HYPERBOLIC SELF-PACED LEARNING FOR SELFSUPERVISED SKELETON-BASED ACTION REPRESENTATIONS
双曲自步学习用于自监督的基于骨架的动作表征
ABSTRACT
摘要
Self-paced learning has been beneficial for tasks where some initial knowledge is available, such as weakly supervised learning and domain adaptation, to select and order the training sample sequence, from easy to complex. However its applicability remains unexplored in unsupervised learning, whereby the knowledge of the task matures during training.
自定进度学习对于已有初步知识的任务(如弱监督学习和领域适应)非常有益,能够按从易到难的顺序选择和排列训练样本序列。然而,其在无监督学习中的适用性仍有待探索,因为任务知识是在训练过程中逐渐成熟的。
We propose a novel HYperbolic Self-Paced model (HYSP) for learning skeletonbased action representations. HYSP adopts self-supervision: it uses data augmentations to generate two views of the same sample, and it learns by matching one (named online) to the other (the target). We propose to use hyperbolic uncertainty to determine the algorithmic learning pace, under the assumption that less uncertain samples should be more strongly driving the training, with a larger weight and pace. Hyperbolic uncertainty is a by-product of the adopted hyperbolic neural networks, it matures during training and it comes with no extra cost, compared to the established Euclidean SSL framework counterparts.
我们提出了一种新颖的双曲自步调模型(HYSP)用于学习基于骨架的动作表征。HYSP采用自监督学习:通过数据增强生成同一样本的两个视图,并通过匹配在线视图与目标视图进行学习。基于"不确定性较低的样本应以更大权重和步调主导训练"的假设,我们提出利用双曲不确定性来确定算法学习步调。这种不确定性是所采用的双曲神经网络的副产品,在训练过程中逐渐成熟,且相比现有欧几里得自监督学习框架无需额外计算成本。
When tested on three established skeleton-based action recognition datasets, HYSP outperforms the state-of-the-art on PKU-MMD I, as well as on 2 out of 3 downstream tasks on NTU-60 and NTU-120. Additionally, HYSP only uses positive pairs and bypasses therefore the complex and computationally-demanding mining procedures required for the negatives in contrastive techniques.
在三个成熟的基于骨架的动作识别数据集上进行测试时,HYSP在PKU-MMD I上表现优于现有最优方法,同时在NTU-60和NTU-120的3个下游任务中有2个表现更优。此外,HYSP仅使用正样本对,因此绕过了对比技术中负样本所需的复杂且计算量大的挖掘过程。
Code is available at https://github.com/paolo mandi ca/HYSP.
代码可在 https://github.com/paolo mandi ca/HYSP 获取。
1 INTRODUCTION
1 引言
Starting from the seminal work of Kumar et al. (2010), the machine learning community has started looking at self-paced learning, i.e. determining the ideal sample order, from easy to complex, to improve the model performance. Self-paced learning has been adopted so far for weakly-supervised learning (Liu et al., 2021; Wang et al., 2021; Sangineto et al., 2019), or where some initial knowledge is available, e.g. from a source model, in unsupervised domain adaption (Liu et al., 2021). Selfpaced approaches use the label (or pseudo-label) confidence to select easier samples and train on those first. However labels are not available in self-supervised learning (SSL) (Chen et al., 2020a; He et al., 2020; Grill et al., 2020; Chen & He, 2021), where the supervision comes from the data structure itself, i.e. from the sample embeddings.
自Kumar等人(2010)的开创性工作以来,机器学习社区开始关注自步学习(self-paced learning),即确定从简单到复杂的理想样本顺序,以提高模型性能。截至目前,自步学习已被应用于弱监督学习(Liu等人,2021;Wang等人,2021;Sangineto等人,2019),或在无监督领域自适应中已有初始知识可用的情况(如来自源模型)(Liu等人,2021)。自步方法利用标签(或伪标签)置信度来选择较简单的样本并优先训练这些样本。然而在自监督学习(SSL)(Chen等人,2020a;He等人,2020;Grill等人,2020;Chen & He,2021)中标签不可用,其监督信号来自数据结构本身,即样本嵌入。
We propose HYSP, the first HYperbolic Self-Paced learning model for SSL. In HYSP, the selfpacing confidence is provided by the hyperbolic uncertainty (Ganea et al., 2018; Shimizu et al., 2021) of each data sample. In more details, we adopt the Poincaré Ball model (Suris et al., 2021; Ganea et al., 2018; Khrulkov et al., 2020; Ermolov et al., 2022) and define the certainty of each sample as its embedding radius. The hyperbolic uncertainty is a property of each data sample in hyperbolic space, and it is therefore available while training with SSL algorithms.
我们提出HYSP,这是首个用于自监督学习(SSL)的双曲自步学习(HYperbolic Self-Paced)模型。在HYSP中,自步学习的置信度由每个数据样本的双曲不确定性(Ganea et al., 2018; Shimizu et al., 2021)提供。具体而言,我们采用庞加莱球模型(Poincaré Ball model)(Suris et al., 2021; Ganea et al., 2018; Khrulkov et al., 2020; Ermolov et al., 2022),并将每个样本的确定性定义为其嵌入半径。双曲不确定性是双曲空间中每个数据样本的属性,因此在用SSL算法训练时可用。
HYSP stems from the belief that the uncertainty of samples matures during the SSL training and that more certain ones should drive the training more prominently, with a larger pace, at each stage of training. In fact, hyperbolic uncertainty is trained end-to-end and it matures as the training proceeds, i.e. data samples become more certain. We consider the task of human action recognition, which has drawn growing attention (Singh et al., 2021; Li et al., 2021; Guo et al., 2022a; Chen et al., 2021a; Kim et al., 2021) due to its vast range of applications, including surveillance, behavior analysis, assisted living and human-computer interaction, while being skeletons convenient light-weight represent at ions, privacy preserving and general iz able beyond people appearance (Xu et al., 2020; Lin et al., 2020a).
HYSP源于这样一种信念:在自监督学习(SSL)训练过程中,样本的不确定性会逐渐成熟,而更确定的样本应在每个训练阶段以更大步伐、更显著地推动训练进程。实际上,双曲不确定性是通过端到端训练逐渐成熟的,即随着训练推进,数据样本会变得更具确定性。我们以人体动作识别任务为例,该领域因在监控、行为分析、辅助生活和人机交互等广泛应用中(Singh等人, 2021; Li等人, 2021; Guo等人, 2022a; Chen等人, 2021a; Kim等人, 2021)展现出骨骼轻量化表示便捷、隐私保护性强且能泛化至不同外貌人群(Xu等人, 2020; Lin等人, 2020a)等优势,正获得越来越多关注。
HYSP builds on top of a recent self-supervised approach, Skeleton C LR (Li et al., 2021), for training skeleton-based action representations. HYSP generates two views for the input samples by data augmentations (He et al., 2020; Chen et al., 2020a; Caron et al., 2020; Grill et al., 2020; Chen & He, 2021; Li et al., 2021), which are then processed with two Siamese networks, to produce two sample representations: an online and a target. The training proceeds by tasking the former to match the latter, being both of them positives, i.e. two views of the same sample. HYSP only considers positives during training and it requires curriculum learning. The latter stems from the vanishing gradients of hyperbolic embeddings upon initialization, due to their initial over confidence (high radius) (Guo et al., 2022b). So initially, we only consider angles, which coincides with starting from the conformal Euclidean optimization. The former is because matching two embeddings in hyperbolic implies matching their uncertainty too, which appears ill-posed for negatives from different samples, i.e. uncertainty is specific of each sample at each stage of training. This bypasses the complex and computationally-demanding procedures of negative mining, which contrastive techniques require*. Both aspects are discussed in detail in Sec. 3.2.
HYSP基于近期提出的自监督方法Skeleton CLR (Li et al., 2021) 进行骨架动作表征训练。该方法通过数据增强 (He et al., 2020; Chen et al., 2020a; Caron et al., 2020; Grill et al., 2020; Chen & He, 2021; Li et al., 2021) 为输入样本生成两个视图,随后使用连体网络处理这两个视图,分别生成在线表征和目标表征。训练过程中,前者需要匹配后者——二者作为同一样本的两个视图构成正样本对。HYSP在训练时仅考虑正样本,并需要课程学习机制。后者源于双曲嵌入初始化时因过度自信(高半径)导致的梯度消失现象 (Guo et al., 2022b),因此初始阶段仅考虑角度参数,这相当于从共形欧几里得优化开始训练。前者则是因为在双曲空间中匹配两个嵌入意味着需要同步匹配其不确定性,而不同样本的负样本对在这种设定下会形成不适定问题——不确定性本质上反映的是每个样本在训练各阶段的特异性。这种方法规避了对比学习所需的复杂且计算密集的负样本挖掘流程*。第3.2节将详细讨论这两个方面。
We evaluate HYSP on three most recent and widely-adopted action recognition datasets, NTU-60, NTU-120 and PKU-MMD I. Following standard protocols, we pre-train with SSL, then transfer to a downstream skeleton-base action classification task. HYSP outperforms the state-of-the-art on PKU-MMD I, as well as on 2 out of 3 downstream tasks on NTU-60 and NTU-120.
我们在三个最新且广泛采用的动作识别数据集NTU-60、NTU-120和PKU-MMD I上评估HYSP。遵循标准流程,我们先用自监督学习(SSL)进行预训练,再迁移到基于骨架的动作分类下游任务。HYSP在PKU-MMD I上超越了当前最优水平,同时在NTU-60和NTU-120的三个下游任务中有两项表现最佳。
2 RELATED WORK
2 相关工作
HYSP embraces work from four research fields, for the first time, as we detail in this section: selfpaced learning, hyperbolic neural networks, self-supervision and skeleton-based action recognition.
HYSP首次融合了四个研究领域的工作,正如我们在本节详述的:自步学习 (self-paced learning)、双曲神经网络 (hyperbolic neural networks)、自监督学习 (self-supervision) 和基于骨架的动作识别 (skeleton-based action recognition)。
2.1 SELF-PACED LEARNING
2.1 自主学习
Self-paced learning (SPL), initially introduced by Kumar et al. (2010) is an extension of curriculum learning (Bengio et al., 2009) which automatically orders examples during training based on their difficulty. Methods for self-paced learning can be roughly divided into two categories. One set of methods (Jiang et al., 2014; Wu et al., 2021) employ it for fully supervised problems. For example, Jiang et al. (2014); Wu et al. (2021) employ it for image classification. Jiang et al. (2014) enhance SPL by considering the diversity of the training examples together with their hardness to select samples. Wu et al. (2021) studies SPL when training with limited time budget and noisy data. The second category of methods employ it for weakly or semi supervised learning. Methods in Sangineto et al. (2019); Zhang et al. (2016a) adopt it for weakly supervised object detection, where Sangineto et al. (2019) iterative ly selects the most reliable images and bounding boxes, while Zhang et al. (2016a) uses saliency detection for self-pacing. Methods in Peng et al. (2021); Wang et al. (2021) employ SPL for semi-supervised segmentation. Peng et al. (2021) adds a regularization term in the loss to learn importance weights jointly with network parameters. Wang et al. (2021) considers the prediction uncertainty and uses a generalized Jensen Shannon Divergence loss. Both categories require the notion of classes and not apply to SSL frameworks, where sample embeddings are only available.
自步学习 (Self-paced learning, SPL) 由Kumar等人 (2010) 首次提出,是对课程学习 (Bengio等人, 2009) 的扩展,它根据样本难度自动调整训练顺序。自步学习方法大致可分为两类。第一类方法 (Jiang等人, 2014; Wu等人, 2021) 将其应用于全监督问题。例如,Jiang等人 (2014) 和Wu等人 (2021) 将其用于图像分类。Jiang等人 (2014) 通过同时考虑训练样本的多样性和难度来增强SPL的样本选择。Wu等人 (2021) 研究了在有限时间预算和噪声数据下的SPL训练。第二类方法将其应用于弱监督或半监督学习。Sangineto等人 (2019) 和Zhang等人 (2016a) 的方法将其用于弱监督目标检测,其中Sangineto等人 (2019) 迭代选择最可靠的图像和边界框,而Zhang等人 (2016a) 使用显著性检测进行自步调节。Peng等人 (2021) 和Wang等人 (2021) 的方法将SPL用于半监督分割。Peng等人 (2021) 在损失函数中添加正则化项,以联合学习重要性权重和网络参数。Wang等人 (2021) 考虑预测不确定性,并使用广义Jensen Shannon散度损失。这两类方法都需要类别概念,因此不适用于仅能获取样本嵌入的SSL框架。
2.2 HYPERBOLIC NEURAL NETWORKS
2.2 双曲神经网络
Hyperbolic representation learning in deep neural networks gained momentum after the pioneering work hyperNNs (Ganea et al., 2018), which proposes hyperbolic counterparts for the classical (Euclidean) fully-connected layers, multi no mi al logistic regression and RNNs. Other representative work has introduced hyperbolic convolution neural networks (Shimizu et al., 2021), hyperbolic graph neural networks (Liu et al., 2019; Chami et al., 2019), and hyperbolic attention networks (Gulcehre et al., 2019). Two distinct aspects have motivated hyperbolic geometry: their capability to encode hierarchies and tree-like structures Chami et al. (2020); Khrulkov et al. (2020), also inspiring Peng et al. (2020) for skeleton-based action recognition; and their notion of uncertainty, encoded by the embedding radius Suris et al. (2021); Atigh et al. (2022), which we leverage here. More recently, hyperbolic geometry has been used with self-supervision (Yan et al., 2021; Suris et al., 2021; Ermolov et al., 2022). Particularly, Suris et al. (2021) and Ermolov et al. (2022) let hierarchical actions and image categories emerge from the unlabelled data using RNNs and Vision Transformers, respectively. Differently, our HYSP uses GCNs and it applies to skeleton data. Moreover, unlike all prior works, HYSP leverages hyperbolic uncertainty to drive the training by letting more certain pairs steer the training more.
双曲表示学习在深度神经网络中的应用始于hyperNNs的开创性工作 (Ganea等人,2018) ,该研究提出了经典(欧几里得)全连接层、多项逻辑回归和RNN的双曲对应版本。其他代表性工作引入了双曲卷积神经网络 (Shimizu等人,2021) 、双曲图神经网络 (Liu等人,2019; Chami等人,2019) 以及双曲注意力网络 (Gulcehre等人,2019) 。双曲几何的推动力来自两个显著特性:其编码层次结构和树状结构的能力 (Chami等人,2020; Khrulkov等人,2020) ——这也启发了Peng等人(2020)在基于骨架的动作识别中的应用;以及通过嵌入半径编码的不确定性概念 (Suris等人,2021; Atigh等人,2022) ,这正是本研究所利用的特性。最近,双曲几何开始与自监督学习结合 (Yan等人,2021; Suris等人,2021; Ermolov等人,2022) 。值得注意的是,Suris等人(2021)和Ermolov等人(2022)分别使用RNN和Vision Transformer从未标注数据中提取层次化动作和图像类别。与之不同,我们的HYSP采用GCN架构并应用于骨架数据。此外,与所有前人工作不同的是,HYSP利用双曲不确定性来驱动训练——通过让置信度更高的样本对主导训练过程。
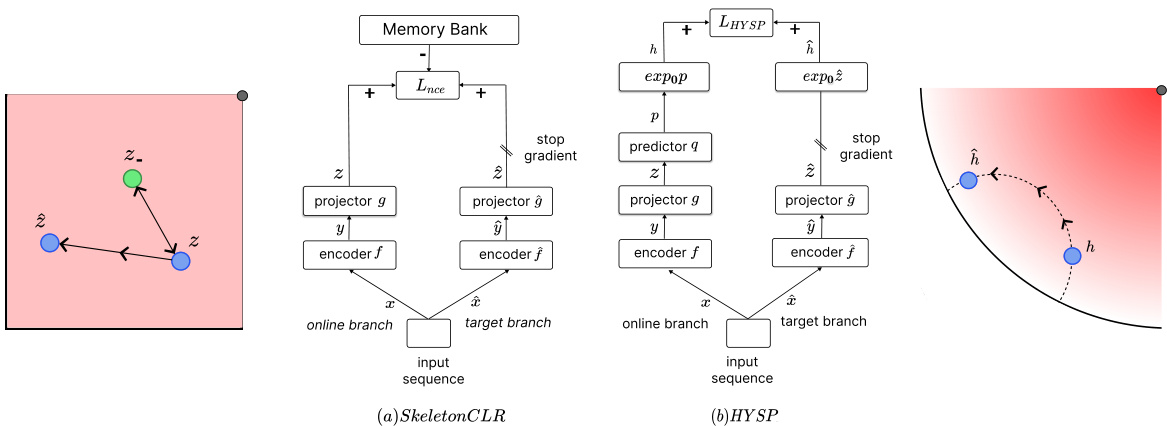
Figure 1: (a) Skeleton C LR is a contrastive learning approach based on pushing the embeddings of two views $x$ and $\hat{x}$ of the same sample (positives) close to each other, while repulsing from embeddings of other samples (negatives). In the represented Euclidean space, on the left side, the attracting/repulsive force is a straight line. (b) The proposed HYSP maps the embeddings into a hyperbolic space, where the sample uncertainty determines the learning pace. The hyperbolic Poincare ball, on the right side, illustrates the embeddings, where the radius indicates the uncertainty. The attractive force proceeds on a circle, orthogonal to the boundary circle. So the force grows polynomial ly with the radius. In HYSP, learning is paced by the uncertainty, which the model learns end-to-end during SSL.
图1: (a) Skeleton CLR是一种基于对比学习的方法, 通过拉近同一样本两个视图 $x$ 和 $\hat{x}$ 的嵌入(正样本), 同时排斥其他样本的嵌入(负样本)。在左侧所示的欧几里得空间中, 吸引/排斥力呈直线作用。(b) 提出的HYSP方法将嵌入映射到双曲空间, 其中样本不确定性决定学习节奏。右侧的双曲Poincare球体展示了嵌入分布, 半径表示不确定性。吸引力沿与边界圆正交的圆周作用, 因此作用力随半径呈多项式增长。在HYSP中, 学习节奏由不确定性决定, 模型在自监督学习(SSL)过程中端到端地学习这一特性。
2.3 SELF-SUPERVISED LEARNING
2.3 自监督学习
Self-supervised learning aims to learn disc rim i native feature representations from unlabeled data. The supervisory signal is typically derived from the input using certain pretext tasks and it is used to pre-train the encoder, which is then transferred to the downstream task of interest. Among all the proposed methods (Noroozi & Favaro, 2016; Zhang et al., 2016b; Gidaris et al., 2018; Caron et al., 2018; 2020), a particularly effective one is the contrastive learning, introduced by SimCLR Chen et al. (2020a). Contrastive learning brings different views of the same image closer (‘positive pairs’), and pushes apart a large number of different ones (‘negative pairs’). MoCo (He et al., 2020; Chen et al., 2020b) partially alleviates the requirement of a large batch size by using a memory-bank of negatives. BYOL (Grill et al., 2020) pioneers on training with positive pairs only. Without the use of negatives, the risk of collapsing to trivial solutions is avoided by means of a predictor in one of the Siamese networks, and a momentum-based encoder with stop-gradient in the other. SimSiam (Chen & He, 2021) further simplifies the design by removing the momentum encoder. Here we draw on the BYOL design and adopt positive-only pairs for skeleton-based action recognition. We experimentally show that including negatives harm training self-supervised hyperbolic neural networks.
自监督学习旨在从未标记数据中学习判别性特征表示。监督信号通常通过特定前置任务从输入数据中生成,用于预训练编码器,随后迁移至目标下游任务。在已有方法中 (Noroozi & Favaro, 2016; Zhang et al., 2016b; Gidaris et al., 2018; Caron et al., 2018; 2020),SimCLR (Chen et al., 2020a) 提出的对比学习尤为有效。该方法使同一图像的不同视角("正样本对")相互靠近,同时推远大量不同图像("负样本对")。MoCo (He et al., 2020; Chen et al., 2020b) 通过负样本记忆库部分缓解了大批量训练需求。BYOL (Grill et al., 2020) 开创性地仅使用正样本对进行训练,通过孪生网络一侧的预测器和另一侧带梯度停止的动量编码器,避免了无负样本时模型坍缩到平凡解的风险。SimSiam (Chen & He, 2021) 进一步简化设计,移除了动量编码器。本文借鉴BYOL框架,在基于骨架的动作识别任务中采用纯正样本对策略。实验表明,引入负样本会损害双曲空间自监督神经网络的训练效果。
2.4 SKELETON-BASED ACTION RECOGNITION
2.4 基于骨架的动作识别
Most recent work in (supervised) skeleton-based action recognition (Chen et al., 2021a;b; Wang et al., 2020) adopts the ST-GCN model of Yan et al. (2018) for its simplicity and performance. We also use ST-GCN. The self-supervised skeleton-based action recognition methods can be broadly divided into two categories. The first category uses encoder-decoder architectures to reconstruct the input (Zheng et al., 2018; Su et al., 2020; Paoletti et al., 2021; Yang et al., 2021; Su et al., 2021). The most representative example is AE-L (Paoletti et al., 2021), which uses Laplacian regular iz ation to enforce representations aware of the skeletal geometry. The other category of methods (Lin et al., 2020a; Thoker et al., 2021; Li et al., 2021; Rao et al., 2021) uses contrastive learning with negative samples. The most representative method is Skeleton C LR (Li et al., 2021) which uses momentum encoder with memory-augmented contrastive learning, similar to MoCo. More recent techniques, CrosSCLR (Li et al., 2021) and AimCLR (Guo et al., 2022a), are based on Skeleton C LR. The former extends it by leveraging multiple views of the skeleton to mine more positives; the latter by introducing extreme augmentations, features dropout, and nearest neighbors mining for extra positives. We also build on Skeleton C LR, but we turn it into positive-only (BYOL), because only uncertainty between positives is justifiable (cf. Sec. FGX-fill-in). BYOL for skeleton-based SSL has first been introduced by Moliner et al. (2022). Differently from them, HYSP introduces self-paced SSL learning with hyperbolic uncertainty.
(监督式)基于骨架的动作识别最新研究(Chen et al., 2021a;b; Wang et al., 2020)多采用Yan等人(2018)提出的ST-GCN模型,因其简洁高效。我们也采用ST-GCN框架。自监督的骨架动作识别方法主要分为两类:第一类采用编码器-解码器架构重构输入(Zheng et al., 2018; Su et al., 2020; Paoletti et al., 2021; Yang et al., 2021; Su et al., 2021),最具代表性的是AE-L(Paoletti et al., 2021),该方法通过拉普拉斯正则化使表征感知骨骼几何结构;第二类方法(Lin et al., 2020a; Thoker et al., 2021; Li et al., 2021; Rao et al., 2021)采用负样本对比学习,代表工作SkeletonCLR(Li et al., 2021)借鉴MoCo框架,结合动量编码器与记忆增强对比学习。后续技术CrosSCLR(Li et al., 2021)和AimCLR(Guo et al., 2022a)均基于SkeletonCLR改进:前者通过多视角骨架数据挖掘更多正样本,后者引入极端数据增强、特征丢弃和最近邻挖掘机制。我们同样以SkeletonCLR为基础,但将其改造为仅使用正样本的BYOL范式(因正样本间的不确定性更具解释性,参见第FGX节)。Moliner等人(2022)首次将BYOL引入骨架自监督学习,而HYSP的创新在于引入双曲不确定性度量的自步学习机制。
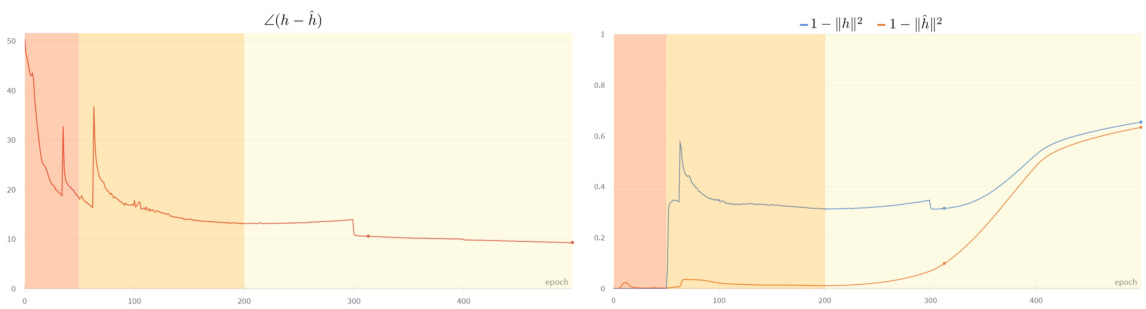
Figure 2: Analysis of the parts of eq. 5, namely (left) the angle between $h$ and h and (right) the quantity $(1-\Vert h\Vert^{2})$ , monotonic with the embedding uncertainty $(1-\Vert h\Vert)$ , during the training phases, i.e. initial (orange), intermediate (yellow), and final (light yellow). See discussion in Sec. 3.2.1.
图 2: 对等式 5 各部分的分析,即 (左) $h$ 与 h 之间的夹角,以及 (右) 与嵌入不确定性 $(1-\Vert h\Vert)$ 单调相关的量 $(1-\Vert h\Vert^{2})$,在训练阶段(初始阶段(橙色)、中间阶段(黄色)和最终阶段(浅黄色))的变化情况。具体讨论见第 3.2.1 节。
3 METHOD
3 方法
We start by motivating hyperbolic self-paced learning, then we describe the baseline Skeleton C LR algorithm and the proposed HYSP. We design HYSP according to the principle that more certain samples should drive the learning process more predominantly. Self-pacing is determined by the sample target embedding, which the sample online embeddings are trained to match. Provided the same distance between target and online values, HYSP gradients are larger for more certain targets†. Since in SSL no prior information is given about the samples, uncertainty needs to be estimated endto-end, alongside the main objective. This is realized in HYSP by means of a hyperbolic mapping and distance, combined with the positives-only design of BYOL (Grill et al., 2020) and a curriculum learning (Bengio et al., 2009) which gradually transitions from the Euclidean to the uncertaintyaware hyperbolic space (Suris et al., 2021; Khrulkov et al., 2020).
我们首先阐述双曲自步学习的动机,随后介绍基准算法Skeleton CLR及提出的HYSP方法。HYSP的设计遵循"确定性更高的样本应主导学习过程"原则:自步节奏由样本目标嵌入决定,在线嵌入通过训练与之匹配。当目标值与在线值距离相同时,HYSP对确定性更高的目标会产生更大梯度†。由于自监督学习(SSL)不提供样本先验信息,不确定性需与主目标同步进行端到端估计。HYSP通过双曲映射与距离度量实现该机制,结合BYOL (Grill等人, 2020)的仅正样本设计,以及从欧式空间逐步过渡到不确定性感知双曲空间 (Suris等人, 2021; Khrulkov等人, 2020) 的课程学习 (Bengio等人, 2009)策略。
3.1 BACKGROUND
3.1 背景
A few most recent techniques (Guo et al., 2022a; Li et al., 2021) for self-supervised skeleton represent ation learning adopt Skeleton C LR Li et al. (2021). That is a contrastive learning approach, which forces two augmented views of an action instance (positives) to be embedded closely, while repulsing different instance embeddings (negatives).
一些最新的自监督骨架表征学习技术 (Guo et al., 2022a; Li et al., 2021) 采用了 Skeleton CLR (Li et al., 2021)。这是一种对比学习方法,它强制将动作实例的两个增强视图(正样本)嵌入相近,同时排斥不同实例的嵌入(负样本)。
Let us consider Fig. $1(a)$ . The positives $x$ and $\hat{x}$ are two different augmentations of the same action sequence, e.g. subject to shear and temporal crop. The samples are encoded into $y=f(x,\theta)$ and $\hat{y}=\hat{f}(\hat{x},\hat{\theta})$ by two Siamese networks, an online $f$ and a target $\hat{f}$ encoder with parameters $\theta$ and $\hat{\theta}$ respectively. Finally the embeddings $z$ and $\hat{z}$ are obtained by two Siamese projector MLPs, $g$ and $\hat{g}$ .
让我们来看图1(a)。正样本 $x$ 和 $\hat{x}$ 是同一动作序列的两种不同增强版本,例如经过剪切和时间裁剪处理。样本通过两个连体网络分别编码为 $y=f(x,\theta)$ 和 $\hat{y}=\hat{f}(\hat{x},\hat{\theta})$ ,其中在线编码器 $f$ 和目标编码器 $\hat{f}$ 的参数分别为 $\theta$ 和 $\hat{\theta}$ 。最终通过两个连体投影器MLP $g$ 和 $\hat{g}$ 获得嵌入表示 $z$ 和 $\hat{z}$ 。
Skeleton C LR also uses negative samples which are embeddings of non-positive instances, queued in a memory bank after each iteration, and dequeued according to a first-in-first-out principle. Positives and negatives are employed within the Noise Contrastive Estimation loss (Oord et al., 2018):
Skeleton C LR 同样使用负样本,这些样本是非正实例的嵌入,在每次迭代后存入记忆库,并按照先进先出原则移除。正样本和负样本被用于噪声对比估计损失 (Oord et al., 2018) 中:
$$
L_{n c e}=-\log\frac{\exp(z\cdot\hat{z}/\tau)}{\exp(z\cdot\hat{z}/\tau)+\sum_{i=1}^{M}\exp(z\cdot m_{i}/\tau)}
$$
$$
L_{n c e}=-\log\frac{\exp(z\cdot\hat{z}/\tau)}{\exp(z\cdot\hat{z}/\tau)+\sum_{i=1}^{M}\exp(z\cdot m_{i}/\tau)}
$$
where $z\cdot\hat{z}$ is the normalised dot product (cosine similarity), $m_{i}$ is a negative sample from the queue and $\tau$ is the softmax temperature hyper-parameter.
其中 $z\cdot\hat{z}$ 是归一化点积(余弦相似度),$m_{i}$ 是队列中的负样本,$\tau$ 是 softmax 温度超参数。
Two aspects are peculiar of Skeleton C LR, important for its robustness and performance: the momentum encoding for $\hat{f}$ and the stop-gradient on the corresponding branch. In fact, the parameters of the target encoder $\hat{f}$ are not updated by back-propagation but by an exponential moving average from the online encoder, i.e $\hat{\theta}\leftarrow\alpha\hat{\theta}+(\dot{1}-\alpha)\dot{\theta}$ , where $\alpha$ is the momentum coefficient. A similar notation and procedure is adopted for $\hat{g}$ . Finally, stop-gradient enables the model to only update the online branch, keeping the other as the reference “target”.
Skeleton C LR有两个独特方面对其鲁棒性和性能至关重要:$\hat{f}$的动量编码以及对应分支上的停止梯度 (stop-gradient)。实际上,目标编码器$\hat{f}$的参数并非通过反向传播更新,而是通过在线编码器的指数移动平均进行更新,即$\hat{\theta}\leftarrow\alpha\hat{\theta}+(\dot{1}-\alpha)\dot{\theta}$,其中$\alpha$为动量系数。$\hat{g}$也采用类似的表示和更新流程。最后,停止梯度机制确保模型仅更新在线分支,而将另一分支固定为参考"目标"。
3.2 HYPERBOLIC SELF-PACED LEARNING
3.2 双曲自步学习 (Hyperbolic Self-Paced Learning)
Basing on Skeleton C LR, we propose to learn by comparing the online $h$ and target $\hat{h}$ representations in hyperbolic embedding space. We do so by mapping the outputs of both branches into the Poincaré ball model centered at 0 by an exponential map (Ganea et al., 2018):
基于Skeleton C LR,我们提出在双曲嵌入空间中通过比较在线$h$和目标$\hat{h}$表示来学习。具体做法是将两个分支的输出通过指数映射(Ganea et al., 2018)映射到以0为中心的庞加莱球模型中:
$$
\hat{h}=E x p_{0}^{c}(\hat{z})=t a n h(\sqrt{c}\left\lVert\hat{z}\right\rVert)\frac{\hat{z}}{\sqrt{c}\left\lVert\hat{z}\right\rVert}
$$
$$
\hat{h}=E x p_{0}^{c}(\hat{z})=t a n h(\sqrt{c}\left\lVert\hat{z}\right\rVert)\frac{\hat{z}}{\sqrt{c}\left\lVert\hat{z}\right\rVert}
$$
where $c$ represents the curvature of the hyperbolic space and $|\cdot|$ the standard Euclidean $L^{2}$ -norm. $h$ and $\hat{h}$ are compared by means of the Poincaré distance:
其中 $c$ 表示双曲空间的曲率,$|\cdot|$ 为标准欧几里得 $L^{2}$ 范数。$h$ 和 $\hat{h}$ 通过庞加莱距离进行比较:
$$
L_{p o i n}(h,\hat{h})=\cosh^{-1}\left(1+2\frac{|h-\hat{h}|^{2}}{\left(1-|h|^{2}\right)\left(1-|\hat{h}|^{2}\right)}\right)
$$
$$
L_{p o i n}(h,\hat{h})=\cosh^{-1}\left(1+2\frac{|h-\hat{h}|^{2}}{\left(1-|h|^{2}\right)\left(1-|\hat{h}|^{2}\right)}\right)
$$
with $\lVert h\rVert$ and $\Vert\hat{h}\Vert$ the radii of $h$ and $\hat{h}$ in the Poincare ball.
其中 $\lVert h\rVert$ 和 $\Vert\hat{h}\Vert$ 为 $h$ 和 $\hat{h}$ 在庞加莱球中的半径。
Following Suris et al. $(2021)^{\ddagger}$ , we define the hyperbolic uncertainty of an embedding $\hat{h}$ as:
根据 Suris 等人 $(2021)^{\ddagger}$ 的研究,我们将嵌入 $\hat{h}$ 的双曲不确定性 (hyperbolic uncertainty) 定义为:
$$
\boldsymbol{u}_{\hat{h}}=1-|\hat{h}|
$$
$$
\boldsymbol{u}_{\hat{h}}=1-|\hat{h}|
$$
Note that the hyperbolic space volume increases with the radius, and the Poincare distance is expone nti ally larger for embeddings closer to the hyperbolic ball edge, i.e. the matching of certain embeddings is penalized exponentially more. Upon training, this yields larger uncertainty for more ambiguous actions, cf. Sec. 4.4 and Appendix A. Next, we detail the self-paced effect on learning.
需要注意的是,双曲空间的体积会随着半径增加而增大,且越靠近双曲球边缘的嵌入,其庞加莱距离会呈指数级增长。也就是说,某些嵌入的匹配会受到指数级的更大惩罚。在训练过程中,这会导致更模糊的动作具有更大的不确定性,具体参见第4.4节和附录A。接下来,我们将详细说明自步学习对训练的影响。
3.2.1 UNCERTAINTY FOR SELF-PACED LEARNING.
3.2.1 自步学习中的不确定性
Learning proceeds by minimizing the Poincare distance via stochastic Riemannian gradient descent (Bonnabel, 2013). This is based on the Riemannian gradient of Eq. 3, computed w.r.t. the online hyperbolic embedding $h$ , which the optimization procedure pushes to match the target $\hat{h}$ :
学习过程通过随机黎曼梯度下降 (Bonnabel, 2013) 最小化庞加莱距离实现。该方法基于式3的黎曼梯度计算,针对在线双曲嵌入 $h$ 进行优化,推动其匹配目标 $\hat{h}$:
$$
\begin{array}{r}{\nabla L_{p o i n}(h,\hat{h})=\frac{(1-|h|^{2})^{2}}{2\sqrt{(1-|h|^{2})(1-|\hat{h}|^{2})+|h-\hat{h}|^{2}}}\left(\frac{h-\hat{h}}{|h-\hat{h}|}+\frac{h|h-\hat{h}|}{1-|h|^{2}}\right)}\end{array}
$$
$$
\begin{array}{r}{\nabla L_{p o i n}(h,\hat{h})=\frac{(1-|h|^{2})^{2}}{2\sqrt{(1-|h|^{2})(1-|\hat{h}|^{2})+|h-\hat{h}|^{2}}}\left(\frac{h-\hat{h}}{|h-\hat{h}|}+\frac{h|h-\hat{h}|}{1-|h|^{2}}\right)}\end{array}
$$
Learning is self-paced, because the gradient changes according to the certainty of the target $\hat{h}$ , i.e. the larger their radius $\lVert\hat{h}\rVert$ , the more certain $\hat{h}$ , and the stronger are the gradients $\nabla L_{p o i n}(h,\hat{h})$ , irrespective of $h$ . We further discuss the training dynamics of Eq. 5. Let us consider Fig. 2, plotting for each training epoch the angle difference between $h$ and $\hat{h}$ , namely $\angle(h-\hat{h})$ , and respectively the quantities $1-|h|^{2}$ and $1-\Vert\hat{h}\Vert^{2}$ :
学习是自定进度的,因为梯度会根据目标 $\hat{h}$ 的确定性而变化,即它们的半径 $\lVert\hat{h}\rVert$ 越大,$\hat{h}$ 越确定,梯度 $\nabla L_{p o i n}(h,\hat{h})$ 就越强,与 $h$ 无关。我们进一步讨论式5的训练动态。让我们考虑图2,它为每个训练周期绘制了 $h$ 和 $\hat{h}$ 之间的角度差,即 $\angle(h-\hat{h})$,以及量 $1-|h|^{2}$ 和 $1-\Vert\hat{h}\Vert^{2}$:
Next, we address two aspects of the hyperbolic optimization: i. the use of negatives is not welldefined in the hyperbolic space and, in fact, leveraging them deteriorates the model performance; ii. the exponential pen aliz ation of the Poincare distance results in gradients which are too small at early stages, causing vanishing gradient. We address these challenges by adopting relatively positive pairs only (Grill et al., 2020) and by curriculum learning (Bengio et al., 2009), as we detail next.
接下来,我们讨论双曲优化的两个问题:i. 负样本在双曲空间中没有明确定义,实际上使用它们会降低模型性能;ii. Poincare距离的指数惩罚导致早期梯度过小,引发梯度消失。我们通过仅采用相对正样本对 (Grill et al., 2020) 和课程学习 (Bengio et al., 2009) 来解决这些挑战,具体如下。
3.2.2 POSITIVE-ONLY LEARNING
3.2.2 仅正样本学习
The Poincare distance is minimized when embeddings $h$ and $\hat{h}$ match, both in terms of angle (cosine distance) and radius (uncertainty). Matching uncertainty of two embeddings only really makes sense for positive pairs. In fact, two views of the same sample may well be required to be known to the same degree. However, repulsing negatives in terms uncertainty is not really justifiable, as the sample uncertainty is detached from the sample identity. This has not been considered by prior work (Ermolov et al., 2022), but it matters experimentally, as we show in Sec. 4.3. We leverage BYOL (Grill et al., 2020) and learn from positive pairs only. Referring to Fig. $1(b)$ , we add a predictor head $q$ to the online branch, to yield the predicted output embedding $p$ . Next, $p$ is mapped into the hyperbolic space to get the embedding $z$ which is pushed to match the target embedding $\hat{z}$ , reference from the stop-gradient branch, using Eq. 3. Note that this simplifies the model and training, as it removes the need for a memory bank and complex negative mining procedures.
当嵌入 $h$ 和 $\hat{h}$ 在角度(余弦距离)和半径(不确定性)上都匹配时,庞加莱距离最小化。两个嵌入的不确定性匹配仅对正样本对真正有意义。事实上,同一样本的两个视图很可能需要以相同的置信度被认知。然而,从不确定性角度排斥负样本并不合理,因为样本的不确定性与样本身份无关。先前的工作 (Ermolov et al., 2022) 未考虑这一点,但实验证明这很关键,如第4.3节所示。我们采用 BYOL (Grill et al., 2020) 并仅从正样本对学习。如图 $1(b)$ 所示,我们在在线分支添加预测头 $q$ ,生成预测输出嵌入 $p$ 。接着,将 $p$ 映射到双曲空间得到嵌入 $z$ ,并通过公式3推动其与来自停止梯度分支的目标嵌入 $\hat{z}$ 匹配。值得注意的是,这简化了模型和训练过程,因为不再需要记忆库和复杂的负样本挖掘流程。
3.2.3 CURRICULUM LEARNING
3.2.3 课程学习
The model random initialization yields starting (high-dimensional) embeddings $
