Revisiting Adversarial Training under Long-Tailed Distributions
重新审视长尾分布下的对抗训练
Xinli Yue, Ningping Mou, Qian Wang, Lingchen Zhao* Key Laboratory of Aerospace Information Security and Trusted Computing, Ministry of Education, School of Cyber Science and Engineering, Wuhan University, Wuhan 430072, China
辛丽月, 牟宁平, 王倩, 赵灵辰* 武汉大学网络空间安全学院, 航空航天信息安全与可信计算教育部重点实验室, 武汉 430072, 中国
Abstract
摘要
Deep neural networks are vulnerable to adversarial attacks, often leading to erroneous outputs. Adversarial training has been recognized as one of the most effective methods to counter such attacks. However, existing adversarial training techniques have predominantly been tested on balanced datasets, whereas real-world data often exhibit a long-tailed distribution, casting doubt on the efficacy of these methods in practical scenarios.
深度神经网络容易受到对抗攻击,往往导致错误输出。对抗训练已被认为是对抗此类攻击的最有效方法之一。然而,现有的对抗训练技术主要是在平衡数据集上进行测试,而现实世界的数据往往呈现出长尾分布,这让人怀疑这些方法在实际场景中的有效性。
In this paper, we delve into adversarial training under long-tailed distributions. Through an analysis of the previous work “RoBal”, we discover that utilizing Balanced Softmax Loss alone can achieve performance comparable to the complete RoBal approach while significantly reducing training overheads. Additionally, we reveal that, similar to uniform distributions, adversarial training under longtailed distributions also suffers from robust over fitting. To address this, we explore data augmentation as a solution and unexpectedly discover that, unlike results obtained with balanced data, data augmentation not only effectively alleviates robust over fitting but also significantly improves robustness. We further investigate the reasons behind the improvement of robustness through data augmentation and identify that it is attributable to the increased diversity of examples. Extensive experiments further corroborate that data augmentation alone can significantly improve robustness. Finally, building on these findings, we demonstrate that compared to RoBal, the combination of BSL and data augmentation leads to a $+6.66%$ improvement in model robustness under AutoAttack on CIFAR-10-LT. Our code is available at: https://github.com/NISPLab/AT-BSL.
在本文中,我们深入探讨了长尾分布下的对抗训练。通过对先前工作“RoBal”的分析,我们发现仅使用平衡Softmax损失(Balanced Softmax Loss)即可实现与完整RoBal方法相当的性能,同时显著减少训练开销。此外,我们揭示出,与均匀分布类似,长尾分布下的对抗训练也存在鲁棒过拟合问题。为了解决这一问题,我们探索了数据增强作为一种解决方案,并意外地发现,与平衡数据下的结果不同,数据增强不仅有效缓解了鲁棒过拟合,还显著提高了鲁棒性。我们进一步研究了数据增强提高鲁棒性的原因,并发现这归因于样本多样性的增加。大量实验进一步证实,仅通过数据增强即可显著提高鲁棒性。最后,基于这些发现,我们证明了与RoBal相比,BSL与数据增强的结合在CIFAR-10-LT上通过AutoAttack测试的模型鲁棒性提高了$+6.66%$。我们的代码可在以下网址获取:https://github.com/NISPLab/AT-BSL。
1. Introduction
1. 引言
It is well-known that deep neural networks (DNNs) are vulnerable to adversarial attacks, where attackers can induce errors in DNNs’ recognition results by adding perturbations that are imperceptible to the human eye [12, 39]. Many researchers have focused on defending against such attacks. Among the various defense methods proposed, adversarial training is recognized as one of the most effective approaches. It involves integrating adversarial examples into the training set to enhance the model’s generalization capability against these examples [20, 31, 42, 45, 53, 54]. In recent years, significant progress has been made in the field of adversarial training. However, we note that almost all studies on adversarial training utilize balanced datasets like CIFAR-10, CIFAR-100 [23], and Tiny-ImageNet [24] for performance evaluation. In contrast, real-world datasets often exhibit an imbalanced, typically long-tailed distribution. Hence, the efficacy of adversarial training in practical systems should be reassessed using long-tailed datasets [14, 40].
众所周知,深度神经网络 (DNNs) 容易受到对抗攻击的影响,攻击者可以通过添加人眼难以察觉的扰动来诱导 DNNs 的识别结果出现错误 [12, 39]。许多研究者致力于防御此类攻击。在提出的各种防御方法中,对抗训练被认为是最有效的方法之一。它通过将对抗样本整合到训练集中,以增强模型对这些样本的泛化能力 [20, 31, 42, 45, 53, 54]。近年来,对抗训练领域取得了显著进展。然而,我们注意到,几乎所有关于对抗训练的研究都使用 CIFAR-10、CIFAR-100 [23] 和 Tiny-ImageNet [24] 等平衡数据集进行性能评估。相比之下,现实世界的数据集通常表现出不平衡的、通常为长尾分布的特征。因此,应该使用长尾数据集重新评估对抗训练在实际系统中的有效性 [14, 40]。

Figure 1. The clean accuracy and robustness under AutoAttack (AA) [5] of various adversarial training methods using WideResNet-34-10 [51] on CIFAR-10-LT [23]. Our method, building upon AT [31] and BSL [36], leverages data augmentation to improve robustness, achieving a $+6.66%$ improvement over the SOTA method RoBal [46]. REAT [26] is a concurrent work with ours, yet to be published.
图 1: 使用 WideResNet-34-10 [51] 在 CIFAR-10-LT [23] 上,各种对抗训练方法在 AutoAttack (AA) [5] 下的干净精度和鲁棒性。我们的方法基于 AT [31] 和 BSL [36],利用数据增强来提高鲁棒性,相比 SOTA 方法 RoBal [46] 实现了 $+6.66%$ 的提升。REAT [26] 是与我们同时进行的工作,尚未发表。
To the best of our knowledge, RoBal [46] is the sole published work that investigates the adversarial robustness under the long-tailed distribution. However, due to its complex design, RoBal demands extensive training time and GPU memory, which somewhat limits its practicality. Upon revisiting the design and principles of RoBal, we find that its most critical component is the Balanced Softmax Loss (BSL) [36]. We observe that combining AT [31] with BSL to form AT-BSL can match RoBal’s effectiveness while significantly reducing training overhead. Following Occam’s Razor principle, where entities should not be multiplied without necessity [19], we advocate using AT-BSL as a substitute for RoBal. In this paper, we base our studies on ATBSL.
据我们所知,RoBal [46] 是唯一一篇研究长尾分布下对抗鲁棒性的已发表工作。然而,由于其复杂的设计,RoBal 需要大量的训练时间和 GPU 内存,这在一定程度上限制了其实用性。回顾 RoBal 的设计和原理,我们发现其最关键的部分是 Balanced Softmax Loss (BSL) [36]。我们观察到,将 AT [31] 与 BSL 结合形成 AT-BSL 可以匹配 RoBal 的效果,同时显著减少训练开销。根据奥卡姆剃刀原则,即“如无必要,勿增实体” [19],我们主张使用 AT-BSL 作为 RoBal 的替代方案。在本文中,我们的研究基于 ATBSL。
2. Related Works
2. 相关工作
Long-Tailed Recognition. Long-tailed distributions refer to a common imbalance in training set where a small portion of classes (head) have massive examples, while other classes (tail) have very few examples [14, 40]. Models trained under such distribution tend to exhibit a bias towards the head classes, resulting in poor performance for the tail classes. Traditional rebalancing techniques aim at addressing the long-tailed recognition problem include re-sampling [21, 38, 41, 56] and cost-sensitive learning [8, 29], which often improve the performance of tail classes at the expense of head classes. To mitigate these adverse effects, some methods handle class-specific attributes through perspectives such as margins [43] and biases [36]. Recently, more advanced techniques like class-conditional sharpness-aware minimization [57], feature clusters compression [27], and global-local mixture consistency cumulative learning [10] have been introduced, further improving the performance of long-tailed recognition. However, these works have been devoted to improving clean accuracy, and investigations into the adversarial robustness of long-tailed recognition remain scant.
长尾识别
Adversarial Training. The philosophy of adversarial training involves integrating adversarial examples into the training set, thereby improving the model’s general iz ability to such examples. Adversarial training addresses a min-max problem, with the inner maximization dedicated to generating the strongest adversarial examples and the outer minimization aimed at optimizing the model parameters. The quintessential method of adversarial training is AT [31], which can be mathematically represented as follows:
对抗训练。对抗训练的理念在于将对抗样本整合到训练集中,从而提升模型对此类样本的泛化能力。对抗训练解决的是一个最小-最大问题,其中内部最大化致力于生成最强的对抗样本,而外部最小化则旨在优化模型参数。对抗训练的经典方法是AT [31],其数学表达如下:

where $x^{\prime}$ is an adversarial example constrained by $\ell_{p}$ norm for clean examples $x,,y$ is the label of $x$ , $\theta_{m}$ is the parameter of the model $m$ , $\epsilon$ is the perturbation size, $\mathcal{L}{\mathrm{max}}$ is the internal maximization loss, and $\mathcal{L}{\mathrm{min}}$ is the external minimization loss.
其中 $x^{\prime}$ 是由 $\ell_{p}$ 范数约束的对抗样本,$x,,y$ 是 $x$ 的标签,$\theta_{m}$ 是模型 $m$ 的参数,$\epsilon$ 是扰动大小,$\mathcal{L}{\mathrm{max}}$ 是内部最大化损失,$\mathcal{L}{\mathrm{min}}$ 是外部最小化损失。
Building upon the foundation of AT [31], subsequent works developed advanced adversarial training techniques such as TRADES [53], MART [42], AWP [45], GAIRAT [54], and LAS-AT [20]. However, these adversarial training methods were predominantly experimented with on balanced datasets like CIFAR-10 and CIFAR-100.
在 AT [31] 的基础上,后续研究开发了先进的对抗训练技术,如 TRADES [53]、MART [42]、AWP [45]、GAIRAT [54] 和 LAS-AT [20]。然而,这些对抗训练方法主要在 CIFAR-10 和 CIFAR-100 等平衡数据集上进行了实验。
Robustness under Long-Tailed Distribution. Previous adversarial training works were concentrated mainly on balanced datasets. However, data in the real world are seldom balanced; they are more commonly characterized by long-tailed distributions [14, 40]. Therefore, a critical criterion for assessing the practical utility of adversarial training should be its performance on long-tailed distributions. To our knowledge, RoBal [46] is the only work that investigates adversarial training on long-tailed datasets. In Section 3, we delve into the components of RoBal, improv- ing the efficacy of long-tailed adversarial training based on our findings. Moreover, some works [30, 44, 47, 49] have already indicated that adversarial training on balanced datasets can lead to significant robustness disparities across classes. Whether this disparity is exacerbated on long-tailed datasets remains an open question for further exploration.
长尾分布下的鲁棒性。以往对抗训练的研究主要集中在平衡数据集上。然而,真实世界中的数据很少是平衡的,它们更常见的是长尾分布 [14, 40]。因此,评估对抗训练实际效用的一个重要标准应该是其在长尾分布上的表现。据我们所知,RoBal [46] 是唯一一个研究长尾数据集上对抗训练的工作。在第 3 节中,我们深入探讨了 RoBal 的组成部分,并根据我们的发现改进了长尾对抗训练的效果。此外,一些工作 [30, 44, 47, 49] 已经指出,在平衡数据集上进行对抗训练可能导致类别间的鲁棒性显著差异。这种差异在长尾数据集上是否会加剧,仍是一个需要进一步探索的开放性问题。
Data Augmentation. In standard training regimes, data augmentation has been validated as an effective tool to mitigate over fitting and improve model generalization, regardless of whether the data distribution is balanced or longtailed [2, 10, 48, 55]. The most commonly utilized augmentation techniques for image classification tasks include random flips, rotations, and crops [15]. More sophisticated augmentation methods like MixUp [52], Cutout [9], and CutMix [50] have been shown to yield superior results in standard training contexts. Furthermore, augmentation strategies such as Augmix [17], AuA [6], RA [7], and TA [33], which employ a learned or random combination of multiple augmentations, have elevated the efficacy of data augmentation to new heights, heralding the advent of the era of automated augmentation.
数据增强 (Data Augmentation)。在标准训练机制中,无论数据分布是平衡的还是长尾的,数据增强已被验证为减轻过拟合并提高模型泛化能力的有效工具 [2, 10, 48, 55]。在图像分类任务中最常用的增强技术包括随机翻转、旋转和裁剪 [15]。MixUp [52]、Cutout [9] 和 CutMix [50] 等更复杂的增强方法在标准训练环境中已被证明能产生更优的结果。此外,Augmix [17]、AuA [6]、RA [7] 和 TA [33] 等增强策略通过使用学习或随机组合的多种增强方法,将数据增强的效果提升到了新的高度,预示着自动化增强时代的到来。
3. Analysis of RoBal
3. RoBal 分析
3.1. Preliminaries
3.1. 预备知识
RoBal [46], in comparison to AT [31], incorporates four additional components: 1) cosine classifier; 2) Balanced Softmax Loss [36]; 3) class-aware margin; 4) TRADES regu- larization [53].
与 AT [31] 相比,RoBal [46] 引入了四个额外组件:1) 余弦分类器;2) Balanced Softmax Loss [36];3) 类别感知边界;4) TRADES 正则化 [53]。
Cosine Classifier. In basic classification tasks employing a standard linear classifier, the predicted logit for class $i$ can be represented as:
余弦分类器。在采用标准线性分类器的基本分类任务中,类别 $i$ 的预测对数几率可以表示为:
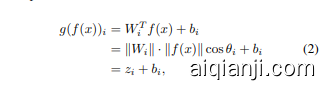
where $g(\cdot)$ is the liner classifer. In this formulation, the prediction depends on three factors: 1) the magnitude of the weight vector $\lVert W_{i}\rVert$ and the feature vector $|f(x)|$ ; 2) the angle between them, expressed as $\cos\theta_{i}$ ; and 3) the bias of the classifier $b_{i}$ .
其中 $g(\cdot)$ 是线性分类器。在这个公式中,预测结果取决于三个因素:1) 权重向量 $\lVert W_{i}\rVert$ 和特征向量 $|f(x)|$ 的幅度;2) 它们之间的夹角,表示为 $\cos\theta_{i}$;以及 3) 分类器的偏差 $b_{i}$。
The above decomposition illustrates that simply by scaling the norm of examples in feature space, the predictions of the examples can be altered. In linear class if i ers, the scale of the weight vector $\lVert W_{i}\rVert$ often diminishes in tail classes, thereby impacting the recognition performance for tail classes. Consequently, [46] endeavors to utilize a cosine classifier [34] to mitigate the scale effects of features and weights. And in the cosine classifier, the predicted logit for class $i$ can be represented as:
上述分解表明,只需通过缩放特征空间中样本的范数,就可以改变样本的预测结果。在线性分类器中,权重向量 $\lVert W_{i}\rVert$ 的尺度通常在尾部类别中减小,从而影响尾部类别的识别性能。因此,[46] 尝试利用余弦分类器 [34] 来减轻特征和权重的尺度效应。在余弦分类器中,类别 $i$ 的预测对数可以表示为:

where $h(\cdot)$ is the cosine classifier, $\Vert\cdot\Vert$ denotes the $\ell_{2}$ norm of the vector, $s$ is the scaling factor.
其中 $h(\cdot)$ 是余弦分类器,$\Vert\cdot\Vert$ 表示向量的 $\ell_{2}$ 范数,$s$ 是缩放因子。
Balanced Softmax Loss. An intuitive and widely adopted approach to addressing class imbalance is to assign classspecific biases during training for the cross-entropy (CE) loss. [46] employs the formulation by [32, 36], denoted as $b_{i}=\tau_{b}\log\left(n_{i}\right)$ , where the modified cross-entropy loss, namely Balanced Softmax Loss (BSL), becomes:
平衡 Softmax 损失。一个直观且广泛采用的解决类别不平衡问题的方法是在训练时为交叉熵 (CE) 损失分配特定类别的偏置。[46] 采用了 [32, 36] 的公式,表示为 $b_{i}=\tau_{b}\log\left(n_{i}\right)$,其中修改后的交叉熵损失,即平衡 Softmax 损失 (BSL),变为:

where $n_{i}$ is the number of examples in the $i$ -th class, and $\tau_{b}$ is a hyper parameter controling the calculation of bias. BSL adapts to the label distribution shift between training and testing by adding specific biases to each class based on the number of examples in each class to improve long-tailed recognition performance [36].
其中 $n_{i}$ 是第 $i$ 类中的样本数量,$\tau_{b}$ 是控制偏差计算的超参数。BSL 通过根据每个类别中的样本数量为每个类别添加特定偏差,适应训练和测试之间的标签分布偏移,从而提高长尾识别性能 [36]。
Class-Aware Margin. However, when considering the margin representation, the margin from the true class $y$ to class $i$ , denoted by $\tau_{b}\log\left(n_{i}/n_{y}\right)$ , becomes negative when $n_{y},>,n_{i}$ , leading to poorer disc rim i native representations and classifier learning for head classes. To address this, [46] introduces a class-aware margin term [34], which assigns a larger margin value to head classes as compensation:
类感知间隔 (Class-Aware Margin)。然而,在考虑间隔表示时,从真实类别 $y$ 到类别 $i$ 的间隔,表示为 $\tau_{b}\log\left(n_{i}/n_{y}\right)$,当 $n_{y},>,n_{i}$ 时会变为负值,导致头部类别的判别表示和分类器学习效果较差。为了解决这个问题,[46] 引入了类感知间隔项 [34],它为头部类别分配了更大的间隔值作为补偿:

The first term increases with $n_{i}$ and reaches its minimum of zero when $n_{i}=n_{\operatorname*{min}}$ , with $\tau_{m}$ as the hyper parameter controlling the trend. The second term, $m_{0},>,0$ , is a uniform boundary for all classes, a common strategy in networks based on cosine class if i ers. Add this class-aware margin $m_{i}$ to $\scriptstyle{\mathcal{L}}{0}$ to become $\mathcal{L}{1}$ :
第一项随着 $n_{i}$ 的增加而增加,并在 $n_{i}=n_{\operatorname*{min}}$ 时达到最小值零,其中 $\tau_{m}$ 是控制趋势的超参数。第二项 $m_{0},>,0$ 是所有类的统一边界,这是基于余弦分类器的网络中的常见策略。将这个类感知的边界 $m_{i}$ 添加到 $\scriptstyle{\mathcal{L}}{0}$ 中,得到 $\mathcal{L}{1}$:

TRADES Regular iz ation. [46] incorporates a $\mathrm{KL}$ regularization term following TRADES [53], thereby modifying the overall loss function to:
TRADES 正则化。[46] 在 TRADES [53] 的基础上引入了 KL 正则化项,从而将整体损失函数修改为:

where $\beta$ serves as a hyper parameter to control the intensity of the TRADES regular iz ation.
其中 $\beta$ 作为超参数,用于控制 TRADES 正则化的强度。
Table 1. The clean accuracy, robustness, time (average per epoch) and memory (GPU) using ResNet-18 [15] on CIFAR-10-LT following the integration of components from RoBal [46] into AT [31]. The best results are bolded. The second best results are underlined. Cos: Cosine Classifier; BSL: Balanced Softmax Loss [36]; CM: Class-aware Margin [46]; TRADES: TRADES Regular iz ation [53].
表 1. 在使用 ResNet-18 [15] 在 CIFAR-10-LT 数据集上,将 RoBal [46] 的组件集成到 AT [31] 中后的干净准确率、鲁棒性、时间(每轮平均)和内存(GPU)。最佳结果加粗显示,次佳结果加下划线。Cos: 余弦分类器;BSL: 平衡 Softmax 损失 [36];CM: 类感知边际 [46];TRADES: TRADES 正则化 [53]。
| 方法 | 组件 | 准确率 | 效率 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cos BSL CM | TRADES | Clean | FGSM | PGD | cW | LSA | AA | Time (s) | Memory (MiB) | ||||
| AT [31] | 54.91 | 32.21 | 28.05 | 28.28 | 28.73 | 26.75 | 21.36 | 946 | |||||
| AT-BSL | √ | 70.21 | 37.44 | 31.91 | 31.45 | 32.25 | 29.48 | 21.00 | 946 | ||||
| AT-BSL-CoS | √ | 71.99 | 39.41 | 34.73 | 30.27 | 29.94 | 28.43 | 22.39 | 946 | ||||
| AT-BSL-Cos-TRADES | √ | √ | 69.31 | 39.62 | 34.87 | 30.19 | 30.15 | 28.64 | 38.91 | 1722 | |||
| RoBal [46] | √ | √ | 人 | 70.34 | 40.50 | 35.93 | 31.05 | 31.10 | 29.54 | 39.03 | 1722 |
3.2. Ablation Studies of RoBal
3.2. RoBal 的消融研究
To investigate the role of each component in RoBal [46], we conduct ablation studies on it. Specifically, we incrementally add each component of RoBal to AT [31] and then evaluate the method’s clean accuracy, robustness, training time per epoch, and memory usage. The results are summarized in Table 1. Note that the parameters utilized in Table 1 adhere strictly to the default settings of [46], and the details about adversarial attacks are in Section 5.1. We observe that the AT-BSL method outperforms AT [31] in terms of clean accuracy and adversarial robustness. However, upon integrating a cosine classifier with AT-BSL, while the robustness under PGD [31] significantly improves, robustness under adaptive attacks like CW [3], LSA [18], and AA [5] notably decreases. This aligns with observations in REAT [26], suggesting that the cosine classifier (scaleinvariant classifier) used in RoBal may lead to gradient vanishing when generating adversarial examples with crossentropy loss. This is attributed to the normalization of weights and features in the classification layer, which substantially reduces the gradient scale, impeding the generation of potent adversarial examples [26]. Further additions of TRADES regular iz ation [53] and class-aware margin do not yield substantial improvements in robustness under AA, yet markedly increase training time and memory consumption. In fact, AT-BSL alone can match the complete RoBal in terms of clean accuracy and robustness under AA. Therefore, in line with Occam’s Razor [19], we advocate using AT-BSL, which renders adversarial training more efficient without sacrificing significant performance. The ${\mathcal{L}}_{m i n}$ formula of AT-BSL is as follows:
为了研究 RoBal [46] 中每个组件的作用,我们对其进行了消融实验。具体来说,我们逐步将 RoBal 的每个组件添加到 AT [31] 中,然后评估该方法的干净准确率、鲁棒性、每轮训练时间和内存使用情况。结果总结在表 1 中。需要注意的是,表 1 中使用的参数严格遵循 [46] 的默认设置,关于对抗攻击的细节见第 5.1 节。我们观察到,AT-BSL 方法在干净准确率和对抗鲁棒性方面优于 AT [31]。然而,当将余弦分类器与 AT-BSL 结合时,虽然 PGD [31] 下的鲁棒性显著提高,但在 CW [3]、LSA [18] 和 AA [5] 等自适应攻击下的鲁棒性明显下降。这与 REAT [26] 中的观察结果一致,表明 RoBal 中使用的余弦分类器(尺度不变分类器)在使用交叉熵损失生成对抗样本时可能导致梯度消失。这是由于分类层中权重和特征的归一化显著降低了梯度规模,阻碍了强对抗样本的生成 [26]。进一步添加 TRADES 正则化 [53] 和类感知间隔并未在 AA 下的鲁棒性方面带来显著提升,但显著增加了训练时间和内存消耗。实际上,仅使用 AT-BSL 就可以在干净准确率和 AA 下的鲁棒性方面与完整的 RoBal 相媲美。因此,根据奥卡姆剃刀原理 [19],我们主张使用 AT-BSL,它可以在不牺牲显著性能的情况下使对抗训练更加高效。AT-BSL 的 ${\mathcal{L}}_{m i n}$ 公式如下:
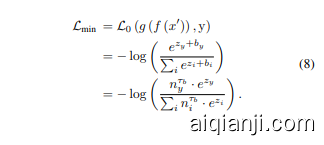

Figure 2. Learning rate scheduling analysis of RoBal [46]. (a) comparison of the learning rate schedules: ‘RoBal Code Schedule’ from the source code and ‘RoBal Paper Schedule’ as described in the publication. (b) the evolution of test robustness under PGD20 [31] using ResNet-18 on CIFAR-10-LT across training epochs.
图 2: RoBal [46] 的学习率调度分析。(a) 学习率调度的比较:源代码中的‘RoBal Code Schedule’和论文中描述的‘RoBal Paper Schedule’。(b) 使用 ResNet-18 在 CIFAR-10-LT 上训练的测试鲁棒性在 PGD20 [31] 下的演变。
3.3. Robust Over fitting and Unexpected Discovery
3.3. 鲁棒过拟合与意外发现
Discrepancy in Learning Rate Scheduling: Paper Description vs. Code Implementation. RoBal [46] asserts that early stopping is not employed, and the results reported are from the final epoch, the 80th epoch. The declared learning rate schedule is an initial rate of 0.1, with decays at the 60th and 70th epochs, each by a factor of 0.1. After executing the source code of RoBal, we observe, as depicted by the blue line in Fig. 2(b), that test robustness remains essentially unchanged after the first learning rate decay (60th epoch), indicating an absence of robust over fitting. It is well-known that adversarial training on CIFAR-10 exhibits significant robust over fitting [37], and given that CIFAR10-LT has less data than CIFAR-10, the absence of robust over fitting on CIFAR-10-LT is contradictory to the assertion that additional data can alleviate robust over fitting in [35].
学习率调度中的差异:论文描述与代码实现。RoBal [46] 声称未采用早停,且报告的结果来自第80个最终周期。声明的学习率调度是初始速率为0.1,在第60和第70周期分别衰减0.1倍。在执行RoBal的源代码后,我们观察到,如图2(b)中的蓝线所示,在第一次学习率衰减(第60周期)后,测试鲁棒性基本保持不变,表明没有出现鲁棒过拟合。众所周知,CIFAR-10上的对抗训练表现出显著的鲁棒过拟合 [37],而CIFAR10-LT的数据量少于CIFAR-10,因此在CIFAR-10-LT上未出现鲁棒过拟合与 [35] 中关于额外数据可以缓解鲁棒过拟合的断言相矛盾。
Upon a meticulous examination of the official code provided by RoBal [46], we discover inconsistencies between the implemented learning rate schedule and what is claimed in the paper. The official code uses a learning rate schedule starting at 0.1, with a decay of 0.1 per epoch after the 60th epoch and 0.01 per epoch after the 75th epoch (the blue line in Fig. 2(a)). This leads to a learning rate as low as 1e26 by the 80th epoch, potentially limiting learning after the 60th epoch and contributing to the similar performance of models at the 60th and 80th epochs as shown in Fig. 2(b).
在对 RoBal [46] 提供的官方代码进行仔细检查后,我们发现其实现的学习率调度与论文中所述存在不一致之处。官方代码使用的学习率调度从 0.1 开始,在第 60 个 epoch 后每 epoch 衰减 0.1,在第 75 个 epoch 后每 epoch 衰减 0.01(图 2(a) 中的蓝线)。这导致在第 80 个 epoch 时学习率低至 1e26,可能限制了第 60 个 epoch 之后的学习,并导致模型在第 60 个和第 80 个 epoch 的表现相似,如图 2(b) 所示。
Subsequently, we adjust the learning rate schedule to what is declared in [46] (the orange line in Fig. 2(a)) and redraw the robustness curve, represented by the orange line in Fig. 2(b). Post-adjustment, a continuous decline in test robustness following the first learning rate decay is observed, aligning with the robust over fitting phenomenon typically seen on CIFAR-10.
随后,我们将学习率调整至 [46] 中声明的值(图 2(a) 中的橙色线),并重新绘制了鲁棒性曲线,如图 2(b) 中的橙色线所示。调整后,观察到在第一次学习率衰减后,测试鲁棒性持续下降,这与 CIFAR-10 上常见的鲁棒过拟合现象一致。
Therefore, adversarial training under long-tailed distributions exhibits robust over fitting, similar to balanced distributions. So, how might we resolve this problem? Several works [4, 13, 35, 37, 45] have attempted to use data augmentation to alleviate robust over fitting on balanced datasets.
因此,长尾分布下的对抗训练表现出与平衡分布类似的鲁棒过拟合。那么,我们如何解决这个问题呢?一些研究 [4, 13, 35, 37, 45] 尝试使用数据增强来缓解平衡数据集上的鲁棒过拟合。
Testing MixUp. [35, 37, 45] suggest that on CIFAR-10, MixUp [52] can alleviate robust over fitting. Therefore, we posit that on the long-tailed version of CIFAR-10, CIFAR10-LT, MixUp would also mitigate robust over fitting. In Fig. 3(a), it is evident that AT-BSL-MixUp, which utilizes MixUp, significantly alleviates robust over fitting compared to AT-BSL. Furthermore, we unexpectedly discover that MixUp markedly improves robustness. This observation is inconsistent with previous findings in balanced datasets [35, 37, 45], where it was concluded that data augmentation alone does not improve robustness.
测试 MixUp。[35, 37, 45] 表明在 CIFAR-10 上,MixUp [52] 可以缓解鲁棒过拟合。因此,我们假设在 CIFAR-10 的长尾版本 CIFAR10-LT 上,MixUp 也会减轻鲁棒过拟合。在图 3(a) 中,明显可以看出,使用 MixUp 的 AT-BSL-MixUp 相比 AT-BSL 显著缓解了鲁棒过拟合。此外,我们意外地发现 MixUp 显著提升了鲁棒性。这一观察结果与之前在平衡数据集上的发现 [35, 37, 45] 不一致,之前的结论是仅通过数据增强无法提升鲁棒性。
Exploring data augmentation. Following the validation of the MixUp hypothesis, our investigation expands to assess whether other augmentation techniques could alleviate robust over fitting and improve robustness. This includes augmentations like Cutout [9], CutMix [50], AugMix [17], TA [33], AuA [6], and RA [7]. Analogous to our analysis of MixUp, we report the robustness achieved by these augmentation techniques during training in Fig. 3. Firstly, our findings indicate that each augmentation technique mitigated robust over fitting, with CutMix, AuA, RA, and TA exhibiting almost negligible instances of this phenomenon. Furthermore, we observe that robustness attained by each augmentation surpasses that of the vanilla AT-BSL, further corroborating that data augmentation alone can improve robustness.
探索数据增强技术。在验证了MixUp假设之后,我们的研究进一步扩展到评估其他增强技术是否能够缓解鲁棒过拟合并提高鲁棒性。这些增强技术包括Cutout [9]、CutMix [50]、AugMix [17]、TA [33]、AuA [6]和RA [7]。与我们对MixUp的分析类似,我们在图3中报告了这些增强技术在训练过程中实现的鲁棒性。首先,我们的研究结果表明,每种增强技术都缓解了鲁棒过拟合,其中CutMix、AuA、RA和TA几乎未出现这种现象。此外,我们观察到,每种增强技术实现的鲁棒性都超过了普通AT-BSL,进一步证实了仅通过数据增强就可以提高鲁棒性。
4. Why Data Augmentation Can Improve Robustness
- 为什么数据增强可以提高鲁棒性
Formulating Hypothesis. We postulate that data augmentation improves robustness by increasing example diversity, thereby allowing models to learn richer representations. Taking RA [7] as an illustrative example, for each training image, RA randomly selects a series of augmentations from a search space consisting of 14 augmentations, namely Identity, ShearX, ShearY, TranslateX, TranslateY, Rotate, Brightness, Color, Contrast, Sharpness, Posterize, Solarize, Auto Contrast, and Equalize, to apply to the image. We initiate an ablation study on RA, testing the impact of each augmentation individually. Specifically, we narrow the search space of RA to a single augmentation, meaning RA is restricted to using only this one augmentation to augment all training examples. From Fig. 4(a), it can be observed that except for Contrast, none of the augmentations alone improve robustness; in fact, augmentations such as Solarize, Auto Contrast, and Equalize significantly underperform compared to AT-BSL. We surmise that this is due to the limited example diversity provided by a single augmentation, thereby resulting in no substantial improvement in robustness.
提出假设。我们假设数据增强通过增加样本多样性来提高鲁棒性,从而使模型能够学习到更丰富的表示。以 RA [7] 为例,对于每张训练图像,RA 从包含 14 种增强操作的搜索空间中随机选择一系列增强操作,即 Identity、ShearX、ShearY、TranslateX、TranslateY、Rotate、Brightness、Color、Contrast、Sharpness、Posterize、Solarize、Auto Contrast 和 Equalize,并将其应用于图像。我们对 RA 进行了消融研究,分别测试了每种增强操作的影响。具体来说,我们将 RA 的搜索空间缩小为单一增强操作,这意味着 RA 只能使用这一种增强操作来增强所有训练样本。从图 4(a) 中可以看出,除了 Contrast 之外,单独使用任何一种增强操作都无法提高鲁棒性;事实上,诸如 Solarize、Auto Contrast 和 Equalize 等增强操作的表现甚至远不如 AT-BSL。我们推测这是由于单一增强操作提供的样本多样性有限,因此无法显著提高鲁棒性。

Figure 3. The evolution of test robustness under PGD-20 using ResNet-18 on CIFAR-10-LT for AT-BSL using different data augmentation strategies across training epochs. For reference, the red dashed lines in each panel represent the robustness of the best checkpoint of AT-BSL. Due to the density of the illustrations, the results have been compartmentalized into four distinct panels: (a), (b), (c), and (d).
图 3. 在 CIFAR-10-LT 上使用 ResNet-18 进行 AT-BSL 时,不同数据增强策略下 PGD-20 的测试鲁棒性随训练轮次的演变。作为参考,每个面板中的红色虚线表示 AT-BSL 最佳检查点的鲁棒性。由于图示密度较高,结果被分为四个独立的面板:(a)、(b)、(c) 和 (d)。
Validating Hypothesis. Subsequently, we explore the impact of the number of types of augmentations on robustness. Specifically, for each trial, we randomly selected $n$ types of augmentations to constitute the search space of RA, with $n,\in,{2,14}$ . Each experiment is repeated five times. As shown in Fig. 4(b), we reveal that robustness progressively improves with the addition of more augmentation methods in the search space of RA. This indicates that as the number of types of augmentations in the search space increases, the variety of augmentations available to examples also grows, leading to greater example diversity. Consequently, the represent at ions learned by the model become more comprehensive, thereby improving robustness. This validates our hypothesis.
验证假设。随后,我们探讨了增强类型数量对鲁棒性的影响。具体而言,对于每次试验,我们随机选择 $n$ 种增强类型来构成 RA 的搜索空间,其中 $n,\in,{2,14}$。每个实验重复五次。如图 4(b) 所示,我们发现随着 RA 搜索空间中增强方法的增加,鲁棒性逐渐提高。这表明随着搜索空间中增强类型数量的增加,样本可用的增强方式也增多,从而导致样本多样性增加。因此,模型学习到的表征更加全面,从而提高了鲁棒性。这验证了我们的假设。
Moreover, to further substantiate our hypothesis, we conduct an ablation study on the three types of augmentations—Solarize, Auto Contrast, and Equalize—which, when used individually, impair robustness. Specifically, we eliminate these three and employ the remaining 11 augmentations as the baseline: RA-11. We then increment ally add
此外,为了进一步验证我们的假设,我们对三种增强方式——Solarize、Auto Contrast 和 Equalize——进行了消融实验,这些增强方式在单独使用时会影响模型的鲁棒性。具体来说,我们剔除了这三种增强方式,并将剩余的 11 种增强方式作为基线:RA-11。然后我们逐步添加这些增强方式。

Figure 4. The robustness under AA for AT-BSL with different augmentations using ResNet-18 on CIFAR-10-LT. (a) Change the augmentation space of RA [7] to a single augmentation, and the horizontal axis represents the name of the single augmentation. (b) The horizontal axis represents the number of types of augmentations in the search space of RA.
图 4. 使用 ResNet-18 在 CIFAR-10-LT 上,不同增强方式下 AT-BSL 在 AA 下的鲁棒性。(a) 将 RA [7] 的增强空间更改为单一增强,横轴表示单一增强的名称。(b) 横轴表示 RA 搜索空间中增强类型的数量。
Table 2. The clean accuracy and robustness under AA for AT-BSL with different augmentations using ResNet-18 on CIFAR-10-LT. The best results are bolded. RA-11 means only using the first 11 augmentations in the search space of RA. The lines below RA-11 indicate additional augmentations based on RA-11, and the last line uses the complete search space of RA. SO: Solarize; AC: AutoContrast; EQ: Equalize.
表 2: 使用 ResNet-18 在 CIFAR-10-LT 上,不同增强方法下 AT-BSL 的干净准确率和对抗鲁棒性 (AA)。最佳结果以粗体显示。RA-11 表示仅使用 RA 搜索空间中的前 11 种增强方法。RA-11 下方的行表示基于 RA-11 的额外增强方法,最后一行使用 RA 的完整搜索空间。SO: 曝光 (Solarize); AC: 自动对比度 (AutoContrast); EQ: 均衡化 (Equalize)。
| 方法 | Clean | FGSM | PGD | CW | LSA | AA |
|---|---|---|---|---|---|---|
| RA-11 | 67.80 | 40.68 | 35.88 | 34.01 | 33.89 | 32.12 |
| SO | 67.60 | 41.43 | 37.04 | 34.52 | 34.05 | 32.76 |
| AC | 68.57 | 41.20 | 36.60 | 34.24 | 34.07 | 32.51 |
| EQ | 68.33 | 41.64 | 36.80 | 34.33 | 34.17 | 32.59 |
| SO+AC | 68.43 | 42.10 | 37.23 | 34.62 | 34.37 | 33.02 |
| SO+EQ | 68.53 | 41.89 | 37.42 | 35.07 | 34.83 | 33.49 |
| AC+EQ | 68.36 | 41.88 | 37.42 | 34.91 | 34.49 | 33.15 |
| SO+AC+EQ | 70.86 | 43.06 | 37.94 | 36.24 | 36.04 | 34.24 |
one to three of the negative augmentations, with the results outlined in Table 2. It is discovered that the more types of augmentations added, the more significant the improvement in robustness. Despite the negative impact of these three augmentations when used in isolation, their inclusion in the search space of RA still contributes to robustness improvement, further validating our hypothesis that data augmentation increases example diversity and thereby improves ro- bustness.
在负面增强中进行一到三种组合,结果如表 2 所示。研究发现,添加的增强类型越多,鲁棒性的提升越显著。尽管这三种增强单独使用时会产生负面影响,但将它们纳入 RA 的搜索空间仍然有助于提升鲁棒性,这进一步验证了我们的假设,即数据增强增加了样本多样性,从而提高了鲁棒性。
5. Experiments
5. 实验
5.1. Settings
5.1. 设置
Datasets. Following [46], we conduct experiments on CIFAR-10-LT and CIFAR-100-LT [23]. Due to space constraints, partial results for CIFAR-100-LT are included in the appendix. In our main experiments, the imbalance ratio (IR) of CIFAR-10-LT is set to 50. Table 6 also provides results for various IRs.
数据集。根据 [46],我们在 CIFAR-10-LT 和 CIFAR-100-LT [23] 上进行实验。由于篇幅限制,CIFAR-100-LT 的部分结果包含在附录中。在我们的主要实验中,CIFAR-10-LT 的不平衡比 (IR) 设置为 50。表 6 还提供了不同 IR 的结果。
Evaluation Metrics. When assessing model robustness, the $l_{\infty}$ norm-bounded perturbation is $\epsilon,=,8/255$ . The attacks carried out include the single-step attack FGSM [12] and several iterative attacks, such as PGD [31], CW [3] and LSA [18], performed over 20 steps with a step size of 2/255. We also employ AutoAttack (AA) [5], considered the strongest attack so far. For all methods, the evaluations are based on both the best checkpoint (selected based on robustness under PGD-20) and the final checkpoint.
评估指标
Comparison Methods. We consider adversarial training methods under long-tailed distributions: RoBal [46] and REAT [26], as well as defenses under balanced distributions: AT [31], TRADES [53], MART [42], AWP [45], GAIRAT [54], and LAS-AT [20].
对比方法。我们考虑了长尾分布下的对抗训练方法:RoBal [46] 和 REAT [26],以及平衡分布下的防御方法:AT [31]、TRADES [53]、MART [42]、AWP [45]、GAIRAT [54] 和 LAS-AT [20]。
Training Details. We train the models using the Stochastic Gradient Descent (SGD) optimizer with an initial learning rate of 0.1, momentum of 0.9, and weight decay of 5e-4. We set the batch size to 128. We set the total number of training epochs to 100, and the learning rate is divided by 10 at the 75th and 90th epoch following [53]. During generating adversarial examples, we enforce a maximum perturbation of 8/255 and a step size of $2/255$ . The number of iterations for internal maximization is fixed at 10, denoting PGD-10, and the impact of PGD steps on robustness is investigated in Table 15. For all experiments related to AT-BSL, we adopt $\tau_{b}=1$ , and the results for different $\tau_{b}$ are provided in Fig. 7. Note that the AT-BSL presented in Tables 3 and 4 represents our own implementation, which differs in training parameters from RoBal [46]. Detailed discussions regarding these discrepancies are provided in the appendix.
训练细节。我们使用随机梯度下降 (SGD) 优化器训练模型,初始学习率为 0.1,动量为 0.9,权重衰减为 5e-4。我们将批量大小设置为 128,总训练轮数设置为 100,并在第 75 轮和第 90 轮时将学习率除以 10,遵循 [53]。在生成对抗样本时,我们强制最大扰动为 8/255,步长为 $2/255$。内部最大化的迭代次数固定为 10,记为 PGD-10,PGD 步骤对鲁棒性的影响在表 15 中进行了研究。对于所有与 AT-BSL 相关的实验,我们采用 $\tau_{b}=1$,不同 $\tau_{b}$ 的结果如图 7 所示。请注意,表 3 和表 4 中展示的 AT-BSL 代表我们自己的实现,其训练参数与 RoBal [46] 不同。有关这些差异的详细讨论在附录中提供。
5.2. Main Results
5.2. 主要结果
As evident from Tables 3 and 4, on CIFAR-10-LT, ATBSL with data augmentation achieves the highest clean accuracy and adversarial robustness on both ResNet-18 and WideResNet-34-10. Note that on WideResNet-34-10, our method, AT-BSL-AuA, demonstrates a significant improvement of $+6.66%$ robustness under AA compared to the SOTA method RoBal. Moreover, in terms of robustness at the final checkpoint, our method significantly outperforms others, demonstrating that data augmentation mitigates robust over fitting.
从表3和表4中可以明显看出,在CIFAR-10-LT数据集上,结合数据增强的ATBSL在ResNet-18和WideResNet-34-10上均实现了最高的干净精度和对抗鲁棒性。值得注意的是,在WideResNet-34-10上,我们的方法AT-BSL-AuA在AA评估下的鲁棒性相比SOTA方法RoBal显著提升了$+6.66%$。此外,在最终检查点的鲁棒性方面,我们的方法显著优于其他方法,这表明数据增强有效缓解了鲁棒过拟合问题。
We present the robustness of different methods across each class in Fig. 5. It is observable that, except for a few classes, our method improves robustness in almost every class, particularly in tail classes (5 to 9 classes) where the improvements are more pronounced. Furthermore, consistent with observations on balanced datasets [30, 44, 47, 49], there is a significant disparity in class-wise robustness. Class 3 remains the least robust despite its example numbers far exceeding that of subsequent classes, which may be attributable to the intrinsic properties of class 3 [46].
我们在图 5 中展示了不同方法在各个类别上的鲁棒性。可以看出,除了少数类别外,我们的方法在几乎所有类别上都提高了鲁棒性,尤其是在尾部类别(5 到 9 类)中改进更为明显。此外,与在平衡数据集上的观察结果一致 [30, 44, 47, 49],类别间的鲁棒性存在显著差异。尽管类别 3 的样本数量远远超过后续类别,但它仍然是最不鲁棒的,这可能归因于类别 3 的内在特性 [46]。
5.3. Futher Analysis
5.3. 进一步分析
Effect of Augmentation Strategies and Parameters. We present in both Table 5 and Fig. 6 the impact of different augmentation strategies and parameters on robustness. Specifically, we conduct experiments using ResNet-18 on CIFAR-10-LT, comparing robustness at the best checkpoint. In addition, in Table 5, we use the best hyper-parameters: mixing rate $\alpha~=~0.3$ for Mixup, window length 17 for Cutout, mixing rate $\alpha=0.1$ for CutMix, and magnitude 8 for RA. As shown in Table 5, various augmentation strategies improve robustness compared to vanilla AT-BSL, with AuA and RA also achieving gains in clean accuracy. Fig. 6 indicates that for MixUp and CutMix, smaller values of $\alpha$ yield better robustness; for Cutout, longer window lengths generally correlate with better robustness; for RA, a moderate magnitude of transformation improves robustness, peaking at magnitude $=8$ , highlighting that excessive augmentation is not always beneficial.
数据增强策略和参数的影响。我们在表 5 和图 6 中展示了不同数据增强策略和参数对鲁棒性的影响。具体来说,我们在 CIFAR-10-LT 上使用 ResNet-18 进行实验,比较最佳检查点的鲁棒性。此外,在表 5 中,我们使用了最佳超参数:Mixup 的混合率 $\alpha~=~0.3$,Cutout 的窗口长度为 17,CutMix 的混合率 $\alpha=0.1$,以及 RA 的强度为 8。如表 5 所示,与普通的 AT-BSL 相比,各种数据增强策略都提高了鲁棒性,AuA 和 RA 还在干净准确率上取得了提升。图 6 表明,对于 MixUp 和 CutMix,较小的 $\alpha$ 值通常能带来更好的鲁棒性;对于 Cutout,较长的窗口长度通常与更好的鲁棒性相关;对于 RA,适度的增强强度能提高鲁棒性,并在强度 $=8$ 时达到峰值,这表明过度的增强并不总是有益的。
Table 3. The clean accuracy and robustness for various algorithms using ResNet-18 on CIFAR-10-LT. The best results are bolded.
Table 4. The clean accuracy and robustness for various algorithms using WideResNet-34-10 on CIFAR-10-LT. The best results are bolded.
表 4: 使用 WideResNet-34-10 在 CIFAR-10-LT 上各种算法的干净准确率和鲁棒性。最佳结果加粗显示。
| Method | Clean | FGSM | PGD | cW | LSA | AA | Clean | FGSM | PGD | cW | LSA | AA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AT [31] | 59.21 | 31.88 | 27.88 | 28.19 | 29.81 | 27.07 | 58.25 | 29.77 | 25.29 | 25.71 | 29.83 | 24.94 |
| TRADES [53] | 51.28 | 31.58 | 28.70 | 28.45 | 28.36 | 27.72 | 53.85 | 30.44 | 26.23 | 26.57 | 26.77 | 25.59 |
| MART [42] | 49.13 | 34.33 | 32.32 | 30.73 | 30.13 | 29.60 | 52.48 | 33.95 | 31.09 | 29.64 | 29.43 | 28.67 |
| AWP [45] | 50.91 | 34.28 | 31.85 | 31.23 | 31.01 | 30.06 | 48.65 | 33.21 | 31.07 | 30.33 | 30.14 | 29.40 |
| GAIRAT[54] | 59.89 | 33.47 | 30.40 | 26.69 | 26.71 | 25.38 | 56.37 | 29.41 | 27.25 | 23.94 | 23.95 | 23.15 |
| LAS-AT [20] | 57.52 | 33.66 | 29.86 | 29.60 | 29.44 | 28.84 | 58.19 | 32.98 | 28.89 | 28.75 | 28.58 | 27.90 |
| RoBal [46] | 72.82 | 41.34 | 36.42 | 32.48 | 31.95 | 30.49 | 70.85 | 35.95 | 27.74 | 27.59 | 26.76 | 25.71 |
| REAT [26] | 73.16 | 41.32 | 35.94 | 35.28 | 35.67 | 33.20 | 67.76 | 34.51 | 27.75 | 28.17 | 31.82 | 26.66 |
| AT-BSL | 73.19 | 41.84 | 35.60 | 34.86 | 35.99 | 32.80 | 65.95 | 33.29 | 27.23 | 27.87 | 31.00 | 26.45 |
| AT-BSL-AuA | 75.17 | 46.18 | 40.84 | 38.82 | 39.23 | 37.15 | 77.27 | 44.73 | 38.06 | 37.14 | 39.05 | 35.11 |

Figure 5. The class-wise example number and robustness under AA for various algorithms on CIFAR-10-LT at the best checkpoint. (a) ResNet-18; (b) WideResNet-34-10.
图 5. CIFAR-10-LT 上不同算法在最佳检查点下的类别样本数量及对抗攻击 (AA) 鲁棒性。(a) ResNet-18;(b) WideResNet-34-10。
Table 5. The clean accuracy and robustness for AT-BSL with different augmentations using ResNet-18 on CIFAR-10-LT. The best results are bolded.
表 5: 在 CIFAR-10-LT 上使用 ResNet-18 的不同增强方法下 AT-BSL 的干净准确率和鲁棒性。最佳结果已加粗。
| 方法 | Clean | FGSM | PGD | cW | LSA | AA |
|---|---|---|---|---|---|---|
| Vanilla | 35.27 | 33.47 | 33.46 | 31.78 | 68.89 | 40.08 |
| MixUp [52] | 65.82 | 41.33 | 38.05 | 34.29 | 33.63 | 32.92 |
| Cutout [9] | 65.12 | 40.25 | 37.86 | 34.10 | 33.46 | 32.83 |
| CutMix [50] | 64.54 | 41.13 | 36.68 | 34.81 | 34.51 | 33.35 |
| AugMix [17] | 67.12 | 70.86 | 40.31 | 35.95 | 34.19 | 34.02 |
| TA [33] | 67.14 | 41.56 | 37.75 | 34.34 | 33.90 | 32.62 |
| AuA [6] | 71.63 | 42.69 | 37.78 | 35.60 | 43.06 | 37.94 |
| RA [7] | 35.47 | 33.69 | 36.24 | 36.04 | 34.24 | 32.51 |
Effect of Hyper parameter $\tau_{b}$ . To investigate the sensitivity of AT-BSL to $\tau_{b}$ , we evaluate the performance of AT-BSL under varying $\tau_{b}$ values. Specifically, we utilize
超参数 $\tau_{b}$ 的影响

Figure 6. The robustness under AA using ResNet-18 on CIFAR10-LT as we vary (a) the mixing rate $\alpha$ for MixUp, (b) the window length for Cutout, (c) the mixing rate $\alpha$ for CutMix, and (d) the magnitude of transformations for RA.
图 6. 在使用 ResNet-18 对 CIFAR10-LT 进行 AA 测试时的鲁棒性,随着 (a) MixUp 的混合率 $\alpha$、(b) Cutout 的窗口长度、(c) CutMix 的混合率 $\alpha$ 和 (d) RA 的变换幅度的变化而变化。

Figure 7. The robustness under AA for various algorithms with different $\tau_{b}$ using ResNet-18. (a): CIFAR-10-LT; (b): CIFAR100-LT.
图 7: 使用 ResNet-18 时,不同 $\tau_{b}$ 下各种算法在 AA 下的鲁棒性。(a): CIFAR-10-LT; (b): CIFAR100-LT.
ResNet-18 with $\tau_{b}$ ranging from 0 to 20. Note that at $\tau_{b}=0$ , the bias $b_{i},=,\tau_{b}\log\left(n_{i}\right)$ added by AT-BSL becomes zero, and Eq.8 reverts to the vanilla CE loss, transforming ATBSL into vanilla AT [31]. The results, depicted in Fig. 7, reveal that on CIFAR10-LT, AT-BSL is quite sensitive to $\tau_{b}$ , achieving optimal robustness at $\tau_{b}=1$ . Conversely, on CIFAR-100-LT, AT-BSL shows less sensitivity to $\tau_{b}$ . Additionally, across tested datasets and $\tau_{b}$ values, AT-BSL with additional data augmentation consistently exhibits significantly higher robustness than vanilla AT-BSL, underscoring the substantial benefits of data augmentation in adversarial training under long-tailed distributions.
ResNet-18 中 $\tau_{b}$ 的取值从 0 到 20。需要注意的是,当 $\tau_{b}=0$ 时,AT-BSL 添加的偏差 $b_{i},=,\tau_{b}\log\left(n_{i}\right)$ 变为零,公式 8 会恢复为普通的 CE 损失,从而将 AT-BSL 转换为普通的 AT [31]。结果显示在图 7 中,表明在 CIFAR10-LT 上,AT-BSL 对 $\tau_{b}$ 非常敏感,并在 $\tau_{b}=1$ 时达到最佳的鲁棒性。相反,在 CIFAR-100-LT 上,AT-BSL 对 $\tau_{b}$ 的敏感性较低。此外,在测试数据集和 $\tau_{b}$ 值的范围内,增加数据增强的 AT-BSL 始终表现出比普通 AT-BSL 显著更高的鲁棒性,这突显了在长尾分布下进行对抗训练时数据增强的显著优势。
Effect of Imbalance Ratio. We further construct longtailed datasets with varying IRs following the protocol of [8, 46] to evaluate the performance of our method. Table 6 illustrates that RA consistently improves the robustness of AT-BSL across various IR settings, further substantiating the finding that data augmentation can improve robustness. Effect of PGD Step Size. To delve into the impact of PGD step size on robustness, we fine-tune the PGD step size from $2/255$ to $1/255$ and $0.5/255$ , while also increasing the PGD steps from 10 to 20 and 40. As depicted in Table 7, it is evident that RA consistently improves the robustness of AT
不平衡比率的影响
表 6: 不同不平衡比率下的性能表现
PGD步长的影响
表 7: 不同PGD步长下的鲁棒性表现
Table 6. The clean accuracy and robustness for various algorithms using ResNet-18 on CIFAR-10-LT with different imbalance ratios. Better results are bolded.
表 6: 使用 ResNet-18 在 CIFAR-10-LT 数据集上不同不平衡比率下各种算法的干净准确性和鲁棒性。更好的结果以粗体显示。
| IR | Method Clean FGSM PGD CW LSA AA |
|---|---|
| 10 | AT-BSL 73.29 47.33 42.04 40.77 41.05 39.12 AT-BSL-RA 79.00 50.98 44.19 42.82 43.10 40.56 |
| 20 | AT-BSL 71.89 44.76 39.40 38.47 38.68 36.74 AT-BSL-RA 75.84 47.62 41.68 39.92 39.82 37.78 |
| 50 | AT-BSL 68.89 40.08 35.27 33.47 33.46 31.78 AT-BSL-RA 70.86 43.06 37.94 36.24 36.04 34.24 |
| 100 | AT-BSL 62.03 35.06 30.95 29.41 29.56 28.01 AT-BSL-RA66.85 38.75 33.69 31.77 31.50 30.00 |
Table 7. The clean accuracy and robustness for various algorithms using ResNet-18 on CIFAR-10-LT training with different PGD step sizes. Better results are bolded.
BSL regardless of the PGD step size. However, we also note a decrease in robustness when compared to the baseline robustness at a PGD step size of 2/255.
表 7. 使用 ResNet-18 在 CIFAR-10-LT 训练集上,不同 PGD 步长下各种算法的干净准确率和鲁棒性。更好的结果加粗显示。
| Size | Method | Clean | FGSM | PGD | CW | LSA | AA |
|---|---|---|---|---|---|---|---|
| 0.5 | AT-BSL | 68.57 | 39.65 | 535.10 | 32.92 | 32.97 | 31.28 |
| 0.5 | AT-BSL-RA | 68.68 | 41.97 | 37.60 | 34.81 | 34.36 | 33.26 |
| 1 | AT-BSL | 68.63 | 39.98 | 35.09 | 33.02 | 33.00 | 31.18 |
| 1 | AT-BSL-RA | 68.93 | 42.71 | 37.85 | 35.30 | 34.79 | 33.51 |
| 2 | AT-BSL | 68.89 | 40.08 | 35.27 | 33.47 | 33.46 | 31.78 |
| 2 | AT-BSL-RA | 70.86 | 43.06 | 37.94 | 36.24 | 36.04 | 34.24 |
无论 PGD 步长如何,BSL 都优于基线。然而,我们也注意到与 PGD 步长为 2/255 的基线鲁棒性相比,鲁棒性有所下降。
6. Conclusion
6. 结论
In this paper, we first dissect the components of RoBal, identifying BSL as a critical component. We then address the issue of robust over fitting in adversarial training under long-tailed distributions and attempt to mitigate it using data augmentation. Surprisingly, we find that data augmentation not only mitigates robust over fitting but also significantly improves robustness. We hypothesize that the improved robustness is due
