Recurrent Generic Contour-based Instance Segmentation with Progressive Learning
基于渐进式学习的循环通用轮廓实例分割
Abstract—Contour-based instance segmentation has been actively studied, thanks to its flexibility and elegance in processing visual objects within complex backgrounds. In this work, we propose a novel deep network architecture, i.e., PolySnake, for generic contour-based instance segmentation. Motivated by the classic Snake algorithm, the proposed PolySnake achieves superior and robust segmentation performance with an iterative and progressive contour refinement strategy. Technically, PolySnake introduces a recurrent update operator to estimate the object contour iterative ly. It maintains a single estimate of the contour that is progressively deformed toward the object boundary. At each iteration, PolySnake builds a semantic-rich representation for the current contour and feeds it to the recurrent operator for further contour adjustment. Through the iterative refinements, the contour progressively converges to a stable status that tightly encloses the object instance. Beyond the scope of general instance segmentation, extensive experiments are conducted to validate the effectiveness and general iz ability of our PolySnake in two additional specific task scenarios, including scene text detection and lane detection. The results demonstrate that the proposed PolySnake outperforms the existing advanced methods on several multiple prevalent benchmarks across the three tasks. The codes and pre-trained models are available at https://github.com/fh2019ustc/PolySnake
摘要—基于轮廓的实例分割因其在处理复杂背景中视觉对象时的灵活性与优雅性而受到广泛研究。本文提出了一种新型深度网络架构PolySnake,用于通用型基于轮廓的实例分割。受经典Snake算法启发,该模型通过迭代渐进式轮廓优化策略实现了卓越且稳健的分割性能。技术上,PolySnake采用循环更新算子对目标轮廓进行迭代估计,始终保持单一轮廓预测并通过渐进形变逼近物体边界。每次迭代时,模型会为当前轮廓构建语义丰富的表征,并将其输入循环算子以进一步调整轮廓。经过多次优化迭代,轮廓最终收敛至紧密包围目标实例的稳定状态。除通用实例分割任务外,我们通过大量实验验证了PolySnake在场景文本检测和车道检测两个特定任务中的有效性与泛化能力。实验结果表明,在三大任务的多个主流基准测试中,PolySnake均超越了现有先进方法。代码与预训练模型已开源:https://github.com/fh2019ustc/PolySnake
Index Terms—Contour-based, Progressive Learning, Instance Segmentation, Text Detection, Lane Detection
索引术语—基于轮廓 (Contour-based)、渐进式学习 (Progressive Learning)、实例分割 (Instance Segmentation)、文本检测 (Text Detection)、车道检测 (Lane Detection)
I. INTRODUCTION
I. 引言
Nstance segmentation is a fundamental computer vision task, aiming to recognize each distinct object in an image along with their associated outlines. It is a challenging task due to background clutter, instance ambiguity, and the complexity of object shapes, etc. The advance of instance segmentation benefits a broad range of visual understanding applications, such as autonomous driving [1], [2], [3], augmented reality [4], [5], robotic grasping [6], [7], surface defect detection [8], [9], [10], text recognition [11], [12], [13], and so on. Over the past few years, instance segmentation has been receiving increased attention and significant progress has been made.
实例分割 (instance segmentation) 是一项基础的计算机视觉任务,旨在识别图像中每个独立对象及其对应的轮廓线。由于背景干扰、实例歧义以及物体形状复杂性等因素,该任务具有较高挑战性。实例分割技术的进步为众多视觉理解应用带来了显著提升,例如自动驾驶 [1][2][3]、增强现实 [4][5]、机器人抓取 [6][7]、表面缺陷检测 [8][9][10]、文字识别 [11][12][13] 等。近年来,实例分割领域持续受到广泛关注并取得了重大进展。
In the literature, most of the state-of-the-art methods [14], [15], [16], [17], [18], [19], [20], [21], [22] adopt a two-
在文献中,大多数最先进的方法 [14]、[15]、[16]、[17]、[18]、[19]、[20]、[21]、[22] 采用了两阶段
Hao Feng, Keyi Zhou, Wengang Zhou, Yufei Yin, Qi Sun, and Houqiang Li are with the CAS Key Laboratory of Technology in Geo-spatial Information Processing and Application System, Department of Electronic Engineering and Information Science, University of Science and Technology of China, Hefei, 230027, China. Hao Feng is also with Zhangjiang Laboratory, Shanghai, China. E-mail: {haof, kyzhou2000, yinyufei, sq008} $@$ mail.ustc.edu.cn; ${\mathrm{zhwg,~lihq}}@$ ustc.edu.cn
Hao Feng、Keyi Zhou、Wengang Zhou、Yufei Yin、Qi Sun 和 Houqiang Li 均任职于中国科学技术大学电子工程与信息科学系,中国科学院空天信息处理与应用系统技术重点实验室,合肥,230027。Hao Feng 同时任职于张江实验室,上海。电子邮箱:{haof, kyzhou2000, yinyufei, sq008} $@$ mail.ustc.edu.cn;${\mathrm{zhwg,~lihq}}@$ ustc.edu.cn
Jiajun Deng is with The University of Adelaide, Australian Institute for Machine Learning. E-mail: jiajun.deng@adelaide.edu.au
Jiajun Deng就职于阿德莱德大学澳大利亚机器学习研究所。电子邮箱:jiajun.deng@adelaide.edu.au

Fig. 1. An illustration of different representations to localize an instance within an image: (b) bounding box; (c) pixel-wise mask; and (d), (f), (h) contour. The images showcase three distinct task scenarios: general instance segmentation (a), scene text detection (f), and lane detection (h).
图 1: 图像中实例定位的不同表示方法示意图:(b) 边界框;(c) 像素级掩码;(d)、(f)、(h) 轮廓。这些图像展示了三种不同的任务场景:通用实例分割 (a)、场景文本检测 (f) 和车道检测 (h)。
stage pipeline for instance segmentation. Typically, they first detect the object instance in the form of bounding boxes (see Fig. 1(b)) and then estimate a pixel-wise segmentation mask (see Fig. 1(c)) within each bounding box. However, the segmentation performance of such methods is limited due to the inaccurate bounding boxes. For example, the classic Mask R-CNN [14] performs a binary classification on a $28\times28$ feature map of a detected instance. Besides, their dense prediction architecture usually suffers from heavy computational overhead [23], limiting their applications in resource-limited scenarios with a real-time requirement.
实例分割的阶段式流水线。通常,它们首先以边界框形式检测对象实例(见图1(b)),然后在每个边界框内估计像素级分割掩码(见图1(c))。然而,由于边界框不准确,这类方法的分割性能受到限制。例如,经典的Mask R-CNN [14] 在检测实例的 $28\times28$ 特征图上执行二元分类。此外,它们的密集预测架构通常面临沉重的计算开销 [23],限制了其在需要实时性的资源受限场景中的应用。
To address the above issues, recent research efforts have been dedicated to designing alternative representations to the pixel-wise segmentation mask. One intuitive representative scheme is the object contour, in the form of a sequence of vertexes along the object silhouette (see Fig. 1(d)). Typically, PolarMask [24], [25] innovative ly applies the angle and distance terms in a polar coordinate system to localize the vertices of the contour, which achieves competitive accuracy. However, in PolarMask [24], [25], contours are constructed from a set of endpoints of concentric rays emitted from the object center, thus restricting the models to handling convex shapes as well as some concave shapes with non-intersecting rays. Another pioneering method is DeepSnake [26] which directly regresses the coordinates of contour vertices in the Cartesian coordinate system. Inspired by the classic Snake algorithm [27], DeepSnake [26] devises a neural network to evolve an initial contour to enclose the object boundary. Nevertheless, the overlarge model size increases the learning difficulty and thus harms the performance. Typically, the performance of DeepSnake [26] drops with more than 4 times contour adjustment. Based on this strong baseline, other methods [28], [29], [30], [31], [32], [33] continue to explore a more effective contour estimation strategy. Although they report promising performance on the challenging benchmarks [34], [35], [36], [37], their contour learning strategies are somewhat heuristic and complex.
为了解决上述问题,最近的研究致力于设计替代逐像素分割掩码的表示方法。一种直观的代表性方案是物体轮廓,即以沿物体轮廓的顶点序列形式呈现(见图1(d))。典型地,PolarMask [24][25]创新性地利用极坐标系中的角度和距离项来定位轮廓顶点,取得了具有竞争力的精度。然而,在PolarMask [24][25]中,轮廓由从物体中心发射的同心射线端点集合构成,因此限制了模型只能处理凸形以及部分射线不相交的凹形。另一项开创性方法是DeepSnake [26],它直接在笛卡尔坐标系中回归轮廓顶点的坐标。受经典Snake算法 [27] 启发,DeepSnake [26] 设计了一个神经网络来演化初始轮廓以包围物体边界。尽管如此,过大的模型尺寸增加了学习难度,从而损害了性能。通常,DeepSnake [26] 的性能在超过4次轮廓调整后会下降。基于这一强基线,其他方法 [28][29][30][31][32][33] 继续探索更有效的轮廓估计策略。尽管它们在具有挑战性的基准测试 [34][35][36][37] 中报告了有希望的性能,但其轮廓学习策略在某种程度上是启发式和复杂的。
In this work, we propose PolySnake, a new deep network architecture for generic contour-based instance segmentation. The idea of our PolySnake is traced back to the classic Snake algorithm [27] that iterative ly deforms an initial polygon to progressively align the object boundary by the optimization of an energy function. Correspondingly, our PolySnake also aims to realize effective automatic contour learning based on iterative and progressive mechanisms simultaneously, different from existing methods. Specifically, given an initial contour of an object instance, PolySnake develops a recurrent update operator to estimate the contour iterative ly. It maintains a single estimate of the contour that is progressively deformed at each iteration. At each iteration, PolySnake first constructs the representation of the contour estimated at the previous iteration. Then, the recurrent operator takes the features as input and estimates the residual displacement to adjust current coarse contour to further outline the object instance. Through the iterative refinements, the contour progressively converges to a stable status that tightly encloses the object instance.
在本工作中,我们提出了PolySnake,这是一种基于通用轮廓的实例分割新深度网络架构。我们PolySnake的灵感可追溯至经典的Snake算法[27],该算法通过能量函数优化迭代地变形初始多边形以逐步贴合目标边界。相应地,我们的PolySnake也旨在基于迭代与渐进机制实现高效的自动轮廓学习,这与现有方法不同。具体而言,给定目标实例的初始轮廓,PolySnake开发了循环更新算子来迭代估计轮廓。它维护着单一轮廓估计,该轮廓在每次迭代中逐步变形。每次迭代时,PolySnake首先构建前一迭代估计的轮廓表征,随后循环算子以这些特征为输入,估计残差位移来调整当前粗糙轮廓以进一步勾勒目标实例。通过迭代优化,轮廓逐步收敛至紧密包围目标实例的稳定状态。
Our PolySnake exhibits a novel design in three aspects, discussed next. Firstly, PolySnake takes a neat network architecture. Due to its recurrent design, the whole model is still lightweight and free from iteration times. Such a lightweight architecture also ensures its real-time ability even under a relatively large number of iterations. Secondly, to achieve a high-quality estimation, we present a multi-scale contour refinement module to further refine the obtained contour by aggregating fine-grained and semantic-rich feature maps. Thirdly, we propose a shape loss to encourage and regularize the learning of object shape, which makes the regressed contour outline the object instance more tightly.
我们的PolySnake在以下三个方面展现出新颖设计。首先,PolySnake采用简洁的网络架构。得益于其循环设计,整个模型仍保持轻量级且不受迭代次数限制。这种轻量架构还确保了即使在较多迭代次数下仍具备实时能力。其次,为实现高质量估计,我们提出多尺度轮廓优化模块,通过聚合细粒度且富含语义的特征图来进一步优化所得轮廓。第三,我们提出形状损失函数以促进和规范物体形状的学习,使回归的轮廓更紧密贴合物体实例。
To evaluate the effectiveness of our PolySnake, we conduct comprehensive experiments on several prevalent instance segmentation benchmark datasets, including SBD [34], Cityscapes [35], COCO [36], and KINS [37]. Furthermore, we validate our PolySnake in other two task scenarios, i.e., scene text detection (see Fig. 1(e, f)) and lane detection (see Fig. 1(g, h)). Distinct from general instance segmentation, scene text detection [38] concentrates solely on segmenting a specific object type, that is text. In lane detection tasks [39], the targeted lane lines inherently lack the closed-loop structure often observed in typical instance segmentation objects. Extensive quantitative and qualitative results demonstrate the merits of our method as well as its superiority over state-ofthe-art methods. Moreover, we validate various design choices of PolySnake through comprehensive studies.
为了评估PolySnake的有效性,我们在多个主流实例分割基准数据集上进行了全面实验,包括SBD [34]、Cityscapes [35]、COCO [36]和KINS [37]。此外,我们还在另外两个任务场景中验证了PolySnake的性能,即场景文本检测(见图1(e, f))和车道线检测(见图1(g, h))。与通用实例分割不同,场景文本检测[38]仅专注于分割特定对象类型——文本。在车道线检测任务[39]中,目标车道线本身缺乏典型实例分割对象常见的闭环结构。大量定量和定性结果证明了我们方法的优势及其相对于最先进方法的优越性。此外,我们通过全面研究验证了PolySnake的各种设计选择。
II. RELATED WORK
II. 相关工作
We mainly discuss the research on instance segmentation in two directions, including mask-based and contour-based. We discuss them in the following.
我们主要从两个方向探讨实例分割的研究,包括基于掩码 (mask-based) 和基于轮廓 (contour-based) 的方法。下文将详细讨论这些内容。
A. Mask-based Instance Segmentation
A. 基于掩码的实例分割
Most recent works perform instance segmentation by predicting pixel-level masks. Some works follow the paradigm of “Detect then Segment” [14], [17], [15], [16], [18], [19], [20], [21], [40]. They usually first detect the bounding boxes and then predict foreground masks in the region of each bounding box. Among them, the classic Mask R-CNN [14] supplements a segmentation branch on Faster R-CNN [41] for per-pixel binary classification in each region proposal. To enhance the feature representation, PANet [17] proposes bottom-up path augmentation to enhance information propagation based on Mask R-CNN [14], and $\mathrm{A^{2}}$ -FPN [20] strengthens pyramidal feature representations through attention-guided feature aggregation. To improve the segmentation parts, Mask Scoring RCNN [16] adds a MaskIoU head to learn the completeness of the predicted masks. HTC [15] and RefineMask [19] integrate cascade into instance segmentation by interweaving detection and segmentation features [15] or fusing the instance features obtained from different stages [19]. Recently, DCT-Mask [18] introduces DCT mask representation to reduce the complexity of mask representation, and BPR [21] proposes the crop-thenrefine strategy to improve the boundary quality.
大多数最新研究通过预测像素级掩码来进行实例分割。部分工作遵循"先检测后分割"范式 [14], [17], [15], [16], [18], [19], [20], [21], [40],通常先检测边界框,然后在每个边界框区域内预测前景掩码。其中经典方法Mask R-CNN [14]在Faster R-CNN [41]基础上增加分割分支,对每个候选区域进行逐像素二分类。为增强特征表示,PANet [17]基于Mask R-CNN提出自底向上路径增强机制来改进信息传播,$\mathrm{A^{2}}$-FPN [20]则通过注意力引导的特征聚合来强化金字塔特征表示。在分割优化方面,Mask Scoring RCNN [16]引入MaskIoU头来学习预测掩码的完整性;HTC [15]和RefineMask [19]分别通过交织检测与分割特征 [15] 或融合多阶段实例特征 [19] 实现级联式实例分割。近期,DCT-Mask [18]采用DCT掩码表示降低复杂度,BPR [21]提出"裁剪-优化"策略来提升边界质量。
There also exist some works that are free of bounding boxes. YOLACT [42] generates several prototype masks over the entire image and predicts a set of coefficients for each instance to combine them. BlendMask [43] directly predicts 2D attention map for each proposal on the top of the FCOS detector [44], and combines them with ROI features. Besides, recent attempts [45], [46], [47], [48] have also applied dynamic convolution kernels trained online, which are then performed on feature maps to generate instance masks.
也存在一些无需边界框的工作。YOLACT [42] 在整个图像上生成多个原型掩码,并为每个实例预测一组系数来组合它们。BlendMask [43] 直接在 FCOS 检测器 [44] 的基础上为每个候选区域预测 2D 注意力图,并将其与 ROI 特征结合。此外,最近的尝试 [45]、[46]、[47]、[48] 还应用了在线训练的动态卷积核,随后在特征图上执行以生成实例掩码。
B. Contour-based Instance Segmentation
B. 基于轮廓的实例分割
Contour-based methods aim to predict a sequence of vertices of object boundaries, which are usually more lightweight than pixel-based methods. Some methods [29], [25], [24] use polar-representation to predict contours directly. Among them, PolarMask [24], [25] extends classic detection algorithm FCOS [44] to instance segmentation, which adds an additional regression head to predict distances from the center point to each boundary vertex. However, performances of such methods are usually limited when dealing with objects with some complex concave shapes. ESE-Seg [29] utilizes Chebyshev polynomials [49] to approximate the shape vector and adds an extra branch on YOLOv3 [50] to regress the coefficients of Chebyshev polynomials.
基于轮廓的方法旨在预测物体边界的一系列顶点,通常比基于像素的方法更轻量。一些方法[29]、[25]、[24]直接采用极坐标表示预测轮廓。其中,PolarMask[24]、[25]将经典检测算法FCOS[44]扩展到实例分割任务,通过增加回归头预测中心点到各边界顶点的距离。但此类方法在处理复杂凹形物体时性能往往受限。ESE-Seg[29]利用切比雪夫多项式[49]逼近形状向量,并在YOLOv3[50]上新增分支回归切比雪夫多项式系数。
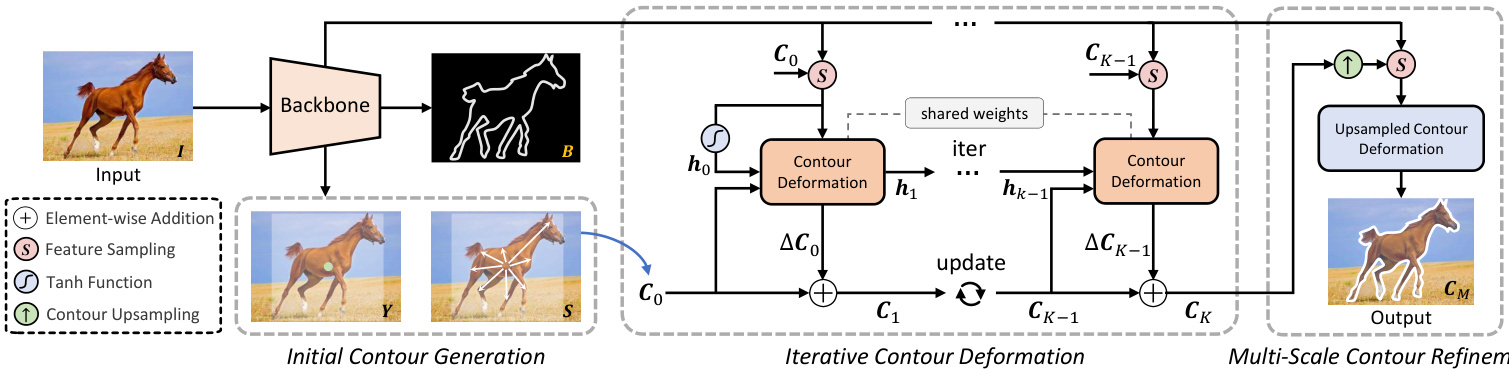
Fig. 2. An overview of the proposed PolySnake framework. PolySnake consists of three modules: Initial Contour Generation (ICG), Iterative Contour Deformation (ICD), and Multi-scale Contour Refinement (MCR). Given an input image $\pmb{I}$ , ICG first initializes a coarse contour $C_{0}$ based on the predicted center heatmap $\mathbf{Y}$ and offset map ${s}$ . Then, in ICD, the obtained contour $C_{0}$ is progressively deformed with $K$ iterations. After that, in MCR, we construct a large-scale but semantic-rich feature map for a further refinement and obtain the output contour $C_{M}$ .

图 2: 提出的PolySnake框架概览。PolySnake包含三个模块: 初始轮廓生成(ICG)、迭代轮廓形变(ICD)和多尺度轮廓优化(MCR)。给定输入图像$\pmb{I}$,ICG首先基于预测的中心热力图$\mathbf{Y}$和偏移图${s}$初始化粗轮廓$C_{0}$。随后在ICD模块中,通过$K$次迭代逐步形变获得的轮廓$C_{0}$。最后在MCR模块中,我们构建大尺度但语义丰富的特征图进行进一步优化,得到输出轮廓$C_{M}$。
Some other works [26], [30], [32], [51], [33] apply Cartesian coordinate representation for vertices, and regress them towards ground-truth object boundaries. Typically, DeepSnake [26] first initializes the contours based on the box predictions, and then applies several contour deformation steps for segmentation. Based on DeepSnake[26], Dance [32] improves the matching scheme between predicted and target contours and introduces an attentive deformation mechanism. ContourRender [51] uses DCT coordinate signature and applies a differentiable renderer to render the contour mesh. Eigencontours [52] proposes a contour descriptor based on low-rank approximation and then incorporates the ei gen contours into an instance segmentation framework. Recently, E2EC [33] applies a novel learnable contour initialization architecture and shows remarkable performance.
其他一些工作[26]、[30]、[32]、[51]、[33]采用笛卡尔坐标系表示顶点,并将其回归到真实物体边界。典型地,DeepSnake[26]首先基于框预测初始化轮廓,然后应用多个轮廓变形步骤进行分割。基于DeepSnake[26],Dance[32]改进了预测轮廓与目标轮廓的匹配方案,并引入了注意力变形机制。ContourRender[51]使用DCT坐标签名,并应用可微分渲染器来渲染轮廓网格。Eigencontours[52]提出了一种基于低秩近似的轮廓描述符,然后将特征轮廓整合到实例分割框架中。最近,E2EC[33]应用了一种新颖的可学习轮廓初始化架构,并展现出卓越性能。
Distinct from existing methodologies, our PolySnake model introduces an innovative iterative and progressive mechanism for learning object contours, thereby achieving precise and robust estimations across a variety of objects.
与现有方法不同,我们的PolySnake模型引入了一种创新的迭代渐进式学习机制来获取物体轮廓,从而实现对各类物体的精准鲁棒估计。
III. METHODOLOGY
III. 方法论
An overview of the proposed PolySnake is shown in Fig. 2. Echoing the methodology of the classic Snake algorithm, PolySnake employs an iterative approach to contour deformation, aiming to precisely align with the object boundary. We develop a recurrent architecture that allows a single estimate of the contour progressively updated at each iteration, and further refine the obtained contour at a larger image scale. Through iterative refinements, the contour steadily envelops the object, eventually stabilizing at a consistent state. For the convenience of understanding, we divide the framework into three modules, including (1) initial contour generation, (2) iterative contour deformation, and (3) multi-scale contour refinement. Each module is discussed in detail in the subsequent sections.
图 2 展示了所提出的 PolySnake 方法概览。延续经典 Snake 算法的思路,PolySnake 采用迭代式轮廓变形策略,旨在实现与物体边界的精确贴合。我们设计了一种循环架构,使得单次轮廓估计能在每次迭代中持续更新,并在更大图像尺度上进一步优化所得轮廓。通过迭代优化,轮廓将逐步包裹目标物体,最终收敛至稳定状态。为便于理解,我们将框架划分为三个模块:(1) 初始轮廓生成,(2) 迭代轮廓变形,(3) 多尺度轮廓优化。后续章节将详细讨论各模块实现。
A. Initial Contour Generation
A. 初始轮廓生成
The Initial Contour Generation (ICG) module is designed to construct preliminary contours for object instances. Leveraging the principles of CenterNet [53], both DeepSnake [26] and Dance [32] initialize a contour from the detected bounding box with a rectangle, whereas E2EC [33] adopts a direct regression of an ordered vertex set to form the initial contour. In our PolySnake, we initialize the coarse contours based on the basic setting of E2EC [33], described next.
初始轮廓生成(ICG)模块旨在为物体实例构建初步轮廓。基于CenterNet[53]的原理,DeepSnake[26]和Dance[32]从检测到的边界框初始化矩形轮廓,而E2EC[33]采用直接回归有序顶点集来形成初始轮廓。在我们的PolySnake中,我们基于E2EC[33]的基本设置初始化粗轮廓,具体描述如下。
Specifically, given an input RGB image $\pmb{I} \in~\mathbb{R}^{H\times W\times3}$ with width $W$ and height $H$ , we first inject it to a backbone network [54], and obtain a feature map $\dot{\pmb{F}}\in\mathbb{R}^{\frac{H}{R}\times\frac{W}{R}\times D}$ , where $R=4$ is the output stride and $D$ denotes the channel number. Then, as shown in Fig. 2, the initial contour is generated with three parallel branches. The first branch predicts a center heatmap $\begin{array}{r}{\dot{\textbf{\emph{Y}}}\in{\bf\Gamma}[0,1]^{\frac{H}{R}\times\frac{W}{R}\times C}}\end{array}$ , where $C$ is the number of object categories. The second branch regresses an offset map $\begin{array}{r l}{S}&{{}\in}&{\mathbb{R}^{\frac{H}{R}\times\frac{W}{R}\times2N_{v}}}\end{array}$ , where $N_{v}$ denotes the vertex number to form an object contour. Let $(x_{i},y_{j})$ denote the center coordinate of an object, then its contour can be obtained by adding the predicted offset ${(\Delta x^{k},\Delta y^{k})|k=1,2,...,N_{v}}$ at $(x_{i},y_{j})$ of $\boldsymbol{S}$ . Moreover, we supplement an extra branch. It predicts a category-agnostic boundary map $\begin{array}{r}{B\in\mathbb{R}^{\frac{H}{R}\times\frac{W}{R}}}\end{array}$ , in which each value is a classification confidence (boundary/nonboundary). Our motivation is that such a branch can help to extract the more fine-grained features for the perception of object boundaries. Note that this branch is only used in the training, which will not cause an extra computation burden for inference. During inference, the instance center can be obtained efficiently based on the max pooling operation [53] on the heatmap $\mathbf{Y}$ . Finally, we obtain the initial contour $C_{0}\in\mathbb{R}^{N_{v}\times2}$ used for the following refinements.
具体来说,给定一个宽度为$W$、高度为$H$的输入RGB图像$\pmb{I} \in~\mathbb{R}^{H\times W\times3}$,我们首先将其输入到主干网络[54]中,获得特征图$\dot{\pmb{F}}\in\mathbb{R}^{\frac{H}{R}\times\frac{W}{R}\times D}$,其中$R=4$为输出步长,$D$表示通道数。接着,如图2所示,初始轮廓通过三个并行分支生成。第一个分支预测中心热图$\begin{array}{r}{\dot{\textbf{\emph{Y}}}\in{\bf\Gamma}[0,1]^{\frac{H}{R}\times\frac{W}{R}\times C}}\end{array}$,其中$C$是目标类别数。第二个分支回归偏移图$\begin{array}{r l}{S}&{{}\in}&{\mathbb{R}^{\frac{H}{R}\times\frac{W}{R}\times2N_{v}}}\end{array}$,其中$N_{v}$表示构成目标轮廓的顶点数。设$(x_{i},y_{j})$为目标中心坐标,则其轮廓可通过在$\boldsymbol{S}$的$(x_{i},y_{j})$处添加预测偏移${(\Delta x^{k},\Delta y^{k})|k=1,2,...,N_{v}}$获得。此外,我们补充了一个额外分支,预测类别无关的边界图$\begin{array}{r}{B\in\mathbb{R}^{\frac{H}{R}\times\frac{W}{R}}}\end{array}$,其中每个值为分类置信度(边界/非边界)。我们的动机是该分支有助于提取更细粒度的特征以感知目标边界。注意此分支仅用于训练,不会增加推理时的计算负担。推理时,实例中心可通过在热图$\mathbf{Y}$上执行最大池化操作[53]高效获得。最终,我们得到用于后续优化的初始轮廓$C_{0}\in\mathbb{R}^{N_{v}\times2}$。
B. Iterative Contour Deformation
B. 迭代轮廓变形
Given the initial contour of an object instance, the Iterative Contour Deformation (ICD) module maintains a single estimation of object contour, which is refined iterative ly. In this way, the initial contour finally converges to a stable state tightly enclosing the object. The architecture of the ICD module is neat, which contributes to the low latency of our method even with a relatively large number of iterations.
给定物体实例的初始轮廓,迭代轮廓变形(ICD)模块会持续维护单一物体轮廓估计,并通过迭代逐步优化。这种方式使得初始轮廓最终收敛至紧密包裹物体的稳定状态。ICD模块架构简洁,即使进行较多轮次迭代,仍能保持方法的低延迟特性。
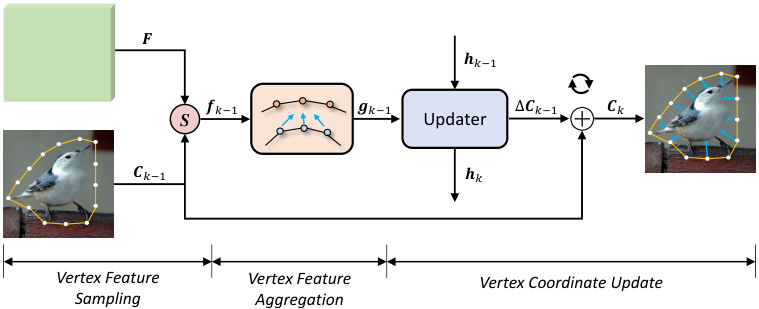
Fig. 3. An illustration of the $k^{t h}$ iteration in the ICD module. “ $\boldsymbol{S}$ ” denotes vertex feature sampling based on bilinear interpolation. “ $\yen123,456$ represents element-wise addition for deforming the current contour.
图 3: ICD模块中第$k^{th}$次迭代的示意图。"$\boldsymbol{S}$"表示基于双线性插值的顶点特征采样。"$\yen123,456$"表示用于变形当前轮廓的逐元素加法。
The workflow of ICD module is illustrated in Fig. 2. Given the feature map $\pmb{F}\in\mathbb{R}^{\frac{H}{R}\times\frac{W}{R}\times D}$ extracted by the backbone network and the initial contour ${\cal C}{0}={p_{0}^{1},\stackrel{.}{p_{0}^{2}},...,p_{0}^{N_{v}}}\in$ $\mathbb{R}^{N_{v}\times2}$ of an object, we deform the object contour iterative ly ${p_{k}^{1},p_{k}^{2},...,p_{k}^{N_{v}}}$ s eiqsu tehnec ep ${C_{1},C_{2},...,C_{K}}$ o, ntwohuerr ew $\begin{array}{r l}{C_{k}}&{{}=}\end{array}$ $N_{v}$ vertices at the $k^{t h}$ iteration, and $K$ is the total iteration number. Note that the two channels of the contour $C_{k}\in\mathbb{R}^{N_{v}\times2}$ denote the horizontal and the vertical coordinates of $N_{v}$ vertices, respectively. After $K$ iterations, we produce the high-quality object contour $C_{K}$ .
ICD模块的工作流程如图2所示。给定骨干网络提取的特征图$\pmb{F}\in\mathbb{R}^{\frac{H}{R}\times\frac{W}{R}\times D}$和物体的初始轮廓${\cal C}{0}={p_{0}^{1},\stackrel{.}{p_{0}^{2}},...,p_{0}^{N_{v}}}\in$ $\mathbb{R}^{N_{v}\times2}$,我们通过迭代变形物体轮廓${p_{k}^{1},p_{k}^{2},...,p_{k}^{N_{v}}}$生成序列${C_{1},C_{2},...,C_{K}}$,其中$C_{k}$表示第$k^{th}$次迭代时的$N_{v}$个顶点,$K$为总迭代次数。需注意轮廓$C_{k}\in\mathbb{R}^{N_{v}\times2}$的两个通道分别表示$N_{v}$个顶点的水平坐标和垂直坐标。经过$K$次迭代后,最终生成高质量物体轮廓$C_{K}$。
As shown in Fig. 3, we illustrate the contour update process at the $k^{t h}$ iteration. Given the feature map $\pmb{F}\in\mathbb{R}^{\frac{\cdot\pmb{H}}{R}\times\frac{W}{R}\times D}$ and the contour $C_{k-1}$ predicted at the ${(k-1)}^{t h}$ iteration, we first sample the vertex-wise feature and then aggregate them for deforming the current contour. We divide the contour update process in ICD module into three sub-processes, including (1) vertex-wise feature sampling, (2) vertex feature aggregation, and (3) vertex coordinate update, as described in the following.
如图 3 所示,我们展示了第 $k^{t h}$ 次迭代时的轮廓更新过程。给定特征图 $\pmb{F}\in\mathbb{R}^{\frac{\cdot\pmb{H}}{R}\times\frac{W}{R}\times D}$ 和第 ${(k-1)}^{t h}$ 次迭代预测的轮廓 $C_{k-1}$,我们首先对顶点特征进行采样,然后聚合这些特征以变形当前轮廓。我们将 ICD 模块中的轮廓更新过程分为三个子过程:(1) 顶点特征采样,(2) 顶点特征聚合,(3) 顶点坐标更新,具体描述如下。
Vertex-wise feature sampling. Given the feature map $\pmb{F}\in\mathbb{R}^{\frac{H}{R}\times\frac{W}{R}\times D}$ of image $\pmb{I}$ and the contour $C_{k-1}\in\mathbb{R}^{N_{v}\times2}$ with $N_{v}$ vertices ${p_{k-1}^{1},p_{k-1}^{2},...,p_{k-1}^{N_{v}}}$ predicted at the (k 1)th iteration, we first retrieve features of these $N_{v}$ vertices. Specifically, given a vertex $\pmb{p}{k-1}^{i}\in\mathbb{R}^{2}$ , we sample its feature vector $F(\pmb{p}{k-1}^{i})\in\mathbb{R}^{D}$ on the feature map $\pmb{F}$ based on the bilinear interpolation. Note that according to classic STN [55], we can compute the gradients to the input $\pmb{F}$ and $C_{k-1}$ for back propagation, thus the module can be trained in an end-to-end manner. After that, we concatenate the feature vectors of the total $N_{v}$ vertices and produce the vertex feature $f_{k-1}\in\mathbb{R}^{N_{v}\times D}$ at the ${(k-1)}^{t h}$ iteration.
逐顶点特征采样。给定图像 $\pmb{I}$ 的特征图 $\pmb{F}\in\mathbb{R}^{\frac{H}{R}\times\frac{W}{R}\times D}$ 和第 $(k-1)$ 次迭代预测的轮廓 $C_{k-1}\in\mathbb{R}^{N_{v}\times2}$ (包含 $N_{v}$ 个顶点 ${p_{k-1}^{1},p_{k-1}^{2},...,p_{k-1}^{N_{v}}}$),我们首先检索这 $N_{v}$ 个顶点的特征。具体而言,给定顶点 $\pmb{p}{k-1}^{i}\in\mathbb{R}^{2}$,我们基于双线性插值从特征图 $\pmb{F}$ 中采样其特征向量 $F(\pmb{p}{k-1}^{i})\in\mathbb{R}^{D}$。根据经典STN [55],可计算输入 $\pmb{F}$ 和 $C_{k-1}$ 的梯度用于反向传播,因此该模块能以端到端方式训练。最后,我们将所有 $N_{v}$ 个顶点的特征向量拼接,生成第 ${(k-1)}^{t h}$ 次迭代的顶点特征 $f_{k-1}\in\mathbb{R}^{N_{v}\times D}$。
Vertex feature aggregation. This module constructs the contour-level representation for $C_{k-1}$ by fusing the vertex features $f_{k-1}$ . Following [26], [32], [33], [38], we use the circle-convolution to fuse the feature of the contour. The circleconvolution operation firstly joins up the head and tail of the input sequence and then applies a standard 1-D convolution on it, which is applicable to capture features of a contour with a polygon topology. In our implementation, we first stack eight circle-convolution layers with residual skip connections for all the layers. Then, we concatenate the features from all the layers and forward them through three $1\times1$ convolutional layers. Finally, we explicitly concatenate the output features with contour coordinate $C_{k-1}\in\mathbb{R}^{N_{v}\times2}$ , obtaining the contour representation $\pmb{g}{k-1}\in\mathbb{R}^{N_{v}\times D_{v}}$ .
顶点特征聚合。该模块通过融合顶点特征$f_{k-1}$为$C_{k-1}$构建轮廓级表示。根据[26]、[32]、[33]、[38],我们采用圆形卷积(circle-convolution)来融合轮廓特征。该操作首先将输入序列首尾相连,然后对其应用标准一维卷积,适用于捕获具有多边形拓扑结构的轮廓特征。具体实现中,我们首先堆叠八个带残差跳跃连接的圆形卷积层,随后拼接所有层的特征并通过三个$1\times1$卷积层。最终将输出特征与轮廓坐标$C_{k-1}\in\mathbb{R}^{N_{v}\times2}$显式拼接,得到轮廓表示$\pmb{g}{k-1}\in\mathbb{R}^{N_{v}\times D_{v}}$。

Fig. 4. Inner structure of the GRU-based vertex coordinate updater.
图 4: 基于GRU的顶点坐标更新器内部结构
Vertex coordinate update. To make the contour enclose the object tightly, we introduce a recurrent update operator that iterative ly updates the currently estimated contour. Fig. 4 illustrates the structure of our GRU-based update operator. It is a gated activation unit based on the GRU cell [56], in which the fully connected layers are replaced with the 1-D convolutional layers. At the $k^{t h}$ iteration, it takes the contour representation $\dot{\pmb{g}}{k-1}\in\mathbb{R}^{N_{v}\times D_{v}}$ as well as the hidden state $\pmb{h}{k-1}\in\mathbb{R}^{N_{v}\times D_{v}}$ as input, differentiates them, and outputs the hidden states $\pmb{h}{k}\in\mathbb{R}^{N_{v}\times D_{v}}$ as follows,
顶点坐标更新。为了使轮廓紧密包围目标物体,我们引入了一种循环更新算子,用于迭代更新当前估计的轮廓。图4展示了基于GRU的更新算子结构。这是一个基于GRU单元[56]的门控激活单元,其中全连接层被一维卷积层取代。在第$k^{t h}$次迭代时,它以轮廓表示$\dot{\pmb{g}}{k-1}\in\mathbb{R}^{N_{v}\times D_{v}}$和隐藏状态$\pmb{h}{k-1}\in\mathbb{R}^{N_{v}\times D_{v}}$作为输入,对它们进行差分处理,并输出隐藏状态$\pmb{h}{k}\in\mathbb{R}^{N_{v}\times D_{v}}$,具体如下:
$$
\begin{array}{r l r}{\lefteqn{z_{k}=\sigma\big(C o n v\big([h_{k-1},g_{k-1}],W_{z}\big)\big),}}\ &{r_{k}=\sigma\big(C o n v\big([h_{k-1},g_{k-1}],W_{r}\big)\big),}\ &{\widetilde{h}{k}=t a n h\big(C o n v\big([r_{k}\odot h_{k-1},g_{k-1}],W_{h}\big)\big),}&\ &{\quad h_{k}=\big(1-z_{k}\big)\odot h_{k-1}+z_{k}\odot\widetilde{h}_{k},}\end{array}
$$
$$
\begin{array}{r l r}{\lefteqn{z_{k}=\sigma\big(C o n v\big([h_{k-1},g_{k-1}],W_{z}\big)\big),}}\ &{r_{k}=\sigma\big(C o n v\big([h_{k-1},g_{k-1}],W_{r}\big)\big),}\ &{\widetilde{h}{k}=t a n h\big(C o n v\big([r_{k}\odot h_{k-1},g_{k-1}],W_{h}\big)\big),}&\ &{\quad h_{k}=\big(1-z_{k}\big)\odot h_{k-1}+z_{k}\odot\widetilde{h}_{k},}\end{array}
$$
where $\odot$ denotes element-wise multiplication; $W_{z}$ , $W_{r}$ , and $W_{h}$ are the weights for the corresponding gates. Note that the initial hidden state $\pmb{h}{0}$ is initialized as the contour feature $\mathbf{\delta}{\mathbf{{g}}{0}}\in$ $\mathbb{R}^{N_{v}\times D_{v}}$ that is processed by the tanh activation function.
其中 $\odot$ 表示逐元素相乘;$W_{z}$、$W_{r}$ 和 $W_{h}$ 是对应门控的权重。注意初始隐藏状态 $\pmb{h}{0}$ 被初始化为轮廓特征 $\mathbf{\delta}{\mathbf{{g}}{0}}\in$ $\mathbb{R}^{N_{v}\times D_{v}}$,该特征经过 tanh 激活函数处理。
After that, two convolutional layers with a ReLU activation follow $\pmb{h}{k}\in\mathbb{R}^{N_{v}\times D_{v}}$ to produce the residual displacement $\Delta C_{k-1}\in\mathbb{R}^{N_{v}\times2}$ , which is used to update the coordinate of current contour $C_{k-1}$ as follows,
随后,两个带有ReLU激活的卷积层处理 $\pmb{h}{k}\in\mathbb{R}^{N_{v}\times D_{v}}$ ,生成残差位移 $\Delta C_{k-1}\in\mathbb{R}^{N_{v}\times2}$ ,并按如下方式更新当前轮廓 $C_{k-1}$ 的坐标:
$$
C_{k}=C_{k-1}+\Delta C_{k-1}.
$$
$$
C_{k}=C_{k-1}+\Delta C_{k-1}.
$$
After $K$ iterations, we obtain the contour prediction $C_{K}\in$ $\mathbb{R}^{N_{v}\times2}$ tightly enclosing an object instance, as shown in Fig. 2.
经过 $K$ 次迭代后,我们得到紧密包围物体实例的轮廓预测 $C_{K}\in$ $\mathbb{R}^{N_{v}\times2}$,如图 2 所示。
C. Multi-scale Contour Refinement
C. 多尺度轮廓优化
The output contour $C_{K}$ is obtained based on the retrieved contour feature from the $\frac{1}{R}$ 1 cale feature map F R R × R ×D. s Note that we set $R=4$ by default, following DeepSnake [26] and E2EC [33]. However, the feature map $\pmb{F}$ is semantically strong, but the high-frequency features on object boundaries are inadequate after all the down sampling and upsampling operations in the network, which brings difficulties to localize the object contours. To this end, we develop the MCR module, aiming to further refine the obtained $C_{K}$ by aggregating a large-scale but semantic-rich feature map.
输出轮廓 $C_{K}$ 是基于从 $\frac{1}{R}$ 尺度特征图 $F_{R} \in \mathbb{R}^{R \times R \times D}$ 中检索到的轮廓特征获得的。需要注意的是,我们默认设置 $R=4$,遵循 DeepSnake [26] 和 E2EC [33] 的做法。然而,特征图 $\pmb{F}$ 虽然语义信息丰富,但在网络经过多次下采样和上采样操作后,物体边界的高频特征仍显不足,这给定位物体轮廓带来了困难。为此,我们开发了 MCR (Multi-scale Context Refinement) 模块,旨在通过聚合大尺度且语义丰富的特征图来进一步细化得到的 $C_{K}$。
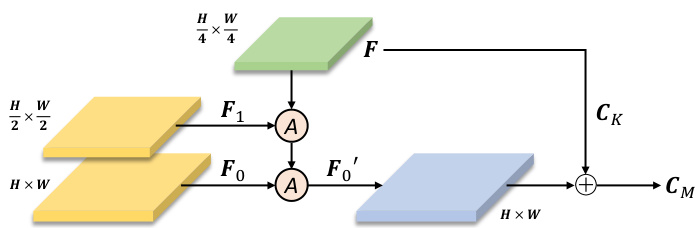
Fig. 5. An overview of the multi-scale contour refinement module. “A” denotes the feature fusion process, following FPN [57].
图 5: 多尺度轮廓细化模块概览。"A"表示特征融合过程,遵循FPN [57]。
Specifically, we first take two additional low-level largescale feature maps from the backbone network (i.e., $F_{0}{\in}$ $\mathbb{R}^{H\times W\times D_{0}}$ and $\begin{array}{r c l}{F_{1}}&{\in}&{\mathbb{R}^{\frac{H}{2}\times\frac{W}{2}\times D_{1}})}\end{array}$ . Note that the highfrequency signals are reserved in ${\cal F}{0}$ and ${\pmb F}{1}$ . Thereafter, as shown in Fig. 5, to aggregate them with the semantically stronger feature map $\pmb{F}$ , we build a simple feature pyramid network [57] to construct feature map $\pmb{F}{0}^{'}\in\mathbb{R}^{H\times W\times\dot{D}_{2}}$ used for following contour refinement.
具体来说,我们首先从主干网络中提取两个额外的低层大尺度特征图(即 $F_{0}{\in}$ $\mathbb{R}^{H\times W\times D_{0}}$ 和 $\begin{array}{r c l}{F_{1}}&{\in}&{\mathbb{R}^{\frac{H}{2}\times\frac{W}{2}\times D_{1}})}\end{array}$)。需要注意的是,高频信号保留在 ${\cal F}{0}$ 和 ${\pmb F}{1}$ 中。随后,如图 5 所示,为了将这些特征图与语义更强的特征图 $\pmb{F}$ 进行聚合,我们构建了一个简单的特征金字塔网络 [57] 来生成用于后续轮廓细化的特征图 $\pmb{F}{0}^{'}\in\mathbb{R}^{H\times W\times\dot{D}_{2}}$。
Based on the feature map $\pmb{F}{0}^{'}$ , we further deform $C_{K}$ to align the object boundary. The contour deformation process is similar to that in the ICD module, except that the GRU-based recurrent update operator is removed. Concretely, given the feature map $\pmb{F}{0}^{'}$ and the current contour $C_{K}$ , we sample the per-vertex features, aggregate them, and directly predict pervertex offset to update the contour $C_{K}$ with a fully connected layer. Finally, we obtain the refined contour estimation, termed as $C_{M}\in\mathbb{R}^{N_{v}\times2}$ , as illustrated in Fig. 2.
基于特征图 $\pmb{F}{0}^{'}$,我们进一步变形 $C_{K}$ 以对齐物体边界。轮廓变形过程与ICD模块类似,只是移除了基于GRU的循环更新算子。具体而言,给定特征图 $\pmb{F}{0}^{'}$ 和当前轮廓 $C_{K}$,我们采样逐顶点特征、聚合这些特征,并通过全连接层直接预测逐顶点偏移量来更新轮廓 $C_{K}$。最终获得精细化轮廓估计结果 $C_{M}\in\mathbb{R}^{N_{v}\times2}$,如图2所示。
$D$ . Training Objectives
$D$ . 训练目标
The training is divided into two stages. Concretely, the ICG and ICD modules are first optimized with the objective as follows,
训练分为两个阶段。具体而言,首先通过以下目标优化ICG和ICD模块,
$$
\mathcal{L}=\mathcal{L}{\mathrm{ICG}}+\mathcal{L}_{\mathrm{ICD}}.
$$
$$
\mathcal{L}=\mathcal{L}{\mathrm{ICG}}+\mathcal{L}_{\mathrm{ICD}}.
$$
Then, we freeze the models and optimize the MCR module with objective $\mathcal{L}_{\mathrm{MCR}}$ . In the following, we separately elaborate them.
随后,我们冻结模型并使用目标函数 $\mathcal{L}_{\mathrm{MCR}}$ 优化MCR模块。下文将分别详述这些步骤。
(1) $\mathcal{L}_{\mathrm{ICG}}$ consists of three terms as follows,
$\mathcal{L}_{\mathrm{ICG}}$ 由以下三项组成,
$$
\mathcal{L}{\mathrm{ICG}}=\mathcal{L}{\mathrm{Y}}+\mathcal{L}{\mathrm{S}}+\mathcal{L}_{\mathrm{B}},
$$
$$
\mathcal{L}{\mathrm{ICG}}=\mathcal{L}{\mathrm{Y}}+\mathcal{L}{\mathrm{S}}+\mathcal{L}_{\mathrm{B}},
$$
where $\mathcal{L}{\mathrm{Y}}$ and $\mathscr{L}{\mathrm{S}}$ are the loss on the predicted center heatmap $\mathbf{Y}$ and offset map $\pmb{S}$ . We follow the classic detector CenterNet [53] to compute $\mathcal{L}{\mathrm{Y}}$ and $\mathscr{L}{\mathrm{S}}$ by only changing the output size of the offset map $\boldsymbol{S}$ from $\frac{H}{R}\stackrel{\cdot}{\times}\frac{W}{R}\stackrel{\cdot}{\times}2N_{v}$ to $\breve{\frac{H}{R}}\times\frac{W}{R}\dot{\times}2$ to directly regress the initial contour with $N_{v}$ vertices. Besides, $\mathscr{L}_{\mathrm{S}}$ is the cross-entropy loss between the predicted boundary map $_B$ and its given ground truth B as follows,
其中 $\mathcal{L}{\mathrm{Y}}$ 和 $\mathscr{L}{\mathrm{S}}$ 分别是预测中心热图 $\mathbf{Y}$ 和偏移图 $\pmb{S}$ 的损失。我们遵循经典检测器 CenterNet [53] 来计算 $\mathcal{L}{\mathrm{Y}}$ 和 $\mathscr{L}{\mathrm{S}}$,仅将偏移图 $\boldsymbol{S}$ 的输出尺寸从 $\frac{H}{R}\stackrel{\cdot}{\times}\frac{W}{R}\stackrel{\cdot}{\times}2N_{v}$ 改为 $\breve{\frac{H}{R}}\times\frac{W}{R}\dot{\times}2$,以直接回归具有 $N_{v}$ 个顶点的初始轮廓。此外,$\mathscr{L}_{\mathrm{S}}$ 是预测边界图 $_B$ 与其给定真实值 B 之间的交叉熵损失,如下所示,
$$
\mathcal{L}{B}=-\sum_{i=1}^{N_{p}}\left[\hat{y}{i}\log(y_{i})+(1-\hat{y}{i})\log(1-y_{i})\right],
$$
$$
\mathcal{L}{B}=-\sum_{i=1}^{N_{p}}\left[\hat{y}{i}\log(y_{i})+(1-\hat{y}{i})\log(1-y_{i})\right],
$$
where $\begin{array}{l}{{N_{p}}=\frac{H}{4}\times\frac{W}{4}}\end{array}$ is the number of pixels in map $B$ $\hat{y}{i}\in[0,1]$ and $\mathbf{\bar{\alpha}}y_{i}\in\bar{{0,1}}$ denote the ground-truth and the predicted confidence score in $\hat{B}$ and $_B$ , respectively.
其中 $\begin{array}{l}{{N_{p}}=\frac{H}{4}\times\frac{W}{4}}\end{array}$ 是特征图 $B$ 中的像素数量,$\hat{y}{i}\in[0,1]$ 和 $\mathbf{\bar{\alpha}}y_{i}\in\bar{{0,1}}$ 分别表示 $\hat{B}$ 和 $_B$ 中的真实置信度得分与预测置信度得分。
(2) $\mathcal{L}_{\mathrm{ICD}}$ is calculated by accumulating the loss over all $K$ iterations as follows,
(2) $\mathcal{L}_{\mathrm{ICD}}$ 的计算方式是对所有 $K$ 次迭代的损失进行累加,具体如下:
$$
\mathcal{L}{\mathrm{ICD}}=\sum_{k=1}^{K}\lambda^{K-k}(\mathcal{L}{R}^{(k)}+\alpha\mathcal{L}_{P}^{(k)}),
$$
$$
\mathcal{L}{\mathrm{ICD}}=\sum_{k=1}^{K}\lambda^{K-k}(\mathcal{L}{R}^{(k)}+\alpha\mathcal{L}_{P}^{(k)}),
$$
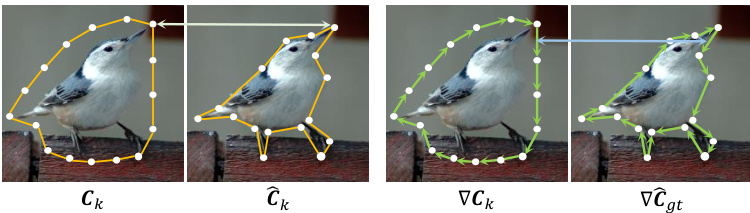
Fig. 6. An illustration of the coordinate regression loss $\mathcal{L}{R}^{(k)}$ (left) and the proposed shape loss $\mathcal{L}{P}^{(k)}$ (right). The loss $\mathcal{L}{R}^{(k)}$ measure the coordinate distance between the predicted contour $C_{k}$ and GT contour $\hat{C}{g t}$ , while $\mathcal{L}_{R}^{(k)}$ encourages the learning of object shape.
图 6: 坐标回归损失 $\mathcal{L}{R}^{(k)}$ (左)与提出的形状损失 $\mathcal{L}{P}^{(k)}$ (右)示意图。损失 $\mathcal{L}{R}^{(k)}$ 衡量预测轮廓 $C_{k}$ 与真实轮廓 $\hat{C}{g t}$ 之间的坐标距离,而 $\mathcal{L}_{R}^{(k)}$ 促进物体形状的学习。
where $\mathcal{L}{R}^{(k)}$ and $\mathcal{L}{P}^{(k)}$ are the coordinate regression loss and our proposed contour shape loss at the iteration, is the temporal weighting factor, and $\alpha$ is the weight of contour shape loss. Here $\lambda$ is less than 1, which means the weight of the loss increases exponentially with the iteration. In Fig. 6, we illustrate the coordinate regression loss $\mathcal{L}{R}^{(k)}$ (left) and the proposed shape loss $\mathcal{L}{P}^{(k)}$ (right). Specifically, we compute the coordinate regression loss by calculating the smooth $L_{1}$ distance [41] between the predicted contour ${C_{k}={p_{k}^{1},p_{k}^{2},...,p_{k}^{N_{v}}}}$ and the ground truth $\hat{C_{g t}}={\hat{p}^{1},\hat{p}^{2},...,\hat{p}^{N_{v}}}$ as follows,
其中 $\mathcal{L}{R}^{(k)}$ 和 $\mathcal{L}{P}^{(k)}$ 分别表示第k次迭代时的坐标回归损失和本文提出的轮廓形状损失,$\lambda$ 是时序权重因子,$\alpha$ 是轮廓形状损失的权重系数。这里 $\lambda$ 小于1,意味着损失权重会随迭代次数呈指数级增长。图6展示了坐标回归损失 $\mathcal{L}{R}^{(k)}$ (左)与提出的形状损失 $\mathcal{L}{P}^{(k)}$ (右)的示意图。具体而言,我们通过计算预测轮廓 $C_{k}={p_{k}^{1},p_{k}^{2},...,p_{k}^{N_{v}}}$ 与真实标注 $\hat{C_{g t}}={\hat{p}^{1},\hat{p}^{2},...,\hat{p}^{N_{v}}}$ 之间的平滑 $L_{1}$ 距离[41]来得到坐标回归损失,计算公式如下:
$$
\mathcal{L}{R}^{(k)}=\sum_{n=1}^{N_{v}}\mathrm{smooth}{L1}(\pmb{p}_{k}^{n},\hat{\pmb{p}}^{n}).
$$
$$
\mathcal{L}{R}^{(k)}=\sum_{n=1}^{N_{v}}\mathrm{smooth}{L1}(\pmb{p}_{k}^{n},\hat{\pmb{p}}^{n}).
$$
$$
\mathcal{L}{P}^{(k)}=\sum_{n=1}^{N_{v}}\mathrm{smooth}{L1}(\Delta\pmb{p}_{k}^{n+1\to n},\Delta\hat{\pmb{p}}^{n+1\to n}).
$$
$$
\mathcal{L}{P}^{(k)}=\sum_{n=1}^{N_{v}}\mathrm{smooth}{L1}(\Delta\pmb{p}_{k}^{n+1\to n},\Delta\hat{\pmb{p}}^{n+1\to n}).
$$
The shape loss encourages the learning of object shape and makes the regressed contour enclose the object tightly.
形状损失 (shape loss) 促使模型学习物体形状,并使回归的轮廓紧密包围目标物体。
(3) $\mathcal{L}{\mathrm{MCR}}$ is calculated as the smooth $L_{1}$ distance [41] between the refined contour ${\cal C}{M}={p_{M}^{1},p_{M}^{2},...,p_{M}^{N_{v}}}$ and its given ground truth $\hat{C_{g t}}$ as follows,
(3) $\mathcal{L}{\mathrm{MCR}}$ 计算为精修轮廓 ${\cal C}{M}={p_{M}^{1},p_{M}^{2},...,p_{M}^{N_{v}}}$ 与其给定真实值 $\hat{C_{g t}}$ 之间的平滑 $L_{1}$ 距离 [41],具体如下:
$$
\mathcal{L}{\mathrm{MCR}}=\sum_{n=1}^{N_{v}}\mathrm{smooth}{L1}(\pmb{p}_{M}^{n},\hat{\pmb{p}}^{n}).
$$
$$
\mathcal{L}{\mathrm{MCR}}=\sum_{n=1}^{N_{v}}\mathrm{smooth}{L1}(\pmb{p}_{M}^{n},\hat{\pmb{p}}^{n}).
$$
IV. EXPERIMENTS
IV. 实验
A. Datasets and Metrics
A. 数据集和指标
Extensive experiments have been conducted on three widely recognized datasets for instance segmentation, as well as two additional datasets specifically focused on scene text detection and lane detection, described in the following.
已在三个广泛认可的实例分割数据集以及两个专门针对场景文本检测和车道检测的数据集上进行了大量实验,具体如下。
SBD [34] dataset consists of 5,623 training and 5,732 testing images, spanning 20 distinct semantic categories. It utilizes images from the PASCAL VOC [58] dataset, but reannotates them with instance-level boundaries. In our study of the SBD dataset, we report the performance of prior works and our PolySnake based on the metrics 2010 VOC $\mathrm{AP}{v o l}$ [59], $\mathrm{AP_{50}}$ , and $\mathrm{AP}{70}$ . $\mathrm{AP}_{v o l}$ is computed as the average of average precision (AP) with nine thresholds from 0.1 to 0.9.
SBD [34] 数据集包含5,623张训练图像和5,732张测试图像,涵盖20个不同的语义类别。该数据集采用PASCAL VOC [58] 数据集的图像,但重新标注了实例级边界。在我们的SBD数据集研究中,基于2010 VOC $\mathrm{AP}{vol}$ [59]、$\mathrm{AP_{50}}$ 和 $\mathrm{AP}{70}$ 指标,报告了先前工作和我们提出的PolySnake的性能表现。$\mathrm{AP}_{vol}$ 是通过0.1至0.9九个阈值的平均精度(AP)取均值计算得出。
TABLE I ABLATIONS OF THE INITIAL CONTOUR GENERATION MODULE ON THE SBD VAL SET [34]. $C_{0}$ AND $C_{K}$ ARE THE OUTPUT CONTOUR OF THE ICG AND ICD MODULES, RESPECTIVELY. SETTINGS USED IN OUR FINAL MODEL ARE UNDERLINED.
表 1: 初始轮廓生成模块在SBD验证集[34]上的消融实验。$C_{0}$和$C_{K}$分别是ICG和ICD模块的输出轮廓。最终模型使用的设置已加下划线。
| 实验 | 轮廓 | 方法 | APvol | AP50 | AP70 |
|---|---|---|---|---|---|
| 边界图 | Co | W/ | 49.5 | 61.2 | 31.9 |
| w/o W/ | 49.3 | 61.0 | 32.2 | ||
| CK | w/o | 59.3 | 66.7 | 54.8 | |
| 顶点数量 | CK | N = 64 | 58.9 | 66.0 | 54.1 |
| N=128 | 59.7 | 66.7 | 54.8 | ||
| N= 192 | 59.2 | 66.2 | 54.3 |
TABLE II ABLATIONS OF THE ITERATIVE CONTOUR DEFORMATION MODULE ON THE SBD VAL SET [34]. SETTINGS USED IN OUR FINAL MODEL ARE UNDERLINED.
表 2: 迭代轮廓变形模块在SBD验证集[34]上的消融实验。最终模型使用的设置已加下划线。
| 实验 | 方法 | APvol | AP50 | AP70 | 参数量 (M) FPS |
|---|---|---|---|---|---|
| ContourFeature | fk gk | 58.6 59.7 | 65.7 66.7 | 53.2 54.8 | 20.3 44.2 22.0 28.8 |
| Update Unit | ConvGRU | 59.7 | 66.7 | 54.8 | 22.0 28.8 |
| ConvLSTM W/ | 59.5 59.7 | 66.4 | 54.6 | 22.1 24.4 | |
| Shared Weights | w/o | 59.6 | 66.7 66.5 | 54.8 55.1 | 22.0 31.0 1 |
| Supervised iters | [1,K] | 59.7 | 66.7 | 54.8 | 22.0 |
| {y} | 58.8 | 66.2 | 54.0 22.0 | ||
| W/ | 59.7 | 66.7 | 54.8 | ||
| Shape Loss | w/o | 59.4 | 66.2 | 54.8 |
Cityscapes [35] dataset is intended for assessing the performance of vision algorithms of semantic urban scene understanding. The dataset contains 5000 images with high-quality annotations of 8 semantic categories. They are further split into 2975, 500, and 1525 images for training, validation, and testing, respectively. Results are evaluated in terms of the AP metric averaged over all categories of the dataset.
Cityscapes [35] 数据集旨在评估语义城市场景理解视觉算法的性能。该数据集包含5000张图像,具有8个语义类别的高质量标注,并进一步划分为2975张训练集、500张验证集和1525张测试集。结果以数据集中所有类别的平均AP (Average Precision) 指标进行评估。
KINS [37] dataset is specifically constructed for amodal instance segmentation [60], which adopts images from the KITTI [61] dataset and annotates them with instance-level semantic annotation. The dataset contains 7474 training and 7517 testing images. We evaluate our approach on seven object categories with the AP metric.
KINS [37] 数据集专为不可见实例分割 (amodal instance segmentation) [60] 而构建,其采用 KITTI [61] 数据集中的图像并进行了实例级语义标注。该数据集包含7474张训练图像和7517张测试图像。我们使用AP (Average Precision) 指标在7个物体类别上评估了所提方法。
COCO [36] dataset stands as a substantial and challenging resource for instance segmentation. It encompasses an extensive collection of images, comprising 115,000 for training, 5,000 for validation, and 20,000 for testing, spanning 80 diverse object categories. A notable feature of the COCO dataset is its inclusion of everyday objects and human figures within its imagery. In our research, we employ the COCO Average Precision (AP) metric as the standard for evaluating the efficacy of other methods and our method.
COCO [36] 数据集是实例分割领域一个庞大且具有挑战性的资源。它包含大量图像,涵盖115,000张训练集、5,000张验证集和20,000张测试集,覆盖80个不同物体类别。该数据集的显著特点是包含了日常物品和人物图像。在我们的研究中,我们采用COCO平均精度(AP)指标作为评估其他方法及我们方法效果的标准。
TABLE III PERFORMANCE OF THE SELECTED ITERATIONS DURING INFERENCE ON THE SBD VAL SET [34]. $C_{0}$ IS OUTPUT INITIAL CONTOUR OF THE ICG MODULE. THE RUNNING EFFICIENCY IS EVALUATED ON A SINGLE RTX $2080\mathrm{TI}$ GPU. THE CONTOUR USED AS THE FINAL OUTPUT OF THE ICD MODULE IS UNDERLINED.
表 III SBD验证集[34]上推理过程中选定迭代的性能表现。$C_{0}$是ICG模块输出的初始轮廓。运行效率在单块RTX $2080\mathrm{TI}$ GPU上评估。作为ICD模块最终输出的轮廓已用下划线标出。
| 轮廓 | APvol | AP50 | AP70 | FPS |
|---|---|---|---|---|
| Co | 49.5 | 61.2 | 31.9 | 51.5 |
| C1 | 56.1 | 65.6 | 49.2 | 48.4 |
| C2 | 58.5 | 66.3 | 53.8 | 45.1 |
| C3 | 59.3 | 66.5 | 54.4 | 37.9 |
| C4 | 59.6 | 66.6 | 54.7 | 34.6 |
| C5 | 59.7 | 66.6 | 54.7 | 30.5 |
| C6 | 59.7 | 66.7 | 54.8 | 28.8 |
| C7 | 59.7 | 66.7 | 54.9 | 26.1 |
| C8 | 59.7 | 66.7 | 54.9 | 23.6 |
| CM | 60.0 | 66.8 | 55.3 | 24.6 |
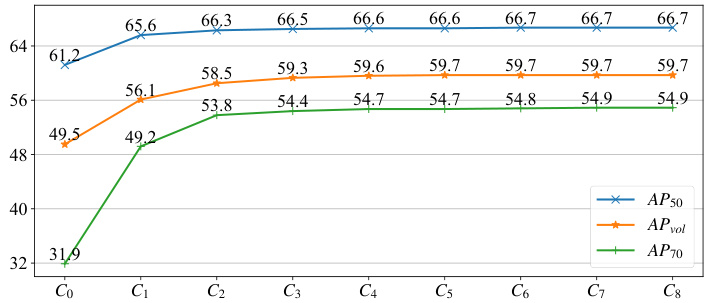
Fig. 7. Performance plot of the selected iterations during inference on the SBD val set [34]. $C_{0}$ is output initial contour of the ICG module.
图 7: 在 SBD 验证集 [34] 上推理过程中选定迭代的性能曲线。$C_{0}$ 是 ICG 模块输出的初始轮廓。
CTW1500 [62] dataset, designed for scene text detection, specifically addresses the challenge of detecting curved texts. It contains 1,500 images, split into 1,000 training and 500 testing images, and features a total of 10,751 text instances, including a significant proportion of curved text. The dataset’s variety includes images sourced from the internet, image libraries, and phone cameras.
CTW1500 [62] 数据集专为场景文本检测设计,特别针对弯曲文本的检测挑战。该数据集包含1,500张图像,分为1,000张训练图像和500张测试图像,共有10,751个文本实例,其中包含大量弯曲文本。数据集的多样性涵盖来自互联网、图像库和手机摄像头的图像。
CULane [63] is a large challenging lane detection dataset. It consists of 9 types of scenarios, including normal, crowd, curve, dazzling light, night, no line, shadow, and arrow. Additionally, it includes a diverse range of environments, capturing both urban and highway settings. In the CULane [63] dataset, the maximum number $M$ of lane lines in the scene is 4.
CULane [63] 是一个大型且具有挑战性的车道检测数据集。它包含9种场景类型,包括正常、拥挤、弯道、眩光、夜间、无线、阴影和箭头。此外,它还涵盖了多样化的环境,包括城市和高速公路场景。在CULane [63]数据集中,场景中车道线的最大数量$M$为4。
B. Implementation Details
B. 实现细节
By default, we set the vertex number $N_{v} = 128$ to form an object contour. The down sampling ratio $R$ and the channel dimension $D$ for feature map $\pmb{F}$ are set as 4 and 64, respectively. The channel dimension $D_{v}$ of contour feature $g_{k,-1}$ is 66. The channel dimension of feature map $F_{0},F_{1}$ , $\pmb{F}{0}^{'}$ in the MCR module are 32, 16, and 8, respectively. We set $\lambda~=~0.8$ and $\alpha=1$ in Equation (9) to calculate loss $\mathcal{L}_{\mathrm{ICD}}$ , respectively. During training, we set the iteration number $K$ as 6 for the SBD [34], Cityscapes [35], COCO [36], and KINS [37] dataset. By default, the iteration number during t
