Robust Learning Through Cross-Task Consistency

通过跨任务一致性实现稳健学习

Abstract

摘要

Visual perception entails solving a wide set of tasks, e.g., object detection, depth estimation, etc. The predictions made for multiple tasks from the same image are not independent, and therefore, are expected to be ‘consistent’. We propose a broadly applicable and fully computational method for augmenting learning with Cross-Task Consistency.1 The proposed formulation is based on inference-path invariance over a graph of arbitrary tasks. We observe that learning with cross-task consistency leads to more accurate predictions and better generalization to out-of-distribution inputs. This framework also leads to an informative unsupervised quantity, called Consistency Energy, based on measuring the intrinsic consistency of the system. Consistency Energy correlates well with the supervised error $'r{=}0.67,$ , thus it can be employed as an unsupervised confidence metric as well as for detection of out-of-distribution inputs $R O C-A U C=0.95$ ). The evaluations are performed on multiple datasets, including Taskonomy, Replica, CocoDoom, and ApolloS cape, and they benchmark cross-task consistency versus various baselines including conventional multi-task learning, cycle consistency, and analytical consistency.

视觉感知涉及解决一系列广泛的任务，例如目标检测、深度估计等。同一图像上多个任务的预测并非独立，因此应保持"一致性"。我们提出了一种通用且完全基于计算的方法，通过跨任务一致性 (Cross-Task Consistency) 来增强学习效果。该方案基于任意任务图上的推理路径不变性。实验表明，跨任务一致性学习能提高预测精度，并增强对分布外输入的泛化能力。该框架还衍生出一个称为一致性能量 (Consistency Energy) 的无监督指标，通过测量系统内在一致性实现。一致性能量与监督误差高度相关 $'r{=}0.67,$ ，可作为无监督置信度度量及分布外输入检测指标 $R O C-A U C=0.95$ )。评估在Taskonomy、Replica、CocoDoom和ApolloS cape等多个数据集上进行，将跨任务一致性与传统多任务学习、循环一致性和解析一致性等基线方法进行了对比。

1. Introduction

1. 引言

What is consistency: suppose an object detector detects a ball in a particular region of an image, while a depth estimator returns a flat surface for the same region. This presents an issue – at least one of them has to be wrong, because they are inconsistent. More concretely, the first prediction domain (objects) and the second prediction domain (depth) are not independent and consequently enforce some constraints on each other, often referred to as consistency constraints.

一致性是什么：假设一个物体检测器在图像的某个区域检测到一个球，而深度估计器却对同一区域返回了一个平面。这就产生了一个问题——至少有一个结果是错误的，因为它们是不一致的。更具体地说，第一个预测域（物体）和第二个预测域（深度）并非相互独立，因此彼此之间存在某些约束，通常被称为一致性约束。

Why is it important to incorporate consistency in learning: first, desired learning tasks are usually predictions of different aspects of one underlying reality (the scene that underlies an image). Hence inconsistency among predictions implies contradiction and is inherently undesirable. Second, consistency constraints are informative and can be used to better fit the data or lower the sample complexity. Also, they may reduce the tendency of neural networks to learn “surface statistics” (superficial cues) [18], by enforcing constraints rooted in different physical or geometric rules. This is empirically supported by the improved generalization of models when trained with consistency constraints (Sec. 5).

为什么在学习中保持一致性很重要：首先，理想的学习任务通常是对同一潜在现实（如图像背后的场景）不同方面的预测。因此，预测间的不一致意味着矛盾，本质上是不理想的。其次，一致性约束具有信息量，可用于更好地拟合数据或降低样本复杂度。此外，通过强制实施基于不同物理或几何规则的约束，它们可能减少神经网络学习"表面统计量"（浅层线索）的倾向[18]。这一点在经验上得到了支持，即使用一致性约束训练的模型具有更好的泛化能力（见第5节）。

Figure 1: Cross-Task Consistent Learning. The predictions made for different tasks out of one image are expected to be consistent, as the underlying scene is the same. This is exemplified by a challenging query and four sample predictions out of it. We propose a general method for learning utilizing data-driven cross-task consistency constraints. The lower and upper rows show the results of the baseline (independent learning) and learning with consistency, which yields higher quality and more consistent predictions. Red boxes provide magnifications. [Best seen on screen]

图 1: 跨任务一致性学习。由于底层场景相同，对同一图像不同任务的预测结果应保持一致性。图中展示了一个具有挑战性的查询及其四个预测示例。我们提出了一种利用数据驱动的跨任务一致性约束进行学习的通用方法。下方和上方两行分别展示了基线（独立学习）和采用一致性学习的结果，后者能产生更高质量且更一致的预测。红色方框为局部放大区域。[建议屏幕观看]

How can we design a learning system that makes consistent predictions: this paper proposes a method which, given an arbitrary dictionary of tasks, augments the learning objective with explicit constraints for cross-task consistency. The constraints are learned from data rather than apriori given relationships.2 This makes the method applicable to any pairs of tasks as long as they are not statistically independent; even if their analytical relationship is unknown, hard to program, or non-differentiable. The primary concept behind the method is ‘inference-path invariance’. That is, the result of inferring an output domain from an input domain should be the same, regardless of the intermediate domains mediating the inference (e.g., RGB $\rightarrow$ normals and RGB $\rightarrow$ depth $\rightarrow$ normals and RGB $\rightarrow$ shading $\rightarrow$ normals are expected to yield the same normal results). When inference paths with the same endpoints, but different intermediate domains, yield similar results, this implies the intermediate domain predictions did not conflict as far as the output was concerned. We apply this concept over paths in a graph of tasks, where the nodes and edges are prediction domains and neural network mappings between them, respectively (Fig. 2(d)). Satisfying this invariance constraint over all paths in the graph ensures the predictions for all domains are in global cross-task agreement.3

如何设计一个能做出一致预测的学习系统：本文提出了一种方法，在给定任意任务字典的情况下，通过显式的跨任务一致性约束来增强学习目标。这些约束是从数据中学习得到的，而非预先给定的关系。这使得该方法适用于任何统计上不独立的成对任务，即使它们的解析关系未知、难以编程或不可微分。

该方法的核心概念是"推理路径不变性"。即无论推理过程中经过哪些中间域（例如 RGB→法线、RGB→深度→法线、RGB→着色→法线），从输入域推断输出域的结果都应相同。当具有相同端点但不同中间域的推理路径产生相似结果时，就意味着这些中间域的预测在输出层面没有产生冲突。我们将这一概念应用于任务图中的路径，其中节点表示预测域，边表示它们之间的神经网络映射（图 2(d)）。满足图中所有路径的这种不变性约束，就能确保所有域的预测达到全局跨任务一致性。

To make the associated large optimization job manageable, we reduce the problem to a ‘separable’ one, devise a tractable training schedule, and use a ‘perceptual loss’ based formulation. The last enables mitigating residual errors in networks and potential ill-posed/one-to-many mappings between domains (Sec. 3).

为了使相关的大规模优化任务变得可管理，我们将问题简化为一个"可分离"的问题，设计了一个易于处理的训练计划，并采用了基于"感知损失"的公式。最后一项措施有助于减轻网络中的残余误差以及领域间潜在的病态/一对多映射问题（第3节）。

Interactive visualization s, trained models, code, and a live demo are available at http://consistency.epfl.ch/.

交互式可视化工具、训练好的模型、代码和实时演示可在 http://consistency.epfl.ch/ 获取。

2. Related Work

2. 相关工作

The concept of consistency and methods for enforcing it are related to various topics, including structured prediction, graphical models [22], functional maps [30], and certain topics in vector calculus and differential topology [10]. We review the most relevant ones in context of computer vision.

一致性的概念及其实现方法涉及多个相关领域，包括结构化预测、图模型 [22]、函数映射 [30] ，以及向量微积分和微分拓扑中的某些主题 [10]。我们将在计算机视觉的背景下回顾其中最相关的内容。

Utilizing consistency: Various consistency constraints have been commonly found beneficial across different fields, e.g., in language as ‘back-translation’ [2, 1, 25, 7] or in vision over the temporal domain [41, 6], 3D geometry [9, 32, 8, 13, 49, 46, 15, 44, 51, 48, 23, 5], and in recognition and (conditional/unconditional) image translation [12, 28, 17, 50, 14, 4]. In computer vision, consistency has been extensively utilized in the cycle form and often between two or few domains [50, 14]. In contrast, we consider consistency in the more general form of arbitrary paths with varied-lengths over a large task set, rather than the special cases of short cyclic paths. Also, the proposed approach needs no prior explicit knowledge about task relationships [32, 23, 44, 51].

利用一致性：各种一致性约束在不同领域中被普遍认为是有益的，例如在语言中的"回译" [2, 1, 25, 7] 或在视觉中的时间域 [41, 6]、3D几何 [9, 32, 8, 13, 49, 46, 15, 44, 51, 48, 23, 5]，以及识别和（条件/无条件）图像转换 [12, 28, 17, 50, 14, 4]。在计算机视觉中，一致性已被广泛用于循环形式，并且通常在两个或少数几个域之间 [50, 14]。相比之下，我们考虑的是更一般形式的一致性，即在大型任务集上具有不同长度的任意路径，而不是短循环路径的特殊情况。此外，所提出的方法不需要事先明确了解任务关系 [32, 23, 44, 51]。

Multi-task learning: In the most conventional form, multi-task learning predicts multiple output domains out of a shared encoder/representation for an input. It has been speculated that the predictions of a multi-task network may be automatically cross-task consistent as the represent ation from which the predictions are made are shared. This has been observed to not be necessarily true in several works [21, 47, 43, 38], as consistency is not directly enforced during training. We also make the same observation (see visuals here) and quantify it (see Fig. 9(a)), which signifies the need for explicit augmentation of consistency in learning.

多任务学习：在最常见的形式中，多任务学习通过共享的编码器/表示对输入预测多个输出域。有推测认为，由于预测基于共享表示，多任务网络的预测可能自动实现跨任务一致性。但多项研究[21, 47, 43, 38]发现这并不必然成立，因为训练过程中并未直接强制一致性。我们同样观察到这一现象（参见可视化示例）并进行了量化分析（见图9(a)），这表明需要在学习中显式增强一致性。

Figure 2: Enforcing Cross-Task Consistency: (a) shows the typical multitask setup where predictions and $\scriptstyle\mathcal{X}\to\mathcal{Y}{2}$ are trained without a notation of consistency. (b) depicts the elementary triangle consistency constraint where the prediction is enforced to be consistent with $\scriptstyle\mathcal{X}\to\mathcal{Y}{2}$ using a function that relates ${\textrm{y}{1}}$ to ${\mathcal{V}{2}}$ (i.e. $y_{1}{\rightarrow}y_{2}$ ). (c) shows how the triangle unit from (b) can be an element of a larger system of domains. Finally, (d) illustrates the generalized case where in the larger system of domains, consistency can be enforced using invariance along arbitrary paths, as long as their endpoints are the same (here the blue and green paths). This is the general concept behind inference-path invariance. The triangle in (b) is the smallest unit of such paths.

图 2: 跨任务一致性约束: (a)展示典型的多任务设置，其中预测和$\scriptstyle\mathcal{X}\to\mathcal{Y}{2}$在没有一致性概念的情况下进行训练。(b)描述基础三角一致性约束，通过关联${\textrm{y}{1}}$和${\mathcal{V}{2}}$的函数(即$y_{1}{\rightarrow}y_{2}$)强制使预测与$\scriptstyle\mathcal{X}\to\mathcal{Y}_{2}$保持一致。(c)展示(b)中的三角单元如何成为更大领域系统的组成部分。(d)说明广义情况：在更大的领域系统中，只要路径端点相同(图中蓝色与绿色路径)，即可通过任意路径上的不变性来实施一致性。这是推理路径不变性背后的核心思想，而(b)中的三角是此类路径的最小单元。

Transfer learning predicts the output of a target task given another task’s solution as a source. The predictions made using transfer learning are sometimes assumed to be cross-task consistent, which is often found to not be the case [45, 36], as transfer learning does not have a specific mechanism to impose consistency by default. Unlike basic multi-task learning and transfer learning, the proposed method includes explicit mechanisms for learning with general data-driven consistency constraints.

迁移学习通过将一个任务的解决方案作为源来预测目标任务的输出。使用迁移学习做出的预测有时被假定为跨任务一致的，但实际情况往往并非如此 [45, 36]，因为迁移学习默认不具备强制一致性的特定机制。与基础的多任务学习和迁移学习不同，所提出的方法包含明确的机制，用于在通用数据驱动的一致性约束下进行学习。

Uncertainty metrics: Among the existing approaches to measuring prediction uncertainty, the proposed Consistency Energy (Sec. 4) is most related to Ensemble Averaging [24], with the key difference that the estimations in our ensemble are from different cues/paths, rather than retraining/reevaluating the same network with different random initi aliz at ions or parameters. Using multiple cues is expected to make the ensemble more effective at capturing uncertainty.

不确定性度量：在现有的预测不确定性测量方法中，提出的Consistency Energy（第4节）与Ensemble Averaging [24]最为相关，关键区别在于我们的集成估计来自不同线索/路径，而非通过不同随机初始化或参数重新训练/评估同一网络。使用多线索有望使集成在捕捉不确定性方面更有效。

3. Method

3. 方法

We define the problem as follows: suppose $\mathcal{X}$ denotes the query domain (e.g., RGB images) and $y={y_{1},...,y_{n}}$ is the set of $n$ desired prediction domains (e.g. normals, depth, objects, etc). An individual datapoint from domains $\left(x,y_{1},...,y_{n}\right)$ is denoted by $(x,y_{1},...,y_{n})$ . The goal is to learn functions that map the query domain onto the prediction domains, i.e. $\mathcal{F}{\boldsymbol{x}}={f_{\boldsymbol{x}\mathscr{y}{j}}|\boldsymbol{y}{j}\in\boldsymbol{y}}$ where $f_{x y_{j}}(x)$ out- puts $y_{j}$ given $x$ . We also define $\mathcal{F}{y}{=}{f_{\mathcal{V}{i}\mathcal{V}{j}}|y_{i},y_{j}{\in}y,i{\neq}j}$ , which is the set of ‘cross-task’ functions that map the prediction domains onto each other; we use them in the consistency constraints. For now assume $\mathcal{F}{y}$ is given apriori and frozen; in Sec. 3.3 we discuss all functions $f\mathrm{s}$ are neural networks in this paper, and we learn $\mathcal{F}{y}$ just like ${\mathcal{F}}_{\mathcal{X}}$ .

我们将问题定义如下：假设$\mathcal{X}$表示查询域（例如RGB图像），$y={y_{1},...,y_{n}}$是$n$个目标预测域（例如法线、深度、物体等）的集合。来自域$\left(x,y_{1},...,y_{n}\right)$的单个数据点记为$(x,y_{1},...,y_{n})$。目标是学习将查询域映射到预测域的函数，即$\mathcal{F}{\boldsymbol{x}}={f_{\boldsymbol{x}\mathscr{y}{j}}|\boldsymbol{y}{j}\in\boldsymbol{y}}$，其中$f_{x y_{j}}(x)$在给定$x$时输出$y_{j}$。我们还定义了$\mathcal{F}{y}{=}{f_{\mathcal{V}{i}\mathcal{V}{j}}|y_{i},y_{j}{\in}y,i{\neq}j}$，这是将预测域相互映射的"跨任务"函数集合，用于一致性约束。目前假设$\mathcal{F}{y}$是预先给定且固定的；在第3.3节中，我们将讨论本文中所有函数$f\mathrm{s}$都是神经网络，并且像${\mathcal{F}}{\mathcal{X}}$一样学习$\mathcal{F}_{y}$。

3.1. Triangle: The Elementary Consistency Unit

3.1. Triangle: 基本一致性单元

A common way of training neural networks in ${\mathcal{F}}{\mathcal{X}}$ , e.g. $f_{x y_{1}}(x)$ , is to find parameters of $f_{\boldsymbol{\mathcal{X}}\mathcal{y}{1}}$ that minimize a loss of the form $\left|f_{\chi y_{1}}(x)-y_{1}\right|$ using a common distance function as $|.|.$ , e.g. $\ell_{1}$ norm. This standard independent learning of $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{i}}\mathrm{s}$ satisfies various desirable properties, including crosstask consistency, if given infinite amount of data, but not under the practical finite data regime. This is shown in Fig. 3 (upper). Thus we introduce additional constraints to guide the training toward cross-task consistency. We define the loss for predicting domain $y_{1}$ from $\mathcal{X}$ while enforcing consistency with domain $y_{2}$ as a directed triangle depicted in Fig. 2(b):

在 ${\mathcal{F}}{\mathcal{X}}$ 中训练神经网络的常见方法，例如 $f_{x y_{1}}(x)$，是通过寻找 $f_{\boldsymbol{\mathcal{X}}\mathcal{y}{1}}$ 的参数，以最小化形如 $\left|f_{\chi y_{1}}(x)-y_{1}\right|$ 的损失，并使用常见的距离函数如 $|.|.$，例如 $\ell_{1}$ 范数。这种对 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{i}}\mathrm{s}$ 的标准独立学习在给定无限数据量时满足包括跨任务一致性在内的各种理想特性，但在实际有限数据情况下则不然。如图 3（上）所示。因此，我们引入额外的约束来引导训练实现跨任务一致性。我们将从 $\mathcal{X}$ 预测域 $y_{1}$ 同时强制与域 $y_{2}$ 一致的损失定义为图 2(b) 中所示的有向三角形：

Figure 3: Impact of disregarding cross-task consistency in learning, illustrated using surface normals domain. Each subfigure shows the results of predicting surface normals out of the prediction of an intermediate domain; using the notation $x{\to}y_{1}{\to}y_{2}$ , here ${\mathscr{X}}$ is RGB image, ${3/2}$ is surface normals, and each column represents a different ${\gg_{1}}$ . The upper row demonstrates the normals are noisy and dissimilar when cross-task consistency is not incorporated in learning of networks. Whereas enforcing consistency when learning results in more consistent and better normals (the lower row). We will show this causes the predictions for the intermediate domains themselves to be more accurate and consistent. More examples available in supplementary material. The Consistency Energy (Sec. 4) captures the variance among predictions in each row.

图 3: 忽略跨任务一致性对学习的影响，以表面法线域为例进行说明。每个子图展示了通过中间域预测结果推导表面法线的效果；使用符号$x{\to}y_{1}{\to}y_{2}$表示，其中${\mathscr{X}}$为RGB图像，${3/2}$为表面法线，每列代表不同的。上排显示当网络学习过程中未纳入跨任务一致性时，法线预测结果存在噪声且不一致。而下排表明在学习时强制保持一致性，可获得更一致且更优的法线结果。我们将证明这会使中间域自身的预测更准确和一致。补充材料提供更多示例。一致性能量（第4节）量化了每行预测结果的方差。

$$
\mathcal{L}{\chi\nu_{1}\nu_{2}}^{t r i a n g l e}\triangleq\left|f_{\chi\nu_{1}}(x)-y_{1}|+|f_{\mathcal{V}{1}\mathcal{V}{2}}\circ f_{\chi\nu_{1}}(x)-f_{\chi\nu_{2}}(x)|+|f_{\chi\nu_{2}}(x)-y_{2}|.\right.
$$

$$
\mathcal{L}{\chi\nu_{1}\nu_{2}}^{t r i a n g l e}\triangleq\left|f_{\chi\nu_{1}}(x)-y_{1}|+|f_{\mathcal{V}{1}\mathcal{V}{2}}\circ f_{\chi\nu_{1}}(x)-f_{\chi\nu_{2}}(x)|+|f_{\chi\nu_{2}}(x)-y_{2}|.\right.
$$

The first and last terms are the standard direct losses for training $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ and $f_{\boldsymbol{{x y}}{2}}$ . The middle term is the consistency term which enforces predicting $y_{2}$ out of the predicted $y_{1}$ yields the same result as directly predicting $y_{2}$ out of $\chi^{4}$ . Thus learning to predict $y_{1}$ and $y_{2}$ are not independent anymore.

首尾两项分别是训练 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ 和 $f_{\boldsymbol{{x y}}{2}}$ 的标准直接损失。中间项是一致性约束项，强制要求通过预测出的 $y_{1}$ 来预测 $y_{2}$ 的结果，应与直接从 $\chi^{4}$ 预测 $y_{2}$ 的结果一致。因此学习预测 $y_{1}$ 和 $y_{2}$ 的过程不再相互独立。

The triangle loss 1 is the smallest unit of enforcing crosstask consistency. Below we make two improving modifications on it via function ‘se par ability’ and ‘perceptual losses’.

三角损失1是实施跨任务一致性的最小单元。下面我们通过函数的"可分性"和"感知损失"对其进行两项改进。

3.1.1 Se par ability of Optimization Parameters

3.1.1 优化参数的可分离性

The loss $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{t r i a n g l e}$ involves simultaneous training of two networks $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ and $f_{\boldsymbol{{x y}}_{2}}$ , thus it is resource demanding. We show Ltriangle can be reduced to a ‘separable’ function [39] resulting in two terms that can be optimized independently.

损失 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{triangle}$ 涉及同时训练两个网络 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ 和 $f_{\boldsymbol{{x y}}_{2}}$ ，因此对资源要求较高。我们证明 Ltriangle 可简化为一个"可分离"函数 [39]，从而得到两个可独立优化的项。

From triangle inequality we can derive:

由三角不等式可得：

$$
\mid f_{y_{1}y_{2}}\circ f_{x y_{1}}(x)-f_{x y_{2}}(x)\mid\leq\mid f_{y_{1}y_{2}}\circ f_{x y_{1}}(x)-y_{2}\mid+\mid f_{x y_{2}}(x)-y_{2}\mid,
$$

$$
\mid f_{y_{1}y_{2}}\circ f_{x y_{1}}(x)-f_{x y_{2}}(x)\mid\leq\mid f_{y_{1}y_{2}}\circ f_{x y_{1}}(x)-y_{2}\mid+\mid f_{x y_{2}}(x)-y_{2}\mid,
$$

which after substitution in Eq. 1 yields:

代入式1后可得：

$$
\mathcal{L}{\chi\ni_{1}\chi_{2}}^{t r i a n g l e}\leq\left|f_{\chi\ni_{1}}(x)-y_{1}\right|+\left|f_{\mathcal{V}{1}\mathcal{V}{2}}\circ f_{\chi_{\mathcal{V}{1}}}(x)-y_{2}\right|+2\left|f_{\chi\mathcal{V}{2}}(x)-y_{2}\right|.
$$

$$
\mathcal{L}{\chi\ni_{1}\chi_{2}}^{t r i a n g l e}\leq\left|f_{\chi\ni_{1}}(x)-y_{1}\right|+\left|f_{\mathcal{V}{1}\mathcal{V}{2}}\circ f_{\chi_{\mathcal{V}{1}}}(x)-y_{2}\right|+2\left|f_{\chi\mathcal{V}{2}}(x)-y_{2}\right|.
$$

The upper bound for $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{t r i a n g l e}$ in inequality 2 can be optimized in lieu of $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{t r i a n g l e}$ its1el2f, as they both have the same minimizer.5 The terms of this bound include either $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}_{1}}$

不等式2中 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{triangle}$ 的上界可以替代 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{triangle}$ 本身进行优化，因为两者具有相同的最小化点。该上界的各项包含 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}_{1}}$

or $f_{\boldsymbol{{x y}}{2}}$ , but not both, hence we now have a loss separable into functions of $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ or $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{Y}}{2}}$ , and they can be optimized independently. The part pertinent to the network $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}_{1}}$ is:

或 $f_{\boldsymbol{{x y}}{2}}$，但不能同时优化两者，因此现在我们可以将损失函数分离为 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ 或 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{Y}}{2}}$ 的函数，并且可以独立优化。与网络 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}_{1}}$ 相关的部分为：

$$
\mathcal{L}{x y_{1}y_{2}}^{s e p a r a t e}\overset{\Delta}{=}|f_{x y_{1}}(x)-y_{1}|+|f_{y_{1}y_{2}\circ{}}f_{x y_{1}}(x)-y_{2}|,
$$

$$
\mathcal{L}{x y_{1}y_{2}}^{s e p a r a t e}\overset{\Delta}{=}|f_{x y_{1}}(x)-y_{1}|+|f_{y_{1}y_{2}\circ{}}f_{x y_{1}}(x)-y_{2}|,
$$

named separate, as we reduced the closed triangle objective $\chi\stackrel{\star_{1}}{\Delta}y_{2}$ ${\textrm{y}{1}}$ in Eq. 1 to two equivalent separate path objectives $x{\to}y_{1}{\to}y_{2}$ and $\chi{\rightarrow}{\gg}{2}$ . The first term of Eq. 3 enforces the general correctness of predicting $y_{1}$ , and the second term enforces its consistency with $_{\mathcal{V}2}$ domain.

将闭合三角形目标 $\chi\stackrel{\star_{1}}{\Delta}y_{2}$ ${\textrm{y}{1}}$ 在公式1中拆分为两个等效的独立路径目标 $x{\to}y_{1}{\to}y_{2}$ 和 $\chi{\rightarrow}{\gg}{2}$ 。公式3的第一项确保预测 $y_{1}$ 的总体正确性，第二项强制其与 $_{\mathcal{V}2}$ 域的一致性。

3.1.2 Reconfiguration into a “Perceptual Loss”

3.1.2 重构为"感知损失"

Training $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ using the loss $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{s e p a r a t e}$ requires a training dataset with multi domain annotations for one input: $(x,y_{1},y_{2})$ . It also relies on availability of a perfect function $f_{y_{1}y_{2}}$ for mapping $y_{1}$ onto $y_{2}$ ; i.e. it demands $y_{2}{=}f_{y_{1}y_{2}}(y_{1})$ . We show how these two requirements can be reduced.

使用损失函数 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{separate}$ 训练 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ 需要一个包含多领域标注的训练数据集：$(x,y_{1},y_{2})$。该方法还依赖于存在一个完美映射函数 $f_{y_{1}y_{2}}$ 能将 $y_{1}$ 映射到 $y_{2}$，即要求满足 $y_{2}{=}f_{y_{1}y_{2}}(y_{1})$。我们将展示如何降低这两个条件的要求。

Again, from triangle inequality we can derive:

根据三角不等式可推导出：

$$
\begin{array}{r}{|f_{y_{1}y_{2}}\circ f_{x y_{1}}(x)-y_{2}|{\leq}|f_{y_{1}y_{2}}\circ f_{x y_{1}}(x)-f_{y_{1}y_{2}}(y_{1})|+}\ {|f_{y_{1}y_{2}}(y_{1})-y_{2}|,\quad\quad}\end{array}
$$

$$
\begin{array}{r}{|f_{y_{1}y_{2}}\circ f_{x y_{1}}(x)-y_{2}|{\leq}|f_{y_{1}y_{2}}\circ f_{x y_{1}}(x)-f_{y_{1}y_{2}}(y_{1})|+}\ {|f_{y_{1}y_{2}}(y_{1})-y_{2}|,\quad\quad}\end{array}
$$

which after substitution in Eq. 3 yields:

代入式3后可得：

$$
\begin{array}{r l r}&{}&{\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{s e p a r a t e}\leq|f_{\mathcal{X}\mathcal{Y}{1}}(x)-y_{1}|+|f_{\mathcal{Y}{1}\mathcal{Y}{2}}\circ f_{\mathcal{X}\mathcal{Y}{1}}(x)-f_{\mathcal{Y}{1}\mathcal{Y}{2}}(y_{1})|+}\ &{}&{|f_{\mathcal{Y}{1}\mathcal{Y}{2}}(y_{1})-y_{2}|.~(5)}\end{array}
$$

$$
\begin{array}{r l r}&{}&{\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{s e p a r a t e}\leq|f_{\mathcal{X}\mathcal{Y}{1}}(x)-y_{1}|+|f_{\mathcal{Y}{1}\mathcal{Y}{2}}\circ f_{\mathcal{X}\mathcal{Y}{1}}(x)-f_{\mathcal{Y}{1}\mathcal{Y}{2}}(y_{1})|+}\ &{}&{|f_{\mathcal{Y}{1}\mathcal{Y}{2}}(y_{1})-y_{2}|.~(5)}\end{array}
$$

Similar to the discussion for inequality 2, the upper bound in inequality 5 can be optimized in lieu of $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{s e p a r a t e}$ as both have the same minimizer.6 As the last term is a constant w.r.t. $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ , the final loss for training $f_{\boldsymbol{x}\boldsymbol{y}_{1}}$ is:

类似于对不等式2的讨论，不等式5的上界可以代替$\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{separate}$进行优化，因为两者具有相同的最小化目标。由于最后一项相对于$f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$是常数，因此训练$f_{\boldsymbol{x}\boldsymbol{y}_{1}}$的最终损失为：

$$
\mathcal{L}{\boldsymbol{x}\boldsymbol{y}{1}\boldsymbol{y}{2}}^{p e n e n t a l}\overset{\triangle}{=}\big|f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-\boldsymbol{y}{1}\big|+\big|f_{\boldsymbol{y}{1}\boldsymbol{y}{2}}\circ f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-f_{\boldsymbol{y}{1}\boldsymbol{y}{2}}(\boldsymbol{y}_{1})\big|.
$$

$$
\mathcal{L}{\boldsymbol{x}\boldsymbol{y}{1}\boldsymbol{y}{2}}^{p e n e n t a l}\overset{\triangle}{=}\big|f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-\boldsymbol{y}{1}\big|+\big|f_{\boldsymbol{y}{1}\boldsymbol{y}{2}}\circ f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-f_{\boldsymbol{y}{1}\boldsymbol{y}{2}}(\boldsymbol{y}_{1})\big|.
$$

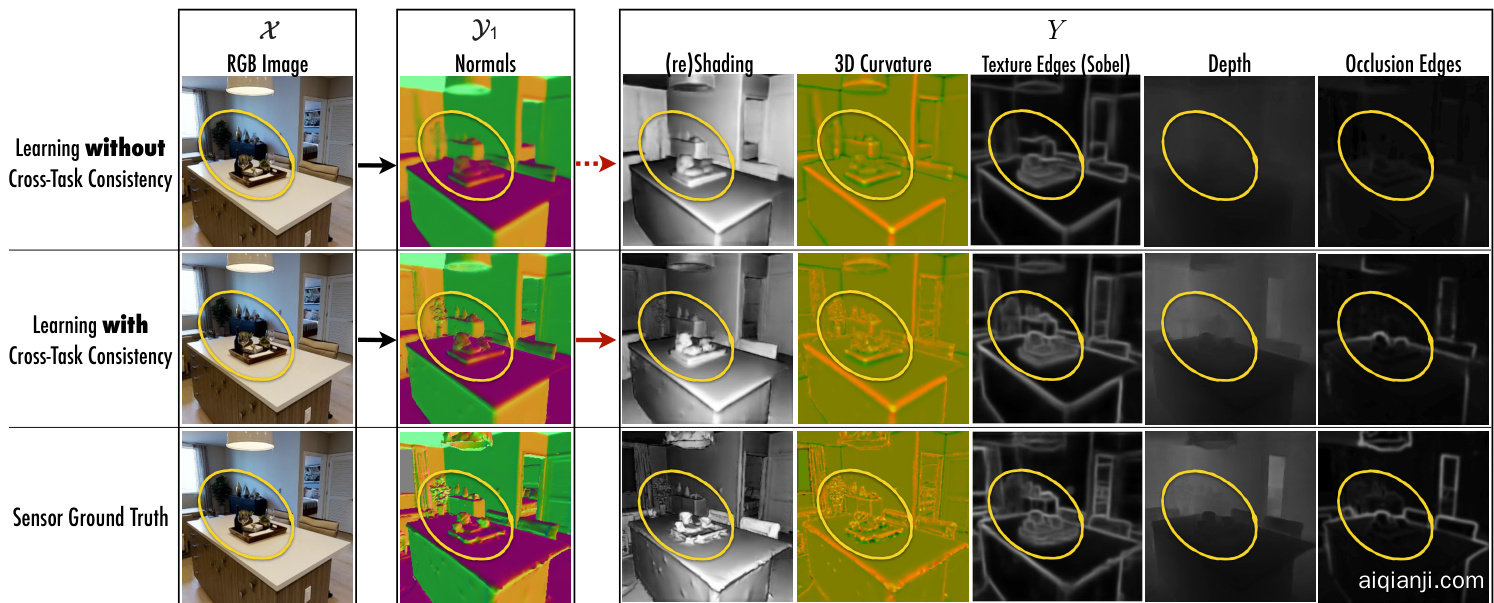
Figure 4: Learning with and without cross-task consistency shown for a sample query. Using the notation $x{\to}y_{1}{\to}Y$ , here ${\mathscr{X}}$ is RGB image, ${\textrm{y}{1}}$ is surface normals, and five domains in $Y$ are reshading, 3D curvature, texture edges (Sobel filter), depth, and occlusion edges. Top row shows the results of standard training of . After convergence of training, the predicted normals $(y_{1})$ are projected onto other domains $(Y)$ which reveals various inaccuracies. This demonstrates such cross-task projections $y_{1}\xrightarrow{}Y$ can provide additional cues to training ${\mathcal{X}}{\rightarrow}\mathcal{D}{1}$ . Middle row shows the results of consistent training of by leveraging $y_{1}\xrightarrow{}Y$ in the loss. The predicted normals are notably improved, especially in hard to predict fine-grained details (zoom into the yellow markers. Best seen on screen). Bottom row provides the ground truth. See video examples at visualization s webpage.

图 4: 展示样本查询中使用与未使用跨任务一致性的学习效果。采用符号$x{\to}y_{1}{\to}Y$表示，其中${\mathscr{X}}$为RGB图像，${\textrm{y}{1}}$为表面法线，$Y$中的五个域分别为重着色、3D曲率、纹理边缘(Sobel滤波器)、深度和遮挡边缘。首行显示标准训练的结果。训练收敛后，预测的法线$(y_{1})$被投影到其他域$(Y)$，暴露出多种不准确性。这表明跨任务投影$y_{1}\xrightarrow{}Y$能为训练${\mathcal{X}}{\rightarrow}\mathcal{D}{1}$提供额外线索。中间行显示通过损失函数利用$y_{1}\xrightarrow{}Y$实现一致性训练的结果，预测法线明显改善，尤其在难以预测的细粒度细节处(放大黄色标记处效果更佳)。末行为真实值。参见可视化网页中的视频示例。

This term $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{{p e r c e p t u a l}}$ no longer includes $y_{2}$ , hence it admits pair training data $(x,y_{1})$ rather than triplets $(x,y_{1},y_{2})$ . Comparing $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{{p e r c e p t u a l}}$ and $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{s e p a r a t e}$ shows the modification boiled down to replacing $y_{2}$ with $\tilde{f}{y_{1}y_{2}}(y_{1})$ . This makes intuitive sense too, as $y_{2}$ is the match of $y_{1}$ in the $y_{2}$ domain.

术语 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{{p e r c e p t u a l}}$ 不再包含 $y_{2}$，因此它接受配对训练数据 $(x,y_{1})$ 而非三元组 $(x,y_{1},y_{2})$。比较 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{{p e r c e p t u a l}}$ 和 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{s e p a r a t e}$ 可以看出，修改的本质是用 $\tilde{f}{y_{1}y_{2}}(y_{1})$ 替换了 $y_{2}$。这也符合直观理解，因为 $y_{2}$ 是 $y_{1}$ 在 $y_{2}$ 域中的对应匹配。

Ill-posed tasks and imperfect networks: If $f_{y_{1}y_{2}}$ is a noisy estimator, then $f_{y_{1}y_{2}}(y_{1}){=}y_{2}{+}n o i s e$ rather than $f_{y_{1}y_{2}}(y_{1}){=}y_{2}$ . Using a noisy $f_{y_{1}y_{2}}$ in $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{s e p a r a t e}$ corrupts the training of $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ since the second loss term does not reach 0 if $f_{x y_{1}}(x)$ correctly outputs $y_{1}$ . That is in contrast to $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{{p e r c e p t u a l}}$ where both terms have the same global minimum and are always 0 if $f_{x y_{1}}(x)$ outputs $y_{1}$ – even when $f_{y_{1}y_{2}}(y_{1}){=}y_{2}{+}n o i s e$ . This is crucial since neural networks are almost never perfect estimators, e.g. due to lacking an optimal training process for them or potential ill-posedness of the task $y_{1}\rightarrow y_{2}$ . Further discussion and experiments are available in supplementary material.

不适定任务与不完美网络：如果 $f_{y_{1}y_{2}}$ 是一个带噪声的估计器，则 $f_{y_{1}y_{2}}(y_{1}){=}y_{2}{+}n o i s e$ 而非 $f_{y_{1}y_{2}}(y_{1}){=}y_{2}$。在 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{s e p a r a t e}$ 中使用带噪声的 $f_{y_{1}y_{2}}$ 会破坏 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ 的训练，因为当 $f_{x y_{1}}(x)$ 正确输出 $y_{1}$ 时，第二损失项不会归零。这与 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{{p e r c e p t u a l}}$ 形成对比——后者两项具有相同的全局最小值，且当 $f_{x y_{1}}(x)$ 输出 $y_{1}$ 时总能归零（即使 $f_{y_{1}y_{2}}(y_{1}){=}y_{2}{+}n o i s e$）。这一特性至关重要，因为神经网络几乎不可能是完美估计器（例如由于训练过程未达最优，或任务 $y_{1}\rightarrow y_{2}$ 本身可能不适定）。补充材料提供了进一步讨论与实验。

Perceptual Loss: The process that led to Eq. 6 can be generally seen as using the loss $\left|g\circ f(x)-g(y)\right|$ instead of $\left|f(x)-y\right|$ . The latter compares $f(x)$ and $y$ in their explicit space, while the former compares them via the lens of function $g$ . This is often referred to as “perceptual loss” in superresolution and style transfer literature [19]–where two images are compared in the representation space of a network pretrained on ImageNet, rather than in pixel space. Similarly, the consistency constraint between the domains $y_{1}$ and $y_{2}$ in Eq. 6 (second term) can be viewed as judging the prediction $f_{x y_{1}}(x)$ against $y_{1}$ via the lens of the network $f_{y_{1}y_{2}}$ ; here $f_{y_{1}y_{2}}$ is a “perceptual loss” for training $f_{\boldsymbol{\mathcal{X}}\mathcal{y}{1}}$ . However, unlike the ImageNet-based perceptual loss [19], this function has the specific and interpret able job of enforcing consistency with another task. We also use multiple $f_{y_{1}y_{i}}\mathbf{s}$ simultaneously which enforces consistency of predicting $y_{1}$ against multiple other domains (Sections 3.2 and 3.3).

感知损失 (Perceptual Loss)：推导出公式6的过程可以概括为使用损失函数$\left|g\circ f(x)-g(y)\right|$替代$\left|f(x)-y\right|$。后者在显式空间中直接比较$f(x)$和$y$，而前者通过函数$g$的视角进行比较。这种损失在超分辨率和风格迁移文献[19]中常被称为"感知损失"——此时两个图像是在ImageNet预训练网络的表征空间而非像素空间进行比较。类似地，公式6中域$y_{1}$和$y_{2}$间的一致性约束（第二项）可视为通过网络$f_{y_{1}y_{2}}$的视角来评判预测值$f_{x y_{1}}(x)$与$y_{1}$的匹配程度；此处$f_{y_{1}y_{2}}$就是用于训练$f_{\boldsymbol{\mathcal{X}}\mathcal{y}{1}}$的"感知损失"。但与基于ImageNet的感知损失[19]不同，该函数具有明确且可解释的职责——强制与其他任务保持一致性。我们还同时使用多个$f_{y_{1}y_{i}}\mathbf{s}$，通过多个其他域来强化$y_{1}$预测的一致性（见3.2和3.3节）。

Figure 5: Schematic summary of derived losses for $f_{\boldsymbol{\mathcal{X}}\mathscr{y}{1}}$ .(a): $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{t r i a n g l e}$ (Eq.1). (b): (Eq.3). (c): (Eq.6). (d): $\mathcal{L}{\mathcal{X Y}_{1}Y}^{p e r c e p t u a l}$ (Eq.7).

图 5: $f_{\boldsymbol{\mathcal{X}}\mathscr{y}{1}}$ 派生损失示意图。(a): $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{t r i a n g l e}$ (公式1)。(b): (公式3)。(c): (公式6)。(d): $\mathcal{L}{\mathcal{X Y}_{1}Y}^{p e r c e p t u a l}$ (公式7)。

3.2. Consistency of with ‘Multiple’ Domains

3.2. 与"多"领域的一致性

The derived $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{{p e r c e p t u a l}}$ loss augments learning of $f_{\boldsymbol{\mathcal{X}}\mathcal{y}{1}}$ with a consistency constraint against one domain $y_{2}$ . Straight forward extension of the same derivation to enforcing consistency of $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ against multiple other domains (i.e. when $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}_{1}}$ is part of multiple simultaneous triangles) yields:

推导出的 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}{2}}^{{perceptual}}$ 损失通过针对一个域 $y_{2}$ 的一致性约束增强了 $f_{\boldsymbol{\mathcal{X}}\mathcal{y}{1}}$ 的学习。将相同推导直接扩展到强制 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ 对多个其他域的一致性（即当 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}_{1}}$ 是多个同时存在的三角形的一部分时）可得到：

$$
\mathcal{L}{\boldsymbol{x}\boldsymbol{y}{1}\boldsymbol{Y}}^{p e r c e p t u a l}\overset{\Delta}{=}|\boldsymbol{Y}|\times|f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-\boldsymbol{y}{1}|+\sum_{\boldsymbol{y}{i}\in\boldsymbol{Y}}|f_{\boldsymbol{y}{1}\boldsymbol{y}{i}}\circ f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-f_{\boldsymbol{y}{1}\boldsymbol{y}{i}}(\boldsymbol{y}_{1})|,
$$

$$
\mathcal{L}{\boldsymbol{x}\boldsymbol{y}{1}\boldsymbol{Y}}^{p e r c e p t u a l}\overset{\Delta}{=}|\boldsymbol{Y}|\times|f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-\boldsymbol{y}{1}|+\sum_{\boldsymbol{y}{i}\in\boldsymbol{Y}}|f_{\boldsymbol{y}{1}\boldsymbol{y}{i}}\circ f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-f_{\boldsymbol{y}{1}\boldsymbol{y}{i}}(\boldsymbol{y}_{1})|,
$$

where $Y$ is the set of domains with which $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ must be consai sstpeencti, aal ncda $|Y|$ fi $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}Y}^{p e r c e p t u a l}$ rd wi h near liet $Y{=}{y_{2}}$ $Y$ .o tFiicge. t5h satu $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}_{2}}^{{p e r c e p t u a l}}$ eiss the derivation of losses for fXY .

其中 $Y$ 是 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ 必须保持一致的域集合，且 $|Y|$ 当 $Y{=}{y_{2}}$ 时 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}Y}^{p e r c e p t u a l}$ 退化为 $\mathcal{L}{\mathcal{X}\mathcal{Y}{1}\mathcal{Y}_{2}}^{{p e r c e p t u a l}}$ ，这是针对 fXY 的损失函数推导。

Fig. 4 shows qualitative results of learning $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}_{1}}$ with and without cross-task consistency for a sample query.

图 4: 展示了在有/无跨任务一致性的情况下，针对示例查询学习 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}_{1}}$ 的定性结果。

3.3. Beyond Triangles: Globally Consistent Graphs

3.3. 超越三角形：全局一致的图

The discussion so far has provided losses for the crosstask consistent training of one function $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ with elementary triangle based units. We also assumed the functions $\mathcal{F}{y}$ were given apriori. The more general multi-task setup is: given a large set of domains, we are interested in learning functions that map the domains onto each other in a globally cross-task consistent manner. This objective can be formulated using a graph $\scriptstyle{\mathcal{G}}=({\mathcal{D}},{\mathcal{F}})$ with nodes representing all of the domains $\scriptstyle{\mathcal{D}}=(x\cup y)$ and edges being neural networks between them $\mathcal{F}{=}(\mathcal{F}{\mathcal{X}}\cup\mathcal{F}_{\mathcal{Y}})$ ; see Fig.2(c).

目前的讨论已为基于基本三角单元的函数 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ 的跨任务一致性训练提供了损失函数。我们还假设函数 $\mathcal{F}{y}$ 是预先给定的。更一般的多任务设置是：给定一个庞大的领域集合，我们希望学习能够以全局跨任务一致的方式将这些领域相互映射的函数。这一目标可以通过图 $\scriptstyle{\mathcal{G}}=({\mathcal{D}},{\mathcal{F}})$ 来表述，其中节点代表所有领域 $\scriptstyle{\mathcal{D}}=(x\cup y)$，边则是它们之间的神经网络 $\mathcal{F}{=}(\mathcal{F}{\mathcal{X}}\cup\mathcal{F}_{\mathcal{Y}})$；见图2(c)。

Extension to Arbitrary Paths: The transition from three domains to a large graph $\mathcal{G}$ enables forming more general consistency constraints using arbitrary-paths. That is, two paths with same endpoint should yield the same results – an example is shown in Fig.2(d). The triangle constraint in Fig.2(b,c) is a special and elementary case of the more general constraint in Fig.2(d), if paths with lengths 1 and 2 are picked for the green and blue paths. Extending the derivations done for a triangle in Sec. 3.1 to paths yields:

扩展到任意路径：从三个领域到大型图 $\mathcal{G}$ 的转变，使得我们能够利用任意路径形成更一般的约束条件。具体而言，两条具有相同终点的路径应当产生相同的结果——图2(d)展示了一个示例。若选择长度为1和2的路径分别作为绿色和蓝色路径，那么图2(b,c)中的三角约束实际上是图2(d)中更一般约束的特殊基础情形。将3.1节中对三角形的推导拓展到路径情形，可得到：

$$
\begin{array}{c}{{\mathcal{L}{\boldsymbol{x}\boldsymbol{y}{1}\boldsymbol{y}{2}...\boldsymbol{y}{k}}^{p e r e p t u a l}=|f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-\boldsymbol{y}{1}|+}}\ {{|f_{\boldsymbol{y}{k-1}\boldsymbol{y}{k}}\circ...\circ f_{\boldsymbol{y}{1}\boldsymbol{y}{2}}\circ f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-f_{\boldsymbol{y}{k-1}\boldsymbol{y}{k}}\circ...\circ f_{\boldsymbol{y}{1}\boldsymbol{y}{2}}(\boldsymbol{y}_{1})|,}}\end{array}
$$

$$
\begin{array}{c}{{\mathcal{L}{\boldsymbol{x}\boldsymbol{y}{1}\boldsymbol{y}{2}...\boldsymbol{y}{k}}^{p e r e p t u a l}=|f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-\boldsymbol{y}{1}|+}}\ {{|f_{\boldsymbol{y}{k-1}\boldsymbol{y}{k}}\circ...\circ f_{\boldsymbol{y}{1}\boldsymbol{y}{2}}\circ f_{\boldsymbol{x}\boldsymbol{y}{1}}(\boldsymbol{x})-f_{\boldsymbol{y}{k-1}\boldsymbol{y}{k}}\circ...\circ f_{\boldsymbol{y}{1}\boldsymbol{y}{2}}(\boldsymbol{y}_{1})|,}}\end{array}
$$

which is the loss for training $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ using the arbitrary consistency path $\mathcal{X}{\rightarrow}\mathcal{Y}{1}{\rightarrow}\mathcal{Y}{2}{\leftarrow}{\rightarrow}\mathcal{Y}{k}$ with length $k$ (full derivation provided in supplementary material). Notice that Eq. 6 is a special case of Eq. 8 if $k{=}2$ . Equation 8 is particularly useful for incomplete graphs; if the function $y_{1}\rightarrow y_{k}$ is missing, consistency between domains $y_{1}$ and $y_{k}$ can still be enforced via transitivity through other domains using Eq. 8.

这是用于训练 $f_{\boldsymbol{\mathcal{X}}\boldsymbol{\mathcal{y}}{1}}$ 的损失函数，其中使用了长度为 $k$ 的任意一致性路径 $\mathcal{X}{\rightarrow}\mathcal{Y}{1}{\rightarrow}\mathcal{Y}{2}{\leftarrow}{\rightarrow}\mathcal{Y}{k}$（完整推导见补充材料）。值得注意的是，当 $k{=}2$ 时，式(6) 是式(8) 的特例。式(8) 对于不完整图特别有用：如果函数 $y_{1}\rightarrow y_{k}$ 缺失，仍然可以通过式(8) 借助其他域的传递性来强制实现域 $y_{1}$ 和 $y_{k}$ 之间的一致性。

Also, extending Eq. 8 to multiple simultaneous paths (as in Eq. 7) by summing the path constraints is straightforward.

此外，通过对路径约束求和，将方程8扩展到多条同时存在的路径（如方程7所示）是直接可行的。

Global Consistency Objective: We define reaching global cross-task consistency for graph $\mathcal{G}$ as satisfying the consistency constraint for all feasible paths in $\mathcal{G}$ . We can write the global consistency objective for $\mathcal{G}$ as $\mathcal{L}{\mathcal{G}}=$ $\textstyle\sum_{p\in{\mathcal{P}}}\mathcal{L}_{p}^{p e r c e p t u a l}$ , where $p$ represents a path and $\mathcal{P}$ is the set of all feasible paths in $\mathcal{G}$ .

全局一致性目标：我们定义图 $\mathcal{G}$ 达到全局跨任务一致性为满足 $\mathcal{G}$ 中所有可行路径的一致性约束。可以将 $\mathcal{G}$ 的全局一致性目标表示为 $\mathcal{L}{\mathcal{G}}=$ $\textstyle\sum_{p\in{\mathcal{P}}}\mathcal{L}_{p}^{perceptual}$，其中 $p$ 表示路径，$\mathcal{P}$ 是 $\mathcal{G}$ 中所有可行路径的集合。

Optimizing the objective $\mathcal{L}{\mathcal{G}}$ directly is intractable as it would require simultaneous training of all networks in $\mathcal{F}$ with a massive number of consistency paths7. In Alg.1 we devise a straightforward training schedule for an approximate optimization of $\mathcal{L}_{\mathcal{G}}$ . This problem is similar to inference in graphical models, where one is interested in marginal distribution of unobserved nodes given some observed nodes by passing “messages” between them through the graph until convergence. As exact inference is usually intractable for un constrained graphs, often an approximate message passing algorithm with various heuristics is used.

直接优化目标函数 $\mathcal{L}{\mathcal{G}}$ 是不可行的，因为这需要同时训练 $\mathcal{F}$ 中所有网络并处理海量一致性路径7。在算法1中，我们设计了一种简单的训练方案来近似优化 $\mathcal{L}_{\mathcal{G}}$。该问题类似于图模型中的推理过程，即通过节点间传递"消息"直至收敛，从而根据已观测节点推断未观测节点的边缘分布。由于无约束图结构通常难以进行精确推理，实践中常采用启发式近似消息传递算法。

Algorithm 1 selects one network $f_{i j}\in\mathcal{F}$ to be trained, selects consistency path(s) $p{\in}\mathcal{P}$ for it, and trains $f_{i j}$ with $p$ for a fixed number of steps using loss 8