Direct3D-S2: Gigascale 3D Generation Made Easy with Spatial Sparse Attention
Direct3D-S2:基于空间稀疏注意力 (Spatial Sparse Attention) 的十亿级3D生成简易方案

Figure 1. Mesh generation results from our method on different input images. Our method can generate detailed and complex 3D shapes The meshes show fine geometry and high visual quality, demonstrating the strength of our approach for high-resolution 3D generation.
图 1: 我们的方法在不同输入图像上的网格生成结果。该方法能生成细节丰富且复杂的三维形状,所展示的网格具有精细几何结构和高度视觉保真度,体现了本方法在高分辨率三维生成方面的优势。
Abstract
摘要
Generating high-resolution $3D$ shapes using volumetric representations such as Signed Distance Functions (SDFs) presents substantial computational and memory challenges. We introduce Direct3D-S2, a scalable 3D generation framework based on sparse volumes that achieves superior output quality with dramatically reduced training costs. Our key innovation is the Spatial Sparse Attention (SSA) mechanism, which greatly enhances the efficiency of Diffusion Transformer (DiT) computations on sparse volumetric data. SSA allows the model to effectively process large token sets within sparse volumes, substantially reducing computational overhead and achieving a $3.9\times$ speedup in the forward pass and a $9.6\times$ speedup in the backward pass. Our framework also includes a variation al auto encoder (VAE) that maintains a consistent sparse volumetric format across input, latent, and output stages. Compared to previous methods with heterogeneous representations in 3D VAE, this unified design significantly improves training efficiency and stability. Our model is trained on public available datasets, and experiments demonstrate that Direct3D-S2 not only surpasses state-of-the-art methods in generation quality and efficiency, but also enables training at $\mathbf{\Delta}I\pmb{0}24^{3}$ resolution using only 8 GPUs, a task typically requiring at least 32 GPUs for volumetric representations at $256^{3}$ resolution, thus making gigascale 3D generation both practical and accessible. Project page: https://www.neural4d.com/research/direct3d-s2.
使用带符号距离函数(SDFs)等体积表示生成高分辨率$3D$形状存在巨大的计算和内存挑战。我们提出Direct3D-S2——一个基于稀疏体素的可扩展3D生成框架,能以显著降低的训练成本实现卓越输出质量。核心创新是空间稀疏注意力(SSA)机制,该机制极大提升了Diffusion Transformer(DiT)在稀疏体素数据上的计算效率。SSA使模型能高效处理稀疏体素中的大规模token集,计算开销大幅降低,前向传播速度提升$3.9\times$,反向传播速度提升$9.6\times$。该框架还包含变分自编码器(VAE),在输入/隐变量/输出阶段均保持一致的稀疏体素格式。相比先前3D VAE中采用异构表示的方法,这种统一设计显著提升了训练效率和稳定性。模型在公开数据集上训练,实验表明Direct3D-S2不仅在生成质量和效率上超越现有最优方法,还能仅用8块GPU完成$\mathbf{\Delta}I\pmb{0}24^{3}$分辨率训练,而传统体素表示在$256^{3}$分辨率下至少需要32块GPU,使得十亿级3D生成既实用又可行。项目页面:https://www.neural4d.com/research/direct3d-s2。
1. Introduction
1. 引言
Generating high-quality 3D models directly from text or images offers significant creative potential, enabling rapid 3D content creation for virtual worlds, product prototyping, and various real-world applications. This capability has garnered increasing attention across domains such as gaming, virtual reality, robotics, and computer-aided design.
从文本或图像直接生成高质量3D模型具有巨大的创作潜力,能够为虚拟世界、产品原型设计和各类现实应用快速创建3D内容。这一能力在游戏、虚拟现实、机器人技术和计算机辅助设计等领域获得了越来越多的关注。
Recently, large-scale 3D generative models based on implicit latent representations have made notable progress. These methods leverage neural fields for shape representation, benefiting from compact latent codes and scalable generation capabilities. For instance, 3 D Shape 2 Vec set [47] pioneered diffusion-based shape synthesis by using a Variational Auto encoder (VAE) [14] to encode 3D shapes into a latent vecset, which can be decoded into neural SDFs or occupancy fields and rendered via Marching Cubes [24]. The latent vecset is then modeled with a diffusion process to generate diverse 3D shapes. CLAY [49] extended this pipeline with Diffusion Transformers (DiT) [30], while TripoSG [18] further improved fidelity through rectified flow transformers and hybrid supervision. However, implicit latent-based methods often rely on VAEs with asymmetric 3D representations, resulting in lower training efficiency that typically requires hundreds of GPUs.
近年来,基于隐式潜在表征的大规模3D生成模型取得了显著进展。这些方法利用神经场进行形状表征,得益于紧凑的潜在编码和可扩展的生成能力。例如,3D Shape2VecSet [47] 开创性地使用变分自编码器 (VAE) [14] 将3D形状编码为潜在向量集,这些向量可解码为神经SDF或占用场,并通过Marching Cubes [24] 进行渲染。随后通过扩散过程对该潜在向量集建模以生成多样化的3D形状。CLAY [49] 采用扩散Transformer (DiT) [30] 扩展了这一流程,而TripoSG [18] 则通过修正流Transformer和混合监督进一步提升了保真度。然而,基于隐式潜在的方法通常依赖具有非对称3D表征的VAE,导致训练效率较低,通常需要数百个GPU。
Explicit latent methods have emerged as a compelling alternative to implicit ones, offering better interpret a bility, simpler training, and direct editing capabilities, while also adopting scalable architectures such as DiT [30]. For instance, Direct3D [39] proposes to use tri-plane latent representations to accelerate training and convergence. XCube [32] introduces hierarchical sparse voxel latent diffusion for $1024^{3}$ sparse volume generation, but only restricted to millions of valid voxels, limiting the final output quality. Trellis [40] integrates sparse voxel representations of $256^{3}$ resolution, with the rendering supervision for the VAE training. In general, due to high memory demands, existing explicit latent methods are limited in output resolution. Scaling to $1024^{3}$ with sufficient latent tokens and valid voxels remains challenging, as the quadratic cost of full attention in DiT renders high-resolution training comput ation ally prohibitive.
显式潜在方法已成为隐式方法的有力替代方案,具有更好的可解释性、更简单的训练过程和直接编辑能力,同时采用了可扩展架构如DiT [30]。例如,Direct3D [39]提出使用三平面潜在表示来加速训练和收敛。XCube [32]引入了分层稀疏体素潜在扩散用于$1024^{3}$稀疏体积生成,但仅限于数百万有效体素,限制了最终输出质量。Trellis [40]集成了$256^{3}$分辨率的稀疏体素表示,并为VAE训练提供渲染监督。总体而言,由于高内存需求,现有显式潜在方法在输出分辨率上受限。扩展到$1024^{3}$分辨率并保持足够的潜在token和有效体素仍具挑战性,因为DiT中全注意力机制的二次计算成本使得高分辨率训练在计算上难以实现。
To address the challenge of high-resolution 3D shape generation, we propose Direct3D-S2, a unified generative framework that utilizes sparse volumetric representations. At the core of our approach is a novel Spatial Sparse Attention (SSA) mechanism, which substantially improves the s cal ability of diffusion transformers in high-resolution 3D shape generation by selectively attending to spatially important tokens via learnable compression and selection modules. Specifically, we draw inspiration from the key principles of Native Sparse Attention (NSA) [46], which integrates compression, selection, and windowing to identify relevant tokens based on global-local interactions. While
为解决高分辨率3D形状生成的挑战,我们提出了Direct3D-S2——一个利用稀疏体素表征的统一生成框架。该方案的核心是新颖的空间稀疏注意力(Spatial Sparse Attention, SSA)机制,通过可学习的压缩和选择模块对空间重要token进行选择性关注,显著提升了扩散Transformer在高分辨率3D形状生成中的可扩展性。具体而言,我们受到原生稀疏注意力(Native Sparse Attention, NSA) [46] 关键原理的启发,该方法通过压缩、选择和窗口化操作,基于全局-局部交互来识别相关token。
NSA is designed for structurally organized 1D sequences, it is not directly applicable to unstructured, sparse 3D data. To adapt it, we redesign the block partitioning to preserve 3D spatial coherence and revise the core modules to accommodate the irregular nature of sparse volumetric tokens. This enables efficient processing of large token sets within sparse volumes. We implement a custom Triton [37] GPU kernel for SSA, achieving a $\ {\bf3.9\times}$ speedup in the forward pass and a $\mathbf{9.6\times}$ speedup in the backward pass compared to Flash Attention-2 at $1024^{3}$ resolution.
NSA专为结构化的1D序列设计,无法直接应用于非结构化、稀疏的3D数据。为此,我们重新设计了块分区机制以保持3D空间连贯性,并改进了核心模块以适应稀疏体素token的不规则特性,从而实现对稀疏体量中大规模token集的高效处理。我们为SSA定制了Triton [37] GPU内核,在1024³分辨率下,其前向传播速度比Flash Attention-2快$\ {\bf3.9\times}$,反向传播速度提升$\mathbf{9.6\times}$。
Our framework also includes a VAE that maintains a consistent sparse volumetric format across input, latent, and output stages. This unified design eliminates the need for cross-modality translation, commonly seen in previous methods using mismatched representations such as point cloud input, 1D vector latent, and dense volume output, thereby improving training efficiency, stability, and geometric fidelity. After the VAE training, the DiT with the proposed SSA will be trained on the converted latents, enabling scalable and efficient high-resolution 3D shape generation.
我们的框架还包含一个VAE (变分自编码器),它在输入、潜变量和输出阶段保持一致的稀疏体素格式。这种统一设计消除了跨模态转换的需求(常见于先前使用不匹配表示的方法,如点云输入、一维向量潜变量和密集体素输出),从而提高了训练效率、稳定性和几何保真度。在VAE训练完成后,采用所提SSA的DiT将在转换后的潜变量上进行训练,实现可扩展且高效的高分辨率3D形状生成。
Extensive experiments demonstrate that our approach successfully achieves high-quality and efficient gigascale 3D generation, a milestone previously unattainable by explicit 3D latent diffusion methods. Compared to prior native 3D diffusion techniques, our model consistently generates highly detailed 3D shapes while considerably reducing computational costs. Notably, Direct3D-S2 requires only 8 GPUs to train on public datasets [8, 9, 20] at a resolution of $1024^{3}$ , in stark contrast to prior state-of-the-art methods, which typically require 32 or more GPUs even for training at $256^{3}$ resolution.
大量实验证明,我们的方法成功实现了高质量、高效的十亿级3D生成,这是显式3D潜在扩散方法 (explicit 3D latent diffusion methods) 此前无法达到的里程碑。与先前的原生3D扩散技术相比,我们的模型在显著降低计算成本的同时,始终能生成高度精细的3D形状。值得注意的是,Direct3D-S2仅需8块GPU即可在公开数据集 [8, 9, 20] 上以 $1024^{3}$ 分辨率进行训练,这与当前最优方法形成鲜明对比——后者即使在 $256^{3}$ 分辨率下训练通常也需要32块或更多GPU。
2. Related work
2. 相关工作
2.1. Multi-view Generation and 3D Reconstruction
2.1. 多视角生成与三维重建
Large-scale 3D generation has been advanced by methods such as [16, 22, 23, 42], which employ multi-view diffusion models [38] trained on 2D image prior models like Stable Diffusion [33] to generate multi-view images of 3D shapes. These multi-view images are then used to reconstruct 3D shapes via generalized sparse-view reconstruction models. Follow-up works [21, 27, 36, 43, 48] further improve the quality and efficiency of reconstruction by incorpora ting different 3D representations. Despite these advances, these methods still face challenges in maintaining multi-view consistency and shape quality. The synthesized images may fail to faithfully represent the underlying 3D structure, which could result in artifacts and reconstruction errors. Another limitation is the reliance on rendering-based supervision, such as Neural Radiance Fields (NeRF) [28] or DMTet [34]. While this avoids the need for direct 3D supervision (e.g., meshes), it adds significant complexity and computational overhead to the training process. Renderingbased supervision can be slow and costly, especially when scaled to large datasets.
大规模3D生成技术已通过[16, 22, 23, 42]等方法取得进展,这些方法采用基于Stable Diffusion [33]等2D图像先验模型训练的多视角扩散模型[38]来生成3D形状的多视角图像。这些多视角图像随后通过广义稀疏视图重建模型进行3D形状重构。后续研究[21, 27, 36, 43, 48]通过融合不同3D表征方式,进一步提升了重建质量和效率。尽管取得这些进展,这些方法在保持多视角一致性和形状质量方面仍面临挑战。合成图像可能无法准确反映底层3D结构,从而导致伪影和重建误差。另一个局限是对基于渲染的监督(如Neural Radiance Fields (NeRF) [28]或DMTet [34])的依赖。虽然这避免了对直接3D监督(如网格)的需求,但显著增加了训练过程的复杂性和计算开销。基于渲染的监督可能速度慢且成本高,特别是在扩展到大型数据集时。
2.2. Large Scale 3D Latent Diffusion Model
2.2. 大规模3D潜在扩散模型
Motivated by recent advances in Latent Diffusion Models (LDMs) [33] in 2D image generation, several methods have extended LDMs to 3D shape generation. These approaches broadly fall into two categories: vecset-based methods and voxel-based methods. Implicit vecset-based methods, such as 3 D Shape 2 Vec set [47], Michelangelo [50], CLAY [49], and CraftsMan 3 D [17], represent 3D shapes using latent vecset and reconstruct meshes through neural SDFs or occupancy fields. However, implicit methods are typically constrained by the size of vecset: larger vecset leads to more complex mappings to the 3D shape and requires longer training times. In contrast, voxel-based methods, such as XCube [32], Trellis [40], and more recent works [11, 45], employ voxel grids as latent representations, providing more interpret ability and easier training. Nevertheless, voxel-based methods face limitations in latent resolution due to cubic growth in GPU memory requirements and high computational costs associated with attention mechanisms. To address this issue, our work specifi- cally targets reducing the computational overhead of attention mechanisms, thereby enabling the generation of high- resolution voxel-based latent representations that were previously infeasible.
受潜在扩散模型 (Latent Diffusion Models, LDMs) [33] 在2D图像生成领域最新进展的启发,多项研究已将LDMs扩展至3D形状生成。这些方法主要分为两类:向量集 (vecset) 基方法与体素 (voxel) 基方法。基于隐式向量集的方法(如3DShape2VecSet [47]、Michelangelo [50]、CLAY [49]和CraftsMan3D [17])通过潜在向量集表示3D形状,并借助神经SDF或占据场重建网格。但隐式方法通常受限于向量集规模:更大的向量集会导致3D形状映射更复杂,且需要更长的训练时间。相比之下,体素基方法(如XCube [32]、Trellis [40]及近期研究[11,45])采用体素网格作为潜在表示,具有更强的可解释性和更易训练的优势。然而,由于GPU内存需求呈立方增长及注意力机制的高计算成本,体素基方法在潜在分辨率方面存在局限。为解决该问题,本研究重点降低注意力机制的计算开销,从而实现了此前无法达成的高分辨率体素基潜在表示生成。
2.3. Efficient Large Tokens Generation
2.3. 高效大Token生成
Generating large tokens efficiently is a challenging problem, especially for high-resolution data. Native Sparse Attention (NSA) [46] addresses this by introducing adaptive token compression that reduce the number of tokens involved in attention computation, while maintaining performance comparable to full attention. NSA has been successfully applied to large language models [31, 46] and video generation [35], showing significant reductions in attention cost. In this paper, we extend token compression to 3D data and propose a new Spatial Sparse Attention (SSA) mechanism. SSA adapts the core ideas of NSA but modifies the block partitioning strategy to respect 3D spatial coherence. We also redesign the compression, selection, and window modules to better fit the properties of sparse 3D token sets. Another line of work, such as linear attention [13], reduces attention complexity by approximating attention weights with linear functions. Variants of this technique have been applied in image [41, 53] and video generation [26] to improve efficiency. However, the absence of non-linear similarity can lead to a significant decline in the performance of the model.
高效生成大型Token是一个具有挑战性的难题,尤其对于高分辨率数据而言。原生稀疏注意力(Native Sparse Attention, NSA) [46]通过引入自适应Token压缩技术来解决这一问题,该技术能在保持与完整注意力相当性能的同时,减少参与注意力计算的Token数量。NSA已成功应用于大语言模型[31,46]和视频生成[35]领域,显著降低了注意力计算成本。本文将该Token压缩技术扩展至三维数据,并提出新型空间稀疏注意力(Spatial Sparse Attention, SSA)机制。SSA继承了NSA的核心思想,但改进区块划分策略以保持三维空间连贯性,同时重新设计了压缩、选择和窗口模块以适配稀疏三维Token集的特性。另一类研究工作如线性注意力[13]通过线性函数近似注意力权重来降低计算复杂度,该技术的变体已应用于图像[41,53]和视频生成[26]领域以提升效率,但非线性相似性特征的缺失可能导致模型性能显著下降。
3. Sparse SDF VAE
3. 稀疏 SDF VAE
While variation al auto encoders (VAEs) have become the cornerstone of 2D image generation by compressing pixel representations into compact latent spaces for efficient diffusion training, their extension to 3D geometry faces fundamental challenges. Unlike images with standardized pixel grids, 3D representations lack a unified structure, such as meshes, point clouds, and implicit fields, each requires specialized processing. This fragmentation forces existing 3D VAEs into asymmetric architectures with compromised efficiency. For instance, prominent approaches [6, 49, 51] based on vecset [47] encode the input point cloud into a vector set latent space before decoding it into SDF field, while Trellis [40] and XCube [32] rely on differentiable rendering or neural kernel surface reconstruction [12] to bridge their latent spaces to usable meshes. These hybrid pipelines introduce computational bottlenecks and geometric approximations that limit their s cal ability to highresolution 3D generation. In this paper, we propose a fully end-to-end sparse SDF VAE that employs a symmetric encoding-decoding network to encode high-resolution sparse SDF volumes into a sparse latent representation, substantially improving training efficiency while maintaining geometric precision.
虽然变分自编码器 (VAE) 通过将像素表示压缩为紧凑的潜在空间以进行高效扩散训练,已成为二维图像生成的基石,但其向三维几何的扩展面临根本性挑战。与具有标准化像素网格的图像不同,三维表示缺乏统一结构,例如网格、点云和隐式场,每种表示都需要专门处理。这种碎片化迫使现有的三维 VAE 采用效率受损的非对称架构。例如,基于 vecset [47] 的主流方法 [6, 49, 51] 将输入点云编码为向量集潜在空间,然后解码为 SDF 场,而 Trellis [40] 和 XCube [32] 则依赖可微分渲染或神经核表面重建 [12] 将其潜在空间桥接到可用网格。这些混合流程引入了计算瓶颈和几何近似,限制了它们在高分辨率三维生成中的可扩展性。在本文中,我们提出了一种完全端到端的稀疏 SDF VAE,采用对称编码-解码网络将高分辨率稀疏 SDF 体积编码为稀疏潜在表示,在保持几何精度的同时显著提高了训练效率。
Given a mesh represented as a signed distance field (SDF) volume $\mathrm{v}$ with resolution $R^{3}$ (e.g., $1024^{3}\rangle$ ), the SSVAE first encodes it into a latent representation $\mathbf{z}=E(V)$ , then reconstructs the SDF through the decoder $\tilde{V}=D(\mathbf{z})$ . Direct processing of dense $R^{3}$ SDF volumes proves comput ation ally prohibitive. To address this, we strategically focus on valid sparse voxels where absolute SDF values fall below threshold $\tau$ :
给定一个以带符号距离场 (SDF) 体素 $\mathrm{v}$ 表示的网格,其分辨率为 $R^{3}$ (例如 $1024^{3}\rangle$),SSVAE 首先将其编码为潜在表示 $\mathbf{z}=E(V)$,然后通过解码器重建 SDF $\tilde{V}=D(\mathbf{z})$。直接处理稠密的 $R^{3}$ SDF 体素在计算上是不可行的。为了解决这个问题,我们策略性地聚焦于绝对 SDF 值低于阈值 $\tau$ 的有效稀疏体素:
$$
V={(\mathbf{x}{i},s(\mathbf{x}{i}))\vert\vert s(\mathbf{x}{i})\vert<\tau}_{i=1}^{\vert V\vert},
$$
$$
V={(\mathbf{x}{i},s(\mathbf{x}{i}))\vert\vert s(\mathbf{x}{i})\vert<\tau}_{i=1}^{\vert V\vert},
$$
where $s(\mathbf{x}{i})$ denotes the SDF value at position $\mathbf{x}_{i}$ .
其中 $s(\mathbf{x}{i})$ 表示位置 $\mathbf{x}_{i}$ 处的 SDF 值。
3.1. Symmetric Network Architecture
3.1. 对称网络架构
Our fully end-to-end SDF VAE framework adopts a symmetric encoder-decoder network architecture, as illustrated in the upper half of Figure 2. Specifically, the encoder employs a hybrid framework combining sparse 3D convolution networks and transformer networks. We first extract local geometric features through a series of residual sparse 3D CNN blocks interleaved with 3D mean pooling operations, progressively down sampling the spatial resolution. We then process the sparse voxels as variable-length tokens and utilize shifted window attention to capture local contextual information between the valid voxels. Inspired by Trellis [40], the feature of each valid voxel is augmented with positional encoding based on its 3D coordinates before being fed into 3D shift window attention layers. This hybrid design outputs sparse latent representations at reduced resolution $\textstyle{\bigl(}{\frac{R}{f}}{\bigr)}^{3}$ , where $f$ denotes the down sampling factor. The decoder of our SS-VAE adopts a symmetric structure with respect to the encoder, leveraging attention layers and sparse 3D CNN blocks to progressively upsample the latent representation and reconstruct the SDF volume $\tilde{V}$ .
我们完全端到端的SDF VAE框架采用了对称的编码器-解码器网络架构,如图2上半部分所示。具体而言,编码器采用了一种结合稀疏3D卷积网络和Transformer网络的混合框架。我们首先通过一系列残差稀疏3D CNN块与3D平均池化操作交错处理,逐步降低空间分辨率进行下采样。随后将稀疏体素处理为可变长度token,并利用移位窗口注意力机制捕捉有效体素间的局部上下文信息。受Trellis [40]启发,每个有效体素的特征在输入3D移位窗口注意力层之前,会基于其3D坐标进行位置编码增强。这种混合设计输出降采样分辨率$\textstyle{\bigl(}{\frac{R}{f}}{\bigr)}^{3}$的稀疏潜在表示,其中$f$表示下采样因子。我们的SS-VAE解码器采用与编码器对称的结构,利用注意力层和稀疏3D CNN块逐步上采样潜在表示,最终重建SDF体$\tilde{V}$。
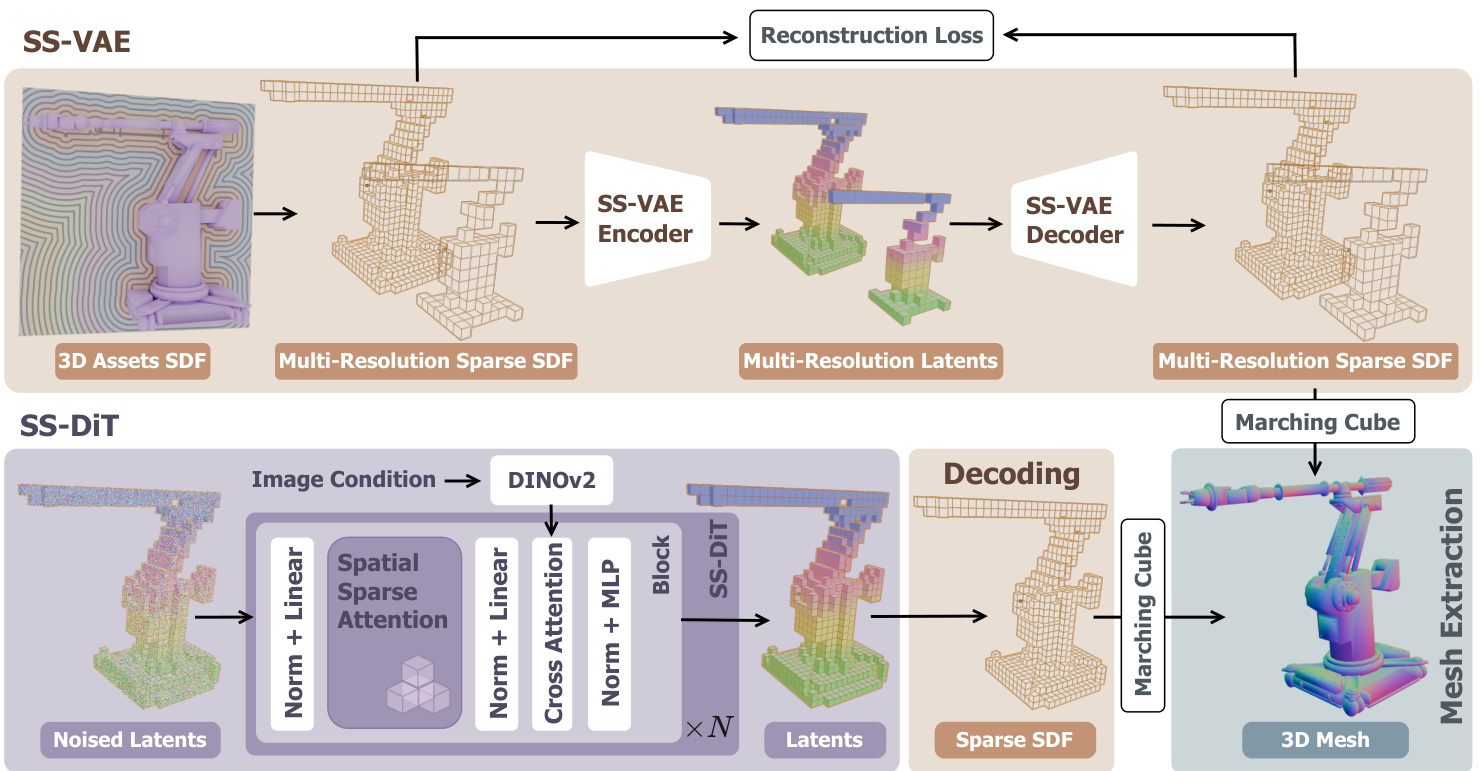
Figure 2. The framework of our Direct3D-S2. We propose a fully end-to-end sparse SDF VAE (SS-VAE), which employs a symmetric encoder-decoder network to efficiently encode high-resolution sparse SDF volumes into sparse latent representations $\mathbf{z}$ . Then we train an image-conditioned diffusion transformer (SS-DiT) based on $\mathbf{z}$ , and design a novel Spatial Sparse Attention (SSA) mechanism that substantially improves the training and inference efficiency of the DiT.
图 2: 我们的Direct3D-S2框架。我们提出了一种完全端到端的稀疏SDF VAE (SS-VAE),它采用对称编码器-解码器网络将高分辨率稀疏SDF体高效编码为稀疏潜在表示$\mathbf{z}$。随后我们基于$\mathbf{z}$训练了一个图像条件扩散Transformer (SS-DiT),并设计了一种新颖的空间稀疏注意力 (SSA) 机制,显著提升了DiT的训练和推理效率。
3.2. Training Losses
3.2. 训练损失
The decoded sparse voxels $\tilde{V}$ contain both the input voxels $\tilde{V}{\mathrm{in}}$ and additional valid voxels $\tilde{V}_{\mathrm{extra}}$ . We enforce supervision on the SDF values across all these spatial positions. To enhance geometric fidelity, we impose additional supervision on the active voxels situated near the sharp edges of the mesh, specifically in regions exhibiting high-curvature variations on the mesh surface. Moreover, the term of KLdivergence regular iz ation is imposed on the latent representation $\mathbf{z}$ to constrain excessive variations in the latent space. The overall training objective of our SS-VAE is formulated as:
解码后的稀疏体素$\tilde{V}$包含输入体素$\tilde{V}{\mathrm{in}}$和额外有效体素$\tilde{V}_{\mathrm{extra}}$。我们对所有这些空间位置的SDF值进行监督。为提高几何保真度,我们在网格锐边附近的高曲率变化区域对活跃体素施加额外监督。此外,在潜在表示$\mathbf{z}$上施加KL散度正则化项以约束潜在空间的过度变化。我们的SS-VAE总体训练目标公式如下:
$$
\mathcal{L}{c}=\frac{1}{\lvert\tilde{V}{c}\rvert}\sum_{(\mathbf{x},\tilde{s}(\mathbf{x}))\in\tilde{V}{c}}\Big\lVert s(\mathbf{x})-\tilde{s}(\mathbf{x})\Big\rVert_{2}^{2},\quad c\in{\mathrm{in,ext,sharp}},
$$
$$
\mathcal{L}{c}=\frac{1}{\lvert\tilde{V}{c}\rvert}\sum_{(\mathbf{x},\tilde{s}(\mathbf{x}))\in\tilde{V}{c}}\Big\lVert s(\mathbf{x})-\tilde{s}(\mathbf{x})\Big\rVert_{2}^{2},\quad c\in{\mathrm{in,ext,sharp}},
$$
$$
\mathcal{L}{\mathrm{total}}=\sum_{c}\lambda_{c}\mathcal{L}{c}+\lambda_{\mathrm{KL}}\mathcal{L}_{\mathrm{KL}},
$$
$$
\mathcal{L}{\mathrm{total}}=\sum_{c}\lambda_{c}\mathcal{L}{c}+\lambda_{\mathrm{KL}}\mathcal{L}_{\mathrm{KL}},
$$
where $\lambda_{\mathrm{in}},\lambda_{\mathrm{ext}},\lambda_{\mathrm{sharp}}$ and $\lambda_{\mathrm{KL}}$ denote the weight of each term.
其中 $\lambda_{\mathrm{in}}$、$\lambda_{\mathrm{ext}}$、$\lambda_{\mathrm{sharp}}$ 和 $\lambda_{\mathrm{KL}}$ 表示各项的权重。
3.3. Multi-resolution Training
3.3. 多分辨率训练
To enhance training efficiency and enable our SS-VAE to encode meshes across varying resolutions, we utilize the multi-resolution training paradigm. Specifically, during each training iteration, we randomly sample a target resolution from the candidate set ${256^{3},384^{3},512^{3},1024^{3}}$ , then tri linearly interpolate the input SDF volume to the selected resolution before feeding it into the SS-VAE.
为提高训练效率并使我们的SS-VAE能够编码不同分辨率的网格,我们采用了多分辨率训练范式。具体而言,在每次训练迭代中,我们从候选集${256^{3},384^{3},512^{3},1024^{3}}$中随机采样一个目标分辨率,然后将输入的SDF体积通过三线性插值调整至选定分辨率,再输入SS-VAE。
4. Spatial Sparse Attention and DiT
4. 空间稀疏注意力与DiT
Through our SS-VAE framework, 3D shapes can be encoded into latent representations z. Following a methodology analogous to Trellis [40], we serialize the latent tokens $\mathbf{z}$ and train a rectified flow transformer-based 3D shape generator conditioned on input images. To ensure efficient generation of high-resolution meshes, we propose spatial sparse attention that substantially accelerates both training and inference processes. Furthermore, we introduce a sparse conditioning mechanism to extract the foreground region of the input images, thereby reducing the number of conditioning tokens. The architecture of the DiT is illustrated in the lower half of Figure 2.
通过我们的SS-VAE框架,3D形状可以被编码为潜在表示z。采用与Trellis [40]类似的方法,我们将潜在token $\mathbf{z}$序列化,并训练一个基于修正流(rectified flow) Transformer的、以输入图像为条件的3D形状生成器。为确保高效生成高分辨率网格,我们提出了空间稀疏注意力机制,显著加速了训练和推理过程。此外,我们引入稀疏条件机制来提取输入图像的前景区域,从而减少条件token的数量。DiT的架构如图2下半部分所示。
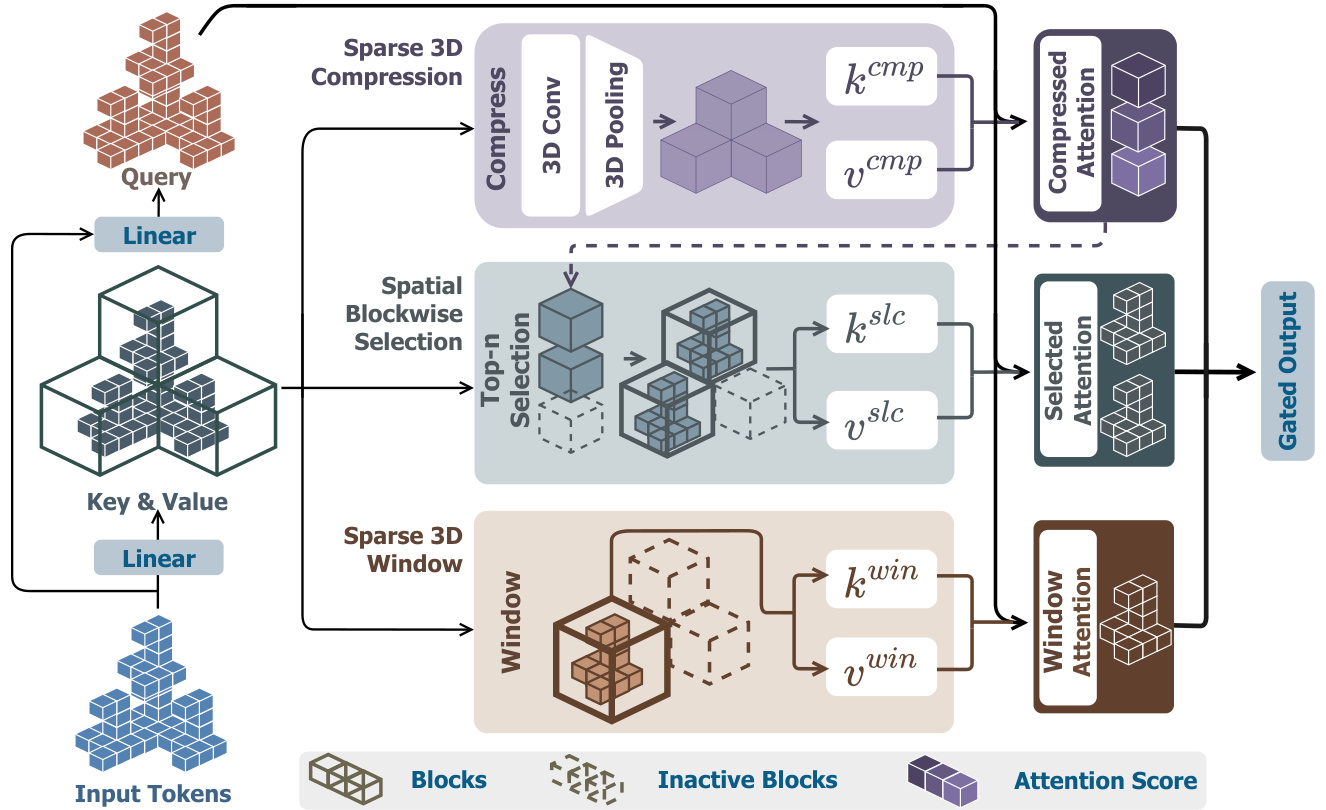
Figure 3. The framework of our Spatial Sparse Attention (SSA). We partition the input tokens into blocks based on their 3D coordinates, and then construct key-value pairs through three distinct modules. For each query token, we utilize sparse 3D compression module to capture global information, while the spatial blockwise selection module selects important blocks based on compression attention scores to extract fine-grained features, and the sparse 3D window module injects local features. Ultimately, we aggregate the final output of SSA from the three modules using predicted gate scores.
图 3: 我们提出的空间稀疏注意力 (SSA) 框架。根据输入 token 的 3D 坐标将其分块,随后通过三个独立模块构建键值对。对于每个查询 token,稀疏 3D 压缩模块用于捕获全局信息,空间分块选择模块则根据压缩注意力分数筛选重要区块以提取细粒度特征,稀疏 3D 窗口模块负责注入局部特征。最终通过预测门控分数聚合三个模块的输出得到 SSA 的最终结果。
4.1. Spatial Sparse Attention
4.1. 空间稀疏注意力 (Spatial Sparse Attention)
Given input tokens q, $\mathbf{\mu},\mathbf{v}\in\mathbb{R}^{N\times d}$ , where $N$ denotes the token length, and $d$ represents the head dimension, the standard full attention is formulated as:
给定输入 tokens q,$\mathbf{\mu},\mathbf{v}\in\mathbb{R}^{N\times d}$,其中 $N$ 表示 token 长度,$d$ 代表头维度 (head dimension),标准全注意力 (full attention) 计算公式为:
$$
{\begin{array}{r l}&{\mathbf{0}{t}=\mathbf{Attn}{\bigl(}\mathbf{q}{t},\mathbf{k},\mathbf{v}{\bigr)}}\ &{\quad=\displaystyle\sum_{i=1}^{N}{\frac{\mathbf{p}{t,i}\mathbf{v}{i}}{N}},\quad t\in[0,N),}\ &{\qquad\quad\sum_{j=1}^{N}\mathbf{p}_{t,j}}\end{array}}
$$
$$
{\begin{array}{r l}&{\mathbf{0}{t}=\mathbf{Attn}{\bigl(}\mathbf{q}{t},\mathbf{k},\mathbf{v}{\bigr)}}\ &{\quad=\displaystyle\sum_{i=1}^{N}{\frac{\mathbf{p}{t,i}\mathbf{v}{i}}{N}},\quad t\in[0,N),}\ &{\qquad\quad\sum_{j=1}^{N}\mathbf{p}_{t,j}}\end{array}}
$$
$$
\mathbf{p}{t,j}=\exp\biggl(\frac{\mathbf{q}{t}^{\top}\mathbf{k}_{j}}{\sqrt{d}}\biggr).
$$
$$
\mathbf{p}{t,j}=\exp\biggl(\frac{\mathbf{q}{t}^{\top}\mathbf{k}_{j}}{\sqrt{d}}\biggr).
$$
As the resolution of SS-VAE escalates, the length of input tokens grows substantially, reaching over $100\mathrm{k}$ at a resolution of $1024^{3}$ , leading to prohibitively low computational efficiency in attention operations. Inspired by NSA (Native Sparse Attention) [46], we proposes Spatial Sparse Attention mechanism, which partitions key and value tokens into spatially coherent blocks based on their geometric relationships and performs blockwise token selection to achieve significant acceleration.
随着SS-VAE分辨率的提升,输入token的长度显著增加,在$1024^{3}$分辨率下超过$100\mathrm{k}$,导致注意力运算的计算效率极低。受NSA (Native Sparse Attention) [46]启发,我们提出空间稀疏注意力机制,该机制根据键值token的几何关系将其划分为空间连贯的块,并通过分块token选择实现显著加速。
where $\mathbf{k}{t}$ and $\mathbf{v}{t}$ represent the selected key and value tokens in each module for query ${\bf q}{t}$ , respectively. $\omega_{t}$ is the gating score for each module, obtained by applying a linear layer followed by a sigmoid activation to the input features.
其中 $\mathbf{k}{t}$ 和 $\mathbf{v}{t}$ 分别表示每个模块中为查询 ${\bf q}{t}$ 选定的键(key)和值(value) token。$\omega_{t}$ 是每个模块的门控分数,通过对输入特征应用线性层和sigmoid激活函数获得。
Sparse 3D Compression. After partitioning input tokens into spatially coherent blocks based on their 3D coordinates, we leverage a compression module to extract block-level representations of the input tokens. Specifically, we first incorporate intra-block positional encoding for each token within a block of size mc3mp, then employ sparse 3D convolution followed by sparse 3D mean pooling to compress the entire block:
稀疏3D压缩。在根据3D坐标将输入Token划分为空间连贯的块后,我们利用压缩模块提取输入Token的块级表示。具体而言,我们首先为尺寸为mc3mp的块内的每个Token加入块内位置编码,随后采用稀疏3D卷积及稀疏3D均值池化来压缩整个块:
$$
\mathbf{k}{t}^{\mathrm{cmp}}=\delta(\mathbf{k}{t}+\mathrm{PE}(\mathbf{k}_{t})),
$$
$$
\mathbf{k}{t}^{\mathrm{cmp}}=\delta(\mathbf{k}{t}+\mathrm{PE}(\mathbf{k}_{t})),
$$
where $\mathbf{k}_{t}^{\mathrm{cmp}}$ denotes the block-level key token, $\mathrm{PE}(\cdot)$ is absolute position encoding, and $\delta(\cdot)$ represents operations of sparse 3D convolution and sparse 3D mean pooling. The sparse 3D compression module effectively captures blocklevel global information while reducing the number of tokens, thereby enhancing computational efficiency.
其中 $\mathbf{k}_{t}^{\mathrm{cmp}}$ 表示块级关键token (key token),$\mathrm{PE}(\cdot)$ 为绝对位置编码 (absolute position encoding),$\delta(\cdot)$ 代表稀疏3D卷积 (sparse 3D convolution) 和稀疏3D均值池化 (sparse 3D mean pooling) 操作。该稀疏3D压缩模块能有效捕获块级全局信息,同时减少token数量,从而提升计算效率。
Spatial Blockwise Selection. The block-level representations only contain coarse-grained information, necessitat- ing the retention of token-level features to enhance the fine details in the generated 3D shapes. However, the excessive number of input tokens leads to computationally inefficient operations if all tokens are utilized. By leveraging the sparse 3D compression module, we compute the attention scores $\mathbf{s}{\mathrm{cmp}}$ between the query q and each compression block, subsequently selecting all tokens within the top $k$ blocks exhibiting the highest scores. The resolution $m_{\mathrm{slc}}$ of the selection blocks must be both greater than and divisible by the resolution $m_{\mathrm{cmp}}$ of the compression blocks. The relevance score ${\mathbf{s}}_{t}^{\mathrm{slc}}$ for a selection block is aggregated from its constituent compression blocks. GQA (Grouped-Query Attention) [4] is employed to further improve computational efficiency, the attention scores of the shared query heads within each group are accumulated as follows:
空间分块选择。块级表征仅包含粗粒度信息,因此需要保留token级别的特征以增强生成3D形状的细节。然而,若使用全部输入token会导致计算效率低下。通过稀疏3D压缩模块,我们计算查询q与每个压缩块之间的注意力得分$\mathbf{s}{\mathrm{cmp}}$,随后选择得分最高的前$k$个块内的所有token。选择块的分辨率$m_{\mathrm{slc}}$必须大于且可被压缩块分辨率$m_{\mathrm{cmp}}$整除。选择块的相关性得分${\mathbf{s}}_{t}^{\mathrm{slc}}$由其组成压缩块聚合得出。采用分组查询注意力(GQA, Grouped-Query Attention) [4]进一步提升计算效率,每组内共享查询头的注意力得分按如下方式累加:
$$
\mathbf{s}{t}^{\mathrm{slc}}=\sum_{i\in\mathcal{B}{\mathrm{cmp}}}\sum_{h=1}^{h_{s}}s_{t,h}^{\mathrm{cmp},i},
$$
$$
\mathbf{s}{t}^{\mathrm{slc}}=\sum_{i\in\mathcal{B}{\mathrm{cmp}}}\sum_{h=1}^{h_{s}}s_{t,h}^{\mathrm{cmp},i},
$$
where $B_{\mathrm{cmp}}$ denotes the set of compression blocks within the selection block, and $h_{s}$ represents the number of shared heads within a group. The top $k$ selection blocks with the highest ${\mathbf{s}}{t}^{\mathrm{slc}}$ scores are selected, and all tokens contained within them are concatenated to form $\mathbf{k}{t}^{\mathrm{slc}}$ and $\mathbf{v}_{t}^{\mathrm{slc}}$ , which are used to compute the spatial blockwise selection attention.
其中 $B_{\mathrm{cmp}}$ 表示选择块内的压缩块集合,$h_{s}$ 代表组内共享注意力头的数量。选取 ${\mathbf{s}}{t}^{\mathrm{slc}}$ 得分最高的前 $k$ 个选择块,将其包含的所有token拼接形成 $\mathbf{k}{t}^{\mathrm{slc}}$ 和 $\mathbf{v}_{t}^{\mathrm{slc}}$,用于计算空间分块选择注意力。
We implement the spatial blockwise selection attention kernel using Triton [37], with two key challenges arising from the sparse 3D voxel structures: 1) the number of tokens varies across different blocks, and 2) tokens within the same block may not be contiguous in HBM. To address these, we first sort the input tokens based on their block indices, then compute the starting index $\mathcal{C}$ of each block as kernel input. In the inner loop, $\mathcal{C}$ dynamically governs the loading of corresponding block tokens. The complete procedure of forward pass is formalized in Algorithm 1.
我们使用Triton [37]实现了空间分块选择注意力内核,稀疏3D体素结构带来了两个关键挑战:1) 不同块之间的token数量存在差异,2) 同一块内的token在HBM中可能不连续。为此,我们首先根据块索引对输入token进行排序,然后计算每个块的起始索引$\mathcal{C}$作为内核输入。在内层循环中,$\mathcal{C}$动态控制对应块token的加载。前向传播的完整流程如算法1所示。
Sparse 3D Window. In addition to sparse 3D compression and spatial blockwise selection modules, we further employ an auxiliary sparse 3D window module to explicitly incorporate localized feature interactions. Drawing inspiration from Trellis [40], we partition the input token-containing voxels into non-overlapping windows of size $m_{\mathrm{win}}^{3}$ . For each token, we formulate its contextual computation by dynamically aggregating active tokens within the corresponding window to form ${\bf k}{t}^{\mathrm{win}}$ and $\mathbf{v}_{t}^{\mathrm{win}}$ , followed by localized self-attention calculation exclusively over this constructed token subset.
稀疏3D窗口。除了稀疏3D压缩和空间分块选择模块外,我们还采用了一个辅助的稀疏3D窗口模块来显式整合局部特征交互。受Trellis [40] 启发,我们将包含输入token的体素划分为不重叠的 $m_{\mathrm{win}}^{3}$ 尺寸窗口。对于每个token,我们通过动态聚合对应窗口内的活跃token来构建 ${\bf k}{t}^{\mathrm{win}}$ 和 $\mathbf{v}_{t}^{\mathrm{win}}$ ,随后仅在此构造的token子集上执行局部自注意力计算。
Through the modules of sparse 3D compression, spatial blockwise selection, and sparse 3D window, corresponding key-value pairs are constructed. Subsequently, attention calculations are performed for each module, and the results are aggregated and weighted according to gate scores to produce the final output of the spatial sparse attention mechanism.
通过稀疏3D压缩、空间分块选择和稀疏3D窗口模块构建对应的键值对,随后对各模块进行注意力计算,并根据门控分数聚合加权结果,最终输出空间稀疏注意力机制。
4.2. Sparse Conditioning Mechanism
4.2. 稀疏条件机制
Existing image-to-3D models [17, 39, 49] typically employ DINO-v2 [29] to extract pixel-level features from conditional images, followed by cross-attention operation with noisy tokens to achieve conditional generation. However, for a majority of input images, more than half of the regions consist of background, which not only introduces additional computational overhead but may also adversely affect the alignment between the generated meshes and the conditional images. To mitigate this issue, we propose a sparse conditioning mechanism that selectively extracts and processes sparse foreground tokens from input images for cross-attention computation. Formally, given an input image $\mathcal{T}$ , the sparse conditioning tokens c are computed as follows:
现有图像转3D模型[17, 39, 49]通常采用DINO-v2[29]从条件图像中提取像素级特征,再通过噪声token的交叉注意力操作实现条件生成。然而对
