RTMO: Towards High-Performance One-Stage Real-Time Multi-Person Pose Estimation
RTMO:迈向高性能单阶段实时多人姿态估计
Abstract
摘要
Real-time multi-person pose estimation presents significant challenges in balancing speed and precision. While two-stage top-down methods slow down as the number of people in the image increases, existing one-stage methods often fail to simultaneously deliver high accuracy and real-time performance. This paper introduces RTMO, a one-stage pose estimation framework that seamlessly integrates coordinate classification by representing keypoints using dual 1-D heatmaps within the YOLO architecture, achieving accuracy comparable to top-down methods while maintaining high speed. We propose a dynamic coordinate classifier and a tailored loss function for heatmap learning, specifically designed to address the incompatibilities between coordinate classification and dense prediction models. RTMO outperforms state-of-the-art onestage pose estimators, achieving $1.1%$ higher AP on COCO while operating about 9 times faster with the same backbone. Our largest model, RTMO-l, attains $74.8%$ AP on COCO val2017 and 141 FPS on a single V100 GPU, demonstrating its efficiency and accuracy. The code and models are available at https://github.com/openmmlab/mmpose/tree/main/projects/rtmo.
实时多人姿态估计在平衡速度与精度方面存在显著挑战。两阶段自上而下方法会随图像中人数增加而减速,而现有单阶段方法往往难以同时实现高精度和实时性能。本文提出RTMO框架,该单阶段姿态估计方案通过YOLO架构内采用双一维热图表示关键点,无缝整合坐标分类,在保持高速的同时达到与自上而下方法相当的精度。我们提出动态坐标分类器和针对热图学习的定制损失函数,专门解决坐标分类与密集预测模型间的兼容性问题。RTMO在COCO数据集上以相同骨干网络实现1.1% AP提升且速度快9倍,超越当前最优单阶段姿态估计器。最大模型RTMO-l在COCO val2017达到74.8% AP,单V100 GPU实现141 FPS,充分展现其高效性与准确性。代码与模型详见https://github.com/openmmlab/mmpose/tree/main/projects/rtmo。
1. Introduction
1. 引言
Multi-person pose estimation (MPPE) is essential in the field of computer vision, with applications ranging from augmented reality to sports analytic. Real-time processing is particularly crucial for applications requiring instant feedback, such as coaching for athlete positioning. Although numerous real-time pose estimation techniques have emerged [3, 16, 17, 31], achieving a balance between speed and accuracy remains challenging.
多人姿态估计 (MPPE) 在计算机视觉领域至关重要,其应用范围从增强现实到运动分析。对于需要即时反馈的应用(如运动员位置指导),实时处理尤为关键。尽管已涌现众多实时姿态估计技术 [3, 16, 17, 31],但在速度与精度之间取得平衡仍具挑战性。
Current real-time pose estimation methods fall into two categories: top-down [3, 16] and one-stage [17, 31]. Top-down methods employ pre-trained detectors to create bounding boxes around subjects, followed by pose estimation for each individual. A key limitation is that their inference time scales with the number of people in the image (see Figure 1). On the other hand, one-stage methods directly predict the locations of keypoints for all individuals in the image. However, current real-time one-stage methods [17, 31, 34] lag in accuracy compared to top-down approaches (see Figure 1). These methods, relying on the YOLO architecture, directly regress the keypoint coordinates, which hinders performance since this technique resembles using a Dirac delta distribution for each keypoint, neglecting the inherent ambiguity and uncertainty [21].
当前的实时姿态估计方法分为两类:自上而下 (top-down) [3, 16] 和单阶段 (one-stage) [17, 31]。自上而下方法使用预训练的检测器在目标周围创建边界框,然后对每个个体进行姿态估计。其关键局限在于推理时间会随图像中人数增加而线性增长 (见图 1)。另一方面,单阶段方法直接预测图像中所有个体的关键点位置。然而,当前实时单阶段方法 [17, 31, 34] 在精度上落后于自上而下方法 (见图 1)。这些基于 YOLO 架构的方法直接回归关键点坐标,由于该技术类似于为每个关键点使用 Dirac delta 分布,忽略了固有的模糊性和不确定性 [21],从而限制了性能。
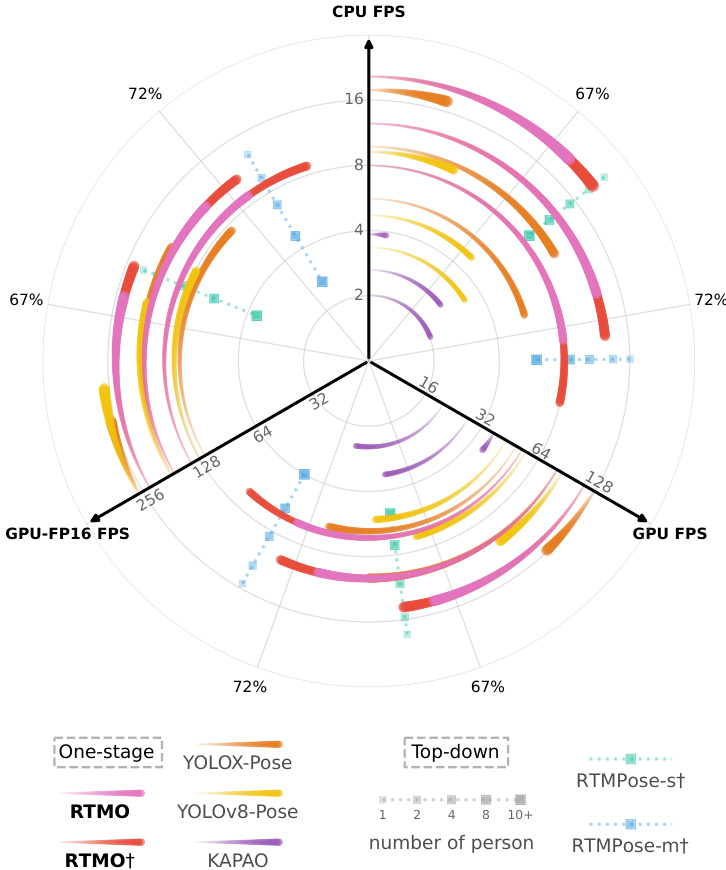
Figure 1. Efficiency and efficacy comparison among real-time pose estimation methods across different inference backends and devices. The radial axes indicate inference speed in Frames Per Second (FPS). The outer circular axis shows Average Precision (AP) on the COCO val2017 dataset. Models marked with $^\dagger$ were trained with additional data beyond the COCO train2017.
图 1: 不同推理后端和设备上实时姿态估计方法的效率与效果对比。径向轴表示以每秒帧数 (FPS) 衡量的推理速度。外圈圆周轴显示在 COCO val2017 数据集上的平均精度 (AP)。标有 $^\dagger$ 的模型使用了超出 COCO train2017 的额外数据进行训练。
Alternatively, the coordinate classification methods employ dual 1-D heatmaps that increase spatial resolution by spreading the probability of keypoint locations over two sets of bins spanning the entire image. This offers more accurate predictions with minimal extra computational cost [16, 23]. However, directly applying coordinate classification to dense prediction scenarios like onestage pose estimation leads to inefficient bin utilization due to global bin distribution across the image and each person occupying only a minor region. Additionally, conventional Kullback–Leibler divergence (KLD) losses treat all samples equally, which is suboptimal for one-stage pose estimation where instance difficulty varies significantly across grids.
或者,坐标分类方法采用双一维热力图,通过将关键点位置的概率分布到覆盖整个图像的两组区间中,从而提高空间分辨率。这种方法能以最小的额外计算成本提供更精确的预测 [16, 23]。然而,在单阶段姿态估计等密集预测场景中直接应用坐标分类,由于区间全局分布于图像且每个人仅占据极小区域,会导致区间利用率低下。此外,传统的Kullback-Leibler散度 (KLD) 损失函数对所有样本一视同仁,这对于网格间实例难度差异显著的单阶段姿态估计来说并非最优方案。
In this work, we overcome the above challenges and incorporate the coordinate classification approach within the YOLO-based framework, leading to the development of Real-Time Multi-person One-stage (RTMO) pose estimation models. RTMO introduces a Dynamic Coordinate Classifier (DCC) that includes dynamic bin allocation localized to bounding boxes and learnable bin representations. Furthermore, we propose a novel loss function based on Maximum Likelihood Estimation (MLE) to effectively train the coordinate heatmaps. This new loss allows learning of per-sample uncertainty, automatically adjusting task difficulty and balancing optimization between hard and easy samples for more effective and harmonized training.
在本工作中,我们克服了上述挑战,将坐标分类方法融入基于YOLO的框架,开发出实时多人单阶段(RTMO)姿态估计模型。RTMO引入了动态坐标分类器(DCC),该分类器包含针对边界框局部化的动态分箱分配和可学习的分箱表征。此外,我们提出了一种基于最大似然估计(MLE)的新型损失函数来有效训练坐标热图。这种新损失函数支持学习每样本不确定性,能自动调整任务难度并平衡难易样本间的优化,从而实现更高效协调的训练。
Consequently, RTMO achieves accuracy comparable to real-time top-down methods and exceeds other lightweight one-stage methods, as shown in Figure 1. Moreover, RTMO demonstrates superior speed when processing multiple instances in an image, outpacing top-down methods with similar accuracy. Notably, RTMO-l attains a $74.8%$ Average Precision (AP) on the COCO val2017 dataset [24] and exhibited 141 frames per second (FPS) on the NVIDIA V100 GPU. On the CrowdPose benchmark [19], RTMOl achieves $73.2%$ AP, a new state of the art for one-stage methods. The key contributions of this work include:
因此,RTMO 实现了与实时自上而下方法相当的精度,并超越了其他轻量级单阶段方法,如图 1 所示。此外,RTMO 在处理图像中的多个实例时表现出更快的速度,超过了精度相近的自上而下方法。值得注意的是,RTMO-l 在 COCO val2017 数据集 [24] 上达到了 74.8% 的平均精度 (AP) ,并在 NVIDIA V100 GPU 上实现了每秒 141 帧 (FPS) 的速度。在 CrowdPose 基准测试 [19] 中,RTMO-l 达到了 73.2% 的 AP,创下单阶段方法的新纪录。本工作的主要贡献包括:
• An innovative coordinate classification technique tailored for dense prediction, utilizing coordinate bins for precise keypoint localization while addressing varying instance sizes and complexities. • A new real-time one-stage MPPE approach that seamlessly integrates coordinate classification with the YOLO architecture, achieving an optimal balance of performance and speed among existing MPPE methods.
• 一种专为密集预测设计的创新坐标分类技术,通过坐标分箱实现精确关键点定位,同时解决不同实例尺寸和复杂度的问题。
• 一种新型实时单阶段多人姿态估计方法,将坐标分类与YOLO架构无缝结合,在现有方法中实现了性能与速度的最佳平衡。
2. Related Works
2. 相关工作
2.1. One-Stage Pose Estimator
2.1. 单阶段姿态估计器
Inspired by advancements in one-stage object detection algorithms [8, 10, 25, 41, 52], a series of one-stage pose estimation methods have emerged [11, 31, 35, 40, 52]. These methods perform MPPE in a single forward pass and directly regress instance-specific keypoints from predetermined root locations. Alternative approaches such as PETR [38] and ED-Pose [47] treat pose estimation as a set prediction problem for end-to-end keypoint regression. Beyond regression-based solutions, techniques like FCPose [32], InsPose [36], and CID [43] utilize dynamic convolution or attention mechanisms to generate instancespecific heatmaps for keypoint localization.
受单阶段目标检测算法[8, 10, 25, 41, 52]进展的启发,一系列单阶段姿态估计方法相继出现[11, 31, 35, 40, 52]。这些方法通过单次前向传播完成多人姿态估计(MPPE),直接从预设的根节点位置回归实例特定的关键点。PETR[38]和ED-Pose[47]等替代方案将姿态估计视为端到端关键点回归的集合预测问题。除基于回归的解决方案外,FCPose[32]、InsPose[36]和CID[43]等技术采用动态卷积或注意力机制来生成实例特定的关键点定位热图。
Compared to two-stage pose estimation methods, onestage approaches eliminate the need for pre-processing (e.g., human detection for top-down methods) and postprocessing (e.g., keypoint grouping for bottom-up methods). This results in two benefits: 1) consistent inference time, irrespective of the number of instances in the image; and 2) a simplified pipeline that facilitates deployment and practical use. Despite these advantages, the existing onestage methods struggle to balance high accuracy with realtime inference. High-accuracy models [43, 47] often depend on resource-intensive backbones like HRNet [39] or Swin [26], making real-time estimation challenging. Conversely, real-time models [31, 34] compromise on performance. Our model addresses this trade-off, delivering both high accuracy and fast real-time inference.
与两阶段姿态估计方法相比,单阶段方法省去了预处理(例如自上而下方法中的人体检测)和后处理(例如自下而上方法中的关键点分组)。这带来两个优势:1) 无论图像中包含多少实例,推理时间保持稳定;2) 简化流程便于部署和实际应用。尽管存在这些优点,现有单阶段方法仍难以平衡高精度与实时推理。高精度模型[43, 47]通常依赖HRNet[39]或Swin[26]等计算密集型主干网络,难以实现实时估计。反之,实时模型[31, 34]则需牺牲性能。我们的模型解决了这一矛盾,同时实现了高精度和快速实时推理。
2.2. Coordinate Classification
2.2. 坐标分类
SimCC [23] and RTMPose [16] have adopted coordinate classification for pose estimation, classifying keypoints into sub-pixel bins along horizontal and vertical axes to achieve spatial discrimination without high-resolution features, balancing accuracy and speed. However, spanning bins across the entire image for dense prediction methods is impractical due to the vast number of bins needed to diminish quantization error, which leads to inefficiency from many bins being superfluous for individual instances. DFL [21] sets bins around a predefined range near each anchor, which may not cover the keypoints of large instances and could induce significant quantization errors for small instances. Our approach assigns bins within localized regions scaled to each instance’s size, which optimizes bin utilization, ensures keypoint coverage, and minimizes quantization error.
SimCC [23] 和 RTMPose [16] 采用坐标分类方法进行姿态估计,将关键点沿水平和垂直轴分类到亚像素区间,以实现无需高分辨率特征的空间区分,平衡了精度与速度。然而,对于密集预测方法而言,将区间覆盖整个图像并不实际,因为需要大量区间来减少量化误差,这会导致许多区间对单个实例而言是冗余的,从而降低效率。DFL [21] 在每个锚点附近的预定义范围内设置区间,但可能无法覆盖大实例的关键点,且对小实例可能产生显著的量化误差。我们的方法将区间分配在与实例大小成比例的局部区域内,从而优化区间利用率,确保关键点覆盖,并最小化量化误差。
2.3. Transformer-Enhanced Pose Estimation
2.3. Transformer增强的姿态估计
Transformer-based architectures have become ubiquitous in pose estimation, leveraging state-of-the-art transformer backbones to improve accuracy as in ViTPose [46], or combining transformer encoders with CNNs to capture spatial relationships [48]. TokenPose [22] and Poseur [33] demonstrate the efficacy of token-based keypoint embedding in both heatmap and regression-based methods, leveraging visual cues and anatomical constraints. Frameworks like PETR [38] and ED-Pose [47] introduce transformers in endto-end multi-person pose estimation, and RTMPose [16] integrates self-attention with a SimCC-based [23] framework for keypoint dependency analysis, an approach also adopted by RTMO. While positional encoding is standard in attention to inform query and key positions, we innovative ly em- ploy it to form representation vectors for each spatial bin, enabling computation of bin-keypoint similarity that facilitates accurate localization predictions.
基于Transformer的架构在姿态估计中已无处不在,它们利用最先进的Transformer主干网络提升精度(如ViTPose [46]),或结合Transformer编码器与CNN来捕捉空间关系[48]。TokenPose [22]和Poseur [33]通过基于热图与回归的方法,展示了基于Token的关键点嵌入在利用视觉线索和解剖学约束方面的有效性。PETR [38]和ED-Pose [47]等框架将Transformer引入端到端多人姿态估计,RTMPose [16]则将自注意力与基于SimCC [23]的框架结合用于关键点依赖分析,RTMO也采用了类似方法。尽管位置编码在注意力机制中用于标记查询和键位置是标准做法,但我们创新性地利用它构建每个空间分区的表征向量,从而计算分区-关键点相似度以实现精准定位预测。
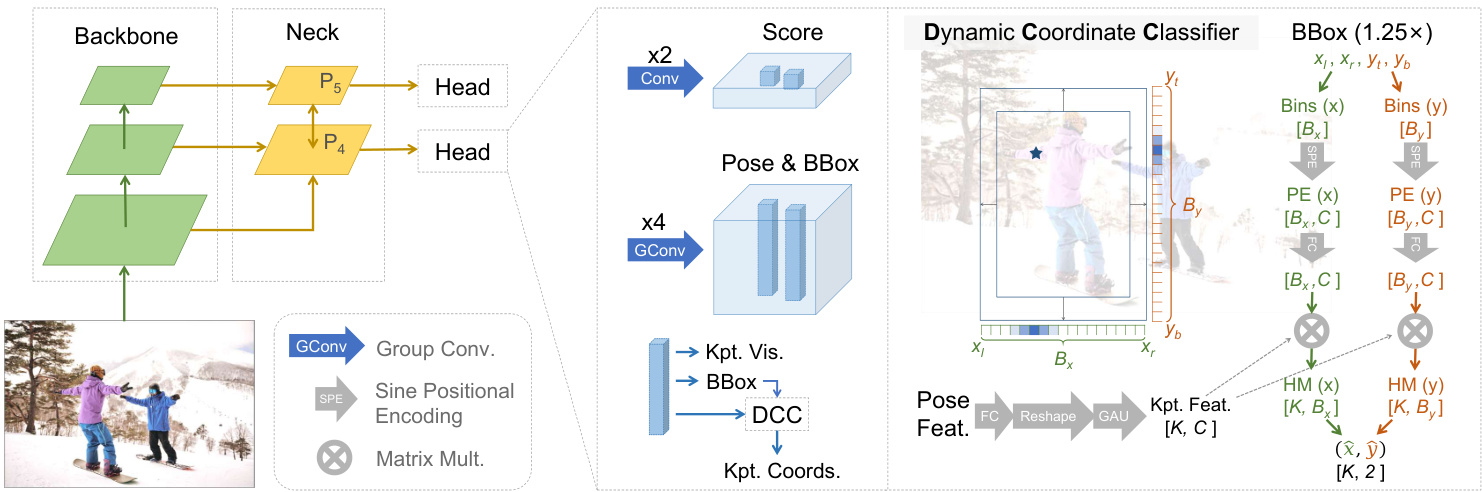
Figure 2. Overview of the RTMO Network Architecture. Its head outputs predictions for the score, bounding box, keypoint coordinates and visibility for each grid cell. The Dynamic Coordinate Classifier translates pose features into $K$ pairs of 1-D heatmaps for both the horizontal and vertical axes, encompassing an expanded region 1.25 times the size of the predicted bounding boxes. From these heatmaps, keypoint coordinates are precisely extracted. $K$ denotes the total number of keypoints.
图 2: RTMO网络架构概览。其头部输出每个网格单元的分数预测、边界框、关键点坐标及可见性。动态坐标分类器 (Dynamic Coordinate Classifier) 将姿态特征转换为 $K$ 对一维热图 (heatmap),分别对应水平轴和垂直轴,覆盖预测边界框1.25倍的扩展区域。关键点坐标从这些热图中精确提取。$K$ 表示关键点总数。
3. Methodology
3. 方法论
In our model, we adopt a YOLO-like architecture, illustrated in Figure 2. The backbone is CSPDarknet [10], and we process the last three feature maps using a Hybrid Encoder [29], yielding spatial features $P_{4}$ and $P_{5}$ with respective down sampling rates of 16 and 32. Each pixel in these features maps to a grid cell uniformly distributed on the original image plane. The network head, utilizing dual convolution blocks at each spatial level, generates a score and corresponding pose features for every grid cell. These pose features are utilized to predict bounding boxes, keypoint coordinates, and visibility. The generation of 1-D heatmap predictions through the Dynamic Coordinate Classifier is detailed in Sec. 3.1 while the proposed heatmap loss based on MLE is presented in Sec. 3.2. The complete training and inference procedures are outlined in Sec. 3.3.
在我们的模型中,采用了类似YOLO的架构,如图2所示。主干网络为CSPDarknet [10],并使用混合编码器(Hybrid Encoder) [29]处理最后三个特征图,生成空间特征$P_{4}$和$P_{5}$,其下采样率分别为16和32。这些特征中的每个像素都映射到原始图像平面上均匀分布的网格单元。网络头部在每个空间级别使用双卷积块,为每个网格单元生成分数和相应的姿态特征。这些姿态特征用于预测边界框、关键点坐标和可见性。通过动态坐标分类器生成一维热图预测的细节详见第3.1节,而基于MLE的提出热图损失在第3.2节中介绍。完整的训练和推理流程概述见第3.3节。
3.1. Dynamic Coordinate Classifier
3.1. 动态坐标分类器
The pose features associated with each grid cell encapsulate the keypoint displacement from the grid. Previous works [11, 31, 35] directly regress these displacement, and thus fall short in performance. Our study explores the integration of coordinate classification with a one-stage pose estimation framework to improve keypoint localization accuracy. A notable limitation of existing coordinate classification methods is their static strategy for bin assignment. To address this problem, we introduce the Dynamic Coordinate Classifier (DCC), which dynamically assigns ranges and forms representations for bins in two 1-D heatmaps, effectively resolving the incompatibilities of coordinate classification in dense prediction contexts.
与每个网格单元关联的位姿特征封装了关键点相对于网格的位移。先前的研究 [11, 31, 35] 直接回归这些位移,导致性能不足。我们的研究探索将坐标分类与单阶段位姿估计框架相结合,以提高关键点定位精度。现有坐标分类方法的一个显著局限是其静态的分箱分配策略。为解决该问题,我们提出动态坐标分类器 (DCC),它动态分配范围并在两个一维热图中构建分箱表示,有效解决了坐标分类在密集预测场景中的兼容性问题。
Dynamic Bin Allocation. Coordinate classification technique employed in top-down pose estimators allocates bins across the entire input image [16, 23], leading to bin wastage in one-stage methods since each subject occupies only a small portion. DFL [21] sets bins within a predefined range near each anchor, which may miss keypoints in larger instances and cause significant quantization errors in smaller ones. DCC addresses these limitations by dynamically assigning bins to align with each instance’s bounding box, ensuring localized coverage. The bounding boxes are initially regressed using a pointwise convolution layer and then expanded by $1.25\mathrm{x}$ to cover all keypoints, even in cases of inaccurate predictions. These expanded bounding boxes are uniformly divided into $B_{x},B_{y}$ bins along horizontal and vertical axes. The $\mathbf{X}$ -coordinate for each horizontal bin is calculated using:
动态分箱分配。自上而下姿态估计器采用的坐标分类技术会在整个输入图像上分配分箱 [16, 23],导致单阶段方法出现分箱浪费,因为每个主体仅占据图像的一小部分。DFL [21] 在每个锚点附近的预定义范围内设置分箱,这可能遗漏较大实例中的关键点,并在较小实例中产生显著量化误差。DCC通过动态分配分箱以匹配每个实例的边界框来解决这些限制,确保局部覆盖。边界框最初通过逐点卷积层回归,然后扩展 $1.25\mathrm{x}$ 以覆盖所有关键点,即使在预测不准确的情况下。这些扩展后的边界框沿水平和垂直轴均匀划分为 $B_{x},B_{y}$ 个分箱。每个水平分箱的 $\mathbf{X}$ 坐标通过以下公式计算:
$$
x_{i}=x_{l}+\left(x_{r}-x_{l}\right)\frac{i-1}{B_{x}-1},
$$
$$
x_{i}=x_{l}+\left(x_{r}-x_{l}\right)\frac{i-1}{B_{x}-1},
$$
where $x_{r},x_{l}$ are the left and right sides of the bounding box, and index $i$ varies from 1 to $B_{x}$ . The y-axis bins are computed similarly. We empirically use $B_{x}~=~192$ and $B_{y}=256$ for all models.
其中 $x_{r},x_{l}$ 是边界框的左右两侧,索引 $i$ 从1变化到 $B_{x}$。y轴分箱的计算方式类似。我们经验性地对所有模型使用 $B_{x}~=~192$ 和 $B_{y}=256$。
Dynamic Bin Encoding. In the context of DCC, the position of each bin varies across grids since their predicted bounding boxes differ. This differs from previous methods [16, 23] where bin coordinates are fixed. Rather than a shared representation for bins across grids used in these methods, DCC generates tailored representations on-the-fly. Specifically, we encode each bin’s coordinates into positional encodings to create bin-specific representations.
动态分箱编码。在DCC的背景下,由于预测边界框不同,每个分箱的位置在网格间会有所变化。这与之前的方法[16, 23]不同,那些方法中分箱坐标是固定的。DCC不是像这些方法那样使用跨网格的共享分箱表示,而是动态生成定制化的表示。具体来说,我们将每个分箱的坐标编码为位置编码,以创建分箱特定的表示。
where $t$ denotes the temperature, $c$ is the index, and $C$ represents the total number of dimension. We refine the positional encoding’s adaptability for our task using a fully connected layer, which applies a learnable linear transformation $\phi$ , thereby optimizing its effectiveness in DCC.
其中 $t$ 表示温度,$c$ 为索引,$C$ 代表总维度数。我们通过全连接层优化位置编码的适应性,该层应用可学习的线性变换 $\phi$,从而提升其在 DCC 中的效果。
The primary objective of DCC is to accurately predict keypoint occurrence probabilities at each bin, informed by bin coordinates and keypoint features. Keypoint features are extracted from the pose feature and refined via a Gated Attention Unit (GAU) module [14] following RTMPose [16], to enhance inter-keypoint consistency. The probability heatmap is generated by multiplying the keypoint features $f_{k}$ with the positional encodings of each bin ${\cal P E}\left(x_{i}\right)$ , followed by a softmax:
DCC的主要目标是通过分箱坐标和关键点特征,准确预测每个分箱中关键点出现的概率。关键点特征从姿态特征中提取,并经由RTMPose [16]提出的门控注意力单元(GAU)模块[14]进行细化,以增强关键点间的一致性。概率热图通过将关键点特征$f_{k}$与每个分箱的位置编码${\cal P E}\left(x_{i}\right)$相乘,再经过softmax运算生成。
$$
\hat{p}{k}\left(x_{i}\right)=\frac{e^{\pmb{f}{k}\cdot\phi\left({P}\pmb{E}\left(x_{i}\right)\right)}}{\sum_{j=1}^{B_{x}}e^{\pmb{f}{k}\cdot\phi\left({P}\pmb{E}\left(x_{j}\right)\right)}},
$$
$$
\hat{p}{k}\left(x_{i}\right)=\frac{e^{\pmb{f}{k}\cdot\phi\left({P}\pmb{E}\left(x_{i}\right)\right)}}{\sum_{j=1}^{B_{x}}e^{\pmb{f}{k}\cdot\phi\left({P}\pmb{E}\left(x_{j}\right)\right)}},
$$
where $\scriptstyle f_{k}$ is the $k$ -th keypoint’s feature vector.
其中 $\scriptstyle f_{k}$ 是第 $k$ 个关键点的特征向量。
3.2. MLE for Coordinate Classification
3.2. 坐标分类的最大似然估计 (MLE)
In classification tasks, one-hot targets and cross-entropy loss are commonly utilized. Label smoothing, like Gaussian label smoothing used in SimCC [23] and RTMPose [16], along with KLD, can improve performance. The Gaussian mean $\mu_{x},\mu_{y}$ and variance σ2 are set to the annotated coordinates and a predefined parameter. The target distribution is defined as:
在分类任务中,通常会使用独热编码目标和交叉熵损失。标签平滑技术(如SimCC [23]和RTMPose [16]中采用的高斯标签平滑)结合KLD可以提升性能。高斯均值$\mu_{x},\mu_{y}$和方差σ2被设定为标注坐标与预设参数。目标分布定义为:
$$
p_{k}\left(x_{i}\mid\mu_{x}\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{\left(x_{i}-\mu_{x}\right)^{2}}{2\sigma^{2}}}\sim{\cal N}\left(x_{i};\mu_{x},\sigma^{2}\right).
$$
$$
p_{k}\left(x_{i}\mid\mu_{x}\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{\left(x_{i}-\mu_{x}\right)^{2}}{2\sigma^{2}}}\sim{\cal N}\left(x_{i};\mu_{x},\sigma^{2}\right).
$$
Importantly, we note that $p_{k}(x_{i}\mid\mu_{x})$ is mathematically identical to the likelihood $p_{k}(\mu_{x}\mid x_{i})$ of the annotation $\mu_{x}$ under a Gaussian error model with true value $x_{i}$ . This symmetrical property arises because the Gaussian distribution is symmetric with respect to its mean. Treating the predicted $\hat{p}{k}(x_{i})$ as the prior of $x_{i}$ , the annotation likelihood for the
值得注意的是,我们指出 $p_{k}(x_{i}\mid\mu_{x})$ 在数学上等同于高斯误差模型中标注 $\mu_{x}$ 关于真值 $x_{i}$ 的似然 $p_{k}(\mu_{x}\mid x_{i})$ 。这种对称性源于高斯分布关于其均值的对称特性。将预测值 $\hat{p}{k}(x_{i})$ 视为 $x_{i}$ 的先验概率时,标注似然
$k$ -th keypoint is:
第 $k$ 个关键点为:
$$
\begin{array}{l}{P\left(\mu_{x}\right)=\displaystyle\sum_{i=1}^{B_{x}}P\left(\mu_{x}\mid x_{i}\right)P\left(x_{i}\right)}\ {\displaystyle\qquad=\displaystyle\sum_{i=1}^{B_{x}}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{\left(x_{i}-\mu_{x}\right)^{2}}{2\sigma^{2}}}\hat{p}{k}\left(x_{i}\right).}\end{array}
$$
$$
\begin{array}{l}{P\left(\mu_{x}\right)=\displaystyle\sum_{i=1}^{B_{x}}P\left(\mu_{x}\mid x_{i}\right)P\left(x_{i}\right)}\ {\displaystyle\qquad=\displaystyle\sum_{i=1}^{B_{x}}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{\left(x_{i}-\mu_{x}\right)^{2}}{2\sigma^{2}}}\hat{p}{k}\left(x_{i}\right).}\end{array}
$$
Maximizing this likelihood models the true distribution of the annotations.
最大化这一似然性可模拟标注的真实分布。
In practice, we employ a Laplace distribution for $P\left(\mu_{x}\mid x_{i}\right)$ and a negative log-likelihood loss:
在实践中,我们采用拉普拉斯分布作为 $P\left(\mu_{x}\mid x_{i}\right)$ 的假设,并使用负对数似然损失函数:
$$
\mathcal{L}{m l e}^{(x)}=-\log\left[\sum_{i=1}^{B_{x}}\frac{1}{\hat{\sigma}}e^{-\frac{\left|x_{i}-\mu_{x}\right|}{2\hat{\sigma}s}}\hat{p}{k}\left(x_{i}\right)\right],
$$
$$
\mathcal{L}{m l e}^{(x)}=-\log\left[\sum_{i=1}^{B_{x}}\frac{1}{\hat{\sigma}}e^{-\frac{\left|x_{i}-\mu_{x}\right|}{2\hat{\sigma}s}}\hat{p}{k}\left(x_{i}\right)\right],
$$
where the instance size $s$ normalizes the error and $\hat{\sigma}$ is the predicted variance. The constant factor is omitted as it does not affect the gradient. The total Maximum Likelihood Estimation (MLE) loss is $\mathcal{L}{m l e}=\mathcal{L}{m l e}^{(x)}+\mathcal{L}_{m l e}^{(y)}$
其中实例大小 $s$ 用于归一化误差,$\hat{\sigma}$ 是预测方差。常数因子被省略,因为它不影响梯度。总的最大似然估计 (MLE) 损失为 $\mathcal{L}{m l e}=\mathcal{L}{m l e}^{(x)}+\mathcal{L}_{m l e}^{(y)}$。
Unlike KLD, our MLE loss allows for learnable variance, representing uncertainty. This uncertainty learning framework automatically adjusts the difficulty of various samples [5, 13]. For hard samples, the model predicts a large variance to ease optimization. For simple samples, it predicts a small variance, aiding in accuracy improvement. With KLD, adopting a learnable variance is problematic - the model leans to predict a large variance to flatten the target distribution as this simplifies learning. More discussion can be found in Sec. 4.4.
与KLD不同,我们的MLE损失允许学习方差以表示不确定性。这种不确定性学习框架能自动调整不同样本的难度 [5, 13]。对于困难样本,模型会预测较大的方差以降低优化难度;对于简单样本,则预测较小的方差以提升准确性。若在KLD中采用可学习方差会导致问题——模型倾向于预测较大方差来扁平化目标分布,因为这会简化学习过程。更多讨论详见第4.4节。
3.3. Training and Inference
3.3. 训练与推理
Training. Our model, adhering to a YOLO-like structure, employs dense grid prediction for human detection and pose estimation. It is crucial for the model to differentiate between positive and negative grids. We extend SimOTA [10] for training, assigning positive grids based on grid scores, bounding box regression, and pose estimation accuracy. The head’s score branch classifies these grids, supervised by varifocal loss [51] $\mathcal{L}_{c l s}$ , with target scores being the Object Keypoint Similarity (OKS) between the predicted pose and the assigned ground truth for each grid.
训练。我们的模型采用类似YOLO的结构,通过密集网格预测实现人体检测与姿态估计。关键在于模型需区分正负网格。我们扩展了SimOTA [10]训练方法,根据网格得分、边界框回归和姿态估计精度分配正网格。头部得分分支通过变焦损失(vari focal loss) [51] $\mathcal{L}_{c l s}$监督网格分类,目标分数为每个网格预测姿态与标注真值之间的目标关键点相似度(OKS)。
Positive grid tokens yield bounding box, keypoint coordinates, and visibility predictions. Keypoint coordinates are derived via the DCC, while other predictions come from pointwise convolution layers. The losses applied are IoU loss for bounding boxes $\mathcal{L}{b b o x}$ , MLE loss for keypoints $\mathcal{L}{m l e}$ , and BCE loss for visibility $\mathcal{L}_{\nu i s}$ .
正向网格token生成边界框、关键点坐标和可见性预测。关键点坐标通过DCC (Discrete Cosine Coordinate) 方法获得,其他预测来自逐点卷积层。采用的损失函数包括:边界框的IoU损失 $\mathcal{L}{b b o x}$、关键点的MLE损失 $\mathcal{L}{m l e}$,以及可见性的BCE损失 $\mathcal{L}_{\nu i s}$。
Given the DCC’s computational demands, we implement a pointwise convolution layer for preliminary coordinate regression, similar to YOLO-Pose [31], to mitigate out-ofmemory issues. This regressed keypoints $\mathrm{kpt}{r e g}$ serves as a proxy in SimOTA for positive grid selection, with the decoded keypoints $\mathrm{kpt}_{d e c}$ later used to calculate OKS. The regression branch’s loss is OKS loss [31]:
考虑到DCC的计算需求,我们实现了类似YOLO-Pose [31]的点式卷积层进行初步坐标回归,以缓解内存不足问题。这些回归关键点$\mathrm{kpt}{reg}$在SimOTA中作为正网格选择的代理,而解码关键点$\mathrm{kpt}_{dec}$随后用于计算OKS。回归分支的损失函数为OKS损失[31]:
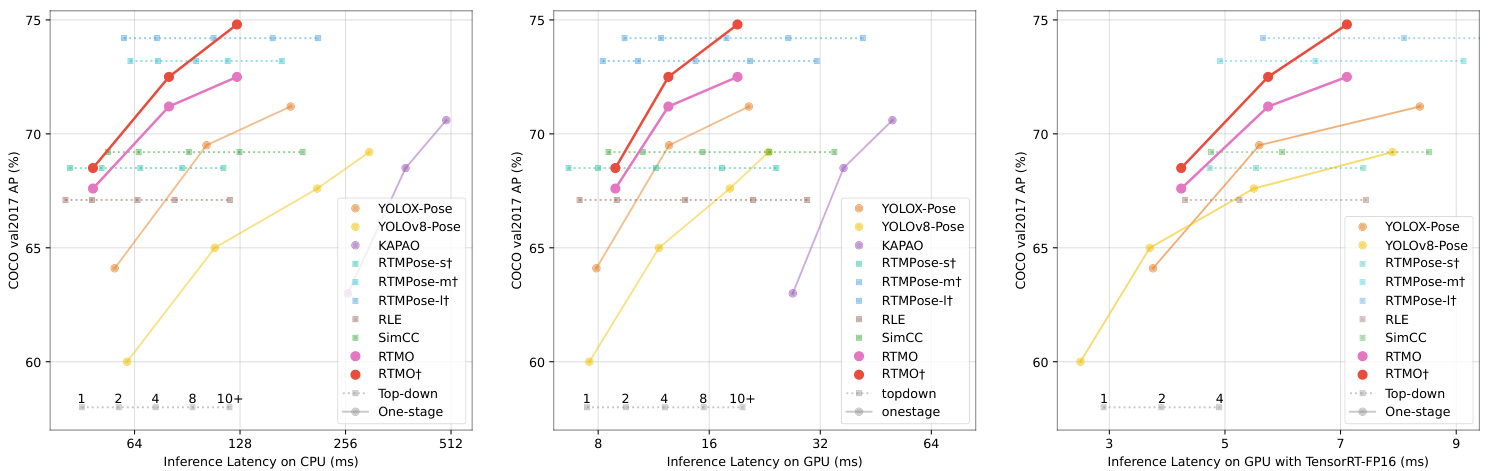
Figure 3. Comparison of RTMO with other real-time multi-person pose estimators. The latency for top-down methods varies depending on the number of instances in the image, as indicated by numerical values in the figures. All models are evaluated without test-time augmentation. $^\dagger$ indicates that the model was trained using additional data beyond the COCO train2017 dataset.
图 3: RTMO与其他实时多人姿态估计器的对比。自上而下方法的延迟会随图像中实例数量变化(如图中数值所示)。所有模型均在未使用测试时增强的情况下进行评估。$^\dagger$表示该模型使用了超出COCO train2017数据集的额外数据进行训练。
$$
\mathcal{L}{p r o x y}=1-\mathrm{OKS}\left(\mathrm{kpt}{r e g},\mathrm{kpt}_{d e c}\right).
$$
$$
\mathcal{L}{p r o x y}=1-\mathrm{OKS}\left(\mathrm{kpt}{r e g},\mathrm{kpt}_{d e c}\right).
$$
The total loss for the proposed model is
所提出模型的总损失为
$$
\mathcal{L}=\lambda_{1}\mathcal{L}{b b o x}+\lambda_{2}\mathcal{L}{m l e}+\lambda_{3}\mathcal{L}{p r o x y}+\lambda_{4}\mathcal{L}{c l s}+\mathcal{L}_{\nu i s},
$$
$$
\mathcal{L}=\lambda_{1}\mathcal{L}{b b o x}+\lambda_{2}\mathcal{L}{m l e}+\lambda_{3}\mathcal{L}{p r o x y}+\lambda_{4}\mathcal{L}{c l s}+\mathcal{L}_{\nu i s},
$$
with hyper parameters $\lambda_{1},\lambda_{2},\lambda_{3}$ , and $\lambda_{4}$ set at $\lambda_{1}=\lambda_{2}=$ $5,\lambda_{3}=10$ , and $\lambda_{4}=2$ .
超参数 $\lambda_{1}$、$\lambda_{2}$、$\lambda_{3}$ 和 $\lambda_{4}$ 分别设置为 $\lambda_{1}=\lambda_{2}=5$、$\lambda_{3}=10$ 以及 $\lambda_{4}=2$。
Inference. During inference, our model employs a score threshold of 0.1 and non-maximum suppression for grid filtering. It then decodes pose features from selected grids into heatmaps, using integral over the heatmaps to derive keypoint coordinates. This selective decoding approach minimizes the number of features for processing, reducing computational cost.
推理。在推理过程中,我们的模型采用0.1的分数阈值和非极大值抑制进行网格筛选,随后将选定网格的姿态特征解码为热力图,通过对热力图积分得到关键点坐标。这种选择性解码方法最大限度地减少了需要处理的特征数量,从而降低了计算成本。
4. Experiments
4. 实验
4.1. Settings
4.1. 设置
Datasets. Experiments were primarily conducted on the COCO2017 Keypoint Detection benchmark [24], comprising approximately 250K person instances with 17 keypoints. Performance comparisons were made with stateof-the-art methods on both the val2017 and test-dev sets. To explore our model’s performance ceiling, training was also extended to include additional datasets: CrowdPose [19], AIC [44], MPII [1], JHMDB [15], Halpe [9], and Pose Track 18 [2]. These annotations were converted to COCO format. RTMO was further evaluated on the CrowdPose benchmark [19], which is known for its high complexity due to crowded and occluded scenes, comprising 20K images and approximately 80K persons with 14 key points.
数据集。实验主要在COCO2017关键点检测基准[24]上进行,该数据集包含约25万个人体实例和17个关键点。我们在val2017和test-dev集上与最先进方法进行了性能对比。为探索模型性能上限,训练还扩展至以下数据集:CrowdPose[19]、AIC[44]、MPII[1]、JHMDB[15]、Halpe[9]和PoseTrack18[2],这些标注均转换为COCO格式。RTMO还在以拥挤遮挡场景著称的高复杂度CrowdPose基准[19]上进行了评估,该数据集包含2万张图像、约8万个人体实例及14个关键点。
OKS-based Average Precision (AP) served as the evaluation metric for both datasets.
基于OKS的平均精度 (AP) 作为两个数据集的评估指标。
Implementation Details. During training, we adopt the image augmentation pipeline from YOLOX [10], incorporating mosaic augmentation, random color adjustments, geometric transformations, and MixUp [50]. Training images are resized to dimensions [480, 800]. Epoch counts are set to 600 and 700 for the COCO and CrowdPose datasets, respectively. The training process is divided into two stages: the first involves
