Abstract
摘要
The dominant paradigm for neural text generation is left-to-right decoding from autoregressive language models. Constrained or controllable generation under complex lexical constraints, however, requires foresight to plan ahead feasible future paths.
神经文本生成的主流范式是通过自回归语言模型进行从左到右的解码。然而,在复杂词汇约束下的受控生成需要前瞻性来规划可行的未来路径。
Drawing inspiration from the $\mathbf{A}^{*}$ search algorithm, we propose NEUROLOGIC A⋆esque,1 a decoding algorithm that incorporates heuristic estimates of future cost. We develop efficient lookahead heuristics that are efficient for large-scale language models, making our method a drop-in replacement for common techniques such as beam search and top-k sampling. To enable constrained generation, we build on NEUROLOGIC decoding (Lu et al., 2021), combining its flexibility in incorporating logical constraints with $\mathbf{A}^{\star}$ esque estimates of future constraint satisfaction.
受 $\mathbf{A}^{*}$ 搜索算法启发,我们提出 NEUROLOGIC A⋆esque——一种融合未来代价启发式估计的解码算法。我们开发了适用于大语言模型的高效前瞻启发函数,使该方法能直接替代集束搜索 (beam search) 和 top-k 采样等常规技术。为实现约束生成,我们在 NEUROLOGIC 解码 (Lu et al., 2021) 基础上进行扩展,将其融入逻辑约束的灵活性与 $\mathbf{A}^{\star}$ esque 的未来约束满足度预测相结合。
Our approach outperforms competitive baselines on five generation tasks, and achieves new state-of-the-art performance on table-totext generation, constrained machine translation, and keyword-constrained generation. The improvements are particularly notable on tasks that require complex constraint satisfaction or in few-shot or zero-shot settings. NEU- ROLOGIC $\mathbf{A}^{\star}$ esque illustrates the power of decoding for improving and enabling new capabilities of large-scale language models.
我们的方法在五项生成任务上超越了竞争基线,并在表格到文本生成(table-to-text generation)、受限机器翻译(constrained machine translation)和关键词约束生成(keyword-constrained generation)任务上取得了新的最先进(state-of-the-art)性能。在需要复杂约束满足的任务,以及少样本(few-shot)或零样本(zero-shot)设置下,改进尤为显著。NEUROLOGIC $\mathbf{A}^{\star}$ 展示了解码在提升和实现大语言模型新能力方面的强大潜力。
1 Introduction
1 引言
The dominant paradigm for neural text generation is based on left-to-right decoding from auto regressive language models such as GPT-2/3 (Radford et al., 2019; Brown et al., 2020). Un- der this paradigm, common decoding techniques such as beam search or top-k/p sampling (Holtzman et al., 2020) determine which token to generate next based on what happened in the past, without explicitly looking ahead into the future. While this lack of foresight often suffices for open-ended text generation – where any coherent text can be acceptable – for constrained text generation, planning ahead is crucial for incorporating all desired content in the generated output (Hu et al., 2017; Dathathri et al., 2019).
神经文本生成的主流范式是基于自回归语言模型(如GPT-2/3 [Radford et al., 2019; Brown et al., 2020])从左到右的解码。在这种范式下,常见的解码技术(如束搜索或top-k/p采样 [Holtzman et al., 2020])仅根据过去已生成的内容决定下一个token,而不会显式地前瞻未来。虽然这种缺乏前瞻性的方式对于开放式文本生成(任何连贯文本均可接受)通常足够,但在约束性文本生成中,提前规划对于整合所有期望内容至关重要 [Hu et al., 2017; Dathathri et al., 2019]。

Figure 1: NEUROLOGIC⋆ leverages lookahead heuristics to guide generations towards those that satisfy the given task-specific constraints. In this example from the COMMONGEN task, although summer is a more likely next word given the already-generated past, NEUROLOGIC $\star$ looks ahead to see that selecting winter results in a generation that incorporates unsatisfied constraint snow with a higher probability later on. Thus, winter is preferred despite being lower probability than summer.
图 1: NEUROLOGIC⋆利用前瞻启发式方法引导生成结果满足特定任务约束。在这个COMMONGEN任务示例中,虽然根据已生成内容summer是更可能的下一个词,但NEUROLOGIC⋆通过前瞻发现选择winter会使后续生成更大概率包含未满足约束snow。因此,尽管winter的概率低于summer,仍被优先选择。
Classical search algorithms such as $\mathbf{A}^{}$ search (Hart et al., 1968; Pearl, 1984; Korf, 1985) ad- dress the challenge of planning ahead by using heuristic estimation of future cost when making decisions. Drawing inspiration from $\mathbf{A}^{}$ search, we develop NEUROLOGIC $\mathbf{A}^{\star}$ esque (shortened to NEUROLOGIC⋆), which combines $\mathbf{A}^{*}$ -like heuristic estimates of future cost (e.g. perplexity, constraint satisfaction) with common decoding algorithms for neural text generation (e.g. beam search, top $k$ sampling), while preserving the efficiency demanded by large-scale neural language models.
经典搜索算法如$\mathbf{A}^{}$搜索 (Hart et al., 1968; Pearl, 1984; Korf, 1985) 通过决策时使用未来成本的启发式估计来应对前瞻性规划的挑战。受$\mathbf{A}^{}$搜索启发,我们开发了NEUROLOGIC$\mathbf{A}^{\star}$esque (简称为NEUROLOGIC⋆),它将$\mathbf{A}^{*}$式的未来成本启发式估计 (如困惑度、约束满足) 与神经文本生成的常见解码算法 (如集束搜索、top $k$采样) 相结合,同时保持大规模神经语言模型所需的高效性。
As selecting the next token to generate based on the optimal future cost is NP-complete (Chen et al.,
在选择下一个基于最优未来成本的Token生成时是NP完全问题 [20]。
2018), we develop lookahead heuristics, which approximate cost at each decoding step based on continuations of the sequence-so-far. Figure 1 shows an example, where NEUROLOGIC $\mathrm{A}^{\star}$ esque guides generation towards a decision that would have been ignored based on the past alone, but is selected after looking ahead and incorporating the probability that constraints are satisfied in the future.
2018), 我们开发了前瞻启发式方法, 该方法基于当前序列的延续来近似计算每个解码步骤的成本。图 1: 展示了一个示例, 其中 NEUROLOGIC 的 $\mathrm{A}^{\star}$ 类算法引导生成朝向一个仅基于过去会被忽略的决策, 但在前瞻并纳入约束在未来可能被满足的概率后被选中。
Our approach builds on NEUROLOGIC Decoding of Lu et al. (2021), a variation of beam-search for controlling generation through rich logic-based lexical constraints expressed in Conjunctive Normal Form (CNF). Our work generalizes Lu et al. (2021) by (1) incorporating novel lookahead heuristics to estimate future contraint satisfaction, and (2) developing additional un constrained variants that can work with an empty set of constraints. These new algorithm variants support broad applications of NEUROLOGIC⋆, including un constrained generation, as demonstrated in our experiments.
我们的方法基于Lu等人(2021)提出的NEUROLOGIC解码技术,这是一种通过合取范式(CNF)表达基于逻辑的丰富词汇约束来控制生成的束搜索变体。本研究在Lu等人(2021)的基础上进行了两项扩展:(1)引入新颖的前瞻启发式方法来预估未来约束满足情况,(2)开发了可处理空约束集的非约束变体算法。如实验所示,这些新算法变体支持NEUROLOGIC⋆的广泛应用场景,包括非约束生成任务。
Extensive experiments across five generation tasks demonstrate that our approach outperforms competitive baselines. We test NEUROLOGIC⋆ in conjunction with both supervised and unsupervised models and find that the performance gain is pronounced especially in zero-shot or few-shot settings. In particular, on the COMMONGEN benchmark, using our proposed decoding algorithm with an off-the-shelf language model outperforms a host of supervised baselines with conventional decoding algorithms. This demonstrates that a strong inference-time algorithm such as NEUROLOGIC⋆ can alleviate the need for costly datasets that are manually annotated for explicit supervision. Moreover, we find that NEUROLOGIC⋆ achieves stateof-the-art performance in various settings, including WMT17 English-German machine translation with lexical constraints (Dinu et al., 2019) and fewshot E2ENLG table-to-text generation (Chen et al., 2020b).
在五项生成任务上的大量实验表明,我们的方法优于竞争基线。我们分别在监督模型和无监督模型中测试了NEUROLOGIC⋆,发现性能提升在零样本或少样本设置中尤为显著。特别是在COMMONGEN基准测试中,使用现成大语言模型搭配我们提出的解码算法,其表现优于采用传统解码算法的多种监督基线。这证明像NEUROLOGIC⋆这样强大的推理时算法,可以减少对人工标注的高成本显式监督数据集的需求。此外,我们发现NEUROLOGIC⋆在多种场景下实现了最先进的性能,包括带词汇约束的WMT17英德机器翻译 (Dinu et al., 2019) 以及少样本的E2ENLG表格到文本生成 (Chen et al., 2020b)。
In summary, we develop NEUROLOGIC $\mathbf{A}^{\star}$ esque, a new decoding algorithm for effective and efficient text generation. To our knowledge this is the first $\mathbf{A}^{*}$ -like algorithm for guided text generation via lookahead heuristics. Our algorithm is versatile, as it can be applied to a variety of tasks via inference-time constraints, reducing the need for costly labeled data. Extensive experiments show its effectiveness on several important generation benchmarks.
总之,我们开发了NEUROLOGIC $\mathbf{A}^{\star}$ esque算法,这是一种用于高效文本生成的新型解码算法。据我们所知,这是首个通过前瞻启发式实现引导式文本生成的类$\mathbf{A}^{*}$算法。该算法具有通用性,可通过推理时约束应用于多种任务,从而减少对昂贵标注数据的需求。大量实验表明,该算法在多个重要生成基准测试中均表现优异。
2 NEUROLOGIC esque Decoding
2 NEUROLOGIC 解码
We describe NEUROLOGIC $\mathbf{A}^{\star}$ esque Decoding (shortened as NEUROLOGIC⋆), our decoding algorithm motivated by $\mathbf{A}^{*}$ search (Hart et al., 1968), a best-first search algorithm that finds high-scoring paths using a heuristic estimate of future return. We first introduce the decoding problem, and then describe our heuristics with a novel lookahead procedure for adapting NEUROLOGIC⋆ search to unconstrained and constrained generation with largescale auto regressive models.
我们介绍NEUROLOGIC $\mathbf{A}^{\star}$ esque解码(简称NEUROLOGIC⋆),这是一种受$\mathbf{A}^{}$搜索(Hart等人,1968年)启发的解码算法。$\mathbf{A}^{*}$搜索是一种最佳优先搜索算法,利用对未来回报的启发式估计来寻找高分路径。我们首先介绍解码问题,然后描述我们的启发式方法,包括一种新颖的前瞻性程序,用于将NEUROLOGIC⋆搜索适配到无约束和约束生成的大规模自回归模型中。
2.1 Decoding Withesque Lookahead
2.1 使用式前瞻解码
Decoding. Sequence-to-sequence generation is the task of generating an output sequence $\mathbf{y}$ given an input sequence $\mathbf{x}$ . We consider standard left-to-right, auto regressive models, $p_{\theta}(\mathbf{y}\vert\mathbf{x})=$ $\begin{array}{r}{\prod_{t=1}^{|\mathbf{y}|}p_{\theta}(y_{t}|\mathbf{y}_{<t},\mathbf{x})}\end{array}$ , and omit $\mathbf{x}$ to reduce clutter. Decoding consists of solving,
解码。序列到序列生成的任务是根据输入序列 $\mathbf{x}$ 生成输出序列 $\mathbf{y}$。我们考虑标准的自左向右自回归模型,$p_{\theta}(\mathbf{y}\vert\mathbf{x})=$ $\begin{array}{r}{\prod_{t=1}^{|\mathbf{y}|}p_{\theta}(y_{t}|\mathbf{y}_{<t},\mathbf{x})}\end{array}$,为简化表达省略 $\mathbf{x}$。解码过程需要求解:
$$
\mathbf{y}_{}=\underset{\mathbf{y}\in\mathcal{V}}{\arg\operatorname*{max}}F(\mathbf{y}).
$$
$$
\mathbf{y}_{}=\underset{\mathbf{y}\in\mathcal{V}}{\arg\operatorname*{max}}F(\mathbf{y}).
$$
Where $\mathcal{V}$ is the set of all sequences. In our setting, the objective $F(\mathbf{y})$ takes the form $s(\mathbf{y})+H(\mathbf{y})$ , where $s(\mathbf{y})$ is $\log p_{\boldsymbol{\theta}}(\mathbf{y})$ , and $H(\mathbf{y})$ is either zero or is a score for satisfying constraints on $\mathbf{y}$ .
其中 $\mathcal{V}$ 是所有序列的集合。在我们的设定中,目标函数 $F(\mathbf{y})$ 的形式为 $s(\mathbf{y})+H(\mathbf{y})$,其中 $s(\mathbf{y})$ 是 $\log p_{\boldsymbol{\theta}}(\mathbf{y})$,而 $H(\mathbf{y})$ 要么为零,要么是对 $\mathbf{y}$ 满足约束条件的评分。
Our method takes the perspective of decoding as discrete search, in which states are partial prefixes, $\mathbf{y}{<t}$ , actions are tokens in vocabulary $\nu$ (i.e. $y_{t}\in$ $\nu$ ) and transitions add a token to a prefix, $\mathbf{y}{<t}\circ y_{t}$ . Each step of decoding consists of 1) expanding a set of candidate next-states, 2) scoring each candidate, and 3) selecting the $k$ best candidates:
我们的方法将解码视为离散搜索过程,其中状态是部分前缀 $\mathbf{y}{<t}$ ,动作是词汇表 $\nu$ 中的 token (即 $y_{t}\in$ $\nu$ ),状态转移通过向当前前缀添加 token 实现 $\mathbf{y}{<t}\circ y_{t}$ 。解码的每一步包含:1) 扩展候选下一状态集合,2) 对每个候选状态评分,3) 选择 $k$ 个最优候选。
$$
\begin{array}{r l}&{Y_{t}^{\prime}={\mathbf y_{<t}\circ y_{t}|\mathbf y_{<t}\in Y_{t-1},y_{t}\in\mathcal{V}},}\ &{Y_{t}=\underset{(\mathbf y_{<t},y_{t})\in Y_{t}^{\prime}}{\arg\mathrm{topk}}\left\lbrace f(\mathbf y_{<t},y_{t})\right\rbrace,}\end{array}
$$
$$
\begin{array}{r l}&{Y_{t}^{\prime}={\mathbf y_{<t}\circ y_{t}|\mathbf y_{<t}\in Y_{t-1},y_{t}\in\mathcal{V}},}\ &{Y_{t}=\underset{(\mathbf y_{<t},y_{t})\in Y_{t}^{\prime}}{\arg\mathrm{topk}}\left\lbrace f(\mathbf y_{<t},y_{t})\right\rbrace,}\end{array}
$$
where $Y_{0} =~{\langle b o s\rangle}$ and $f(\cdot)$ is a scoring function that approximates the objective $F$ . Common decoding algorithms such as beam search score candidates without considering future tokens, e.g., $f(\mathbf{y}{<t},y_{t})=\log p_{\theta}(\mathbf{y}_{\le t}).$
其中 $Y_{0} =~{\langle b o s\rangle}$,且 $f(\cdot)$ 是近似目标 $F$ 的评分函数。常见的解码算法(如束搜索)在评分候选序列时不考虑未来 token,例如 $f(\mathbf{y}{<t},y_{t})=\log p_{\theta}(\mathbf{y}_{\le t}).$
Lookahead heuristics. Our method incorporates an estimate of the future into candidate selection. Ideally, we want to select candidates that are on optimal trajectories, replacing Equation 2 with:
前瞻启发式。我们的方法将未来预估纳入候选选择中。理想情况下,我们希望选择处于最优轨迹上的候选,将公式2替换为:
$$
Y_{t}={(y<t,y_{t}) Y_{t}^{}}{{topk}}{{{y}>t}{{max}}F(y{<t},y_{t},{y}_{>t})}.
$$
However, computing Equation 3 presents two difficulties: 1) the objective $F(\mathbf{y})$ may be unknown or difficult to compute, and 2) the space of future trajectories $\mathbf{y}_{>t}$ is prohibitively large.
然而,计算方程3存在两个难点:1) 目标函数 $F(\mathbf{y})$ 可能未知或难以计算;2) 未来轨迹空间 $\mathbf{y}_{>t}$ 过于庞大。
Motivated by $\mathbf{A}^{*}$ search (Hart et al., 1968), a best-first search algorithm that finds high-scoring paths by selecting actions that maximize,
受 $\mathbf{A}^{*}$ 搜索 (Hart et al., 1968) 的启发,这是一种通过选择最大化得分路径动作的最佳优先搜索算法,
$$
f(a)=s(a)+h(a),
$$
$$
f(a)=s(a)+h(a),
$$
where $s(a)$ is the score-so-far and $h(a)$ is a heuris- tic estimate of the future score. We approximate the objective using a lightweight heuristic $h(\cdot)$ ,
其中 $s(a)$ 是当前得分,$h(a)$ 是对未来得分的启发式估计。我们使用轻量级启发式 $h(\cdot)$ 来近似目标函数。
$$
Y_{t}={y{ t} Y_{t}^{}}{{topk}}{s(y{t})+{y{>t}}{{max}}h({y}{<t},y_{t},{y}_{>t})},
$$
where $s(\mathbf{y}{\le t})=\log p_{\theta}(\mathbf{y}_{\le t}).$ . To make the search tractable, we search over a set of lookahead continuations, approximating Equation 3 as,
其中 $s(\mathbf{y}{\le t})=\log p_{\theta}(\mathbf{y}{\le t})$。为使搜索可行,我们在前瞻延续集上进行搜索,将方程3近似为
where each element $\mathbf{y}{t+1:t+\ell}$ of $\mathcal{L}{\ell}(\mathbf{y}_{\le t})$ is a length $\ell$ continuation of $\mathbf{y}{\le}t$ . Beam search corresponds to setting $\ell$ and $h$ to 0.
其中 $\mathcal{L}{\ell}(\mathbf{y}{\le t})$ 的每个元素 $\mathbf{y}{t+1:t+\ell}$ 都是 $\mathbf{y}_{\le t}$ 的长度为 $\ell$ 的延续。束搜索 (beam search) 对应将 $\ell$ 和 $h$ 设为 0。
$\mathbf{A}^{\star}$ esque decoding. Beam search, $\mathbf{A}^{}$ search, and our method fall under a general class of algorithms that differ based on (1) which candidates are expanded, (2) which candidates are pruned, (3) how candidates are scored (Meister et al., 2020). We inherit the practical advantages of beam search-style expansion and pruning, while drawing on $\mathbf{A}^{*}$ -like heuristics to incorporate estimates of the future, and refer to our method as $\mathbf{A}^{\star}$ esque decoding.
$\mathbf{A}^{\star}$ 式解码。束搜索 (beam search)、$\mathbf{A}^{}$ 搜索和我们的方法都属于一类通用算法,其区别在于:(1) 扩展哪些候选,(2) 剪枝哪些候选,(3) 如何对候选进行评分 [20]。我们继承了束搜索式扩展和剪枝的实用优势,同时借鉴 $\mathbf{A}^{*}$ 类启发式方法来纳入未来估计,并将我们的方法称为 $\mathbf{A}^{\star}$ 式解码。
Generating lookaheads. We compare several methods for generating the lookaheads $\mathcal{L}{\ell}(\mathbf{y}_{\le t})$ .
生成前瞻。我们比较了几种生成前瞻 $\mathcal{L}{\ell}(\mathbf{y}_{\le t})$ 的方法。
We also consider a relaxation which interpolates between providing the greedy token and a uniform mixture of tokens as input at each step. Specifically, we adjust the model’s probabilities with a temperature, $\tilde{p}{\theta}(y_{t}|\mathbf y_{<t})=\mathrm{softmax}(s_{t}/\tau)$ , where $s_{t}\bar{\in}\mathbb{R}^{|\mathcal{V}|}$ is a vector of logits, and feed the expected token embedding as input at step $t$ ,
我们还考虑了一种松弛方法,它在每一步输入时在贪婪token和token的均匀混合之间进行插值。具体来说,我们用一个温度参数调整模型的概率分布:$\tilde{p}{\theta}(y_{t}|\mathbf y_{<t})=\mathrm{softmax}(s_{t}/\tau)$,其中$s_{t}\bar{\in}\mathbb{R}^{|\mathcal{V}|}$是logits向量,并在步骤$t$时将期望的token嵌入作为输入。
$$
e_{t}=\mathbb{E}{y_{t}\sim\tilde{p}(y_{t}|\mathbf{y}{<t})}[E(y_{t})],
$$
$$
e_{t}=\mathbb{E}{y_{t}\sim\tilde{p}(y_{t}|\mathbf{y}{<t})}[E(y_{t})],
$$
where $E\in\mathbb{R}^{|\mathcal{V}|\times d}$ is the model’s token embedding matrix. This soft lookahead moves from providing the greedy token as input $(\tau\rightarrow0)$ ) to a uniform mixture of tokens $\prime\tau\rightarrow\infty$ ) based on the value of temperature $\tau$ . When using the soft lookahead, we use $\tilde{p}$ in place of $p$ when scoring tokens. The soft (and greedy) lookahead is efficient, but only explores a single trajectory.
其中 $E\in\mathbb{R}^{|\mathcal{V}|\times d}$ 是该模型的token嵌入矩阵。这种软前瞻机制会根据温度参数 $\tau$ 的取值,从提供贪婪token作为输入 $(\tau\rightarrow0)$ )过渡到token的均匀混合状态 $(\tau\rightarrow\infty$ )。使用软前瞻时,我们用 $\tilde{p}$ 替代 $p$ 来对token进行评分。这种软(及贪婪)前瞻机制效率很高,但仅探索单一路径。
The beam lookahead trades off efficiency for exploration, returning a set $\mathcal{L}{\ell}$ containing the top $k$ candidates obtained by running beam search for $\ell$ steps starting from $\mathbf{y}_{<t}$ .
前瞻束搜索在效率与探索之间进行权衡,返回一个集合 $\mathcal{L}{\ell}$ ,其中包含从 $\mathbf{y}_{<t}$ 开始运行 $\ell$ 步束搜索得到的前 $k$ 个候选结果。
Finally, the sampling lookahead explores beyond the highly-probable beam search continuations, generating each $\mathbf{y}{t+1:t+\ell}\in\mathcal{L}_{\ell}$ using,
最后,采样前瞻探索超越了高概率的束搜索延续,使用每个$\mathbf{y}{t+1:t+\ell}\in\mathcal{L}_{\ell}$生成,
$$
y_{t^{\prime}}\sim p_{\theta}(y|\mathbf{y}_{<t^{\prime}}),
$$
$$
y_{t^{\prime}}\sim p_{\theta}(y|\mathbf{y}_{<t^{\prime}}),
$$
for $t^{\prime}$ from $_{t+1}$ to $t{+}\mathrm{k}$ .
对于 $t^{\prime}$ 从 $_{t+1}$ 到 $t{+}\mathrm{k}$。
Next, we move to our proposed lookahead heuristics, starting with the un constrained setting.
接下来,我们转向提出的前瞻启发式方法,从无约束设置开始。
2.2 Un constrained Generation with NEUROLOGIC⋆
2.2 基于NEUROLOGIC⋆的无约束生成
First we consider a standard decoding setting,
首先我们考虑一个标准的解码设置,
$$
\underset{\mathbf{y}\in\mathcal{Y}}{\arg\operatorname*{max}}\log p_{\theta}(\mathbf{y}|\mathbf{x}).
$$
$$
\underset{\mathbf{y}\in\mathcal{Y}}{\arg\operatorname*{max}}\log p_{\theta}(\mathbf{y}|\mathbf{x}).
$$
We score candidates based on a combination of the history and estimated future, by using the likelihood of the lookahead as a heuristic. That is, at the tth step of decoding, we use Equation 5:
我们通过结合历史记录和预估未来来评估候选方案,使用前瞻可能性作为启发式方法。具体来说,在解码的第t步,我们使用公式5:
$$
h(\mathbf{y}{\le t+\ell})=\lambda\log p_{\theta}(\mathbf{y}{t+1:t+\ell}|\mathbf{y}_{\le t},\mathbf{x}),
$$
$$
h(\mathbf{y}{\le t+\ell})=\lambda\log p_{\theta}(\mathbf{y}{t+1:t+\ell}|\mathbf{y}_{\le t},\mathbf{x}),
$$
where $\lambda$ controls how much we rely on the estimated future versus the history, similar to weighted $\mathbf{A}^{*}$ (Pohl, 1970).
其中 $\lambda$ 控制我们对预估未来值与历史值的依赖程度,类似于加权 $\mathbf{A}^{*}$ (Pohl, 1970)。
2.3 NEUROLOGIC $\star$ for Constrained Generation
2.3 NEUROLOGIC $\star$ 约束生成
Our lookahead heuristics lend themselves to decoding with lexical constraints in a way that standard beam search does not. For constrained generation, we build on and generalize NEUROLOGIC decoding algorithm of Lu et al. (2021)– a beam-based search algorithm that supports a wide class of logical constraints for lexically constrained generation– with estimates of future contraint satisfaction.
我们的前瞻启发式方法适用于带词汇约束的解码,而标准束搜索则不具备这一特性。针对约束生成任务,我们在Lu等人(2021)提出的NEUROLOGIC解码算法基础上进行了扩展和泛化。该基于束搜索的算法通过预估未来约束满足情况,支持广泛类别的逻辑约束用于词汇约束生成。
Background of NEUROLOGIC. NEUROLOGIC Lu et al. (2021) accepts lexical constraints in Conjunctive Normal Form (CNF):
NEUROLOGIC的背景。NEUROLOGIC Lu等人(2021) 接受合取范式(CNF)的词汇约束:
$$
\underbrace{\left(D_{1}\vee D_{2}\cdot\cdot\cdot\vee D_{i}\right)}{C_{1}}\wedge\cdot\cdot\wedge\underbrace{\left(D_{i^{\prime}}\vee D_{i^{\prime}+1}\cdot\cdot\cdot\vee D_{N}\right)}{C_{M}}
$$
$$
\underbrace{\left(D_{1}\vee D_{2}\cdot\cdot\cdot\vee D_{i}\right)}{C_{1}}\wedge\cdot\cdot\wedge\underbrace{\left(D_{i^{\prime}}\vee D_{i^{\prime}+1}\cdot\cdot\cdot\vee D_{N}\right)}{C_{M}}
$$
where each $D_{i}$ represents a single positive or negative constraint, $D({\bf a},{\bf y})$ or $\neg D({\bf a},{\bf y})$ , enforcing the phrase a to be included in or omitted from y. Lu et al. (2021) refer to each constraint $D_{i}$ as a literal, and each disjunction $C_{j}$ of literals as a clause.
其中每个 $D_{i}$ 代表一个正向或负向约束条件 $D({\bf a},{\bf y})$ 或 $\neg D({\bf a},{\bf y})$ ,强制要求短语a必须包含在y中或从y中排除。Lu等人 (2021) 将每个约束 $D_{i}$ 称为字面量 (literal) ,将字面量的每个析取式 $C_{j}$ 称为子句 (clause) 。
NEUROLOGIC is a beam-based approximate search for an objective which seeks fluent sequences in which all clauses are satisfied:
NEUROLOGIC是一种基于束搜索的近似目标搜索方法,旨在寻找所有子句都满足的流畅序列:
$$
\arg\operatorname*{max}{\mathbf{y}\in\mathcal{Y}}p_{\boldsymbol{\theta}}(\mathbf{y}|\mathbf{x})-\lambda^{\prime}\sum_{j=1}^{M}(1-C_{j}),
$$
$$
\arg\operatorname*{max}{\mathbf{y}\in\mathcal{Y}}p_{\boldsymbol{\theta}}(\mathbf{y}|\mathbf{x})-\lambda^{\prime}\sum_{j=1}^{M}(1-C_{j}),
$$
where $\lambda^{\prime}\gg0$ penalizes unsatisfied clauses. At each step of the search, NEUROLOGIC scores each of the $k\times|\mathcal{V}|$ candidates $(\mathbf{y}{<t},y_{t})$ based on whether they (partially) satisfy new constraints,
其中 $\lambda^{\prime}\gg0$ 用于惩罚未满足的子句。在搜索的每一步,NEUROLOGIC 根据是否(部分)满足新约束来对 $k\times|\mathcal{V}|$ 个候选 $(\mathbf{y}{<t},y_{t})$ 进行评分。
$$
f(\mathbf{y}{\le t})=\log p_{\theta}(\mathbf{y}{\le t}|\mathbf{x})+\lambda_{1}\operatorname*{max}{D(\mathbf{a},\mathbf{y}_{\le t})}\frac{|\hat{\mathbf{a}}|}{|\mathbf{a}|},
$$
$$
f(\mathbf{y}{\le t})=\log p_{\theta}(\mathbf{y}{\le t}|\mathbf{x})+\lambda_{1}\operatorname*{max}{D(\mathbf{a},\mathbf{y}_{\le t})}\frac{|\hat{\mathbf{a}}|}{|\mathbf{a}|},
$$
where the maximization is over a set of unsatisfied multi-token constraints a tracked by NEUROLOGIC, and $\hat{\mathbf{a}}$ is the prefix of a in the ongoing generation. For example, for $\mathbf{y}_{\le t}=\mathbf{\epsilon}^{\leftarrow}$ “The boy climbs an apple” and constraint $\mathbf{a}{=}^{\mathsf{e}}$ "apple tree”, a is "apple". Intuitively, this function rewards candidates that are in the process of satisfying a constraint.
其中最大化操作针对NEUROLOGIC跟踪的一组未满足的多token约束a,$\hat{\mathbf{a}}$是当前生成过程中a的前缀。例如,对于$\mathbf{y}_{\le t}=\mathbf{\epsilon}^{\leftarrow}$"男孩爬上一棵苹果"和约束$\mathbf{a}{=}^{\mathsf{e}}$"苹果树",a即为"苹果"。直观上,该函数会奖励那些正在满足约束的候选序列。
In lieu of taking the top- $k$ scoring candidates (Equation 5), NEUROLOGIC prunes candidates that contain clauses that violate constraints, groups the candidates to promote diversity, and selects highscoring candidates from each group. We use the same pruning and grouping approach, and refer the reader to Lu et al. (2021) for further details.
NEUROLOGIC 并非直接选择得分最高的前 $k$ 个候选 (公式5),而是剪除包含违反约束子句的候选,对候选进行分组以提升多样性,并从每组中选出高得分候选。我们采用相同的剪枝与分组方法,具体细节请参阅 Lu et al. (2021) [20]。
NEUROLOGIC⋆ decoding. Our method improves upon the NEUROLOGIC scoring function with an estimate of future constraint satisfaction. Our key addition is a lookahead heuristic that adjusts a candidate $\left(\mathbf{y}{<t},{y}_{t}\right)$ ’s score proportional to the probability of satisfying additional constraints in the lookahead yt+1:t+ℓ:
NEUROLOGIC⋆解码。我们的方法改进了NEUROLOGIC评分函数,通过预估未来约束满足情况。核心改进是引入前瞻启发式策略,该策略根据前瞻窗口yt+1:t+ℓ内满足额外约束的概率,按比例调整候选序列$\left(\mathbf{y}{<t},{y}_{t}\right)$的得分:
$$
\begin{array}{r l}{h_{\mathrm{future}}(\mathbf{y}{\le t+\ell})=}{\lambda_{2}\underset{D(\mathbf{a},\mathbf{y}{\le t})}{\operatorname*{max}}\log p_{\theta}(D(\mathbf{a},\mathbf{y}{t+1:t+\ell})|\mathbf{x},\mathbf{y}_{\le t}),}\end{array}
$$
$$
\begin{array}{r l}&{h_{\mathrm{future}}(\mathbf{y}{\le t+\ell})=}\ &{\lambda_{2}\underset{D(\mathbf{a},\mathbf{y}{\le t})}{\operatorname*{max}}\log p_{\theta}(D(\mathbf{a},\mathbf{y}{t+1:t+\ell})|\mathbf{x},\mathbf{y}_{\le t}),}\end{array}
$$
where we define the probability that constraint a is satisfied using the most probable sub sequence,
我们定义约束a通过最可能子序列满足的概率,
$$
\begin{array}{r}{p_{\theta}(D(\mathbf{a},\mathbf{y}{t+1:t+\ell})|\mathbf{x},\mathbf{y}{\le t})=\qquad}\ {\underset{t^{\prime}\in[t,t+\ell]}{\operatorname*{max}}p_{\theta}(\mathbf{y}{t^{\prime}:t^{\prime}+|\mathbf{a}|}=\mathbf{a}|\mathbf{x},\mathbf{y}_{<t^{\prime}}),}\end{array}
$$
$$
\begin{array}{r}{p_{\theta}(D(\mathbf{a},\mathbf{y}{t+1:t+\ell})|\mathbf{x},\mathbf{y}{\le t})=\qquad}\ {\underset{t^{\prime}\in[t,t+\ell]}{\operatorname*{max}}p_{\theta}(\mathbf{y}{t^{\prime}:t^{\prime}+|\mathbf{a}|}=\mathbf{a}|\mathbf{x},\mathbf{y}_{<t^{\prime}}),}\end{array}
$$
$\lambda_{2}$ is a scaling hyper parameter for the heuristic.
$\lambda_{2}$ 是一个用于启发式方法的缩放超参数。
Intuitively, this lookahead heuristic brings two benefits. When $y_{t}$ is a token that would satisfy a multi-token constraint, the lookahead incorporates the score of the full constraint. When $y_{t}$ is a token that is not part of a constraint, the lookahead allows for incorporating the score of a future constraint that would be satisfied if $y_{t}$ was selected.
直观上,这种前瞻启发式方法带来两个好处。当 $y_{t}$ 是满足多token约束的token时,前瞻机制会纳入完整约束的分数。当 $y_{t}$ 不属于任何约束时,前瞻机制允许纳入未来可能因选择 $y_{t}$ 而满足的约束分数。
We add our lookahead heuristic to the NEUROLOGIC scoring function (Equation 8), and call the resulting decoding procedure NEUROLOGIC $\mathbf{A}^{\star}$ esque (or, NEUROLOGIC⋆ in short).
我们将前瞻启发式方法加入NEUROLOGIC评分函数(公式8),并将由此产生的解码过程称为NEUROLOGIC $\mathbf{A}^{\star}$风格(简称NEUROLOGIC⋆)。
Table 1: Tasks and setups considered in this work.
| Task | Supervision | Constraints |
| CommonsenseGeneration | zero+full | w/ |
| MachineTranslation | full | w/ |
| Table-to-textGeneration | few | w/ |
| QuestionGeneration | zero | w/ |
| CommonsenseStory Generation | full | w/o |
表 1: 本研究中考虑的任务与设置。
| 任务 | 监督方式 | 约束条件 |
|---|---|---|
| 常识生成 (Commonsense Generation) | 零样本+全监督 | 有约束 |
| 机器翻译 (Machine Translation) | 全监督 | 有约束 |
| 表格到文本生成 (Table-to-text Generation) | 少样本 | 有约束 |
| 问题生成 (Question Generation) | 零样本 | 有约束 |
| 常识故事生成 (Commonsense Story Generation) | 全监督 | 无约束 |
3 Experiments: Constrained Generation
3 实验:受限生成
We present experimental results on various constrained generation benchmarks: COMMONGEN (§3.1), constrained machine translation (§3.2), table-to-text generation (§3.3), and interrogative sentence generation (§3.4). NEUROLOGIC⋆ consistently outperforms NEUROLOGIC and all previous approaches. The improvement is especially substantial in zero-shot and few-shot cases where the search problem is much harder.
我们在多个受限生成基准测试上展示了实验结果:COMMONGEN(第3.1节)、受限机器翻译(第3.2节)、表格到文本生成(第3.3节)以及疑问句生成(第3.4节)。NEUROLOGIC⋆始终优于NEUROLOGIC及所有先前方法,在搜索问题更为困难的零样本和少样本场景中提升尤为显著。
Experimental setups. We explore a variety of experimental setups (Table 1). In terms of supervision, we consider different configurations of zeroshot, few-shot and full-shot. The former two supervision regimes are particularly important as many realistic generation application do not come with many manually-annotated labeled data. Additionally, we study both constrained and un constrained tasks, even though we focus on the former.
实验设置。我们探索了多种实验设置(表1)。在监督方式方面,我们考虑了零样本(zero-shot)、少样本(few-shot)和全样本(full-shot)的不同配置。前两种监督机制尤为重要,因为许多实际生成应用缺乏大量人工标注数据。此外,尽管我们主要关注约束性任务,但同时也研究了非约束性任务。
Evaluation metrics. We use the following automatic metrics that are commonly used for evaluating text generation: BLEU (Papineni et al., 2002), ROUGE (Lin, 2004), METEOR (Banerjee and Lavie, 2005), CIDEr (Vedantam et al., 2015), SPICE (Anderson et al., 2016) and NIST (Lin and Hovy, 2003). Any other domain specific metrics are detailed in each task description.
评估指标。我们采用以下常用于文本生成评估的自动指标:BLEU (Papineni et al., 2002)、ROUGE (Lin, 2004)、METEOR (Banerjee and Lavie, 2005)、CIDEr (Vedantam et al., 2015)、SPICE (Anderson et al., 2016) 和 NIST (Lin and Hovy, 2003)。各任务描述中会详述其他领域特定指标。
3.1 Constrained Commonsense Generation
3.1 受限常识生成
COMMONGEN (Lin et al., 2020) is a constrained commonsense generation task with lexical constraints.
COMMONGEN (Lin et al., 2020) 是一个带有词汇约束的常识生成任务。
Table 2: Performance of various decoding methods with supervised or off-the-shelf GPT-2 on the COMMONGEN test set, measured with automatic and human evaluations. We only tried NEUROLOGIC⋆ (greedy) in the unsupervised setting because of the computational cost. The best numbers are bolded and the second best ones are underlined.
| DecodeMethod | AutomaticEvaluation | HumanEvaluation | ||||||||
| ROUGE-LBLEU-4 | METEOR | CIDEr | SPICE | Coverage | Quality | Plausibility | yConceptsOverall | |||
| Supervised | ||||||||||
| CBS (Anderson etal.,2017) | 38.8 | 20.6 | 28.5 | 12.9 | 27.1 | 97.6 | 2.27 | 2.35 | 2.51 | 2.23 |
| GBS (Hokamp and Liu, 2017) | 38.2 | 18.4 | 26.7 | 11.7 | 26.1 | 97.4 | 2.06 | 2.17 | 2.29 | 2.01 |
| DBA(Post andVilar,2018a) | 38.3 | 18.7 | 27.7 | 12.4 | 26.3 | 97.5 | 2.23 | 2.30 | 2.43 | 2.15 |
| NEUROL0GIC (Lu etal.,2021) | 42.8 | 26.7 | 30.2 | 14.7 | 30.3 | 97.7 | 2.54 | 2.56 | 2.67 | 2.50 |
| NEUROLOGIC(greedy) | 43.6 | 28.2 | 30.8 | 15.2 | 30.8 | 97.8 | 2.66 | 2.67 | 2.73 | 2.59 |
| NEUROLOGIC★ (sample) | 43.4 | 27.9 | 30.8 | 15.3 | 31.0 | 97.7 | 2.64 | 2.64 | 2.74 | 2.58 |
| NEUROLOGIC★ (beam) | 43.2 | 28.2 | 30.7 | 15.2 | 31.0 | 97.6 | 2.68 | 2.67 | 2.76 | 2.60 |
| Unsupervised | ||||||||||
| TSMH (Zhang et al.,2020) | 24.7 | 2.2 | 14.5 | 3.6 | 15.4 | 71.5 | 1.85 | 1.92 | 1.95 | 1.63 |
| NEUROL0GIC (Lu et al.,2021) | 41.9 | 24.7 | 29.5 | 14.4 | 27.5 | 96.7 | 2.64 | 2.52 | 2.68 | 2.50 |
| NEUROLOGIC★ (greedy) | 44.3 | 28.6 | 30.7 | 15.6 | 29.6 | 97.1 | 2.78 | 2.70 | 2.77 | 2.70 |
表 2: 监督学习或现成 GPT-2 模型在 COMMONGEN 测试集上采用不同解码方法的性能表现,通过自动评估和人工评估进行衡量。由于计算成本限制,我们仅在无监督设置下尝试了 NEUROLOGIC⋆ (贪婪解码)。最优数值加粗显示,次优数值加下划线。
| 解码方法 | 自动评估 | 人工评估 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ROUGE-L | BLEU-4 | METEOR | CIDEr | SPICE | 覆盖率 | 质量 | 合理性 | 概念完整性 | ||
| 监督学习 | ||||||||||
| CBS (Anderson et al., 2017) | 38.8 | 20.6 | 28.5 | 12.9 | 27.1 | 97.6 | 2.27 | 2.35 | 2.51 | 2.23 |
| GBS (Hokamp and Liu, 2017) | 38.2 | 18.4 | 26.7 | 11.7 | 26.1 | 97.4 | 2.06 | 2.17 | 2.29 | 2.01 |
| DBA (Post and Vilar, 2018a) | 38.3 | 18.7 | 27.7 | 12.4 | 26.3 | 97.5 | 2.23 | 2.30 | 2.43 | 2.15 |
| NEUROLOGIC (Lu et al., 2021) | 42.8 | 26.7 | 30.2 | 14.7 | 30.3 | 97.7 | 2.54 | 2.56 | 2.67 | 2.50 |
| NEUROLOGIC (贪婪解码) | 43.6 | 28.2 | 30.8 | 15.2 | 30.8 | 97.8 | 2.66 | 2.67 | 2.73 | 2.59 |
| NEUROLOGIC⋆ (采样) | 43.4 | 27.9 | 30.8 | 15.3 | 31.0 | 97.7 | 2.64 | 2.64 | 2.74 | 2.58 |
| NEUROLOGIC⋆ (束搜索) | 43.2 | 28.2 | 30.7 | 15.2 | 31.0 | 97.6 | 2.68 | 2.67 | 2.76 | 2.60 |
| 无监督学习 | ||||||||||
| TSMH (Zhang et al., 2020) | 24.7 | 2.2 | 14.5 | 3.6 | 15.4 | 71.5 | 1.85 | 1.92 | 1.95 | 1.63 |
| NEUROLOGIC (Lu et al., 2021) | 41.9 | 24.7 | 29.5 | 14.4 | 27.5 | 96.7 | 2.64 | 2.52 | 2.68 | 2.50 |
| NEUROLOGIC⋆ (贪婪解码) | 44.3 | 28.6 | 30.7 | 15.6 | 29.6 | 97.1 | 2.78 | 2.70 | 2.77 | 2.70 |
Table 3: Example generations for the COMMONGEN task across supervised NEUROLOGIC⋆and baselines, including GBS (Hokamp and Liu, 2017), DBA (Post and Vilar, 2018a), and NEUROLOGIC (Lu et al., 2021)
| Words | Method | Generation |
| cut | GBS | Cutapieceofwoodtouseasafence. |
| piece | DBA | Cutapieceofwood touse as afence. |
| use | NEUROLOGIC | Piece ofwood usedfor cutting. |
| poom | NEURoLoGIc*A man cuts a piece of wood using a circular saw. | |
| ball | GBS | A dog is run over by a ball and mouth agape. |
| sop | DBA | A dog is run over by a ball and bites his mouth. |
| mouth | NEUROLOGIC | A dog is running and chewing on aballinitsmouth. |
| run | NEUROLOGIc * A dog running with a ball in its mouth. | |
| sop | GBS | Soap andwaterscrubbeddogwith a towel. |
| scrub | DBA | Soap andwater on a dog and scrubbed skin. |
| soap | NEUROLOGIC | A dogis scrubbinghis paws with soap andwater. |
| water | NEURoLoGIc* A man is scrubbing a dog with soap and water. |
表 3: COMMONGEN任务在监督式NEUROLOGIC⋆与基线方法(包括GBS (Hokamp和Liu,2017)、DBA (Post和Vilar,2018a)和NEUROLOGIC (Lu等人,2021))上的生成示例
| 词语 | 方法 | 生成结果 |
|---|---|---|
| cut | GBS | Cutapieceofwoodtouseasafence. |
| piece | DBA | Cutapieceofwood touse as afence. |
| use | NEUROLOGIC | Piece ofwood usedfor cutting. |
| poom | NEURoLoGIc*A man cuts a piece of wood using a circular saw. | |
| ball | GBS | A dog is run over by a ball and mouth agape. |
| sop | DBA | A dog is run over by a ball and bites his mouth. |
| mouth | NEUROLOGIC | A dog is running and chewing on aballinitsmouth. |
| run | NEUROLOGIc * A dog running with a ball in its mouth. | |
| sop | GBS | Soap andwaterscrubbeddogwith a towel. |
| scrub | DBA | Soap andwater on a dog and scrubbed skin. |
| soap | NEUROLOGIC | A dogis scrubbinghis paws with soap andwater. |
| water | NEURoLoGIc* A man is scrubbing a dog with soap and water. |
Given a set of concepts (e.g., {throw, run, javelin, track}), the task is to generate a coherent sentence describing a plausible scenario using all of the given concepts (e.g., “a man runs on a track and throws a javelin.”).
给定一组概念(例如 {投掷, 跑步, 标枪, 跑道}),任务是生成一个连贯的句子,描述一个使用所有给定概念的合理场景(例如“一名男子在跑道上跑步并投掷标枪。”)。
Approach and Baselines. Following Lu et al. (2021), we enforce that each given concept $c_{i}$ must appear in output y under some morphological inflection. We experiment with both supervised and zero-shot settings. In the supervised setting, we formulate it as conditional sentence generation task and finetune GPT-2 (Radford et al., 2019) as a sequence-to-sequence model. In the zero-shot setting, we use GPT-2 off-the-shelf (no fine-tuning), and rely on constrained decoding to guide the generations. We compare with previous constrained decoding algorithms, including CBS (Anderson et al., 2017), GBS (Hokamp and Liu, 2017), DBA (Post and Vilar, 2018a), NEUROLOGIC (Lu et al.,
方法与基线。遵循 Lu et al. (2021) 的方法,我们强制要求每个给定概念 $c_{i}$ 必须以某种形态变化出现在输出 y 中。我们在监督学习和零样本两种设置下进行实验。在监督学习设置中,我们将其表述为条件语句生成任务,并将 GPT-2 (Radford et al., 2019) 微调为序列到序列模型。在零样本设置中,我们直接使用现成的 GPT-2 (不进行微调),并依赖约束解码来引导生成。我们与之前的约束解码算法进行比较,包括 CBS (Anderson et al., 2017)、GBS (Hokamp and Liu, 2017)、DBA (Post and Vilar, 2018a)、NEUROLOGIC (Lu et al.
- and TSMH (Zhang et al., 2020)
- 和 TSMH (Zhang 等人, 2020)
Metrics Following Lin et al. (2020), we report automatic generation metrics as well as coverage, defined as the average percentage of the provided concepts that are present in lemmatized outputs. Additionally, we conduct human evaluation on 100 test examples with workers from Amazon Mechanical Turk (AMT). We include our evaluation template in Figure 5 of Appendix A. Workers are given a pair of concepts and a model generation, and asked to rate each pair on language quality, scenario plausibility, coverage of given concepts, and an overall score, in the Likert scale: Agree, Neutral, and Disagree. Each pair is rated by 3 workers.
指标
遵循 Lin 等人 (2020) 的方法,我们报告了自动生成指标以及覆盖率 (coverage),后者定义为词形还原输出中包含所提供概念的平均百分比。此外,我们对来自 Amazon Mechanical Turk (AMT) 的众包工作者进行了 100 个测试示例的人工评估。附录 A 的图 5 中包含了我们的评估模板。工作者会获得一组概念和一个模型生成结果,并被要求按照 Likert 量表 (Agree, Neutral, Disagree) 对每组进行语言质量、场景合理性、给定概念覆盖率和总体评分的评分。每组由 3 名工作者进行评分。
Results. Table 2 compares different constrained decoding methods on top of the finetuned and offthe-shelf GPT-2, in supervised and zero-shot settings respectively. The key observations are:
结果。表 2 比较了在微调版和现成 GPT-2 基础上采用的不同约束解码方法,分别在监督学习和零样本设置下的表现。主要观察结果包括:
- NEUROLOGIC⋆ outperforms all previous constrained-decoding methods in both supervised and zero-shot settings. Surprisingly, unsupervised NEUROLOGIC⋆ outperforms all supervised methods based on human evaluation.
- NEUROLOGIC⋆ 在监督学习和零样本设置下均优于所有先前的约束解码方法。令人惊讶的是,未经监督的 NEUROLOGIC⋆ 在人工评估中超越了所有监督学习方法。
- Compared to vanilla NEUROLOGIC, NEUROLOGIC⋆ improves the generation quality while maintaining high constraint satisfaction. The difference is especially substantial in the zero-shot case, where there is more room for incorporating constraint-driven signals due to the lack of supervision and the large output space.
- 与基础版NEUROLOGIC相比,NEUROLOGIC⋆在保持高约束满足率的同时提升了生成质量。这一差异在零样本场景中尤为显著,由于缺乏监督信号且输出空间庞大,约束驱动信号在此具有更大的优化空间。
- NEUROLOGIC⋆ reaches similar performance with different lookahead strategies, among which beam lookahead slightly outperforms the others based on human evaluation, and greedy lookahead has the lowest runtime.
- NEUROLOGIC⋆ 在不同前瞻策略下达到相近性能,其中基于人工评估的束搜索前瞻 (beam lookahead) 略优于其他策略,而贪心前瞻 (greedy lookahead) 运行时最短。
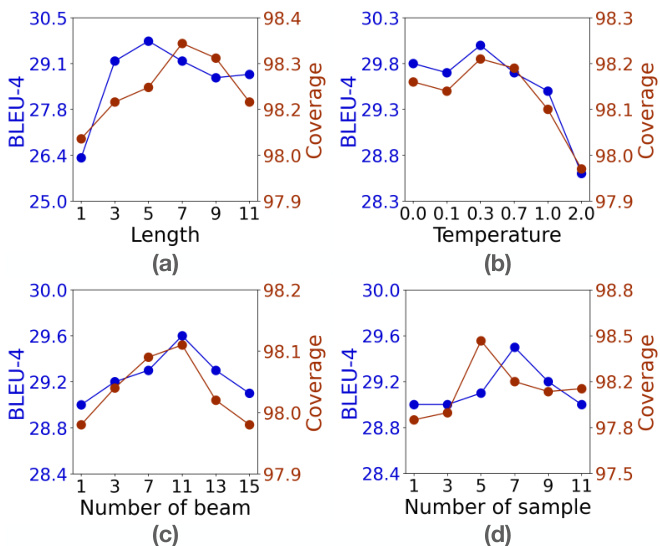
Figure 2: Performance (y-axis) of supervised GPT-2 in terms of BLEU-4 and Coverage with varying lookahead parameters ( $\mathbf{\check{X}}$ -axis) on COMMONGEN validationset.
图 2: 监督式 GPT-2 在 COMMONGEN 验证集上,随着前瞻参数 ( $\mathbf{\check{X}}$ -轴) 变化,BLEU-4 和覆盖率 (y-轴) 的性能表现。
Studying lookahead strategies. With an infinite lookahead length $\ell$ and number of lookaheads $|\mathcal{L}{\ell}|$ , lookahead decoding exactly solves Equation 3. For practical choices of $\ell$ and $|\mathcal{L}_{\ell}|$ , we empirically study how varying the lookahead strategy and hyper parameters affects performance. In Figure 2, we study the greedy, soft, beam, and sampling lookahead strategies (§2.1).
研究前瞻策略。在无限前瞻长度 $\ell$ 和前瞻数量 $|\mathcal{L}{\ell}|$ 的情况下,前瞻解码精确求解方程3。针对实际选择的 $\ell$ 和 $|\mathcal{L}_{\ell}|$ ,我们通过实验研究不同前瞻策略和超参数对性能的影响。在图2中,我们研究了贪婪、软性、束搜索和采样前瞻策略(§2.1)。
Figure 2(a) shows the effect of increasing the lookahead horizon $\ell$ for the greedy strategy. Increasing the horizon improves up to one point – e.g., 5-7 steps – then decreases thereafter, likely due to the difficulty of long-horizon approximation.
图 2(a) 展示了贪心策略中前瞻步长 $\ell$ 增加的效果。增大前瞻步长会在一段范围内(例如5-7步)提升效果,之后性能开始下降,这可能是由于长程近似难度增加所致。
Figure 2(b) studies the temperature in the soft lookahead, showing that greedy $\mathit{\Omega}_{\mathcal{T}}^{\prime}=0.0\rangle$ ) performs well, with slight gains if $\tau$ is carefully selected. The results suggest that one can safely bypass tuning $\tau$ using fast, greedy lookahead.
图 2(b) 研究了软前瞻中的温度参数,表明贪婪策略 ( $\mathit{\Omega}_{\mathcal{T}}^{\prime}=0.0\rangle$ ) 表现良好,若谨慎选择 $\tau$ 可获得小幅提升。结果表明,通过快速贪婪前瞻策略可安全跳过 $\tau$ 调参环节。
Next, Figure 2(c) shows that with beam lookahead, increasing the beam width improves performance up to a certain point (here, 11). Similarly, increasing the number of samples with sampling lookahead improves over a single sample, and then reaches an inflection point (Figure 2(d)).
接下来,图 2(c) 显示,在使用波束前瞻 (beam lookahead) 时,增大波束宽度 (beam width) 能在一定范围内提升性能 (此处为 11)。类似地,在使用采样前瞻 (sampling lookahead) 时,增加采样数量相比单次采样有所改善,随后达到拐点 (图 2(d))。
3.2 Constrained Machine Translation
3.2 受限机器翻译
It is often critical to have control over machine translation output. For example, domain-specific dictionaries can be incorporated to force a model
控制机器翻译输出通常至关重要。例如,可以整合领域专用词典来强制模型
| 方法 | Dinuetal. | MarianMT | ||
|---|---|---|---|---|
| BLUE | Term% | BLUE | Term% | |
| 无约束 | 25.8 | 76.3 | 32.9 | 85.0 |
| train-by-app. train-by-rep. | 26.0 | 92.9 | — | — |
| Post andVilar(2018a) | 26.0 25.3 | 94.5 82.0 | — | — |
| 33.0 | 94.3 | |||
| NEUROLOGIC | 26.5 | 95.1 | 33.4 | 97.1 |
| NEUROLOGIC★ (贪婪) | 26.7 | 95.8 | 33.7 | 97.2 |
| NEUROLOGIC★ (采样) | 26.6 | 95.4 | 33.7 | 97.2 |
| NEUROLOGIC★ (束搜索) | 26.6 | 95.8 | 33.6 | 97.2 |
Table 4: Results on constrained machine translation. The left section uses the same two-layer transformer model as Dinu et al. (2019) for fair comparisons. The right one decodes a stronger Marian MT EN-DE model. The highlighted methods modify training data specifically for constrained decoding, and thus cannot be applied to off-the-shelf models. The best numbers are bolded and the second best ones are underlined.
表 4: 受限机器翻译结果。左侧部分采用与Dinu等人 (2019) 相同的双层Transformer模型以确保公平比较。右侧解码了更强的Marian MT英德模型。高亮显示的方法专门针对受限解码修改了训练数据,因此无法直接应用于现成模型。最优结果以粗体标示,次优结果以下划线标示。
Table 5: Constrained Machine Translation performance broken down by the number of constraint
