From Hours to Minutes: Lossless Acceleration of Ultra Long Sequence Generation up to 100K Tokens
从小时到分钟:无损加速超长序列生成至10万Token
Generating ultra-long sequences with large language models (LLMs) has become increasingly crucial but remains a highly time-intensive task, particularly for sequences up to 100K tokens. While traditional speculative decoding methods exist, simply extending their generation limits fails to accelerate the process and can be detrimental. Through an in-depth analysis, we identify three major challenges hindering efficient generation: frequent model reloading, dynamic key-value (KV) management and repetitive generation. To address these issues, we introduce TOKENSWIFT, a novel framework designed to substantially accelerate the generation process of ultra-long sequences while maintaining the target model’s inherent quality. Experimental results demonstrate that TOKENSWIFT achieves over $\mathsfit{3\times}$ speedup across models of varying scales (1.5B, 7B, 8B, 14B) and architectures (MHA, GQA). This acceleration translates to hours of time savings for ultra-long sequence generation, establishing TOKENSWIFT as a scalable and effective solution at unprecedented lengths. Code can be found at github.com/bigai-nlco/TokenSwift.
使用大语言模型生成超长序列变得越来越重要,但仍然是一项非常耗时的任务,特别是对于长达100K Token的序列。虽然存在传统的推测解码方法,但仅仅扩展其生成限制并不能加速过程,反而可能有害。通过深入分析,我们确定了阻碍高效生成的三大挑战:频繁的模型重载、动态键值(KV)管理和重复生成。为了解决这些问题,我们引入了TOKENSWIFT,这是一个旨在显著加速超长序列生成过程,同时保持目标模型固有质量的新框架。实验结果表明,TOKENSWIFT在不同规模(1.5B、7B、8B、14B)和架构(MHA、GQA)的模型上实现了超过$\mathsfit{3\times}$的加速。这种加速为超长序列生成节省了数小时的时间,使TOKENSWIFT成为在空前长度上的可扩展且有效的解决方案。代码可在github.com/bigai-nlco/TokenSwift找到。
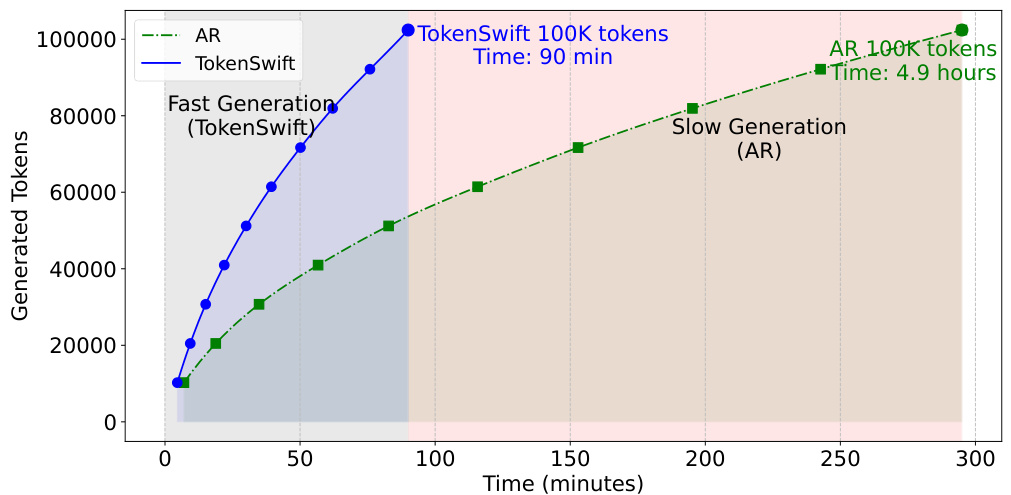
Figure 1. Comparison of the time taken to generate 100K tokens using auto regressive (AR) and TOKENSWIFT with prefix length of 4096 on LLaMA3.1-8b. As seen, TOKENSWIFT accelerates the AR process from nearly 5 hours to just 90 minutes.
图 1: 在 LLaMA3.1-8b 上使用自回归 (AR) 和 TOKENSWIFT (前缀长度为 4096) 生成 100K Token 所需时间的比较。如图所示,TOKENSWIFT 将 AR 过程从近 5 小时加速至仅 90 分钟。
1. Introduction
1. 引言
Recent advances in large language models (LLMs), amplified by their long context capacities (Wu et al., 2024; Ding et al., 2024), have demonstrated remarkable proficiency in intricate reasoning (Jaech et al., 2024; Guo et al., 2025), agentic thinking (Shinn et al., 2023; Yao et al., 2023; Li et al., 2024a), and creative writing (Wang et al.,
大语言模型 (LLMs) 的最新进展
2023; Mik hay lov ski y, 2023), etc. These advancements necessitate the ability to generate lengthy sequences, e.g., o1-like (Jaech et al., 2024) reasoning tends to generate protracted chain-of-thought trajectories before reaching final conclusions. However, a critical challenge impeding the practical deployment of such applications is the extensive time required to produce ultra-long sequences. For instance, generating 100K tokens with LLaMA3.1- 8B can take approximately five hours (Figure 1), a duration that is im practically long for the development of sophisticated applications, let alone recent gigantic models such as LLaMA3.1-405B (AI@Meta, 2024) and DeepSeek-600B (Liu et al., 2024a). Addressing this bottleneck is essential for harnessing the full potential of LLMs in real-world scenarios.
2023; Mik hay lov ski y, 2023) 等。这些进展需要生成长序列的能力,例如 o1-like (Jaech et al., 2024) 推理在得出结论之前往往会生成冗长的链式思维轨迹。然而,阻碍此类应用实际部署的一个关键挑战是生成超长序列所需的大量时间。例如,使用 LLaMA3.1-8B 生成 100K Token 可能需要大约五个小时 (图 1),这对于复杂应用的开发来说是不切实际的,更不用说最近的巨型模型如 LLaMA3.1-405B (AI@Meta, 2024) 和 DeepSeek-600B (Liu et al., 2024a) 了。解决这一瓶颈对于在现实场景中充分发挥大语言模型的潜力至关重要。
A straightforward solution is to take advantage of recent success in speculative decoding (SD) (Leviathan et al., 2023; Chen et al., 2023), which employs a draft-then-verify strategy to expedite generation while preserving lossless accuracy; see Appendix A and Section 5.1 for detailed background and relevant literature. However, these methods are generally tailored for generating short sequences, e.g., TriForce (Sun et al., 2024a) and MagicDec (Chen et al., 2024a) are limited to generating 256 and 64 tokens, respectively. Directly extending their generation length to 100K tokens would inevitably encounter failures due to KV cache budget constraints. Furthermore, even when applied to optimized KV cache architectures such as Group Query Attention (GQA), these methods yield only marginal acceleration gains for short-sequence generation, as evidenced in Tables 1 and 3. This observation leads to a pivotal research question:
一个直接的解决方案是利用推测解码 (Speculative Decoding, SD) 最近的成功 (Leviathan et al., 2023; Chen et al., 2023),该策略采用先起草后验证的方法来加速生成,同时保持无损精度;详细背景和相关文献请参见附录 A 和第 5.1 节。然而,这些方法通常是为生成短序列量身定制的,例如 TriForce (Sun et al., 2024a) 和 MagicDec (Chen et al., 2024a) 分别只能生成 256 和 64 个 Token。直接将它们的生成长度扩展到 100K Token 将不可避免地因 KV 缓存预算限制而遭遇失败。此外,即使应用于优化后的 KV 缓存架构,如群组查询注意力 (Group Query Attention, GQA),这些方法在短序列生成中也仅能带来微小的加速增益,如表 1 和表 3 所示。这一观察引出了一个关键的研究问题:
Is it possible to achieve model-agnostic lossless accelerations, akin to those seen in short-sequence SDs, for generating ultra-long sequences, with minimal training overhead?
是否可以在最小化训练开销的情况下,实现模型无关的无损加速,类似于在短序列 SD 中看到的效果,以生成超长序列?
To answer this question, we conduct an in-depth analysis (§2) and identify three key challenges: (1) frequent model reloading: frequently reloading model for each token generation introduces a significant delay, primarily due to memory access times rather than computation. (2) Prolonged Growing of KV Cache, the dynamic management of key-value (KV) pairs, which grow with the sequence length, adds complexity in maintaining model efficiency. (3) repetitive content generation, the issue of repetitive generation becomes more pronounced as the sequence length increases, leading to degraded output quality.
为了回答这个问题,我们进行了深入分析(§2),并确定了三个关键挑战:(1) 频繁的模型重载:为每个Token生成频繁重载模型会引入显著的延迟,这主要是由于内存访问时间而非计算。(2) KV缓存持续增长:随着序列长度的增加,键值对(KV)的动态管理增加了维护模型效率的复杂性。(3) 重复内容生成:随着序列长度的增加,重复生成问题变得更加明显,导致输出质量下降。
Building on these insights, we introduce our framework TOKENSWIFT, which utilizes $n$ -gram retrieval and dynamic KV cache updates to accelerate ultra-long sequence generation. Specifically, we employ multi-token generation and token re utilization to enable the LLM (i.e. target model) to draft multiple tokens in a single forward pass, alleviating the first challenge of frequent model reloading (§3.2). As the generation progresses, we dynamically update the partial KV cache at each iteration, reducing the KV cache loading time (§3.3). Finally, to mitigate the issue of repetitive outputs, we apply contextual penalty to constrain the generation process, ensuring the diversity of output (§3.4).
基于这些见解,我们提出了TOKENSWIFT框架,该框架利用$n$-gram检索和动态KV缓存更新来加速超长序列生成。具体来说,我们采用多Token生成和Token重用技术,使大语言模型(即目标模型)能够在一次前向传递中生成多个Token,从而缓解频繁模型重载的第一个挑战(§3.2)。随着生成的进行,我们在每次迭代中动态更新部分KV缓存,减少了KV缓存加载时间(§3.3)。最后,为了缓解输出重复的问题,我们应用上下文惩罚来约束生成过程,确保输出的多样性(§3.4)。
In $\S4_{,}$ , we conduct extensive experiments to evaluate TOKENSWIFT across different model scales and architectures. In summary, we highlight our advantages as:
在第4节中,我们进行了广泛的实验,以评估TOKENSWIFT在不同模型规模和架构上的表现。总结来说,我们的优势体现在:
- To the best of our knowledge, TOKENSWIFT is the first to accelerate ultra-long sequence generation up to 100K with lossless accuracy of target LLMs, while demonstrating significant superiority over enhanced baselines. 2. TOKENSWIFT consistently achieves over $\mathsfit{3\times}$ speedup compared to AR across varying prefix lengths, model architectures, and model scales in generating 100K tokens, reducing the AR process from nearly 5 hours to 90 minutes on LLaMA3.1-8b. 3. TOKENSWIFT achieves progressively higher speedup compared to AR as the generation length increases, while enhancing diversity in ultra-long sequence generation (as measured by Distinct-n (Li et al., 2016)).
- 据我们所知,TOKENSWIFT 是首个在加速超长序列生成(长达100K)的同时,保持目标大语言模型无损精度的技术,并在增强基线模型上展现出显著优势。
- TOKENSWIFT 在不同前缀长度、模型架构和模型规模下生成100K Token时,始终实现超过 $\mathsfit{3\times}$ 的加速,将LLaMA3.1-8b上的自回归 (AR) 过程从近5小时缩短至90分钟。
- TOKENSWIFT 在生成长度增加时,与AR相比实现了逐步更高的加速,同时增强了超长序列生成的多样性(通过Distinct-n (Li et al., 2016) 衡量)。
2. Challenges
2. 挑战
Accelerating long sequence generation is nevertheless a non-trivial task, even built upon prior success in speculative decoding (SD). In this section, we identify critical challenges encountered in accelerating ultra-long sequence generation.
加速长序列生成仍然是一个非平凡的任务,即使在推测解码(SD)之前的成功基础上也是如此。在本节中,我们识别了在加速超长序列生成过程中遇到的关键挑战。
Challenge I: Frequent Model Reloading One fundamental speed obstacle lies in the auto regressive (AR) generation scheme of LLM. For each token, the entire model must be loaded from GPU’s storage unit to the computing unit (Yuan et al., 2024), which takes significantly more time than the relatively small amount of computation performed (as shown in Table 2). Consequently, the primary bottleneck in generation stems from I/O memory access rather than computation.
挑战 I: 频繁的模型重载
一个根本的速度障碍在于大语言模型的自回归 (AR) 生成方案。对于每个 Token,整个模型必须从 GPU 的存储单元加载到计算单元 (Yuan et al., 2024),这比相对较少的计算量所花费的时间要多得多 (如表 2 所示)。因此,生成的主要瓶颈源于 I/O 内存访问而非计算。
Table 1. Experimental results of TriForce (Sun et al., 2024a) and MagicDec (Chen et al., 2024a) with default parameters on LLaMA3.1-8b. The Batch Size of MagicDec is set to 1.
表 1. TriForce (Sun 等, 2024a) 和 MagicDec (Chen 等, 2024a) 在 LLaMA3.1-8b 上使用默认参数的实验结果。MagicDec 的 Batch Size 设置为 1。
| 方法 | 生成长度 | 草稿形式 | 加速比 |
|---|---|---|---|
| TriForce | 256 | 独立草稿 | 1.02 |
| MagicDec | 64 | 自我推测 | 1.20 |
| MagicDec | 64 | 独立草稿 | 1.06 |
Table 2. Taking NVIDIA A100 80G and LLaMA3.1-8b as example, MAX refers to the scenario with a maximum context window 128K. The calculation method is from Yuan et al. (2024).
表 2: 以 NVIDIA A100 80G 和 LLaMA3.1-8b 为例,MAX 表示最大上下文窗口为 128K 的场景。计算方法来自 Yuan 等人 (2024)。
| 内存 | 计算 |
|---|---|
| 带宽:2.04e12B/s | BF16:312e12FLOPS |
| 模型权重:15.0 GB | 最大操作数:83.9GB |
| 加载时间:7.4ms | 最大计算时间:0.3ms |
▷ When generating ultra-long sequence, such as 100K tokens, the GPU must reload the model weights over 100,000 times. This repetitive process poses the challenge: How can we reduce the frequency of model reloading?
▷ 在生成超长序列(例如 100K Token)时,GPU 必须重新加载模型权重超过 10 万次。这一重复过程带来了挑战:我们如何减少模型重新加载的频率?
Challenge II: Prolonged Growing of KV Cache Previous studies, such as TriForce (Sun et al., 2024a) and MagicDec (Chen et al., 2024a) have demonstrated that, a small KV cache budget can be used during the drafting phase to reduce the time increase caused by the loading enormous KV cache. While their one-time compression strategy at the prefill stage can handle scenarios with long prefixes and short outputs, it fails to address cases involving ultra-long outputs, as the growing size of KV cache would far exceed the allocated length budget.
挑战二:KV缓存的持续增长
先前的研究,如TriForce (Sun et al., 2024a) 和 MagicDec (Chen et al., 2024a) 已经证明,在草拟阶段可以使用较小的KV缓存预算来减少因加载庞大KV缓存而增加的时间。虽然它们在预填充阶段的一次性压缩策略可以处理长前缀和短输出的场景,但无法应对超长输出的情况,因为KV缓存不断增长的规模将远远超过分配的长度预算。
$\triangleright T o$ dynamically manage partial KV cache within limited budget during ultra-long sequence generation, the challenge lies in determining when and how to dynamically update the KV cache.
$\triangleright T o$ 在超长序列生成过程中,如何在有限的预算内动态管理部分 KV 缓存,其挑战在于确定何时以及如何动态更新 KV 缓存。
Challenge III: Repetitive Content Generation The degeneration of AR in text generation tasks — characterized by output text that is bland, incoherent, or gets stuck in repetitive loops — is a widely studied challenge (Holtzman et al., 2020; Nguyen et al., 2024; Hewitt et al., 2022). When generating sequences of considerable length, e.g., 100K, the model tends to produce repetitive sentences (Figure 5).
挑战 III:重复内容生成
AR(自回归)在文本生成任务中的退化问题——表现为生成文本平淡、不连贯或陷入重复循环——是一个被广泛研究的挑战(Holtzman et al., 2020; Nguyen et al., 2024; Hewitt et al., 2022)。当生成长度较长的序列时,例如 100K,模型往往会生成重复的句子(图 5)。
$\vartriangleright$ Since our objective is lossless acceleration and repetition is an inherent problem in LLMs, eliminating this issue is not our focus. However, it is still essential and challenging to mitigate repetition patterns in ultra-long sequences.
$\vartriangleright$ 由于我们的目标是无损加速,而重复是大语言模型中的一个固有问题,因此消除这一问题并非我们的重点。然而,在超长序列中减轻重复模式仍然是至关重要且具有挑战性的。
3. TOKENSWIFT
3. TOKENSWIFT
To achieve lossless acceleration in generating ultra-long sequences, we propose tailored solutions for each challenge inherent to this process. These solutions are seamlessly integrated into a unified framework, i.e. TOKENSWIFT.
为了实现超长序列生成中的无损加速,我们针对这一过程中固有的每个挑战提出了定制化的解决方案。这些解决方案被无缝集成到一个统一的框架中,即 TOKENSWIFT。
3.1. Overview
3.1. 概述
The overall framework is depicted in Figure 2. TOKENSWIFT generate a sequence of draft tokens with selfdrafting, which are then passed to the target (full) model for validation using a tree-based attention mechanism (See Appendix E for more tree-based attention details). This process ensures that the final generated output aligns with the target model’s predictions, effectively achieving lossless acceleration.
整体框架如图 2 所示。TOKENSWIFT 通过自生成生成一系列草稿 Token,然后使用基于树的注意力机制(详见附录 E)将这些 Token 传递给目标(完整)模型进行验证。这一过程确保最终生成的输出与目标模型的预测一致,从而实现无损加速。
OKENSWIFT is lightweight because the draft model is the target model itself with a partial KV cache. This eliminates the need to train a separate draft LLM; instead, only $\gamma$ linear layers need to be trained, where $\gamma+1^{1}$ represents the number of logits predicted in a single forward pass. In addition, during the verification process, once we obtain the target tokens from the target model with full KV cache, we directly compare draft tokens with target tokens sequentially to ensure that the process is lossless (He et al., 2024).
TOKENSWIFT 之所以轻量,是因为草稿模型本身就是目标模型,只是带有部分 KV 缓存。这消除了训练独立草稿大语言模型的需求;相反,只需训练 $\gamma$ 个线性层,其中 $\gamma+1^{1}$ 表示单次前向传播中预测的 Logits 数量。此外,在验证过程中,一旦我们从带有完整 KV 缓存的目标模型中获取目标 Token,我们会依次将草稿 Token 与目标 Token 直接比较,以确保过程无损 (He et al., 2024)。
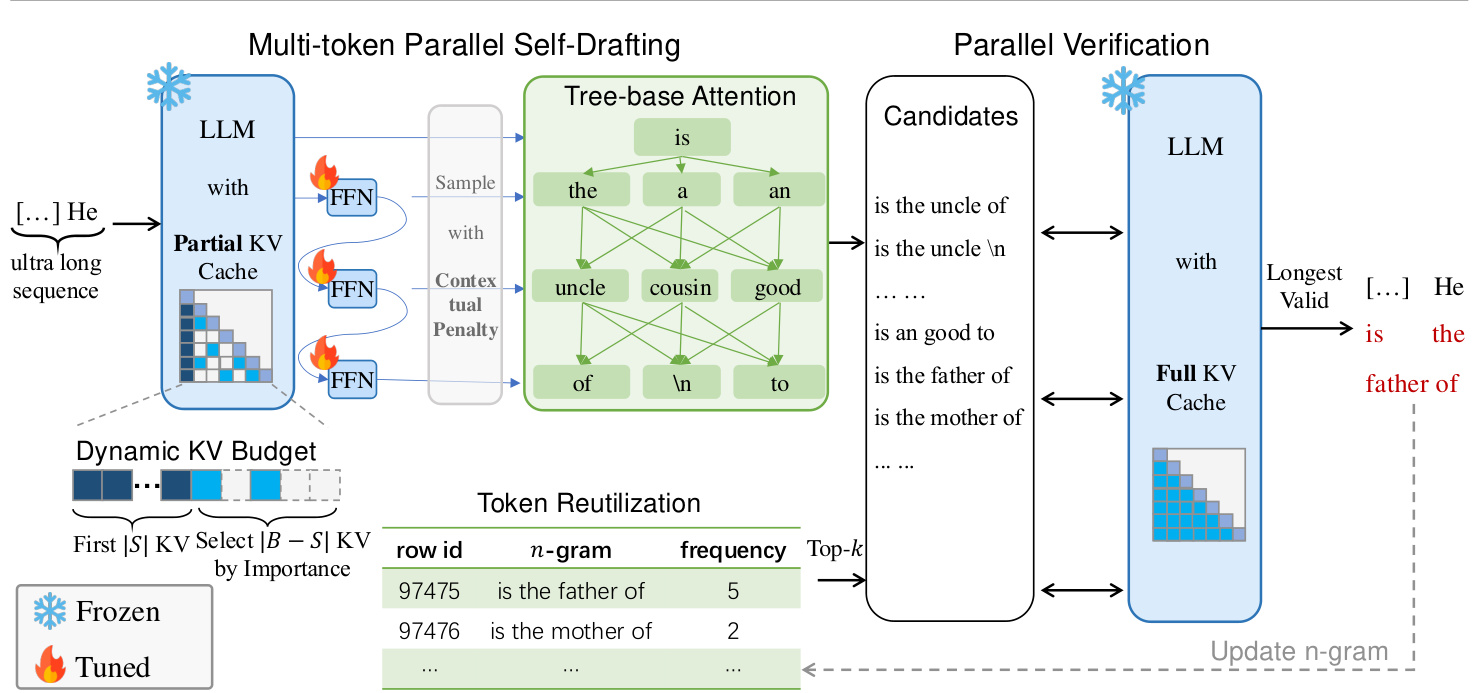
Figure 2. Illustration of TOKENSWIFT Framework. First, target model (LLM) with partial KV cache and three linear layers outputs 4 logits in a single forward pass. Tree-based attention is then applied to construct candidate tokens. Secondly, top $k$ candidate 4-grams are retrieved accordingly. These candidates compose draft tokens, which are fed into the LLM with full KV cache to generate target tokens. The verification is performed by checking if draft tokens match exactly with target tokens (Algorithm 1). Finally, we randomly select one of the longest valid draft tokens, and update $n$ -gram table and KV cache accordingly.
图 2: TOKENSWIFT 框架示意图。首先,具有部分 KV 缓存和三个线性层的目标模型(大语言模型)在单次前向传播中输出 4 个 logits。然后应用基于树的注意力机制来构建候选 token。其次,相应地检索前 $k$ 个候选 4-gram。这些候选组成草稿 token,并将其输入具有完整 KV 缓存的大语言模型中以生成目标 token。验证通过检查草稿 token 是否与目标 token 完全匹配来进行(算法 1)。最后,我们随机选择一个最长的有效草稿 token,并相应地更新 $n$-gram 表和 KV 缓存。
3.2. Multi-token Generation and Token Re utilization
3.2. 多Token生成与Token重用
Multi-token Self-Drafting Inspired by Medusa (Cai et al., 2024), we enable the LLM to generate multiple draft tokens in a single forward pass by incorporating $\gamma$ additional linear layers. However, we empirically note that the additional linear layers should not be independent of each other. Specifically, we propose the following structure:
多Token自草稿生成

where $h_{0}$ denotes the last hidden state of LLM, $f_{i}(\cdot)$ represents the $i$ -th linear layer, $h_{i}$ refers to the $i\cdot$ -th hidden representation, $g(\cdot)$ represents the LM Head of target model, and $l_{i}$ denotes output logits. This structure aligns more closely with the AR nature of the model. Moreover, this adjustment incurs no additional computational cost.
其中 $h_{0}$ 表示大语言模型的最后一个隐藏状态,$f_{i}(\cdot)$ 表示第 $i$ 个线性层,$h_{i}$ 表示第 $i$ 个隐藏表示,$g(\cdot)$ 表示目标模型的 LM Head,$l_{i}$ 表示输出的 logits。这种结构更符合模型的 AR 特性。此外,这种调整不会产生额外的计算成本。
Token Re utilization Given the relatively low acceptance rate of using linear layers to generate draft tokens, we propose a method named token re utilization to further reduce the frequency of model reloads. The idea behind token re utilization is that some phrases could appear frequently, and they are likely to reappear in subsequent generations.
Token 重复利用
Specifically, we maintain a set of tuples ${(\mathcal{G},\mathcal{F})},$ where $\mathcal{G}={x_{i+1},...,x_{i+n}}$ represents an $n$ -gram and $\mathcal{F}$ denotes its corresponding frequency $\mathcal{F}$ within the generated token sequence ${\cal{S}}={x_{0},x_{1},...,x_{t-1}}$ by time step $t\left(t\geqslant n\right)$ . After obtaining ${p_{0},\ldots,p_{3}}$ as described in $\S3.4,$ we retrieve the top $k$ most frequent $n$ -grams beginning with
具体来说,我们维护一组元组 ${(\mathcal{G},\mathcal{F})},$ 其中 $\mathcal{G}={x_{i+1},...,x_{i+n}}$ 表示一个 $n$ -gram,而 $\mathcal{F}$ 表示其在生成 Token 序列 ${\cal{S}}={x_{0},x_{1},...,x_{t-1}}$ 中到时间步 $t\left(t\geqslant n\right)$ 为止的对应频率 $\mathcal{F}$。在按照 $\S3.4$ 所述获取 ${p_{0},\ldots,p_{3}}$ 后,我们检索以这些概率开头的前 $k$ 个最频繁的 $n$ -grams。
token arg max $p_{0}$ to serve as additional draft tokens.
token arg max $p_{0}$ 作为额外的草稿 token。
Although this method can be applied to tasks with long prefixes, its efficacy is constrained by the limited decoding steps, which reduces the opportunities for accepting $n$ -gram candidates. Additionally, since the long prefix text is not generated by the LLM itself, a distribution al discrepancy exists between the generated text and the authentic text (Mitchell et al., 2023). As a result, this method is particularly suitable for generating ultra-long sequences.
尽管该方法可应用于具有长前缀的任务,但其效果受限于有限的解码步骤,这减少了接受 $n$ 元候选词的机会。此外,由于长前缀文本并非由大语言模型自身生成,生成文本与真实文本之间存在分布差异 (Mitchell et al., 2023)。因此,该方法特别适合生成超长序列。
3.3. Dynamic KV Cache Management
3.3. 动态 KV 缓存管理
Dynamic KV Cache Updates Building upon the findings of Xiao et al. (2024), we preserve the initial $|S|$ KV pairs within the cache during the drafting process, while progressively evicting less important KV pairs. Specifically, we enforce a fixed budget size $|B|,$ ensuring that the KV cache at any given time can be represented as:
动态KV缓存更新基于Xiao等人(2024)的研究成果,我们在草拟过程中保留缓存中的初始$|S|$个KV对,同时逐步淘汰重要性较低的KV对。具体而言,我们强制执行固定预算大小$|B|$,确保在任何给定时间点的KV缓存可以表示为:
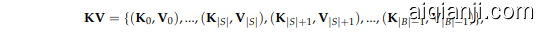
where the first $|S|$ pairs remain fixed, and the pairs from position $|S|$ to $|B|-1$ are ordered by decreasing importance. As new tokens are generated, less important KV pairs are gradually replaced, starting from the least important ones at position $|B|-1$ and moving towards position $|S|$ . Once replacements extend beyond the |S| position, we re calculate the importance scores of all preceding tokens and select the most relevant $\left|B\right|-\left|S\right|$ pairs to reconstruct the cache. This process consistently preserves the critical information required for ultra-long sequence generation.
其中前 $|S|$ 对保持固定,从位置 $|S|$ 到 $|B|-1$ 的对按重要性递减排序。随着新 Token 的生成,从位置 $|B|-1$ 开始,逐渐替换重要性较低的 KV 对,直到位置 $|S|$。一旦替换超过 |S| 位置,我们会重新计算所有前导 Token 的重要性分数,并选择最相关的 $\left|B\right|-\left|S\right|$ 对来重建缓存。这一过程始终保留超长序列生成所需的关键信息。
Importance Score of KV pairs We rank the KV pairs based on the importance scores derived from the dot product between the query (Q) and key (K), i.e. ${\bf Q}{\bf K}^{\overleftarrow{T}}$ .
键值对重要性评分
In the case of Group Query Attention (GQA), since each K corresponds to a group of $\mathcal{Q}={\mathbf{Q}{0},...,\mathbf{Q}{g-1}},$ direct dot-product computation is not feasible. Unlike methods such as SnapKV (Li et al., 2024c), we do not replicate the K. Instead, we partition the $\mathcal{Q},$ as shown in Equation (2):
在 Group Query Attention (GQA) 的情况下,由于每个 K 对应一组 $\mathcal{Q}={\mathbf{Q}{0},...,\mathbf{Q}{g-1}},$ 直接进行点积计算是不可行的。与 SnapKV (Li et al., 2024c) 等方法不同,我们不会复制 K。相反,我们对 $\mathcal{Q},$ 进行分区,如公式 (2) 所示:
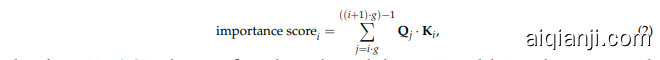
where for position $i,\mathbf{Q}{j}$ in the group $\mathcal{Q}{i}$ are dot-product with the same $\mathbf{K}_{i},$ and their results are aggregated to obtain the final importance score. This approach enhances memory saving while preserving the quality of the attention mechanism, ensuring that each query is effectively utilized without introducing unnecessary redundancy.
其中对于位置 $i,\mathcal{Q}{i}$ 组中的 $\mathbf{Q}{j}$ 与相同的 $\mathbf{K}_{i},$ 进行点积,并将结果聚合以获得最终的重要性分数。这种方法在保持注意力机制质量的同时增强了内存节省,确保每个查询都被有效利用而不引入不必要的冗余。
3.4. Contextual Penalty and Random N-gram Selection
3.4. 上下文惩罚与随机 N-gram 选择
The penalized sampling approach proposed in (Keskar et al., 2019) suggests applying a penalty to all generated tokens. However, when generating ultra-long sequences, the set of generated tokens may cover nearly all common words, which limits the ability to sample appropriate tokens. Therefore, we propose an improvement to this method.
(Keskar et al., 2019) 提出的惩罚采样方法建议对所有生成的 Token 施加惩罚。然而,在生成超长序列时,生成的 Token 集可能几乎覆盖所有常见单词,这限制了采样合适 Token 的能力。因此,我们对该方法提出改进。
Specifically, we introduce a fixed penalty window W and apply penalty value $\theta$ to the most recent $W$ tokens, denoted as $\mathbb{W}$ , generated up to the current position, as illustrated in Equation (3):
具体来说,我们引入了一个固定的惩罚窗口 W,并对最近生成的 W 个 Token(记为 $\mathbb{W}$)应用惩罚值 $\theta$,如公式 (3) 所示:
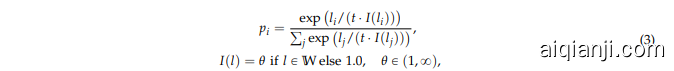
where $t$ denotes temperature, $l_{i}$ and $p_{i}$ represent the logit and probability of $i$ -th token. This adjustment aims to maintain diversity while still mitigating repetitive generation.
其中 $t$ 表示温度,$l_{i}$ 和 $p_{i}$ 分别表示第 $i$ 个 Token 的 logit 和概率。此调整旨在保持多样性的同时,减少重复生成。
Algorithm 1 TOKENSWIFT
算法 1 TOKENSWIFT
Random $n$ -gram Selection In our experiments, we observe that the draft tokens provided to the target model for parallel validation often yield multiple valid groups. Building on this observation, we randomly select one valid $n$ -gram to serve as the final output. By leveraging the fact that multiple valid $n$ -grams emerge during verification, we ensure that the final output is both diverse and accurate.
随机 $n$ -gram 选择
In summary, the overall flow of our framework is presented in Algorithm 1.
总之,我们的框架的整体流程在算法 1 中展示。
4. Experiments
4. 实验
In this section, we demonstrate the capability of TOKENSWIFT in accelerating ultra-long sequences generation.
在本节中,我们展示了TOKENSWIFT在加速超长序列生成方面的能力。
4.1. Setup
4.1. 设置
We conduct experiments on a variety of models, including YaRN-LLaMA2-7b-128k (Peng et al., 2024), LLaMA3.1-8b (AI@Meta, 2024) and Qwen2.5-(1.5b,7b,14b) (Qwen et al., 2025). For all models, we use the Base version, as the output length of Instruct version is limited (Bai et al., 2024). The inference experiments are performed on the test set of PG-19 (Rae et al., 2020).
我们在多种模型上进行了实验,包括 YaRN-LLaMA2-7b-128k (Peng 等, 2024)、LLaMA3.1-8b (AI@Meta, 2024) 和 Qwen2.5-(1.5b,7b,14b) (Qwen 等, 2025)。对于所有模型,我们均使用基础版本,因为指导版本的输出长度有限 (Bai 等, 2024)。推理实验在 PG-19 (Rae 等, 2020) 的测试集上进行。
Training and Inference Details We train linear layers in Section 3.2 using the first 8K tokens of training data, for datasets longer than 8K tokens, from PG-19 (Rae et al., 2020). The number of extra decoding heads is set to 3 across all models.
训练与推理细节
我们使用 PG-19 (Rae et al., 2020) 数据集中前 8K Token 的训练数据来训练第 3.2 节中的线性层,对于超过 8K Token 的数据集也是如此。所有模型的额外解码头数量均设置为 3。
Inference is performed on a single NVIDIA A100-SXM4-80GB. When generating 100K tokens, the models are prefilled with 2K, 4K or 8K tokens as prompt from a random sample of the PG-19 test set (See Appendix F.2 for ablation on prefill length). The maximum budget of the partial cache is determined by the length of the prompt. For further training and inference details, please refer to Appendix B.
推理在单个 NVIDIA A100-SXM4-80GB 上进行。当生成 100K 个 Token 时,模型会从 PG-19 测试集的随机样本中预填充 2K、4K 或 8K 个 Token 作为提示(有关预填充长度的消融实验,请参见附录 F.2)。部分缓存的最大预算由提示的长度决定。有关进一步训练和推理的详细信息,请参阅附录 B。
Evaluation Metrics We evaluate the overall acceptance rate and speedup for all methods. Unlike Leviathan et al. $(2023)^{3}$ , our acceptance rate α is defined as:
评估指标
Table 3. Experimental results for LLaMA2 and LLaMA3.1 under varying prefix lengths, generating sequences from 20K to 100K tokens. α denotes the acceptance rate of all draft tokens (Equation (4)), while $\times$ represents the speedup ratio relative to AR (Equation (5)). TriForce* refers to our improved version, and Medusa* indicates the model we retrained (§4.1).
表 3: LLaMA2 和 LLaMA3.1 在不同前缀长度下的实验结果,生成序列从 20K 到 100K Tokens。α 表示所有草稿 Tokens 的接受率 (公式 (4)),而 $\times$ 表示相对于 AR 的加速比 (公式 (5))。TriForce* 指我们改进的版本,Medusa* 表示我们重新训练的模型 (§4.1)。
| 方法 | 生成长度 | 预填充长度 2048 | 预填充长度 4096 | 预填充长度 8192 | 预填充长度 2048 | 预填充长度 4096 | 预填充长度 8192 |
|---|---|---|---|---|---|---|---|
| YaRN-LLaMA2-7b-128k (MHA) | LLaMA3.1-8b (GQA) | ||||||
| α | ×(>1) | α | ×(>1) | α | ×(>1) | ||
| Medusa* | 20K | 0.43 | 0.96 | 0.39 | 0.85 | 0.40 | 0.83 |
| TriForce* | 20K | 0.80 | 1.50 | 0.89 | 1.51 | 0.92 | 1.36 |
| TOKENSWIFT | 20K | 0.73±0.09 | 2.11±0.14 | 0.68±0.09 | 2.02±0.20 | 0.64±0.08 | 1.91±0.12 |
| Medusa* | 40K | 0.52 | 1.08 | 0.42 | 0.86 | 0.43 | 0.88 |
| TriForce* | 40K | 0.84 | 1.64 | 0.93 | 1.67 | 0.96 | 1.49 |
| TOKENSWIFT | 40K | 0.82±0.06 | 2.60±0.05 | 0.79±0.06 | 2.56±0.09 | 0.79±0.05 | 2.50±0.07 |
| Medusa* | 60K | 0.59 | 1.18 | 0.47 | 0.95 | 0.45 | 0.91 |
| TriForce* | 60K | 0.85 | 1.76 | 0.95 | 1.83 | 0.97 | 1.62 |
| TOKENSWIFT | 60K | 0.87±0.04 | 2.92±0.04 | 0.85±0.04 | 2.89±0.06 | 0.85±0.04 | 2.84±0.05 |
| Medusa* | 80K | 0.61 | 1.17 | 0.51 | 0.99 | 0.47 | 0.93 |
| TriForce* | 80K | 0.84 | 1.86 | 0.95 | 1.98 | 0.97 | 1.74 |
| TOKENSWIFT | 80K | 0.89±0.03 | 3.13±0.04 | 0.88±0.04 | 3.10±0.06 | 0.88±0.03 | 3.05±0.03 |
| Medusa* | 100K | 0.62 | 1.15 | 0.52 | 0.99 | 0.47 | 0.91 |
| TriForce* | 100K | 0.82 | 1.94 | 0.96 | 2.14 | 0.97 | 1.86 |
| TOKENSWIFT | 100K | 0.90±0.02 | 3.25±0.05 | 0.90±0.03 | 3.23±0.06 | 0.90±0.02 | 3.20±0.02 |
where $a_{i}$ represents the number of tokens accepted at the $i\cdot$ -th time step, $\gamma+1$ denotes the number of draft tokens generated at each time step, and $T$ represents the total number of time steps. The speedup is denotes as $\times,$ which is the ratio of AR latency to TOKENSWIFT latency, given by:
其中 $a_{i}$ 表示在第 $i\cdot$ 个时间步接受的 token 数量,$\gamma+1$ 表示每个时间步生成的草稿 token 数量,$T$ 表示总时间步数。加速比表示为 $\times,$ 它是 AR 延迟与 TOKENSWIFT 延迟的比值,由下式给出:

where latency refers to the average time required to generate a single token.
其中延迟指的是生成单个Token所需的平均时间。
We use Distinct $n$ (Li et al., 2016) to measure the diversity of generated content, i.e., repetition. A higher value indicates greater diversity and lower repetition (Table 6).
我们使用 Distinct $n$ (Li et al., 2016) 来衡量生成内容的多样性,即重复性。值越高表示多样性越大,重复性越低(表 6)。
Baselines We compare TOKENSWIFT with two baselines: TriForce*: The original TriForce (Sun et al., 2024a) employs a static KV update strategy, which cannot accelerate the generation of 100K tokens. The results in Table 3 correspond to our improved version of TriForce, which incorporates dynamic KV update . Medusa*: To ensure lossless ness, we adopt the Medusa (Cai et al., 2024) training recipe and incorporate the verification method of TOKENSWIFT. Both Medusa heads and tree structure are consistent with TOKENSWIFT.
基线方法 我们将TOKENSWIFT与两种基线方法进行比较:TriForce*:原始TriForce(Sun et al., 2024a)采用静态KV更新策略,无法加速生成100K个Token。表3中的结果对应我们改进后的TriForce版本,该版本加入了动态KV更新。Medusa*:为了确保无损性,我们采用了Medusa(Cai et al., 2024)的训练方法,并融入了TOKENSWIFT的验证方法。Medusa的头部和树结构均与TOKENSWIFT一致。
The recent released MagicDec (Chen et al., 2024a) primarily focuses on acceleration for large throughput, and when the batch size is 1, LLaMA3.1-8b does not exhibit any acceleration for short text generation, let alone for ultra-long sequences. Therefore, it is excluded from our baseline.
近期发布的 MagicDec (Chen et al., 2024a) 主要关注大吞吐量的加速,当批次大小为 1 时,LLaMA3.1-8b 在短文本生成上并未表现出任何加速效果,更不用说超长序列了。因此,它被排除在我们的基线之外。
4.2. Main Results
4.2. 主要结果
The experimental results are presented in Table 3 and Table 4. We evaluate TOKENSWIFT at different generation lengths of 20K, 40K, 60K, 80K and 100K, reporting speedup $\times$ and acceptance rate $\alpha$ by taking the average and standard deviation of 5 experiments to avoid randomness. Notably, the results for TOKENSWIFT and Medusa* show a balanced trade-off between speed and quality, in contrast to TriForce*, which suffers from low quality due to the absence of any repetition penalty.
实验结果如表 3 和表 4 所示。我们在 20K、40K、60K、80K 和 100K 的不同生成长度下评估了 TOKENSWIFT,报告了加速比 $\times$ 和接受率 $\alpha$,并通过取 5 次实验的平均值和标准差来避免随机性。值得注意的是,TOKENSWIFT 和 Medusa* 的结果在速度和质量之间表现出平衡的权衡,而 TriForce* 由于缺乏任何重复惩罚,导致质量较低。
TOKENSWIFT significantly outperforms all baselines across generation lengths. As shown in Table 3, across all engths, TOKENSWIFT demonstrates superior acceleration performance compared to all baselines on models with
TOKENSWIFT在各生成长度上显著优于所有基线模型。如表 3 所示,在所有长度上,TOKENSWIFT在模型上展现出比所有基线更优越的加速性能。
4To compare with LLaMA3.1-8b, we pretrained a draft model based on LLaMA3.1-8b. See Appendix C for details.
为了与 LLaMA3.1-8b 进行比较,我们基于 LLaMA3.1-8b 预训练了一个草稿模型。详见附录 C。
Table 4. Experimental results of TOKENSWIFT for Qwen2.5 across different scales under prefix length 4096, generating sequences from 20K to 100K tokens. $T_{A R}$ and T TOKEN SWIFT denote the actual time required (in minutes) for AR and TOKENSWIFT, respectively. $\Delta_{T}$ represents the number of minutes saved by TOKENSWIFT compared to AR.
表 4: 不同规模下 Qwen2.5 模型在前缀长度为 4096 时,生成 20K 到 100K Token 序列的 TOKENSWIFT 实验结果。$T_{A R}$ 和 $T_{TOKENSWIFT}$ 分别表示 AR 和 TOKENSWIFT 实际所需的时间(分钟)。$\Delta_{T}$ 表示 TOKENSWIFT 相比 AR 节省的时间(分钟)。
| Gen.Len. | Qwen2.5-1.5B | x(> 1) | TAR | TTOKENSWIFT | △T | Qwen2.5-7B | x(> 1) | TAR | TTOKENSWIFT | △T | α | Qwen2.5-14B | x(> 1) | TAR | TTOKENSWIFT | △T | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20K | 0.69±0.11 | 1.69±0.17 | 12.00 | 7.20 | -4.80 | 0.64±0.07 | 2.00±0.16 | 15.60 | 7.80 | -7.80 | 0.67±0.06 | 2.12±0.13 | 29.40 | 13.80 | -15.60 | |||||
| 40K | 0.80±0.06 | 2.31±0.09 | 36.00 | 15.60 | -20.40 | 0.77±0.05 | 2.64±0.10 | 47.40 | 18.00 | -29.40 | 0.78±0.03 | 2.68±0.10 | 89.40 | 33.60 | -55.80 | |||||
| 60K | 0.85±0.04 | 2.69±0.07 | 73.80 | 27.60 | -46.20 | 0.78±0.08 | 2.86±0.25 | 95.40 | 33.60 | -61.80 | 0.82±0.02 | 23.01±0.13 | 184.20 | 61.20 | -123.00 | |||||
| 80K | 0.87±0.03 | 2.95±0.06 | 124.20 | 42.00 | -82.20 | 0.80±0.09 | 3.07±0.30 | 161.40 | 52.80 | -108.60 | 0.83±0.02 | 23.20±0.13 | 312.60 | 97.80 | -214.80 | |||||
| 100K | 0.89±0.07 | 3.13±0.07 | 187.80 | 60.00 | -127.80 | 0.82±0.09 | 3.23±0.28 | 244.20 | 75.60 | -168.60 | 0.84±0.02 | 3.34±0.10 | 474.60 | 142.20 | -332.40 |
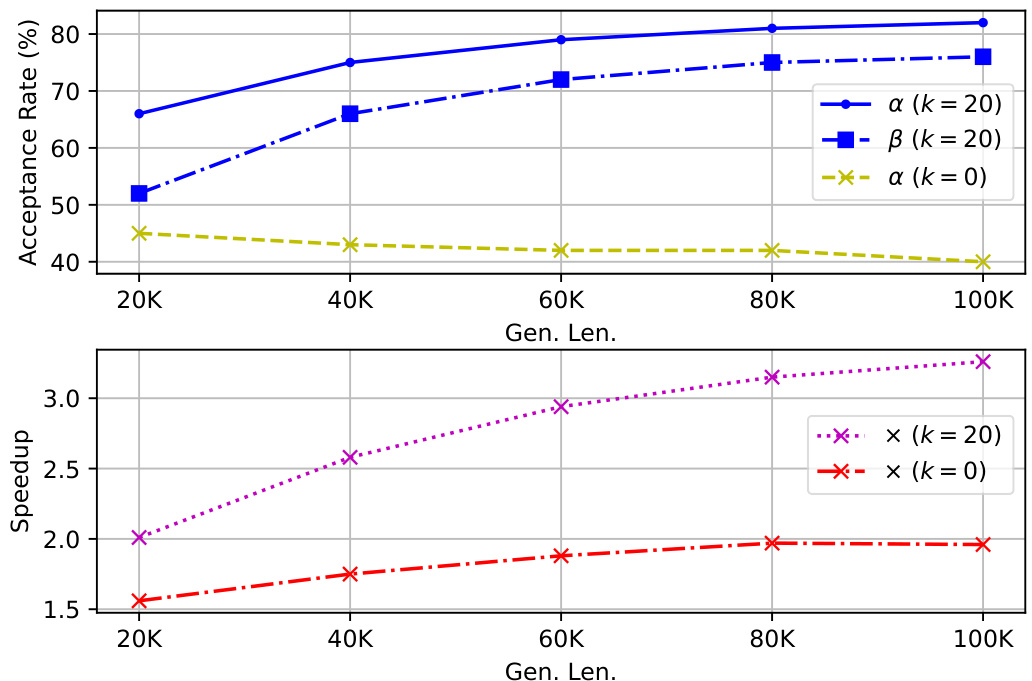
Figure 3. Upper: The acceptance rate α for $k=20$ and $k=0$ , along with the $n$ -gram acceptance rate $\beta$ for $k=20$ , plotted against varying generation lengths. Lower: The speedup $\times$ achieved at different generation lengths.
图 3: 上:$k=20$ 和 $k=0$ 的接受率 $\alpha$,以及 $k=20$ 的 $n$-gram 接受率 $\beta$,随生成长度变化的情况。下:不同生成长度下实现的加速倍数 $\times$。
different architectures (MHA, GQA). Moreover, TOKENSWIFT demonstrates remarkable robustness, showing virtually no impact when tested with varying prefix lengths.
不同架构 (MHA, GQA)。此外,TOKENSWIFT 表现出显著的鲁棒性,在使用不同前缀长度进行测试时几乎不受影响。
Longer generations amplify the speedup benefits. As the generation length increases, the speed improvement of TOKENSWIFT becomes increasingly evident. Two key factors drive this trend: Firstly, AR experiences longer KV cache loading times as the number of tokens grows, whereas TOKENSWIFT mitigates this issue by utilizing dynamic KV pruning. Secondly, the acceptance rate improves as the number of tokens increases, primarily due to the higher $n$ -grams acceptance rate. As the $n$ -grams pool composed of generated tokens grows larger, the candidate $n$ -grams become more diverse and accurate (Figure 3).
生成长度越长,TOKENSWIFT 的加速优势越明显。随着生成长度的增加,TOKENSWIFT 的速度提升变得越来越显著。这一趋势主要由两个关键因素驱动:首先,随着 token 数量的增加,AR 的 KV 缓存加载时间变长,而 TOKENSWIFT 通过动态 KV 剪枝缓解了这一问题。其次,随着 token 数量的增加,接受率提高,这主要归因于更高的 $n$ -grams 接受率。随着由生成的 token 组成的 $n$ -grams 池变得更大,候选 $n$ -grams 变得更加多样化和准确(图 3)。
Larger models yield greater speedup benefits. The impact of frequent model reloading varies with model scale, as larger models require more time due to the increased parameters. As shown in Table 4, TOKENSWIFT demonstrates robust performance across models of different scales, with the acceleration advantage becoming more pronounced for larger models. In particular, when generating 100K tokens, TOKENSWIFT saves up to 5.54 hours for 14B model.
更大规模的模型带来更显著的加速效益。频繁的模型重载影响因模型规模而异,因为更大的模型由于参数增多而需要更多时间。如表 4 所示,TOKENSWIFT 在不同规模的模型上均表现出稳健的性能,且对更大模型的加速优势更为明显。特别是当生成 100K tokens 时,TOKENSWIFT 为 14B 模型节省了多达 5.54 小时。
4.3. Ablation Studies
4.3. 消融研究
We conduct comprehensive ablation studies on TOKENSWIFT using LLaMA3.1-8b. For all experiments, the prefix length is 4096.
我们使用 LLaMA3.1-8b 对 TOKENSWIFT 进行了全面的消融研究。所有实验中,前缀长度均为 4096。
4.3.1. TOKEN RE UTILIZATION
4.3.1. Token 重复利用
We define the $n$ -gram acceptance rate $\beta$ similarly to Equation (4). Let $a_{i}^{\prime}$ denote the length of accepted $n$ -gram candidate at iteration $i$ . Then $\beta$ is given by:
我们定义 $n$ -gram 接受率 $\beta$ 与公式 (4) 类似。设 $a_{i}^{\prime}$ 表示在第 $i$ 次迭代时接受的 $n$ -gram 候选长度,则 $\beta$ 由下式给出:

From Figure 3, we observe that removing token re utilization $(k=0)$ ) leads to a significant decrease in both acceptance rate $\alpha$ and speedup $\times$ . Furthermore, as the generation length increases, the acceptance rate $\alpha$ for $k=0$ slightly drops. This trend stems from the fact that, in ultra-long sequences, the KV cache cannot be compressed indefinitely. In contrast, TOKENSWIFT $(k=20)$ ) shows an increasing acceptance rate as the sequence length grows, demonstrating the effectiveness of token re utilization in reducing the frequency of model reloading.
从图 3 中我们观察到,移除 token 重用 $(k=0)$ 会导致接受率 $\alpha$ 和加速比 $\times$ 显著下降。此外,随着生成长度的增加,$k=0$ 的接受率 $\alpha$ 略有下降。这一趋势源于在超长序列中,KV 缓存无法无限压缩。相比之下,TOKENSWIFT $(k=20)$ 的接受率随着序列长度的增加而上升,展示了 token 重用在减少模型重新加载频率方面的有效性。
Table 5. The ablation experiment results on KV management.
表 5. KV管理的消融实验结果
| Gen.Len. | 全缓存 | 部分缓存 | 动态部分缓存 | |
|---|---|---|---|---|
| 20K | α | 0.42 | 0.19 | 0.45 |
| ×(>1) | 1.36 | 0.94 | 1.56 | |
| 40K | α | 0.42 | 0.16 | 0.43 |
| ×(>1) | 1.42 | 1.03 | 1.75 | |
| 60K | α | 0.42 | 0.18 | 0.42 |
| ×(>1) | 1.45 | 1.19 | 1.88 | |
| 80K | α | 0.42 | 0.19 | 0.42 |
| ×(>1) | 1.46 | 1.31 | 1.97 | |
| 100K | α | 0.42 | 0.21 | 0.40 |
| ×(>1) | 1.47 | 1.44 | 1.96 |
Table 6. The ablation experiment results on contextual penalty using different sampling methods. Light cell represents the settings adopted by TOKENSWIFT. We take $\theta=1.2$ , $W=$ 1024.
表 6: 使用不同采样方法的上下文惩罚消融实验结果。浅色单元格表示 TOKENSWIFT 采用的设置。我们取 $\theta=1.2$,$W=1024$。
| Distinct-1 | Distinct-2 | Distinct-3 | Distinct-4 | AVG. | X | |
|---|---|---|---|---|---|---|
| top-p w/o.penalty | 0.15 | 0.25 | 0.29 | 0.31 | 0.25 | 3.42 |
| 0.09 | 0.15 | 0.18 | 0.20 | 0.16 | 3.53 | |
| r-sampling w/o.penalty | 0.25 | 0.43 | 0.49 | 0.53 | 0.43 | 3.42 |
| 0.06 | 0.10 | 0.12 | 0.13 | 0.11 | 3.57 | |
| min-p w/o.penalty | 0.41 | 0.71 | 0.81 | 0.82 | 0.69 | 3.27 |
| 0.07 | 0.11 | 0.14 | 0.15 | 0.12 | 3.58 |
4.3.2. DYNAMIC KV UPDATES
4.3.2. 动态KV更新
To evaluate the effectiveness of TOKENSWIFT’s dynamic KV update policy, we experiment with three different strategies of managing KV cache during drafting:
为了评估TOKENSWIFT的动态KV更新策略的有效性,我们实验了三种不同的草稿生成过程中管理KV缓存的策略:
‚ Full Cache: Retaining full KV cache throughout drafting. ‚ Partial Cache: Updating partial KV cache only once during the prefill phase. ‚ Dynamic Partial Cache: Dynamically updating KV cache as described in $\S3.3$
- 全缓存:在整个起草阶段保留完整的KV缓存。
- 部分缓存:在预填充阶段仅更新部分KV缓存。
- 动态部分缓存:如 $\S3.3$ 所述,动态更新KV缓存。
For a fair comparison, token re utilization is disabled (i.e. $k=0$ ). As shown in Table 5, Partial Cache leads to a low acceptance rate, resulting in reduced speedup. While Full Cache achieves a higher acceptance rate, its computational overhead negates the speedup gains. In contrast, Dynamic Partial Cache adopted by TOKENSWIFT strikes a balanced trade-off, achieving both high acceptance rate and significant speedup. As a result, Dynamic Partial Cache can effectively manage partial KV under ultra-long sequence generation.
为了公平比较,Token 重复利用被禁用(即 $k=0$)。如表 5 所示,Partial Cache 导致接受率较低,从而降低了加速效果。而 Full Cache 实现了较高的接受率,但其计算开销抵消了加速收益。相比之下,TOKENSWIFT 采用的 Dynamic Partial Cache 实现了平衡的权衡,既达到了高接受率,又实现了显著的加速效果。因此,Dynamic Partial Cache 能够有效管理超长序列生成中的部分 KV 缓存。
4.3.3. CONTEXTUAL PENALTY
4.3.3. 上下文惩罚
As an orthogonal method to min $p$ , top $p$ , and $\eta$ -sampling for mitigating the repetition, contextual penalty demonstrates effectiveness across different sampling methods.
作为最小化 $p$、top $p$ 和 $\eta$ 采样的正交方法,上下文惩罚在不同采样方法中展示了有效性。
As shown in Table 6, without contextual penalty, the diversity of generated sequences is significantly lower for all sampling methods. The most striking improvement emerges in min $p$ sampling (See Appendix D for more sampling details), where the average Distinct $n$ score surges from 0.12 to 0.69 with only an $8%$ compromise in speedup. These results clearly highlight the impact of contextual penalty in mitigating repetitive token generation. It can seamlessly integrate with existing sampling methods to enhance the quality of ultra-long sequence generation.
如表 6 所示,在没有上下文惩罚的情况下,所有采样方法生成的序列多样性都显著降低。最显著的改进出现在 min $p$ 采样中 (更多采样细节见附录 D),其中平均 Distinct $n$ 分数从 0.12 飙升至 0.69,而加速性能仅降低了 $8%$。这些结果清楚地凸显了上下文惩罚在减少重复 Token 生成方面的影响。它可以无缝集成到现有的采样方法中,以提升超长序列生成的质量。
In addition, we can find that the higher the diversity, the lower the speedup. Therefore, if TriForce is combined with context penalty, the speedup in Table 3 will drop further.
此外,我们可以发现多样性越高,加速比越低。因此,如果 TriForce 与上下文惩罚结合使用,表 3 中的加速比将进一步下降。
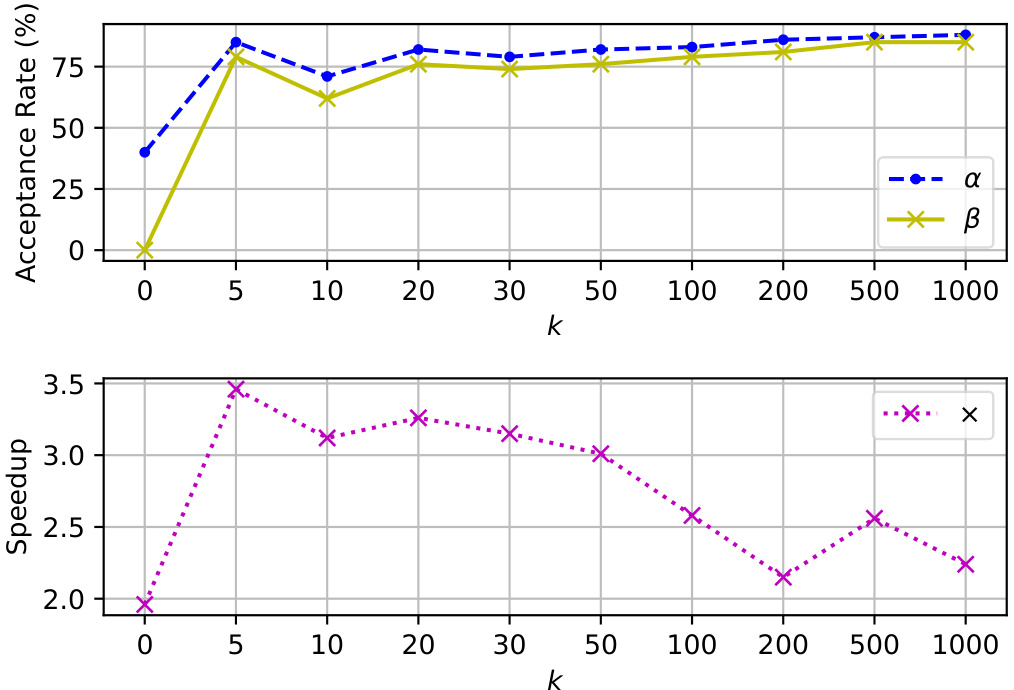
Figure 4. Upper: The acceptance rate $\alpha$ and $n$ -gram acceptance rate $\beta$ versus varying $k$ . Lower: The speedup $\times$ versus varying $k$
图 4: 上:接受率 $\alpha$ 和 $n$ -gram 接受率 $\beta$ 随 $k$ 变化的情况。下:加速比 $\times$ 随 $k$ 变化的情况。
Table 7. Acceptance rate α $\left(k=0\right)$ ) and speedup $\times$ across different tree configurations. Each configuration is represented by a 4-digit array: they represent the number of candidates for different decoding heads in §3.2.
表 7: 不同树配置下的接受率 α($\left(k=0\right)$)和加速比 $\times$。每个配置由一个 4 位数数组表示:它们代表第 3.2 节中不同解码头的候选数量。
Table 8. Distinct-n score across different penalty value θ. 1.0 indicate that no penalty is applied. We take $W=1024$ (See Appendix F.3 for ablation on $W$ ).
表 8: 不同惩罚值 θ 下的 Distinct-n 分数。1.0 表示未应用惩罚。我们取 $W=1024$(关于 $W$ 的消融实验见附录 F.3)。
| Gen.Len. | [3,3,3,3] | [1,9,9,9] | [1,3,3,3] (Ours) | |
|---|---|---|---|---|
| 20K | α | 0.44 | 0.50 | 0.45 |
| x(>1) | 1.34 | 0.53 | 1.56 | |
| 40K | α | 0.43 | 0.52 | 0.43 |
| x(>1) | 1.58 | 0.67 | 1.75 | |
| 60K | α | 0.43 | 0.53 | 0.42 |
| x(>1) | 1.75 | 0.78 | 1.88 | |
| 80K | α | 0.43 | 0.55 | 0.42 |
| x(>1) | 1.85 | 0.88 | 1.97 | |
| 100K | α | 0.42 | 0.57 | 0.40 |
| x(>1) | 1.91 | 0.96 | 1.96 |
| Distinct-1 | Distinct-2 | Distinct-3 | Distinct-4 | AVG. | |
|---|---|---|---|---|---|
| 1.0 | 0.07 | 0.11 | 0.14 | 0.15 | 0.12 |
| 1.1 | 0.08 | 0.13 | 0.15 | 0.16 | 0.13 |
| 1.2 | 0.41 | 0.71 | 0.81 | 0.82 | 0.69 |
| 1.3 | 0.57 | 0.86 | 0.93 | 0.95 | 0.83 |
| 1.4 | 0.52 | 0.73 | 0.76 | 0.77 | 0.70 |
| 1.5 | 0.74 | 0.96 | 0.98 | 0.99 | 0.92 |
4.4. Discussions
4.4. 讨论
In this section, we explore the effects of different hyper parameters on TOKENSWIFT.
在本节中,我们探讨了不同超参数对 TOKENSWIFT 的影响。
4.4.1. TREE CONFIGURATION
4.4.1. 树配置
Due to the time-consuming nature of finding the optimal tree in Medusa (Cai et al., 2024) and its limited impact on accelerating ultra-long sequences generation, we employ a simple 3-ary tree in tree attention. See Appendix B for the tree structure.
由于在 Medusa (Cai et al., 2024) 中找到最优树的过程耗时且对加速超长序列生成的影响有限,我们在树注意力中采用了简单的三叉树。树结构详见附录 B。
As shown in Table 7, [1,9,9,9] has the highest acceptance rate but the lowest speedup. This is because more candidates increase the acceptance rate, but also increase the verification burden. Similarly, by comparing [1,3,3,3] and [3,3,3,3], we can find that the first head (i.e., the original head of target model) achieves relatively high prediction accuracy when using KV compression, so choosing the top-1 token as candidate is sufficient. To balance the trade-off of acceptance rate and verification efficiency, we adopt [1,3,3,3] as the configuration of TOKENSWIFT.
如表 7 所示,[1,9,9,9] 的接受率最高,但加速比最低。这是因为更多的候选会增加接受率,但也会增加验证负担。同样,通过比较 [1,3,3,3] 和 [3,3,3,3],我们可以发现,在使用 KV 压缩时,第一个头 (即目标模型的原始头) 实现了相对较高的预测准确率,因此选择 top-1 token 作为候选就足够了。为了平衡接受率和验证效率,我们采用 [1,3,3,3] 作为 TOKENSWIFT 的配置。
4.4.2. N-GRAM CANDIDATES
4.4.2. N-GRAM 候选集
As illustrated in Figure 4, increasing $k$ enhances the $n$ -gram acceptance rate $\beta$ due to a larger pool of $n$ -gram candidates. However, an excessive number of candidates can strain the verification process, leading to reduced speedup $\times$ .
如图 4 所示,随着 $k$ 的增加,由于 $n$-gram 候选池的扩大,$n$-gram 接受率 $\beta$ 得到提升。然而,过多的候选词会给验证过程带来压力,导致加速比 $\times$ 下降。
Interestingly, a lower $k$ does not always result in a lower $\beta$ . For instance, $k=5$ achieves a higher $\beta$ than $k=20$ , resulting in both a higher acceptance rate $\alpha$ and greater speedu $_p\times$ . However, at $k=5$ , the lack of diversity among the candidates leads to increased repetition, which in turn degrades the quality of generation.
有趣的是,较低的 $k$ 并不总是导致较低的 $\beta$。例如,$k=5$ 实现了比 $k=20$ 更高的 $\beta$,从而获得了更高的接受率 $\alpha$ 和更大的速度 $_{p}\times$。然而,在 $k=5$ 时,候选者之间缺乏多样性导致重复增加,进而降低了生成的质量。
4.4.3. PENALTY VALUE $\theta$
4.4.3. 惩罚值 $\theta$
As a key component of TOKENSWIFT, contextual penalty significantly reduces repetition in generated text. We examine the effect of two parameters present in contextual penalty, i.e. penalty value $\theta$ and penalty window $W$ .
作为 TOKENSWIFT 的关键组件,上下文惩罚显著减少了生成文本中的重复。我们研究了上下文惩罚中两个参数的影响,即惩罚值 $\theta$ 和惩罚窗口 $W$。
Table 8 presents the impact of introducing contextual penalty on diversity. Without any penalty $(\theta=0)$ ), the generated sequences exhibit severe repetition, with an average Distinct $n$ score of only 0.12. As the value of $\theta$ increases gradually to 1.2, the diversity improves significantly, highlighting the effectiveness of contextual penalty in enhancing the diversity of ultra-long sequence generation.
表 8 展示了引入上下文惩罚对多样性的影响。在没有惩罚 $(\theta=0)$ 的情况下,生成的序列表现出严重的重复,平均 Distinct $n$ 得分仅为 0.12。随着 $\theta$ 的值逐渐增加到 1.2,多样性显著提高,凸显了上下文惩罚在增强超长序列生成多样性方面的有效性。
4.4.4. CASE STUDY
4.4.4. 案例研究
Figure 5 presents a case study on the impact of the contextual penalty. Without the Contextual Penalty, repetitions appear at about 5K tokens, compared to 60K with the penalty applied. Additionally, generation without the penalty exhibits word-for-word repetition, whereas generation with the penalty primarily demonstrates semanticlevel repetition, highlighting its effectiveness in mitigating redundancy.
图 5: 上下文惩罚影响的案例研究。在不使用上下文惩罚的情况下,重复现象出现在大约 5K Token 处,而应用惩罚后则出现在 60K Token 处。此外,未应用惩罚的生成表现出逐字重复,而应用惩罚的生成则主要表现出语义层面的重复,凸显了其在减少冗余方面的有效性。
5. Related Works
- 相关工作
5.1. Speculative Decoding
5.1. 推测解码 (Speculative Decoding)
Recent advancements in speculative decoding have significantly accelerated large language model (LLM) inference through diverse methodologies. Speculative decoding (Leviathan et al., 2023; Chen et al., 2023) traditionally leverages smaller draft models to propose candidate tokens for verification by the target model. Early works like SpecTr (Sun et al., 2023) introduced optimal transport for multi-candidate selection, while SpecInfer (Miao et al., 2024) and Medusa (Cai et al., 2024) pioneered tree-based structures with tree-aware attention and multi-head decoding to enable parallel verification of multiple candidates. Subsequent innovations, such as Sequoia (Chen et al., 2024b) and EAGLE-2 (Li et al., 2024d), optimized tree construction using dynamic programming and reordering strategies, while Hydra (Ankner et al., 2024) and ReDrafter (Cheng et al., 2024) enhanced tree dependencies through sequential or recurrent heads. Hardware-aware optimization s, exemplified by SpecExec (Sv ir sch evski et al., 2024) and Triforce (Sun et al., 2024a), further improved efficiency by leveraging hierarchical KV caching and quantized inference.
推测解码 (Speculative Decoding) 领域的最新进展通过多种方法显著加速了大语言模型 (LLM) 的推理。传统推测解码 (Leviathan et al., 2023; Chen et al., 2023) 利用较小的草稿模型提出候选 Token,供目标模型验证。早期的研究如 SpecTr (Sun et al., 2023) 引入了最优传输用于多候选选择,而 SpecInfer (Miao et al., 2024) 和 Medusa (Cai et al., 2024) 则开创了基于树结构的树感知注意力和多头解码,实现了多个候选的并行验证。随后的创新,如 Sequoia (Chen et al., 2024b) 和 EAGLE-2 (Li et al., 2024d),通过动态规划和重排序策略优化了树构建,而 Hydra (Ankner et al., 2024) 和 ReDrafter (Cheng et al., 2024) 则通过顺序或循环头增强了树的依赖关系。硬件感知优化方法,如 SpecExec (Sv ir sch evski et al., 2024) 和 Triforce (Sun et al., 2024a),通过利用分层 KV 缓存和量化推理进一步提高了效率。
Self-speculative approaches eliminate the need for external
