Atom of Thoughts for Markov LLM Test-Time Scaling
用于马尔可夫大语言模型测试时间扩展的思维原子
Abstract
摘要
Large Language Models (LLMs) achieve superior performance through training-time scaling, and test-time scaling further enhances their capabilities by conducting effective reasoning during inference. However, as the scale of reasoning increases, existing test-time scaling methods suffer from accumulated historical information, which not only wastes computational resources but also interferes with effective reasoning. To address this issue, we observe that complex reasoning progress is often achieved by solving a sequence of independent sub questions, each being self-contained and verifiable. These sub questions are essentially atomic questions, relying primarily on their current state rather than accumulated history, similar to the memoryless transitions in a Markov process. Based on this observation, we propose Atom of Thoughts (AOT), where each state transition in the reasoning process consists of decomposing the current question into a dependency-based directed acyclic graph and contracting its sub questions, forming a new atomic question state. This iterative decomposition-contraction process continues until reaching directly solvable atomic questions, naturally realizing Markov transitions between question states. Furthermore, these atomic questions can be seamlessly integrated into existing test-time scaling methods, enabling AOT to serve as a plug-in enhancement for improving reasoning capabilities. Experiments across six benchmarks demonstrate the effectiveness of AOT both as a standalone framework and a plug-in enhancement. Notably, on HotpotQA, when applied to gpt-4omini, AOT achieves an $80.6%$ F1 score, surpassing o3-mini by $3.4%$ and DeepSeek-R1 by $10.6%$ . The code will be available at https://github.com/qixucen/atom.
大语言模型 (LLMs) 通过训练时的扩展获得卓越的性能,而测试时的扩展通过在推理过程中进行有效推理进一步增强了它们的能力。然而,随着推理规模的增加,现有的测试时扩展方法受到累积历史信息的影响,这不仅浪费了计算资源,还干扰了有效的推理。为了解决这个问题,我们观察到复杂的推理过程通常通过解决一系列独立的子问题来实现,每个子问题都是自包含且可验证的。这些子问题本质上是原子问题,主要依赖于它们当前的状态而不是累积的历史,类似于马尔可夫过程中的无记忆转移。基于这一观察,我们提出了 Atom of Thoughts (AOT) ,其中推理过程中的每个状态转移包括将当前问题分解为基于依赖的有向无环图,并收缩其子问题,形成一个新的原子问题状态。这种迭代的分解-收缩过程持续进行,直到达到可直接解决的原子问题,自然而然地实现了问题状态之间的马尔可夫转移。此外,这些原子问题可以无缝集成到现有的测试时扩展方法中,使 AOT 成为一个提升推理能力的插件增强。在六个基准测试上的实验证明了 AOT 作为独立框架和插件增强的有效性。值得注意的是,在 HotpotQA 上,当应用于 gpt-4omini 时,AOT 实现了 80.6% 的 F1 分数,超过了 o3-mini 的 3.4% 和 DeepSeek-R1 的 10.6%。代码将在 https://github.com/qixucen/atom 上提供。
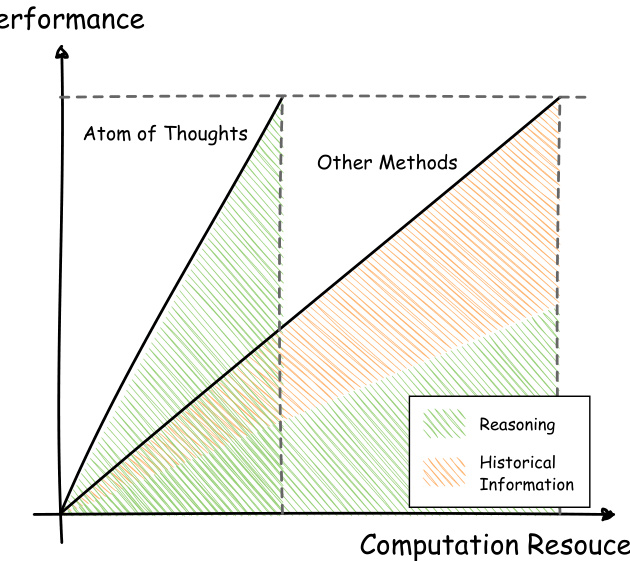
Figure 1: Comparison of computational resource allocation in test-time scaling methods. Traditional testtime scaling methods allocate computational resources partially to process historical information, while AOT dedicates all computational resources to reasoning directly related to the current atomic question state.
图 1: 测试时扩展方法中计算资源分配的对比。传统的测试时扩展方法将计算资源部分分配给处理历史信息,而 AOT 将所有计算资源用于直接与当前原子问题状态相关的推理。
1 Introduction
1 引言
Large Language Models (LLMs) demonstrate significant scaling effects, with their capabilities showing predictable improvements as model parameters and training data increase, leading to enhanced performance across diverse domains (Kaplan et al., 2020). While this scaling law faces bottlenecks in high-quality data availability, test-time scaling offers an alternative solution by forcing LLMs to engage in effective logical reasoning during inference to improve performance on diverse tasks (Snell et al., 2024; Mu en nigh off et al., 2025; Hou et al., 2025; Zhang et al., 2024a).
大语言模型 (Large Language Models, LLMs) 展示了显著的规模效应,随着模型参数和训练数据的增加,其能力呈现出可预测的提升,从而在多个领域中表现更好 (Kaplan et al., 2020)。尽管这一规模效应在高质量数据的可用性上面临瓶颈,但测试时的规模扩展提供了一种替代解决方案,通过迫使LLMs在推理过程中进行有效的逻辑推理,从而提升在多样化任务中的表现 (Snell et al., 2024; Mu en nigh off et al., 2025; Hou et al., 2025; Zhang et al., 2024a)。
However, existing test-time scaling methods excessively maintain historical information during reasoning, as they rely heavily on complex structural dependencies throughout the reasoning process. Chain-based methods must preserve the entire reasoning history to generate each subsequent step (Wei et al., 2022; Zhang et al., 2023), while tree-based approaches require tracking both ancestor and sibling relationships for branch selection (Yao et al., 2023; Zhou et al., 2024; Ding et al., 2024). Graph-based structures further compound these challenges through arbitrary node dependencies. As the scale of reasoning increases, the accumulation of historical dependencies not only wastes substantial computational resources but also interferes with the model’s ability to reason effectively, as illustrated in Figure 1.
然而,现有的测试时缩放方法在推理过程中过度维护历史信息,因为它们在整个推理过程中严重依赖复杂的结构依赖关系。基于链式的方法必须保留整个推理历史以生成每个后续步骤 (Wei et al., 2022; Zhang et al., 2023),而基于树的方法则需要跟踪祖先和兄弟关系以进行分支选择 (Yao et al., 2023; Zhou et al., 2024; Ding et al., 2024)。基于图的结构通过任意的节点依赖关系进一步加剧了这些挑战。随着推理规模的增加,历史依赖的积累不仅浪费了大量计算资源,还干扰了模型的有效推理能力,如图 1 所示。
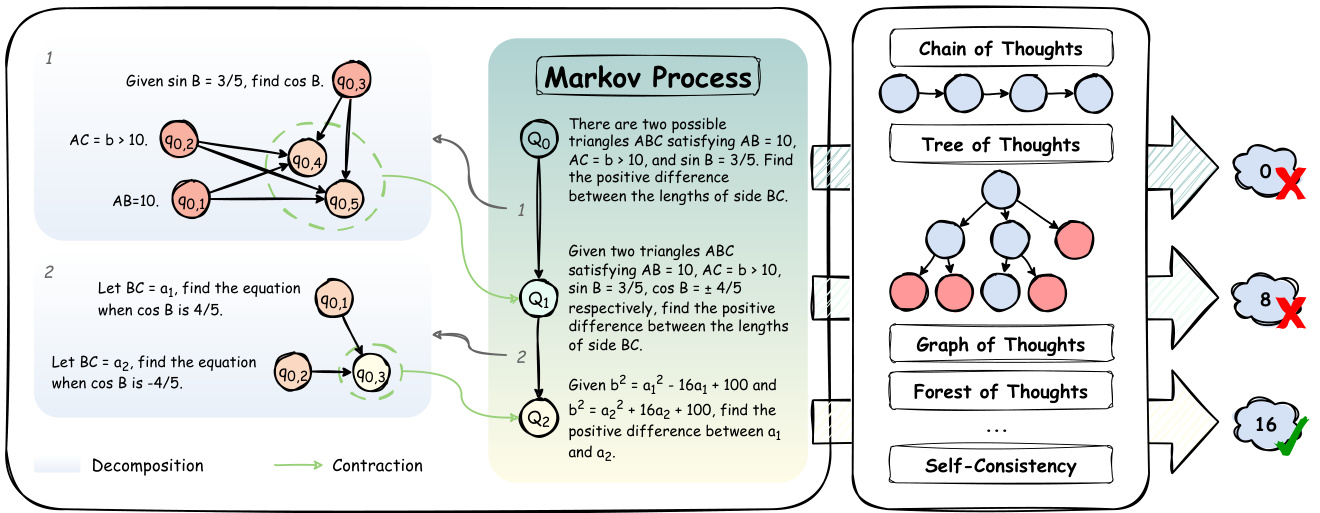
Figure 2: The overview of AOT. The left portion illustrates our Markov process where each state $Q_{i}$ represents an atomic reasoning state derived through DAG decomposition and contraction from its predecessor. The right portion demonstrates AOT’s integration capability with existing test-time scaling methods (e.g., CoT, ToT). A key feature of this integration is that any intermediate state $Q_{i}$ from our Markov process can serve as an entry point $(Q_{0})$ for other methods, enabling flexible composition while maintaining answer equivalence with the original question. This design allows AOT to function both as a standalone iterative framework and as a preprocessing module that can enhance existing approaches through structural optimization.
图 2: AOT 概览。左侧部分展示了我们的马尔可夫过程,其中每个状态 $Q_{i}$ 表示通过 DAG 分解和收缩从其前驱状态得到的原子推理状态。右侧部分展示了 AOT 与现有测试时扩展方法(例如 CoT、ToT)的集成能力。这种集成的关键特征是,我们马尔可夫过程中的任何中间状态 $Q_{i}$ 都可以作为其他方法的入口点 $(Q_{0})$,从而实现灵活组合,同时保持与原始问题的答案等价性。这种设计使 AOT 既能作为一个独立的迭代框架运行,也能作为一个预处理模块,通过结构优化增强现有方法。
Human reasoning often progresses through solving a sequence of independent sub questions, a fundamental principle established in cognitive science (Simon, 1962) and problem-solving theory (Polya, 1945). When solving a complex problem, we naturally identify and resolve self-evident sub questions first, then seamlessly incorporate these solutions to reformulate a simplified problem state, rather than maintaining detailed reasoning processes for resolved components. This progression closely resembles a Markov process (Markov, 1906), where each state represents a question, and state transitions occur through resolving partial problems to form new, independent questions.
人类推理通常通过解决一系列独立的子问题来推进,这是认知科学 (Simon, 1962) 和问题解决理论 (Polya, 1945) 中确立的基本原则。在解决复杂问题时,我们自然会先识别并解决显而易见的子问题,然后无缝地整合这些解决方案,重新构建一个简化的问题状态,而不是为已解决的组件保留详细的推理过程。这一过程与马尔可夫过程 (Markov, 1906) 非常相似,其中每个状态代表一个问题,而状态转换通过解决部分问题形成新的独立问题来实现。
Inspired by this Markov nature of human reasoning, we propose Atom of Thoughts (AOT), a framework that realizes the Markov-style reasoning process. Our key insight is that each reasoning state can be defined as a simplified problem equivalent to the original one, where partial reasoning steps are either transformed into known conditions or excluded as incorrect explorations. This definition is achieved through a two-phase state transition mechanism: first decomposing the current question into a dependency-based directed acyclic graph (DAG) to capture rich structural information, then contracting sub questions into a new independent question. This iterative decomposition-contraction process continues until reaching directly solvable atomic questions, ensuring each state transition depends only on the current state while progressively reducing problem complexity.
受人类推理的马尔可夫性质启发,我们提出了思维原子(Atom of Thoughts,AOT),一个实现马尔可夫风格推理过程的框架。我们的核心观点是,每个推理状态可以定义为一个与原始问题等价的简化问题,其中部分推理步骤要么转化为已知条件,要么被排除为错误探索。这一定义通过两阶段状态转移机制实现:首先将当前问题分解为基于依赖关系的有向无环图(DAG)以捕捉丰富的结构信息,然后将子问题压缩为一个新的独立问题。这种迭代的分解-压缩过程持续进行,直到达到可直接解决的原子问题,确保每个状态转移仅依赖于当前状态,同时逐步降低问题复杂度。
This design endows AOT with two key advantages. First, AOT eliminates the need for maintaining and computing historical information when scaling computational resources. Second, these atomic questions can be seamlessly integrated into existing test-time scaling frameworks, allowing AOT to function as either a standalone framework or a plug-in enhancement for improving the overall reasoning capabilities.
该设计为 AOT 带来了两个关键优势。首先,AOT 在扩展计算资源时无需维护和计算历史信息。其次,这些原子问题可以无缝集成到现有的测试时扩展框架中,使 AOT 既可以作为独立框架运行,也可以作为插件增强功能来提升整体推理能力。
In summary, our contributions are as follows:
我们的贡献如下:
• Atom of Thoughts. We introduce AOT, a novel reasoning framework with Markov property that progressively decomposes problems into atomic units. This approach significantly reduces computational resources wasted on historical information processing, allowing the model to focus on effective reasoning during test-time scaling.
• 思维原子 (Atom of Thoughts)。我们提出了 AOT,一种具有马尔可夫性质的新型推理框架,它将问题逐步分解为原子单元。这种方法显著减少了在处理历史信息时浪费的计算资源,使模型能够在测试阶段扩展时专注于有效推理。
• Plug-In Enhancement. The atomic questions derived by AOT can be directly integrated into existing test-time scaling methods (Bi et al., 2024; Wang et al., 2023b), enhancing both their performance and cost efficiency.
插件增强。AOT 生成的原子问题可以直接集成到现有的测试时间扩展方法中 (Bi et al., 2024; Wang et al., 2023b),提升其性能和成本效率。
• Extensive Evaluation. Experiments across six benchmarks demonstrate the effectiveness of AOT both as a standalone framework and as a plug-in enhancement. AOT outperforms all baselines, and notably on HotpotQA dataset, enables gpt-4o-mini to surpass reasoning models: o3-mini by $3.4%$ and DeepSeek- R1 by $10.6%$ .
• 广泛评估。在六个基准上的实验证明了 AOT 作为独立框架和插件增强的有效性。AOT 优于所有基线,尤其是在 HotpotQA 数据集上,使 gpt-4o-mini 超越了推理模型:o3-mini 提高了 $3.4%$,DeepSeek-R1 提高了 $10.6%$。
2 Related Work
2 相关工作
2.1 Reasoning Framework
2.1 推理框架
Chain-of-Thought (Wei et al., 2022) prompting has emerged as a fundamental technique for enhancing LLMs’ reasoning. Decomposition methods like Least-to-Most (Zhou et al., 2023) and Plan-andSolve (Wang et al., 2023a) prompting parse complex problems into sequential subtasks. Iterative optimization approaches like Self-Refine (Madaan et al., 2023), Step-Back (Zheng et al., 2024) prompting and Progressive-Hint Prompting (Zheng et al., 2023) refine solutions through cyclic feedback or abstraction. Multi-path aggregation techniques like Self-Consistency CoT (Wang et al., 2023b) and LLM-Blender (Jiang et al., 2023) further improve reasoning reliability by multitrajectory consensus.
Chain-of-Thought (Wei et al., 2022) 提示已成为增强大语言模型推理能力的基础技术。Least-to-Most (Zhou et al., 2023) 和 Plan-and-Solve (Wang et al., 2023a) 等分解方法将复杂问题解析为顺序子任务。Self-Refine (Madaan et al., 2023)、Step-Back (Zheng et al., 2024) 和 Progressive-Hint Prompting (Zheng et al., 2023) 等迭代优化方法通过循环反馈或抽象来优化解决方案。Self-Consistency CoT (Wang et al., 2023b) 和 LLM-Blender (Jiang et al., 2023) 等多路径聚合技术通过多轨迹共识进一步提高了推理的可靠性。
More sophisticated frameworks structure the represent ation of reasoning space through dedicated formalisms: Tree of Thoughts (Yao et al., 2023) enables systematic exploration of multiple reasoning paths, while Graph of Thoughts (Besta et al., 2024) represents reasoning processes as dynamic graphs with backtracking mechanisms. Addressing fundamental limitations in resampling-based paradigms, Thought Space Explorer (Zhang and Liu, 2024) strategically explores under-sampled regions of the solution space. These frameworks serve as universal augmentation of LLMs reasoning, enhancing their capacity across various domains, with their principles being widely adopted in agentic workflows for code generation, question answering, and data science applications (Hong et al., 2024b; Zhang et al., 2024a; Hong et al., 2024a;
更复杂的框架通过专用的形式化方法来构建推理空间的表示:思维树(Tree of Thoughts)(Yao et al., 2023) 支持对多条推理路径的系统性探索,而思维图(Graph of Thoughts)(Besta et al., 2024) 则将推理过程表示为具有回溯机制的动态图。针对基于重采样范式的基本限制,思维空间探索器(Thought Space Explorer)(Zhang and Liu, 2024) 策略性地探索解决方案空间中未被充分采样的区域。这些框架作为大语言模型推理的通用增强手段,提升了其在各个领域的能力,其原则在代码生成、问答和数据科学应用等智能体工作流程中被广泛采用 (Hong et al., 2024b; Zhang et al., 2024a; Hong et al., 2024a)。
Zhang et al., 2025; Xiang et al., 2025; Zhang et al., 2024b).
Zhang et al., 2025; Xiang et al., 2025; Zhang et al., 2024b).
2.2 Test-time Scaling
2.2 测试时缩放
Test-time scaling approaches have demonstrated the value of extended computation during inference. Supervised fine-tuning on long chain-of-thought traces has proven effective at enhancing models’ capabilities to conduct extended reasoning (Yeo et al., 2025; Yao et al., 2025). Building on this foundation, reinforcement learning methods have enabled models to automatically learn optimal inference expansion strategies, allowing for adaptive scaling of the reasoning process (Kimi et al., 2025; Zeng et al., 2025; DeepSeek-AI, 2025). Framework- based approaches have further expanded these capabilities by extending inference through external systems, incorporating techniques like verification, budget forcing, and ensemble methods (Zhang et al., 2024a; Saad-Falcon et al., 2024; Chen et al., 2024). These complementary approaches demonstrate how strategic use of additional computation during inference through learned behaviors, automated scaling, and system-level interventions can substantially enhance model performance.
测试时扩展方法展示了在推理过程中进行扩展计算的价值。通过对长思维链的监督微调,证明其能有效增强模型进行扩展推理的能力 (Yeo et al., 2025; Yao et al., 2025)。在此基础上,强化学习方法使模型能够自动学习最优推理扩展策略,从而实现推理过程的自适应扩展 (Kimi et al., 2025; Zeng et al., 2025; DeepSeek-AI, 2025)。基于框架的方法通过外部系统扩展推理,结合了验证、预算强制和集成方法等技术,进一步扩展了这些能力 (Zhang et al., 2024a; Saad-Falcon et al., 2024; Chen et al., 2024)。这些互补的方法展示了通过习得行为、自动扩展和系统级干预在推理过程中战略性地使用额外计算如何显著提升模型性能。
However, these approaches universally maintain extensive historical information throughout the reasoning process, leading to computational inefficiency and potential interference with effective reasoning. In contrast, AOT introduces a Markovian perspective that eliminates the need for historical dependency tracking, enabling more efficient resource allocation while maintaining compatibility with existing test-time scaling methods.
然而,这些方法在推理过程中普遍保持了大量的历史信息,导致计算效率低下,并可能干扰有效的推理。相比之下,AOT 引入了马尔可夫视角,消除了对历史依赖跟踪的需求,从而在保持与现有测试时扩展方法兼容的同时,实现更高效的资源分配。
3 An Overview of AOT
3 AOT概述
This section presents an overview of AOT from a probabilistic modeling perspective. We first examine how traditional reasoning chains work and then introduce our dependency-based graph structures and their contraction mechanisms to enhance the modeling capability of reasoning processes.
本节从概率建模的角度概述了AOT。我们首先探讨了传统推理链的工作原理,然后介绍了基于依赖关系的图结构及其收缩机制,以增强推理过程的建模能力。
3.1 Reasoning Chain
3.1 推理链
Chain-of-Thought (CoT) prompting enables LLMs to progressively propose intermediate thoughts $T_{i}$ when solving a problem. As discussed earlier, this approach requires maintaining a complete reasoning history, which can be formalized as a probabilistic sampling procedure:
思维链 (Chain-of-Thought, CoT) 提示使大语言模型在解决问题时能够逐步提出中间思维 $T_{i}$ 。如前所述,这种方法需要维护完整的推理历史,可以形式化为概率采样过程:

Here, $\mathcal{T}={T_{0},T_{1},...,T_{N}}$ represents the sequence of intermediate thoughts generated by the LLM. Each thought $T_{i}$ depends on the previous thoughts $\tau_{<i}$ and the initial question $Q_{0}$ .
这里,$\mathcal{T}={T_{0},T_{1},...,T_{N}}$ 表示大语言模型生成的中间思考序列。每个思考 $T_{i}$ 依赖于之前的思考 $\tau_{<i}$ 和初始问题 $Q_{0}$。
To explore chain-based methods with different node definitions, Least-to-Most (Zhou et al., 2023) replaces the intermediate thoughts $T_{i}$ with subquestions $Q_{i}$ , resulting in a different formulation of the reasoning chain:
为探索基于链的方法的不同节点定义,Least-to-Most (Zhou et al., 2023) 将中间思考 $T_{i}$ 替换为子问题 $Q_{i}$,从而形成了不同的推理链形式:

where $\mathcal{Q}={Q_{0},Q_{1},\dots,Q_{N}}$ is the sequence of sub questions.
其中 $\mathcal{Q}={Q_{0},Q_{1},\dots,Q_{N}}$ 是子问题的序列。
In an ideal scenario where the reasoning chain $\mathcal{Q}$ exhibits the Markov property, each sub question $Q_{i+1}$ would only depend on its immediate predecessor $Q_{i}$ , similar to how humans naturally solve complex problems by resolving independent subquestions and reformulating simplified states. This leads to:
在理想情况下,若推理链 $\mathcal{Q}$ 满足马尔可夫性质,每个子问题 $Q_{i+1}$ 将仅依赖于其直接前驱 $Q_{i}$,这类似于人类通过解决独立子问题并重新表述简化状态来自然解决复杂问题的方式。由此可得:

However, achieving true Markov property in realworld reasoning tasks is challenging. We adopt the sub question-based node structure from reasoning chains as states while exploring a two-phase state transition mechanism consisting of decomposition and contraction to address this challenge.
然而,在现实世界的推理任务中实现真正的马尔可夫属性具有挑战性。我们采用基于子问题的节点结构作为状态,同时探索由分解和收缩组成的两阶段状态转换机制以应对这一挑战。
3.2 Dependency Directed Acyclic Graph
3.2 依赖有向无环图
AOT utilizes temporary DAG structures to decompose the current question, unlike existing methods that maintain complex dependencies throughout the reasoning process. This DAG structure serves as a scaffold during state transitions, providing rich structural information to guide the complete state transition process, specifically functioning as the decomposition phase to facilitate the subsequent contraction phase.
AOT 利用临时 DAG (Directed Acyclic Graph) 结构来分解当前问题,与现有方法不同,后者在整个推理过程中保持复杂的依赖关系。这种 DAG 结构在状态转换过程中充当支架,提供丰富的结构信息来指导完整的状态转换过程,具体作为分解阶段,以促进后续的收缩阶段。
The DAG $\mathcal{G}$ is defined as:
图 $\mathcal{G}$ 定义为:

In our DAG definition, nodes represent subquestions $Q_{i}$ , and edges $(Q_{j},Q_{i})$ indicate that $Q_{j}$ con- tains necessary information for solving $Q_{i}$ . A major challenge in constructing Markov processes stems from the dependencies of various information in complex reasoning scenarios, and this defini- tion provides structural information for identifying dependencies through rule-based determination.
在我们的有向无环图定义中,节点表示子问题 $Q_{i}$,边 $(Q_{j},Q_{i})$ 表示 $Q_{j}$ 包含解决 $Q_{i}$ 所需的信息。构建马尔可夫过程的主要挑战源于复杂推理场景中各种信息的依赖性,而该定义为通过基于规则的确定来识别依赖关系提供了结构信息。
Based on their dependency relationships, all subquestion nodes can be categorized into two types:
基于它们的依赖关系,所有子问题节点可以分为两类:
Independent sub questions $\mathcal{Q}_{\mathrm{ind}}$ (nodes without incoming edges):
独立子问题 $\mathcal{Q}_{\mathrm{ind}}$(没有入边的节点):
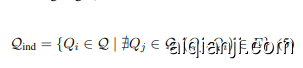
Dependent sub questions $\mathcal{Q}_{\mathrm{dep}}$ (nodes with incoming edges):
依赖子问题 $\mathcal{Q}_{\mathrm{dep}}$(具有入边的节点):

The key assumption of acyclicity in our DAG is guaranteed by this edge definition: since subquestions are generated following natural language order, any sub question $Q_{i}$ can only depend on previously generated sub questions $Q_{<i}$ . Even in the maximally connected case where each subquestion links to all its predecessors, acyclicity is maintained, as any additional edges would create cycles by connecting to future nodes while violating the natural language order.
我们DAG(有向无环图)中无环性的关键假设通过边的定义得到保证:由于子问题是按照自然语言顺序生成的,任何子问题 $Q_{i}$ 只能依赖于之前生成的子问题 $Q_{<i}$。即使在最大连接的情况下,每个子问题都连接到其所有前驱节点,无环性仍然得以保持,因为任何额外的边都会通过连接到未来节点而创建循环,从而违反自然语言顺序。
3.3 Contraction
3.3 收缩
The contraction phase transforms the temporary DAG structure into the next atomic state while preserving the Markov property. To ensure this Markov process is meaningful, we must maintain state atomicity while ensuring progress in the reasoning process. As the reasoning progresses, new conclusions and information are continuously derived, necessitating the selective discarding of information to maintain atomic states. AOT addresses this by treating results from $\mathcal{Q}{\mathrm{ind}}$ as either given conditions or eliminated process information, while contracting $\mathcal{Q}{\mathrm{dep}}$ into an independent question as the next state. This contracted question maintains solution equivalence to $Q_{i}$ , ensuring the reasoning process stays on track.
收缩阶段将临时的 DAG 结构转换为下一个原子状态,同时保留马尔可夫性质。为了确保这一马尔可夫过程有意义,我们必须在保持状态原子性的同时,确保推理过程的进展。随着推理的进展,新的结论和信息不断被推导出来,因此需要选择性地丢弃信息以维持原子状态。AOT 通过将 $\mathcal{Q}{\mathrm{ind}}$ 的结果视为给定条件或消除的过程信息来解决这个问题,同时将 $\mathcal{Q}{\mathrm{dep}}$ 收缩为一个独立问题作为下一个状态。这个收缩后的问题保持与 $Q_{i}$ 的解等价,确保推理过程保持在正确的轨道上。
The reasoning process is formally described in Algorithm 1, which shows how AOT iterates through decomposition and contraction steps. This
推理过程在算法 1 中正式描述,展示了 AOT 如何通过分解和收缩步骤进行迭代。
Algorithm 1 Algorithm of AOT
算法 1 AOT 算法
iterative process continues until it reaches a maximum number $D$ , which is assigned by the depth of the first generated graph $\mathcal{G}_{0}$ to prevent infinite decomposition. The process can be formalized as:
迭代过程持续进行,直到达到最大次数 $D$,这是由首次生成的图 $\mathcal{G}_{0}$ 的深度分配的,以防止无限分解。该过程可以形式化为:

4 The Design Details of AOT
4 AOT 的设计细节
This section details the implementation of AOT’s core components: decomposition and contraction, which together form one iteration of state transition in the Markov reasoning process, as illustrated in Figure 2. Through structured decomposition and principled contraction, our approach establishes a foundation for iterative reasoning that can flexibly integrate with other methods while balancing computational efficiency and reasoning depth.
本节详细介绍了 AOT 核心组件的实现:分解和收缩,这两者共同构成了马尔可夫推理过程中一次状态转移的迭代,如图 2 所示。通过结构化分解和原则性收缩,我们的方法为迭代推理奠定了基础,同时平衡了计算效率和推理深度,并能灵活与其他方法集成。
4.1 Decomposition
4.1 分解
Dependency Directed Acyclic Graph. Addressing the challenge of excessive historical information maintenance, our decomposition phase intro- duces an efficient dependency extraction mechanism that only temporarily captures rich structural information, which provides the foundation for subsequent simplification. This process starts with decomposing the current question into granular subquestions, then leverages LLMs’ zero-shot capabilities to efficiently identify inter-question dependencies. The dependency extraction is achieved through a JSON-formatted LLM invocation that progressively labels each sub question’s dependencies by indexing its upstream questions (see Appendix B.2 for annotation prompt templates).
依赖有向无环图。为了解决历史信息维护过多的问题,我们的分解阶段引入了一种高效的依赖提取机制,该机制仅临时捕获丰富的结构信息,为后续的简化奠定了基础。这一过程从将当前问题分解为细粒度的子问题开始,然后利用大语言模型的零样本能力高效识别问题间的依赖关系。依赖提取通过 JSON 格式的大语言模型调用来实现,逐步标记每个子问题的依赖关系,通过索引其上游问题来完成(参见附录 B.2 中的标注提示模板)。
4.2 Contraction
4.2 收缩
Sub questions Contracting. Based on the dependency relationships identified in DAG structure, AOT performs contraction through a single LLM invocation. This process constructs an independent contracted question by selectively integrating information from independent sub questions as known conditions and incorporating the descriptions of current dependent sub questions into the main body. This process maintains answer equivalence throughout the Markov chain while continuously eliminating the test-time of solved independent sub questions in past iterations when solving the contracted question independently. The elimination of the dependency relationships from independent sub questions and the generated contracted question facilitates the transmission of key information that causes dependency. (see Appendix B.3 for contraction prompt templates).
子问题合同化。基于DAG结构中识别的依赖关系,AOT通过单次大语言模型调用执行合同化过程。该过程通过选择性地将来自独立子问题的信息作为已知条件,并将当前依赖子问题的描述整合到主体中,构建一个独立的合同化问题。该过程在整个马尔可夫链中保持答案的等价性,同时在独立解决合同化问题时逐步消除过去迭代中已解决的独立子问题的测试时间。消除独立子问题与生成的合同化问题之间的依赖关系,有助于传递导致依赖的关键信息。(合同化提示模板参见附录B.3)。
Markov Property Maintenance. Through this contraction process, AOT effectively eliminates redundant information in historical reasoning steps to reduce the test-time required for solving questions in subsequent states. The contraction mechanism ensures that each state generated in the process depends only on its immediate predecessor, preserving the Markov property while progressively simplifying inherent complexity of the question in the current state.
马尔可夫性质保持。通过这种收缩过程,AOT 有效地消除了历史推理步骤中的冗余信息,以减少后续状态中解决问题所需的测试时间。收缩机制确保过程中生成的每个状态仅依赖于其直接前驱,在保持马尔可夫性质的同时,逐步简化当前状态中问题的固有复杂性。
4.3 Integration
4.3 集成
Iterative Process. The pipeline of AOT operates through an iterative process where each state transition step involves question decomposition followed by contraction. The contracted question from each iteration serves as the input for the next decomposition phase. As the number of iterations increases, the test-time scales up in an attempt to achieve more robust and effective reasoning.
迭代过程
Termination Mechanism. To optimize test-time efficiency, AOT incorporates an automated termination mechanism that uses LLM evaluation to assess solution quality through answer comparison. After each contraction step, an LLM examines three key elements: the execution results of the original question $Q_{i}$ , the decomposed DAG structure $\mathcal{G}i$ , and the independent execution results of contracted question $Q_{i+1}$ . The LLM synthesizes these elements to generate a comprehensive answer for $Q_{i}$ . If this synthesized answer demonstrates consistency with the answer produced by $Q_{i+1}$ , the iterative process continues. Upon termination, AOT combines the current contracted question with the union of independent subquestions $\mathcal{Q}{d e p}=\bigcup{j=1}^{i}\mathcal{Q}{d e p{j}}$ accumulated from all previous iterat ions to form a complete solution to the initial question $Q_{0}$ . This structure provides a solution composed entirely of independent questions, maintaining semantic independence of each sub question while ensuring completeness of whole solution.
终止机制。为了优化测试时效率,AOT 引入了一种自动终止机制,该机制通过大语言模型评估来比较答案,从而评估解决方案的质量。在每次收缩步骤之后,大语言模型会检查三个关键要素:原始问题 $Q_{i}$ 的执行结果、分解后的 DAG 结构 $\mathcal{G}i$,以及收缩问题 $Q_{i+1}$ 的独立执行结果。大语言模型综合这些要素,生成 $Q_{i}$ 的全面答案。如果该综合答案与 $Q_{i+1}$ 生成的答案一致,则迭代过程继续。终止时,AOT 将当前收缩问题与之前所有迭代中累积的独立子问题 $\mathcal{Q}{d e p}=\bigcup{j=1}^{i}\mathcal{Q}{d e p{j}}$ 结合,形成初始问题 $Q_{0}$ 的完整解决方案。此结构提供了一个完全由独立问题组成的解决方案,在保证整个解决方案完整性的同时,保持了每个子问题的语义独立性。
Integration Through Configurable Termination.
通过可配置终止实现集成
Building upon this termination mechanism, AOT enables seamless integration with existing test-time scaling methods by allowing any intermediate state to serve as an entry point. This flexibility comes from AOT’s configurable termination strategy - often just a single decomposition-contraction cycle - before passing this simplified question to other methods (refer to the right portion of Figure 2). This approach leverages AOT’s structural optimization capabilities as a preprocessing step while al- lowing other methods to operate on a more manageable question. The contracted question passed to subsequent methods maintains answer equivalence with the original question while AOT’s initial structural simplification helps redirect computational resources towards more direct and effective reasoning. The seamless transition between methods is facilitated by the atomic state representation in our Markov process, ensuring that essential question characteristics are preserved while unnecessary historical information is eliminated.
在此基础上,AOT通过允许任何中间状态作为入口点,实现了与现有测试阶段扩展方法的无缝集成。这种灵活性源自AOT可配置的终止策略——通常只是一个分解-收缩周期——在将简化后的问题传递给其他方法之前(参见图2右侧部分)。该方法利用AOT的结构优化能力作为预处理步骤,同时允许其他方法在更易处理的问题上进行操作。传递给后续方法的收缩问题在保持与原始问题答案等价的同时,AOT的初始结构简化有助于将计算资源重新导向更直接和有效的推理。方法之间的无缝过渡由我们马尔可夫过程中的原子状态表示所促进,确保在消除不必要的历史信息的同时保留问题的关键特征。
mechanism confirm the essential it y of our design choices.
机制确认了我们设计选择的重要性。
5.1 Experimental Setup
5.1 实验设置
Datasets. We evaluate AOT using gpt-4o-mini-0718 as the backbone model, chosen for its strong performance-efficiency trade-off. Our evaluation covers four categories of reasoning tasks: mathematical reasoning (MATH (Hendrycks et al., 2021) with numerical answers and GSM8K (Cobbe et al., 2021)), knowledge-intensive reasoning (MMLU-CF (Zhao et al., 2024)), logical reasoning (multiple-choice subsets of BBH (Suzgun et al., 2023), see Appendix D.1 for details), and multi-hop reasoning (HotpotQA (Yang et al., 2018) and LongBench (Bai et al., 2024) which test models’ ability to connect information across multiple contexts). We use the first 1,000 examples from each dataset’s test set, except for GSM8K where we use its complete test set (1,319 examples) and LongBench where we use the combined MuSiQue (Trivedi et al., 2022) and 2 Wiki Multi Hop QA (Ho et al., 2020) subsets (400 examples).
数据集。我们使用 gpt-4o-mini-0718 作为骨干模型来评估 AOT,选择该模型是因为其在性能与效率之间有良好的平衡。我们的评估涵盖了四类推理任务:数学推理(MATH (Hendrycks et al., 2021) 包含数值答案和 GSM8K (Cobbe et al., 2021))、知识密集型推理(MMLU-CF (Zhao et al., 2024))、逻辑推理(BBH (Suzgun et al., 2023) 的多选子集,详见附录 D.1)以及多跳推理(HotpotQA (Yang et al., 2018) 和 LongBench (Bai et al., 2024),这些任务测试模型在多个上下文中连接信息的能力)。我们使用每个数据集的测试集的前 1,000 个示例,但 GSM8K 除外,我们使用其完整的测试集(1,319 个示例),而 LongBench 我们使用 MuSiQue (Trivedi et al., 2022) 和 2 Wiki Multi Hop QA (Ho et al., 2020) 子集的组合(400 个示例)。
Baselines. Our baselines include classical prompting methods (Chain-of-Thought (CoT), CoT with Self-Consistency (CoT-SC, $n=5$ ), Self-Refine, and Analogical Reasoning (Yasunaga et al., 2024)) and advanced reasoning frameworks (agentic workflow AFlow (Zhang et al., 2024a) and Forest of Thought (FoT)). For FoT, we implement it using Tree of Thoughts with branch number $b$ $=3$ , chosen for its general iz ability across diverse tasks. All experiments are averaged over three runs, with detailed reproduction settings in Appendix D.
基线。我们的基线包括经典的提示方法(思维链 (Chain-of-Thought, CoT)、带自一致性 (Self-Consistency, CoT-SC, $n=5$) 的思维链、自我优化 (Self-Refine) 和类比推理 (Analogical Reasoning, Yasunaga et al., 2024))以及高级推理框架(智能工作流 AFlow (Zhang et al., 2024a) 和思维森林 (Forest of Thought, FoT))。对于 FoT,我们使用分支数 $b$ $=3$ 的思维树 (Tree of Thoughts) 实现,因其在多样化任务中的通用性而选择。所有实验均进行三次运行取平均值,详细复现设置见附录 D。
5 Experiments
5 实验
We conduct comprehensive experiments to examine AOT through extensive benchmark evaluation on six standard datasets, reasoning models comparison, test-time optimization experiments, and ablation studies. Our main results demonstrate consis- tent improvements across different reasoning tasks, with significant gains especially in multi-hop reasoning. Through comparison with state-of-the-art reasoning models, we show AOT’s effectiveness as a general framework. Our test-time optimization experiments further validate AOT’s adaptability and efficiency. Finally, ablation studies on key components like DAG structure and decomposition
我们通过六个标准数据集上的广泛基准评估、推理模型对比、测试时优化实验和消融研究,进行了全面的实验来检验AOT。我们的主要结果表明,在不同的推理任务中,AOT均取得了持续的改进,尤其是在多跳推理方面表现尤为显著。通过与最先进的推理模型进行对比,我们展示了AOT作为一个通用框架的有效性。我们的测试时优化实验进一步验证了AOT的适应性和高效性。最后,对DAG结构和分解等关键组件的消融研究
5.2 Experimental Results and Analysis.
5.2 实验结果与分析
Main Results As shown in Table 1, AOT demonstrates consistent improvements across different reasoning tasks. AOT achieves strong performance on mathematics tasks, with AOT ∗ reaching $84.9%$ on MATH and $95.1%$ on GSM8K $(+1.9%$ over AFlow on MATH, $+1.1%$ over FoT( $\scriptstyle\left(n=8\right)$ on GSM8K). The most notable improvements are in multi-hop QA tasks, where our base version achieves $80.6%$ F1 score on HotpotQA $(+7.1%$ over AFlow). Similar improvements on LongBench ( $68.8%$ , $+7.5%$ over AFlow) further demonstrate the effectiveness of AOT’s atomic state represent ation in long context scenarios.
主要结果如表 1 所示,AOT 在不同推理任务中表现出一致的改进。AOT 在数学任务中表现强劲,AOT ∗ 在 MATH 上达到 $84.9%$,在 GSM8K 上达到 $95.1%$(在 MATH 上比 AFlow 高 $+1.9%$,在 GSM8K 上比 FoT( $\scriptstyle\left(n=8\right)$ 高 $+1.1%$)。最显著的改进是在多跳问答任务中,我们的基础版本在 HotpotQA 上实现了 $80.6%$ 的 F1 分数(比 AFlow 高 $+7.1%$)。在 LongBench 上的类似改进($68.8%$,比 AFlow 高 $+7.5%$)进一步证明了 AOT 的原子状态表示在长上下文场景中的有效性。
Table 1: Performance Comparison Across Tasks $(%)$ . We evaluate three variants: the base version (AOT), a version integrated with FoT (AOT $(d{=}1)+\mathrm{FoT}(n{=}2))$ , and a computationally intensive version (AOT ∗) that uses LLM to select the optimal answer from three runs. Results are reported as exact match accuracy for MATH, GSM8K, BBH, and MMLU-CF, and F1 scores for HotpotQA and LongBench.
表 1: 任务性能对比 $(%)$。我们评估了三个变体:基础版本 (AOT)、与 FoT 集成的版本 (AOT $(d{=}1)+\mathrm{FoT}(n{=}2))$,以及计算密集型版本 (AOT ∗),该版本使用大语言模型从三次运行中选择最优答案。结果以 MATH、GSM8K、BBH 和 MMLU-CF 的精确匹配准确率,以及 HotpotQA 和 LongBench 的 F1 分数报告。
| 方法 | MATH GSM8K | BBH | MMLU-CF | HotpotQA | LongBench | 平均 |
|---|---|---|---|---|---|---|
| CoT | 78.3 | 90.9 | 78.3 | 69.6 | 57.6 | 73.7 |
| CoT-SC (n=5) | 81.8 | 92.0 | 83.4 | 71.1 | 58.6 | 75.5 |
| Self-Refine | 78.7 | 91.7 | 80.0 | 69.7 | 58.2 | 74.4 |
| Analogical Prompting | 65.4 | 87.2 | 72.5 | 65.8 | 52.9 | 68.1 |
| AFlow | 83.0 | 93.5 | 76.0 | 69.5 | 61.0 | 76.1 |
| FoT (n=8) | 82.5 | 94.0 | 82.4 | 70.6 | 59.1 | 75.9 |
| AoT (d=1) + FoT (n=2) | 82.6 | 94.2 | 82.2 | 69.7 | 58.4 | 75.8 |
| AoT (Ours) | 83.6 | 95.0 | 86.0 | 70.9 | 68.5 | 80.8 |
| AoT (Ours) | 84.9 | 95.1 | 87.4 | 71.2 | 68.8 | 81.4 |
Table 2: Comparison of Reasoning Model Performance on Multi-hop QA Tasks. Results show F1 scores and Hit rates $(\mathrm{F}1>0)$ for HotpotQA and LongBench across different models.
表 2: 多跳问答任务中推理模型性能对比。结果显示不同模型在 HotpotQA 和 LongBench 上的 F1 分数和命中率 $(\mathrm{F}1>0)$。
| 方法 | HotpotQA | LongBench |
|---|---|---|
| QwQ | F1 68.1 | Hit 82.4 |
| CoT | DeepSeek-R1 03-mini | F1 70.0 |
| gpt-4o-mini | F1 77.2 80.6 | |
| AoT | 03-mini | F1 81.4 |
| Hit 91.4 |
Reasoning Models Comparison Results. We compare AOT with several reasoning models, including $\mathsf{Q}\mathsf{w}\mathsf{Q}{\mathrm{-}32\mathsf{B}\mathrm{-}\mathsf{P}\mathsf{r e v i e w}}$ (Qwen-Team, 2024), DeepSeek-R1 (DeepSeek-AI, 2025), and o3-mini-2025-01-31(OpenAI, 2025). Notably, o3-mini demonstrates remarkable raw performance with a $77.2%$ F1 score on HotpotQA, surpassing our previous best baseline AFlow $73.5%$ F1) in the main experiments, highlighting its strength as a foundation model. When integrated into our framework, even a relatively modest model like gpt-4omini achieves an impressive $80.6%$ F1 score. Fur- thermore, employing o3-mini as the backbone of AOT leads to exceptional results: the F1 score increases to $81.4%$ and the Hit rate reaches $91.4%$ on HotpotQA. On the LongBench subset, our framework with o3-mini achieves a $63.3%$ F1 score and $72.1%$ Hit rate, establishing new state-of-the-art performance across all metrics. Due to the computational constraints and stability considerations, we evaluated on the first 100 examples from the Musique subset of LongBench, which may result in slightly higher scores compared to our main experiments in Table 1.
推理模型对比结果。我们将 AOT 与多种推理模型进行了比较,包括 $\mathsf{Q}\mathsf{w}\mathsf{Q}{\mathrm{-}32\mathsf{B}\mathrm{-}\mathsf{P}\mathsf{r e v i e w}}$ (Qwen-Team, 2024)、DeepSeek-R1 (DeepSeek-AI, 2025) 和 o3-mini-2025-01-31 (OpenAI, 2025)。值得注意的是,o3-mini 在 HotpotQA 上展现了卓越的原始性能,F1 得分为 $77.2%$,超过了我们在主实验中的最佳基线 AFlow ($73.5%$ F1),凸显了其作为基础模型的优势。当将其集成到我们的框架中时,即使是像 gpt-4omini 这样相对较小的模型,也能达到令人印象深刻的 $80.6%$ F1 得分。此外,将 o3-mini 作为 AOT 的骨干模型,带来了卓越的结果:在 HotpotQA 上,F1 得分提高至 $81.4%$,命中率达到 $91.4%$。在 LongBench 子集上,我们的框架与 o3-mini 结合,实现了 $63.3%$ 的 F1 得分和 $72.1%$ 的命中率,在所有指标上均达到了新的最先进水平。由于计算限制和稳定性考虑,我们评估了 LongBench 的 Musique 子集的前 100 个示例,这可能导致得分略高于表 1 中的主实验结果。
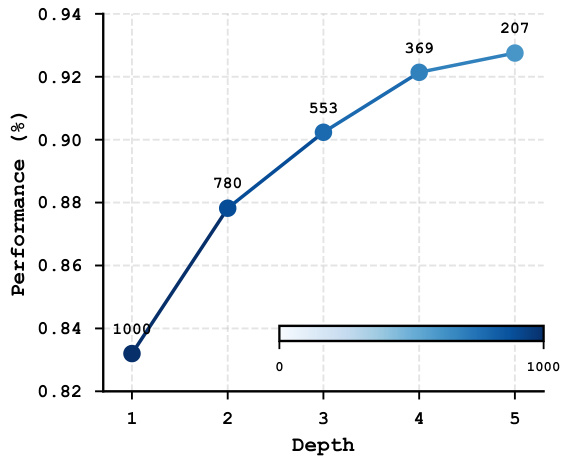
Performance vs Iteration Depth on MATH Figure 3: Performance scaling with transition times on MATH dataset. Darker blue indicates larger sample sizes at shallower depths, as most problems are solved with fewer decomposition steps.
图 3: 在 MATH 数据集上性能随迭代深度的变化。深蓝色表示在较浅深度下样本量较大,因为大多数问题在较少的分解步骤中就能解决。
Test-Time Optimization Results. We investigate the test-time scaling behavior of AOT through two sets of experiments. First, as shown in Figure 3, we analyze the performance scaling of AOT on MATH dataset. Unlike the dynamic iteration limit determined by problem-specific graph structures described in Section 3, here we set a uniform maximum of 5 iterations to explicitly examine the depth-wise scaling behavior. Since each iteration produces an evaluable solution, we can track performance across different iteration depths. All 1000 test samples naturally generate solutions at depth 1, while fewer samples proceed to deeper iterations (dropping to 207 at depth 5), as many problems achieve satisfactory solutions at earlier depths. The results demonstrate that AOT exhibits consistent accuracy improvements from $83.2%$ to $92.7%$ as the iteration depth increases, with the performance gains gradually tapering. This pattern suggests that while deeper iterations continue to benefit overall performance, many problems can be effectively solved with fewer iterations, providing a natural trade-off between computational cost and solution quality.
测试时优化结果
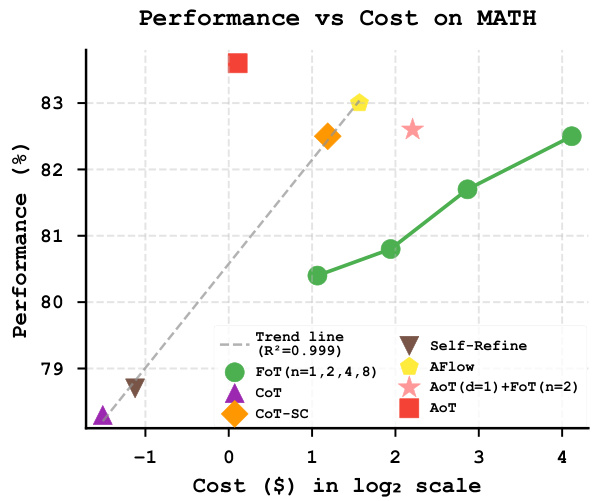
Figure 4: Performance comparison on MATH dataset showing computational efficiency. The green line shows FoT scaling with varying tree numbers $(2^{k},k=$ $0,1,2,\ldots)$ , while the gray trend line (representing other baseline methods) together demonstrate the trade-off between performance gains and computational costs. AOT $(d{=}1)$ combined with $\mathrm{FoT}(n{=}2)$ achieves slightly better performance to standalone FoT $\scriptstyle\left(n=8\right)$ while requiring substantially less computation.
图 4: MATH 数据集上的性能比较,展示了计算效率。绿线展示了 FoT 在不同树数量 $(2^{k},k=$ $0,1,2,\ldots)$ 下的扩展情况,而灰色趋势线(代表其他基线方法)共同展示了性能提升与计算成本之间的权衡。AOT $(d{=}1)$ 结合 $\mathrm{FoT}(n{=}2)$ 在需要更少计算的情况下,实现了比独立 FoT $\scriptstyle\left(n=8\right)$ 稍好的性能。
In our second experiment (Figure 4), we examine the effectiveness of AOT as a plug-in for existing test-time scaling methods. When integrated with FoT, AOT demonstrates promising efficiency. This efficiency gain stems from how AOT restructures the reasoning process: by iterative ly solving sub-problems and using them as known conditions for subsequent steps, it eliminates redundant derivations. This leads to substantially reduced test-time demands in the FoT phase while achieving slightly better performance, demonstrating how our approach can systematically optimize existing test-time scaling methods.
在我们的第二个实验(图 4)中,我们研究了 AOT 作为现有测试时缩放方法的插件的有效性。当与 FoT 集成时,AOT 展示了显著的效率提升。这种效率提升源于 AOT 如何重构推理过程:通过迭代地解决子问题并将它们作为后续步骤的已知条件,它消除了冗余的推导。这导致在 FoT 阶段的测试时需求大幅减少,同时实现了略微更好的性能,展示了我们的方法如何系统地优化现有的测试时缩放方法。
Cost Analysis. Through analyzing computational efficiency as shown in Figure 4, our AOT achieves superior efficiency by reaching competitive performance at significantly lower computational costs compared to existing methods. This enhanced efficiency can be attributed to our atomic state representation that preserves only necessary information while eliminating redundant computations. Notably, AOT demonstrates the steepest performance-to-cost ratio among all compared methods, indicating it achieves the highest marginal improvement in accuracy per unit of computational investment.
成本分析。通过分析图 4 中展示的计算效率,我们的 AOT 在显著降低计算成本的同时达到了具有竞争力的性能,从而实现了卓越的效率。这种效率的提升归功于我们的原子状态表示,它仅保留了必要的信息,同时消除了冗余计算。值得注意的是,AOT 在所有对比方法中展示了最陡峭的性能成本比,表明它在单位计算投资中实现了最高的边际精度提升。
Table 3: Ablation Study on AOT Components $(%)$ . Removing the decomposition phase causes notable performance drops, while removing the DAG structure but keeping decomposition leads to even larger degradation.
表 3: AOT 组件消融研究 $(%)$ 。移除分解阶段会导致显著的性能下降,而移除 DAG 结构但保留分解则会导致更大的性能下降。
| 方法 | MATH | GSM8K |
|---|---|---|
| AoT (Full) | 83.6 | 95.0 |
| AoT w/o Decomposition | 82.9 | 94.8 |
| AoT w/o DAG Structure | 82.7 | 94.3 |
Ablation Study. We conduct ablation studies to analyze the contribution of key components in AOT. As shown in Table 3, removing the decomposition phase (i.e., no extracted independent or dependent sub-problems as guidance) causes notable performance drops, while removing the DAG structure but keeping the decomposition phase (i.e., only extracting the first semantically independent subproblem as guidance) leads to even larger degradation. Without decomposition structure, the LLM struggles to capture crucial dependencies between sub questions in the contraction phase, resulting in contracted questions that often contain redundant information. Moreover, providing single subproblem guidance without proper structural information disrupts the parallel relationships between sub-problems. This reveals a critical insight: imperfect structural guidance can be more detrimental than no guidance at all (see Appendix C.1 for examples).
消融研究。我们进行消融研究以分析 AOT 中关键组件的贡献。如表 3 所示,移除分解阶段(即没有提取独立或依赖的子问题作为指导)会导致显著的性能下降,而移除 DAG 结构但保留分解阶段(即仅提取第一个语义独立的子问题作为指导)会导致更大的性能下降。没有分解结构时,大语言模型难以在收缩阶段捕捉子问题之间的关键依赖关系,导致生成的收缩问题通常包含冗余信息。此外,在没有适当结构信息的情况下提供单一子问题指导会破坏子问题之间的并行关系。这揭示了一个关键见解:不完善的结构指导可能比没有指导更有害(示例见附录 C.1)。
6 Conclusion
6 结论
In this paper, we introduced Atom of Thoughts (AOT), a novel framework that transforms complex reasoning processes into a Markov process of atomic questions. By implementing a two-phase transition mechanism of decomposition and contraction, AOT eliminates the need to maintain historical dependencies during reasoning, allowing models to focus computational resources on the current question state. Our extensive evaluation across diverse benchmarks demonstrates that AOT serves effectively both as a standalone framework and as a plug-in enhancement for existing test-time scaling methods. These results validate AOT’s ability to enhance LLMs’ reasoning capabilities while optimizing computational efficiency through its Markov-style approach to question decomposition and atomic state transitions.
本文介绍了原子思维(Atom of Thoughts,AOT)这一新颖框架,它将复杂的推理过程转化为原子问题的马尔可夫过程。通过实现分解和收缩的两阶段转换机制,AOT消除了在推理过程中维护历史依赖的需求,使模型能够将计算资源集中在当前问题状态上。我们在多样化的基准测试中进行了广泛评估,结果表明AOT既可以作为独立框架,也可以作为现有测试时扩展方法的插件增强。这些结果验证了AOT通过其马尔可夫式的问题分解和原子状态转换,能够在优化计算效率的同时增强大语言模型的推理能力。
7 Limitations
7 局限性
A key limitation of AOT lies in its Markov state transition process without a well-designed reflection mechanism. When the initial DAG decompo- sition fails to properly model parallel relationships between sub questions or captures unnecessary dependencies, it can negatively impact subsequent contraction and reasoning process, a scenario that occurs frequently in practice. The framework currently lacks the ability to detect and rectify such poor decomposition s, potentially leading to compounded errors in the atomic state transitions. This limitation suggests the need for future research into incorporating effective reflection and adjustment mechanisms to improve the robustness of DAGbased decomposition.
AOT 的一个关键局限在于其缺乏精心设计的反思机制的马尔可夫状态转移过程。当初始的有向无环图 (DAG) 分解未能正确建模子问题之间的平行关系或捕获了不必要的依赖关系时,它可能会对后续的收缩和推理过程产生负面影响,这种情况在实践中经常发生。该框架目前缺乏检测和纠正此类不良分解的能力,可能导致原子状态转移中的错误累积。这一局限表明,未来的研究需要探索如何引入有效的反思和调整机制,以提高基于 DAG 分解的鲁棒性。
8 Ethics Statement
8 伦理声明
While this work advances the computational efficiency and test-time scaling capabilities of language models through the AOT framework, we acknowledge that these models process information and conduct reasoning in ways fundamentally different from human cognition. Making direct comparisons between our Markov reasoning process and human thought patterns could be misleading and potentially harmful. The atomic state represent ation and dependency-based decomposition proposed in this research are computational constructs designed to optimize machine reasoning, rather than models of human cognitive processes. Our work merely aims to explore more efficient ways of structuring machine reasoning through reduced computational resources and simplified state transitions, while recognizing the distinct nature of artificial and human intelligence. We encourage users of this technology to be mindful of these limitations and to implement appropriate safeguards when deploying systems based on our framework.
尽管这项工作通过 AOT 框架提升了语言模型的计算效率和测试时扩展能力,但我们承认这些模型处理信息和进行推理的方式与人类认知有本质上的不同。将我们的马尔可夫推理过程与人类思维模式直接比较可能会产生误导,甚至可能是有害的。本研究中提出的原子状态表示和基于依赖的分解是为了优化机器推理而设计的计算结构,而不是人类认知过程的模型。我们的工作仅仅旨在通过减少计算资源和简化状态转换来探索更高效的机器推理结构,同时认识到人工智能与人类智能的本质差异。我们鼓励该技术的用户在使用基于我们框架的系统时,注意这些限制并采取适当的保障措施。
References
参考文献
Yushi Bai, Xin Lv, Jiajie Zhang, Hongchang Lyu, Jiankai Tang, Zhidian Huang, Zhengxiao Du, Xiao Liu, Aohan Zeng, Lei Hou, Yuxiao Dong, Jie Tang, and Juanzi Li. 2024. Longbench: A bilingual, multitask benchmark for long context understanding. In ACL (1), pages 3119–3137. Association for Computational Linguistics.
Yushi Bai, Xin Lv, Jiajie Zhang, Hongchang Lyu, Jiankai Tang, Zhidian Huang, Zhengxiao Du, Xiao Liu, Aohan Zeng, Lei Hou, Yuxiao Dong, Jie Tang, and Juanzi Li. 2024. Longbench: 一个用于长上下文理解的双语多任务基准。在 ACL (1) 中,第 3119–3137 页。计算语言学协会。
Maciej Besta, Nils Blach, Ales Kubicek, Robert Gersten- berger, Michal Podstawski, Lukas Gianinazzi, Joanna
Maciej Besta, Nils Blach, Ales Kubicek, Robert Gerstenberger, Michal Podstawski, Lukas Gianinazzi, Joanna
Dongfu Jiang, Xiang Ren, and Bill Yuchen Lin. 2023. Llm-blender: Ensembling large language models with pairwise ranking and generative fusion. In ACL (1), pages 14165–14178. Association for Computational Linguistics.
Dongfu Jiang, Xiang Ren 和 Bill Yuchen Lin. 2023. LLM-Blender: 通过成对排序和生成融合集成大语言模型. 在 ACL (1) 中, 页码 14165–14178. 计算语言学协会.
Jared Kaplan, Sam McCandlish, Tom Henighan, Tom B. Brown, Benjamin Chess, Rewon Child, Scott Gray, Alec Radford, Jeffrey Wu, and Dario Amodei. 2020. Scaling laws for neural language models. CoRR, abs/2001.08361.
Jared Kaplan、Sam McCandlish、Tom Henighan、Tom B. Brown、Benjamin Chess、Rewon Child、Scott Gray、Alec Radford、Jeffrey Wu 和 Dario Amodei。2020。神经语言模型的缩放定律。CoRR, abs/2001.08361。
Kimi, Angang Du, Bofei Gao, Bowei Xing, Changjiu Jiang, Cheng Chen, Cheng Li, Chenjun Xiao, Chenzhuang Du, Chonghua Liao, et al. 2025. Kimi k1. 5: Scaling reinforcement learning with llms. arXiv preprint arXiv:2501.12599.
Kimi, Angang Du, Bofei Gao, Bowei Xing, Changjiu Jiang, Cheng Chen, Cheng Li, Chenjun Xiao, Chenzhuang Du, Chonghua Liao, 等. 2025. Kimi k1. 5: 使用大语言模型扩展强化学习. arXiv 预印本 arXiv:2501.12599.
Aman Madaan, Niket Tandon, Prakhar Gupta, Skyler Hallinan, Luyu Gao, Sarah Wiegreffe, Uri Alon, Nouha Dziri, Shrimai Prabhumoye, Yiming Yang, Shashank Gupta, Bodhi s at twa Prasad Majumder, Katherine Hermann, Sean Welleck, Amir Yazdanbakhsh, and Peter Clark. 2023. Self-refine: Iterative refinement with self-feedback. In NeurIPS.
Aman Madaan, Niket Tandon, Prakhar Gupta, Skyler Hallinan, Luyu Gao, Sarah Wiegreffe, Uri Alon, Nouha Dziri, Shrimai Prabhumoye, Yiming Yang, Shashank Gupta, Bodhi s at twa Prasad Majumder, Katherine Hermann, Sean Welleck, Amir Yazdanbakhsh, 和 Peter Clark. 2023. Self-refine: 自我反馈的迭代优化. 在 NeurIPS.
Andrey Andre yevich Markov. 1906. Extension of the law of large numbers to dependent quantities. Izv. Fiz.-Matem. Obsch. Kazan Univ.(2nd Ser), 15(1):135– 156.
Andrey Andreyevich Markov. 1906. 大数定律在依赖量上的扩展. Izv. Fiz.-Matem. Obsch. Kazan Univ.(2nd Ser), 15(1):135–156.
Niklas Mu en nigh off, Zitong Yang, Weijia Shi, Xiang Lisa Li, Li Fei-Fei, Hannaneh Hajishirzi, Luke Z ett le moyer, Percy Liang, Emmanuel Candès, and Tatsunori Hashimoto. 2025. s1: Simple test-time scaling. Preprint, arXiv:2501.19393.
Niklas Muennighoff, Zitong Yang, Weijia Shi, Xiang Lisa Li, Li Fei-Fei, Hannaneh Hajishirzi, Luke Zettlemoyer, Percy Liang, Emmanuel Candès, and Tatsunori Hashimoto. 2025. s1: 简单的测试时扩展。预印本, arXiv:2501.19393.
OpenAI. 2025. OpenAI o3-mini: Pushing the frontier of cost-effective reasoning.
OpenAI. 2025. OpenAI o3-mini:推动高效推理的前沿
G Polya. 1945. How to solve it: A new aspect of mathematical method.
G Polya. 1945. 如何解决:数学方法的新视角。
Qwen-Team. 2024. QwQ: Reflect deeply on the boundaries of the unknown.
Qwen-Team. 2024. QwQ: 深度反思未知的边界
Jon Saad-Falcon, Adrian Gamarra Lafuente, Shlok Natarajan, Nahum Maru, Hristo Todorov, Etash Guha, Estefany Kelly Buchanan, Mayee F. Chen, Neel Guha, Christopher Ré, and Azalia Mirhoseini. 2024. Archon: An architecture search framework for inference-time techniques. CoRR, abs/2409.15254.
Jon Saad-Falcon、Adrian Gamarra Lafuente、Shlok Natarajan、Nahum Maru、Hristo Todorov、Etash Guha、Estefany Kelly Buchanan、Mayee F. Chen、Neel Guha、Christopher Ré 和 Azalia Mirhoseini。2024。Archon:一种用于推理时技术的架构搜索框架。CoRR,abs/2409.15254。
Herbert A Simon. 1962. The architecture of complexity. Proceedings of the American Philosophical Society, 106(6):467–482.
Herbert A Simon. 1962. 复杂性的结构。美国哲学学会会刊,106(6):467–482。
Charlie Snell, Jaehoon Lee, Kelvin Xu, and Aviral Kumar.
