FingerFlex: Inferring Finger Trajectories from ECoG signals

FingerFlex: 从ECoG信号推断手指轨迹

Abstract

摘要

Motor brain-computer interface (BCI) development relies critically on neural time series decoding algorithms. Recent advances in deep learning architectures allow for automatic feature selection to approximate higher-order dependencies in data. This article presents the FingerFlex model - a convolutional encoder-decoder architecture adapted for finger movement regression on electro cor tico graphic (ECoG) brain data. State-of-the-art performance was achieved on a publicly available BCI competition IV dataset 4 with a correlation coefficient between true and predicted trajectories up to 0.74. The presented method provides the opportunity for developing fully-functional high-precision cortical motor braincomputer interfaces.

运动脑机接口(BCI)的开发高度依赖于神经时间序列解码算法。深度学习架构的最新进展使得自动特征选择能够近似数据中的高阶依赖关系。本文提出FingerFlex模型——一种适用于皮层脑电(ECoG)数据手指运动回归的卷积编码器-解码器架构。在公开可用的BCI竞赛IV数据集4上实现了最先进的性能，真实轨迹与预测轨迹之间的相关系数高达0.74。该方法为开发功能齐全的高精度皮层运动脑机接口提供了可能。

Introduction

引言

Brain-computer interface

脑机接口

One of the promising rehabilitation tools for people with disabilities is the brain-computer interface (BCI) (Lebedev and Nicolelis 2006; Bamdad, Zarshenas, and Auais 2015; Yuan and He 2014). In general, developing a functioning BCI involves interpreting neural signals to extract relevant information from the brain. The extracted features, i.e. control parameters can be used in the restoration of the lost functions and ability augmentation via controlling external devices. Specifically, motor BCIs aim to decode movementrelated information in the sensory-motor cortex into meaningful behavioral patterns, such as joint movement or finger flexion (Tam et al. 2019; Volkova et al. 2019).

脑机接口 (BCI) (Lebedev and Nicolelis 2006; Bamdad, Zarshenas, and Auais 2015; Yuan and He 2014) 是残障人士极具前景的康复工具之一。通常，开发功能性BCI需要解析神经信号以提取大脑中的相关信息。这些提取的特征（即控制参数）可通过控制外部设备，用于恢复丧失的功能或增强能力。具体而言，运动型BCI旨在将感觉运动皮层中与运动相关的信息解码为有意义的动作模式，例如关节运动或手指屈伸 (Tam et al. 2019; Volkova et al. 2019)。

Recording of the neural activity

神经活动记录

Brain activity is analyzed using electro physiological methods measuring single neuron or population level electric potentials. Most methods allowing to capture spiking activity, such as op to genetics, single-unit and multi-unit recordings are highly-invasive. At the same time, population level recording tools, such as electroencephalogram (EEG) and magneto e ncep halo gram (MEG) require no surgical intervention, albeit lack spacial resolution due to a voltage leakage in the human scalp and movement-related artifacts (Neil Cuffin and Cohen 1979; Hamalainen et al. 1993; Jackson and Bolger 2014). The electro cor tico gram (ECoG) used in this study lies in between these methods, estimated to register localized activity of $10^{5}$ neurons on the cortical surface (Engel et al. 2005). ECoG electrodes are placed over the surface of the cortex with approximately $1~\mathrm{cm}$ inter-electrode distance. Electro cor tico gram provides higher spatial resolution and superior signal quality compared to EEG and MEG with a tradeoff of portability and invasive ness.

脑活动通过测量单个神经元或群体水平电位的电生理方法进行分析。大多数能捕捉尖峰活动的方法（如光遗传学、单单元和多单元记录）都具有高度侵入性。而群体水平记录工具（如脑电图(EEG)和脑磁图(MEG)）虽无需手术干预，但由于头皮电压泄漏和运动伪影导致空间分辨率不足 (Neil Cuffin和Cohen 1979; Hamalainen等 1993; Jackson和Bolger 2014)。本研究使用的皮层脑电图(ECoG)介于这些方法之间，估计能记录皮层表面约$10^{5}$个神经元的局部活动 (Engel等 2005)。ECoG电极以约$1~\mathrm{cm}$的间距放置在皮层表面，与EEG和MEG相比具有更高的空间分辨率和更优的信号质量，但牺牲了便携性和侵入性。

Movement correlates in the human brain

人类大脑中的运动相关性

The primary brain area involved in the movement processing is primary motor cortex (PMC) (Kakei, Hoffman, and Strick 1999). The adjacent brain areas - supplementary motor area (SMA) and somatosensory cortex take part into motor planning and receive peripheral inputs on the body position and environment (Tam et al. 2019). Planning and exe- cuting motor programs change the activity of single neurons in the cortical sheet of the motor areas (Kakei, Hoffman, and Strick 1999). Spiking activity in a synchronized neuronal population, in turn, contributes to the change in local field potentials registered via surface electrodes (Buzsaki, Anastassiou, and Koch 2012). Despite the lack of an exact areato-muscle correspondence in the motor cortex, overlapping regions associated with different muscle groups and even fingers can be distinguished (Schieber 2001; Mar janine j ad, Taherian, and Valero-Cuevas 2017; Georg o poul os and Carpenter 2015).

参与运动处理的主要脑区是初级运动皮层 (PMC) (Kakei, Hoffman, and Strick 1999)。相邻脑区——辅助运动区 (SMA) 和体感皮层参与运动规划，并接收关于身体位置和环境的周围输入 (Tam et al. 2019)。规划和执行运动程序会改变运动区皮层单神经元的活动 (Kakei, Hoffman, and Strick 1999)。同步神经元群中的尖峰活动反过来又会导致通过表面电极记录的局部场电位变化 (Buzsaki, Anastassiou, and Koch 2012)。尽管运动皮层中没有精确的脑区与肌肉对应关系，但可以区分与不同肌肉群甚至手指相关的重叠区域 (Schieber 2001; Marjaninejad, Taherian, and Valero-Cuevas 2017; Georgopoulos and Carpenter 2015)。

Another feature of population activity in the cortex is that its local field potential comprises a set of independent oscillatory processes (Buzsaki and Draguhn 2004). It was shown that changes in alpha band $(8-13{\mathrm{ Hz}})$ ) power, also known as mu-rhythm, beta $(13{-}35~\mathrm{Hz})$ ), gamma $(35–100~\mathrm{Hz})$ and high-gamma $\mathrm{(100-250~Hz)}$ correlate significantly with ongoing movement patterns (Tam et al. 2019; Mar janine j ad, Taherian, and Valero-Cuevas 2017). It is thus possible to use frequency-decomposed or time-frequency represented signal instead of raw time series data.

大脑皮层群体活动的另一个特征是，其局部场电位由一组独立的振荡过程组成 (Buzsaki and Draguhn 2004)。研究表明，阿尔法频段 $(8-13{\mathrm{ Hz}})$ 功率（也称为μ节律）、贝塔频段 $(13{-}35~\mathrm{Hz})$ 、伽马频段 $(35–100~\mathrm{Hz})$ 以及高伽马频段 $\mathrm{(100-250~Hz)}$ 的变化与当前运动模式显著相关 (Tam et al. 2019; Marjanine Jad, Taherian, and Valero-Cuevas 2017)。因此，可以使用频率分解或时频表示的信号代替原始时间序列数据。

The primary purpose of this study is to improve existing solutions for decoding a continuous finger trajectory based solely on ECoG-registered brain oscillator y patterns in the

本研究的主要目的是改进现有解决方案，仅基于ECoG记录的大脑振荡模式来解码连续手指轨迹。

sensor i motor cortex.

传感器 i 运动皮层。

Related work

相关工作

While some studies concentrated on classifying finger activations (Hotson et al. 2016; Onaran, Ince, and Cetin 2011; Yao and Shoaran 2019), the others predicted hand translations (Pistohl et al. 2008; Nakanishi et al. 2013; Bundy et al. 2016; Sliwowski et al. 2022) and gestures (Pan et al. 2018; Branco et al. 2017), numerous approaches were presented for solving finger trajectory prediction task.

一些研究专注于手指动作分类 (Hotson et al. 2016; Onaran, Ince, and Cetin 2011; Yao and Shoaran 2019)，另一些则预测手部平移 (Pistohl et al. 2008; Nakanishi et al. 2013; Bundy et al. 2016; Sliwowski et al. 2022) 和手势 (Pan et al. 2018; Branco et al. 2017)。针对手指轨迹预测任务，目前已提出多种解决方案。

Liang and Bougrain (2012) and Flamary (2012) presented the first attempts to decode one-dimensional finger flexions on the publicly available BCI Competition dataset IV (Schalk et al. 2007). The former study employed switching linear models, while the latter - linear regression with rigorous feature selection, which allowed to win the competition. Nakanishi et al. (2014) used sparsed linear regression on frequency band decomposed signal achieving comparable results both on the BCI competition dataset and data gathered by their team. With the advancement of deep learning (LeCun, Bengio, and Hinton 2015) techniques over the following years, neural network approaches were more frequently used in consequent studies. For example, Xie, Schwartz, and Prasad (2018) used long short-term memory based (Hochreiter and Schmid huber 1997) architecture to decode finger trajectory. Jubien et al. (2019) compared different conventional machine learning methods with artificial neural network approaches on the same task to conclude that deep learning solves the task with higher accuracy. The method developed by Frey et al. (2021) presented the opportunity for developing a generalized decoder for neural data yielding high performance over a variety of tasks including finger trajectory regression over the ECoG data. The attempt to build an interpret able convolutional neural network was made by Petrosyan et al. (2021), which is highly relevant for neuroscience research on details of motor encoding in the human brain. Lastly, a new type of features based on Riemann geometry (Congedo, Barachant, and Bhatia 2017) was introduced in the finger movement decoding task by Yao, Zhu, and Shoaran (2022) used consequently with linear discriminators and support vector machine (SVM) regressors.

Liang和Bougrain (2012) 以及Flamary (2012) 首次尝试在公开的BCI Competition数据集IV (Schalk等, 2007) 上解码一维手指弯曲信号。前者采用切换线性模型，后者通过严格特征选择的线性回归方法赢得了比赛。Nakanishi等 (2014) 对频带分解信号使用稀疏线性回归，在BCI竞赛数据集和团队自采数据上都取得了可比结果。

随着深度学习 (LeCun, Bengio和Hinton 2015) 技术的发展，神经网络方法在后续研究中得到更广泛应用。例如Xie, Schwartz和Prasad (2018) 采用基于长短期记忆网络 (Hochreiter和Schmidhuber 1997) 的架构解码手指轨迹。Jubien等 (2019) 对比了传统机器学习方法与人工神经网络在该任务上的表现，证实深度学习能获得更高精度。

Frey等 (2021) 开发的神经数据通用解码器在包括ECoG数据手指轨迹回归在内的多任务中表现优异。Petrosyan等 (2021) 尝试构建可解释卷积神经网络，这对研究人脑运动编码的神经机制具有重要意义。Yao, Zhu和Shoaran (2022) 最新引入基于黎曼几何 (Congedo, Barachant和Bhatia 2017) 的特征表示方法，配合线性判别器和支持向量机 (SVM) 回归器进行手指运动解码。

The novelty of this work is primarily addressed by the use of different decoding paradigm based on the encoderdecoder architecture, which transforms feature time series into a target time series through a set of convolutions, deconvolutions, and skip-connections. Our research aims to prove this approach can outperform existing conventional machine learning solutions based on thorough feature extraction, as well as deep learning models implemented by the other research teams in a finger flexion decoding task.

这项工作的创新性主要体现在采用了基于编码器-解码器架构的全新解码范式，通过一系列卷积、反卷积和跳跃连接将特征时间序列转换为目标时间序列。我们的研究旨在证明，在手指弯曲解码任务中，该方法能够超越基于精细特征提取的传统机器学习方案，以及其它研究团队实现的深度学习模型。

Methods

方法

Dataset

数据集

The primary dataset for training the model was the BCI competition IV dataset 4 (Schalk et al. 2007). The dataset contains electro cor tico graphic recordings of three anonymous patients with corresponding finger movement information, represented as a one-dimensional coordinate denoting the finger fold. The recording grids consist of 48-64 electrodes evenly distributed in grids of 6x8, 8x8, and other shapes. The authors of a dataset imposed a limitation on ECoG electrode distribution information. The channels were shuffled beforehand and the electrode positions relative to the brain were not provided either. ECoG was recorded at a sampling frequency of 1000 Hertz, while finger movements were sampled at $25\mathrm{Hz}$ with a data glove.

训练模型的主要数据集是BCI竞赛IV数据集4 (Schalk et al. 2007)。该数据集包含三名匿名患者的皮层脑电图记录及对应的手指运动信息，后者以一维坐标表示手指弯曲程度。记录网格由48-64个电极组成，均匀分布在6x8、8x8等不同形状的网格中。数据集作者对ECoG电极分布信息进行了限制：通道数据已预先打乱，且未提供电极在大脑中的相对位置。皮层脑电图采样频率为1000赫兹，而手指运动数据通过数据手套以$25\mathrm{Hz}$采样。

The subjects were instructed to move a particular finger after a cue, which was presented as a corresponding word (e.g., ”thumb”) on a computer monitor. Each cue lasted for two seconds and was followed by a two-second resting period during which the screen was blank. More details on the experimental procedure and recording setup can be found in the dataset description (Miller and Schalk 2008).

受试者被要求在提示后移动特定手指，提示以相应单词（如"拇指"）形式呈现在电脑显示器上。每个提示持续两秒，随后是两秒的空白屏幕休息期。有关实验程序和记录设置的更多细节可在数据集描述中查阅 (Miller and Schalk 2008)。

Data preprocessing and feature extraction

数据预处理与特征提取

Data preprocessing can be divided into two parts: preprocessing of ECoG signals and preprocessing of the finger movement data (Figure 1). The ECoG preprocessing pipeline consisted of the following steps. Firstly, data standar diz ation and subtraction of the median from each channel was performed. Then, band-pass and band-stop filters were used to filter frequencies in the range of 40 to $300\mathrm{Hz}$ and remove the power grid frequency of $50\mathrm{Hz}$ and its harmonics. The frequency range from 40 to $300\mathrm{Hz}$ constitutes gamma and high-gamma components of the local field potential signal, which were chosen as the main predictors for the task.

数据预处理可分为两部分：ECoG信号预处理和手指运动数据预处理 (图 1)。ECoG预处理流程包括以下步骤：首先对每个通道进行数据标准化并减去中值，接着使用带通和带阻滤波器过滤40至$300\mathrm{Hz}$频率范围，并去除$50\mathrm{Hz}$工频及其谐波。40至$300\mathrm{Hz}$频段构成局部场电位信号的伽马与高伽马成分，这些成分被选为该任务的主要预测指标。

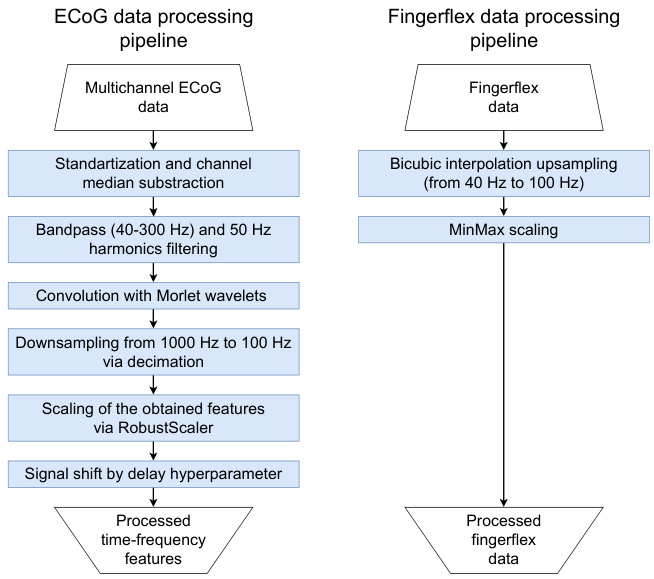
Figure 1: ECoG and finger motion data processing pipeline

图 1: ECoG和手指运动数据处理流程

As a method of explicit extraction of time-frequency represent ation of the signal, the convolution with complex Morlet wavelets was chosen. Wavelet decomposition allows capturing specific frequency components of a signal change in time. Forty wavelet kernels were created with base frequencies ranging from 40 to $300\mathrm{Hz}$ evenly spaced on a logarithmic scale. The convolution operation of selected wavelets with each channel was performed and the amplitudes of resulting analytical signals were extracted as an absolute value of a complex-valued vector. As a result of this operation for each ECoG channel, a spec tr ogram is obtained of shape: (number of wavelets, number of time points in a time window). Then, the sampling rate was then lowered from $1000~\mathrm{Hz}$ to $100~\mathrm{Hz}$ by decimation for the correspondence to a motion capture time series. Next, the obtained timefrequency envelopes were standardized with respect to 0.1 and 0.9 quantiles, and the values not falling within this range were then taken equal to the corresponding scaler boundary values to combat outliers. This operation was done using the Robust Scale r class from the scikit-learn library, which was fitted on the training set and applied to both the training and validation sets. Lastly, to account for the delay between brain activity and actual movements, the forward shift of ECoG data with respect to the finger movement time series was introduced. The exact value of the shift can be regarded as a tunable hyper parameter within the relevant physiological range: $0-200\mathrm{ms}$ .

作为信号时频表征的显式提取方法，我们选择了与复Morlet小波的卷积运算。小波分解能够捕捉信号随时间变化的特定频率成分。我们创建了40个小波核，其基频在40至$300\mathrm{Hz}$范围内按对数尺度均匀分布。对每个通道执行选定小波的卷积运算后，提取所得解析信号的振幅作为复值向量的绝对值。该运算为每个ECoG通道生成一个形状为（小波数量，时间窗口内时间点数）的频谱图。随后通过降采样将采样率从$1000~\mathrm{Hz}$降至$100~\mathrm{Hz}$，以匹配动作捕捉时间序列。接着，使用0.1和0.9分位数对获得的时频包络进行标准化处理，超出该范围的值被截断至相应边界以消除异常值。此操作通过scikit-learn库的RobustScaler类实现，该缩放器在训练集上拟合后同时应用于训练集和验证集。最后，为补偿大脑活动与实际运动之间的延迟，对ECoG数据相对于手指运动时间序列进行了前向位移，位移量可作为可调超参数在$0-200\mathrm{ms}$生理范围内调整。

The preprocessing of finger movement data consisted of two steps. First, to keep the sampling frequencies of finger movements and time-frequency time series matched, upsampling from $25\mathrm{Hz}$ to $100\mathrm{Hz}$ using bicubic interpolation was conducted. Second, MinMax scaling was applied.

手指运动数据的预处理包含两个步骤。首先，为了使手指运动和时频时间序列的采样频率匹配，使用双三次插值法将采样频率从 $25\mathrm{Hz}$ 上采样至 $100\mathrm{Hz}$。其次，应用了最小-最大缩放 (MinMax scaling)。

The model architecture

模型架构

The final model is designed in the same way as the convolutional auto encoder with a set of additions and improvements. The architecture of the model is depicted on Figure 2

最终模型的设计方式与卷积自编码器类似，但增加了一系列改进。模型架构如图 2 所示

As the input, the model takes a window of ECoG features of arbitrary length and returns the corresponding window of predicted movements; however, during the training process, the length of such a window is fixed and equal to 256 time points (2.56 secs). Initially, the model performs dimensionality reduction using a regular convolutional layer. Next comes a set of convolutional encoder layers. Each encoder layer consists of a 1D convolution layer, layer normalization, GeLU activation function, dropout layer, and maximum pooling with stride equals 2. This part of the model is responsible for encoding the features of the time window fragments. Encoder layer architecture is inspired by wav2vec architecture (Schneider et al. 2019).

模型输入任意长度的ECoG特征窗口，输出对应的预测运动窗口；但在训练过程中，该窗口长度固定为256个时间点（2.56秒）。模型首先通过常规卷积层进行降维，随后接一组卷积编码层。每个编码层包含一维卷积层、层归一化、GeLU激活函数、Dropout层以及步长为2的最大池化。这部分结构负责对时间窗口片段特征进行编码，其设计灵感源自wav2vec架构 (Schneider et al. 2019)。

This is followed by a symmetrical set of convolutional decoder layers, each of which uses for further prediction not only information from the previous layer, but also from the symmetrical encoder layer. In other words, skip connections like those of the UNet model (Ronne berger, Fischer, and Brox 2015) were added. Skip connections make it possible to use for prediction not only the generalized representation in the latent space obtained by the encoder, but also the original local features, which ultimately increases the accuracy of the final model. The model is completed by a $1\times1$ convolution layer that uses the resulting set of features from each point in time to predict the coordinates of each of the five fingers at that point.

随后是一组对称的卷积解码器层，每层不仅利用前一层的特征进行预测，还结合了对称编码器层的信息。换言之，该模型添加了类似UNet (Ronneberger, Fischer, and Brox 2015) 的跳跃连接结构。跳跃连接使得预测过程既能利用编码器生成的潜在空间全局表征，又能保留原始局部特征，从而提升最终模型的精度。模型末端通过 $1\times1$ 卷积层整合每个时间点的特征集，预测该时刻五根手指的坐标位置。

Training details

训练细节

The BCI competition IV dataset 4 was already divided into training and validation sets, the recording of each of the three patients was divided into 2 parts, where the first part of 6.5 minutes duration constitutes training subset and the second part of 3.5 minutes long constitutes validation data subset. The model was trained and optimized using only the training subset, while the validation set was used for the performance measurement and hyper parameter adjustment. Due to lack of alignment of electrode grid shapes between subjects and intentional mixing of electrodes done by the dataset creators, the model was trained for each subject individually. Note that over fitting due to a hyper parameter search using the validation set was addressed by performing ablation study using only one subject provided in the dataset. The same model was trained on the other patients without any additional hyper parameter adjustment.

BCI竞赛IV数据集4已预先划分为训练集和验证集，每位患者的记录分为两部分：前6.5分钟构成训练子集，后3.5分钟构成验证数据子集。模型仅使用训练子集进行训练和优化，验证集则用于性能评估和超参数调整。由于受试者间电极网格形状未对齐且数据集创建者故意混排电极，模型需针对每位受试者单独训练。需注意的是，通过仅使用数据集中一名受试者进行消融研究，解决了因验证集超参数搜索导致的过拟合问题。相同模型在其他患者数据上训练时未进行额外超参数调整。

Loss function The loss function was chosen as the half sum of the mean squared error (MSE) and the mean cosine distance. Since the metric of the final score is correlation, it is essential to include it in the loss for training process. However, the correlation itself is not an optimal optimization criterion when working with small windows, since it is too sensitive to insignificant noise within this window in those cases when there is no movenet. Therefore, instead of a correlation loss, it was decided to use the cosine distance. The ablation study was conducted to test whether the combination of MSE and cosine similarity metrics performed better than any of those metrics alone. Nevertheless, due to the evaluation criteria at BCI competition IV, correlation coefficient (CC) metric was used to evaluate and compare model performance.

损失函数
损失函数选择为均方误差 (MSE) 和平均余弦距离之和的一半。由于最终评分的指标是相关性，因此必须将其纳入训练过程的损失中。然而，在处理小窗口时，相关性本身并不是一个最优的优化标准，因为在没有运动的情况下，它对窗口内不显著的噪声过于敏感。因此，决定使用余弦距离代替相关性损失。通过消融实验验证了 MSE 和余弦相似度指标的组合是否比单独使用任一指标表现更好。尽管如此，根据 BCI competition IV 的评估标准，仍采用相关系数 (CC) 指标来评估和比较模型性能。

Hyper parameters The number of features on each of the layers of the encoder as a result of the experiments was taken equal to (32, 32, 64, 64, 128, 128). The number of features in the decoder layers is symmetrical with respect to the bottleneck. The stride size was taken equal to 2 to reduce the sampling rate of the original window as gradually as possible, which allows better extraction of common features.

超参数
编码器各层的特征数根据实验结果设定为 (32, 32, 64, 64, 128, 128)。解码器各层的特征数与瓶颈层呈对称分布。步长设为2以尽可能渐进地降低原始窗口的采样率，这有助于更好地提取共性特征。

The learning rate was picked according to the Pytorch Lightning library’s automatic learning rate finder recommendation and was set fixed to $8.4\cdot10^{-5}$ .

学习率根据Pytorch Lightning库的自动学习率查找器推荐选取，并固定设置为 $8.4\cdot10^{-5}$ 。

As was previously mentioned, wavelet number, loss function combination coefficients and the delay between ECoG and hand movement time series can be considered as the tunable hyper parameters.

如前所述，小波数量、损失函数组合系数以及ECoG信号与手部运动时间序列之间的延迟可视为可调超参数。

Results

结果

Model development

模型开发

Every subsequently improved model was trained for 30 epochs. Model weights trained during the epoch preceding over fitting of the model were chosen for inference. The model refinement took several important steps to achieve the final performance.

每个后续改进的模型都训练了30个周期。选择模型过拟合前一个周期训练的权重进行推理。模型优化经历了几个重要步骤以实现最终性能。

Architecture refinement Baseline encoder-decoder architecture, trained on unscaled absolute values of waveletconvoluted signals, yielded average correlation value of 0.2 on the first subject (Table 1). However, adding data scaling both for ECoG features and finger movements improved results using the same architecture by more than two-fold, to 0.45 on average on the first subject. It can be speculated that this win in performance is due to highly variable absolute values of the time-frequency representation of the signal. The electro physiological recordings consistently show a $1/f$ relationship between signal spectral power and a corresponding frequency (Buzsaki and Draguhn 2004), leading to a multiple-fold difference between signal power in highly distinct frequency bands. A modification of the encoderdecoder architecture parameters, which are mainly a number of features in each layer and the number of layers allowed to increase the average correlation coefficient furth