Meta-Learning through Hebbian Plasticity in Random Networks

通过随机网络中的赫布可塑性进行元学习

Elias Najarro and Sebastian Risi IT University of Copenhagen 2300 Copenhagen, Denmark enaj@itu.dk, sebr@itu.dk

Elias Najarro 和 Sebastian Risi
哥本哈根信息技术大学
丹麦哥本哈根 2300
enaj@itu.dk, sebr@itu.dk

Abstract

摘要

Lifelong learning and adaptability are two defining aspects of biological agents. Modern reinforcement learning (RL) approaches have shown significant progress in solving complex tasks, however once training is concluded, the found solutions are typically static and incapable of adapting to new information or perturbations. While it is still not completely understood how biological brains learn and adapt so efficiently from experience, it is believed that synaptic plasticity plays a prominent role in this process. Inspired by this biological mechanism, we propose a search method that, instead of optimizing the weight parameters of neural networks directly, only searches for synapse-specific Hebbian learning rules that allow the network to continuously self-organize its weights during the lifetime of the agent. We demonstrate our approach on several reinforcement learning tasks with different sensory modalities and more than 450K trainable plasticity parameters. We find that starting from completely random weights, the discovered Hebbian rules enable an agent to navigate a dynamical 2D-pixel environment; likewise they allow a simulated 3D quadrupedal robot to learn how to walk while adapting to morphological damage not seen during training and in the absence of any explicit reward or error signal in less than 100 timesteps. Code is available at https://github.com/enajx/He bbi an MetaL earning.

终身学习与适应能力是生物智能体的两大核心特征。现代强化学习(RL)方法在解决复杂任务方面取得了显著进展，但训练结束后所得解决方案通常是静态的，无法适应新信息或环境扰动。尽管生物大脑如何高效地从经验中学习与适应的机制尚未完全阐明，但突触可塑性被认为在此过程中起着关键作用。受此生物机制启发，我们提出了一种搜索方法：不直接优化神经网络权重参数，而是搜索特定突触的赫布学习规则(Hebbian learning rules)，使网络能在智能体生命周期内持续自组织调整权重。我们在多个具有不同感官模态的强化学习任务中验证了该方法，涉及超过45万个可训练可塑性参数。实验表明：从完全随机权重出发，所发现的赫布规则能使智能体在动态2D像素环境中自主导航；同样使模拟3D四足机器人在100个时间步内学会行走，并能适应训练中未出现的形态损伤，且无需任何显式奖励或误差信号。代码详见https://github.com/enajx/HebbianMetaLearning。

1 Introduction

1 引言

Agents controlled by neural networks and trained through reinforcement learning (RL) have proven to be capable of solving complex tasks [1–3]. However once trained, the neural network weights of these agents are typically static, thus their behaviour remains mostly inflexible, showing limited adaptability to unseen conditions or information. These solutions, whether found by gradient-based methods or black-box optimization algorithms, are often immutable and overly specific for the problem they have been trained to solve [4, 5]. When applied to a different tasks, these networks need to be retrained, requiring many extra iterations.

通过强化学习(RL)训练并由神经网络控制的AI智能体(AI Agent)已被证明能够解决复杂任务[1-3]。然而一旦训练完成，这些智能体的神经网络权重通常是静态的，其行为基本保持固定，对未见过的条件或信息表现出有限的适应性。无论是基于梯度的方法还是黑盒优化算法找到的这些解决方案，通常都是不可变的，并且针对训练解决的问题过于特定[4,5]。当应用于不同任务时，这些网络需要重新训练，需要大量额外的迭代。

Unlike artificial neural networks, biological agents display remarkable levels of adaptive behavior and can learn rapidly [6, 7]. Although the underlying mechanisms are not fully understood, it is well established that synaptic plasticity plays a fundamental role [8, 9]. For example, many animals can quickly walk after being born without any explicit supervision or reward signals, seamlessly adapting to their bodies of origin. Different plasticity-regulating mechanisms have been suggested which can be encompassed in two main ideal-type families: end-to-end mechanisms which involve top-down feedback propagating errors [10] and local mechanisms, which solely rely on local activity in order to regulate the dynamics of the synaptic connections. The earliest proposed version of a purely local mechanism is known as Hebbian plasticity, which in its simplest form states that the synaptic strength between neurons changes proportionally to the correlation of activity between them [11].

与人工神经网络不同，生物智能体展现出惊人的适应行为水平并能快速学习 [6, 7]。虽然其底层机制尚未完全明晰，但学界公认突触可塑性起着基础性作用 [8, 9]。例如，许多动物出生后无需显式监督或奖励信号即可快速行走，无缝适应与生俱来的身体结构。现有研究提出了两类主要的理想型可塑性调节机制：涉及自上而下误差传播的端到端机制 (end-to-end mechanisms) [10]，以及仅依赖局部活动来调节突触连接动态的局部机制。最早提出的纯局部机制被称为赫布可塑性 (Hebbian plasticity)，其最简形式表明神经元间的突触强度会随二者活动相关性成比例变化 [11]。

34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, Canada.

第34届神经信息处理系统大会 (NeurIPS 2020)，加拿大温哥华。

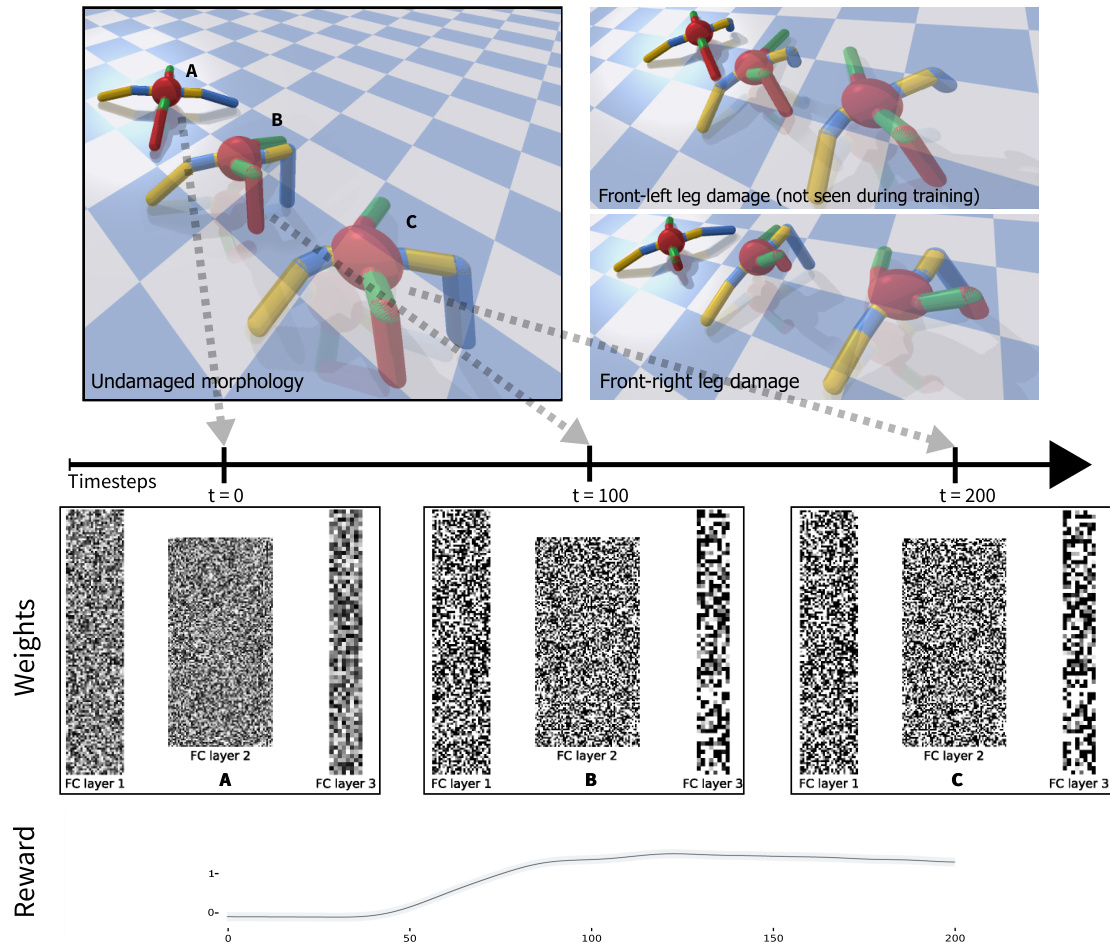
Figure 1: Hebbian Learning in Random Networks. Starting from random weights, the discovered learning rules allow fast adaptation to different morphological damage without an explicit reward signal. The figure shows the weights of the network at three different timesteps (A, B, C) during the lifetime of the robot with standard morphology (top-left). Each column represents the weights of each of the network layers at the different timesteps. At $\scriptstyle{\mathrm{t=0}}$ (A) the weights of the network are initial is ed randomly by sampling from an uniform distribution $\mathbf{w}\in\mathrm{U}[-0.1,0.1]$ , thereafter their dynamics are determined by the evolved Hebbian rules and the sensory input from the environment. After a few timesteps the quadruped starts to move which reflects in an increase in the episodic reward (bottom row). The network with the same Hebbian rules is able to adapt to robots with varying morphological damage, even ones not seen during training (top right).

图 1: 随机网络中的赫布学习。从随机权重开始，所发现的学习规则允许在没有明确奖励信号的情况下快速适应不同的形态损伤。该图展示了机器人标准形态下生命周期中三个不同时间步（A、B、C）的网络权重（左上角）。每列代表不同时间步各网络层的权重。在$\scriptstyle{\mathrm{t=0}}$时（A），网络权重通过均匀分布$\mathbf{w}\in\mathrm{U}[-0.1,0.1]$随机初始化，随后其动态由进化的赫布规则和来自环境的感官输入决定。经过几个时间步后，四足机器人开始移动，这反映在情景奖励的增加上（底部行）。具有相同赫布规则的网络能够适应具有不同形态损伤的机器人，甚至包括训练期间未见过的损伤（右上角）。

The rigidity of non-plastic networks and their inability to keep learning once trained can partially be attributed to them traditionally having both a fixed neural architecture and a static set of synaptic weights. In this work we are therefore interested in algorithms that search for plasticity mechanisms that allow agents to adapt during their lifetime [12–15]. While recent work in this area has focused on determining both the weights of the network and the plasticity parameters, we are particularly intrigued by the interesting properties of randomly-initial is ed networks in both machine learning [16–18] and neuroscience [19]. Therefore, we propose to search for plasticity rules that work with randomly initial is ed networks purely based on a process of self-organisation.

非塑性网络的刚性及其训练后无法持续学习的特点，部分可归因于它们传统上同时具有固定的神经架构和静态的突触权重集合。因此，在本研究中，我们关注的是寻找能让智能体在其生命周期内适应的可塑性机制算法 [12-15]。尽管该领域近期研究集中于同时确定网络权重和可塑性参数，但我们对随机初始化网络在机器学习 [16-18] 和神经科学 [19] 中表现出的有趣特性尤为着迷。为此，我们提出探索仅基于自组织过程、适用于随机初始化网络的可塑性规则。

To accomplish this, we optimize for connection-specific Hebbian learning rules that allow an agent to find high-performing weights for non-trivial reinforcement learning tasks without any explicit reward during its lifetime. We demonstrate our approach on two continuous control tasks and show that such a network reaches a higher performance than a fixed-weight network in a vision-based RL task. In a 3-D locomotion task, the Hebbian network is able to adapt to damages in the morphology of a simulated quadrupedal robot which has not been seen during training, while a fixed-weight network fails to do so. In contrast to fixed-weight networks, the weights of the Hebbian networks continuously vary during the lifetime of the agent; the evolved plasticity rules give rise to the emergence of an attractor in the weight phase-space, which results in the network quickly converging to highperforming dynamical weights.

为实现这一目标，我们针对连接特异性赫布学习规则 (Hebbian learning rules) 进行优化，使智能体能在生命周期内无需显式奖励的情况下，为复杂强化学习任务找到高性能权重。我们在两项连续控制任务中验证了该方法，并证明此类网络在基于视觉的强化学习任务中表现优于固定权重网络。在3D运动任务中，赫布网络能够适应训练中未出现的模拟四足机器人形态损伤，而固定权重网络则无法做到。与固定权重网络不同，赫布网络的权重在智能体生命周期内持续变化；进化出的可塑性规则促使权重相空间中出现吸引子，使网络快速收敛至高性能动态权重。

We hope that our demonstration of random Hebbian networks will inspire more work in neural plasticity that challenges current assumptions in reinforcement learning; instead of agents starting deployment with finely-tuned and frozen weights, we advocate for the use of more dynamical neural networks, which might display dynamics closer to their biological counterparts. Interestingly, we find that the discovered Hebbian networks are remarkably robust and can even recover from having a large part of their weights zeroed out.

我们希望随机Hebbian网络的演示能够启发更多关于神经可塑性的研究，挑战当前强化学习中的假设；我们主张使用更具动态性的神经网络，而非让智能体在部署时使用经过精细调整且固定不变的权重，这样的网络可能展现出更接近生物神经系统的动态特性。有趣的是，我们发现这些被发现的Hebbian网络具有极强的鲁棒性，甚至能在大部分权重被置零后恢复功能。

In this paper we focus on exploring the potential of Hebbian plasticity to master reinforcement learning problems. Meanwhile, artificial neural networks (ANNs) have been the object of great interest by neuroscientists for being capable of explaining some neuro biological data [20], while at the same time being able to perform certain visual cognitive tasks at a human-level. Likewise, demonstrating how random networks – solely optimised through local rules – are capable of reaching competitive performance in complex tasks may contribute to the pool of plausible models for understanding how learning occurs in the brain. Finally, we hope this line of research will further help promoting ANN-based RL frameworks to study how biological agents learn [21].

本文重点探索赫布可塑性(Hebbian plasticity)在强化学习问题中的应用潜力。与此同时，人工神经网络(ANN)因其能解释部分神经生物学数据[20]，同时具备人类水平的视觉认知能力，正受到神经科学界的广泛关注。同样地，证明仅通过局部规则优化的随机网络如何在复杂任务中达到竞争性表现，可能为理解大脑学习机制提供新的理论模型。最后，我们希望这项研究能进一步推动基于ANN的强化学习框架，用以探索生物智能体( biological agents)的学习机制[21]。

2 Related work

2 相关工作

Meta-learning. The aim in meta-learning or learning-to-learn [22, 23] is to create agents that can learn quickly from ongoing experience. A variety of different methods for meta-learning already exist [24–29]. For example, Wang et al. [27] showed that a recurrent LSTM network [30] can learn to reinforcement learn. In their work, the policy network connections stay fixed during the agent’s lifetime and learning is achieved through changes in the hidden state of the LSTM. While most approaches, such as the work by Wang et al. [27], take the environment’s reward as input in the inner loop of the meta-learning algorithms (either as input to the neural network or to adjust the network’s weights), we do not give explicit rewards during the agent’s lifetime in the work presented here.

元学习 (Meta-learning)。元学习或学会学习 [22, 23] 的目标是创建能够从持续经验中快速学习的 AI智能体。目前已存在多种不同的元学习方法 [24–29]。例如，Wang 等人 [27] 证明循环 LSTM 网络 [30] 可以学会强化学习。在他们的工作中，策略网络连接在智能体生命周期内保持固定，学习是通过 LSTM 隐藏状态的变化实现的。虽然大多数方法 (如 Wang 等人 [27] 的工作) 在元学习算法的内部循环中将环境奖励作为输入 (要么作为神经网络的输入，要么用于调整网络权重)，但在本文提出的工作中，我们在智能体生命周期内不提供显式奖励。

Typically, during meta-training, networks are trained on a number of different tasks and then tested on their ability to learn new tasks. A recent trend in meta-learning is to find good initial weights (e.g. through gradient descent [28] or evolution [29]), from which adaptation can be performed in a few iterations. One such approach is Model-Agnostic Meta-Learning (MAML) [28], which allows simulated robots to quickly adapt to different goal directions. Hybrid approaches bringing together gradient-based learning with an unsupervised Hebbian rules have also proven to improve performance on supervised-learning tasks [31].

通常，在元训练过程中，网络会在多个不同任务上进行训练，然后测试其学习新任务的能力。元学习领域的一个最新趋势是寻找良好的初始权重（例如通过梯度下降 [28] 或进化算法 [29]），从而只需少量迭代即可完成适配。其中一种方法是模型无关元学习（Model-Agnostic Meta-Learning，MAML）[28]，该方法能让仿真机器人快速适应不同的目标方向。将基于梯度的学习与无监督赫布规则相结合的混合方法，也被证明能提升监督学习任务的性能 [31]。

A less explored meta-learning approach is the evolution of plastic networks that undergo changes at various timescales, such as in their neural connectivity while experiencing sensory feedback. These evolving plastic networks are motivated by the promise of discovering principles of neural adaptation, learning, and memory [13]. They enable agents to perform a type of meta-learning by adapting during their lifetime through evolving recurrent networks that can store activation patterns [32] or by evolving forms of local Hebbian learning rules that change the network’s weights based on the correlated activation of neurons (“what fires together wires together”). Instead of relying on Hebbian learning rules, early work [14] tried to explore the optimization of the parameters of a parameter is ed learning rule that is applied to all connections in the network. Most related to our approach is early work by Floreano and Urzelai [33], who explored the idea of starting networks with random weights and then applying Hebbian learning. This approach demonstrated the promise of evolving Hebbian rules but was restricted to only four different types of Hebbian rules and small networks (12 neurons, 144 connections) applied to a simple robot navigation task.

一种较少被探索的元学习方法是通过演化具有不同时间尺度可塑性变化的网络（例如在接收感官反馈时改变神经连接）。这些可演化塑性网络的灵感源于发现神经适应、学习与记忆机制的潜力[13]。它们使智能体能够通过以下方式实现某种元学习：在生命周期中适应可存储激活模式的演化循环网络[32]，或演化局部赫布学习规则（Hebbian learning rules）的形式，根据神经元的相关激活来改变网络权重（"同步激活的神经元会相互连接"）。早期研究[14]没有依赖赫布学习规则，而是尝试探索对网络中所有连接应用的参数化学习规则进行参数优化。与我们的方法最相关的是Floreano和Urzelai的早期工作[33]，他们探索了从随机权重初始化网络再应用赫布学习的方法。该方法展现了演化赫布规则的潜力，但仅限于四种赫布规则类型和小型网络（12个神经元，144个连接），应用于简单的机器人导航任务。

Instead of training local learning rules through evolutionary optimization, recent work showed it is also possible to optimize the plasticity of individual synaptic connections through gradient descent [15]. However, while the trainable parameters in their work only determine how plastic each connection is, the black-box optimization approach employed in this paper allows each connection to implement its own Hebbian learning rule.

近期研究表明，除了通过进化优化训练局部学习规则外，还可以通过梯度下降优化单个突触连接的可塑性 [15]。然而，虽然他们研究中的可训练参数仅决定每个连接的塑性程度，但本文采用的黑盒优化方法允许每个连接实现其自身的赫布学习规则。

Self-Organization. Self-organization plays a critical role in many natural systems [34] and is an active area of research in complex systems. It also recently gaining more prominence in machine learning, with graph neural networks being a noteworthy example [35]. The recent work by Mordvintsev et al. [36] on growing cellular automata through local rules encoded by a neural network has interesting parallels to the work we present here; in their work the growth of 2D images relies on self-organization while in our work it is the network’s weights themselves that self-organize. A benefit of self-organizing systems is that they are very robust and adaptive. The goal in our proposed approach is to take a step towards similar levels of robustness for neural network-based RL agents.

自组织。自组织在许多自然系统中起着关键作用 [34]，也是复杂系统研究中一个活跃的领域。近年来，它在机器学习领域也日益受到重视，图神经网络就是一个显著的例子 [35]。Mordvintsev 等人 [36] 最近通过神经网络编码的局部规则来生长细胞自动机的工作，与我们在此展示的研究有有趣的相似之处；在他们的工作中，二维图像的生长依赖于自组织，而在我们的工作中，是网络权重本身在进行自组织。自组织系统的一个优势在于它们非常健壮且具有适应性。我们提出的方法的目标是朝着为基于神经网络的强化学习智能体实现类似水平的健壮性迈进一步。

Neuroscience. In biological nervous systems, the weakening and strengthening of synapses through synaptic plasticity is assumed to be one of the key mechanisms for long-term learning [8, 9]. Evolution shaped these learning mechanisms over long timescales, allowing efficient learning during our lives. What is clear is that the brain can rewire itself based on experiences we undergo during our lifetime [37]. Additionally, animals are born with a highly structured brain connectivity that allows them to learn quickly form birth [38]. However, the importance of random connectivity in biological brains is less well understood. For example, random connectivity seems to play a critical role in the prefrontal cortex [39], allowing an increase in the dimensionality of neural representations. Interestingly, it was only recently shown that these theoretical models matched experimental data better when random networks were combined with simple Hebbian learning rules [19].

神经科学。在生物神经系统中，通过突触可塑性实现的突触强弱变化被认为是长期学习的关键机制之一 [8, 9]。进化在漫长的时间尺度上塑造了这些学习机制，使我们能够在生命过程中高效学习。可以明确的是，大脑能够根据我们一生中的经历进行自我重塑 [37]。此外，动物出生时就具备高度结构化的大脑连接，使其从出生起就能快速学习 [38]。然而，随机连接在生物大脑中的重要性尚不明确。例如，随机连接在前额叶皮层中似乎起着关键作用 [39]，能够增加神经表征的维度。有趣的是，直到最近才证明当随机网络与简单的赫布学习规则结合时，这些理论模型与实验数据更匹配 [19]。

The most well-known form of synaptic plasticity occurring in biological spiking networks is spiketiming-dependent plasticity (STDP). On the other hand, artificial neural networks have continuous outputs which are usually interpreted as an abstraction of spiking networks in which the continuous output of each neuron represents a spike-rate coding average –instead of spike-timing coding– of a neuron over a long time window or, equivalent, of a subset of spiking neurons over a short time window; in this scenario, the relative timing of the pre and post-synaptic activity does not play a central role anymore [40, 41]. Spike-rate-dependent plasticity (SRDP) is a well documented phenomena in biological brains [42, 43]. We take inspiration from this work, showing that random networks combined with Hebbian learning can also enable more robust meta-learning approaches.

生物脉冲网络中最著名的突触可塑性形式是脉冲时间依赖可塑性 (STDP) 。另一方面，人工神经网络具有连续输出，通常被解释为脉冲网络的抽象——其中每个神经元的连续输出代表长时间窗口内神经元的脉冲频率编码平均值 (而非脉冲时间编码) ，或等效地代表短时间窗口内脉冲神经元子集的平均值；在此场景下，突触前后活动的相对时间不再起核心作用 [40, 41] 。脉冲频率依赖可塑性 (SRDP) 是生物大脑中已被充分记录的现象 [42, 43] 。我们受此启发，证明随机网络结合赫布学习也能实现更稳健的元学习方法。

3 Meta-learning through Evolved Local Learning Rules

3 通过进化局部学习规则进行元学习

The main steps of our approach can be summarized as follows: (1) An initial population of neural networks with random synapse-specific learning rules is created, (2) each network is initial is ed with random weights and evaluated on a task based on its accumulated episodic reward, with the network weights changing at each timestep following the discovered learning rules, and (3) a new population is created through an evolution strategy [44], moving the learning-rule parameters towards rules with higher cumulative rewards. The algorithm then starts again at (2), with the goal to progressively discover more and more efficient learning rules that can work with arbitrary initial is ed networks.

我们的方法主要步骤如下：(1) 创建具有随机突触特异性学习规则的初始神经网络群体，(2) 每个网络以随机权重初始化，并根据其累积情景奖励在任务上进行评估，网络权重在每个时间步根据发现的学习规则进行更新，(3) 通过进化策略[44]创建新群体，将学习规则参数向具有更高累积奖励的规则方向调整。然后算法从(2)重新开始，目标是逐步发现能适用于任意初始化网络的、越来越高效的学习规则。

In more detail, the synapse-specific learning rules in this paper are inspired by biological Hebbian mechanisms. We use a generalized Hebbian ABCD model [45, 46] to control the synaptic strength between the artificial neurons of relatively simple feed forward networks. Specifically, the weights of the agent are randomly initialized and updated during its lifetime at each timestep following:

具体来说，本文中突触特异性学习规则的灵感来源于生物赫布机制。我们采用广义赫布ABCD模型 [45, 46] 来控制相对简单的前馈网络中人工神经元之间的突触强度。具体而言，智能体的权重被随机初始化，并在其生命周期中的每个时间步按以下方式更新：

$$
\Delta w_{i j}=\eta_{w}\cdot(A_{w}o_{i}o_{j}+B_{w}o_{i}+C_{w}o_{j}+D_{w}),
$$

$$
\Delta w_{i j}=\eta_{w}\cdot(A_{w}o_{i}o_{j}+B_{w}o_{i}+C_{w}o_{j}+D_{w}),
$$

where $w_{i j}$ is the weight between neuron $i$ and $j$ , $\eta_{w}$ is the evolved learning rates, evolved correlation terms $A_{w}$ , evolved pre synaptic terms $B_{w}$ , evolved post synaptic terms $C_{w}$ , with $o_{i}$ and $o_{j}$ being the pre synaptic and post synaptic activation s respectively. While the coefficients $A,B,C$ explicitly determine the local dynamics of the network weights, the evolved coefficient $D$ can be interpreted as an individual inhibitory/excitatory bias of each connection in the network. In contrast to previous work, our approach is not limited to uniform plasticity [47, 48] (i.e. each connection has the same amount of plasticity) or being restricted to only optimizing a connection-specific plasticity value [15]. Instead, building on the ability of recent evolution strategy implementations to scale to a large number of parameters [44], our approach allows each connection in the network to have both a different learning rule and learning rate.

其中 $w_{i j}$ 是神经元 $i$ 和 $j$ 之间的权重，$\eta_{w}$ 是演化学习率，演化相关项 $A_{w}$，演化突触前项 $B_{w}$，演化突触后项 $C_{w}$，而 $o_{i}$ 和 $o_{j}$ 分别是突触前和突触后的激活值。虽然系数 $A,B,C$ 明确决定了网络权重的局部动态，但演化系数 $D$ 可以解释为网络中每个连接的个体抑制/兴奋偏置。与之前的工作不同，我们的方法不仅限于均匀可塑性 [47, 48] (即每个连接具有相同的可塑性量) 或仅限于优化连接特定的可塑性值 [15]。相反，基于最近演化策略实现扩展到大量参数的能力 [44]，我们的方法允许网络中的每个连接具有不同的学习规则和学习率。

We hypothesize that this Hebbian plasticity mechanism should give rise to the emergence of an attractor in weight phase-space, which leads the randomly-initial is ed weights of the policy network to quickly converge towards high-performing values, guided by sensory feedback from the environment.

我们假设这种赫布可塑性机制会在权重相空间中形成一个吸引子，引导策略网络随机初始化的权重在环境感知反馈的指导下快速收敛到高性能值。

3.1 Optimization details

3.1 优化细节

The particular population-based optimization algorithm that we are employing is an evolution strategy (ES) [49, 50]. ES have recently shown to reach competitive performance compared to other deep reinforcement learning approaches across a variety of different tasks [44]. These black-box optimization methods have the benefit of not requiring the back propagation of gradients and can deal with both sparse and dense rewards. Here, we adapt the ES algorithm by Salimans et al. [44] to not optimize the weights directly but instead finding the set of Hebbian coefficients that will dynamically control the weights of the network during its lifetime based on the input from the environment.

我们采用的特定基于种群的优化算法是进化策略 (ES) [49, 50]。最近的研究表明，在各种不同任务中，ES 与其他深度强化学习方法相比能达到相当的性能 [44]。这些黑盒优化方法的优点是不需要梯度反向传播，并且可以处理稀疏和密集奖励。在此，我们采用 Salimans 等人 [44] 的 ES 算法，但不对权重进行直接优化，而是寻找一组 Hebbian 系数，这些系数将根据环境输入在网络生命周期内动态控制其权重。

In order to evolve the optimal local learning rules, we randomly initialise both the policy network’s weights w and the Hebbian coefficients h by sampling from an uniform distribution $\mathbf{w}\in\mathbf{U}[-0.1$ , 0.1] and $\mathbf{h}\in\mathrm{U}[-1,1$ ] respectively. Subsequently we let the ES algorithm evolve $\mathbf{h}$ , which in turn determines the updates to the policy network’s weights at each timestep through Equation 1.

为了演化出最优的局部学习规则，我们通过均匀分布随机初始化策略网络的权重w和Hebbian系数h，分别采样自$\mathbf{w}\in\mathbf{U}[-0.1$，0.1]和$\mathbf{h}\in\mathrm{U}[-1,1$]。随后让ES算法演化$\mathbf{h}$，进而通过公式1决定策略网络权重在每个时间步的更新。

At each evolutionary step $t$ we compute the task-dependent fitness of the agent $F(\mathbf{h}_ {\mathbf{t}})$ , we populate a new set of $n$ candidate solutions by sampling normal noise $\epsilon_{i}=\mathcal{N}(\bar{0,1})$ and adding it to the current best solution $\mathbf{h_{t}}$ , subsequently we update the parameters of the solution based on the fitness evaluation of each of the $i\in n$ candidate solutions:

在每个进化步骤 $t$ 中，我们计算AI智能体的任务相关适应度 $F(\mathbf{h}_ {\mathbf{t}})$，通过采样正态噪声 $\epsilon_{i}=\mathcal{N}(\bar{0,1})$ 并将其添加到当前最优解 $\mathbf{h_{t}}$ 来生成一组新的 $n$ 个候选解，随后根据每个候选解 $i\in n$ 的适应度评估更新解的参数：

$$
\mathbf{h_{t+1}}=\mathbf{h_{t}}+\frac{\alpha}{n\sigma}\sum_{i=1}^{n}F(\mathbf{h_{t}}+\sigma\epsilon_{i})\cdot\epsilon_{i},
$$

$$
\mathbf{h_{t+1}}=\mathbf{h_{t}}+\frac{\alpha}{n\sigma}\sum_{i=1}^{n}F(\mathbf{h_{t}}+\sigma\epsilon_{i})\cdot\epsilon_{i},
$$

where $\alpha$ modulates how much the parameters are updated at each generation and $\sigma$ modulates the amount of noise introduced in the candidate solutions. It is important to note that during its lifetime the agent does not have access to this reward.

其中 $\alpha$ 调节每代参数的更新幅度，$\sigma$ 调节候选解中引入的噪声量。需注意，智能体在其生命周期内无法获取此奖励。

We compare our Hebbian approach to a standard fixed-weight approach, using the same ES algorithm to optimise either directly the weights or learning rule parameters respectively. All the code necessary to evolve both the Hebbian networks as well as the static networks with the ES algorithm is available at https://github.com/enajx/He bbi an MetaL earning.

我们将基于赫布学习 (Hebbian learning) 的方法与标准固定权重方法进行对比，使用相同的进化策略 (ES) 算法分别直接优化权重或学习规则参数。进化赫布网络和静态网络所需的全部代码已开源：https://github.com/enajx/HebbianMetaLearning。

Figure 2: Test domains. The random Hebbian network approach introduced in this paper is tested on the CarRacing-v0 environment [51] and a quadruped locomotion task. In the robot tasks, the same network has to adapt to three morph o logie s while only seeing two of them during the training phase (standard Ant-v0 morphology, morphology with damaged right front leg and unseen morphology with damaged left front leg) without any explicit reward feedback.

图 2: 测试领域。本文提出的随机赫布网络方法在 CarRacing-v0 环境 [51] 和四足机器人运动任务中进行了测试。在机器人任务中，同一网络需要适应三种形态结构 (标准 Ant-v0 形态、右前腿受损形态以及在训练阶段未见的左前腿受损形态)，且不依赖任何显式奖励反馈。

4 Experimental Setups

4 实验设置

We demonstrate our approach on two continuous control environments with different sensory modalities (Fig. 2). The first is a challenging vision-based RL task, in which the goal is to drive a racing car through procedurally generated tracks as fast possible. While not appearing too complicated, the tasks was only recently solved (achieving a score of more than 900 averaged over 100 random rollouts) [52–54]. The second domain is a complex 3-D locomotion task that controls a four-legged robot [55]. Here the information of the environment is represented as a one-dimensional state vector.

我们在两种具有不同感知模态的连续控制环境中展示了我们的方法 (图 2)。第一个是基于视觉的强化学习任务，目标是以最快速度驾驶赛车通过程序生成的赛道。虽然看起来不太复杂，但该任务直到最近才被解决 (在100次随机测试中平均得分超过900) [52–54]。第二个领域是控制四足机器人的复杂3D运动任务 [55]，这里的环境信息以一维状态向量表示。

Vision-based environment As a vision-based environment, we use the CarRacing-v0 domain [51], build with the Box2D physics engine. The output state of the environment is resized and normalised, resulting in a observational space of 3 channels (RGB) of $84\times84$ pixels each. The policy network consists of two convolutional layers, activated by hyperbolic tangent and interposed by pooling layers which feed a 3-layers feed forward network with [128, 64, 3] nodes per layer with no bias. This network has 92,690 weight parameters, 1,362 corresponding to the convolutional layers and

基于视觉的环境 作为基于视觉的环境，我们使用CarRacing-v0领域[51]，该环境基于Box2D物理引擎构建。环境输出状态经过尺寸调整和归一化处理，形成3通道(RGB)的观测空间，每通道为$84\times84$像素。策略网络包含两个卷积层，采用双曲正切激活函数，中间穿插池化层，最终接入一个3层前馈网络，各层节点数分别为[128, 64, 3]且无偏置项。该网络共包含92,690个权重参数，其中1,362个属于卷积层。

91,328 to the fully connected ones. The three network outputs control three continuous actions (left/right steering, acceleration, break). Under the ABCD mechanism this results in 456,640 Hebbian coefficients including the lifetime learning rates $\eta$ .

91,328个全连接节点。这三个网络输出控制三个连续动作（左/右转向、加速、刹车）。在ABCD机制下，这产生了456,640个赫布系数（Hebbian coefficients），其中包括终身学习率$\eta$。

In this environment, only the weights of the fully connected layers are controlled by the Hebbian plasticity mechanism, while the 1,362 parameters of the convolutional layers remain static during the lifetime of the agent. The reason being that there is no natural definition of what the pre synaptic and post synaptic activity of a convolution filter may be, hence making the interpretation of Hebbian plasticity for convolutional layers challenging. Furthermore, previous research on the human visual cortex indicates that the representation of visual stimuli in the early regions of the ventral stream are compatible with the representations of convolutional layers trained for image recognition [56], therefore suggesting that the variability of the parameters of convolutional layers should be limited. The evolutionary fitness is calculated as -0.1 every frame and $+1000/N$ for every track tile visited, where $N$ is the total number of tiles in the generated track.

在此环境中，只有全连接层的权重受到赫布可塑性机制控制，而卷积层的1,362个参数在智能体生命周期内保持静态。原因在于卷积滤波器的突触前和突触后活动缺乏自然定义，这使得赫布可塑性在卷积层的解释具有挑战性。此外，先前关于人类视觉皮层的研究表明，腹侧流早期区域对视觉刺激的表征与图像识别训练的卷积层表征相符[56]，因此建议限制卷积层参数的变异性。进化适应度按每帧-0.1计算，每访问一个赛道区块获得 $+1000/N$ ，其中 $N$ 是生成赛道中的区块总数。

3-D Locomotion Task For the quadruped, we use a 3-layer feed forward network with [128, 64, 8] nodes per layer, no bias and hyperbolic tangent as activation function. This architectural choice leads to a network with 12,288 synapses. Under the ABCD plastic mechanism, which has 5 coefficients per synapse, this translates to a set of 61,440 Hebbian coefficients including the lifetime learning rates $\eta$ . For the state-vector environment we use the open-source Bullet physics engine and its pyBullet python wrapper [57] that includes the “Ant” robot, a quadruped with 13 rigid links, including four legs and a torso, along with 8 actuated joints [58]. It is modeled after the ant robot in the MuJoCo simulator [59] and constitutes a common benchmark in RL [28]. The robot has an input size of 28, comprising the positional and velocity information of the agent and an action space of 8 dimensions, controlling the motion of each of the 8 joints. The fitness function of the quadruped agent selects for distance travelled during a period of 1,000 timesteps along a fixed axis.

三维运动任务
对于四足机器人，我们使用一个3层前馈网络，每层节点数为[128, 64, 8]，无偏置项并采用双曲正切作为激活函数。该架构形成包含12,288个突触的网络。在ABCD可塑性机制下（每个突触含5个系数），这相当于包含61,440个赫布系数的集合，其中包含终身学习率$\eta$。

对于状态向量环境，我们采用开源的Bullet物理引擎及其pyBullet Python语言封装库[57]，其中包含"Ant"机器人——一个由13个刚性连杆（含四条腿和躯干）及8个驱动关节组成的四足机器人[58]。该模型基于MuJoCo模拟器中的蚂蚁机器人[59]，是强化学习领域的常用基准[28]。机器人输入维度为28（包含智能体的位置和速度信息），动作空间为8维（控制8个关节的运动）。四足智能体的适应度函数选取沿固定轴在1,000个时间步内移动的距离。

The parameters used for the ES algorithm to optimize both the Hebbian and static networks are the following: a population size 200 for the CarRacing-v0 domain and size 500 for the quadruped, reflecting the higher complexity of this domain. Other parameters were the same for both domains and reflect typical ES settings (ES algorithms are typically more robust to different hyper parameters than other RL approaches [44]), with a learning rate $\alpha{=}0.2$ , $\alpha$ decay $\mathord{\left[=\mathrm{0.995}\right.}$ , $\sigma{=}0.1$ , and $\sigma$ decay $=0.999$ . These hyper parameters were found by trial-and-error and worked best in prior experiments.

用于优化赫布网络和静态网络的ES算法参数如下：CarRacing-v0域种群规模为200，四足机器人域为500（反映该领域更高复杂度）。其他参数在两个领域保持一致，采用典型ES设置（相比其他强化学习方法[44]，ES算法通常对超参数更具鲁棒性）：学习率$\alpha{=}0.2$、$\alpha$衰减率$\mathord{\left[=\mathrm{0.995}\right.}$、$\sigma{=}0.1$、$\sigma$衰减率$=0.999$。这些超参数通过试错法确定，在先前实验中表现最佳。

4.1 Results

4.1 结果

For each of the two domains, we performed three independent evolutionary runs (with different random seeds) for both the static and Hebbian approach. We performed additional ablation studies on restricted forms of the generalised Hebbian rule, which can be found in the Appendix.

对于这两个领域，我们分别针对静态方法和Hebbian方法进行了三次独立的进化实验（使用不同的随机种子）。我们还对广义Hebbian规则的受限形式进行了额外的消融研究，具体内容可参见附录。

Vision-based Environment To test how well the evolved solutions generalize, we compare the cumulative rewards averaged over 100 rollouts for the highest-performing Hebbian-based approach and traditional fixed-weight approach. The set of local learning rules found by the ES algorithm yield a reward of $872{\pm}11$ , while the static-weights solution only reached a performance of $711\pm16$ The numbers for the Hebbian network are slightly below the performance of the state-of-the-art approaches in this domain which rely on additional neural attention mechanisms $(914\pm15$ [54]), but on par with deep RL approaches such as PPO $865\pm159$ [54]). The competitive performance of the Hebbian learning agent is rather surprising, since it starts every one of the 100 rollouts with completely different random weights but through the tuned learning rules it is able to adapt quickly. While the Hebbian network takes slightly longer to reach a high training performance, likely because of the increased parameter space (see Appendix), the benefits are a higher generality when tested on procedurally generated tracks not seen during training.

基于视觉的环境测试
为了评估进化解决方案的泛化能力，我们对比了基于赫布学习(Hebbian-based)的最高性能方法与固定权重传统方法在100次运行中的平均累积奖励。进化策略(ES)算法发现的局部学习规则集合获得了$872{\pm}11$的奖励值，而静态权重方案仅达到$711\pm16$的表现。赫布网络的数值略低于该领域依赖额外神经注意力机制的最先进方法$(914\pm15$ [54])，但与PPO等深度强化学习方法($865\pm159$ [54])相当。赫布学习智能体的竞争力表现令人惊讶——尽管它在100次运行中每次都从完全不同的随机权重开始，但通过调优的学习规则能快速适应。虽然赫布网络因参数空间增大(见附录)需要稍长时间达到高训练性能，但其优势在于面对训练时未见的程序化生成赛道时展现出更强的泛化能力。

3-D Locomotion Task For the locomotion task, we created three variations of a 4-legged robot such as to mimic the effect of partial damage to one of its legs (Fig. 2). The choice of these morph o logie s is intended to create a task that would be difficult to master for a neural network that is not able to adapt. During training, both the static-weights and the Hebbian plastic networks follow the same set-up: at each training step the policy is optimised following the ES algorithm described in Section 3.1 where the fitness function consists of the average distance walked of two morph o logie s, the standard one and the one with damage on the right front leg. The third morphology (damaged on left front leg) is left out of training loop in order to subsequently evaluate the generalisation of the networks.

三维运动任务
针对运动任务，我们创建了四足机器人的三种变体，以模拟其中一条腿部分受损的效果(图2)。这些形态的选择旨在构建一项对无法自适应神经网络而言难以掌握的任务。训练过程中，静态权重网络与Hebbian可塑性网络采用相同设置：每个训练步骤中，策略按照3.1节描述的ES算法进行优化，适应度函数由两种形态(标准形态和右前腿受损形态)的平均行走距离构成。第三种形态(左前腿受损)被排除在训练循环外，以便后续评估网络的泛化能力。

Table 1: Average distance travelled by the highest-performing quadrupeds evolved with both local rules (Hebbian) and static weights, across 100 rollouts. While the Hebbian learning approach finds a solution for the seen and unseen morph o logie s (defined as moving away from the initial start position at least 100 units of length), the static-weights agent can only develop locomotion for the two morph o logie s that were present during training.

Quadruped Damage	Seen / Unseen during training	Learning Rule	Distancetravelled	Solved
NoDamage	Seen	Hebbian	1051±113	True
NoDamage	Seen	staticweights	1604±171	True
Right front leg	Seen	Hebbian	1019±116	True
Right front leg	Seen	staticweights	1431±54	True
Left front leg	Unseen	Hebbian	452±95	True
Leftfront leg	Unseen	static weights	68±56	False

表 1: 采用局部规则(Hebbian)和静态权重进化的最高性能四足机器人在100次运行中的平均