Reconstruction vs. Generation: Taming Optimization Dilemma in Latent Diffusion Models

重构 vs 生成：化解潜在扩散模型中的优化困境

Abstract

摘要

Latent diffusion models with Transformer architectures excel at generating high-fidelity images. However, recent studies reveal an optimization dilemma in this two-stage design: while increasing the per-token feature dimension in visual tokenizers improves reconstruction quality, it requires substantially larger diffusion models and more training iterations to achieve comparable generation perfor- mance. Consequently, existing systems often settle for suboptimal solutions, either producing visual artifacts due to information loss within tokenizers or failing to converge fully due to expensive computation costs. We argue that this dilemma stems from the inherent difficulty in learning un constrained high-dimensional latent spaces. To ad- dress this, we propose aligning the latent space with pretrained vision foundation models when training the visual tokenizers. Our proposed VA-VAE (Vision foundation model Aligned Variation al Auto Encoder) significantly expands the reconstruction-generation frontier of latent diffusion models, enabling faster convergence of Diffusion Transformers (DiT) in high-dimensional latent spaces. To exploit the full potential of VA-VAE, we build an enhanced DiT baseline with improved training strategies and architecture designs, termed Lightning D iT. The integrated system achieves state-of-the-art (SOTA) performance on ImageNet $256\times256$ generation with an FID score of 1.35 while demonstrating remarkable training efficiency by reaching an FID score of 2.11 in just 64 epochs – representing an over $2l\times$ convergence speedup compared to the original DiT. Models and codes are available at github.com/hustvl/Lightning D iT.

基于 Transformer 架构的潜在扩散模型在生成高保真图像方面表现出色。然而，最近的研究揭示了这种两阶段设计中的一个优化困境：虽然在视觉 Tokenizer 中增加每个 Token 的特征维度可以提高重建质量，但它需要更大的扩散模型和更多的训练迭代才能实现相当的生成性能。因此，现有系统通常采用次优解决方案，要么由于 Tokenizer 内的信息丢失而产生视觉伪影，要么由于昂贵的计算成本而无法完全收敛。我们认为，这种困境源于学习无约束高维潜在空间的固有难度。为了解决这个问题，我们建议在训练视觉 Tokenizer 时，将潜在空间与预训练的视觉基础模型对齐。我们提出的 VA-VAE (Vision foundation model Aligned Variational Auto Encoder) 显著扩展了潜在扩散模型的重建-生成边界，使得 Diffusion Transformers (DiT) 在高维潜在空间中能够更快地收敛。为了充分发挥 VA-VAE 的潜力，我们构建了一个增强的 DiT 基线，改进了训练策略和架构设计，称为 Lightning DiT。集成系统在 ImageNet $256\times256$ 生成任务上实现了最先进的 (SOTA) 性能，FID 得分为 1.35，同时在仅 64 个 epoch 内达到了 2.11 的 FID 得分，展示了显著的训练效率——与原始 DiT 相比，收敛速度提高了超过 $2l\times$。模型和代码可在 https://github.com/hustvl/Lightning DiT 获取。

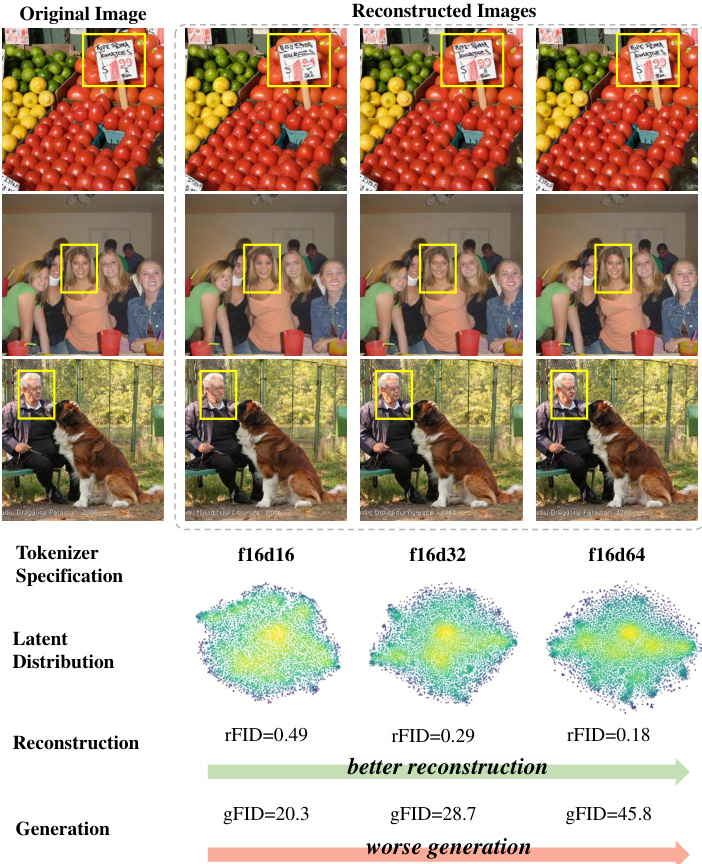
Figure 1. Optimization dilemma within latent diffusion models. In latent diffusion models, increasing the dimension of the visual tokenizer enhances detail reconstruction but significantly reduces generation quality. (In tokenizer specification, “f” and “d” represent the down sampling rate and dimension, respectively. All results are evaluated on ImageNet $256\times256$ dataset with a fixed compute budget during diffusion model training.)

图 1: 潜在扩散模型中的优化困境。在潜在扩散模型中，增加视觉 Tokenizer 的维度可以增强细节重建，但会显著降低生成质量。（在 Tokenizer 的规格中，“f”和“d”分别表示下采样率和维度。所有结果均在 ImageNet $256\times256$ 数据集上评估，并且在扩散模型训练期间使用固定的计算预算。）

1. Introduction

1. 引言

The latent diffusion model [34] utilizes a continuous-valued variation al auto encoder (VAE) [18], or visual tokenizer, to compress visual signals and thereby reduce the computational demands of high-resolution image generation. The performance of these visual tokenizers, particularly their compression and reconstruction capabilities, plays a crucial role in determining the overall system effectiveness [5, 7]. A straightforward approach to enhance the reconstruction capability is to increase the feature dimension of visual tokens, which effectively expands the information capacity of the latent representation. Recently, several influential textto-image works [5, 7, 21] have explored higher-dimensional tokenizers compared to the widely adopted VAE in Stable Diffusion [31, 34], as these tokenizers offer improved detail reconstruction, enabling finer generative quality.

潜在扩散模型 (Latent Diffusion Model) [34] 利用连续值的变分自编码器 (VAE) [18] 或视觉分词器来压缩视觉信号，从而降低高分辨率图像生成的计算需求。这些视觉分词器的性能，尤其是其压缩和重建能力，在决定整体系统有效性方面起着至关重要的作用 [5, 7]。增强重建能力的一个直接方法是增加视觉Token的特征维度，这有效地扩展了潜在表示的信息容量。最近，一些有影响力的文本生成图像工作 [5, 7, 21] 探索了比 Stable Diffusion [31, 34] 中广泛采用的 VAE 更高维度的分词器，因为这些分词器提供了更好的细节重建能力，从而实现了更精细的生成质量。

However, as research has advanced, an optimization dilemma has emerged between reconstruction and generation performance in latent diffusion models [7, 14, 17]. Specifically, while increasing token feature dimension improves the tokenizer’s reconstruction accuracy, it significantly degrades the generation performance (see Fig. 1). Currently, two common strategies exist to address this issue: the first involves scaling up model parameters, as demonstrated by Stable Diffusion 3 [7], which shows that higher-dimensional tokenizers can achieve stronger generation performance with a significantly larger model capacity—however, this approach requires significantly more training compute, making it prohibitively expensive for most practical applications. The second strategy is to deliberately limit the tokenizer’s reconstruction capacity, e.g. Sana [4, 42], W.A.L.T [14], for faster convergence of diffusion model training. Yet, this compromised reconstruction quality inherently limits the upper bound of generation performance, leading to imperfect visual details in generated results. Both approaches involve inherent trade-offs and do not provide an effective control to the underlying optimization dilemma.

然而，随着研究的深入，潜在扩散模型在重建和生成性能之间出现了优化困境 [7, 14, 17]。具体来说，虽然增加 Token 特征维度可以提高分词器的重建精度，但它会显著降低生成性能（见图 1）。目前，解决这一问题的常见策略有两种：第一种是扩大模型参数，如 Stable Diffusion 3 [7] 所示，它表明更高维度的分词器在显著更大的模型容量下可以实现更强的生成性能——然而，这种方法需要显著更多的训练计算资源，使其在大多数实际应用中成本过高。第二种策略是刻意限制分词器的重建能力，例如 Sana [4, 42] 和 W.A.L.T [14]，以加速扩散模型训练的收敛。然而，这种妥协的重建质量本质上限制了生成性能的上限，导致生成结果中的视觉细节不完美。这两种方法都涉及固有的权衡，并未对潜在的优化困境提供有效的控制。

In this paper, we propose a straightforward yet effective approach to this optimization dilemma. We draw inspiration from Auto-Regressive (AR) generation, where increasing the codebook size of discrete-valued VAEs leads to low codebook utilization [44, 49]. Through visualizing the latent space distributions across different feature dimensions (see Fig. 1), we observe that higher-dimensional tokenizers learn latent representations in a less spread-out manner, evidenced by more concentrated high-intensity areas in the distribution visualization. This analysis suggests that the optimization dilemma stems from the inherent difficulty of learning un constrained high-dimensional latent spaces from scratch. To address this issue, we develop a vision foundation model guided optimization strategy for continuous VAEs [18] in latent diffusion models. Our key finding demonstrates that learning latent representations guided by vision foundation models significantly enhances the generation performance of high-dimensional tokenizers while preserving their original reconstruction capabilities (see Fig. 2).

本文提出了一种简单而有效的优化方法来解决这一困境。我们受到自回归（Auto-Regressive, AR）生成的启发，发现离散值的变分自编码器（VAE）在增加码本大小时会导致码本利用率低下 [44, 49]。通过可视化不同特征维度的潜在空间分布（见图 1），我们观察到高维的Token化器学习的潜在表示更加集中，分布可视化中的高密度区域更加集中。这一分析表明，优化困境源于从零开始学习无约束的高维潜在空间的固有难度。为了解决这一问题，我们开发了一种基于视觉基础模型（vision foundation model）的优化策略，用于潜在扩散模型中的连续VAE [18]。我们的关键发现表明，在视觉基础模型的指导下学习潜在表示，能够显著提升高维Token化器的生成性能，同时保持其原有的重建能力（见图 2）。

Our main technical contribution is the Vision Foundation model alignment Loss (VF Loss), a plug-and-play mod- ule that aligns latent representations with pre-trained vision foundation models [16, 29] during tokenizer training. While naively initializing VAE encoders with pre-trained vision foundation models has proven ineffective [23]—likely because the latent representation quickly deviates from its initial state to optimize reconstruction—we find that a carefully designed joint reconstruction and alignment loss is crucial. Our alignment loss is specifically crafted to regularize high-dimensional latent spaces without overly constraining their capacity. First, we enforce both element-wise and pair-wise similarities to ensure comprehensive regularization of global and local structures in the feature space. Second, we introduce a margin in the similarity cost to provide controlled flexibility in the alignment, thereby preventing over-regular iz ation. Additionally, we investigate the impact of different vision foundation models.

我们的主要技术贡献是视觉基础模型对齐损失（VF Loss），这是一个即插即用的模块，在Tokenizer训练过程中将潜在表示与预训练的视觉基础模型 [16, 29] 对齐。虽然使用预训练的视觉基础模型初始化VAE编码器已被证明是无效的 [23]——可能是因为潜在表示会迅速偏离其初始状态以优化重建——但我们发现，精心设计的联合重建和对齐损失是至关重要的。我们的对齐损失专门设计用于正则化高维潜在空间，而不会过度限制其能力。首先，我们强制执行元素级和配对级相似性，以确保特征空间中全局和局部结构的全面正则化。其次，我们在相似性成本中引入了一个边距，以提供对齐中的可控灵活性，从而防止过度正则化。此外，我们还研究了不同视觉基础模型的影响。

Figure 2. Reconstruction-generation frontier of latent diffusion models. VA-VAE improves the feature distribution of highdimensional latent. Through alignment with vision foundation models, we expand the frontier between reconstruction and generation in latent diffusion models.

图 2: 潜在扩散模型的重构-生成边界。VA-VAE 改进了高维潜在特征分布。通过与视觉基础模型对齐，我们扩展了潜在扩散模型中重构与生成之间的边界。

To evaluate the generation performance, we couple the proposed Vision foundation model Aligned VAE (VA-VAE) with Diffusion Transformers (DiT) [30] to create a latent diffusion model. To fully exploit the potential of VA-VAE, we build an enhanced DiT framework through advanced diffusion training strategies and transformer architectural improvements, which we name Lightning D iT. Our contributions achieve the following significant milestones:

为了评估生成性能，我们将提出的视觉基础模型对齐变分自编码器 (VA-VAE) 与扩散 Transformer (DiT) [30] 结合，创建了一个潜在扩散模型。为了充分利用 VA-VAE 的潜力，我们通过先进的扩散训练策略和 Transformer 架构改进构建了一个增强的 DiT 框架，我们将其命名为 Lightning DiT。我们的贡献实现了以下重要里程碑：

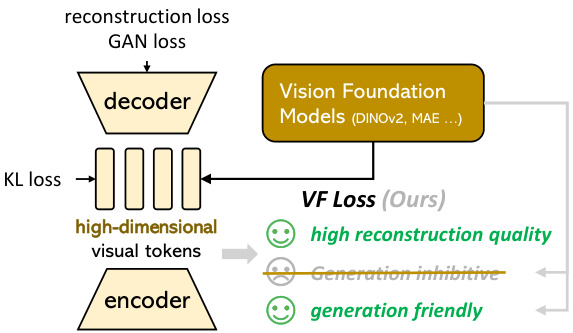
Figure 3. The proposed Vision foundation model Aligned VAE (VA-VAE). Vision foundation models are used to guide the training of high-dimensional visual tokenizers, effectively mitigating the optimization dilemma and improve generation performance.

图 3: 提出的视觉基础模型对齐 VAE (VA-VAE)。视觉基础模型用于指导高维视觉 tokenizer 的训练，有效缓解优化困境并提升生成性能。

2. Related Work

2. 相关工作

2.1. Tokenizers for Visual Generation

2.1. 用于视觉生成的 Tokenizer

Visual tokenizers, represented by variation al auto encoders (VAEs) [18], leverage an encoder-decoder architecture to create continuous visual representations, facilitating the compression and reconstruction of visual signals. While VAEs operate in continuous space, VQVAE [40] introduces discrete representation learning through a learnable codebook for quantization. VQGAN [6] further enhances this discrete approach by incorporating adversarial training, establishing itself as a cornerstone for auto regressive (AR) generation frameworks [2]. However, these discrete approaches face a fundamental challenge: as revealed in [44], larger codebooks improve reconstruction fidelity but lead to poor codebook utilization, adversely affecting generation performance. Recent works propose different solu- tions to this utilization problem: SeQ-GAN [13] explores the role of semantic information in generation. MAGVITv2 [44] introduces Look-up Free Quantization (LFQ), while VQGAN-LC [49] leverages CLIP [33] vision features for codebook initialization, achieving near-complete codebook utilization.

视觉分词器 (Visual Tokenizer)，以变分自编码器 (VAEs) [18] 为代表，利用编码器-解码器架构创建连续的视觉表示，促进视觉信号的压缩和重建。虽然 VAEs 在连续空间中操作，但 VQVAE [40] 通过可学习的码本 (codebook) 引入了离散表示学习。VQGAN [6] 通过引入对抗训练进一步增强了这种离散方法，成为自回归 (AR) 生成框架的基石 [2]。然而，这些离散方法面临一个根本性挑战：如 [44] 所示，较大的码本虽然提高了重建保真度，但会导致码本利用率低下，从而对生成性能产生不利影响。最近的工作提出了不同的解决方案：SeQ-GAN [13] 探讨了语义信息在生成中的作用。MAGVITv2 [44] 引入了无查找量化 (Look-up Free Quantization, LFQ)，而 VQGAN-LC [49] 则利用 CLIP [33] 的视觉特征进行码本初始化，实现了接近完全的码本利用率。

Interestingly, continuous VAE-based latent diffusion systems [34] encounter a parallel optimization challenge: increasing the tokenizer’s feature dimensionality enhances reconstruction quality but degrades generation performance, necessitating substantially higher training costs [4, 7, 23]. Despite the significance of this trade-off in both discrete and continuous domains, current literature lacks comprehensive analysis and effective solutions for continuous VAE optimization. Our work addresses this fundamental limitation by introducing vision foundation model alignment into continuous VAE training. This principled approach resolves the optimization dilemma by structuring the latent space according to well-established visual representations, enabling efficient training of diffusion models in higher-dimensional latent spaces. Importantly, our solution maintains the computational efficiency of diffusion model training as it requires no additional parameters, while significantly accelerating convergence by over $2.5\times$ .

有趣的是，基于连续 VAE 的潜在扩散系统 [34] 也面临着类似的优化挑战：增加分词器的特征维度可以提高重建质量，但会降低生成性能，从而导致训练成本大幅增加 [4, 7, 23]。尽管这种权衡在离散和连续域中都具有重要意义，但当前文献缺乏对连续 VAE 优化的全面分析和有效解决方案。我们的工作通过将视觉基础模型对齐引入连续 VAE 训练，解决了这一根本性限制。这种原则性的方法通过根据成熟的视觉表示构建潜在空间，解决了优化困境，从而能够在高维潜在空间中高效训练扩散模型。重要的是，我们的解决方案保持了扩散模型训练的计算效率，因为它不需要额外的参数，同时将收敛速度显著加速了超过 $2.5\times$。

2.2. Fast Convergence of Diffusion Transformers

2.2. 扩散 Transformer 的快速收敛

Diffusion Transformers [30] are currently the most popular implementation of latent diffusion models [3, 7, 10, 26, 28]. Due to their remarkable s cal ability, they have proven effective across various text-to-image and text-to-video tasks. However, they suffer from slow convergence speeds. Previous works have proposed various solutions: SiT [27] enhances DiT’s efficiency through Rectified Flow integration, while MDT [11] and MaskDiT [47] achieve faster convergence by incorporating mask image modeling. REPA [45] accelerates convergence by aligning DiT features with vision foundation models like DINOv2 [29] during training.

扩散Transformer (Diffusion Transformer) [30] 是目前最流行的隐扩散模型 (latent diffusion models) [3, 7, 10, 26, 28] 的实现。由于其出色的可扩展性，它们已在各种文本到图像和文本到视频任务中证明了其有效性。然而，它们的收敛速度较慢。先前的工作提出了多种解决方案：SiT [27] 通过整合 Rectified Flow 提高了 DiT 的效率，而 MDT [11] 和 MaskDiT [47] 则通过引入掩码图像建模实现了更快的收敛。REPA [45] 通过在训练期间将 DiT 特征与视觉基础模型（如 DINOv2 [29]）对齐，加速了收敛。

Different from these approaches, we identify that a major bottleneck in efficient latent diffusion training lies in the tokenizer itself. We propose a principled approach that optimizes the latent space learned by the visual tokenizer. Unlike methods that combine diffusion loss with auxiliary losses [11, 45, 47], which incur additional computational costs during training, our approach achieves faster convergence without modifying the diffusion models. Additionally, we add several optimization s in terms of training strategies and architecture designs to the original DiT implementation that further accelerate training.

与这些方法不同，我们发现高效潜在扩散训练的一个主要瓶颈在于Tokenizer本身。我们提出了一种优化视觉Tokenizer学习的潜在空间的原则性方法。与将扩散损失与辅助损失相结合的方法 [11, 45, 47] 不同，这些方法在训练过程中会产生额外的计算成本，而我们的方法无需修改扩散模型即可实现更快的收敛。此外，我们在原始DiT实现的基础上，在训练策略和架构设计方面增加了多项优化，进一步加速了训练。

*Relationship to REPA [45]: Both our work and REPA [45] utilize vision foundation models to aid in diffusion training, yet the motivations and approaches are entirely different. REPA aims to employ vision foundation models to constrain DiT, thereby enhancing the convergence speed of generative models. In contrast, our work takes into account both the reconstruction and generative capabilities within the latent diffusion model, with the objective of leveraging foundation models to regulate the highdimensional latent space of the tokenizer, thereby resolving the optimization conflict between the tokenizer and the generative model.

与REPA [45]的关系：我们的工作和REPA [45]都利用视觉基础模型来辅助扩散训练，但动机和方法完全不同。REPA旨在通过视觉基础模型来约束DiT，从而提高生成模型的收敛速度。相比之下，我们的工作同时考虑了潜在扩散模型中的重建和生成能力，目标是利用基础模型来调节分词器的高维潜在空间，从而解决分词器和生成模型之间的优化冲突。

3. Align VAE with Vision Foundation Models

3. 对齐 VAE 与视觉基础模型

In this section, we introduce VA-VAE, a visual tokenizer trained through vision foundation model alignment. The key approach involves constraining the tokenizer’s latent space by leveraging the feature space of the foundation model, which enhances its suitability for generative tasks.

在本节中，我们介绍了VA-VAE，这是一个通过视觉基础模型对齐训练的视觉Token化器。其关键方法是通过利用基础模型的特征空间来约束Token化器的潜在空间，从而增强其在生成任务中的适用性。

As illustrated in Figure 3, our architecture and training process mainly follows LDM [34], employing a VQGAN [6] model architecture with a continuous latent space, constrained by KL loss. Our key contribution lies in the design of Vision Foundation model alignment loss, VF loss, which substantially optimizes the latent space without altering the model architecture or training pipeline, effectively resolving the optimization dilemma discussed in Section 1.

如图 3 所示，我们的架构和训练过程主要遵循 LDM [34]，采用具有连续潜在空间的 VQGAN [6] 模型架构，并受 KL 损失约束。我们的关键贡献在于设计了视觉基础模型对齐损失 (Vision Foundation model alignment loss, VF loss)，该损失在不改变模型架构或训练流程的情况下显著优化了潜在空间，有效解决了第 1 节中讨论的优化困境。

The VF loss consists of two components: marginal cosine similarity loss and marginal distance matrix similarity loss. These components are carefully crafted as a straightforward, plug-and-play module that is decoupled from the VAE architecture. We will explain each part in detail below.

VF 损失由两个部分组成：边际余弦相似度损失和边际距离矩阵相似度损失。这些组件经过精心设计，作为一个简单、即插即用的模块，与VAE架构解耦。我们将在下面详细解释每个部分。

3.1. Marginal Cosine Similarity Loss

3.1. 边缘余弦相似度损失

During training, a given image $I$ is processed by both the encoder of visual tokenizer and a frozen vision foundation model, resulting in image latents $Z$ and foundational visual representations $F$ . As shown in Eq. 1, we project $Z$ to match the dimensionality of $F$ using a linear transformation, where $W~\in~\mathbb{R}^{d_{f}\times d_{z}}$ respectively, producing $Z^{\prime}\in\mathbb{R}^{d_{f}}$ .

在训练过程中，给定图像 $I$ 会同时通过视觉分词器 (visual tokenizer) 的编码器和冻结的视觉基础模型 (frozen vision foundation model) 进行处理，生成图像潜在表示 $Z$ 和基础视觉表示 $F$ 。如公式 1 所示，我们使用线性变换将 $Z$ 投影以匹配 $F$ 的维度，其中 $W~\in~\mathbb{R}^{d_{f}\times d_{z}}$ ，生成 $Z^{\prime}\in\mathbb{R}^{d_{f}}$ 。

As defined in Eq. 2, the loss function $\mathcal{L}{\mathrm{mcos}}$ minimizes the similarity gap between corresponding features $z{i j}^{\prime}$ and $f_{i j}$ from feature matrices $Z^{\prime}$ and $F$ at each spatial location $(i,j)$ . For each pair, we compute the cosine similar- ity $\frac{z_{i j}^{\prime}\cdot f_{i j}}{\parallel z_{i j}^{\prime}\parallel\parallel f_{i j}\parallel}$ and subtract a margin $m_{1}$ . The ReLU function ensures that only pairs with similarities below $m_{1}$ con- tribute to the loss, focusing alignment on less similar pairs. The final loss is averaged over all positions in the $h\times w$ feature grid.

如公式 2 所定义，损失函数 $\mathcal{L}{\mathrm{mcos}}$ 最小化来自特征矩阵 $Z^{\prime}$ 和 $F$ 的对应特征 $z{i j}^{\prime}$ 和 $f_{i j}$ 在每个空间位置 $(i,j)$ 处的相似性差距。对于每一对特征，我们计算余弦相似度 $\frac{z_{i j}^{\prime}\cdot f_{i j}}{\parallel z_{i j}^{\prime}\parallel\parallel f_{i j}\parallel}$ 并减去一个边界值 $m_{1}$。ReLU 函数确保只有相似度低于 $m_{1}$ 的特征对才会对损失有贡献，从而将对齐集中在相似度较低的特征对上。最终的损失在 $h\times w$ 特征网格中的所有位置上取平均。

3.2. Marginal Distance Matrix Similarity Loss

3.2. 边际距离矩阵相似性损失

Complementary to $\mathcal{L}_{\mathrm{mcos}}$ , which enforces point-to-point absolute alignment, we also aim for the relative distribution distance matrices within the features to be as similar as possible. To achieve this, we propose the marginal distance matrix similarity loss.

作为对 $\mathcal{L}_{\mathrm{mcos}}$ 的补充，它强制了点对点的绝对对齐，我们还希望特征内的相对分布距离矩阵尽可能相似。为了实现这一点，我们提出了边际距离矩阵相似性损失。

In Eq. 3, the distance matrix similarity Loss aligns the internal distributions of feature matrices $z$ and $f$ . Here, $N=h\times w$ represents the total number of elements in each flattened feature map. For each pair $(i,j)$ , we compute the absolute value of the cosine similarity difference between the corresponding vectors in feature matrices $z$ and $f$ , thus promoting closer alignment of their relative structures. Similarly, we subtract a margin $m_{2}$ to relax the constraint. The ReLU function ensures that only pairs with differences exceeding $m_{2}$ contribute to the loss.

在公式 3 中，距离矩阵相似度损失函数对齐了特征矩阵 $z$ 和 $f$ 的内部分布。其中，$N=h\times w$ 表示每个展平特征图中的元素总数。对于每一对 $(i,j)$，我们计算特征矩阵 $z$ 和 $f$ 中对应向量的余弦相似度差异的绝对值，从而促进它们相对结构的更紧密对齐。同样地，我们减去一个边界值 $m_{2}$ 以放松约束。ReLU 函数确保只有差异超过 $m_{2}$ 的对才会对损失函数产生影响。

训练技巧	训练样本	轮次	FID-50k↓
DiT-XL/2 [30]	400k× 256	80	19.50
训练策略
+Rectified Flow [24] +batchsizex4&lrx2	400k×256	80	17.20 16.59
+AdamWβ2 =0.95 [1]	100k×1024	16.61
+ Logit Normal Sampling [7]		13.99
+VelocityDirection Loss [43]		12.52
架构改进
+ SwiGLU FFN [35]	100k× 1024 +patch size=1 & VA-VAE (Sec.3)	80	10.10
+ RMS Norm [46]	9.25
+Rotary Pos Embed [36]	7.13
	4.29

Table 1. Performance of Lightning D iT. With SD-VAE [34], Lightning D iT achieves FID $\cdot50\mathrm{k}{=}7.13$ on ImageNet classconditional generation, using $94%$ fewer training samples compared to the original DiT [30]. We show that the original DiT can also achieve exceptional performance by leveraging advanced design techniques.

表 1: Lightning D iT 的性能。通过使用 SD-VAE [34]，Lightning D iT 在 ImageNet 类条件生成上实现了 FID $\cdot50\mathrm{k}{=}7.13$，并且比原始 DiT [30] 减少了 $94%$ 的训练样本。我们展示了原始 DiT 通过利用先进的设计技术也能实现卓越的性能。

3.3. Adaptive Weighting

3.3. 自适应加权

In Figure 3, the original reconstruction loss and KL loss are both sum losses, which places the VF loss on a completely different scale, making it challenging to adjust the weight for stable training. Inspired by GAN Loss [6], we employ an adaptive weighting mechanism. Before backpropagation, we calculate the gradients of $L_{\mathrm{vf}}$ and $L_{\mathrm{rec}}$ on the last convolutional layer of the encoder, as shown in Eq 4. The adaptive weighting is set as the ratio of these two gradients, ensuring that $L_{\mathrm{vf}}$ and $\boldsymbol{L}_{\mathrm{rec}}$ have similar impacts on model optimization. This alignment significantly reduces the adjustment range of the VF Loss.

在图 3 中，原始的重建损失和 KL 损失都是总和损失，这使得 VF 损失处于完全不同的尺度上，难以调整权重以实现稳定的训练。受 GAN Loss [6] 的启发，我们采用了一种自适应加权机制。在反向传播之前，我们计算 $L_{\mathrm{vf}}$ 和 $L_{\mathrm{rec}}$ 在编码器最后一个卷积层上的梯度，如公式 4 所示。自适应权重被设置为这两个梯度的比率，确保 $L_{\mathrm{vf}}$ 和 $\boldsymbol{L}_{\mathrm{rec}}$ 对模型优化有相似的影响。这种对齐显著减少了 VF 损失的调整范围。

Then we get VF Loss with adaptive weighting like Eq 5. The purpose of adaptive weighting is to quickly align our loss scales across different VAE training pipelines. On this basis, we can still use manually tuned hyper parameters to further improve performance.

然后我们得到了如公式5所示的自适应加权VF Loss。自适应加权的目的是快速对齐不同VAE训练流程中的损失尺度。在此基础上，我们仍然可以使用手动调优的超参数来进一步提升性能。

We will evaluate the significant role of VF loss in achieving the latent diffusion Pareto frontier for both reconstruction and generation in our forthcoming experiments.

我们将在接下来的实验中评估 VF 损失在实现重建和生成的潜在扩散帕累托前沿中的重要作用。

4. Improved Diffusion Transformer

4. 改进的扩散Transformer

In this section, we introduce our Lightning D iT. Diffusion Transformers (DiT) [30] has gained considerable success as a foundational model for text-to-image [3, 7] and text-tovideo generation tasks [28, 32]. However, its convergence speed on ImageNet is significantly slow, resulting in high experimental iteration costs. Previous influential work like

在本节中，我们介绍我们的 Lightning D iT。Diffusion Transformers (DiT) [30] 作为文本到图像 [3, 7] 和文本到视频生成任务 [28, 32] 的基础模型取得了相当大的成功。然而，它在 ImageNet 上的收敛速度显著较慢，导致实验迭代成本较高。之前的有影响力工作如

Table 2. VF loss Improves Generation Performance. The f16d16 tokenizer specification is widely used [22, 34]. As dimensionality increases, we observe that (1) higher dimensions improve reconstruction but reduce generation quality, highlighting an optimization dilemma within the latent diffusion framework; (2) VF Loss significantly enhances generative performance in high-dimensional tokenizers with minimal impact on reconstruction.

表 2: VF 损失提升生成性能。f16d16 Tokenizer 规范被广泛使用 [22, 34]。随着维度的增加，我们观察到 (1) 更高的维度改善了重建但降低了生成质量，凸显了潜在扩散框架内的优化困境； (2) VF 损失显著提升了高维度 Tokenizer 的生成性能，同时对重建的影响最小。

Tokenizer	Spec.	ReconstructionPerformance	GenerationPerformance (FID-10K)↓
		rFID↓	PSNR↑
LDM [34]	f16d16	0.49	26.10
LDM+VF1oss (MAE)[16]	f16d16	0.51	26.01
LDM+VF1oss(DINOv2)[29]	f16d16	0.55	25.29
LDM [34]	f16d32	0.26	28.59
LDM+VF1oss (MAE)[16]	f16d32	0.28	28.33
LDM+VF1oss(DINOv2)[29]	f16d32	0.28	27.96
LDM [34]	f16d64	0.17	31.03
LDM+VF1oss (MAE) [16]	f16d64	0.15	31.03
LDM+VF1oss(DINOv2)[29]	f16d64	0.14	30.71

DINOv2 [29], ConvNeXt [25], and EVA [9] demonstrates how incorporating advanced design strategies can revitalize classic methods [15, 48]. In our work, we aim to extend the potential of the DiT architecture and explore the boundaries of how far the DiT can go. While we do not claim any individual optimization detail as our original contribution, we believe an open-source, fast-converging training pipeline for DiT will greatly support the community’s ongoing research on diffusion transformers.

DINOv2 [29]、ConvNeXt [25] 和 EVA [9] 展示了如何通过引入先进的设计策略来振兴经典方法 [15, 48]。在我们的工作中，我们旨在扩展 DiT 架构的潜力，并探索 DiT 的边界。虽然我们并不声称任何个别优化细节是我们的原创贡献，但我们相信，一个开源、快速收敛的 DiT 训练管道将极大地支持社区在扩散 Transformer 领域的持续研究。

We utilize the SD-VAE [34] with the f8d4 specification as the visual tokenizer and employ DiT-XL/2 as our experimental model. We show the optimization routine in Table 1. Each model has been trained for 80 epochs and sampled with a dopri5 integrator, which has less NFE than the original DiT for fast inference. To ensure a fair comparison, no sample optimization methods such as cfg interval [20] and timestep shift [21] are used. We adopt three categories of optimization strategies. At the computational level, we implement torch.compile [38] and bfloat16 training for acceleration. Additionally, we increase the batch size and reduce the $\beta_{2}$ of AdamW to 0.95, drawing from previous work AuraFlow [8]. For diffusion optimization, we incorporate Rectified Flow [24, 27], logit normal dis- tribution (lognorm) sampling [7], and velocity direction loss [43]. At the model architecture level, we apply common Transformer optimization s, including RMSNorm [46], SwiGLU [35], and RoPE [36]. During training, we observe that some acceleration strategies are not orthogonal. For example, gradient clipping is effective when used alone but tends to reduce performance when combined after lognorm sampling and velocity direction loss.

我们采用 SD-VAE [34] 的 f8d4 规范作为视觉分词器，并使用 DiT-XL/2 作为实验模型。我们在表 1 中展示了优化流程。每个模型都训练了 80 个 epoch，并使用 dopri5 积分器进行采样，该积分器比原始 DiT 的 NFE 更少，以实现快速推理。为了确保公平比较，没有使用诸如 cfg interval [20] 和 timestep shift [21] 等样本优化方法。我们采用了三类优化策略。在计算层面，我们实现了 torch.compile [38] 和 bfloat16 训练以加速。此外，我们借鉴了之前的工作 AuraFlow [8]，增加了批量大小并将 AdamW 的 $\beta_{2}$ 降低到 0.95。对于扩散优化，我们引入了 Rectified Flow [24, 27]、logit 正态分布 (lognorm) 采样 [7] 和速度方向损失 [43]。在模型架构层面，我们应用了常见的 Transformer 优化方法，包括 RMSNorm [46]、SwiGLU [35] 和 RoPE [36]。在训练过程中，我们观察到一些加速策略并不是正交的。例如，梯度裁剪在单独使用时有效，但在与 lognorm 采样和速度方向损失结合后往往会降低性能。

Our optimized model, Lightning D iT, achieves an FID of 7.13 $(c f g=I)$ with SD-VAE at around 80 epochs on ImageNet class-conditional generation, which is only $6%$ of the training volume required by the original DiT and SiT models over 1400 epochs. Previous great work MDT [11] or REPA [45] achieved similar convergence performance with the help of Mask Image Modeling (MIM) and representation alignment. Our results show that, even without any complex training pipeline, naive DiT could still achieve very competitive performance. This optimized architecture has been of great help in our following rapid experiment validation.

我们的优化模型 Lightning DiT 在 ImageNet 类条件生成任务中，使用 SD-VAE 在大约 80 个 epoch 时达到了 7.13 的 FID $(c f g=I)$，这仅相当于原始 DiT 和 SiT 模型在 1400 个 epoch 中所需训练量的 $6%$。之前的重要工作 MDT [11] 或 REPA [45] 在掩码图像建模 (MIM) 和表示对齐的帮助下实现了相似的收敛性能。我们的结果表明，即使没有任何复杂的训练流程，简单的 DiT 仍然可以实现非常具有竞争力的性能。这种优化架构对我们后续的快速实验验证大有帮助。

5. Experiments

5. 实验

In this section, our main objective is to achieve the reconstruction and generation frontier (see Figure 2) of reconstruction and generation within the latent diffusion system by leveraging VF loss proposed in Section 3. With the support of Lightning D iT introduced in Section 4, we demonstrate how VF loss effectively resolves the optimization dilemma, from the perspective of convergence, s cal ability, and overall system performance.

在本节中，我们的主要目标是通过利用第3节提出的VF损失，在潜在扩散系统中实现重建与生成的边界（见图2）。在第4节引入的Lightning DiT的支持下，我们从收敛性、可扩展性和整体系统性能的角度，展示了VF损失如何有效解决优化困境。

5.1. Implementation Details

5.1. 实现细节

We introduce our latent diffusion system in detail. For the visual tokenizer, we employ an architecture and training strategy mainly following to LDM [34]. Specifically, we utilize the VQGAN [6] network structure, omitting quantization and applying KL Loss to regulate the continuous latent space. To enable multi-node training, we scale the learning rate and global batch size to $1e{-4}$ and 256, respectively, following a setup from MAR [22]. We train three different $f16$ tokenizers: one without VF loss, one using VF loss $(M A E)$ , and another using VF loss $(D I N O\nu2)$ . Here $f$ denotes the do