Scale E qui variance Improves Siamese Tracking

尺度等变性提升孪生跟踪性能

Abstract

摘要

Siamese trackers turn tracking into similarity estimation between a template and the candidate regions in the frame. Mathematically, one of the key ingredients of success of the similarity function is translation e qui variance. Non-translation-e qui variant architectures induce a positional bias during training, so the location of the target will be hard to recover from the feature space. In real life scenarios, objects undergoe various transformations other than translation, such as rotation or scaling. Unless the model has an internal mechanism to handle them, the similarity may degrade. In this paper, we focus on scaling and we aim to equip the Siamese network with additional built-in scale e qui variance to capture the natural variations of the target a priori. We develop the theory for scalee qui variant Siamese trackers, and provide a simple recipe for how to make a wide range of existing trackers scalee qui variant. We present SE-SiamFC, a scale-e qui variant variant of SiamFC built according to the recipe. We conduct experiments on OTB and VOT benchmarks and on the synthetically generated T-MNIST and S-MNIST datasets. We demonstrate that a built-in additional scale e qui variance is useful for visual object tracking.

Siamese跟踪器将跟踪任务转化为模板与帧中候选区域之间的相似性估计。从数学角度看，相似度函数成功的关键要素之一是平移等变性 (translation equivariance)。非平移等变的架构会在训练过程中引入位置偏差，导致难以从特征空间恢复目标位置。在现实场景中，目标除了平移还会经历旋转、缩放等多种变换。除非模型具备内部机制处理这些变换，否则相似度可能会下降。本文聚焦缩放变换，旨在为Siamese网络赋予额外的内置尺度等变性 (scale equivariance)，从而先验地捕捉目标的自然形变。我们建立了尺度等变Siamese跟踪器的理论框架，并给出通用方案使现有跟踪器具备尺度等变性。基于该方案，我们提出了SiamFC的尺度等变改进版本SE-SiamFC。在OTB、VOT基准测试及合成的T-MNIST、S-MNIST数据集上的实验表明，内置的额外尺度等变性对视觉目标跟踪具有显著价值。

1. Introduction

1. 引言

Siamese trackers turn tracking into similarity estimation between a template and the candidate regions in the frame. The Siamese networks are successful because the similarity function is powerful: it can learn the variances of appearance very effectively, to such a degree that even the association of the frontside of an unknown object to its backside is usually successful. And, once the similarity is effective, the location of the candidate region is reduced to simply selecting the most similar candidate.

Siamese跟踪器将跟踪任务转化为模板与帧中候选区域之间的相似度估计。这类网络之所以成功，关键在于其强大的相似度函数：它能高效学习外观变化，甚至能成功关联未知物体的正面与背面。一旦相似度计算有效，候选区域定位就简化为选择最相似的候选对象。

Mathematically, one of the key ingredients of the success of the similarity function is translation e qui variance, i.e. a translation in the input image is to result in the proportional translation in feature space. Non-translation-e qui variant archi tec ture s will induce a positional bias during training, so the location of the target will be hard to recover from the feature space [21, 38]. In real-life scenarios, the target will undergo more transformations than just translation, and, unless the network has an internal mechanism to handle them, the similarity may degrade. We start from the position that e qui variance to common transformations should be the guiding principle in designing conceptually simple yet robust trackers. To that end, we focus on scale e qui variance for trackers in this paper.

从数学角度看，相似度函数成功的关键要素之一是平移等变性 (translation equivariance)，即输入图像的平移应导致特征空间中的成比例平移。不具备平移等变性的架构会在训练过程中引入位置偏差，导致难以从特征空间恢复目标位置 [21, 38]。现实场景中，目标往往经历比平移更复杂的变换，若网络缺乏内部机制处理这些变换，相似度可能会降低。我们以"对常见变换保持等变性应作为设计简洁鲁棒跟踪器指导原则"为出发点，本文重点研究跟踪器的尺度等变性。

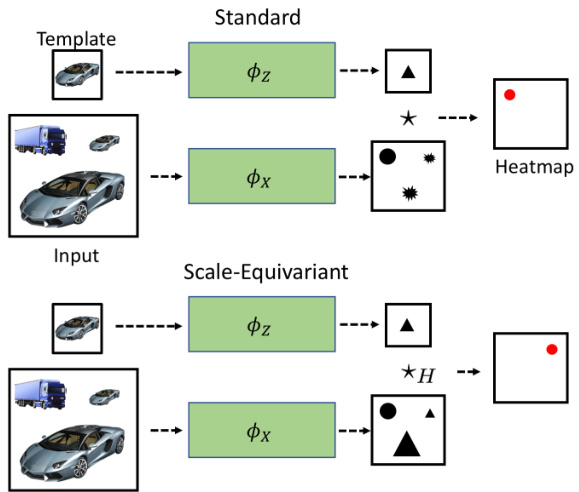
Figure 1: The standard version (top) and the scalee qui variant version (bottom) of a basic tracker. The scalee qui variant tracker has an internal notion of scale which allows for the distinction between similar objects which only differ in scale. The operator $\star$ denotes convolution, and $\star_{H}$ stands for scale-convolution.

图 1: 基础跟踪器的标准版本 (top) 和 scalee qui 变体版本 (bottom)。scalee qui 变体跟踪器具有内部尺度概念，可区分仅尺度不同的相似对象。运算符 $\star$ 表示卷积，$\star_{H}$ 表示尺度卷积。

Measuring scale precisely is crucial when the camera zooms its lens or when the target moves into depth. However, scale is also important in distinguishing among objects in general. In following a marching band or in analyzing a soccer game, or when many objects in the video have a similar appearance (a crowd, team sports), the similarity power of Siamese trackers has a hard time locating the right target. In such circumstances, spatial-scale equivariance will provide a richer and hence more disc rim i native descriptor, which is essential to differentiate among several similar candidates in an image. And, even, as we will demonstrate, when the sequence does not show variation over scale, proper scale measurement is important to keep the target bounding box stable in size.

精确测量尺度在相机镜头变焦或目标向纵深移动时至关重要。然而，尺度对于一般物体区分同样重要。无论是追踪行进乐队、分析足球比赛，还是处理视频中外观相似的多个物体（如人群、团队运动），连体跟踪器的相似性匹配能力都难以准确定位目标。此时，空间尺度等变性将提供更丰富、更具判别力的描述符，这对区分图像中多个相似候选目标至关重要。我们还将证明，即使序列未呈现尺度变化，正确的尺度测量对于保持目标边界框尺寸稳定也具有重要意义。

The common way to implement scale into a tracker is to train the network on a large dataset where scale variations occur naturally. However, as was noted in [20], such training procedures may lead to learning groups of re-scaled duplicates of almost the same filters. As a consequence, interscale similarity estimation becomes unreliable, see Figure 1 top. Scale-e qui variant models have an internal notion of scale and built-in weight sharing among different filter scales. Thus, scale e qui variance aims to produce the same distinction for all sizes, see Figure 1 bottom.

在跟踪器中实现尺度变化的常见方法是在自然存在尺度变化的大规模数据集上训练网络。然而，如文献[20]所指出的，这种训练过程可能导致学习到几乎相同滤波器的多组缩放副本。其后果是尺度间相似性估计变得不可靠（见图1顶部）。而尺度等变（scale-equivariant）模型具有内部尺度概念，并在不同滤波器尺度间内置权重共享机制，因此尺度等变性旨在对所有尺寸产生相同的判别特征（见图1底部）。

In this paper, we aim to equip the Siamese network with spatial and scale e qui variance built-in from the start to capture the natural variations of the target a priori. We aim to improve a broad class of tracking algorithms by enhancing their capacity of candidate distinction. We adopt recent advances [28] in convolutional neural networks (CNNs) which handle scale variations explicitly and efficiently.

本文旨在为孪生网络内置空间与尺度等变性，从一开始就捕获目标的自然先验变化。我们通过增强候选区分能力来改进广泛的跟踪算法类别。采用卷积神经网络(CNNs)领域的最新进展[28]，该方法能显式且高效地处理尺度变化。

While scale-e qui variant convolutional models have lead to success in image classification [28, 33], we focus on their usefulness in object localization. Where scale estimation has been used in the localization for tracking, it typically relies on brute-force multi-scale detection with an obvious computational burden [8, 2], or on a separate network to estimate the scale [6, 22]. Both approaches will require attention to avoid bias and the propagation thereof through the network. Our new method treats scale and scale equivariance as a desirable fundamental property, which makes the algorithm conceptually easier. Hence, scale e qui variance should be easy to merge into an existing network for tracking. Then, scale e qui variance will enhance the performance of the tracker without further modification of the network or extensive data augmentation during the learning phase.

虽然尺度等变卷积模型在图像分类领域取得了成功[28, 33]，但我们关注的是它们在目标定位中的实用性。在跟踪定位中使用尺度估计时，通常依赖于计算负担明显的暴力多尺度检测[8, 2]，或是依赖单独的网络来估计尺度[6, 22]。这两种方法都需要注意避免偏差及其在网络中的传播。我们的新方法将尺度和尺度等变视为理想的基本属性，这使得算法在概念上更简单。因此，尺度等变应该很容易融入现有的跟踪网络。这样，尺度等变将在不进一步修改网络或学习阶段进行大量数据增强的情况下，提升跟踪器的性能。

We make the following contributions:

我们做出以下贡献：

• We propose the theory for scale-e qui variant Siamese trackers and provide a simple recipe of how to make a wide range of existing trackers scale-e qui variant. • We propose building blocks necessary for efficient implementation of scale e qui variance into modern Siamese trackers and implement a scale-e qui variant extension of the recent SiamFC $^+$ [38] tracker. • We demonstrate the advantage of scale-e qui variant Siamese trackers over their conventional counterparts on popular benchmarks for sequences with and without apparent scale changes.

• 我们提出了尺度等变 (scale-equivariant) 孪生跟踪器的理论，并提供了如何使多种现有跟踪器实现尺度等变的简单方案。
• 我们提出了在现代孪生跟踪器中高效实现尺度等变所需的构建模块，并基于近期 SiamFC$^+$ [38] 跟踪器实现了尺度等变扩展版本。
• 我们在多个流行基准测试中证明了尺度等变孪生跟踪器相对于传统方法的优势，无论测试序列是否存在明显尺度变化。

2. Related Work

2. 相关工作

Siamese tracking The challenge of learning to track arbitrary objects can be addressed by deep similarity learning [2]. The common approach is to employ Siamese networks to compute the embeddings of the original patches. The embeddings are then fused to obtain a location estimate. Such formulation is general, allowing for a favourable flexibility in the design of the tracker. In [2] Bertinetto et al. employ off-line trained CNNs as feature extractors. The authors compare dot-product similarities between the feature map of the template with the maps coming from the current frame and measure similarities on multiple scales. Held et al. [14] suggest a detection-based Siamese tracker, where the similarity function is modeled as a fullyconnected network. Extensive data augmentation is applied to learn a similarity function, which generalizes for various object transformations. Li et al. [22] consider tracking as a one-shot detection problem to design Siamese region-proposal-networks [25] by fusing the features from a fully-convolutional backbone. The recent ATOM [6] and DIMP [3] trackers employ a multi-stage tracking framework, where an object is coarsely localized by the online classification branch, and subsequently refined in its position by the estimation branch. From a Siamese perspective, in both [6, 3] the object embeddings are first fused to produce an initial location and subsequently processed by the IoU-Net [17] to enhance the precision of the bounding box.

孪生网络跟踪
通过学习深度相似性来追踪任意物体的挑战可以通过深度相似性学习解决 [2]。常见方法是使用孪生网络计算原始图像块的嵌入表示，再通过融合这些嵌入来获得位置估计。这种框架具有通用性，为跟踪器设计提供了良好的灵活性。Bertinetto等人在 [2] 中采用离线训练的CNN作为特征提取器，通过比较模板特征图与当前帧多尺度特征图之间的点积相似度进行匹配。Held等人 [14] 提出了一种基于检测的孪生跟踪器，使用全连接网络建模相似度函数，并通过大量数据增强使相似度函数能泛化到各种物体形变。Li等人 [22] 将跟踪视为单样本检测问题，通过融合全卷积主干网络特征设计了孪生区域提议网络 [25]。最新的ATOM [6] 和DIMP [3] 跟踪器采用多阶段框架：在线分类分支粗定位目标后，由估计分支精调位置。从孪生网络视角看，这两项研究 [6, 3] 都先融合物体嵌入生成初始位置，再通过IoU-Net [17] 处理以提高边界框精度。

The aforementioned references have laid the foundation for most of the state-of-the-art trackers. These methods share an implicit or explicit attention to translation equivariance for feature extraction. The decisive role of translation e qui variance is noted in [2, 21, 38]. Bertinetto et al. [2] utilize fully-convolutional networks where the output directly commutes with a shift in the input image as a function of the total stride. Li et al. [21] suggest a training strategy to eliminate the spatial bias introduced in nonfully-convolutional backbones. Along the same line, Zhang and Peng [38] demonstrated that deep state-of-the-art models developed for classification are not directly applicable for localization. And hence these models are not directly applicable to tracking as they induce positional bias, which breaks strict translation e qui variance. We argue that transformations, other then translation, such as rotation may be equally important for certain classes of videos like sports and following objects in the sea or in the sky. And we argue that scale transformation is common in the majority of sequences due to the changing distances between objects and the camera. In this paper, we take on the latter class of transformations for tracking.

上述研究为当前最先进的追踪器奠定了基础。这些方法在特征提取时都隐式或显式地关注了平移等变性 (translation equivariance)。[2, 21, 38] 均指出平移等变性的决定性作用：Bertinetto等人 [2] 采用全卷积网络，其输出会随输入图像平移而发生相应偏移（偏移量为总步长的函数）；Li等人 [21] 提出消除非全卷积主干网络引入空间偏置的训练策略；Zhang和Peng [38] 则证明，为分类任务开发的先进深度模型会因产生位置偏置而破坏严格平移等变性，故不能直接用于定位任务。我们认为除平移外，旋转等变换对体育赛事、海上/空中目标追踪等特定视频类型同样重要。而由于目标与相机距离变化，尺度变换在多数序列中更为普遍。本文主要研究后一类变换在追踪中的应用。

E qui variant CNNs Various works on transformatione qui variant convolutional networks have been published recently. They extend the built-in property of translatione qui variance of conventional CNNs to a broader set of transformations. Mostly considered was roto-translation, as demonstrated on image classification [4, 5, 15, 30, 27, 26], image segmentation [31] and edge detection [33].

等变卷积网络
近期发表了多项关于等变卷积网络的研究工作。这些研究将传统CNN固有的平移等变特性扩展到了更广泛的变换集合。其中最常见的应用是旋转平移变换，已在图像分类 [4, 5, 15, 30, 27, 26] 、图像分割 [31] 和边缘检测 [33] 等领域得到验证。

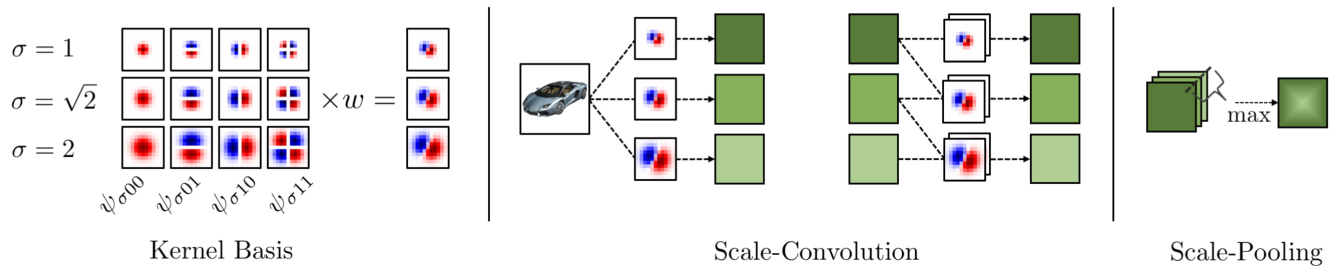
Figure 2: Left: convolutional kernels use a fixed kernel basis on multiple scales, each with a set of trainable weights. Middle: a representation of scale-convolution using Equation 6 for the first and all subsequent layers. Right: a scheme of scalepooling, which transforms a 3D-signal into a 2D one without losing scale e qui variance. As an example, we use a basis of 4 functions and 3 scales with a step of $\sqrt{2}$ . Only one channel of each convolutional layer is demonstrated for simplicity.

图 2: 左图: 卷积核在多个尺度上使用固定的核基组，每组具有可训练权重。中图: 使用公式6对首层及后续所有层进行尺度卷积的示意图。右图: 尺度池化方案，将3D信号转换为2D信号同时保持尺度等变性。示例中采用4个基函数和3个尺度(步长$\sqrt{2}$)。为简化演示，每个卷积层仅展示一个通道。

One of the first works on scale-translation-e qui variant convolutional networks was by Marcos et al. [24]. In order to process images on multiple scales, the authors resize and convolve the input of each layer multiple times, forming a stack of features which corresponds to variety of scales. The output of such a convolutional layer is a vector whose length encodes the maximum response in each position among different scales. The direction of the vector is derived from the scale, which gave the maximum. The method has almost no restrictions in the choice of admissible scales. As this approach relies on rescaling the image, the obtained models are significantly slower compared to conventional CNNs. Thus, this approach is not suitable for being applied effectively in visual object tracking.

关于尺度平移等变卷积网络的首批研究之一由Marcos等人[24]提出。为处理多尺度图像，作者对每层输入进行多次缩放和卷积操作，形成对应不同尺度的特征堆栈。此类卷积层的输出是一个向量，其长度编码了不同尺度下各位置的最大响应值，向量方向则源自产生最大响应的尺度。该方法对可选用尺度几乎没有任何限制。由于依赖图像重缩放，所得模型相比传统CNN速度显著下降，因此该方案不适用于视觉目标跟踪的高效应用。

Worrall & Welling [32] propose Deep Scale-Spaces, an e qui variant model which generalizes the concept of scalespace to deep networks. The approach uses filter dilation to analyze the images on different scales. It is almost as fast as a conventional CNN with the same width and depth. As the method is restricted to integer scale factors it is unsuited to applications in tracking where the scene dictates arbitrary scale factors.

Worrall & Welling [32] 提出了深度尺度空间 (Deep Scale-Spaces)，这是一个将尺度空间概念推广到深度网络的等变模型。该方法通过滤波器膨胀来分析不同尺度下的图像，其速度几乎与具有相同宽度和深度的传统 CNN 相当。由于该方法仅限于整数比例因子，因此不适用于场景需要任意比例因子的跟踪应用。

Almost simultaneously, three papers [28, 1, 39] were proposed to implement scale-translation-e qui variant networks with arbitrary scales. What they have in common is that they use a pre-calculated and fixed basis defined on multiple scales. All filters are then calculated as a linear combination of the basis and trainable weights. As a result, no rescaling is used. We prefer to use [28], as Sosnovik et al. propose an approach for building general scaletranslation-e qui variant networks with an algorithm for the fast implementation of the scale-convolution.

几乎同时，三篇论文 [28, 1, 39] 提出了实现任意尺度的尺度平移等变网络的方法。它们的共同点是使用了在多尺度上预计算并固定的基。所有滤波器随后通过基与可训练权重的线性组合计算得出，因此无需重新缩放。我们更倾向于采用 [28] 的方法，因为 Sosnovik 等人提出了一种构建通用尺度平移等变网络的方案，并提供了快速实现尺度卷积的算法。

To date, the application of scale-e qui variant networks was mostly demonstrated in image classification. Almost no attention was paid to tasks that involve object localization, such as visual object tracking. As we have noted above, it is a fundamentally different case. To the best of our knowledge, we demonstrate the first application of transformation-e qui variant CNNs to visual object tracking.

迄今为止，尺度等变网络 (scale-equivariant networks) 的应用主要集中于图像分类领域。对于涉及目标定位的任务（如视觉目标跟踪），几乎无人关注。正如前文所述，这是完全不同的应用场景。据我们所知，我们首次将变换等变卷积神经网络 (transformation-equivariant CNNs) 应用于视觉目标跟踪领域。

3. Scale-E qui variant Tracking

3. Scale-Equivariant Tracking

In this work, we consider a wide range of modern trackers which can be described by the following formula:

在本研究中，我们考虑了多种现代跟踪器，它们可以用以下公式描述：

$$
h(z,x)=\phi_{X}(x)\star\phi_{Z}(z)
$$

$$
h(z,x)=\phi_{X}(x)\star\phi_{Z}(z)
$$

where $z,x$ are the template and the input frame, and $\phi_{X},\phi_{Z}$ are the functions which process them, and $\star$ is the convolution operator which implements a connection between two signals. The resulting value $h(z,x)$ is a heatmap that can be converted into a prediction by relatively simple calculations. Functions $\phi_{X},\phi_{Z}$ here can be para met rize d as feed-forward neural networks. For our analysis, it is both suitable if the weights of these networks are fixed or updated during training or inference. This pipeline describes the majority of Siamese trackers such as [2, 22, 21] and the trackers based on correlation filters [7, 8].

其中 $z,x$ 是模板和输入帧，$\phi_{X},\phi_{Z}$ 是处理它们的函数，$\star$ 是实现两个信号之间连接的卷积运算符。结果值 $h(z,x)$ 是一个热图，可以通过相对简单的计算转换为预测。这里的函数 $\phi_{X},\phi_{Z}$ 可以参数化为前馈神经网络。对于我们的分析，无论这些网络的权重在训练或推理过程中是固定的还是更新的，都是合适的。这个流程描述了大多数连体跟踪器 [2, 22, 21] 以及基于相关滤波器的跟踪器 [7, 8]。

3.1. Convolution is all you need

3.1. 卷积即一切

Let us consider some mapping $g$ . It is e qui variant under a transformation $L$ if and only if there exists $L^{\prime}$ such that $g\circ L=L^{\prime}\circ g$ . If $L^{\prime}$ is the identity mapping, then the function $g$ is invariant under this transformation. A function of multiple variables is e qui variant when it is e qui variant with respect to each of the variables. In our analysis, we consider only transformations that form a transformation group, in other words, $L\in G$ .

让我们考虑某个映射 $g$。当且仅当存在 $L^{\prime}$ 使得 $g\circ L=L^{\prime}\circ g$ 时，该映射在变换 $L$ 下是等变的。若 $L^{\prime}$ 是恒等映射，则函数 $g$ 在此变换下是不变的。当多元函数对每个变量都具有等变性时，该函数就是等变的。在我们的分析中，仅考虑构成变换群的变换，即 $L\in G$。

Theorem 1. A function given by Equation 1 is e qui variant under a transformation $L$ from group $G$ if and only if $\phi_{X}$ and $\phi_{Z}$ are constructed from $G$ -e qui variant convolutional layers and $\star$ is the $G$ -convolution.

定理 1. 由方程 1 给出的函数在群 $G$ 的变换 $L$ 下是等变的 (equivariant) ，当且仅当 $\phi_{X}$ 和 $\phi_{Z}$ 由 $G$-等变卷积层构成，且 $\star$ 是 $G$-卷积。

The proof of Theorem 2 is given in the supplementary material. A simple interpretation of this theorem is that a tracker is e qui variant to transformations from $G$ if and only if it is fully $G$ -convolutional. The necessity of fullyconvolutional trackers is well-known in tracking community and is related to the ability of the tracker to capture the main variations in the video — the translation. In this paper, we seek to extend this ability to scale variations as well. Which, due to Theorem 2 boils down to using scaleconvolution and building fully scale-translation convolutional trackers.

定理2的证明见补充材料。该定理的一个简单解释是：当且仅当跟踪器是完全$G$-卷积时，它对来自$G$的变换具有等变性。全卷积跟踪器的必要性在跟踪领域众所周知，这与跟踪器捕捉视频中主要变化（即平移）的能力有关。本文旨在将这种能力扩展到尺度变化。根据定理2，这最终归结为使用尺度卷积并构建完全尺度-平移卷积跟踪器。

3.2. Scale Modules

3.2. 规模模块

where cases with $s>1$ are referred to as upscale and with $s~<~1$ as downscale. Standard convolutional layers and convolutional networks are translation e qui variant but not scale-e qui variant [28].

其中，$s>1$ 的情况称为放大，$s~<~1$ 的情况称为缩小。标准卷积层和卷积网络具有平移等变性 (translation e qui variant) ，但不具备尺度等变性 (scale-e qui variant) [28]。

Parametric Scale-Convolution In order to build scalee qui variant convolutional networks, we follow the method proposed by Sosnovik et al. [28]. We begin by choosing a complete basis of functions defined on multiple scales. Choosing the center of the function to be the point $(0,0)$ in coordinates $(u,v)$ , we use functions of the following form:

参数化尺度卷积
为了构建尺度等变卷积网络，我们遵循Sosnovik等人[28]提出的方法。首先选择定义在多尺度上的完备函数基，将函数中心设为坐标$(u,v)$中的点$(0,0)$，采用如下形式的函数：

$$
\psi_{\sigma n m}(u,v)=A\frac{1}{\sigma^{2}}H_{n}\Big(\frac{u}{\sigma}\Big)H_{m}\Big(\frac{v}{\sigma}\Big)e^{-\frac{u^{2}+v^{2}}{2\sigma^{2}}}
$$

$$
\psi_{\sigma n m}(u,v)=A\frac{1}{\sigma^{2}}H_{n}\Big(\frac{u}{\sigma}\Big)H_{m}\Big(\frac{v}{\sigma}\Big)e^{-\frac{u^{2}+v^{2}}{2\sigma^{2}}}
$$

Here $H_{n}$ is a Hermite polynomial of the $n$ -th order, and $A$ is a constant used for normalization. In order to build a basis of $N$ functions, we iterate over increasing pairs of $n$ and $m$ . As the basis is complete, the number of functions $N$ is equal to the number of pixels in the original filter. We build such a basis for a chosen set of equidistant scales $\sigma$ and fix it:

这里 $H_{n}$ 是第 $n$ 阶的 Hermite 多项式，$A$ 是用于归一化的常数。为了构建包含 $N$ 个函数的基组，我们遍历递增的 $n$ 和 $m$ 对。由于基组是完备的，函数数量 $N$ 等于原始滤波器的像素数。我们为选定的一组等距尺度 $\sigma$ 构建这样的基组并固定它：

The result of this operation is a stack of features each of which corresponds to a different scale. We end up with a 3- dimensional representation of the signal — 2-dimensional translation $^+$ scale. We follow [28] and denote scale- convolution as $\star_{H}$ in order to distinguish it with the standard one. Figure 2 demonstrates how a kernel basis is formed and how scale-convolutional layers work.

该操作的结果是一组特征堆栈，每个特征对应不同的尺度。我们最终得到信号的三维表示——二维平移 $^+$ 尺度。我们遵循 [28] 的表示方法，将尺度卷积记为 $\star_{H}$ 以区别于标准卷积。图 2 展示了核基的形成方式以及尺度卷积层的工作原理。

Fast $\textbf{1}\times\textbf{1}$ Scale-Convolution An essential building block of many backbone deep networks such as ResNets [13] and Wide ResNets [36] is a $1\times1$ convolutional layer. We follow the interpretation of these layers proposed in [23] — it is a linear combination of channels. Thus, it has no spatial resolution. In order to build a scale-e qui variant counterpart of $1\times1$ convolution, we do not utilize a kernel basis. As we pointed out before, the signal is stored as a 3 dimensional tensor for each channel. Therefore, for a kernel defined on $N_{S}$ scales, the convolution of the signal with this kernel is just a 3-dimensional convolution with a kernel of size $1\times1$ in spatial dimension, and with $N_{S}$ values in depth. This approach for $1\times1$ scale-convolution is faster than the special case of the algorithm proposed in [28].

快速 $\textbf{1}\times\textbf{1}$ 尺度卷积
ResNets [13] 和 Wide ResNets [36] 等许多主干深度网络的基本构建模块是 $1\times1$ 卷积层。我们遵循 [23] 提出的解释——它是通道的线性组合，因此不具备空间分辨率。为了构建 $1\times1$ 卷积的尺度等变对应物，我们不使用核基。如前所述，每个通道的信号存储为三维张量。因此，对于在 $N_{S}$ 个尺度上定义的核，信号与该核的卷积仅是一个空间维度为 $1\times1$、深度为 $N_{S}$ 值的三维卷积。这种 $1\times1$ 尺度卷积方法比 [28] 提出的算法特例更快。

Padding Although zero padding is a standard approach in image classification for saving the spatial resolution of the image, it worsens the localization properties of convolutional trackers [21, 38]. Nevertheless, a simple replacement of standard convolutional layers with scale-e qui variant ones in very deep models is not possible without padding. Scalee qui variant convolutional layers have kernels of a bigger spatial extent because they are defined on multiple scales. For these reasons, we use circular padding during training and zero padding during testing in our models.

填充
尽管零填充 (zero padding) 是图像分类中用于保持图像空间分辨率的常规方法，但它会削弱卷积跟踪器的定位性能 [21, 38]。然而，在极深度模型中，若完全不使用填充，则无法直接用尺度等变 (scale-equivariant) 卷积层替换标准卷积层。由于尺度等变卷积层在多尺度上定义，其核具有更大的空间范围。因此，我们在模型训练时采用循环填充 (circular padding)，测试时使用零填充。

The introduced padding does not affect the feature maps which are obtained with kernels defined on small scales. It does not violate the translation e qui variance of a network. We provide an experimental proof in supplementary material.

引入的填充不会影响由小尺度核定义的特征图，且不会破坏网络的平移等变性。补充材料中提供了实验证明。

Kernels of convolutional layers are para met rize d by trainable weights $w$ in the following way:

卷积层的核 (kernel) 通过可训练权重 $w$ 以下列方式进行参数化:

$$
\kappa_{\sigma}=\sum_{i}\Psi_{\sigma i}w_{i}
$$

$$
\kappa_{\sigma}=\sum_{i}\Psi_{\sigma i}w_{i}
$$

Scale-Pooling In order to capture correlations between different scales and to transform a 3-dimensional signal into a 2-dimensional one, we utilize global max pooling along the scale axis. This operation does not eliminate the scale-e qui variant properties of the network. We found that it is useful to additionally incorporate this module in the places where conventional CNNs have spatial max pooling or strides. The mechanism of scale-pooling is illustrated in Figure 2.

尺度池化
为了捕捉不同尺度间的相关性并将三维信号转换为二维信号，我们沿尺度轴采用全局最大池化。该操作不会破坏网络的尺度等变性。我们发现，在传统CNN使用空间最大池化或步长的位置额外引入该模块具有积极作用。尺度池化机制如图2所示。

Here $L_{s}$ is rescaling implemented as bicubic interpolation. Although it is a relatively slow operation, it is used only once in the tracker and does not heavily affect the inference time. The proof of the e qui variance of this convolution is provided in supplementary material.

这里 $L_{s}$ 是通过双三次插值 (bicubic interpolation) 实现的缩放操作。尽管这是一个相对较慢的运算，但它在跟踪器中仅使用一次，不会显著影响推理时间。该卷积的等变性证明详见补充材料。

3.3. Extending a Tracker to Scale E qui variance

3.3. 扩展跟踪器以实现尺度等变性

We present a recipe to extend a tracker to scale equivariance.

我们提出了一种扩展跟踪器以实现尺度等变性的方法。

The obtained tracker produces a heatmap $h(z,x)$ defined on scale and translation. Therefore, each position is assigned a vector of features that has both the measure of similarity and the scale relation between the candidate and the template. If additional scale-pooling is included, then all scale information is just aggregated in the similarity score.

获得的跟踪器生成一个定义在尺度和平移上的热图 $h(z,x)$。因此，每个位置都被分配了一个特征向量，该向量既包含候选与模板之间的相似度度量，也包含它们之间的尺度关系。如果包含额外的尺度池化(scale-pooling)，那么所有尺度信息就仅聚合在相似度分数中。

Note that the overall structure of the tracker, as well as the training and inference procedures are not changed. Thus, the recipe allows for a simple extension of a tracker with little cost of modification.

需要注意的是，跟踪器的整体结构以及训练和推理流程均未改变。因此，该方案只需对跟踪器进行简单扩展，修改成本极低。

4. Scale-E qui variant SiamFC

4. 尺度等变 SiamFC

While the proposed algorithm is applicable to a wide range of trackers, in this work, we focus on Siamese trackers. As a baseline we choose SiamFC [2]. This model serves as a starting point for modifications for the many modern high-performance Siamese trackers.

虽然所提出的算法适用于多种跟踪器，但在本工作中我们主要关注孪生网络跟踪器。作为基线，我们选择了SiamFC [2]。该模型是许多现代高性能孪生跟踪器进行修改的起点。

4.1. Architecture

4.1. 架构

Given the recipe, here we discuss the actual implementation of the scale-e qui variant SiamFC tracker (SE-SiamFC).

根据该方案，我们在此讨论尺度均衡变体SiamFC跟踪器(SE-SiamFC)的实际实现。

In the first step of the recipe, we assess the range of scales in the domain (dataset). In sequences presented in most of the tracking benchmarks, like OTB or VOT, objects change their size relatively slowly from one frame to the other. The maximum scale change usually does not exceed a factor of $1.5-2$ . Therefore, we use 3 scales with a step of $\sqrt{2}$ as the basis for the scale-convolutions. The next step in the recipe is to represent the tracker as it is done in Equation 1. SiamFC localizes the object as the coordinate argmax of the heatmap $h(z,x)=\phi_{Z}(z)\star\phi_{X}(x)$ , where $\phi_{Z}~=~\phi_{X}$ are convolutional Siamese backbones. Next, in step number 3, we modify the backbones by replacing standard convolutions by scale-e qui variant convolutions. We follow step 4 and utilize scale-pooling in the backbones in order to capture additional scale correlations between features of various scales. According to step 5, the connecting correlation is replaced with non-parametric scale-convolution. SiamFC computes its similarity function as a 2-dimensional map, therefore, we follow step 6 and add extra scale-pooling in order to transform a 3-dimensional heatmap into a 2-dimensional one. Now, we can use exactly the same inference algorithm as in the original paper [2]. We use the standard approach of scale estimation, based on the greedy selection of the best similarity for 3 different scales.

在配方的第一步中，我们评估了领域(数据集)中的尺度范围。在大多数跟踪基准测试(如OTB或VOT)呈现的序列中，物体在帧与帧之间的尺寸变化相对缓慢。最大尺度变化通常不超过1.5-2倍。因此，我们使用步长为√2的3个尺度作为尺度卷积的基础。配方的下一步是将跟踪器表示为公式1中的形式。SiamFC通过热图h(z,x)=φZ(z)⋆φX(x)的坐标argmax来定位目标，其中φZ=φX是卷积孪生骨干网络。接着，在第三步中，我们通过用尺度等变卷积替换标准卷积来修改骨干网络。我们执行第四步，在骨干网络中使用尺度池化以捕获不同尺度特征之间的额外尺度相关性。根据第五步，连接相关性被替换为非参数尺度卷积。由于SiamFC将其相似度函数计算为二维映射，因此我们遵循第六步并添加额外的尺度池化，将三维热图转换为二维热图。现在，我们可以使用与原论文[2]完全相同的推理算法。我们采用基于3种不同尺度的最佳相似度贪婪选择的标准尺度估计方法。

4.2. Weight Initialization

4.2. 权重初始化

An important ingredient of a successful model training is the initialization of its weights. A common approach is to use weights from an Imagenet [9] pre-trained model [22, 38, 21]. In our case, however, this requires additional steps, as there are no available scale-e qui variant models pretrained on the Imagenet. We present a method for initializing a scale-e qui variant model with weights from a pretrained conventional CNN. The key idea is that a scalee qui variant network built according to Section 3.3 contains a sub-network that is identical to the one of the non-scalee qui variant counterpart. As the kernels of scale-e qui variant models are parameterized with a fixed basis and trainable weights, our task is to initialize these weights.

成功训练模型的一个重要因素是其权重的初始化。常见方法是使用在ImageNet [9]上预训练模型的权重[22, 38, 21]。然而，在我们的案例中，由于没有可用的在ImageNet上预训练的尺度等变(scale-e qui variant)模型，这需要额外的步骤。我们提出了一种方法，用于利用预训练的传统CNN权重来初始化尺度等变模型。关键思想是，根据第3.3节构建的尺度等变网络包含一个与非尺度等变对应网络完全相同的子网络。由于尺度等变模型的卷积核是通过固定基和可训练权重参数化的，我们的任务是初始化这些权重。

We begin by initializing the inter-scale correlations by setting to 0 all weights responsible for these connections.

我们首先通过将所有负责这些连接的权重设为0来初始化跨尺度相关性。

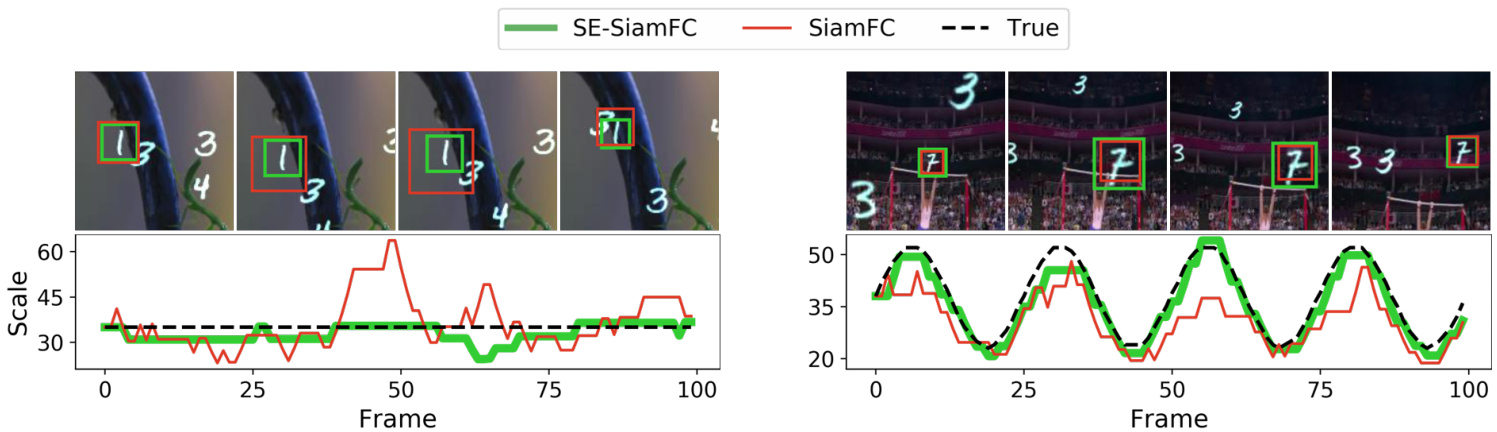
Figure 3: Top: examples of simulated T-MNIST and S-MNIST sequences. Bottom: scale estimation for e qui variant and non-e qui variant models. In the S-MNIST example, SE-SiamFC can estimate the scale more accurately. In the T-MNIST example, our model better preserves the scale of the target unchanged, while the non-scale-e qui variant model is prone to oscillations in its scale estimate.

图 3: 上: 模拟T-MNIST和S-MNIST序列的示例。下: 等变与非等变模型的尺度估计结果。在S-MNIST示例中，SE-SiamFC能更准确地估计尺度。在T-MNIST示例中，我们的模型能更好地保持目标尺度不变，而非尺度等变模型的尺度估计容易出现振荡。

At this moment, up to scale-pooling, the scale-e qui variant model consists of several networks parallel to, yet disconnected from one another, where the only difference is the size of their filters. For the convolutional layers with a nonunitary spatial extent, we initialize the weights such that the kernels of the smallest scale match those of the source model. Given a source kernel $\kappa^{\prime}(u,v)$ and a basis $\Psi_{\sigma i}(u,v)$ with $\sigma=1$ , weights $w_{i}$ are chosen to satisfy the linear system derived from Equation 5:

此时，在尺度池化之前，尺度等变模型由多个并行但彼此独立的网络组成，这些网络唯一的区别在于滤波器尺寸。对于具有非单位空间范围的卷积层，我们初始化权重使最小尺度的核与源模型匹配。给定源核 $\kappa^{\prime}(u,v)$ 和基 $\Psi_{\sigma i}(u,v)$ (其中 $\sigma=1$)，选择权重 $w_{i}$ 以满足由公式5导出的线性系统：

$$
\kappa_{1}(u,v)=\sum_{i}\Psi_{1i}(u,v)w_{i}=\kappa^{\prime}(u,v),\quad\forall u,v
$$

$$
\kappa_{1}(u,v)=\sum_{i}\Psi_{1i}(u,v)w_{i}=\kappa^{\prime}(u,v),\quad\forall u,v
$$

As the basis is complete by construction, its matrix form is invertible. The system has a unique solution with respect to $w_{i}$ :

由于该基在构造上是完备的，其矩阵形式可逆。该系统关于 $w_{i}$ 存在唯一解：

$$
w_{i}=\sum_{u,v}\Psi_{1i}^{-1}(u,v)\kappa^{\prime}(u,v)
$$

$$
w_{i}=\sum_{u,v}\Psi_{1i}^{-1}(u,v)\kappa^{\prime}(u,v)
$$

All $1\times1$ scale-convolutional layers are identical to standard $1\times1$ convolutions after zeroing out inter-scale correlations. We copy these weights from the source model. We provide an additional illustration of the proposed initialization method in the supplementary material.

所有 $1\times1$ 尺度卷积层在消除尺度间相关性后与标准 $1\times1$ 卷积层完全相同。我们直接从源模型复制这些权重。补充材料中提供了所提初始化方法的额外图示说明。

5. Experiments and Results

5. 实验与结果

5.1. Translation-Scaling MNIST

5.1. 平移缩放MNIST

To test the ability of a tracker to cope with translation and scaling, we conduct an experiment on a simu- lated dataset with controlled factors of variation. We construct the datasets of translating (T-MNIST) and translatingscaling (S-MNIST) digits.

为了测试跟踪器处理平移和缩放的能力，我们在一个模拟数据集上进行了实验，该数据集控制了变化因素。我们构建了平移数字(T-MNIST)和平移缩放数字(S-MNIST)的数据集。

In particular, to form a sequence, we randomly sample up to 8 MNIST digits with backgrounds from the GOT10k

特别是，为了形成一个序列，我们从GOT10k中随机采样最多8个带有背景的MNIST数字。

Tracker	T/T	T/S	S/T	S/S	#Params
SiamFC	0.64	0.62	0.64	0.63	999 K
SE-SiamFC	0.76	0.69	0.77	0.70	999 K

Table 1: AUC for models trained on T-MNIST and SMNIST. T/S indicates that the model was trained on TMNIST and tested on S-MNIST datasets. Bold numbers represent the best result for each of the training/testing scenarios.

表 1: 在 T-MNIST 和 SMNIST 上训练模型的 AUC 值。T/S 表示模型在 TMNIST 上训练并在 S-MNIST 数据集上测试。加粗数字代表每种训练/测试场景中的最佳结果。

dataset [16]. Then, on each of the digits in the sequence independent ly, a smoothed Brownian motion model induces a random translation. Simultaneously, for S-MNIST, a smooth scale change in the range [0.67, 1.5] is induced by the sine rule:

数据集 [16]。然后，对于序列中的每个数字独立地，平滑布朗运动模型会引入随机平移。同时，对于S-MNIST，通过正弦规则在[0.67, 1.5]范围内引入平滑的尺度变化：

$$
s_{i}(t)=\frac{h-l}{2}\big[\sin(\frac{t}{4}+\beta_{i})+1)\big]+l
$$

$$
s_{i}(t)=\frac{h-l}{2}\big[\sin(\frac{t}{4}+\beta_{i})+1)\big]+l
$$

where $s_{i}(t)$ is the scale factor of the $i$ -th digit in the $t$ -th frame, $h,l$ are upper and lower bounds for scaling, and $\beta_{i}\in$ $[0,100]$ is a phase, sampled randomly for each of the digits. In total, we simulate 1000 sequences for training and 100 for validation. Each sequence has a length of 100 frames. We compare two configurations of the tracker: (i) SiamFC with a shallow backbone and (ii) its scale-e qui variant version SE-SiamFC. We conduct the experiments acco