Multi-View Hyper complex Learning for Breast Cancer Screening
多视角超复数学习在乳腺癌筛查中的应用
Abstract—Traditionally, deep learning methods for breast cancer classification perform a single-view analysis. However, radiologists simultaneously analyze all four views that compose a mammography exam, owing to the correlations contained in mammography views, which present crucial information for identifying tumors. In light of this, some studies have started to propose multi-view methods. Nevertheless, in such existing architectures, mammogram views are processed as independent images by separate convolutional branches, thus losing correlations among them. To overcome such limitations, in this paper, we propose a methodological approach for multi-view breast cancer classification based on parameterized hyper complex neural networks. Thanks to hyper complex algebra properties, our networks are able to model, and thus leverage, existing correlations between the different views that comprise a mammogram, thus mimicking the reading process performed by clinicians. This happens because hyper complex networks capture both global properties, as standard neural models, as well as local relations, i.e., inter-view correlations, which real-valued networks fail at modeling. We define architectures designed to process two-view exams, namely PHResNets, and four-view exams, i.e., PHYSEnet and PHYBOnet. Through an extensive experimental evaluation conducted with publicly available datasets, we demonstrate that our proposed models clearly outperform real-valued counterparts and state-of-the-art methods, proving that breast cancer classification benefits from the proposed multi-view architectures. We also assess the method general iz ability beyond mammogram analysis by considering different benchmarks, as well as a finerscaled task such as segmentation. Full code and pretrained models for complete reproducibility of our experiments are freely available at https://github.com/ispamm/PHBreast.
摘要—传统上，用于乳腺癌分类的深度学习方法仅进行单视图分析。然而，由于乳腺X光检查视图间存在相关性，放射科医师会同时分析构成乳腺X光检查的所有四个视图，这些相关性为识别肿瘤提供了关键信息。鉴于此，一些研究开始提出多视图方法。然而，在此类现有架构中，乳腺X光视图被独立的卷积分支作为独立图像处理，从而丢失了它们之间的相关性。为克服这些限制，本文提出了一种基于参数化超复数神经网络的多视图乳腺癌分类方法。得益于超复数代数特性，我们的网络能够建模并利用构成乳腺X光的不同视图间的现有相关性，从而模拟临床医生的阅片过程。这是因为超复数网络既能像标准神经模型一样捕获全局属性，又能捕获实值网络无法建模的局部关系（即视图间相关性）。我们定义了处理双视图检查的架构PHResNets，以及处理四视图检查的架构PHYSEnet和PHYBOnet。通过在公开数据集上进行的广泛实验评估，我们证明所提模型明显优于实值对应模型和最先进方法，证实乳腺癌分类能从所提多视图架构中受益。我们还通过考虑不同基准测试及更精细的分割任务，评估了该方法在乳腺X光分析之外的泛化能力。实验完整复现所需的全部代码和预训练模型已开源：https://github.com/ispamm/PHBreast。
Index Terms—Multi-View Learning, Hyper complex Neural Networks, Hyper complex Algebra, Breast Cancer Screening
索引术语 - 多视图学习 (Multi-View Learning)、超复数神经网络 (Hypercomplex Neural Networks)、超复数代数 (Hypercomplex Algebra)、乳腺癌筛查 (Breast Cancer Screening)
I. INTRODUCTION
I. 引言
Among the different types of cancer that affect women worldwide, breast cancer alone accounts for almost one-third, making it by far the cancer with highest incidence among women [1]. For this reason, early detection of this disease is of extreme importance and, to this end, screening mammography is performed annually on all women above a certain age [2], [3]. During a mammography exam, two views of the breast are taken, thus capturing it from above, i.e., the cr a nio caudal (CC) view, and from the side, i.e., the medio lateral oblique (MLO) view. More in detail, the CC and MLO views of the same breast are known as ips i lateral views, while the same view of both breasts as bilateral views. Importantly, when reading a mammogram, radiologists examine the views by performing a double comparison, that is comparing ips i lateral views along with bilateral views, as each comparison provides valuable information. Such multi-view analysis has been found to be essential in order to make an accurate diagnosis of breast cancer [4], [5].
在全球影响女性的各类癌症中，仅乳腺癌就占近三分之一，成为目前女性发病率最高的癌症 [1]。因此，该疾病的早期检测至关重要。为此，所有达到特定年龄的女性每年都要接受乳腺X光筛查 [2][3]。
乳腺X光检查会拍摄乳房的两种视图：从上向下拍摄的头尾位 (CC) 视图，以及从侧面拍摄的内外侧斜位 (MLO) 视图。具体而言，同一乳房的CC和MLO视图称为同侧视图，而双侧乳房的相同视图则称为双侧视图。值得注意的是，放射科医生在解读乳腺X光片时，会通过双重对比进行分析——既比较同侧视图，又比较双侧视图，因为每种对比都能提供有价值的信息。研究发现，这种多视图分析对于准确诊断乳腺癌至关重要 [4][5]。
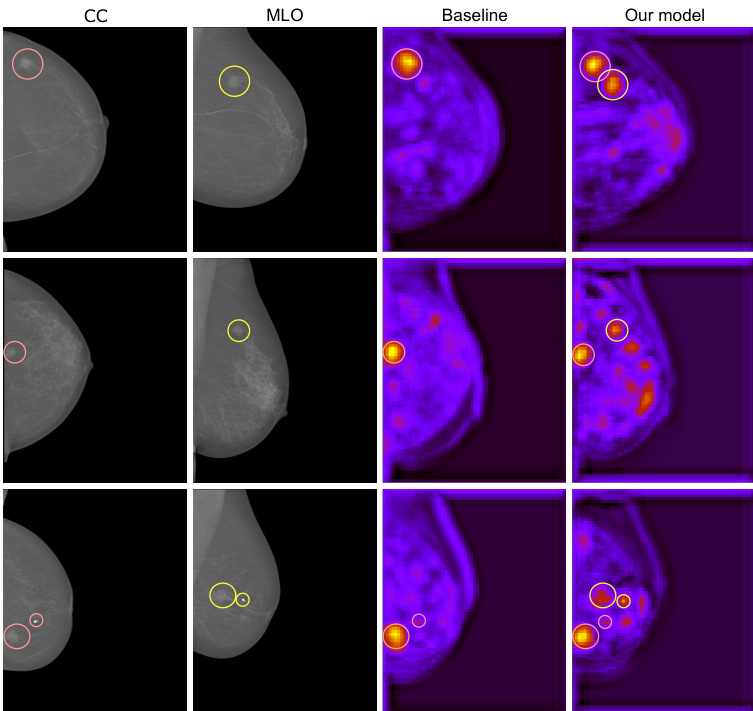
Fig. 1. Visualization of hyper complex multi-view learning. In the figure, there are the two views (CC and MLO) corresponding to one breast containing a malignant mass (highlighted in red and green in the respective views). Then, we show the activation maps of a baseline, i.e. the real-valued counterpart of our network (SEnet), and the proposed hyper complex architecture (PHYSEnet). Unlike the network in the real domain, ours learns from both views as it is visible that there are highlighted areas corresponding to both views.
图 1: 超复数多视图学习的可视化示意图。图中展示了包含恶性肿块（分别在CC和MLO视图中用红色和绿色高亮显示）的同一乳房对应的两个视图。随后，我们展示了基线模型（即我们网络中实值对应的SEnet）与提出的超复数架构（PHYSEnet）的激活图。与实域网络不同，我们的模型能从两个视图中学习，这体现在激活图中同时存在对应两个视图的高亮区域。
Recently, many works are employing deep learning (DL)- based methods in the medical field and, especially, for breast cancer classification and detection with encouraging results [6]–[17]. Inspired by the multi-view analysis performed by radiologists, several recent studies try to adopt a multi-view architecture in order to obtain a more robust and performing model [18]–[29].
近来，许多研究在医学领域采用基于深度学习 (DL) 的方法，特别是在乳腺癌分类和检测方面取得了令人鼓舞的成果 [6]–[17]。受放射科医师多视角分析的启发，近期多项研究尝试采用多视角架构以获得更鲁棒且性能更优的模型 [18]–[29]。
The general approach taken by these works consists in designing a neural network with different branches dedicated to processing the different views. However, there are several issues associated with this procedure. To begin with, a recent study [19] observes that this kind of model can favor one of the two views during learning, thus not truly taking advantage of the multi-view input. Additionally, the model might fail entirely in leveraging the correlated views and actually worsen the performance with respect to its single-view counterpart [19], [30]. Thus, it is made clear that improving the ability of deep networks to truly exploit the information contained in multiple views is still a largely open research question. To address and overcome these problems, we employ a novel technique in deep learning that relies on exotic algebraic systems, such as qua tern ions and, more in general, hyper complex ones.
这些研究采用的通用方法是设计一个具有不同分支的神经网络，专门用于处理不同视图。然而，这种方法存在若干问题。首先，最近的一项研究 [19] 指出，这类模型在学习过程中可能会偏向其中一个视图，从而无法真正利用多视图输入的优势。此外，模型可能完全无法利用相关视图，甚至导致性能比单视图版本更差 [19][30]。因此，如何提升深度网络真正利用多视图中信息的能力，仍然是一个亟待解决的研究问题。为解决并克服这些问题，我们采用了一种依赖非常规代数系统（如四元数及更广义的超复数）的深度学习新技术。
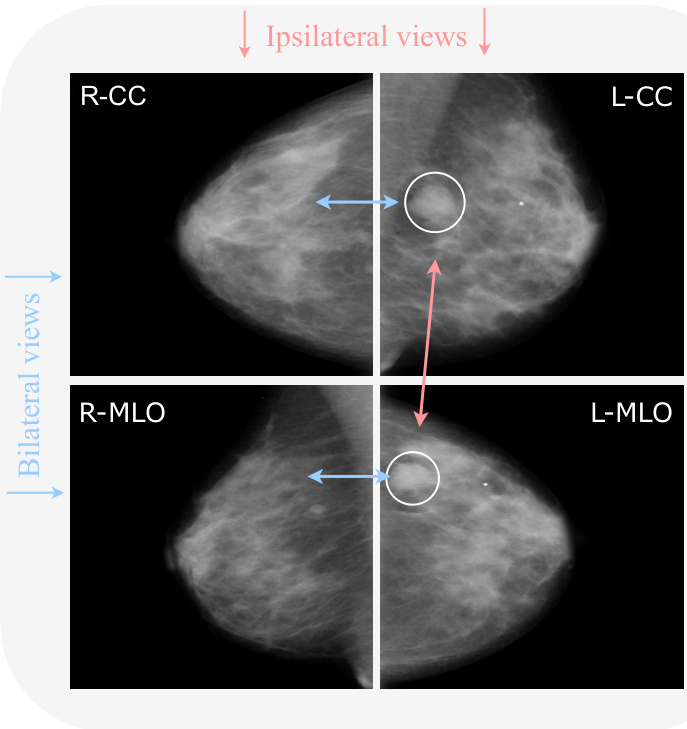
Fig. 2. Example of a mammography exam from the CBIS-DDSM dataset with the four views: left CC (L-CC), right CC (R-CC), left MLO (L-MLO), and right MLO (R-MLO). Horizontal couples are bilateral views (blue), while vertical couples are ips i lateral views (red). Arrows indicate the relations among views. Bilateral relations reveal an asymmetry (as there is a mass on the left that is not present on the right. Ips i lateral relations give a better view of the specific mass.
图 2: CBIS-DDSM数据集中乳腺X光检查的示例，包含四个视图：左头尾位 (L-CC)、右头尾位 (R-CC)、左斜侧位 (L-MLO) 和右斜侧位 (R-MLO)。水平成对的是双侧视图 (蓝色)，垂直成对的是同侧视图 (红色)。箭头表示视图之间的关系。双侧关系显示出不对称性 (因为左侧有一个肿块而右侧没有)。同侧关系提供了该肿块的更清晰视图。
In recent years, quaternion neural networks (QNNs) have gained a lot of interest in a variety of applications [31]–[36]. The reason for this is the particular properties that characterize these models. As a matter of fact, thanks to the quaternion algebra rules on which these models are based (e.g., the Hamilton product), quaternion networks possess the capability of modeling interactions between input channels. Thus, they capture internal latent relations within them and additionally reduce the total number of parameters by $75%$ , while still attaining comparable performance to their real-valued counterparts. Furthermore, built upon the idea of QNNs, the recent parameterized hyper complex neural networks (PHNNs) generalize hyper complex multiplications as a sum of $n$ Kronecker products, where $n$ is a hyper parameter that controls in which domain the model operates [37], [38], going beyond quaternion algebra. Thus, they improve previous shortcomings by making these models applicable to any $n$ -dimensional input (instead of just 3D/4D as the quaternion domain) thanks to the introduction of the parameterized hyper complex multiplication (PHM) and convolutional (PHC) layer [37], [38].
近年来，四元数神经网络(QNNs)在各类应用中引起了广泛关注[31]–[36]。这源于该模型独特的性质：基于四元数代数规则(如Hamilton积)构建的网络能够建模输入通道间的交互关系，从而捕捉其内部潜在关联，并将参数量减少75%，同时保持与实数网络相当的性能。进一步地，基于QNNs思想提出的参数化超复数神经网络(PHNNs)将超复数乘法推广为n个Kronecker积之和，其中n作为超参数控制模型运算域[37][38]，突破了四元数代数的限制。通过引入参数化超复数乘法(PHM)和卷积(PHC)层[37][38]，这类模型可适用于任意n维输入(而非仅限于3D/4D的四元数域)，从而改进了先前局限。
Motivated by the problems mentioned above and the benefits of hyper complex models, we propose a framework of multi-view learning for breast cancer classification based on PHNNs, taking a completely different approach with respect to the literature. More in detail, we propose a family of parameterized hyper complex ResNets (PHResNets) able to process ips i lateral views corresponding to one breast, i.e., two views. Additionally, we design two parameterized hypercomplex networks for four views, namely PHYBOnet and PHYSEnet. PHYBOnet involves a bottleneck with $n=4$ to process learned features in a joint fashion, performing a patient-level analysis. Instead, PHYSEnet is characterized by a shared encoder with $n=2$ to learn stronger representations of the ips i lateral views by sharing the weights between bilateral ones, focusing on a breast-level analysis.
受到上述问题和超复数模型优势的启发，我们提出了一种基于PHNNs的多视角乳腺癌分类框架，这与文献中的方法完全不同。具体而言，我们提出了一系列参数化超复数ResNet（PHResNet）模型，能够处理对应于单侧乳房（即两个视角）的同侧视图。此外，我们还设计了两种用于四视角的参数化超复数网络：PHYBOnet和PHYSEnet。PHYBOnet采用$n=4$的瓶颈结构以联合方式处理学习到的特征，实现患者级别的分析；而PHYSEnet则通过$n=2$的共享编码器，在双侧视图间共享权重来学习更强的同侧视图表征，侧重于乳房级别的分析。
The advantages of our approach are manifold. Firstly, instead of handling the m ammo graphic views independently, which results in losing significant correlations, our models process them as a unique component, without breaking the original nature of the exam. Secondly, thanks to hyper complex algebra properties, the proposed models are endowed with the capability of preserving existing latent relations between views by modeling and capturing their interactions, as shown in Fig. 1. In fact, hyper complex networks have been shown to effectively model not only global relations as standard deep learning networks but also local relations [32]. In the context of the mammography exam, these local relations are essential since they represent the complementary information contained in the multiple views, which are critical for a correct diagnosis and represent a fundamental step of the reading process performed by radiologists [4], [5]. In this sense, with the proposed approach in the hyper complex domain, we can say that our networks mimic the examination process of radiologists in real-life settings. Thirdly, our parameterized hyper complex networks are characterized by the number of free parameters halved, when $n=2$ , and reduced by $1/4$ , when $n=4$ , with respect to their real-valued counterparts. Finally, our proposed approach is both portable and flexible. It can be seamlessly applied to other medical exams involving multiple views or modalities, signifying its portability. Furthermore, any neural network can be easily defined within the hyper complex domain by simply integrating PHC layers, thus highlighting its flexibility. To the best of our knowledge, this is the first time that hyper complex models have been investigated for multi-view medical exams, particularly in the context of mammography.
我们方法的优势是多方面的。首先，与独立处理乳腺钼靶视图(这会导致重要相关性丢失)不同，我们的模型将其作为独特组件处理，同时保持检查的原始特性。其次，得益于超复数代数特性，所提模型能够通过建模和捕获视图间交互来保持潜在的现有关系，如图1所示。实际上，超复数网络不仅能像标准深度学习网络那样有效建模全局关系，还能建模局部关系[32]。在乳腺钼靶检查中，这些局部关系至关重要，因为它们代表了多视图包含的互补信息——这对正确诊断至关重要，也是放射科医师阅片过程的基本步骤[4][5]。就此而言，采用超复数域的所提方法，可以说我们的网络模拟了现实环境中放射科医师的检查过程。第三，当$n=2$时，我们的参数化超复数网络自由参数数量减半；当$n=4$时，参数数量减少$1/4$（相较于实数域对应模型）。最后，所提方法兼具可移植性和灵活性：它能无缝应用于其他涉及多视图或多模态的医学检查，体现其可移植性；此外，通过简单集成PHC层，任何神经网络都能轻松在超复数域中定义，彰显其灵活性。据我们所知，这是首次将超复数模型应用于多视图医学检查(尤其是乳腺钼靶)的研究。
We evaluate the effectiveness of our approach on two publicly available benchmark datasets of mammography images, namely CBIS-DDSM [39] and INbreast [2]. We conduct a meticulous experimental evaluation that demonstrates how our proposed models, owing to the aforementioned abilities, possess the means for properly leveraging information contained in multiple m ammo graphic views and thus exceed the performance of both real-valued baselines and state-of-the-art methods. Finally, we further validate the proposed method on two additional benchmark datasets, i.e., Chexpert [40] for chest $\mathrm{\DeltaX}$ -rays and BraTS19 [41], [42] for brain MRI, to prove the general iz ability of the proposed approach in different applications and medical exams, going beyond mammograms and classification.
我们在两个公开可用的乳腺X光影像基准数据集上评估了所提方法的有效性，分别是CBIS-DDSM [39]和INbreast [2]。通过细致的实验验证，我们证明了所提出的模型凭借前文所述能力，能够有效利用多视角乳腺X光影像中的信息，其性能不仅超越了实数基线方法，更优于当前最先进的技术。此外，我们还在另外两个基准数据集上进行了进一步验证：用于胸部X光的Chexpert [40]和用于脑部MRI的BraTS19 [41][42]，以此证明该方法在乳腺X光分类之外的多种医学影像应用场景中具有普适性 (generalizability)。
The rest of the paper is organized as follows. Section II gives a detailed overview of the multi-view approach for breast cancer analysis, delving into why it is important to design a painstaking multi-view method. Section III provides theoretical aspects and concepts of hyper complex models, and Section IV presents the proposed method. The experiments are set up in Section V and evaluated in Section VI. A summary of the proposed models with specific data cases is provided in Section VIII, while conclusions are drawn in Section IX.
本文其余部分组织结构如下。第II节详细概述了乳腺癌分析的多视角方法，深入探讨为何需要精心设计多视角方法。第III节介绍超复数模型的理论基础和概念，第IV节阐述所提出的方法。实验设置见第V节，评估结果见第VI节。第VIII节通过具体数据案例对所提模型进行总结，第IX节给出结论。
II. MULTI-VIEW APPROACH IN BREAST CANCERANALYSIS
II. 乳腺癌分析中的多视角方法
There exist several types of medical exams for the detection process of breast cancer, such as mammography, ultrasound, biopsy, and so on. Among these, mammography is considered the best imaging method for breast cancer screening and the most effective for early detection [3]. A mammography exam comprises four X-ray images produced by the recording of two views for each breast: the CC view, which is a top to bottom view, and the MLO view, which is a side view. The diagnosis procedure adopted by radiologists consists in looking for specific abnormalities, the most common being masses, calcification s, architectural distortions of breast tissue, and a symmetries [2]. During the reading of a mammography exam, employing multiple views is crucial in order to make an accurate diagnosis, as they retain highly correlated characteristics, which, in reality, represent complementary information. Admittedly, comparing ips i lateral views (CC and MLO views of the same breast) helps to detect eventual tumors, as sometimes they are visible only in one of the two views, and additionally helps to analyze the 3D structure of masses. Whereas, studying bilateral views (same view of both breasts) helps to locate masses as a symmetries between them are an indicating factor [5]. An example of a complete mammogram exam with ips i lateral and bilateral views is shown in Fig. 2.
乳腺癌检测过程中存在多种医学检查方法，如乳腺X线摄影（mammography）、超声检查、活组织检查等。其中，乳腺X线摄影被视为乳腺癌筛查的最佳影像学方法，也是早期检测最有效的手段[3]。一次乳腺X线检查包含四张X光图像，通过每侧乳房两个视角拍摄获得：CC位（自上而下视角）和MLO位（侧视角）。放射科医师采用的诊断流程需寻找特定异常表现，最常见包括肿块、钙化灶、乳腺组织结构扭曲以及不对称征[2]。
解读乳腺X线影像时，采用多视角对比对精准诊断至关重要，因为这些视角间存在高度关联特征，实际构成互补信息。公认的是，同侧视图（同一乳房的CC位与MLO位）对比有助于发现潜在肿瘤（某些情况下肿瘤仅在单一视角可见），并能辅助分析肿块的三维结构；而双侧视图（双乳相同视角）对比则可通过不对称征象定位肿块，此类不对称具有指示意义[5]。图2展示了一个包含同侧与双侧视图的完整乳腺X线检查示例。
Given the multi-view nature of the exam and the multi-view approach employed by radiologists, many works are focusing on utilizing two or four views for the purpose of classifying breast cancer, with the goal of leveraging the information coming from ips i lateral and/or bilateral views. Indeed, studies have shown that a model employing multiple views can learn to generalize better compared to its single-view counterpart, increasing its disc rim i native power, while also reducing the number of false positives and false negatives [6], [9], [18].
考虑到乳腺检查的多视角特性以及放射科医师采用的多视角诊断方法，许多研究致力于利用双视角或四视图进行乳腺癌分类，旨在整合同侧和/或双侧乳腺影像的信息。研究表明，与单视角模型相比，多视角模型能够提升泛化能力、增强判别力，同时降低假阳性与假阴性率 [6] [9] [18]。
Several works show the advantages of leveraging multiple views by adopting simple approaches. For instance, one approach involves simply averaging the predictions generated by the same model when provided with two ips i lateral views [6], which can be classified as a late-fusion approach. However, late-fusion methods ignore local interactions between views [29]. In contrast to late-fusion, also early-fusion techniques have been employed. These techniques involve the concatenation of feature vectors into a single vector [43]. Nevertheless, the issue with early fusion is that it treats the resulting vector as a unimodal input, potentially failing to fully exploit the complementary nature of the views [44], [45]. Instead, more complex approaches consist in designing multi-view architectures that exploit correlations for learning and not just at inference time, like late-fusion methods. Recent techniques such as these propose architectures comprising multiple convolutional neural networks (CNNs) paths or columns, where each column processes a different view and their output is subsequently concatenated together and fed to a number of fully connected layers to obtain the final output [18]–[25]. A recent paper proposes an approach to utilize the complete mammography exam, thus comprised of four views [18]. Alternatively, a number of works [20]–[22], [26] adopt the same idea of having multiple columns but instead focus on using just two ips i lateral views.
多项研究表明，采用简单方法利用多视图具有优势。例如，一种方法仅对同一模型提供的双侧视图预测结果进行平均处理[6]，可归类为后融合(late-fusion)方法。但后融合方法忽略了视图间的局部交互[29]。与后融合不同，早期融合技术也被采用，其通过将特征向量拼接为单一向量实现[43]。然而早期融合的问题在于将结果向量视为单模态输入，可能无法充分利用视图的互补特性[44][45]。更复杂的方法则是设计多视图架构，不仅在推理阶段、更在学习阶段利用视图相关性。这类最新技术提出包含多个卷积神经网络(CNN)路径或分支的架构，每个分支处理不同视图，输出结果经拼接后输入全连接层获得最终输出[18][25]。近期有论文提出利用完整乳腺X光检查（含四个视图）的方法[18]。另有多项研究[20][22][26]采用相同多分支思路，但仅聚焦于使用双侧视图。
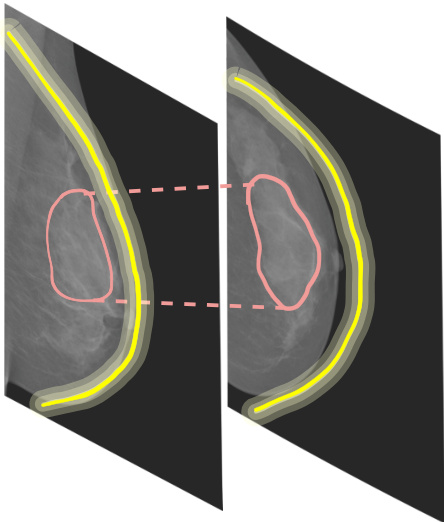
Fig. 3. Global and local relations. Global relations are intra-view features, e.g., the shape of the breast (depicted in shades of yellow). Local relations are inter-view features, e.g., textures (depicted in red).
图 3: 全局与局部关系。全局关系是视图内部特征 (如乳房的形状，用黄色阴影表示)。局部关系是视图间特征 (如纹理，用红色表示)。
Even though multimodal methods have been employed in a variety of recent deep learning works for breast cancer analysis, not much attention has been paid to how the DL model actually leverages information contained in the multiple views. Indeed, a recent study shows that such multimodal approaches might actually fail to exploit such information, leading to a counter-intuitive situation in which the single-view counterpart outperforms the multi-view one [19]. Therefore, just employing an architecture with multiple columns for each view is not enough to really leverage the knowledge coming from the correlated inputs [19]. Even in other applications of multimodal learning (e.g., involving speech or text), it is a common phenomenon that DL networks that are not properly modeled, fail to utilize the information contained in the different input modalities [30]. Although the context may differ, this underlying issue is a common concern in the multimodal and multi-view scenarios. Therefore, when processing multi-view exams, a painstaking and meticulous method has to be developed. To this end, we propose a method based on hyper complex algebra, whose properties are described in the following sections.
尽管多模态方法已广泛应用于近期乳腺癌分析的深度学习研究中，但人们很少关注深度学习模型如何真正利用多视角中包含的信息。事实上，最新研究表明，这类多模态方法可能实际上未能有效利用此类信息，导致单视角模型反超多视角模型的违反直觉现象 [19]。因此，仅采用为每个视角配备多分支的架构并不足以真正利用相关输入的知识 [19]。即便在其他多模态学习应用中（如涉及语音或文本的场景），建模不当的深度学习网络无法利用不同输入模态信息的现象也十分普遍 [30]。虽然具体情境不同，但这一根本问题在多模态和多视角场景中普遍存在。因此，在处理多视角检查时，必须开发细致周密的方法。为此，我们提出了一种基于超复数代数的方法，其特性将在后续章节详述。
III. QUATERNION AND HYPER COMPLEX NEURALNETWORKS
III. 四元数与超复数神经网络
Quaternion and hyper complex neural networks have their foundations in a hyper complex number system $\mathbb{H}$ equipped with its own algebra rules to regulate additions and multiplications. Hyper complex numbers generalize a plethora of algebraic systems, including complex numbers $\mathbb{C}$ , qua tern ions $\mathbb{Q}$ and octonions $\mathbb{O}$ , among others. A generic hyper complex number is defined as
四元数与超复数神经网络的基础在于超复数系统 $\mathbb{H}$，该系统拥有独立的代数规则来规范加法和乘法运算。超复数推广了多种代数体系，包括复数 $\mathbb{C}$、四元数 $\mathbb{Q}$ 和八元数 $\mathbb{O}$ 等。通用超复数的定义为
$$
h=h_{0}+h_{1}\hat{\imath}{1}+...+h_{i}\hat{\imath}{i}+...+h_{n-1}\hat{\imath}_{n-1},
$$
$$
h=h_{0}+h_{1}\hat{\imath}{1}+...+h_{i}\hat{\imath}{i}+...+h_{n-1}\hat{\imath}_{n-1},
$$
whereby $h_{0},\ldots,h_{n-1}$ are the real-valued coefficients and $\hat{\i}{i},\dots,\hat{\i}{n-1}$ the imaginary units. The first coefficient $h_{0}$ represents the real component, while the remaining ones compose the imaginary part. Therefore, the algebraic subsets of $\mathbb{H}$ are identified by the number of imaginary units and by the algebraic rules that govern the interactions among them. For instance, a complex number has just one imaginary unit, while a quaternion has three imaginary units. In the latter domain, the vector product is not commutative so the Hamilton product has been introduced to multiply two qua tern ions. Interestingly, a real number can be expressed through eq. (1) by setting $i=0$ and considering the real part only. Being hyper complex algebras part of the Cayley-Dickson algebras, they always have a dimension equal to a power of 2, therefore it is important to note that subset domains exist solely at predefined dimensions, i.e., $n=2,4,8,16,\dots$ , while no algebra rules have been discovered yet for other values.
其中 $h_{0},\ldots,h_{n-1}$ 为实值系数，$\hat{\i}{i},\dots,\hat{\i}{n-1}$ 为虚数单位。首项系数 $h_{0}$ 表示实部，其余系数构成虚部。因此，$\mathbb{H}$ 的代数子集可通过虚数单位数量及其相互作用规则来定义。例如，复数仅含一个虚数单位，而四元数包含三个虚数单位。在后者的数域中，由于向量乘法不满足交换律，汉密尔顿积被引入以实现四元数乘法。值得注意的是，实数可通过令 $i=0$ 并仅保留实部，由公式 (1) 表示。作为凯莱-迪克森代数中的超复数代数，其维度总是2的幂次方，因此需注意子数域仅存在于预设维度（即 $n=2,4,8,16,\dots$），目前尚未发现其他维度的代数规则。
The addition operation is performed through an elementwise addition of terms, i.e., $h+p=(h_{0}+p_{0})+(h_{1}+p_{1})+...+$ $(h_{i}+p_{i})\hat{\imath}{i}+...+(h_{n-1}+p_{n-1})\hat{\imath}{n-1}$ . Similarly, the product between a quaternion and a scalar value $\alpha\in\mathbb R$ can be formulated with $\alpha h=\alpha h_{0}+\alpha h_{1}+...+\alpha h_{i}\hat{\imath}{i}+...+\alpha h_{n-1}\hat{\imath}{n-1}$ by multiplying the scalar to real-valued components. Nevertheless, with the increasing of $n$ , Cayley-Dickson algebras lose some properties regarding the vector multiplication, and more specific formulas need to be introduced to model this operation because of imaginary units interplays [46]. Indeed, as an example, qua tern ions and octonions products are not commutative due to imaginary unit properties for which $\hat{\i}{1}\hat{\i}{2}\neq\hat{\i}{2}\hat{\i}{1}$ . Therefore, quaternion convolutional neural network (QCNN) layers are based on the Hamilton product, which organizes the filter weight matrix to be encapsulated into a quaternion as $\mathbf{W}=\mathbf{W}{0}+\mathbf{W}{1}\boldsymbol{\hat{\imath}}{1}+\mathbf{W}{2}\boldsymbol{\hat{\imath}}{2}+\mathbf{W}{3}\boldsymbol{\hat{\imath}}{3}$ and to perform convolution with the quaternion input ${\bf x}={\bf x}{0}+{\bf x}{1}\hat{\imath}{1}+{\bf x}{2}\hat{\imath}{2}+{\bf x}{3}\hat{\imath}_{3}$ as:
加法运算通过逐项元素相加实现，即 $h+p=(h_{0}+p_{0})+(h_{1}+p_{1})+...+$ $(h_{i}+p_{i})\hat{\imath}{i}+...+(h_{n-1}+p_{n-1})\hat{\imath}{n-1}$。类似地，四元数与标量值 $\alpha\in\mathbb R$ 的乘积可表示为 $\alpha h=\alpha h_{0}+\alpha h_{1}+...+\alpha h_{i}\hat{\imath}{i}+...+\alpha h_{n-1}\hat{\imath}{n-1}$，即对实值分量进行标量乘法。然而随着 $n$ 增大，Cayley-Dickson代数在向量乘法方面会损失部分性质，由于虚数单位的相互作用，需要引入更特定的公式来建模该运算 [46]。例如，四元数和八元数的乘法不具备交换性，因为虚数单位满足 $\hat{\i}{1}\hat{\i}{2}\neq\hat{\i}{2}\hat{\i}{1}$。因此，四元数卷积神经网络 (QCNN) 层基于汉密尔顿积实现，其将滤波器权重矩阵封装为四元数形式 $\mathbf{W}=\mathbf{W}{0}+\mathbf{W}{1}\boldsymbol{\hat{\imath}}{1}+\mathbf{W}{2}\boldsymbol{\hat{\imath}}{2}+\mathbf{W}{3}\boldsymbol{\hat{\imath}}{3}$，并与四元数输入 ${\bf x}={\bf x}{0}+{\bf x}{1}\hat{\imath}{1}+{\bf x}{2}\hat{\imath}{2}+{\bf x}{3}\hat{\imath}_{3}$ 进行如下卷积运算：
$$
\mathbf{W}\mathbf{x}=\left[\begin{array}{c c c c}{\mathbf{W}{0}}&{-\mathbf{W}{1}}&{-\mathbf{W}{2}}&{-\mathbf{W}{3}}\ {\mathbf{W}{1}}&{\mathbf{W}{0}}&{-\mathbf{W}{3}}&{\mathbf{W}{2}}\ {\mathbf{W}{2}}&{\mathbf{W}{3}}&{\mathbf{W}{0}}&{-\mathbf{W}{1}}\ {\mathbf{W}{3}}&{-\mathbf{W}{2}}&{\mathbf{W}{1}}&{\mathbf{W}{0}}\end{array}\right]*\left[\begin{array}{c c c c}{\mathbf{x}{0}}\ {\mathbf{x}{1}}\ {\mathbf{x}{2}}\ {\mathbf{x}_{3}}\end{array}\right].
$$
$$
\mathbf{W}\mathbf{x}=\left[\begin{array}{c c c c}{\mathbf{W}{0}}&{-\mathbf{W}{1}}&{-\mathbf{W}{2}}&{-\mathbf{W}{3}}\ {\mathbf{W}{1}}&{\mathbf{W}{0}}&{-\mathbf{W}{3}}&{\mathbf{W}{2}}\ {\mathbf{W}{2}}&{\mathbf{W}{3}}&{\mathbf{W}{0}}&{-\mathbf{W}{1}}\ {\mathbf{W}{3}}&{-\mathbf{W}{2}}&{\mathbf{W}{1}}&{\mathbf{W}{0}}\end{array}\right]*\left[\begin{array}{c c c c}{\mathbf{x}{0}}\ {\mathbf{x}{1}}\ {\mathbf{x}{2}}\ {\mathbf{x}_{3}}\end{array}\right].
$$
Processing multidimensional inputs with QCNNs has several advantages. Indeed, due to the reusing of filter sub matrices $\mathbf{W}_{i}$ , $\begin{array}{l l l}{i}&{=}&{0,\ldots,3}\end{array}$ in eq. (2), QCNNs are defined with $1/4$ free parameters with respect to real-valued counterparts with the same architecture structure. Moreover, sharing the filter sub matrices among input components allows QCNNs to capture internal relations in input dimensions and to preserve correlations among them [32], [47]. However, this approach is limited to 4D inputs, thus various knacks are usually employed to apply QCNNs to different 3D inputs, such as RGB color images. In these cases, a padding channel is concatenated to the three-channel image to build a 4D image adding, however, useless information. Similarly, when processing grayscale images with QCNNs, the single channel has to be replicated in order to be fed into the quaternionvalued network, without annexing any additional information for the model. Recently, novel approaches proposed to parameter ize hyper complex multiplications and convolutions to maintain QCNNs and hyper complex algebras advantages, while extending their applicability to any $n\mathrm{D}$ input [37], [38]. The core idea of these methods is to develop the filter matrix $\mathbf{W}$ as a parameterized sum of Kronecker products:
使用QCNN处理多维输入具有多重优势。由于在公式(2)中重复使用滤波器子矩阵 $\mathbf{W}_{i}$ ( $i=0,\ldots,3$ )，QCNN的自由参数数量仅为同架构实值网络的1/4。此外，通过在输入分量间共享滤波器子矩阵，QCNN能够捕捉输入维度间的内在关联并保持其相关性[32][47]。但该方法仅适用于4D输入，因此通常需要特殊技巧将QCNN应用于RGB彩色图像等3D输入——此时需通过填充通道构建4D图像，但会引入冗余信息。类似地，处理灰度图像时需复制单通道以适配四元数网络，同样未增添有效信息。最新研究提出参数化超复数乘法和卷积运算的方法[37][38]，在保留QCNN和超复数代数优势的同时，将其适用范围扩展至任意$n\mathrm{D}$输入。这些方法的核心思想是将滤波器矩阵$\mathbf{W}$构建为克罗内克积的参数化组合：
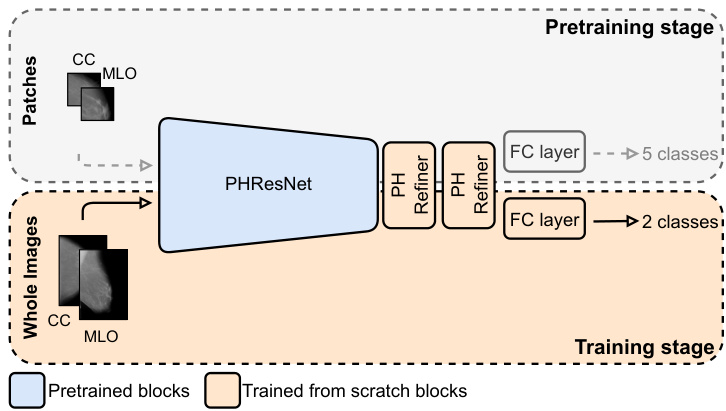
Fig. 4. Training pipeline and PHResNet overview. We employ a pertaining stage to overcome issues presented in Section efsubsec:training. During this stage, the PHResNet is trained on patches extracted from the original mammogram. They are classified into five classes: background or normal, benign and malignant calcification s and masses, respectively. At downstream time, i.e., when training on whole images, two PH convolutional refiner blocks are added and trained from scratch together with the final classification layer.
图 4: 训练流程与PHResNet架构概览。我们采用预训练阶段来解决第efsubsec:training节所述问题。在此阶段，PHResNet通过从原始乳腺X光片中提取的 patches 进行训练，这些 patches 被分为五类：背景/正常组织、良性钙化、恶性钙化、良性肿块和恶性肿块。在下游阶段（即整图训练时），会新增两个PH卷积精炼块 (PH convolutional refiner blocks) 并与最终分类层一起从头开始训练。
$$
\mathbf{W}=\sum_{i=0}^{n}\mathbf{A}{i}\otimes\mathbf{F}_{i},
$$
$$
\mathbf{W}=\sum_{i=0}^{n}\mathbf{A}{i}\otimes\mathbf{F}_{i},
$$
whereby $n$ is a tunable or user-defined hyper parameter that determines the domain in which the model operates (i.e., $n=4$ for the quaternion domain, $n=8$ for octonions, and so on). The matrices $\mathbf{A}{i}$ encode the algebra rules, that is the filter organization for convolutional layers, while the matrices $\mathbf{F}_{i}$ enclose the weight filters. Both these elements are completely learned from data during training, thus grasping algebra rules or adapting them, if no algebra exists for the specific value of $n$ , directly from inputs. The PHC layer is malleable to operate in any $n\mathrm{D}$ domain by easily setting the hyper parameter $n$ , thus extending QCNNs advantages to every multidimensional input. Indeed, PHNNs can process color images in their natural domain $(n:=:3)$ ) without adding any uninformative channel (as previously done for QCNNs), while still exploiting latent relations between channels. Moreover, due to the data-driven fashion in which this approach operates, PHNNs with $n=4$ outperform QCNNs both in terms of prediction accuracy and training as well as inference time [37], [38]. Furthermore, PHC layers employ $1/n$ free parameters with respect to real-valued counterparts, so the user can govern both the domain and the parameters reduction by simply setting the value of $n$ .
其中 $n$ 是一个可调或用户定义的超参数，用于确定模型运行的域（即四元数域对应 $n=4$，八元数对应 $n=8$，以此类推）。矩阵 $\mathbf{A}{i}$ 编码代数规则，即卷积层的滤波器组织结构，而矩阵 $\mathbf{F}_{i}$ 则包含权重滤波器。这两类元素均在训练过程中完全从数据中学习，从而掌握代数规则或直接根据输入调整规则（若特定 $n$ 值不存在对应代数）。通过简单设置超参数 $n$，PHC 层可灵活适应任意 $n\mathrm{D}$ 域，从而将 QCNNs 的优势扩展到所有多维输入。实际上，PHNNs 能在自然域 $(n=3)$ 处理彩色图像，无需添加任何无信息通道（如 QCNNs 先前所做），同时仍能利用通道间的潜在关联。此外，由于该方法采用数据驱动方式，$n=4$ 的 PHNNs 在预测精度、训练及推理时间方面均优于 QCNNs [37][38]。值得注意的是，PHC 层使用的自由参数数量仅为实数对应版本的 $1/n$，因此用户仅需设定 $n$ 值即可同时控制运算域和参数量缩减。
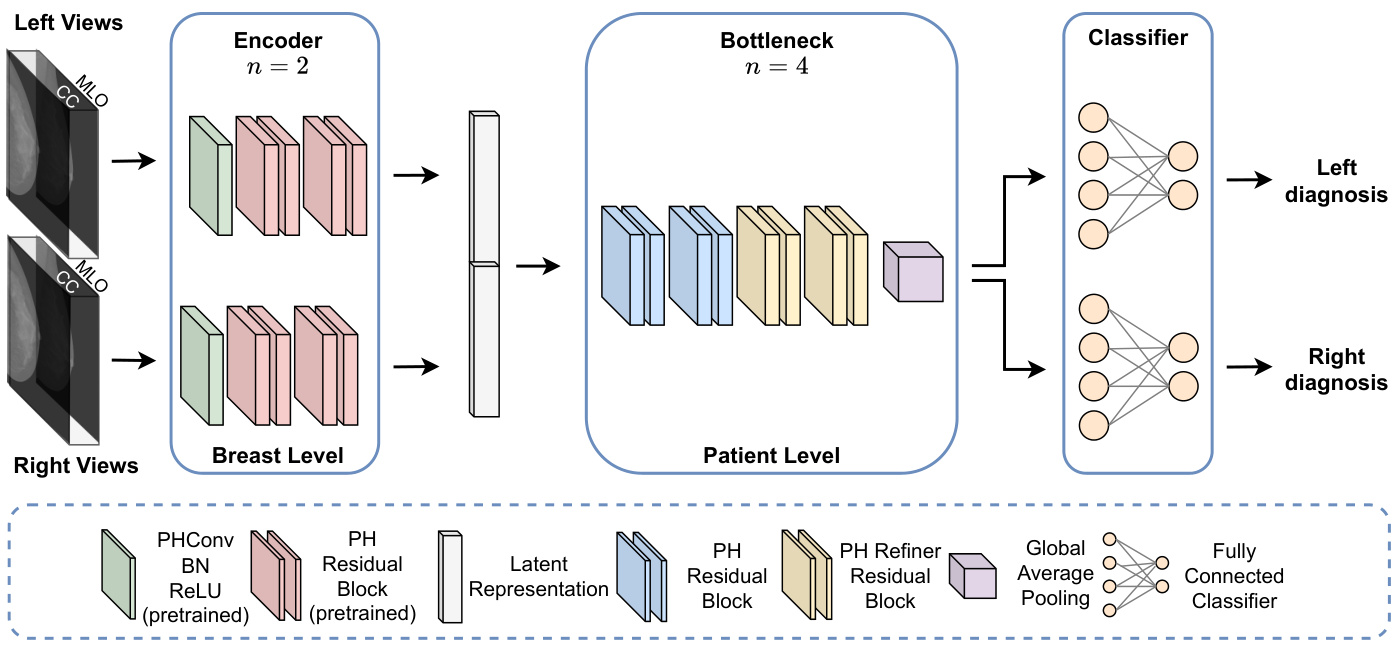
Fig. 5. PHYBOnet architecture. The model first performs a breast-level analysis by taking as input two pairs of ips i lateral views that are handled by two pretrained PH encoder branches with $n=2$ . The learned latent representations are then processed in a joint fashion by four PH residual blocks with $n=4$ Finally, the outputs from the two branches are fed to a separate final fully connected layer after a global average pooling operation.
图 5: PHYBOnet架构。该模型首先通过输入两对同侧视图进行乳腺级别分析，这些视图由两个预训练的PH编码器分支处理（$n=2$）。学习到的潜在表征随后通过四个PH残差块（$n=4$）以联合方式处理。最后，两个分支的输出在经过全局平均池化操作后，分别馈入独立的最终全连接层。
The reason behind the success of hyper complex models is their ability to model not only global relations as standard neural networks but also local relations. Global dependencies are related to spatial relations among pixels of the same level (i.e., for an RGB image, the R, G, and B channels are different levels). Instead, local dependencies implicitly link different levels. In the latter case, implicit local relations for an RGB image are the natural link that exists within the three-channel components defining a pixel. This kind of correlation among the different levels of the input is usually not taken into account by conventional neural networks that operate in the real domain, as they consider the pixels at different levels as sets of de correlated points [32]. Considering the multiple dimensions/levels of a sample as unrelated components may break the inner nature of the data, losing information about the inner structure of the sample. Instead, PHNNs can explore both global and local relations, not losing crucial information. Indeed, global relations are modeled as in conventional models, e.g., with convolutional operations. Rather, thanks to the formulation of convolution defined in Eq. 2, the filter sub matrices are shared among input dimensions, i.e., the different levels, thus hyper complex networks are endowed with the ability to model also local relations. In the context of mammography, the different views can be regarded as the color channels of an RGB image. Thus, global relations are intraview features, such as the shape of the breast. In contrast, local relations are inter-view features, thus encompassing the interdependencies found across the various views. A depiction of such relations in the context of a mammography exam can be seen in Fig. 3. Indeed, local relations are an inherent part of multi-view data. Nevertheless, standard neural networks have been shown to ignore such relations [32]. Therefore, hyper complex algebra may be a powerful tool to leverage mammogram views as it is able to describe multidimensional data preserving its inner structure [38].
超复数模型成功的原因在于它们不仅能像标准神经网络那样建模全局关系，还能捕捉局部关联。全局依赖性与同层级像素间的空间关系相关（例如RGB图像中R、G、B通道属于不同层级），而局部依赖性则隐式连接不同层级。以RGB图像为例，其隐含的局部关系就是构成像素的三个通道组件之间天然存在的联系。传统实数域神经网络通常忽略这种输入数据不同层级间的相关性，它们将不同层级的像素视为互不关联的点集[32]。若将样本的多维度/层级视为无关组件，可能会破坏数据的内在特性，丢失样本内部结构信息。相比之下，PHNN（超复数神经网络）能同时探索全局与局部关系，避免关键信息丢失。其中全局关系通过常规操作（如卷积运算）建模，而借助公式(2)定义的卷积形式，滤波器子矩阵在输入维度（即不同层级）间共享，因此超复数网络也具备建模局部关系的能力。
在乳腺X光检查场景中，不同视角可类比RGB图像的色彩通道：全局关系对应视角内特征（如乳房形状），局部关系则对应跨视角特征，涵盖不同视图间的相互依赖关系。图3展示了乳腺检查中这类关系的示意图。实际上，局部关系是多视图数据与生俱来的特性，但标准神经网络已被证明会忽略这种关联[32]。因此，超复数代数可能是利用乳腺X光视图的强大工具，因其能描述多维数据同时保留内在结构[38]。
IV. PROPOSED METHOD
IV. 提出的方法
In the following section, we expound the proposed approach and we delineate the structure of our models and the training recipes we adopt. More in detail, we design ad hoc networks for two-view and four-view exams, i.e., a complete mammography exam.
在以下部分，我们将阐述所提出的方法，并详细说明模型结构及采用的训练方案。具体而言，我们针对双视图检查和四视图检查（即完整的乳腺X光检查）设计了专用网络。
A. Multi-view PHResNet
A. 多视角 PHResNet
The core idea of our method is to take advantage of the information contained in multiple views through PHC layers in order to obtain a more performant and robust classifier for breast cancer.
我们方法的核心思想是通过PHC层利用多视图中的信息，以获得性能更强、鲁棒性更好的乳腺癌分类器。
ResNets are among the most widespread models for medical image classification [6], [9], [15], [18], [19], [48], [49]. They are characterized by residual connections that ensure proper gradient propagation during training. A ResNet block is typically defined by:
ResNets 是医学图像分类领域应用最广泛的模型之一 [6], [9], [15], [18], [19], [48], [49]。其核心特征是通过残差连接确保训练过程中的梯度正常传播。典型的 ResNet 块定义为：
$$
\begin{array}{r}{\mathbf{y}=\mathcal{F}(\mathbf{x})+\mathbf{x},}\end{array}
$$
$$
\begin{array}{r}{\mathbf{y}=\mathcal{F}(\mathbf{x})+\mathbf{x},}\end{array}
$$
where $\mathcal F(\ensuremath{\mathbf{x}})$ is usually composed by interleaving convolutional layers, batch normalization (BN) and ReLU activation functions. When equipped with PHC layers, real-valued convolu- tions are replaced with PHC to build PHResNets, therefore $\mathcal{F}(\mathbf{x})$ becomes:
其中 $\mathcal F(\ensuremath{\mathbf{x}})$ 通常由交替的卷积层、批归一化 (BN) 和 ReLU 激活函数组成。当配备 PHC 层时，实值卷积被替换为 PHC 以构建 PHResNets，因此 $\mathcal{F}(\mathbf{x})$ 变为：
$$
\mathcal{F}(\mathbf{x})=\mathrm{BN}\left(\mathrm{PHC}\left(\mathrm{ReLU}\left(\mathrm{BN}\left(\mathrm{PHC}\left(\mathbf{x}\right)\right)\right)\right)\right),
$$
$$
\mathcal{F}(\mathbf{x})=\mathrm{BN}\left(\mathrm{PHC}\left(\mathrm{ReLU}\left(\mathrm{BN}\left(\mathrm{PHC}\left(\mathbf{x}\right)\right)\right)\right)\right),
$$
in which $\mathbf{x}$ can be any multidimensional input with correlated components. It is worth noting that PH models generalize realvalued counterparts and also mono dimensional inputs. As a
其中 $\mathbf{x}$ 可以是具有相关分量的任意多维输入。值得注意的是，PH模型不仅推广了实值对应模型，还适用于单维输入。
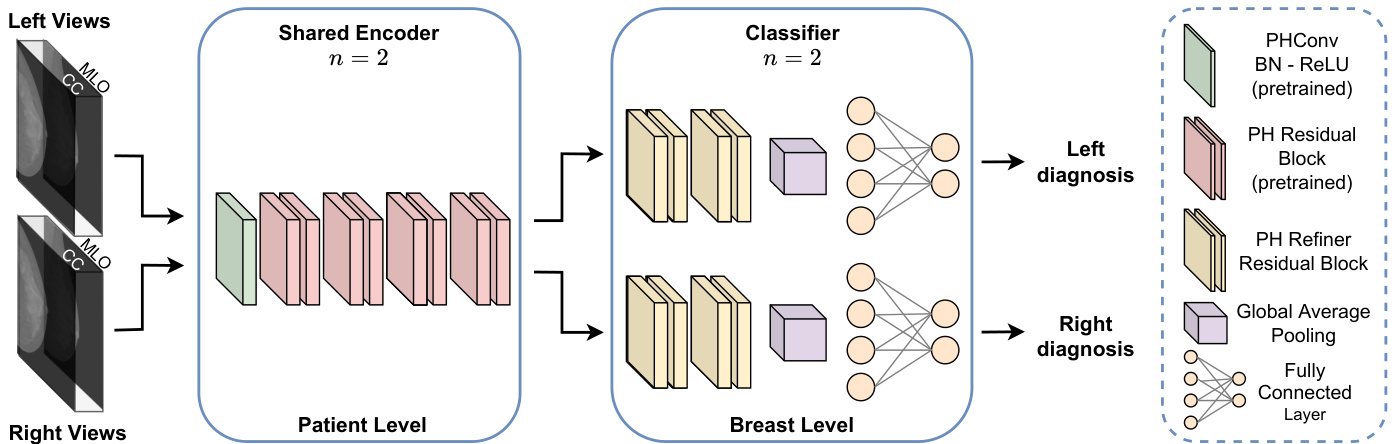
Fig. 6. PHYSEnet architecture. The model comprises an initial deep patient-level framework that takes as input two pairs of ips i lateral views which are processed by a pretrained shared PHResNet18 with $n=2$ that serves as the encoder. Ultimately, the two learned latent representations are fed to the respective classification branch composed of PH refiner residual blocks with global average pooling and the final fully connected layer to perform the breast-level learning.
图 6: PHYSEnet架构。该模型包含一个初始的深度患者级框架，输入为两对同侧视图，由预训练的共享PHResNet18 (n=2) 作为编码器进行处理。最终，两个学习到的潜在表征被送入各自的分类分支，该分支由带有全局平均池化的PH细化残差块和最终的全连接层组成，以执行乳腺级别的学习。
matter of fact, a PH model with $n=1$ is equivalent to a real-valued model receiving 1D inputs.
事实上，当 $n=1$ 时，PH 模型等价于接收一维输入的实值模型。
B. PH architectures for two views
B. 双视图的PH架构
The proposed multi-view architecture in the case of two views is straightforward. We employ PHResNets and we fix the hyper parameter $n=2$ . The model is depicted in Fig. 4 together with the training strategy we deploy. The two views of the same breast, i.e., ips i lateral views, are fed to the network as a multidimensional input (channel-wise) enabling PHC layers to exploit their correlations. We adopt ips i lateral views because, as mentioned in Section VI-B, they help in both the detection and classification process, unlike bilateral views which aid only in the former.
所提出的双视图多视角架构较为简单。我们采用PHResNets并固定超参数$n=2$。该模型及训练策略如图4所示。同一乳房的两个视角（即同侧视图）以多维输入（通道维度）形式馈入网络，使PHC层能够利用其相关性。我们选用同侧视图是因为，如第VI-B节所述，它们同时有助于检测和分类过程，而异侧视图仅对前者有帮助。
Ultimately, the model produces a binary prediction indicating the presence of either a malignant or benign/normal finding (depending on the dataset). In such a manner, the model is able to process the two mammograms as a unique entity by preserving the original multidimensional structure as elucidated in Section III [32]. As a consequence, it is endowed with the capacity to exploit both global and local relations, i.e., the interactions between the highly correlated views, mimicking the diagnostic process of radiologists.
最终，该模型会生成一个二元预测，用于指示是否存在恶性或良性/正常发现（具体取决于数据集）。通过这种方式，模型能够将两张乳腺X光片作为一个独特实体进行处理，同时保留原始的多维结构，如第三节 [32] 所述。因此，该模型具备利用全局和局部关系的能力，即高度相关视图之间的相互作用，从而模拟放射科医师的诊断过程。
C. PH architectures for four views
C. 四视图的PH架构
- PHYBOnet: The first model we propose is shown in Fig. 5, namely Parameterized Hyper complex Bottleneck network (PHYBOnet). PHYBOnet is based on an initial breastlevel focus and a consequent patient-level one, through the following components: two encoder branches for each breast side with $n~=~2$ , a bottleneck with the hyper parameter $n=4$ and two final classifier layers that produce the binary prediction relative to the corresponding side. Each encoder takes as input two views (CC and MLO) and has the objective of learning a latent representation of the ips i lateral views. The learned latent representations are then merged together and processed by the bottleneck which has $n$ set to 4 in order for PHC layers to grasp correlations among them. Indeed, in this way we additionally obtain a light network since the number of parameters is reduced by $1/4$ .
- PHYBOnet：我们提出的第一个模型如图5所示，即参数化超复数瓶颈网络 (PHYBOnet)。该模型基于初始乳房层级关注和后续患者层级关注，通过以下组件实现：两侧乳房各设两个编码器分支（$n~=~2$），一个超参数为$n=4$的瓶颈层，以及两个最终分类层用于生成对应侧的二元预测。每个编码器以两个视图（CC和MLO）作为输入，旨在学习同侧视图的潜在表征。习得的潜在表征经合并后由瓶颈层处理（此处$n$设为4），使PHC层能捕捉其间的相关性。实际上，这种方式还实现了网络轻量化，因为参数量减少了$1/4$。
- PHYSEnet: The second architecture we present, namely Parameterized Hyper complex Shared Encoder network (PHYSEnet), is depicted in Fig. 6. It has a broader focus on the patient-level analysis through an entire PHResNet18 with $n=$ 2 as the encoder model, which takes as input two ips i lateral views. The weights of the encoder are shared between left and right inputs to jointly analyze the whole information of the patient. Then, two final classification branches, consisting of residual blocks and a final fully connected layer, perform a breast-level analysis to output the final prediction for each breast. This design allows the model to leverage information from both ips i lateral and bilateral views. Indeed, thanks to PHC layers, ips i lateral information is leveraged as in the case of two views, while by sharing the encoder between the two sides, the model is also able to take advantage of bilateral information.
- PHYSEnet：我们提出的第二种架构，即参数化超复数共享编码器网络 (PHYSEnet)，如图 6 所示。它通过一个完整的 PHResNet18（其中 $n=$ 2 作为编码器模型）更广泛地关注患者层面的分析，该模型以两个同侧视图作为输入。编码器的权重在左右输入之间共享，以共同分析患者的全部信息。然后，两个最终分类分支（由残差块和一个最终全连接层组成）执行乳房层面的分析，输出每个乳房的最终预测。这种设计使模型能够利用同侧和双侧视图的信息。事实上，得益于 PHC 层，同侧信息可以像两个视图的情况一样被利用，而通过在两侧共享编码器，模型还能够利用双侧信息。
D. Training procedure
D. 训练流程
Training a classifier from scratch for this kind of task is very difficult for a number of reasons. To begin, neural models require huge volumes of data for training, but there are only a handful of publicly available datasets for breast cancer, which also present a limited number of examples. Additionally, a lesion occupies only a tremendously small portion of the original image, thus making it arduous to be detected by a model [6].
针对此类任务从头训练分类器存在诸多困难。首先，神经网络模型需要海量训练数据，但公开可用的乳腺癌数据集寥寥无几，且样本数量有限。此外，病灶在原图像中占比极小，导致模型检测难度极大 [6]。
To overcome these challenges, we deploy an ad hoc pretraining strategy, illustrated in Fig. 4 divided into two main steps. First, we pretrain the model on patches of mammograms and, second, we involve the pretrained weights to initialize the network for training on whole images. Specifically, in the first step patches are extracted from the original mammograms by taking 20 patches for each lesion present in the dataset: 10 of background or normal tissue and 10 around the region of interest (ROI) in question. Aiming to utilize this classifier for the training of whole mammograms with two views, we also require two views at the patch level. The definition of two views for patches is straightforward. For all lesions that are visible in both views of the breast, patches around that lesion are taken for both views. Thus, the patch classifier takes as input two-view $224\times224$ patches of the original mammogram, concatenated along the channel dimension and classifies them into one of the following five classes: ext it background or normal, benign calcification, malignant calcification, benign mass, and malignant mass [6]. At downstream time, i.e., when training on whole images, the network is initialized with the pretrained weights to classify exams as either malignant or benign. Indeed, pre training on patches is a way to exploit the fine-grained detail characteristic of mammograms which is crucial for discriminating between malignant and benign findings, that would otherwise be lost due to the resizing of images [6], [18]. Such training strategy plays a determining role in boosting the performance of the models as we demonstrate in the experimental Section VI.
为克服这些挑战，我们采用了一种专门的预训练策略，如图4所示，该策略分为两个主要步骤。首先，我们在乳腺X光片的小块上进行模型预训练；其次，利用预训练权重初始化网络，以在整个图像上进行训练。具体而言，第一步从原始乳腺X光片中提取小块，数据集中每个病灶对应提取20个小块：10个来自背景或正常组织，10个来自相关感兴趣区域(ROI)周边。为了使该分类器能用于训练包含两个视角的完整乳腺X光片，我们在小块层面也要求两个视角。定义小块的双视角很简单：对于乳房两个视角中都可见的所有病灶，分别从两个视角提取该病灶周边的小块。因此，小块分类器的输入是原始乳腺X光片双视角的$224\times224$小块（沿通道维度拼接），并将其分类为以下五类之一：背景或正常组织、良性钙化、恶性钙化、良性肿块和恶性肿块[6]。在下游阶段（即在整个图像训练时），网络使用预训练权重初始化，用于将检查分类为恶性或良性。实际上，小块预训练是利用乳腺X光片细粒度细节特征的方法，这对区分恶性和良性结果至关重要，否则这些细节会因图像尺寸调整而丢失[6][18]。如实验章节VI所示，这种训练策略对提升模型性能具有决定性作用。
V. EXPERIMENTAL SETUP
五、实验设置
In this section, we describe the experimental setup of our work that comprises the datasets we consider, the metrics employed for evaluation, model architectures details and training hyper parameters.
在本节中，我们将介绍实验设置，包括使用的数据集、评估指标、模型架构细节以及训练超参数。
A. Data
A. 数据
We validate the proposed method with two publicly available datasets of mammography images, whose sample summary is presented in Tab. I. We additionally demonstrate the general iz ability and flexibility of the proposed method on two additional tasks and datasets described herein.
我们使用两个公开可用的乳腺X光影像数据集验证了所提出的方法，其样本摘要如表1所示。此外，我们还通过本文描述的两个额外任务和数据集，展示了所提方法的泛化能力和灵活性。
- CBIS-DDSM: The Curated Breast Imaging Subset of DDSM (CBIS-DDSM) [39] is an updated and standardized version of the Digital Database for Screening Mammography (DDSM). It contains 2478 scanned film mammography images in the standard DICOM format and provides both pixellevel and whole-image labels from biopsy-proven pathology results. Furthermore, for each lesion, the type of abnormality is reported: calcification (753 cases) or mass (891 cases). Importantly, the dataset does not contain healthy cases but only positive ones (i.e., benign or malignant), where for the majority of them a biopsy was requested by the radiologist in order to make a final diagnosis, meaning that the dataset is mainly comprised of the most difficult cases. Additionally, the dataset provides the data divided into splits containing only masses and only calcification s, respectively, in turn split into official training and test sets, characterized by the same level of difficulty. CBIS-DDSM is employed for the training of the patch classifier as well as whole-image classifier in the twoview scenario. It is not used for four-view experiments as the official training/test splits do not contain enough full-exam cases and creating different splits would result in data leakage between patches and whole images. Finally, the images are resized to $600\times500$ and are augmented with a random rotation between $-25$ and $+25$ degrees and a random horizontal and vertical flip [6], [8].
- CBIS-DDSM：DDSM精选乳腺影像子集 (CBIS-DDSM) [39] 是数字化乳腺筛查数据库 (DDSM) 的标准化升级版本。该数据集包含2478张标准DICOM格式的扫描胶片乳腺X光影像，并提供基于活检病理结果的像素级和全图标注。每处病灶均标注异常类型：钙化灶 (753例) 或肿块 (891例)。值得注意的是，该数据集仅包含阳性病例 (即良性或恶性)，不含健康病例，其中多数病例需放射科医师通过活检确诊，表明数据集主要由疑难病例构成。此外，数据集按病灶类型划分为仅含肿块和仅含钙化灶的子集，每个子集又分为官方训练集和测试集，且难度水平保持一致。CBIS-DDSM用于双视角场景下的局部分类器和全图分类器训练，未用于四视角实验，因其官方训练/测试划分未包含足够完整检查病例，且重新划分会导致局部图像与全图数据泄露。最终图像统一调整为$600×500$分辨率，并采用随机旋转 ($-25$至$+25$度) 及随机水平/垂直翻转进行数据增强 [6][8]。
- INbreast: The second dataset employed in this study, INbreast [2], is a database of full-field digital mammography (FFDM) images. It contains 115 mammography exams for a total of 410 images, involving several types of lesions, among which are masses and calcification s. The data splits are not provided, thus they are manually created by splitting the dataset patient-wise in a stratified fashion, using $20%$ of the data for testing. Finally, INbreast does not provide pathological confirmation of malignancy but BI-RADS labels. Therefore, in the aim of obtaining binary labels, we consider BI-RADS categories 4, 5 and 6 as positive and 1, 2 as negative, whilst ruling out category 3 following the approach of [6]. INbreast is utilized for experiments in both the two-view and fourview scenarios and the same preprocessing as CBIS-DDSM is applied. Finally, as can be seen in Tab. I, the dataset is highly imbalanced. To tackle this issue, in addition to using the same data augmentation techniques employed for CBIS-DDSM, we deploy a weighted loss during training, as elaborated in Section V-C.
- INbreast: 本研究采用的第二个数据集INbreast [2]是一个全视野数字乳腺摄影(FFDM)图像数据库。它包含115例乳腺检查，共计410张图像，涉及多种类型的病变，包括肿块和钙化。该数据集未提供预设划分，因此我们采用分层方式按患者手动划分数据集，其中20%数据用于测试。需要注意的是，INbreast未提供恶性肿瘤的病理学确认，而是采用BI-RADS标注。为获得二分类标签，我们参照[6]的方法，将BI-RADS 4、5、6类视为阳性，1、2类视为阴性，同时排除3类病例。该数据集被用于双视图和四视图场景的实验，并采用与CBIS-DDSM相同的预处理流程。如表1所示，该数据集存在严重不平衡问题。为此，除了采用与CBIS-DDSM相同的数据增强技术外，我们还在训练阶段使用了加权损失函数（详见第V-C节）。
TABLE I DATA DISTRIBUTION FOR SPLITS OF CBIS-DDSM AND FOR INBREAST WHEN CONSIDERING TWO AND FOUR VIEWS. IN THE WHOLE TABLE, TWO VIEWS OF THE SAME BREAST ARE COUNTED AS ONE INSTANCE.
表 1: CBIS-DDSM 和 INbreast 数据集在考虑双视图和四视图时的数据分布。全表中，同一乳房的两个视图计为一个实例。
| CBIS-DDSM | |||||
|---|---|---|---|---|---|
| Mass split | Mass-calc split | ||||
| Malignant | Benign | Malignant | Benign/Normal | ||
| Train | 254 | 255 | 480 | 582 | |
| Test | 59 | 83 | 104 | 149 | |
| INbreast | |||||
| Two views | Four views | ||||
| Malignant | Benign | Malignant | Benign/Normal | ||
| Train | 34 | 89 | 85 | ||
| Test | 14 | 39 | 8 | 22 |
- CheXpert: The CheXpert [40] dataset contains 224,316 chest X-rays with both frontal and lateral views and provides labels corresponding to 14 common chest radio graphic observations. Images are resized to $320\times320$ [40] for training and the same augmentation operations as before are applied.
- CheXpert: CheXpert [40] 数据集包含224,316张包含正位和侧位视图的胸部X光片，并提供14种常见胸部放射学观察结果的标签。训练时将图像尺寸调整为$320\times320$ [40]，并应用与之前相同的增强操作。
- BraTS19: BraTS19 [41], [42], [50] is a dataset of multimodal brain MRI scans, providing four modalities for each exam, segmentation maps, demographic information (such as age) and overall survival (OS) data as the number of days, for 210 patients. For training, volumes are resized to $128\times128\times128$ and augmented via random scaling between 1 and 1.1 [51] for the task of overall survival prediction. Rather, for segmentation, 2D axial slices are extracted from the volumes and the original shape of $240\times240$ is maintained.
- BraTS19: BraTS19 [41], [42], [50] 是一个多模态脑部MRI扫描数据集，为210名患者提供每次检查的四种模态、分割图、人口统计信息（如年龄）以及以天数为单位的总生存期 (OS) 数据。在训练中，为总生存期预测任务，体积被调整为 $128\times128\times128$ 并通过1到1.1之间的随机缩放进行增强 [51]。而对于分割任务，则从体积中提取2D轴向切片，并保持原始 $240\times240$ 的形状。
B. Evaluation metrics
B. 评估指标
We adopt AUC (Area Under the ROC Curve) as the main performance metric to evaluate our models, as it is one of the most common metrics employed in medical imaging tasks [6], [18]–[20]. The ROC curve summarizes the trade-off between True Positive Rate (TPR) and False Positive Rate (FPR) for a predictive model using different probability thresholds. To further assess network performance, we additionally evaluate our models in terms of classification accuracy. Finally, we employ the Dice score for the segmentation task, which measures the pixel-wise agreement between a predicted mask and its corresponding ground truth.
我们采用AUC (Area Under the ROC Curve)作为评估模型的主要性能指标，因为这是医学影像任务中最常用的指标之一 [6], [18]–[20]。ROC曲线总结了预测模型在不同概率阈值下真阳性率(TPR)与假阳性率(FPR)之间的权衡关系。为进一步评估网络性能，我们还通过分类准确率对模型进行评价。最后，在分割任务中采用Dice分数衡量预测掩膜与真实标注之间的像素级吻合度。
C. Training details
C. 训练细节
We train our models to minimize the binary cross-entropy loss using Adam optimizer [52], with a learning rate of $10^{-5}$ for classification experiments and $2\times10^{-4}$ for segmentation. Regarding two-view models, the batch size is 8 for PHResNet18, 2 for PHResNet50 and 32 for PHUNet. Instead, for four-view models the batch size is set to 4. Notably, in our initial experiments concerning four-view exams, we employed a standard cross-entropy loss. However, the models struggled to generalize due to the high class imbalance within the dataset. Consequently, to address this issue and achieve meaningful results, we adopted a weighted loss [53], [54] assigning a weight to positive examples equal to the number of benign/normal examples divided by the number of positive examples. We adopt two regular iz ation techniques: weight decay at $5\times10^{-4}$ and early stopping.
我们训练模型时使用Adam优化器[52]最小化二元交叉熵损失，分类实验的学习率为$10^{-5}$，分割任务则为$2\times10^{-4}$。对于双视图模型，PHResNet18的批次大小为8，PHResNet50为2，PHUNet为32；而四视图模型的批次大小统一设为4。值得注意的是，在初期四视图检查实验中，我们采用标准交叉熵损失函数，但由于数据集中类别高度不平衡，模型难以泛化。为此，我们改用加权损失[53][54]以取得有效结果——将良性/正常样本数除以阳性样本数作为阳性样本权重。我们采用两种正则化技术：权重衰减系数设为$5\times10^{-4}$，并实施早停策略。
- Two-view architectures: We perform the experimental validation with two ResNet backbones: PHResNet18 and PHResNet50. The networks have the same structure as in the original paper [38] with some variations. In the first convolutional layer, the number of channels in input is set to be equal to the hyper parameter $n~=~2$ and we omit the max pooling operation since we apply a global average pooling operation, after which we add 4 refiner residual blocks constructed with the bottleneck design [55]. Ultimately, the output of such blocks is fed to the final fully connected layer responsible for classification. The backbone network is initialized with the patch classifier weights, while the refiner blocks and final layer are trained from scratch, following the approach of [6]. In both hyper complex and real domains, the models take as input two views as if they were a single multidimensional (channel-wise) entity.
- 双视图架构：我们采用两种ResNet主干网络进行实验验证：PHResNet18和PHResNet50。这些网络结构与原论文[38]基本一致，但存在一些调整。在第一个卷积层中，输入通道数设置为等于超参数$n~=~2$，并省略了最大池化操作（因为我们采用了全局平均池化）。随后添加了4个采用瓶颈结构[55]设计的细化残差块。这些块的输出最终送入负责分类的全连接层。主干网络使用补丁分类器的权重进行初始化，而细化块和最终层则遵循[6]的方法从头开始训练。无论在超复数域还是实数域，模型都将两个视图作为单一多维（通道维度）实体输入。
- Four-view architectures: Here, we expound the architectural details of the proposed models when considering as input the whole mammogram exam. Also in this case, we use as baselines the respective real-valued counterparts, the bottleneck model (BOnet) and the shared encoder network (SEnet), for which the structural details are the same as in the hyper complex domain.
- 四视图架构：在此，我们详细阐述了将整个乳腺X光检查作为输入时所提出模型的架构细节。同样地，我们采用各自的实数域对应模型作为基线，即瓶颈模型 (BOnet) 和共享编码器网络 (SEnet) ，其结构细节与超复数域中的模型保持一致。
The first proposed model is PHYBOnet. We start from a PHResNet18 and divide its blocks such that the first part of the network serves as an encoder for each side and the remaining blocks compose the bottleneck. Thus, the encoders comprise a first $3\times3$ convolutional layer with a stride of 1, together with batch normalization and ReLU, and the first 4 residual blocks of ResNet18, as shown in Fig. 5. Then, the bottleneck is composed of 8 residual blocks and a global average pooling layer, with the first 4 residual blocks being the standard remaining blocks of ResNet18, and the last 4 the refiner residual blocks employed also in the architecture with two views. Finally, the two outputs are fed to the respective fully connected layer, each responsible to produce the prediction related to its side. The second proposed architecture, PHYSEnet, presents as shared encoder model a whole PHResNet18, while the two classifier branches are comprised of the 4 refiner blocks with a global average pooling layer and the final classification layer. For both proposed models, the choice of PHResNet18 as backbone instead of PHResNet50 is motivated by the results obtained in the experimental evaluation in the two-view scenario described in Subsection VI-B2.
首个提出的模型是PHYBOnet。我们从PHResNet18出发，将其模块划分，使网络的前半部分作为各侧的编码器，剩余模块构成瓶颈部分。因此，编码器包含一个步长为1的初始3×3卷积层（带批归一化和ReLU激活）以及ResNet18的前4个残差块，如图5所示。随后，瓶颈部分由8个残差块和全局平均池化层构成，其中前4个残差块是ResNet18的标准剩余模块，后4个为双视图架构中也采用的精炼残差块。最终，两个输出分别送入各自的全连接层，各负责生成对应侧的预测结果。第二个提出的架构PHYSEnet采用完整的PHResNet18作为共享编码器模型，两个分类器分支则由4个精炼块（含全局平均池化层）和最终分类层组成。选择PHResNet18而非PHResNet50作为这两个模型的骨干网络，是基于第VI-B2小节所述双视图场景实验评估结果而定的。
TABLE II RESULTS FOR PATCH CLASS IF I ERS ON CBIS DATASET CONTAINING BOTH MASS AND CALC. THE PHRESNETS OUTPERFORM REAL-VALUED COUNTERPARTS.
表 2: 包含肿块和钙化的 CBIS 数据集上 PATCH CLASS IF I ERS 的结果。PHResNet 优于实值对应模型。
| 模型 | 准确率 (%) |
|---|---|
| ResNet18 | 74.942 |
| PHResNet18 | 76.825 |
| ResNet50 | 75.989 |
| PHResNet50 | 77.338 |
At training time, both for PHYBOnet and PHYSEnet, the encoder portions of the networks are initialized with the patch classifier weights, while the rest is trained from scratch. Rather, in a second set of experiments conducted only with PHYSEnet, the whole architecture is initialized with the weights of the best whole-image two-view classifier trained on CBIS-DDSM.
在训练阶段，无论是PHYBOnet还是PHYSEnet，网络的编码器部分均使用补丁分类器的权重进行初始化，其余部分则从头开始训练。而在仅针对PHYSEnet进行的第二组实验中，整个架构采用在CBIS-DDSM上训练的最佳全图像双视图分类器的权重进行初始化。
VI. EXPERIMENTAL EVALUATION
六、实验评估
In this section, we present an exhaustive evaluation of our method, firstly investigating preliminary experiments without pre training and then in detail with two multi-view scenarios. We validate our proposed framework by comparing it against real-valued counterparts and state-of-the-art models for multiview breast cancer classification. Finally, we show the efficacy and the general iz ability of the proposed architectures by going beyond breast cancer, considering two additional medical problems regarding multi-view chest $\boldsymbol{\mathrm X}$ -rays and multimodal brain MRIs. For all experiments, the mean AUC and accuracy over multiple runs are reported together with the standard deviation.
在本节中，我们对所提方法进行了全面评估：首先探究无预训练的初步实验，随后针对两种多视角场景展开详细分析。通过将所提框架与实数域对应方法及当前最优的多视角乳腺癌分类模型进行对比，我们验证了其有效性。最后，我们通过超越乳腺癌范畴的扩展实验（涉及多视角胸部$\boldsymbol{\mathrm X}$光片和多模态脑部MRI两个额外医学问题），证明了所提架构的效能与泛化能力。所有实验均报告多次运行的平均AUC、准确率及标准差。
A. Preliminary experiments
A. 初步实验
- Whole-image without pre training: We conduct preliminary experiments to evaluate the ability of the models to learn from data without any form of pre training (first part of Tab. III). We test four different architectures on whole mammograms of CBIS-DDSM considering the mass data split. We employ PHResNet18 and PHResNet50 compared against their real-valued counterparts ResNet18 and ResNet50, respectively. Herein, it is evident that all the models involved are not able to learn properly and struggle to discriminate between images containing a benign lesion from images containing a malignant lesion. In fact, distinguishing the malignancy of an abnormality from the whole image only is extremely challenging because the lesion itself occupies a minuscule portion of the entire image. Nevertheless, even with poor performance, it is already evident that the proposed PHResNets are able to capture more information contained in the correlated views and thus reach a higher AUC and accuracy with respect to the real-valued models in all the experiments. Indeed, the bestperforming model, i.e., the PHResNet50, achieves an AUC of 0.70 and accuracy of $70.657%$ . Although the networks reach good results considering the limited number of examples for training, to overcome the challenge of learning from whole mammograms, all further experiments exploit the pre training strategy described in Subsection IV-D.
- 整图无预训练：我们通过初步实验评估模型在无任何预训练情况下从数据中学习的能力（表 III 第一部分）。在CBIS-DDSM乳腺摄影整图（肿块数据划分）上测试了四种架构，分别对比PHResNet18/PHResNet50与其实数对应模型ResNet18/ResNet50。结果显示所有模型均难以有效区分良性/恶性病变图像——仅凭整图判断异常恶性度本身极具挑战性，因病灶仅占图像极小部分。但即使性能欠佳，PHResNet仍能明显捕获关联视图中的更多信息，在所有实验中均比实数模型获得更高AUC（PHResNet50最佳达0.70）和准确率（70.657%）。尽管在有限训练样本下取得尚可结果，为克服整图学习难题，后续实验均采用IV-D节所述的预训练策略。
TABLE III RESULTS FOR TWO-VIEW MODELS. FOR CBIS DATASET - MASS SPLIT, WE PERFORM EXPERIMENTS WITH NO PRE TRAINING AND WITH PRE TRAINING ON PATCHES. FOR CBIS DATASET - MASS AND CALC SPLIT, EXPERIMENTS ARE CONDUCTED WITH MODELS PRETRAINED ON PATCHES. FOR THE INBREAST DATASET, WE PRETRAIN THE MODELS ON PATCHES AND THEN ON WHOLE CBIS IMAGES (PATCHES $^+$ CBIS). RESULTS INDICATED IN BOLD AND UNDERLINED TEXT REPRESENT THE BEST AND SECOND-BEST OUTCOMES. OUR METHODS EXCEED REAL-VALUED BASELINES AND STATE-OF-THE-ARTMODELS IN EACH TEST WE CONDUCT.
表 III 双视图模型结果。对于 CBIS 数据集 - 肿块分割，我们进行了无预训练和基于图像块 (patches) 预训练的对比实验。对于 CBIS 数据集 - 肿块和钙化分割，所有模型均采用基于图像块的预训练。在 INbreast 数据集上，我们先用图像块预训练模型，再在整个 CBIS 图像上微调 (patches $^+$ CBIS)。加粗和下划线标注的结果分别表示最优和次优表现。我们的方法在所有测试中都超越了实值基线模型和当前最先进模型。
| 数据集 | 模型 | 参数量 | 预训练方式 | AUC | 准确率 (%) |
|---|---|---|---|---|---|
| CBIS (肿块) | ResNet18 ResNet50 | 11M 16M | × | 0.646 ± 0.008 | 64.554 ± 2.846 |
| 0.663 ± 0.011 | 67.606 ± 1.408 | ||||
| PHResNet18 (ours) | 5M | 0.660 ± 0.020 | 67.371 ± 2.846 | ||
| PHResNet50 (ours) | 8M | 0.700 ± 0.002 | 70.657 ± 1.466 | ||
| CBIS (肿块) | ResNet18 | 26M | 图像块 | 0.710 ± 0.018 | 70.892 ± 3.614 |
| ResNet50 | 32M | 0.724 ± 0.007 | 73.474 ± 1.076 | ||
| Shared ResNet[19] | 12M | 0.735 ± 0.014 | 72.769 ± 2.151 | ||
| Breast-wise-model[18] | 23M | 0.705 ± 0.011 | 69.484 ± 2.151 | ||
| DualNet [56] | 13M | 0.705 ± 0.018 | 69.719 ± 1.863 | ||
| PHResNet18 (ours) | 13M | 0.737 ± 0.004 | 74.882 ± 1.466 | ||
| PHResNet50 (ours) | 16M | 0.739 ± 0.004 | 75.352 ± 1.409 | ||
| CBIS (肿块和钙化) | ResNet18 | 26M | 图像块 | 0.659 ±0.012 | 66.271 ± 1.271 |
| ResNet50 | 32M | 0.659 ± 0.013 | 65.217 ± 3.236 | ||
| PHResNet18 (ours) | 13M | 0.677 ± 0.005 | 68.116 ± 1.388 | ||
| PHResNet50 (ours) | 16M | 0.676 ± 0.014 | 67.062 ± 0.995 | ||
| INbreast | ResNet18 | 26M | 图像块 + CBIS | 0.789 ± 0.073 | 81.887 ± 1.509 |
| ResNet50 | 32M | 0.755 ± 0.063 | 77.358 ± 7.825 | ||
| PHResNet18 (ours) | 13M | 0.793 ± 0.071 | 83.019 ± 5.723 | ||
| PHResNet50 (ours) | 16M | 0.759 ± 0.045 | 80.000 ± 6.382 |
- Patch classifier: Preliminary experiments also include the pre training phase of patch class if i ers, which is carried out with the purpose of overcoming the problems described in Subsection IV-D and extracting crucial information concerning the lesions. Table II reports the results of these experiments. We can observe that at the patch level, there is a great gap in performance between our parameterized hyper complex models and real ones, with PHResNet50 yielding $77.338%$ accuracy, further exhibiting the ability of PHC layers to leverage latent relations between multi-dimensional inputs.
- 分块分类器：初步实验还包括分块分类器的预训练阶段，旨在解决第 IV-D 节所述问题并提取病灶关键信息。表 II 展示了这些实验结果。我们观察到在分块级别，参数化超复数模型与实数模型存在显著性能差距，其中 PHResNet50 达到了 77.338% 准确率，进一步证明了 PHC 层利用多维输入间潜在关系的能力。
B. Experiments with two views
B. 双视图实验
- State-of-the-art methods for comparison: We first compare the proposed PHResNets against the respective realvalued baseline models (ResNet18 and ResNet50) and thereafter against three state-of-the-art multi-view architectures [18], [19], [56]. The model proposed in [56] processes frontal and lateral chest X-rays, employing as backbone Dense Net 121, while methods proposed in [18], [19] are designed for mammography images. To ensure a fair comparison with our own networks, new runs were conducted for these models, following the same experimental setup, data, and pre training technique as employed for our models. Additionally, original architectures proposed in [18], [19] employ as backbone a variation of the standard ResNet50, namely ResNet22, which was designed specifically for the purpose of handling high-resolution images. However, in our case the mammograms are resized as explained in Subsection V-A, thus we straightforwardly use the more proper ResNet18 instead. Finally, since [18] proposes networks designed to handle four views, to compare this approach with ours, we employ the proposed breast-wise-model by trivially considering only half of it: instead of having four ResNet columns (one per each view and side) we consider only two columns for the CC and MLO views of one side only.
- 用于对比的先进方法：我们首先将提出的PHResNets与相应的实值基线模型（ResNet18和ResNet50）进行比较，随后再与三种先进的多视图架构[18]、[19]、[56]进行对比。[56]提出的模型处理正位和侧位胸部X光片，采用DenseNet121作为主干网络，而[18]、[19]提出的方法专为乳腺X光图像设计。为确保与我们的网络进行公平比较，这些模型按照与我们模型相同的实验设置、数据和预训练技术重新运行。此外，[18]、[19]提出的原始架构采用标准ResNet50的变体ResNet22作为主干网络，该变体专为处理高分辨率图像设计。但在我们的案例中，乳腺X光片已按第V-A小节所述调整尺寸，因此直接使用更合适的ResNet18。最后，由于[18]提出的网络设计用于处理四个视图，为将该方法与我们的方法进行比较，我们仅简单采用其提出的乳房单侧模型的一半：即仅保留单侧CC和MLO视图的两个ResNet列，而非原本四个视图（每侧各一）的四列结构。
- Results: The results of the experiments we conduct in the two-view scenario are reported in Tab. III, together with the number of parameters for each model we train.
- 结果: 我们在双视图场景下进行的实验结果与各训练模型的参数量一同呈现在表 III 中。
Firstly, the advantages of the employed pre training strategy are clear by comparing the results in the top part of the table with the part corresponding to the pre training on patches. Most importantly, the center of the table reveals that PHResNets clearly outperform both baseline counterparts implemented in the real domain and all other state-of-the-art methods, with PHResNet50 yielding 0.739 AUC and $75.352%$ accuracy in the mass split. Our approach achieves the best results also for the mass and calc splits. Although the overall performance is reduced in this case, it is expected since calcification s are harder to classify and, in fact, most works in the literature focus only on mass detection/classification [5], [13], [14], [27], [28]. In this case, PHResNet18 performs better than PHResNet50, which might be due to PHResNet50 resulting over-parameterized for the dataset. In fact, the latter achieves in general similar results to smaller PHResNet18, even in the case of the mass split. Nonetheless, in both data splits, the two highest AUC and accuracy values are obtained by the two PHResNets, demonstrating the advantages of our approach. On top of that, it is interesting to notice how our proposed models present the lowest standard deviation on AUC and accuracy over different runs, which may indicate less sensibility to initi aliz ation and generally more robustness. Moreover, we have also conducted statistical significance tests to further validate our results. For example, in the case of mass classification with pre training, the $p$ -value between PHResNet18 and ResNet18 is 0.057, while between PHResNet50 and ResNet50 is 0.022, which are both statistically significant for a significance level of 0.10. Ultimately, compared with the baseline real-valued networks, PHC-based models possess half the number of free parameters and, even so, are still able to outperform them, further proving how the hyper complex approach truly takes advantage of the correlations found in mammogram views.
首先，通过比较表格顶部与基于图像块预训练部分的结果，可以明显看出所采用预训练策略的优势。最重要的是，表格中部数据显示PHResNet系列模型在肿块分割任务中明显优于实数域实现的基线模型及其他最先进方法，其中PHResNet50取得了0.739的AUC值和75.352%的准确率。我们的方法在肿块和钙化分割任务中也取得了最佳结果。虽然钙化分类的整体性能有所下降（这符合预期，因为钙化病灶更难分类，事实上现有文献[5][13][14][27][28]大多仅关注肿块检测/分类），但PHResNet18在此表现出优于PHResNet50的性能，可能是由于PHResNet50对该数据集存在过参数化问题。值得注意的是，两种数据分割情况下，最高AUC和准确率均由PHResNet系列包揽，充分证明了本方法的优越性。此外，我们提出的模型在不同训练轮次中展现出最低的AUC和准确率标准差，表明其对初始化敏感度更低且具有更强的鲁棒性。通过统计显著性检验进一步验证了结果：在预训练后的肿块分类任务中，PHResNet18与ResNet18的p值为0.057，PHResNet50与ResNet50的p值为0.022（显著性水平0.10条件下均具有统计显著性）。最终，与实数域基线网络相比，基于PHC的模型仅需一半自由参数量即可实现更优性能，这再次验证了超复数方法在有效利用乳腺X光视图间相关性方面的优势。
TABLE IV RESULTS FOR FOUR-VIEW MODELS ON INBREAST. WE PRETRAIN MODELS ON CBIS PATCHES AS WELL AS PATCHES AND THEN WHOLE CBIS IMAGES FOR FURTHER FINE-TUNING. RESULTS INDICATED IN BOLD AND UNDERLINED TEXT REPRESENT THE BEST AND SECOND-BEST OUTCOMES.
表 4: INBREAST数据集上四视图模型的结果。我们在CBIS图像块上进行模型预训练，随后结合图像块和完整CBIS图像进行微调。加粗和下划线文本分别表示最佳和次优结果。
| 模型 | 参数量 | 预训练方式 | AUC | 准确率 (%) |
|---|---|---|---|---|
| BOnetconcat | 27M | 0.756 ± 0.047 | 70.000 ± 4.216 | |
| SEnet | 41M | 0.786 ± 0.090 | 73.333±12.824 | |
| View-wise-model[18] | 24M | 0.768 ± 0.072 | 75.333±6.182 | |
| Breast-wise-model[18] | 24M | 0.734 ± 0.027 | 72.667 ± 7.717 | |
| PHYBOnet (ours) | 7M | 0.764 ± 0.061 | 70.000 ± 7.601 | |
| PHYSEnet (ours) | 20M | 0.798 ± 0.071 | 77.333 ± 7.717 | |
| SEnet | 41M | Patches +CBIS | 0.796 ±0.096 | 79.333±8.273 |
| PHYSEnet (ours) | 20M | Patches +CBIS | 0.814 ± 0.060 | 82.000 ± 6.864 |
Then, an additional set of experiments is conducted with the INbreast dataset to further validate the proposed method. In this case, the models are initialized with the weights of the best whole-image classifier trained with CBIS-DDSM. Despite INbreast containing a very limited number of images, the features learned on CBIS-DDSM are transferred effectively so that the models are able to attain even better performance, i.e., an AUC of 0.793 and $83.019%$ accuracy obtained by PHResNet18. Also in this case, both PHResNets exceed the respective realvalued baselines and reduce the standard deviation, proving once more the general iz ability of the networks and the ability of PHC layers to draw on the relations of m ammo graphic views to achieve more accurate predictions.
随后，使用INbreast数据集进行了另一组实验以进一步验证所提方法。在此情况下，模型采用在CBIS-DDSM上训练的最佳全图分类器的权重进行初始化。尽管INbreast包含的图像数量非常有限，但从CBIS-DDSM学习到的特征被有效迁移，使得模型能够获得更优性能——PHResNet18取得了0.793的AUC值和83.019%的准确率。同样在此实验中，两种PHResNet均超越其对应的实数基线模型并降低了标准差，再次证明了网络的泛化能力以及PHC层利用乳腺摄影视图间关系实现更精准预测的能力。
Moreover, we can also observe that, throughout all the experiments with pre training, the performance of PHResNet18 and PHResNet50 is comparable. The reason for this may be that PHResNet50 might result over parameterized for the relatively small datasets employed. For this reason, for four-view architectures we adopt PHResNet18 instead of PHResNet50 as the backbone, also considering the fact that the subset of complete exams further reduces the number of examples.
此外，我们还可以观察到，在所有预训练实验中，PHResNet18 和 PHResNet50 的性能表现相当。这可能是因为 PHResNet50 在相对较小的数据集上容易出现过参数化。因此，对于四视角架构，我们采用 PHResNet18 而非 PHResNet50 作为主干网络，同时考虑到完整检查的子集会进一步减少样本数量。
To conclude, experiments presented in Tab. III serve also as an ablation study. In fact, the main component of the networks that we propose are PHC layers and by removing them the models turn out to be equivalent to their realvalued counterparts, which we have thoroughly tested in each scenario.
综上所述，表 III 中的实验也起到了消融研究的作用。实际上，我们所提出网络的主要组成部分是 PHC 层，移除这些层后，模型将等同于其对应的实值版本，这一点我们在每种场景下都进行了充分测试。
C. Experiments with four views
C. 四视图实验
- State-of-the-art methods for comparison: We first compare the proposed architectures against the respective baseline models implemented in the real domain (BOnet and SEnet), and further against two state-of-the-art approaches designed for breast cancer [18]. Specifically, we employ as comparison their best-performing model, the view-wise-model, along with the breast-wise-model, since we already consider it for the case of two views. The same considerations mentioned in Subsection VI-B1 apply herein as well: ResNet22 is replaced with ResNet18, and new runs are conducted with the same dataset and pre training procedure as our models to guarantee a fair comparison.
- 用于对比的先进方法：我们首先将提出的架构与实域中实现的基线模型（BOnet和SEnet）进行对比，并进一步与两种针对乳腺癌设计的前沿方法[18]进行比较。具体而言，我们采用其性能最佳的视图级模型（view-wise-model）和乳房级模型（breast-wise-model）作为对比基准，因为这两种模型已考虑双视图情况。第VI-B1小节提到的相同注意事项在此同样适用：将ResNet22替换为ResNet18，并采用与我们的模型相同的数据集和预训练流程重新运行实验以确保公平对比。
- Results: In Tab. IV, we can observe the number of free parameters for each model and the results on the INbreast dataset with four views. Since this is a small dataset, in order to avoid over fitting, we perform cross-validation considering 5 different splits.
- 结果：在表 IV 中，我们可以观察到每个模型的自由参数数量以及在 INbreast 数据集上四种视图的结果。由于这是一个小数据集，为了避免过拟合，我们考虑了 5 种不同的分割进行交叉验证。
The proposed PH models reach higher accuracy and AUC with respect to the equivalent real-valued baselines, achieving so with half/a quarter of the number of free parameters, thus highlighting the role that correlations between m ammo graphic views play in making the right prediction if exploited properly, as our hyper complex models are able to do. Importantly, our PHYSEnet largely outperforms all other models, attaining an AUC of 0.798 and accuracy of $77.333%$ , proving how the simultaneous exploitation of ips i lateral views, related to PHC layers, and the shared weights between bilateral views of the encoder model results in a more performing classifier. Indeed, PHYSEnet has an initial deep patient-level block that encodes view embeddings by sharing weights between the two sides, providing a more powerful representation with respect to the ones given by the breast-level encoders of PHYBOnet. Interestingly, our second proposed network, PHYBOnet with $n=4$ , is also able to compete with the best models in the state-of-the-art, surpassing the breast-wise model and having overall comparable performance with only 7M parameters. Furthermore, we have performed statistical significance tests to corroborate our findings. For example, the $p$ -value between PHYSEnet and the state-of-the-art Breast-wise-model is 0.076 which is statistically significant for a significance level of 0.10.
所提出的PH模型在达到同等实值基线更高准确率和AUC的同时，仅需一半/四分之一的可训练参数量，这凸显了乳腺影像视图间相关性在正确预测中的关键作用——当这些相关性被恰如我们的超复数模型这般有效利用时。值得注意的是，PHYSEnet显著优于所有其他模型，取得了0.798的AUC和77.333%的准确率，这证明了同时利用与PHC层相关的同侧视图信息，以及编码器模型中双侧视图间权重共享机制，能构建出性能更优的分类器。实际上，PHYSEnet通过初始的深度患者级模块，在双侧视图间共享权重来编码视图嵌入，相比PHYBOnet的乳房级编码器能生成更具表现力的特征表示。有趣的是，我们提出的第二个网络PHYBOnet（n=4）仅用700万参数就与当前最优模型性能相当，超越了乳房级模型。此外，我们进行了统计显著性检验以验证结论：例如PHYSEnet与当前最优乳房级模型间的p值为0.076，在0.10显著性水平上具有统计显著性。
Ultimately, we also test the most performing architecture, that is PHYSEnet, together with its equivalent implemented in the real domain, using as initialization the weights of the best whole-image two-view model trained with CBIS-DDSM. Both models benefit from the learned features on whole images instead of patches, gaining a boost in performance. However, the greater improvement is attained by the PHC version of the network, which once again surpasses the performance of all other experiments with an AUC of 0.814 and accuracy of $82%$ .
最终，我们还测试了性能最佳的架构PHYSEnet及其在实数域中的等效实现，使用在CBIS-DDSM上训练的最佳全图双视图模型的权重进行初始化。两种模型都受益于在全图上而非图像块上学到的特征，从而获得了性能提升。然而，PHC版本的网络取得了更大的改进，再次以0.814的AUC和$82%$的准确率超越了所有其他实验的性能。
In conclusion, by comparing our method against the respective real-valued models in Tab. IV, these experiments also serve as ablation studies, as explained in Section VI-B2.
总之，通过与表 IV 中各自的实值模型进行比较，这些实验也可作为消融研究，如第 VI-B2 节所述。
D. Generalizing beyond mammograms
D. 超越乳腺X光片的泛化
We conduct three additional sets of experiments to further validate the efficacy of the proposed method and its generalizability to different medical scenarios and on a finer-scaled task, i.e., segmentation.
我们进行了三组额外实验，以进一步验证所提方法的有效性及其在不同医疗场景下的泛化能力，以及在更精细任务（即分割任务）上的表现。
- Multi-view multi-label chest $X$ -ray classification: The task consists in classifying the 14 most common chest diseases from multi-view X-rays. The evaluation is then conducted on a subset of five labels according to the original task [40]. Since the exam comprises two views, we employ a PHResNet with $n=2$ and compare it against its real-valued counterpart. As shown in Tab. V, PHResNet outperforms the real-valued ResNet, achieving an AUC of 0.722. We additionally compare our approach with the single-view model that won the CheXpert challenge, i.e., DeepAUC [57], which directly trains their network to classify the five evaluation labels instead of the whole 14. Their model is a single-view architecture, and the best performance was achieved through an ensemble of networks. To ensure a fair comparison, we conduct a new run using a single model and compare it with our approach, i.e., PHDeepAUC with $n=2$ , which is a multiview adaptation of DeepAUC operating in the hyper complex domain. Additionally, we modify the original DeepAUC to handle multiple views for a more straightforward comparison with our method. As can be seen in Tab. V, PHDeepAUC yields the highest AUC of 0.867, outperforming the best model proposed in the original challenge. Moreover, it is noteworthy that the multi-view version of DeepAUC performs worse than the original single-view model. Indeed, as described in Section II, these types of networks tend to overfit on one of the two views and, because of this, it might occur that the single-view model surpasses its multi-view respective [19], as it happens in this example. This result further validates the efficacy of our multi-view approach based on hyper complex algebra, which instead effectively exploits information from both views and thus outperforms both multi-view and singleview state-of-the-art DeepAUC.
- 多视角多标签胸部X光分类：该任务旨在从多视角X光片中分类14种最常见胸部疾病。根据原始任务[40]，评估在五个标签子集上进行。由于检查包含两个视角，我们采用$n=2$的PHResNet模型，并与其实数版本进行对比。如表V所示，PHResNet以0.722的AUC值优于实数版ResNet。我们还与赢得CheXpert挑战赛的单视角模型DeepAUC[57]进行了对比，该模型直接训练网络分类五个评估标签而非全部14个标签。其最佳性能通过模型集成实现，为保障公平比较，我们使用单一模型重新运行测试。同时构建了超复数域下的多视角适配版本PHDeepAUC ($n=2$)，并将原始DeepAUC修改为多视角版本以便直接对比。如表V所示，PHDeepAUC以0.867的AUC值超越原挑战赛最佳模型。值得注意的是，多视角版DeepAUC性能反而不及原单视角模型。如第II节所述，此类网络易在某一视角上过拟合，导致单视角模型可能优于多视角版本[19]，本例即印证该现象。该结果进一步验证了基于超复数代数的多视角方法的有效性——我们的方案能充分利用双视角信息，从而在性能上超越多视角与单视角的state-of-the-art DeepAUC模型。
Finally, these results prove the general iz ability of the proposed method with respect to other types of medical exams. In other words, the ability of hyper complex networks to learn a more effective representation of a multi-view exam remains consistent across different medical imaging scenarios, such as chest $\mathrm{\DeltaX}$ -rays.
最后，这些结果证明了所提方法在其他类型医学检查上的泛化能力。换言之，超复数网络学习多视图检查更有效表征的能力，在不同医学影像场景（如胸部 $\mathrm{\DeltaX}$ 光片）中保持一致。
- Multimodal overall survival prediction: For this set of experiments, we consider one of the official tasks of the BraTS19 challenge [50], which is the prediction of the overall survival (OS) in number of days for each patient. The task evaluation is done considering three different classes: shortterm (less than 10 months), mid-term (between 10 and 15 months), and long-term (more than 15 months) survivors. For this task, we employ a PHResNet18 3D, thus defining 3D parameterized hyper complex convolutions. Specifically, the input consists of two modalities, T2 and FLAIR, and the age parameter. The volumes are processed by the PHResNet18 3D for which we set $n=2$ , while the age input is handled by a linear layer. Then, the learned features of the MRIs and the age are summed together [51] and processed by two fully connected layers to produce the final output, i.e., the estimated number of survival days. We train this architecture and its real-valued respective, ResNet18 3D, with an MSE loss. Moreover, we compare our method against a state-of-the-art architecture, Post-hoc [51], for which we conduct a new run, and its counterpart in the hyper complex domain, PH Posthoc. They employ as input the volumes corresponding to all four modalities provided by BraTS19 and the age parameter. Thus, we set the hyper parameter $n=4$ for the branch that processes the MRIs, and $n=1$ for the PHM layer that handles the age input. All the models are evaluated through the official online evaluation platform of the challenge on the provided validation set and the results are reported in Tab. VI. Both hyper complex networks surpass their respective realvalued counterparts, with PHResNet18 3D achieving the highest accuracy 0.517, surpassing the state-of-the-art approach in both real and hyper complex domains. Importantly, PH Post-hoc, which comprises only 91K parameters, outperforms ResNet18 3D, which instead has 33M parameters, further highlighting the power of exploiting not only global relations, as standard neural networks, but also local relations, thanks to hyper complex operations.
- 多模态总体生存期预测：本组实验基于BraTS19挑战赛[50]的官方任务之一，即预测每位患者以天为单位的总体生存期(OS)。任务评估采用三类划分：短期(小于10个月)、中期(10至15个月)和长期(超过15个月)生存者。我们采用PHResNet18 3D架构，定义三维参数化超复数卷积运算。具体输入包含T2和FLAIR两种模态及年龄参数，其中影像数据由PHResNet18 3D处理(设$n=2$)，年龄参数通过线性层处理。随后将MRI学习特征与年龄特征相加[51]，经两个全连接层生成最终输出(预估生存天数)。该架构及其实数域对应模型ResNet18 3D均采用MSE损失函数训练。我们与先进架构Post-hoc51及其超复数域变体PH Post-hoc进行对比，后者输入采用BraTS19提供的全部四种模态影像及年龄参数，故设置MRI处理分支超参数$n=4$，年龄处理PHM层$n=1$。所有模型均通过挑战赛官方在线验证平台评估，结果如Tab. VI所示。两个超复数网络均超越其实数域对应模型，其中PHResNet18 3D以0.517准确率创最优，同时超越实数域和超复数域现有方法。值得注意的是，仅含91K参数的PH Post-hoc优于3300万参数的ResNet18 3D，这凸显了超复数运算不仅能捕捉标准神经网络的全局关系，还能利用局部关系的优势。
TABLE V RESULTS FOR MULTI-VIEW MULTI-LABEL CLASSIFICATION ON CHEXPERT.
表 5: CHEXPERT数据集上的多视图多标签分类结果
| 模型 | 参数量 | AUC |
|---|---|---|
| ResNet18 | 11M | 0.645 ± 0.164 |
| PHResNet18 | 5M | 0.722 ± 0.184 |
| DeepAUC (单视图) [57] | 6M | 0.834 ± 0.002 |
| DeepAUC (多视图) | 6M | 0.820 ± 0.012 |
| PHDeepAUC (n=2) | 3M | 0.867 ± 0.009 |
TABLE VI RESULTS FOR OS PREDICTION ON OFFICIAL VALIDATION DATASET OFBRATS19.
| Model | Params | Accuracy |
| Post-hoc [51] | 310K | 0.414 |
| PH Post-hoc (n = 4) | 91K | 0.448 |
| ResNet183D | 33M | 0.414 |
| PHResNet18 3D (n = 2) | 16M | 0.517 |
表 6: BRATS19官方验证数据集上的OS预测结果
| 模型 | 参数量 | 准确率 |
|---|---|---|
| Post-hoc [51] | 310K | 0.414 |
| PH Post-hoc (n = 4) | 91K | 0.448 |
| ResNet183D | 33M | 0.414 |
| PHResNet18 3D (n = 2) | 16M | 0.517 |
To conclude, the experiment results in Tab. VI prove the flexibility of the method with respect to a different task, i.e., regression, and medical exam, i.e., brain MRI, as the hyper complex networks far exceed the respective models in the real domain. Finally, these results also show that the proposed architectures can not only learn good representations from different views, i.e., a different angle of the same subject, but also from multiple modalities, i.e., the same view but containing different information.
综上所述，表 VI 中的实验结果证明了该方法在不同任务（即回归）和医学检查（即脑部 MRI）方面的灵活性，因为超复数网络远超实数域中的相应模型。最后，这些结果还表明，所提出的架构不仅可以从不同视角（即同一主题的不同角度）学习良好表征，还能从多模态数据（即相同视角但包含不同信息）中学习。
Fig. 7. From the left, a sample exam from the INbreast dataset containing a benign calcification on the left side and a malignant mass on the right side. Then, activation maps to visualize the learned latent representations of PHYSEnet and SEnet at encoder and classifier level. Lastly, the saliency map for PHYSEnet containing the most relevant pixels according to the gradient.
图 7: 从左至右依次为：INbreast数据集中包含左侧良性钙化和右侧恶性肿块的样本图像；PHYSEnet和SEnet在编码器与分类器层级学习到的潜在表征可视化激活图；基于梯度计算的PHYSEnet显著性图（突出显示最相关像素）。
TABLE VII RESULTS FOR BRAIN TUMOR SEGMENTATION ON BRATS19.
表 7: BRATS19 脑肿瘤分割结果
| Model | Params | Dice Score |
|---|---|---|
| UNet | 31M | 0.826 ± 0.017 |
| PHUNet | 15M | 0.825 ± 0.018 |
- Multimodal brain tumor segmentation: Lastly, in this section, we demonstrate how this framework can easily be extended for different tasks and employed with any network architecture. To this end, we conduct experiments regarding brain tumor segmentation from multimodal slices extracted from MRI volumes, specifically focusing on whole-tumor segmentation, one of the tasks of the original challenge. We define the more appropriate UNet [58] in the hyper complex domain, i.e. PHUNet, and set the parameter $n=2$ considering the same modalities as for the OS prediction. The two models in the real and hyper complex domain yield a very similar Dice score average of about $83%$ on BraTS19 [41], as reported in Tab. VII, proving the validity of the proposed approach also for finer-scaled tasks. Moreover, we believe these results can be further improved in future works that mainly focus on tasks such as detection and segmentation, employing more complex networks and extending to a 3D segmentation scenario.
- 多模态脑肿瘤分割：最后，在本节中，我们展示了该框架如何轻松扩展到不同任务并与任何网络架构结合使用。为此，我们针对从MRI体积中提取的多模态切片进行脑肿瘤分割实验，特别关注全肿瘤分割这一原始挑战任务之一。我们在超复数域中定义了更合适的UNet [58]，即PHUNet，并设置参数$n=2$，考虑与OS预测相同的模态。如Tab. VII所示，实数域和超复数域的两种模型在BraTS19 [41]上获得了非常相似的Dice分数平均值（约$83%$），证明了该方法在更精细任务中的有效性。此外，我们认为这些结果可以在未来工作中通过采用更复杂的网络并扩展到3D分割场景，主要聚焦于检测和分割等任务来进一步提升。
VII. VISUALIZING MULTI-VIEW LEARNING
VII. 多视图学习可视化
In this section, we provide a visualization of how the hypercomplex models are able to model information from different views, depicted in Fig. 7. Specifically, we employ our bestperforming model PHYSEnet and compare it against its realvalued counterpart SEnet. We consider a patient from INbreast with a benign finding in the left breast and a malignant mass in the right breast. We show the activation maps at two different levels of the architecture, i.e., after the encoder and after the refiner blocks (classifier). We obtain the activation maps by computing the average of feature channels. Regarding the left views, by observing the activation maps of PHYSEnet, especially at the encoder level, we can see how it has learned a more focused representation, as the regions corresponding to the benign calcification are highlighted. While in the maps of SEnet, all areas of the breast are accentuated. But most importantly, in the right views the multi-view learning ability of the hyper complex model is more visible. In fact, from the activation maps of PHYSEnet, it is clear that the network is learning from both views, as two areas are highlighted, corresponding to the location of the mass in the CC view and the MLO view. On the other hand, in the activation maps of SEnet, only one highlighted area appears, corresponding to the CC view only. Thus, it seems that the real model, unlike the PH network, is relying on only one view, not truly leveraging both views, as it also appears from Fig. 1. Moreover, sometimes a mass is visible only in one of the two views [3], [6]. In these situations, if the network has predominantly learned to depend on information from just one view, e.g., the CC view, it might mis classify cases where the mass is exclusively visible in the other view, e.g., the MLO view. This challenge is commonly encountered in multiview breast cancer analysis, as elaborated in Section II and documented in the existing literature [5], [19]. Precisely for this reason, we propose the use of hyper complex algebra to address this issue and enable the network to effectively learn from both views without over fitting to one view type.
在本节中，我们通过图7展示了超复数模型如何从不同视角建模信息。具体而言，我们采用性能最佳的PHYSEnet模型，并与其实数值对照模型SEnet进行比较。研究对象为INbreast数据库中一名左乳良性病灶、右乳恶性肿块的患者。我们展示了架构中两个不同层级的激活图：(1) 编码器输出层；(2) 优化块（分类器）输出层。激活图通过计算特征通道平均值获得。
在左乳视角中，通过观察PHYSEnet的激活图（特别是编码器层级），可见其学习了更聚焦的表征——良性钙化对应区域被显著激活，而SEnet的激活图则强化了整个乳房区域。更重要的是，在右乳视角中，超复数模型的多视角学习能力更为显著。PHYSEnet的激活图清晰显示网络同时从CC视图和MLO视图中学习，肿块在两个视图中的对应位置均被高亮标注；而SEnet仅显示CC视图对应的单个激活区域。这表明与PH网络不同，实值模型仅依赖单一视图（如图1所示），未能真正利用双视图信息。
值得注意的是，临床实践中肿块可能仅在某单一视图中可见 [3][6]。若网络过度依赖特定视图（如CC视图），则可能误判仅在其他视图（如MLO视图）中显现的肿块病例。这正是多视角乳腺癌分析的常见挑战（如第II节所述 [5][19]）。为此，我们提出采用超复数代数方法，使网络能均衡学习双视图特征，避免对单一视图类型的过拟合。
Finally, for the hyper complex network, we additionally compute the saliency map in Fig. 7. Moreover, we provide saliency maps and visualization s obtained with Grad-CAM [59] for different patients in Fig. 8, comparing the realvalued SEnet against its hyper complex respective PHYSEnet. Saliency maps are computed for each side separately, using gradients of the class-dependent output over the input [60] in order to visualize which area of the two-view input is most influential for the model decision. By looking at the last column of Fig. 7 we can see in the right side the highlighted pixels that indeed correspond to the malignant mass, while the left-side map is darker and no pixel region is particularly accentuated since there are no malignant findings in the left breast. Interestingly, the maps for the left side differ between activation maps and saliency maps. This point highlights how the learned representation, visualized as activation maps, leverages patient-level information, i.e. from both sides, while the classification decision visualized in the saliency map has no highlighted area as the left view is classified as benign. In conclusion, by considering two well-established explain able techniques in Fg. 8, we further validate the visualization s provided in Fig. 1 and Fig. 7. In fact, also from these maps, it is evident how the proposed approach has the ability to effectively model local relations between views. On the contrary, the real-valued network seems to overfit on the CC view, which is indeed a typical behavior and challenge encountered in the literature [19] that we specifically address in this paper through our hyper complex architectures.
最后，针对超复数网络，我们在图7中额外计算了显著图。此外，图8展示了使用Grad-CAM [59] 为不同患者生成的显著图与可视化结果，将实数版SEnet与其对应的超复数版PHYSEnet进行对比。显著图分别对双侧单独计算，通过输入数据上类别相关输出的梯度 [60] 来可视化双视角输入中对模型决策影响最大的区域。观察图7最后一列可见，右侧高亮像素确实对应恶性肿块，而左侧图谱较暗且无特别突出的像素区域——因为左乳并无恶性病灶。值得注意的是，左侧的激活图与显著图存在差异。这一点揭示了学习表征（以激活图呈现）如何利用患者层面的双侧信息，而显著图中呈现的分类决策（因左视图被判定为良性）则无高亮区域。综上所述，通过图8中两种成熟的可解释性技术，我们进一步验证了图1与图7提供的可视化结果。事实上，这些图谱也清晰表明：所提方法能有效建模视图间的局部关联。相比之下，实数网络似乎对CC视图存在过拟合，这正是文献 [19] 中记载的典型现象与挑战——本文通过超复数架构对此进行了针对性解决。
TABLE VIII MODELS USE CASES SUMMARY. THE TICKS $\checkmark$ MEAN THAT THE MODEL CAN BE ADOPTED IN THE SPECIFIC CASE IF OUR PRETRAINED WEIGHTS ARE EMPLOYED. THIS IS BECAUSE WITHOUT ROI ANNOTATIONS IT IS NOT POSSIBLE TO TRAIN A PATCH CLASSIFIER, THUS THE PRE TRAINING STAGE CANNOT BE PERFORMED.
表 VIII: 模型用例总结。标记 $\checkmark$ 表示如果采用我们的预训练权重，该模型可用于特定场景。这是因为在没有 ROI (Region of Interest) 标注的情况下无法训练 patch 分类器，因此无法执行预训练阶段。
| 用例 | PHResNet18 | PHResNet50 | PHYBOnet | PHYSEnet |
|---|---|---|---|---|
| 单视图 | ||||
| 双视图 | √ | × | ||
| 四视图 | × | √ | ||
| 有 ROI 标注 | √ | |||
| 无 ROI 标注 | √ | √ | √ | |
| 低内存占用 | ||||
| 小规模数据集 | √ | |||
| 其他问题 |
VIII. HOW DO I CHOOSE THE BEST MODEL FOR MY DATA?
VIII. 如何为我的数据选择最佳模型？
In this section, we aim at answering the reader question Which model do I employ on my data and for my problem?
在本节中，我们旨在回答读者的问题：我应该针对我的数据和问题使用哪种模型？
We consider multiple scenarios, including datasets with 1, 2, or 4 views, whether ROI annotations are available or not, the memory constraints, the size of the dataset, and whether the proposed models are easily exportable to other kinds of medical imaging problems. Table VIII reports the applicability of each network we propose in the above-mentioned scenarios. In detail, the main difference between PHYBOnet and PHYSEnet lies in their complexity and parameter count. PHYBOnet is designed as a lightweight model comprising only 7 million parameters. Despite its reduced complexity, PHYBOnet exhibits competitive performance, as demonstrated by the experimental results shown in Section VI-C2. In contrast, PHYSEnet is a more intricate model with 20 million parameters that stands out as the top-performing model among all the networks tested, as indicated in Section VI-C2. In summary, the main advantage of PHYBOnet is its lightweight nature, which allows it to be computationally efficient while still delivering competitive results thanks to the ability to exploit both global and local relations. While PHYSEnet, with its larger parameter count and the same ability, excels in terms of performance. Moreover, while we prove the crucial role of pre training for breast cancer classification tasks, especially when only scarce data is available, this is only applicable in the case of datasets with provided ROI annotations. Nevertheless, our methods can be applied even in datasets where ROI observations are missing, since we provide pretrained models and weights1 to overcome this limitation. We believe that Table VIII may help the reader clarify which model better fits specific cases and may increase the usability of our approach in future research and in different medical fields.
我们考虑了多种场景，包括具有1、2或4个视图的数据集，是否提供ROI标注，内存限制，数据集规模，以及所提模型能否轻松迁移到其他类型的医学影像问题。表VIII展示了我们提出的各网络在上述场景中的适用性。具体而言，PHYBOnet与PHYSEnet的主要区别在于复杂性和参数量。PHYBOnet被设计为仅含700万参数的轻量级模型，尽管复杂度降低，如第VI-C2节实验结果所示，它仍展现出具有竞争力的性能。相比之下，PHYSEnet是包含2000万参数的更复杂模型，如第VI-C2节所示，它在所有测试网络中表现最佳。总之，PHYBOnet的主要优势在于其轻量特性，这使其在保持计算效率的同时，通过利用全局和局部关系的能力仍能提供有竞争力的结果。而PHYSEnet凭借更多参数和相同能力，在性能方面表现更优。此外，虽然我们证明了预训练对乳腺癌分类任务的关键作用（特别是在数据稀缺时），但这仅适用于提供ROI标注的数据集。尽管如此，我们的方法仍可应用于缺失ROI标注的数据集，因为我们提供了预训练模型和权重1来克服这一限制。我们相信表VIII能帮助读者明确哪种模型更适合特定案例，并可能提升我们方法在未来研究和不同医学领域中的可用性。
Fig. 8. Saliency and Grad-CAM maps of different patients. Circles indicate malignant masses, while red and yellow correspond to the CC and MLO view, respectively. We show the saliency maps and visualization s obtained with Grad-CAM of SEnet and PHYSEnet. By looking at the highlighted areas, it is visible from both explain ability techniques that the hyper complex network effectively models local relations, i.e. the complementary information contained in the two views, unlike its real-valued counterpart.
图 8: 不同患者的显著性和 Grad-CAM 热力图。圆圈表示恶性肿块，红色和黄色分别对应 CC 视图和 MLO 视图。我们展示了 SEnet 和 PHYSEnet 通过 Grad-CAM 获得的显著性图谱和可视化结果。通过观察高亮区域可以看出，这两种可解释性技术都表明超复数网络能有效建模局部关系（即两个视图包含的互补信息），而其实数值对应模型则不具备这种特性。
IX. CONCLUSIONS
IX. 结论
In this paper, we have introduced an innovative approach for breast cancer classification that handles multi-view mammograms as radiologists do, thus leveraging information contained in ips i lateral views as well as bilateral. Thanks to hyper complex algebra properties, neural models are endowed with the capability of capturing and truly exploiting correlations between views and thus outperforming state-of-theart models. At the same time, we demonstrate how our approach generalizes considering different imaging exams as well as proving its efficacy on finer-scaled tasks, while also being flexible to be adopted in any existing neural network. For future work, it would be interesting to extend to an unsupervised learning scenario and expand the work done on finer-scaled tasks considering more recent models, such as transformer-based networks. We believe that our approach is a real breakthrough for this research field and that it may pave the way to novel methods capable of processing medical imaging exams with techniques closer to radiologists and to human understanding.
本文提出了一种创新的乳腺癌分类方法，该方法像放射科医生一样处理多视角乳腺X光片，从而利用同侧视图和双侧视图中的信息。得益于超复数代数特性，神经模型能够捕获并真正利用视图间的相关性，从而超越了现有最优模型。同时，我们展示了该方法如何推广到不同的影像检查，并证明了其在更精细任务上的有效性，同时具有灵活适配任何现有神经网络的特性。未来工作可延伸至无监督学习场景，并基于更新模型（如基于Transformer的网络）扩展更精细任务的研究。我们相信该方法为该研究领域带来了真正突破，可能为开发出更接近放射科医生和人类理解方式的医学影像处理方法开辟新途径。
