Model Merging in Pre-training of Large Language Models

大语言模型预训练中的模型合并

Abstract

摘要

Model merging has emerged as a promising technique for enhancing large language models, though its application in large-scale pre-training remains relatively unexplored. In this paper, we present a comprehensive investigation of model merging techniques during the pre-training process. Through extensive experiments with both dense and Mixture-of-Experts (MoE) architectures ranging from millions to over 100 billion parameters, we demonstrate that merging checkpoints trained with constant learning rates not only achieves significant performance improvements but also enables accurate prediction of annealing behavior. These improvements lead to both more efficient model development and significantly lower training costs. Our detailed ablation studies on merging strategies and hyper parameters provide new insights into the underlying mechanisms while uncovering novel applications. Through comprehensive experimental analysis, we offer the open-source community practical pre-training guidelines for effective model merging.

模型合并已成为增强大语言模型的一项前景广阔的技术，但其在大规模预训练中的应用仍相对未被探索。本文全面研究了预训练过程中的模型合并技术。通过对参数规模从数百万到超过1000亿的密集结构和专家混合 (MoE) 架构进行大量实验，我们发现：使用恒定学习率训练的检查点进行合并不仅能显著提升性能，还能准确预测退火行为。这些改进既能提高模型开发效率，又能大幅降低训练成本。我们对合并策略和超参数的详细消融研究为底层机制提供了新见解，同时揭示了新颖应用。通过全面的实验分析，我们为开源社区提供了有效的模型合并实用预训练指南。

Date: May 18, 2025 Correspondence: Yunshui Li at liyunshui@bytedance.com

日期：2025年5月18日
通讯作者：Yunshui Li (liyunshui@bytedance.com)

1 Introduction

1 引言

Modern large language models (LLMs) [1, 12, 36, 40, 48] have demonstrated remarkable capabilities with widespread applications across diverse tasks. Despite their exceptional performance in fundamental tasks, LLMs still face several critical challenges, including the extensive pre-training costs, discounted effectiveness of domain-specific post-training, imprecisely-predictable performance scaling, as well as the instability of large-scale training. Model merging [49], as a relatively young topic, presents a promising approach to alleviate these practical challenges.

现代大语言模型 [1, 12, 36, 40, 48] 已展现出卓越能力，并在多种任务中得到广泛应用。尽管在基础任务中表现优异，大语言模型仍面临若干关键挑战，包括高昂的预训练成本、领域微调效果不佳、性能扩展难以精确预测，以及大规模训练的不稳定性。模型融合 [49] 作为新兴研究方向，为解决这些实际问题提供了可行路径。

Recently, the benefits of model merging have been primarily studied in the post-training stage, where several models fine-tuned on different downstream tasks are combined into a single but more versatile model [18, 51, 57]. For example, using the DARE [51] method to merge WizardLM [45] with WizardMath [29] shows a significant performance enhancement on GSM8K [7], raising its score from 2.2 to 66.3. In contrast, research on model merging during the pre-training phase remains scarce. Such pre-training merging typically involves combining checkpoints from a single training trajectory, as explored in LAWA [23] which utilizes model merging to accelerate the LLM training. However, as the model and data scales dramatically, independent researchers struggle to evaluate model merging’s impact on large-scale models, mainly due to limited access to intermediate checkpoints from extensive pre-training. Although DeepSeek [26] and LLaMA-3 [11] have both indicated their employment of model merging techniques for model development, detailed information regarding these techniques has not been publicly disclosed.

最近，模型合并的优势主要在研究后训练阶段得到验证，该阶段将针对不同下游任务微调的多个模型合并为一个更具通用性的单一模型 [18, 51, 57]。例如，使用 DARE [51] 方法合并 WizardLM [45] 和 WizardMath [29] 后，模型在 GSM8K [7] 上的性能显著提升，得分从 2.2 跃升至 66.3。相比之下，预训练阶段的模型合并研究仍较为匮乏。此类预训练合并通常涉及整合单一训练轨迹中的检查点，如 LAWA [23] 通过模型合并加速大语言模型训练所探索的方案。然而，随着模型规模和数据量的急剧增长，独立研究者难以评估模型合并对大规模模型的影响，主要受限于获取大规模预训练中间检查点的渠道。尽管 DeepSeek [26] 和 LLaMA-3 [11] 均声明采用模型合并技术进行模型开发，但相关技术细节尚未公开披露。

In this work, we mainly focus on model merging during the pre-training stage, introducing Pre-trained Model Average (PMA), a novel strategy for model-level weight merging during pre-training. To comprehensively evaluate PMA, we trained a diverse set of LLMs of varying sizes and architectures from scratch, including Dense models [11] with parameters spanning from 411M to 70B, as well as Mixture-of-Experts (MoE) architectures [38] with activated/total parameters ranging from 0.7B/7B to 20B/200B. We first investigate the performance impact of PMA and establish systematic evaluations across different phases of the warmup-stable-decay (WSD) learning schedule, which lately becomes a popular choice of $_{l r}$ scheduler for LLM pre-training since [15]. Experimental results demonstrate that model merging during the stable training phase yields consistent performance gains at different training steps. More remarkably, applying PMA at early-stage of the cosine-decay phase usually achieve comparable or even superior performance to their final-stage annealing counterparts. These findings suggest that during the extensively lengthy pre-training stage with constant lr, PMA can serve as a fast, reliable yet low-cost simulator for the annealed performance, enabling both faster validation cycles and significant computational savings.

在本工作中，我们主要关注预训练阶段的模型合并，引入了预训练模型平均（PMA），这是一种在预训练期间进行模型级权重合并的新策略。为了全面评估PMA，我们从头开始训练了多种不同规模和架构的大语言模型，包括参数范围从411M到70B的Dense模型[11]，以及激活/总参数范围从0.7B/7B到20B/200B的混合专家（MoE）架构[38]。我们首先研究了PMA对性能的影响，并在预热-稳定-衰减（WSD）学习计划的不同阶段建立了系统评估，该计划自[15]以来已成为大语言模型预训练中$_{l r}$调度器的流行选择。实验结果表明，在稳定训练阶段进行模型合并可以在不同的训练步骤中获得一致的性能提升。更值得注意的是，在余弦衰减阶段的早期应用PMA通常可以达到甚至优于最终阶段退火对应模型的性能。这些发现表明，在持续学习率下进行长时间预训练时，PMA可以作为一种快速、可靠且低成本的退火性能模拟器，既能加快验证周期，又能显著节省计算资源。

Building upon our PMA framework, we first evaluate its performance with various prevalent merging strategies, including Simple Moving Average (SMA) [20], Weighted Moving Average (WMA) [32] and Exponential Moving Average (EMA) [17]. Notably, our experiments demonstrate that the performance differences among these methods gradually become negligible. We further investigate how these important factors of PMA, namely, the interval between each merging checkpoint, the number of models involved in merging, and the size of the model, would affect merging performance. Our analysis reveals two important findings: First, the optimal merging interval exhibits a clear scaling relationship with model size. Second, incorporating more checkpoints in the merging process consistently improves performance once training is completed.

基于我们的PMA框架，我们首先评估了其与多种主流合并策略的性能表现，包括简单移动平均(SMA) [20]、加权移动平均(WMA) [32]和指数移动平均(EMA) [17]。值得注意的是，实验表明这些方法之间的性能差异逐渐变得微不足道。我们进一步研究了PMA的关键因素——每次合并检查点之间的间隔、参与合并的模型数量以及模型规模——如何影响合并性能。分析揭示了两个重要发现：首先，最优合并间隔与模型规模存在明显的比例关系；其次，在训练完成后，合并更多检查点能持续提升性能。

Furthermore, we also investigated whether PMA could produce more effective initialization weights for the consecutive continued training (CT) or supervised fine-tuning (SFT) [42] stages to enhance the downstream model performance. We practically observed that entering CT and SFT stages with PMA applied could yield smoother GradNorm curves, which thus helps stabilize the training dynamics yet without harming the performance, compared to initializing these stages with the latest available checkpoint as usual. This finding inspire a novel application of model merging for training stabilization, which we dubbed as PMA-init. We demonstrate that in scenarios when the LLM training experiences severe irrecoverable loss spikes with broken training dynamics, applying PMA-init over $N$ preceding checkpoints to resume training, enables reliable recovery from unstable training trajectories.

此外，我们还研究了PMA是否能通过为后续持续训练(CT)或有监督微调(SFT)[42]阶段生成更有效的初始化权重来提升下游模型性能。实际观察发现，与常规采用最新检查点初始化相比，应用PMA进入CT和SFT阶段能产生更平滑的GradNorm曲线，从而在保持性能的同时稳定训练动态。这一发现启发了模型合并技术用于训练稳定的创新应用，我们将其命名为PMA-init。实验证明，当大语言模型训练遭遇不可恢复的严重损失峰值且训练动态崩溃时，对前$N$个检查点应用PMA-init恢复训练，能够可靠地从不稳定训练轨迹中实现恢复。

In summary, our paper makes the following key contributions:

总之，我们的论文做出了以下关键贡献：

2 Related Work

2 相关工作

Model merging is an emerging field undergoing rapid development, with diverse applications across various domains. Typically, model merging is implemented during the post-training phase [18, 51, 57], where multiple models fine-tuned on different downstream tasks are combined by merging their weights. This process effectively integrates the distinct capabilities of each individual model, resulting in a unified model that exhibits robust and comprehensive performance.

模型合并是一个快速发展的新兴领域，在各领域具有多样化应用。通常，模型合并是在训练后阶段[18, 51, 57]实施的，通过合并权重将针对不同下游任务微调的多个模型组合起来。该过程能有效整合各独立模型的独特能力，最终形成具有强大综合性能的统一模型。

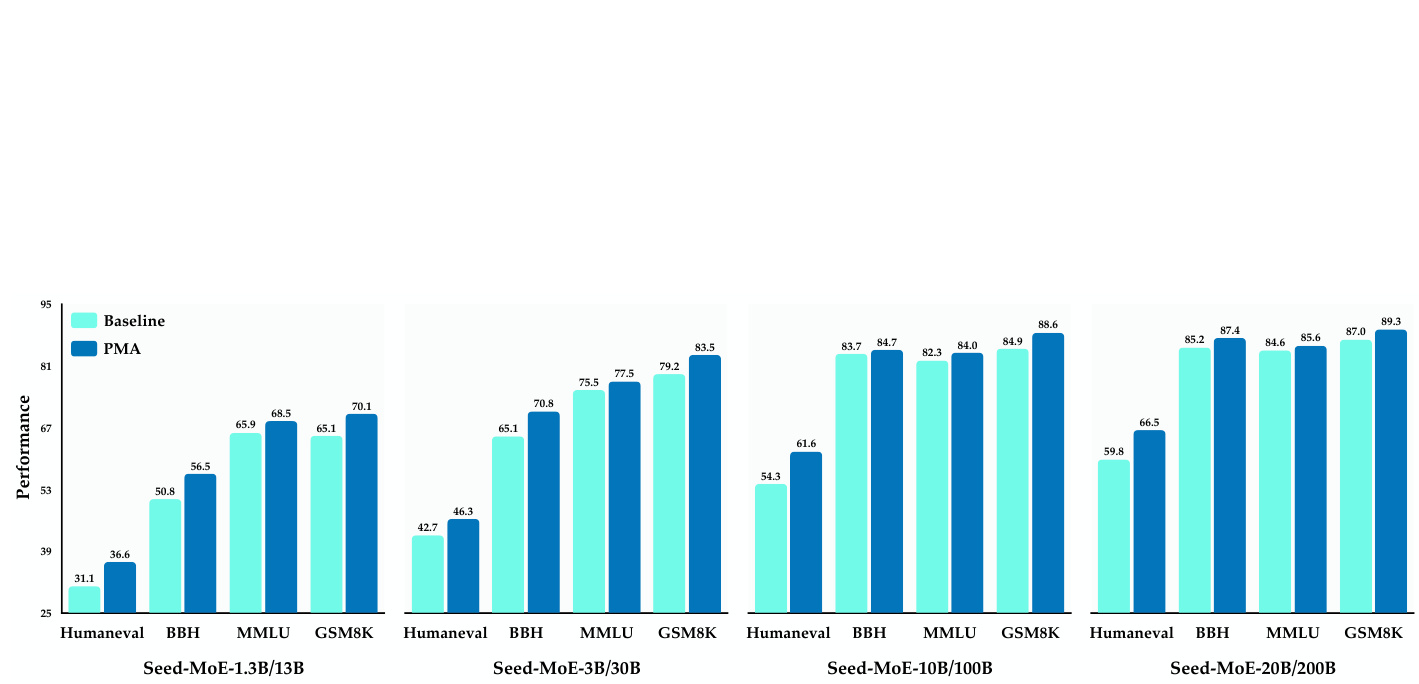
Figure 1 Comparison of downstream task performance for MoE models of varying sizes under stable training, before and after model merging.

图 1: 模型合并前后，不同规模MoE模型在稳定训练下的下游任务性能对比。

Recently, several methods have advanced this field significantly. For instance, Task Arithmetic [18], TiesMerging [46], and AdaMerging [50] integrate Vision Transformer (ViT) models [9] trained on distinct visual classification tasks, producing a single model capable of multi-task object classification. PAPA [21] integrates the broad applicability of ensembling with the computational efficiency of weight averaging. MetaGPT [57] frames model merging as a multi-task learning problem, aiming to minimize the average loss between the merged model and individual task-specific models. Fisher Merging [30] employs a weighted fusion of model parameters, with weights determined by the Fisher information matrix. RegMean [19] elegantly addresses the merging process by formulating it as a linear regression problem solvable through closed-form solutions. Evolutionary-model-merge [2] efficiently optimizes merging coefficients using evolutionary algorithms. Additionally, DARE [51] merges multiple task-specific language models into a versatile unified model by randomly dropping and subsequently rescaling the delta parameters.

近期，多项研究显著推动了该领域发展。例如，Task Arithmetic [18]、TiesMerging [46] 和 AdaMerging [50] 通过整合在不同视觉分类任务上训练的 Vision Transformer (ViT) 模型 [9]，生成能执行多任务物体分类的单一模型。PAPA [21] 将集成学习的广泛适用性与权重平均的计算效率相结合。MetaGPT [57] 将模型融合构建为多任务学习问题，旨在最小化融合模型与各任务专用模型间的平均损失。Fisher Merging [30] 采用基于Fisher信息矩阵加权的模型参数融合方法。RegMean [19] 通过将融合过程表述为可闭式求解的线性回归问题，提供优雅解决方案。Evolutionary-model-merge [2] 利用进化算法高效优化融合系数。此外，DARE [51] 通过随机丢弃并重新缩放增量参数，将多个任务专用语言模型融合为多功能统一模型。

However, research on model merging during the pre-training phase remains relatively limited. Such studies typically refer to incorporating checkpoints within a single training trajectory during large language model (LLM) pre-training. For example, LAWA [13, 23, 25] demonstrated that merging checkpoints at intermediate stages can significantly accelerate training. Sanyal et al. [35] further indicated that checkpoint averaging combined with a high learning rate in pre-training trajectories contributes to faster convergence. Additionally, Checkpoint Merging [27] provided a comprehensive evaluation of the effectiveness of merging checkpoints at different stages during the pre-training of the Baichuan2 [47] LLM. Furthermore, technical reports of large-scale models such as Deepseek V3 [26] and LLaMA3.1 [11] also mention the use of model merging techniques during pre-training, although detailed methodologies have not been publicly disclosed. This paper primarily explores techniques for model merging within the pre-training paradigm. To the best of our knowledge, this is the first study to provide detailed technical insights into scaling model merging methods to significantly larger model sizes. We also discuss practical approaches for effective model merging and analyze its potential capabilities as well as its limitations.

然而，关于预训练阶段模型合并的研究仍相对有限。这类研究通常涉及在大语言模型(LLM)预训练过程中整合单一训练轨迹中的检查点(checkpoint)。例如，LAWA [13, 23, 25] 证明合并中间阶段的检查点能显著加速训练。Sanyal等人 [35] 进一步指出，检查点平均化与预训练轨迹中的高学习率结合有助于更快收敛。此外，Checkpoint Merging [27] 对百川2(Baichuan2) [47] 大语言模型预训练中不同阶段合并检查点的有效性进行了全面评估。值得注意的是，Deepseek V3 [26] 和LLaMA3.1 [11] 等大规模模型的技术报告也提及了预训练阶段使用模型合并技术，但具体方法尚未公开披露。本文主要探索预训练范式下的模型合并技术。据我们所知，这是首个详细阐述如何将模型合并方法扩展到更大模型规模的技术研究。我们还讨论了有效模型合并的实践方法，并分析了其潜在能力与局限性。

3 Preliminaries

3 预备知识

In this section, we describe the fundamental experimental framework, introduce the notations and concepts used in model merging, and present multiple variants of model merging techniques.

在本节中，我们将描述基础实验框架，介绍模型合并中使用的符号和概念，并展示模型合并技术的多种变体。

Experimental setup. In terms of model architecture, we independently trained a series of MoE and dense models. We employ a Warmup-Stable-Decay (WSD) learning rate scheduler [15], which begins with a short warmup period, followed by an extended period of stable training at a constant learning rate, and concludes with annealing to a relatively small learning rate. The learning rates are determined according to scaling law guidelines [4, 24], employing optimal values for training on an internal pre training corpus comprising trillions of tokens. Although specific model architectures and datasets have not yet been publicly released, we posit that our findings are not strongly tied to these particular choices, as subsequent experiments primarily focus on MoE structures. Related conclusions for dense models are provided in the Appendix A. For evaluation, we primarily report results on open-source benchmarks in both few-shot and zero-shot settings, including: ARC-Challenge [6], BBH [39], DROP [10], WinoGrande [34], HellaSwag [54], MMLU [14], C-Eval [16], TriviaQA [22], Ape210K [55], GSM8K [7], MATH [55], MBPP [3], HumanEval [5], AGIEval [56], GPQA [33], and MMLU-Pro [41]. The weighted average score across these benchmarks serves as the model’s comprehensive performance metric. Unless otherwise specified, we report this score as the model’s performance metric to ensure evaluation reliability.

实验设置。在模型架构方面，我们独立训练了一系列混合专家（MoE）模型和密集模型。我们采用Warmup-Stable-Decay (WSD)学习率调度器[15]，该调度器以短暂的预热期开始，随后在恒定学习率下进行长时间稳定训练，最后退火至相对较小的学习率。学习率根据扩展法则指导[4,24]确定，采用在包含数万亿token的内部预训练语料库上进行训练的最佳值。尽管具体模型架构和数据集尚未公开，但我们认为研究结果与这些特定选择关联性不强，因为后续实验主要聚焦于MoE结构。密集模型的相关结论见附录A。评估方面，我们主要报告少样本和零样本设置下开源基准测试的结果，包括：ARC-Challenge[6]、BBH[39]、DROP[10]、WinoGrande[34]、HellaSwag[54]、MMLU[14]、C-Eval[16]、TriviaQA[22]、Ape210K[55]、GSM8K[7]、MATH[55]、MBPP[3]、HumanEval[5]、AGIEval[56]、GPQA[33]和MMLU-Pro[41]。这些基准测试的加权平均分数作为模型的综合性能指标。除非另有说明，我们均以该分数作为模型性能指标以确保评估可靠性。

Notions and concepts. Our main focus is on model merging during pre-training, where the merged entities are sequential checkpoints along the training trajectory. Suppose we aim to merge $N$ models, with each model’s parameters denoted as $M_{i}$ (where $i$ ranges from 1 to $N$ ). Each model has an associated weighting coefficient $w_{i}$ , and the merged model $M_{a v g}$ is computed as:

概念与定义。我们主要关注预训练过程中的模型合并，其中被合并的实体是训练轨迹上的连续检查点。假设我们需要合并 $N$ 个模型，每个模型的参数表示为 $M_{i}$ (其中 $i$ 的取值范围为1到 $N$)。每个模型都有一个关联的权重系数 $w_{i}$，合并后的模型 $M_{a v g}$ 计算公式为：

$$
M_{\mathrm{avg}}=\sum_{i=1}^{N}w_{i}M_{i}.
$$

$$
M_{\mathrm{avg}}=\sum_{i=1}^{N}w_{i}M_{i}.
$$

We assume that the data consumption of these models form an arithmetic sequence with a common difference $V$ , formulated as:

我们假设这些模型的数据消耗构成一个公差为 $V$ 的等差数列，其表达式为：

$$
V=T_{i+1}-T_{i},
$$

$$
V=T_{i+1}-T_{i},
$$

where $T_{i}$ represents the cumulative number of tokens consumed by the $i$ -th model.

其中 $T_{i}$ 表示第 $i$ 个模型消耗的累计 token 数量。

Model merging variants. Model merging techniques vary primarily in how they assign weights ( $w_{i}$ ) to individual models. This paper examines three popular approaches for weight assignment, namely the Simple Moving Average (SMA), Exponential Moving Average (EMA), and Weighted Moving Average (WMA).

模型合并变体。模型合并技术的主要区别在于如何为单个模型分配权重 ($w_{i}$)。本文研究了三种流行的权重分配方法，分别是简单移动平均 (SMA)、指数移动平均 (EMA) 和加权移动平均 (WMA)。

The first approach, Simple Moving Average (SMA), treats all models equally. For instance, when combining 10 models, each model is assigned a weight of $w_{i}=0.1$ . The SMA is formulated as:

第一种方法，简单移动平均 (Simple Moving Average, SMA)，对所有模型一视同仁。例如，当组合10个模型时，每个模型的权重为 $w_{i}=0.1$。SMA的公式如下：

$$
M_{\mathrm{avg}}={\frac{1}{N}}\sum_{i=1}^{N}M_{i}.
$$

$$
M_{\mathrm{avg}}={\frac{1}{N}}\sum_{i=1}^{N}M_{i}.
$$

The second approach, Exponential Moving Average (EMA), emphasizes later models by assigning weights that decay exponentially, making EMA more sensitive to recent changes. The EMA is expressed recursively as:

第二种方法是指数移动平均 (Exponential Moving Average, EMA)，它通过指数衰减的权重分配来强调后续模型，使得EMA对近期变化更加敏感。EMA的递归表达式为：

$$
M_{\mathrm{avg}}^{(i)}=\alpha\cdot M_{i}+(1-\alpha)\cdot M_{\mathrm{avg}}^{(i-1)},i\in[2,N],
$$

$$
M_{\mathrm{avg}}^{(i)}=\alpha\cdot M_{i}+(1-\alpha)\cdot M_{\mathrm{avg}}^{(i-1)},i\in[2,N],
$$

Here, $\alpha$ , the smoothing factor (typically between 0 and 1), controls the balance between the current model $M_{i}$ and the previous EMA result $M_{\mathrm{avg}}^{(i-1)}$ .

这里，$\alpha$（平滑因子，通常介于0和1之间）控制当前模型$M_{i}$与先前EMA结果$M_{\mathrm{avg}}^{(i-1)}$之间的平衡。

The third approach, Weighted Moving Average (WMA), also prioritizes recent models but uses a distinct weighting scheme. In WMA, each model is assigned a specific weight, often increasing linearly for later models (e.g., $w_{i}=i$ ). The weighted sum is then normalized to compute the average, formulated as follows:

第三种方法，加权移动平均 (Weighted Moving Average, WMA)，同样优先考虑近期模型，但采用不同的加权方案。在WMA中，每个模型被分配特定权重（通常后期模型权重线性递增，例如 $w_{i}=i$），随后对加权和进行归一化计算平均值，公式如下：

$$
M_{\mathrm{avg}}=\sum_{i=1}^{N}{\frac{w_{i}}{w_{\mathrm{sum}}}}M_{i},\quad w_{\mathrm{sum}}=\sum_{i=1}^{N}w_{i}.
$$

$$
M_{\mathrm{avg}}=\sum_{i=1}^{N}{\frac{w_{i}}{w_{\mathrm{sum}}}}M_{i},\quad w_{\mathrm{sum}}=\sum_{i=1}^{N}w_{i}.
$$

These methods offer flexible ways to combine models based on their recency and relevance. Choosing the right approach depends on the specific application and desired emphasis on newer data.

这些方法提供了根据模型的新近性和相关性进行灵活组合的方式。选择合适的方法取决于具体应用场景以及对新数据的侧重程度。

4 Experiments

4 实验

In this section, we delve into the experimental core of our study, systematically addressing six critical questions surrounding model merging in the context of pre-training: 1) How does model merging affect performance? 2)

在本节中，我们将深入探讨研究的实验核心，系统性地解决预训练背景下模型合并的六个关键问题：1) 模型合并如何影响性能？2)

How do different merging methods affect final performance? 3) How to determine the optimal interval and number of weights to merge for various model sizes? 4) Do merged pre-trained models contribute to better downstream training? 5) Does model merging improve the stability of training? 6) What processes unfold during model merging? Through these experiments, we aim to provide comprehensive insights into model merging, offering practical guidance for its application and shedding light on its theoretical underpinnings.

不同合并方法如何影响最终性能？
3) 如何为不同规模的模型确定最优权重合并间隔和数量？
4) 合并的预训练模型是否能提升下游训练效果？
5) 模型合并能否提高训练稳定性？
6) 模型合并过程中会发生哪些变化？
通过这些实验，我们旨在全面解析模型合并机制，为其实际应用提供指导，并揭示其理论基础。

4.1 How does model merging affect model performance?

4.1 模型合并如何影响模型性能？

Current learning rate schedule methods mainly involve constant learning rates or cosine annealing. In our model pre-training, we employed the Warmup-Stable-Decay (WSD) strategy [15], which combines a constant learning rate phase with a subsequent cosine decay phase [28]. To explore the effects of model merging under different learning rate schedules, we conducted experiments during both constant learning rate phase and cosine dacay phase.

当前学习率调度方法主要包括恒定学习率和余弦退火。在我们的模型预训练中，采用了Warmup-Stable-Decay (WSD)策略[15]，该策略将恒定学习率阶段与后续的余弦衰减阶段[28]相结合。为了探究不同学习率调度下模型合并的效果，我们在恒定学习率阶段和余弦衰减阶段均进行了实验。

In the constant learning rate phase, we merged fully trained models of various sizes. As shown in Figure 1, the merged models exhibited significant performance improvements across multiple downstream tasks. For example, on the Humaneval benchmark, Seed-MoE-1.3B/13B improved from 31.1 to 36.6 points, and SeedMoE-10B/100B increased from 54.3 to 61.6 points. While larger models showed less pronounced gains on certain benchmarks, such as BBH, this was likely due to the near-saturation of these metrics. Overall, the improvements were robust and consistent across model sizes.

在恒定学习率阶段，我们合并了不同规模的已训练完整模型。如图1所示，合并后的模型在多个下游任务中均表现出显著性能提升。例如，在Humaneval基准测试中，Seed-MoE-1.3B/13B从31.1分提升至36.6分，Seed-MoE-10B/100B从54.3分提升至61.6分。虽然较大模型在某些基准测试(如BBH)上增益幅度较小，但这可能是由于这些指标已接近饱和。总体而言，性能提升在不同规模模型间均保持稳健且一致。

Next, we performed model merging in the cosine annealing phase by collecting weights from the annealing stages of Seed-MoE-1.3B/13B, Seed-MoE-10B/100B, and Seed-MoE-15B/150B. As depicted in Figure 2, as the learning rate gradually decreased, the models converged steadily, with performance continuing to improve. Interestingly, at the early annealing stage, the results of PMA were comparable to those at the end of the annealing process. In some cases, particularly for larger models, the merged models even surpassed those naturally annealed.

接下来，我们在余弦退火阶段通过收集来自Seed-MoE-1.3B/13B、Seed-MoE-10B/100B和Seed-MoE-15B/150B退火阶段的权重进行模型合并。如图2所示，随着学习率逐渐降低，模型稳定收敛，性能持续提升。有趣的是，在退火初期，PMA（参数均值平均）的结果与退火末期相当。在某些情况下，尤其是较大规模的模型，合并后的模型甚至超越了自然退火的模型。

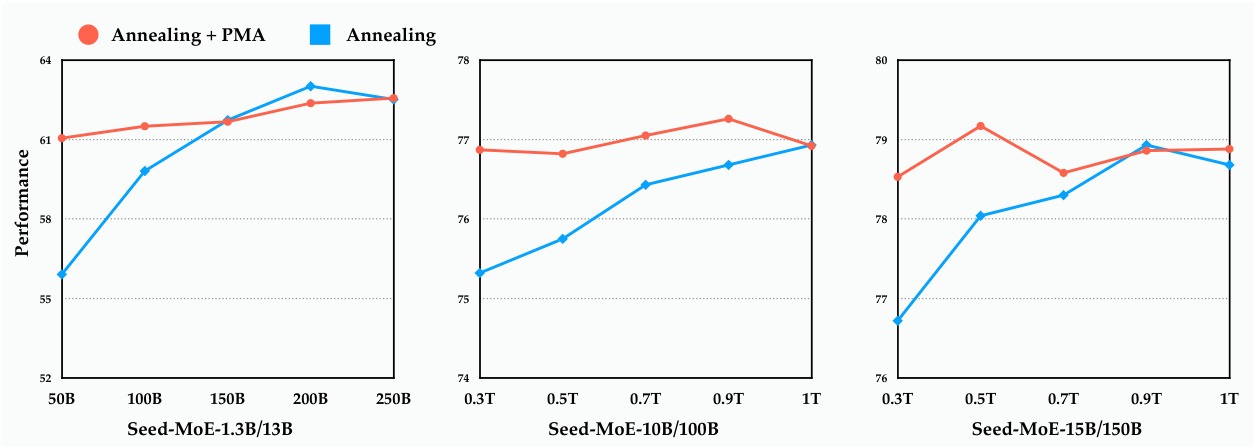
Figure 2 Comparison of overall performance for MoE models of varying sizes under annealing training, before and after model merging. The learning rate follows a cosine schedule during the annealing process. The x-axis shows the count of training tokens.

图 2: 不同规模MoE模型在退火训练前后的整体性能对比。退火过程中学习率采用余弦调度。x轴表示训练token数量。

These findings raised a question: could we simplify the training process by using only the Warmup-Stable phases alongside PMA, skipping the decay phase, and avoiding learning rate adjustments? To investigate, we forked two training runs from the stable phase of Seed-MoE-1.3B/13B at 1.4T tokens. One continued with a constant learning rate, while another underwent annealing, each training for an additional 250B tokens. We then merged the models trained with the constant learning rate. As shown in Figure 3, early in training, the merged models significantly outperformed both the constant learning rate and annealed models. Even later, their performance was comparable to the annealed models.

这些发现引发了一个问题：我们是否可以仅使用预热-稳定阶段和PMA来简化训练过程，跳过衰减阶段并避免学习率调整？为了探究这一点，我们从Seed-MoE-1.3B/13B在1.4T token处的稳定阶段分叉了两个训练运行。一个保持恒定学习率继续训练，另一个进行退火，各自额外训练了250B token。随后我们合并了恒定学习率训练的模型。如图3所示，在训练早期，合并模型的表现显著优于恒定学习率和退火模型。即便在后期，其性能仍与退火模型相当。

This suggests that pre-training with a constant learning rate, combined with model merging, can effectively match the performance of an annealed model at any point in the training process without the need for learning rate annealing. This approach accelerates model validation and significantly reduces computational resource demands.

这表明，采用恒定学习率进行预训练并结合模型合并，能有效匹配训练过程中任意阶段采用退火学习率的模型性能，且无需实施学习率退火。该方法可加速模型验证过程，并显著降低计算资源需求。

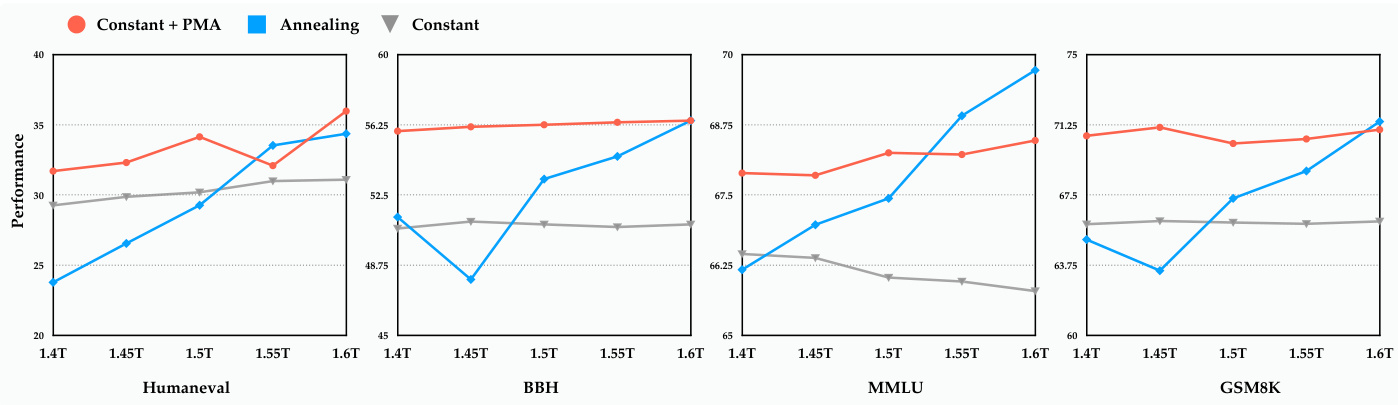
Figure 3 Comparison of downstream task performance between model merging results under stable training and the real annealed model. The $_\textrm{x}$ -axis shows the count of training tokens.

图 3: 稳定训练下的模型合并结果与真实退火模型在下游任务性能上的对比。横轴 ($_\textrm{x}$) 表示训练 token 的数量。

4.2 How do different merging methods affect final performance?

4.2 不同合并方法如何影响最终性能？

In this section, we systematically evaluate how different merging strategies affect the performance of merged models. Specifically, we focus on three distinct approaches: EMA, WMA, and SMA. The EMA method employs exponentially decaying weights $w_{i}=\alpha(1-\alpha)^{N-i}$ , giving higher importance to more recent checkpoints. WMA assigns linearly increasing weights $w_{i}=i$ , also prioritizing more recent checkpoints. In contrast, SMA applies uniform weighting, treating all checkpoints equally regardless of their position in the training sequence.

在本节中，我们系统评估了不同合并策略对合并模型性能的影响。具体而言，我们聚焦于三种不同方法：EMA、WMA和SMA。EMA方法采用指数衰减权重$w_{i}=\alpha(1-\alpha)^{N-i}$，对较新的检查点赋予更高重要性。WMA采用线性递增权重$w_{i}=i$，同样优先考虑较新的检查点。相比之下，SMA采用均匀加权，无论检查点在训练序列中的位置如何，均平等对待所有检查点。

We conducted experiments on Seed-MoE-1.3/13B and showed the results in Figure 4. At 204B training tokens, all merging methods enhanced model performance compared to the pre-merged model, but WMA delivered the best results. This suggests that in the early phases of training, when model weights undergo significant changes, assigning higher weights to checkpoints with more training tokens produces superior models. This is further supported by the fact that $\mathrm{EMA}{\alpha=0.2}$ outperforms $\mathrm{EMA}_{\alpha=0.1}$ . However, as training advances to later stages and model weights stabilize, the performance differences between merging methods diminish. For its simplicity and stability, we primarily use SMA for model merging in subsequent experiments.

我们在 Seed-MoE-1.3/13B 上进行了实验，结果如图 4 所示。在训练 204B token 时，所有合并方法相比合并前模型都提升了性能，但 WMA (Weighted Moving Average) 表现最佳。这表明在训练初期模型权重变化剧烈时，为训练 token 更多的检查点分配更高权重能产生更优模型。$\mathrm{EMA}{\alpha=0.2}$ 优于 $\mathrm{EMA}_{\alpha=0.1}$ 的现象进一步佐证了这一点。但随着训练进入后期阶段且模型权重趋于稳定，不同合并方法间的性能差异逐渐缩小。出于简洁性和稳定性考虑，我们在后续实验中主要采用 SMA (Simple Moving Average) 进行模型合并。

4.3 How to determine the optimal interval and number of weights to merge for various model sizes?

4.3 如何为不同规模的模型确定最佳权重合并间隔和数量？

Beyond the merging technique itself, two other factors may also affect the effectiveness of model merging: the interval $V$ between selected models and the number of models $N$ . We performed ablation studies on the Seed-MoE-1.3/13B model to investigate these effects, starting with the impact of the interval. As illustrated in the upper part of Figure 5, we fixed $N=10$ and tested intervals of $V=4\mathrm{B}$ , 8B, 16B, and 32B. Notably, at 204B with $V=32\mathrm{B}$ , we reduced $N$ to 6 due to insufficient models. In the early stage of training, at 204B tokens, merged results with $V=16\mathrm{B}$ and $V=32\mathrm{B}$ under performed the baseline. This is likely because large intervals incorporated unstable weights from the initial training phase, leading to significant weight disparities and suboptimal outcomes. As training progressed and weights stabilized, the performance gap across different $V$ settings gradually narrowed. In practice, the optimal interval scales with model size, following these observed patterns: an interval of around 8B tokens for 1.3B/13B models, 4B tokens for 0.7B/7B models, and approximately 80B tokens for 10B/100B models. This aligns with the tendency of larger models to use larger batch sizes [31].

除了模型融合技术本身，还有两个因素可能影响融合效果：所选模型之间的间隔 $V$ 和模型数量 $N$。我们在Seed-MoE-1.3/13B模型上进行了消融实验，首先探究间隔的影响。如图5上半部分所示，固定 $N=10$ 并测试了 $V=4\mathrm{B}$、8B、16B和32B的间隔。值得注意的是，在204B tokens且 $V=32\mathrm{B}$ 时，由于模型不足我们将 $N$ 降至6。训练初期（204B tokens时），$V=16\mathrm{B}$ 和 $V=32\mathrm{B}$ 的融合结果表现逊于基线，这可能是因为大间隔引入了训练初期的不稳定权重，导致显著权重差异和次优结果。随着训练推进和权重稳定，不同 $V$ 设置间的性能差距逐渐缩小。实践表明，最优间隔随模型规模变化：1.3B/13B模型约8B tokens，0.7B/7B模型约4B tokens，10B/100B模型约80B tokens，这与大模型倾向于使用更大批量的趋势一致 [31]。

Next, we set $V=8\mathrm{B}$ and explored how the number of merged models $N$ affects performance, testing $N=3$ , $_6$ , 10, and 15. As shown in the lower part of Figure 5, early in training, incorporating more models introduced unstable weights, which reduced the performance of merged models. However, once training was complete, merging a larger number of models led to significant performance improvements. Notably, the overall performance for $N=3$ was nearly 1 point lower than for $N=15$ . To strike a balance betwee computational cost and performance gains, we opted for $N=10$ in further experiments.

接下来，我们设定 $V=8\mathrm{B}$，并探究合并模型数量 $N$ 对性能的影响，测试了 $N=3$、$6$、10 和 15。如图 5 下半部分所示，在训练初期，合并更多模型会引入不稳定的权重，从而降低合并模型的性能。然而，一旦训练完成，合并更多模型会带来显著的性能提升。值得注意的是，$N=3$ 时的整体性