Neural Pre-Processing: A Learning Framework for End-to-end Brain MRI Pre-processing

Neural Pre-Processing: 端到端脑部MRI预处理的学xi框架

Abstract. Head MRI pre-processing involves converting raw images to an intensity-normalized, skull-stripped brain in a standard coordinate space. In this paper, we propose an end-to-end weakly supervised learning approach, called Neural Pre-processing (NPP), for solving all three sub-tasks simultaneously via a neural network, trained on a large dataset without individual sub-task supervision. Because the overall objective is highly under-constrained, we explicitly disentangle geometricpreserving intensity mapping (skull-stripping and intensity normalization) and spatial transformation (spatial normalization). Quantitative results show that our model outperforms state-of-the-art methods which tackle only a single sub-task. Our ablation experiments demonstrate the importance of the architecture design we chose for NPP. Furthermore, NPP affords the user the flexibility to control each of these tasks at inference time. The code and model are freely-available at https: //github.com/Novestars/Neural-Pre-processing.

摘要：头部MRI预处理涉及将原始图像转换为标准坐标空间中强度归一化且去除颅骨的脑部图像。本文提出一种端到端弱监督学习方法——神经预处理(NPP)，通过在大规模数据集上训练的神经网络同时解决这三个子任务，且无需单独的子任务监督。由于整体目标高度欠约束，我们显式解耦了保持几何特性的强度映射(去颅骨和强度归一化)与空间变换(空间归一化)。定量结果表明，该模型在仅处理单个子任务的先进方法中表现更优。消融实验验证了我们为NPP设计的架构重要性。此外，NPP在推理时允许用户灵活控制每个子任务。代码与模型已在https://github.com/Novestars/Neural-Pre-processing开源。

Keywords: Neural network $^{-1}$ Pre-processing · Brain MRI.

关键词：神经网络 $^{-1}$ · 预处理 · 脑部MRI

1 Introduction

1 引言

Brain magnetic resonance imaging (MRI) is widely-used in clinical practice and neuroscience. Many popular toolkits for pre-processing brain MRI scans exist, e.g., FreeSurfer [9], FSL [25], AFNI [5], and ANTs [3]. These toolkits divide up the pre-processing pipeline into sub-tasks, such as skull-stripping, intensity normalization, and spatial normalization/registration, which often rely on computationally-intensive optimization algorithms.

脑磁共振成像 (MRI) 在临床实践和神经科学领域应用广泛。目前已有许多流行的脑 MRI 扫描预处理工具包，例如 FreeSurfer [9]、FSL [25]、AFNI [5] 和 ANTs [3]。这些工具包将预处理流程划分为多个子任务，例如颅骨剥离、强度归一化和空间归一化/配准，这些任务通常依赖于计算密集型的优化算法。

Recent works have turned to machine learning-based methods to improve preprocessing efficiency. These methods, however, are designed to solve individual sub-tasks, such as SynthStrip [15] for skull-stripping and Voxelmorph [4] for registration. Learning-based methods have advantages in terms of inference time and performance. However, solving sub-tasks independently and serially has the drawback that each step’s performance depends on the previous step. In this paper, we propose a neural network-based approach, which we term Neural PreProcessing (NPP), to solve three basic tasks of pre-processing simultaneously.

最近的研究转向基于机器学习的方法以提高预处理效率。然而这些方法仅针对单个子任务设计，例如用于颅骨剥离的SynthStrip [15] 和用于配准的Voxelmorph [4]。基于学习的方法在推理时间和性能方面具有优势，但独立且串行解决子任务会带来每个步骤的性能依赖于前序步骤的缺陷。本文提出一种基于神经网络的方法（我们称为神经预处理(NPP)），可同步解决预处理中的三项基础任务。

NPP first translates a head MRI scan into a skull-stripped and intensitynormalized brain using a translation module, and then spatially transforms to the standard coordinate space with a spatial transform module. As we demonstrate in our experiments, the design of the architecture is critical for solving these tasks together. Furthermore, NPP offers the flexibility to turn on/off different pre-processing steps at inference time. Our experiments demonstrate that NPP achieves state-of-the-art accuracy in all the sub-tasks we consider.

NPP首先通过一个翻译模块将头部MRI扫描转换为经过颅骨剥离和强度归一化的大脑图像，随后利用空间变换模块将其转换到标准坐标空间。如实验所示，这种架构设计对协同解决这些任务至关重要。此外，NPP在推理阶段可灵活开启/关闭不同的预处理步骤。实验表明，NPP在我们考察的所有子任务中都达到了最先进的精度水平。

2 Methods

2 方法

2.1 Model

2.1 模型

As shown in Fig. 1, our model contains two modules: a geometry-preserving translation module, and a spatial-transform module.

如图 1 所示，我们的模型包含两个模块：几何保持转换模块和空间变换模块。

Geometry-preserving Translation Module. This module converts a brain MRI scan to a skull-stripped and intensity normalized brain. We implement it using a U-Net style [23] $f_{\theta}$ architecture (see Fig. 1), where $\theta$ denotes the model weights. We operational ize skull stripping and intensity normalization as a pixelwise multiplication of the input image with a scalar multiplier field $\chi$ , which is the output of the U-Net $f_{\theta}$ :

几何保持转换模块。该模块将脑部MRI扫描转换为去颅骨且强度归一化的脑部图像。我们采用U-Net风格[23]的$f_{\theta}$架构实现该模块（见图1），其中$\theta$表示模型权重。我们将去颅骨和强度归一化操作实现为输入图像与标量乘子场$\chi$的逐像素相乘，该乘子场是U-Net $f_{\theta}$的输出：

$$
T_{\theta}(x)=f_{\theta}(x)\otimes x,
$$

$$
T_{\theta}(x)=f_{\theta}(x)\otimes x,
$$

where $\bigotimes$ denotes the element-wise (Hadamard) product.

其中 $\bigotimes$ 表示逐元素 (Hadamard) 乘积。

Such a parameter iz ation allows us to impose constraints on $\chi$ . In this work, we penalize high-frequencies in $\chi$ , via the total variation loss described below. Another advantage of $\chi$ is that it can be computed at a lower resolution to boost both training and inference speed, and then up-sampled to the full resolution grid before being multiplied with the input image. This is possible because the multiplier $\chi$ is spatially smooth. In contrast, if we have $f_{\theta}$ directly compute the output image, doing this at a lower resolution means we will inevitably lose high frequency information. In our experiments, we take advantage of this by having the model output the multiplicative field at a grid size that is $1/2$ of the original input grid size along each dimension.

这样的参数化允许我们对 $\chi$ 施加约束。在本工作中，我们通过下文描述的总变差损失来惩罚 $\chi$ 中的高频成分。$\chi$ 的另一个优势是可以在较低分辨率下计算以提升训练和推理速度，随后在与输入图像相乘前上采样至完整分辨率网格。这种操作之所以可行，是因为乘数 $\chi$ 具有空间平滑性。相比之下，若直接让 $f_{\theta}$ 计算输出图像，在较低分辨率下操作将不可避免地丢失高频信息。实验中，我们利用这一特性，让模型输出的乘性场网格尺寸沿每个维度均为原始输入网格尺寸的 $1/2$。

Spatial Transformation Module. Spatial normalization is implemented as a variant of the Spatial Transformer Network (STN) [17]; in our implementation, the STN outputs the 12 parameters of an affine matrix $\boldsymbol{\phi}{a f f}$ . The STN takes as input the bottleneck features from the image translation network $f_{\theta}$ and feeds it through a multi-layer perceptron (MLP) that projects the features to a 12-dimensional vector encoding the affine transformation matrix. This affine transformation is in turn applied to the output of the image translation module $T_{\boldsymbol{\theta}}(\boldsymbol{x})$ via a differentiable resampling layer [17].

空间变换模块。空间归一化通过空间变换网络 (Spatial Transformer Network, STN) [17] 的变体实现；在我们的实现中，STN 输出仿射矩阵 $\boldsymbol{\phi}{a f f}$ 的 12 个参数。STN 以图像翻译网络 $f_{\theta}$ 的瓶颈特征作为输入，并通过多层感知机 (MLP) 将特征投影为编码仿射变换矩阵的 12 维向量。该仿射变换随后通过可微分重采样层 [17] 作用于图像翻译模块 $T_{\boldsymbol{\theta}}(\boldsymbol{x})$ 的输出。

Fig. 1: (Top) An overview of Neural Pre-processing. (Bottom) The network archie c ture of Neural Pre-processing

图 1: (上) 神经预处理 (Neural Pre-processing) 概览。(下) 神经预处理的网络架构

2.2 Loss Function

2.2 损失函数

The objective to minimize is composed of two terms. The first term is a reconstruction loss $L_{r e c}$ . In this paper, we use SSIM [29] for $L_{r e c}$ . The second term penalizes $T_{\theta}$ from making high-frequency intensity changes to the input image, encapsulating our prior knowledge that skull-stripping and MR bias field correction involve a pixel-wise product with a spatially smooth field. In this work, we use a total variation penalty [22] $L_{T V}$ on the multiplier field $\chi$ , which promotes sparsity of spatial gradients in $\chi$ . The final objective is:

最小化目标由两项组成。第一项是重建损失 $L_{r e c}$。本文使用 SSIM [29] 作为 $L_{r e c}$。第二项惩罚 $T_{\theta}$ 对输入图像进行高频强度变化，体现了我们的先验知识：颅骨剥离和 MR 偏置场校正涉及与空间平滑场的逐像素乘积。本工作采用总变分惩罚 [22] $L_{T V}$ 作用于乘子场 $\chi$，以促进 $\chi$ 中空间梯度的稀疏性。最终目标为：

$$
\underset{\theta}{\arg\operatorname*{min}}L_{r e c}(T_{\theta}(x)\circ\varPhi_{a f f},x_{g t})+\lambda L_{T V}(\chi),
$$

$$
\underset{\theta}{\arg\operatorname*{min}}L_{r e c}(T_{\theta}(x)\circ\varPhi_{a f f},x_{g t})+\lambda L_{T V}(\chi),
$$

where $x_{g t}$ is the pre-processed ground truth images, $\lambda\geq0$ controls the trade-off between the two loss terms, and $\circ$ denotes a spatial transformation.

其中 $x_{g t}$ 是预处理后的真实图像，$\lambda\geq0$ 控制两个损失项之间的权衡，$\circ$ 表示空间变换。

Conditioning on $\lambda$ . Classically, hyper parameters like $\lambda$ are tuned on a held-out validation set - a computationally-intensive task which requires training multiple models corresponding to different values of $\lambda$ . To avoid this, we condition on $\lambda$ in $f_{\theta}$ by passing in $\lambda$ as an input to a separate MLP $h_{\phi}(\lambda)$ (see Fig. 1), which generates a $\lambda$ -conditional scale and bias for each channel of the decoder layers. $h_{\phi}$ can be interpreted as a hyper network [12,28,14] which generates a conditional scale and bias similar to adaptive instance normalization (AdaIN) [16].

以 $\lambda$ 为条件。传统上，像 $\lambda$ 这样的超参数会在保留的验证集上进行调优，这是一项计算密集型任务，需要针对不同的 $\lambda$ 值训练多个模型。为了避免这种情况，我们通过将 $\lambda$ 作为输入传递给单独的 MLP $h_{\phi}(\lambda)$ (见图 1)，在 $f_{\theta}$ 中以 $\lambda$ 为条件，该 MLP 为解码器层的每个通道生成 $\lambda$ 条件缩放和偏置。$h_{\phi}$ 可解释为一种超网络 [12,28,14]，其生成的缩放和偏置类似于自适应实例归一化 (AdaIN) [16]。

Specifically, for a given decoder layer with $C$ intermediate feature maps ${z_{1},...,z_{C}}$ , $h_{\phi}(\lambda)$ generates the parameters to scale and bias each channel $z_{c}$ such that the the channel values are computed as:

具体来说，对于具有 $C$ 个中间特征图 ${z_{1},...,z_{C}}$ 的给定解码器层，$h_{\phi}(\lambda)$ 生成用于缩放和偏置每个通道 $z_{c}$ 的参数，使得通道值计算如下：

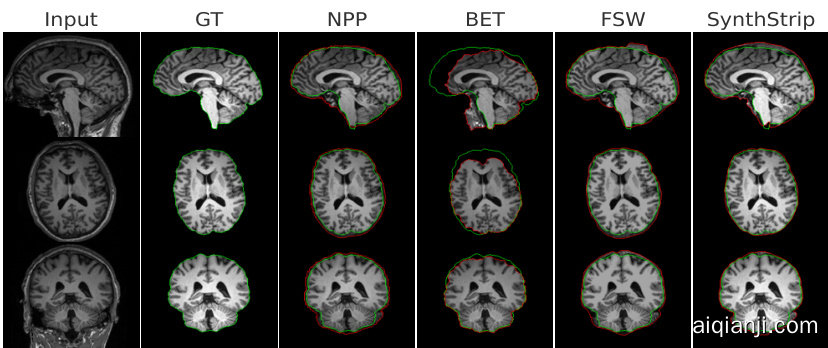
Fig. 2: Representative slices for skull-stripping. From top to bottom: coronal, axial and sagittal views. Green and red contours depict ground truth and estimated brain masks, respectively.

图 2: 颅骨剥离的代表性切片。从上到下：冠状面、轴向面和矢状面视图。绿色和红色轮廓分别表示真实脑掩膜和估计脑掩膜。

$$
\hat{z}{c}=\alpha_{c}z_{c}+\beta_{c},
$$

$$
\hat{z}{c}=\alpha_{c}z_{c}+\beta_{c},
$$

for $c\in{1,...,C}$ . Here, $\alpha_{c}$ and $\beta_{c}$ denote the scale and bias of channel $c$ , conditioned on $\lambda$ . This is repeated for every decoder layer, except the final layer.

对于 $c\in{1,...,C}$。这里，$\alpha_{c}$ 和 $\beta_{c}$ 表示通道 $c$ 的缩放和偏置，其值由 $\lambda$ 决定。该操作在每个解码器层重复进行（最后一层除外）。

3 Experiments

3 实验

Training details. We created a large-scale dataset of 3D T1-weighted (T1w) brain MRI volumes by aggregating 7 datasets: GSP [13], ADNI [21], OASIS [20], ADHD [24], ABIDE [30], MCIC [11], and COBRE [1]. The whole training set contains 10,083 scans. As ground-truth target images, we used FreeSurfer generated skull-stripped, intensity-normalized and affine-registered (to so-called MNI atlas coordinates) images.

训练细节。我们通过整合7个数据集构建了一个大规模3D T1加权(T1w)脑部MRI体素数据集：GSP [13]、ADNI [21]、OASIS [20]、ADHD [24]、ABIDE [30]、MCIC [11]和COBRE [1]。整个训练集包含10,083次扫描。作为真实目标图像，我们采用了FreeSurfer生成的去颅骨、强度归一化且经过仿射配准(至所谓的MNI图谱坐标)的图像。

We train NPP with ADAM [19] and a batch size of 2, for a maximum of 60 epochs. The initial learning rate is 1e-4 and then decreases by half after 30 epochs. We use random gamma transformation as a data augmentation technique, with parameter log gamma (-0.3,0.3). We randomly sampled $\lambda$ from a log-uniform distribution on $(-3,1)$ for each mini-batch.

我们使用ADAM [19]训练NPP，批大小为2，最多60个周期。初始学习率为1e-4，30个周期后减半。采用随机伽马变换作为数据增强技术，参数log gamma (-0.3,0.3)。每个小批量中从$(-3,1)$的对数均匀分布随机采样$\lambda$。

Architecture Details. $f_{\theta}$ is a U-Net-style architecture containing an encoder and decoder with skip connections in between. The encoder and decoder have 5 levels and each level consists of 2 consecutive 3D convolutional layers. Specifically, each 3D convolutional layer is followed by an instance normalization layer and LeakyReLU (negative slope of 0.01). In the bottleneck, we use three transformer blocks to enhance the ability of capturing global information [27]. Each transformer block contains a self-attention layer and a MLP layer. For the transformer block, we use patch size 1x1x1, 8 attention heads, and an MLP expansion ratio of 1. We perform token iz ation by flattening the 3D CNN feature maps into a 1D sequence.

架构细节。$f_{\theta}$ 采用 U-Net 风格架构，包含编码器和解码器，中间通过跳跃连接相连。编码器和解码器各有 5 层，每层由 2 个连续的 3D 卷积层组成。具体而言，每个 3D 卷积层后接一个实例归一化层和 LeakyReLU（负斜率为 0.01）。在瓶颈部分，我们使用三个 Transformer 模块来增强捕获全局信息的能力 [27]。每个 Transformer 模块包含一个自注意力层和一个 MLP 层。对于 Transformer 模块，我们使用 1x1x1 的 patch 大小、8 个注意力头和 MLP 扩展比为 1。我们通过将 3D CNN 特征图展平为一维序列来进行 Token 化。

Table 1: Supported sub-tasks and average runtime for each method. Skullstripping (SS), intensity normalization (IN) and spatial normalization (SN). Units are sec, bold is best.

表 1: 各方法支持的子任务及平均运行时间。颅骨剥离(SS)、强度归一化(IN)和空间归一化(SN)。单位为秒，加粗为最优值。

方法	SS	IN	SN	GPU	CPU
SynthStrip BET Freesurfer	16.5 9.1	- 262.2 747.2 481.5	671.6

Table 2: Performance on intensity normalization. Higher is better, bold is best.

方法	重建SSIM	重建PSNR	偏置SSIM	偏置PSNR
FSL	98.5	34.2	92.5	39.2
FS	98.9	35.7	92.1	39.3
NPP	99.1	36.2	92.7	39.4

表 2: 强度归一化性能对比。数值越高越好，加粗为最优结果。

The hyper network, $h_{\phi}$ , is a 3-layer MLP with hidden layers 512, 2048 and 496. The STN MLP is composed of a global average pooling layer and a 2-layer MLP with hidden layers of size 256 and 12. The 2-layer MLP contains: linear(256 channels); ReLU; linear(12 channels); Tanh. Note an identity matrix is added to the output affine matrix.

超网络 (hyper network) $h_{\phi}$ 是一个包含512、2048和496隐藏层的3层MLP。STN MLP由全局平均池化层和具有256、12隐藏层的2层MLP组成。该2层MLP包含：线性层(256通道)；ReLU激活；线性层(12通道)；Tanh激活。注意输出仿射矩阵会叠加一个单位矩阵。

Baselines. We chose three popular and widely-used tools, SynthStrip [15], FSL [25], and FreeSurfer [9], as baselines. SynthStrip (SS) is a learning-based skull-stripping method, while FSL and FreeSurfer (FS) is a cross-platform brain processing package containing multiple tools. FSL’s Brain Extraction Tool (BET) and FMRIB’s Automated Segmentation Tool are for skull stripping and MR bias field correction, respectively. FS uses a watershed method for skull-stripping, a model-based tissue segmentation for intensity normalization and bias field correction.

基线方法。我们选择了三种流行且广泛使用的工具作为基线：SynthStrip [15]、FSL [25] 和 FreeSurfer [9]。SynthStrip (SS) 是一种基于学习的颅骨剥离方法，而 FSL 和 FreeSurfer (FS) 是包含多种工具的跨平台脑处理套件。FSL 的脑提取工具 (BET) 和 FMRIB 的自动分割工具分别用于颅骨剥离和 MR 偏置场校正。FS 采用分水岭法进行颅骨剥离，并基于模型的组织分割实现强度归一化和偏置场校正。

3.1 Runtime analyses

3.1 运行时分析

The primary advantage of NPP is runtime. As shown in Table 1, for images with resolution $256\times256\times256$ , NPP requires less than 3 sec on a GPU and less than 8 sec on a CPU for all three pre-processing tasks. This is in part due to the fac