Geodesic Distance Histogram Feature for Video Segmentation

用于视频分割的测地距离直方图特征

Abstract. This paper proposes a geodesic-distance-based feature that encodes global information for improved video segmentation algorithms. The feature is a joint histogram of intensity and geodesic distances, where the geodesic distances are computed as the shortest paths between superpixels via their boundaries. We also incorporate adaptive voting weights and spatial pyramid configurations to include spatial information into the geodesic histogram feature and show that this further improves results. The feature is generic and can be used as part of various algorithms. In experiments, we test the geodesic histogram feature by incorporating it into two existing video segmentation frameworks. This leads to significantly better performance in 3D video segmentation benchmarks on two datasets.

摘要。本文提出了一种基于测地距离的特征，该特征通过编码全局信息来改进视频分割算法。该特征是强度与测地距离的联合直方图，其中测地距离通过超像素边界之间的最短路径计算得到。我们还引入了自适应投票权重和空间金字塔配置，将空间信息融入测地直方图特征，并证明这能进一步提升效果。该特征具有通用性，可作为多种算法的组成部分。实验中，我们通过将测地直方图特征集成到两个现有视频分割框架中进行测试。在两个数据集的3D视频分割基准测试中，该方法显著提升了性能。

1 Introduction

1 引言

Video segmentation is an important pre-processing step for many high-level video applications such as action recognition [1], scene understanding [2], or 3D reconstruction [3]. A more compact representation not only reduces the subsequent processing space and time requirements, but also provides sets of visual segments that contain meaningful cues for higher-level computer vision tasks. However, generating super vox els from videos is a significantly more difficult task than superpixel segmentation from images, due to the heavy computational cost and the extra temporal dimension. Specifically, well delineated spatio-temporal video segments can be used for tracking bounded regions, foreground moving objects, or semantic understanding. For example, locating the movement of hands is helpful for gesture or action recognition, and separating foreground/background can pin-point the region-of-interest for detecting moving objects. Therefore, these spatio-temporal segments should be temporally consistent in order to be beneficial for these computer vision tasks.

视频分割是许多高级视频应用的重要预处理步骤，例如动作识别 [1]、场景理解 [2] 或 3D 重建 [3]。更紧凑的表示不仅能减少后续处理的空间和时间需求，还能提供包含高级计算机视觉任务有意义线索的视觉片段集合。然而，由于高昂的计算成本和额外的时间维度，从视频生成超体素 (super voxel) 比从图像生成超像素 (superpixel) 分割要困难得多。具体而言，清晰划分的时空视频片段可用于跟踪边界区域、前景运动物体或语义理解。例如，定位手部运动有助于手势或动作识别，而分离前景/背景可以精确定位检测运动物体的感兴趣区域。因此，这些时空片段需要保持时间一致性才能对这些计算机视觉任务有益。

For video segmentation s that are initialized from super pixels, the main goal is to consider the connections between neighboring super pixels and to decide which ones belong to the same spatio-temporal cluster. The connections are usually represented as a spatio-temporal graph, where the nodes are the super pixels and the edges connect super pixels that are adjacent to each other. The edges are weighted based on the similarity distances between pairs of super pixels. Previous work [4, 5] proposed a variety of features corresponding to a wide range of low and mid-level image cues from super pixels. For example, the within-frame similarities were computed from boundary magnitude, color, texture, and shape, and the temporal connections were defined by the direction of optical flow or motion trajectories. Importantly, the aforementioned features that were used for video segmentation encode only local information, extracted from within each superpixel. One would expect improved performance when combining local and global features, if the appropriate global features per superpixel were extracted.

对于从超像素初始化的视频分割，其主要目标是考虑相邻超像素之间的连接关系，并确定哪些属于同一时空簇。这些连接通常表示为时空图，其中节点是超像素，边连接彼此相邻的超像素。边的权重基于超像素对之间的相似性距离计算。先前工作[4,5]提出了多种特征，对应超像素中各种低层和中层图像线索。例如，帧内相似性通过边界强度、颜色、纹理和形状计算，而时间连接则由光流方向或运动轨迹定义。值得注意的是，上述用于视频分割的特征仅编码从每个超像素内部提取的局部信息。若能提取每个超像素的适当全局特征，结合局部与全局特征可预期性能提升。

Fig. 1: The segmentation results on video “monkey” from Segtrack v2 dataset [6]. Top row: original frames with superimposed ground-truth (green). Second row: segmentation results of the PGP algorithm ([7]) using their four predefined features. Third row: result of PGP with our feature integrated. Fourth row: segmentation result of spectral clustering with the6 features proposed in [8]. Bottom row: segmentation result of spectral clustering with our feature integrated. Our results show better temporal consistency and less over-segmentation.

图 1: Segtrack v2数据集[6]中视频"monkey"的分割结果。首行: 叠加真实标注(绿色)的原始帧。第二行: 使用四种预定义特征的PGP算法([7])分割结果。第三行: 整合我们特征的PGP算法结果。第四行: 采用文献[8]提出的6个特征的谱聚类分割结果。末行: 整合我们特征的谱聚类分割结果。我们的方法展现出更好的时间一致性和更少的过分割现象。

The geodesic distance has been shown to be effective for image segmentation problems [9, 10] but its applications in the video domain have been limited [11, 10, 12, 13]. In this work, we propose a complete methodology for the use of geodesic distance histogram features in the video segmentation problem. The histogram feature describes the superpixel-of-interest by the distribution of the geodesic distances from it, to all other super pixels in the same frame. The representation compactly encodes global similarity relations between segments. Thus, we want to use per-frame geodesic distance information to associate super pixels both within and across frames. However, the nature of this global representation, poses several challenges that need to be addressed, in order to successfully use geodesic distance histograms for video segmentation:

测地线距离 (geodesic distance) 已被证明能有效解决图像分割问题 [9, 10]，但它在视频领域的应用仍十分有限 [11, 10, 12, 13]。本文提出了一套完整的方法论，将测地线距离直方图特征应用于视频分割问题。该直方图特征通过计算目标超像素 (superpixel-of-interest) 与同帧其他所有超像素之间的测地线距离分布来描述其特征。这种表示方法能紧凑地编码分割区域间的全局相似性关系。因此，我们希望利用逐帧测地线距离信息来建立帧内及帧间超像素的关联。然而，这种全局表示的特性带来了若干挑战，必须解决这些挑战才能成功将测地线距离直方图应用于视频分割：

In this paper, we address these issues in order to derive a geodesic histogram feature that is appropriate for video segmentation tasks. In essence, we introduce the necessary local information in the global representation, in order to disambiguate associations across frames. For a given superpixel, we first extract the soft boundary map of the frame where it belongs, then we compute geodesic distances from the superpixel-of-interest to all other super pixels in the same frame using the boundary scores. If we were performing per frame segmentation, a 1D histogram of these scores would suffice [10]. However, due to motion, this 1D histogram is not robust across frames. As observed previously [13], a 2D joint histogram of intensity and geodesic distance is much more robust. To encode more spatial information into the feature, we compute multiple geodesic histograms in a spatial pyramid [14]. Finally, we weigh the bins with respect to their spatial distance from the superpixel-of-interest, in order to favor potentially discriminative neighborhood information. We show in experiments that when we add our complete geodesic histogram feature into existing frameworks, the resulting segmentation s are greatly improved, especially in 3D segmentation accuracy and temporal consistency. The feature is also fast to compute, without increasing significantly processing time for the existing frameworks. The geodesic histogram features are added into two state-of-the-art video segmentation frameworks that are based on superpixel clustering, and tested on two popular datasets using standard 3D segmentation benchmarks.

本文针对这些问题，提出了一种适用于视频分割任务的测地直方图特征。其核心思想是在全局表征中引入必要的局部信息，以消除跨帧关联的歧义性。对于给定超像素，我们首先提取其所属帧的软边界图，随后利用边界得分计算该目标超像素到同帧内所有其他超像素的测地距离。若进行逐帧分割，这些得分的1D直方图即可满足需求[10]。但由于运动因素，这种1D直方图在跨帧时缺乏鲁棒性。如先前研究[13]所示，强度与测地距离的2D联合直方图具有更强的鲁棒性。为在特征中编码更多空间信息，我们在空间金字塔[14]中计算多重测地直方图。最后，根据各分箱与目标超像素的空间距离进行加权，以增强潜在判别性邻域信息。实验表明，当我们将完整的测地直方图特征加入现有框架时，分割结果（特别是3D分割精度与时序一致性）获得显著提升。该特征计算速度快，不会显著增加现有框架的处理时间。我们将测地直方图特征集成到两个基于超像素聚类的前沿视频分割框架中，并采用标准3D分割基准在两个流行数据集上进行测试。

The rest of paper is organized as follows: Section 2 discusses related work. Section 3 discusses the motivation, computation, and analysis of the proposed geodesic histogram features. Implementation details are described in Section 3.4. Section 4 presents the experimental results. Section 5 concludes the paper and discusses other possible applications.

本文其余部分组织结构如下：第2节讨论相关工作。第3节阐述所提出的测地直方图特征 (geodesic histogram features) 的动机、计算和分析，具体实现细节见第3.4节。第4节展示实验结果。第5节总结全文并探讨其他潜在应用场景。

2 Related Work

2 相关工作

Many video segmentation works propose diverse features to capture various kinds of information in order to estimate the similarity between the components of the video. Appearance can be represented by features based on color [5, 15], texture [16], and soft boundaries [17]. Motion related features have also been utilized often, including short-term motion features based on optical flow [18, 19] and long-term motion features based on trajectories [20, 21, 22, 23]. Superpixel shape is used to compute the similarities among super pixels across frames [15]. Some works discuss the choice of features to use [8] as well as the method to incorporate various kinds of features into affinity matrices [4].

许多视频分割工作提出了多种特征来捕捉各类信息，以估计视频组件之间的相似性。外观可通过基于颜色 [5, 15]、纹理 [16] 和软边界 [17] 的特征来表示。运动相关特征也常被使用，包括基于光流的短期运动特征 [18, 19] 和基于轨迹的长期运动特征 [20, 21, 22, 23]。超像素形状用于计算跨帧超像素之间的相似性 [15]。部分研究探讨了特征的选择 [8] 以及将各类特征整合到亲和力矩阵中的方法 [4]。

Geodesic distances provide appearance-based similarity estimates. Geodesic distances have been applied widely on segmentation related problems on images [9, 13, 10]. A feature based on geodesic distance for matching images of deformed objects has been introduced in [13]. The authors showed that the geodesic distance could be invariant to object deformations, by encoding pixels as color histograms on the surrounding pixels that have the same geodesic distances. The geodesic distance is also used to propose object segments on images [9], which is based on the correlation between the object boundary and the change in the geodesic distance transform. Several video segmentation methods have employed geodesic distance for various purposes. The salient object segmentation framework uses a geodesic distance in each frame to estimate the objectness of super pixels [11] on a per frame basis. Further work further proposes a spatio-temporal geodesic distance [10] that extends image segmentation to video segmentation. However, the proposed spatio-temporal distance has to be constrained to be temporally non-decreasing to preserve the metric property, thus limiting the robustness of the method.

测地距离提供基于外观的相似性估计。测地距离已广泛应用于图像分割相关问题[9,13,10]。文献[13]提出了一种基于测地距离的特征，用于匹配变形物体的图像。作者表明，通过将像素编码为具有相同测地距离的周围像素的颜色直方图，测地距离可以不受物体变形的影响。测地距离还被用于提出图像上的物体分割[9]，该方法基于物体边界与测地距离变换变化之间的相关性。多种视频分割方法出于不同目的采用了测地距离。显著物体分割框架在每帧中使用测地距离来估计超像素的物体性[11]。进一步的研究提出了时空测地距离[10]，将图像分割扩展到视频分割。然而，所提出的时空距离必须约束为时间非递减以保持度量属性，从而限制了该方法的鲁棒性。

In this paper, we propose a feature based on geodesic distance to estimate the similarity between the super pixels in the video. We consider the frame-wise distribution of the geodesic distances, i.e., the histogram of geodesic distances from each superpixel to all other super pixels in the same frame. This representation compactly encodes the relative similarity distances between the segment containing the superpixel-of-interest to all the other segments on the frame. This global information therefore serves as a complement to the set of to the set of appearance, motion, and shape-based features which only encode information from the inner region of the superpixel-of-interest.

本文提出了一种基于测地线距离的特征，用于估计视频中超像素之间的相似性。我们考虑了测地线距离的逐帧分布，即同一帧中每个超像素到所有其他超像素的测地线距离直方图。该表示方法紧凑地编码了包含目标超像素的片段与帧上所有其他片段之间的相对相似距离。因此，这种全局信息可作为外观、运动和基于形状的特征集的补充，这些特征仅编码来自目标超像素内部区域的信息。

3 Geodesic Distance Histogram Feature

3 测地距离直方图特征

Given a frame of the video, let $X$ be the set of super pixels: $X={x_{1},\ldots,x_{n}}$ . The frame is then represented by a non-negative, undirected graph $G=(X,E)$ , where each value in $E$ is associated with a pair of neighboring super pixels in $X$ , and the edge weight is computed as the boundary strength between the two super pixels. The geodesic distance between any two super pixels $x_{i},x_{j}\in X$ is defined as the weight of the shortest path between the two super pixels in $G$ .

给定视频的一帧，设 $X$ 为超像素(super pixel)集合：$X={x_{1},\ldots,x_{n}}$。该帧可表示为非负无向图 $G=(X,E)$，其中 $E$ 的每个值对应 $X$ 中相邻超像素对，边权重计算为两个超像素间的边界强度。任意两个超像素 $x_{i},x_{j}\in X$ 之间的测地距离(geodesic distance)定义为 $G$ 中两超像素最短路径的权重。

Given a superpixel $x_{i}$ on a frame, the geodesic distance between $x_{i}$ and all other super pixels in the same frame is computed and pooled into a geodesic distance histogram. This histogram contains the global information of the frame with respect to $x_{i}$ in terms of geodesic distance distribution, and can be used for computing pair-wise superpixel similarity both within and across frames.

给定帧上的一个超像素 $x_{i}$，计算其与同帧内所有其他超像素的测地距离，并汇总为测地距离直方图。该直方图以测地距离分布形式蕴含了帧相对于 $x_{i}$ 的全局信息，可用于计算帧内及跨帧的超像素对相似度。

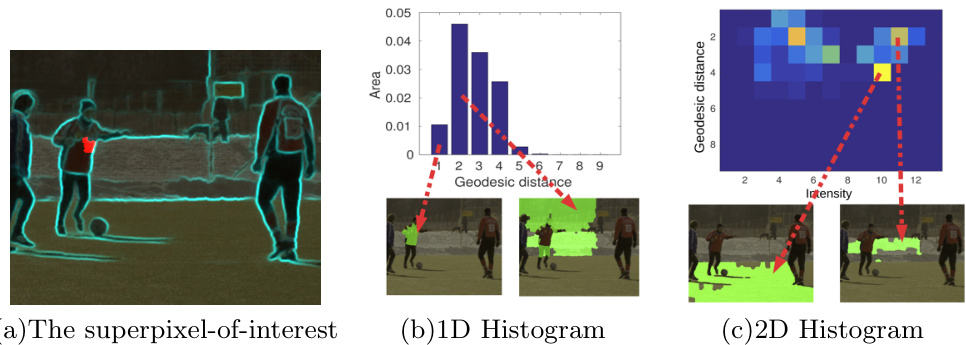
Fig. 2: The figure shows an example of 1D (geodesic distances) and 2D (intensitygeodesic distances) histogram features. (a): frame 1 of video “soccer” from Chen’s Xiph.org dataset [24], with soft boundary scores highlighted, and a superpixel-ofinterest marked in red. (b) and (c): the 1D and 2D histograms of the superpixelof-interest, and the frame regions (green) that correspond to the selected bins and cells of the 1D and 2D histograms, respectively. (b) shows that the bins of the 1D histogram contain mixed information, while the cells in (c) contain regions that are more semantically homogeneous.

图 2: 该图展示了1D (测地距离) 和2D (强度-测地距离) 直方图特征的示例。(a): Chen的Xiph.org数据集[24]中视频"soccer"的第1帧, 高亮显示了软边界分数, 并用红色标记了感兴趣的超像素。(b) 和 (c): 感兴趣超像素的1D和2D直方图, 以及分别对应1D和2D直方图所选区间和单元的帧区域 (绿色)。(b) 显示1D直方图的区间包含混合信息, 而 (c) 中的单元包含语义更同质的区域。

3.1 1D Geodesic Distance Histogram.

3.1 一维测地距离直方图

The simplest approach is to use an 1D histogram to describe the distribution of the geodesic distances, where a bin of the histogram represents the number of super pixels with a particular geodesic distance. This is similar to the concept of critical level sets [9], where each critical level defines a group of super pixels having their geodesic distances less than a certain threshold. Each bin of the histogram is then associated with a region in the image.

最简单的方法是使用一维直方图来描述测地距离的分布，其中直方图的每个区间代表具有特定测地距离的超像素数量。这与关键水平集 [9] 的概念类似，其中每个关键水平定义了一组测地距离小于特定阈值的超像素。直方图的每个区间随后与图像中的一个区域相关联。

In order to keep our feature relatively constant across frames, the value of each bin should stay approximately the same. This means that the regions associated with each bin also remain relatively stable. Considering the superpixel (in red) shown in Fig. 2(a), two regions corresponding to the first two bins of the histogram are visualized in Fig. 2(b). The first bin collects the votes of all superpixels with the lowest geodesic distance interval, forming the region indicated by the leftmost arrow. However, the region corresponding to the second bin is the combination of super pixels from different semantic regions. The value of the second bin is therefore not robust since these regions could potentially move in different ways, and end up voting for different bins in subsequent frames.

为了使我们的特征在帧间保持相对稳定，每个直方图条柱(bin)的数值应大致保持不变。这意味着与每个条柱相关联的区域也需保持相对稳定。以图2(a)中红色标注的超像素(superpixel)为例，图2(b)可视化了直方图前两个条柱对应的两个区域。第一个条柱汇集了所有具有最低测地距离区间的超像素投票，形成最左侧箭头指示的区域。然而，第二个条柱对应的区域却混合了来自不同语义区域的超像素。因此第二个条柱的数值不具备鲁棒性，因为这些区域可能会以不同方式移动，最终在后续帧中投票给不同的条柱。

3.2 2D Intensity-Geodesic Distance Histogram.

3.2 二维强度-测地距离直方图

We incorporate the intensity feature as an additional cue to complement the geodesic distance, on order to constrain bins to correspond to individual regions instead of disparate groups of regions. Thus the histogram becomes a 2D table where each cell is voted for by the super pixels that have a particular pair of geodesic distance and intensity. The joint distribution of intensity-geodesic distance was originally proposed in [13], where the joint distribution was expected to be stable and informative under a wide range of deformations.

我们将强度特征作为补充线索与测地距离结合，以约束分箱对应独立区域而非分散的区域组。因此直方图转化为二维表格，其中每个单元格由具有特定测地距离-强度值对的超像素投票生成。这种强度-测地距离联合分布最初由[13]提出，该研究预期该联合分布在多种形变下能保持稳定性和信息量。

Fig. 3: The figures visualize the similarities between the superpixel-of-interest in Fig. 2(a) on a later frame (frame 49) to all other super pixels. Warmer color represents higher similarity. (a): original frame. (b): the similarity map based on 1D geodesic distance histograms. (c): the similarity map based on 2D intensity-geodesic distance histograms. The figure shows that the 2D histogram is more robust than the 1D histogram for across-frame matching: there are multiple super pixels located in multiple regions that have similar 1D histograms with the superpixel-of-interest, while only the super pixels located within the upper-body region have the most similar 2D histograms.

图 3: 这些图展示了图 2(a) 中感兴趣的超像素在后续帧(第49帧)与所有其他超像素之间的相似性。暖色调表示更高的相似度。(a): 原始帧。(b): 基于一维测地距离直方图的相似性图。(c): 基于二维强度-测地距离直方图的相似性图。该图表明，对于跨帧匹配，二维直方图比一维直方图更具鲁棒性：存在多个位于不同区域的超像素与感兴趣超像素具有相似的一维直方图，而只有位于上半身区域的超像素具有最相似的二维直方图。

Fig. 2(c) visualizes the intensity-geodesic distance histogram of a superpixelof-interest (shown in red in Fig. 2(a)). Notice that the second bin of the 1D histogram equals to the sum of all cells in the second row of the 2D histogram, and the region from the second bin in the 1D histogram is now separated into multiple smaller regions corresponding to these cells. This is a desired effect given that each of the cells in the 2D histogram contains super pixels from the same semantic region as the 1D case. We also visualized the cell with the highest value in Fig. 2(c), which corresponds to the super pixels within the entire grass field. Such a region is likely to be stable across frames and remain connected. This implies that as long as the intermediate boundaries remain the same, these regions would still contribute to the same cells in the histogram.

图 2(c) 展示了目标超像素(图 2(a) 中红色标记部分)的强度-测地距离直方图。值得注意的是，一维直方图的第二个柱状区间等于二维直方图第二行所有单元格的累加值，且一维直方图第二个柱状区间对应的区域现被细分为与这些单元格对应的多个子区域。这种效果符合预期，因为二维直方图中每个单元格包含的超像素与一维情况同属一个语义区域。我们在图 2(c) 中还标注了数值最大的单元格，该区域对应整片草场范围内的超像素。这类区域在连续帧间往往保持稳定且连通，这意味着只要中间边界保持不变，这些区域仍会对直方图中相同单元格产生贡献。

To compute the similarity distance between two histograms, we can use the $\chi^{2}$ distance or the Earth Mover’s Distance. Following [13], the $\chi^{2}$ distance between two 2D histograms $H_{p}$ and $H_{q}$ with size $M\times N$ is defined by:

为了计算两个直方图之间的相似距离，我们可以使用 $\chi^{2}$ 距离或推土机距离 (Earth Mover’s Distance)。根据 [13]，大小为 $M\times N$ 的两个二维直方图 $H_{p}$ 和 $H_{q}$ 之间的 $\chi^{2}$ 距离定义为：

$$
\chi^{2}(H_{p},H_{q})={\frac{1}{2}}{\sum}_{k=1}^{K}{\sum}_{m=1}^{M}{\frac{[H_{p}(k,m)-H_{q}(k,m)]^{2}}{H_{p}(k,m)+H_{q}(k,m)}}
$$

$$
\chi^{2}(H_{p},H_{q})={\frac{1}{2}}{\sum}_{k=1}^{K}{\sum}_{m=1}^{M}{\frac{[H_{p}(k,m)-H_{q}(k,m)]^{2}}{H_{p}(k,m)+H_{q}(k,m)}}
$$

The Earth Mover’s Distance (EMD) is computed as the sum of the 1D EMDs at each intensity bin of the 2D histogram.

推土机距离 (Earth Mover’s Distance, EMD) 通过计算二维直方图每个强度区间的1D EMD之和获得。

Fig. 3 visualizes the similarity values computed based on 1D and 2D feature histograms from the superpixel-of-interest in Fig. 2(a) on a later video frame. In the color scheme, higher similarity is represented by the warmer color. The figure shows that the 1D histogram is less robust than the 2D histogram: there are multiple regions having similar 1D histograms with the superpixel-of-interest, and the superpixel with the highest 1D histogram similarity is in the background. In contrast, the superpixel with the highest similarity using the 2D histogram falls within the same upper-body region, a desirable result.

图 3 展示了基于图 2(a) 中感兴趣超像素的 1D 和 2D 特征直方图在后续视频帧上计算的相似度值。在配色方案中，较高的相似度用较暖的颜色表示。该图显示 1D 直方图比 2D 直方图的鲁棒性更低：存在多个区域与感兴趣超像素具有相似的 1D 直方图，且 1D 直方图相似度最高的超像素位于背景中。相比之下，使用 2D 直方图获得最高相似度的超像素位于同一上半身区域，这是理想的结果。

3.3 Spatial Information

3.3 空间信息

Pooling methods such as histograms discard spatial information, such as image distance relationships or local neighborhood patterns. We encode spatial cues in two ways: 1) by embedding spatial distances into the voting weight of each superpixel, and 2) by adopting a commonly used spatial pyramid scheme [14].

直方图等池化方法会丢弃空间信息，例如图像距离关系或局部邻域模式。我们通过两种方式编码空间线索：1) 将空间距离嵌入每个超像素的投票权重中；2) 采用常用的空间金字塔方案 [14]。

Spatial distance voting weight For a given superpixel $x$ , its histogram feature is constructed by its intensity and geodesic distances to all other pixels in the same frame. To take the spatial location of these other super pixels into account, the geodesic distances are weighted by the spatial distance of those super pixels to $x$ . In particular, the weighting of superpixel $y$ to the histogram bins of superpixel $x$ in frame $f$ is defined by:

空间距离投票权重 对于给定的超像素 $x$，其直方图特征由强度值及与同帧其他像素的测地距离构成。为考虑其他超像素的空间位置关系，这些测地距离会根据对应超像素与 $x$ 的空间距离进行加权。具体而言，在帧 $f$ 中超像素 $y$ 对超像素 $x$ 直方图分箱的加权计算定义为：

$$
w e i g h t_{y}=\frac{|y|}{|f|}\times\exp(-\mu\times L_{2}(x,y))
$$

$$
w e i g h t_{y}=\frac{|y|}{|f|}\times\exp(-\mu\times L_{2}(x,y))
$$

where $\left|\cdot\right|$ is the area and $L_{2}(\cdot)$ is the Euclidean distance between two super pixels center locations.

其中 $\left|\cdot\right|$ 表示面积，$L_{2}(\cdot)$ 表示两个超像素中心位置之间的欧氏距离。

The area component normalizes the influence of super pixels of different sizes. The exponential ensures that nearby super pixels contribute more to the geodesic histogram of $x$ . This is especially helpful for super pixels that belong to smaller segments, for which most other super pixels have large geodesic distances, that would dominate the histogram. Hence two small regions that are locally different would have very similar histograms. The parameter $\mu$ of the exponential controls the trade-off between global and local information.

面积分量用于归一化不同大小超像素的影响。指数项确保邻近超像素对$x$的测地直方图贡献更大，这对属于较小分段的超像素尤为重要——由于其他多数超像素具有较大测地距离会主导直方图，若不如此，两个局部不同的小区域将产生高度相似的直方图。指数中的参数$\mu$控制着全局与局部信息的平衡。

Spatial pyramid histogram Inspired by the popularity of spatial pyramids [14], we incorporated the pyramid scheme into the construction of our feature histogram to encode more spatial information into the features. We implemented two scales of the spatial pyramid: 1x1 and 2x2 grids over a given frame. A histogram is extracted from each cell of the grid. Histograms from the same scale are concatenated.

空间金字塔直方图
受空间金字塔 [14] 流行度的启发，我们将金字塔方案融入特征直方图的构建中，以将更多空间信息编码到特征中。我们实现了两种尺度的空间金字塔：在给定帧上使用1x1和2x2的网格。从网格的每个单元中提取一个直方图，并将同一尺度的直方图进行拼接。

3.4 Implementation Details

3.4 实现细节

Our features are constructed from the intensity and boundary probability maps. For more robust boundary extraction, we also experiment with two different boundary map methods: spatial edge maps using structured forests [25], and motion boundary maps using the method proposed in [26].

我们的特征基于强度和边界概率图构建。为了获得更稳健的边界提取效果，我们还实验了两种不同的边界图方法：使用结构化森林 [25] 生成的空间边缘图，以及采用 [26] 所提方法生成的运动边界图。

Given the combined edge map and the superpixel graph, the geodesic distance feature for each superpixel is computed using Dijkstra’s algorithm in $O(|X||E|l o g|X|)$ , with the cost of a path being the accumulated boundary scores between one superpixel to another.

给定组合边缘图和超像素图，每个超像素的测地距离特征使用 Dijkstra 算法在 $O(|X||E|l o g|X|)$ 时间内计算得出，路径成本为从一个超像素到另一个超像素之间累积的边界得分。

We empirically set the intensity dimension of the feature histogram at 13 bins, and the geodesic dimension at 9 bins.

我们经验性地将特征直方图的强度维度设为13个区间，测地维度设为9个区间。

4 Experiments

4 实验

In this section, we describe our experiments using the geodesic histogram features for video segmentation. We incorporated our features into two existing frameworks that are based on different clustering algorithms: spectral clustering [8] and parametric graph partitioning [7]. Spectral clustering performs dimensionality reduction on an affinity matrix based on eigenvalues, while parametric graph partitioning directly performs the clustering on the superpixel graph by modeling $L_{p}$ affinity matrices probabilistic ally. Also, the method in [8] generates coarse-to-fine hierarchical segmentation results, while [7] only outputs a single level of segmentation.

在本节中，我们描述了利用测地线直方图特征进行视频分割的实验。我们将这些特征整合到基于两种不同聚类算法的现有框架中：谱聚类 [8] 和参数化图分割 [7] 。谱聚类基于特征值对亲和矩阵进行降维处理，而参数化图分割则通过概率化建模 $L_{p}$ 亲和矩阵直接在超像素图上执行聚类。此外，[8] 中的方法生成由粗到细的分层分割结果，而 [7] 仅输出单层分割。

The experiments were conducted on the Segtrack V2 [6] and Chen’s Xiph.org [24] datasets, covering a wide range of scenarios for evaluating video segmentation algorithms. We evaluate our segmentation results using the metrics proposed in [27], including 3D Accuracy (AC), 3D Under-segmentation Error (UE), 3D Boundary Recall (BR), and 3D Boundary Precision (BP). All experiments were conducted with the exact same set of initial super pixels and other parameter settings.

实验在Segtrack V2 [6]和Chen's Xiph.org [24]数据集上进行，涵盖了评估视频分割算法的多种场景。我们采用[27]提出的指标评估分割结果，包括三维准确率(AC)、三维欠分割错误(UE)、三维边界召回率(BR)和三维边界精确率(BP)。所有实验均采用完全相同的初始超像素集及其他参数设置。

4.1 Video Segmentation Using Spectral Clustering

4.1 基于谱聚类 (Spectral Clustering) 的视频分割

We first evaluate the performance of the framework by adding our feature to spectral clustering [8]. We use the same 6 features as [8]: short term temporal, long term temporal, spatio temporal appearance, spatio temporal motion, across boundary appearance, and across boundary motion. The affinity matrix was computed by combining the 6 affinity matrices computed from each feature. We combined the original computed affinity matrix with the geodesic histogram features in order to preserve the algorithm settings and superpixel configurations. The similarity distances based on our features were computed using the $\chi^{2}$ distance.

我们首先通过将我们的特征添加到谱聚类 [8] 中来评估框架的性能。我们使用与 [8] 相同的6个特征：短期时间、长期时间、时空外观、时空运动、跨边界外观和跨边界运动。通过组合从每个特征计算的6个亲和矩阵来计算亲和矩阵。我们将原始计算的亲和矩阵与测地直方图特征相结合，以保留算法设置和超像素配置。基于我们特征的相似性距离使用 $\chi^{2}$ 距离计算。

Fig. 4 shows the evaluation results of spectral clustering with and without our feature on Segtrack v2 and Chen Xiph.org datasets. We tested four settings of our feature: (i) 2D histogram using only spatial edge maps to compute geodesic distances and without spatial distance voting weight (2D - 0), (ii) 2D histogram using spatial edge maps and spatial distance voting weight with $\mu=0.02$ (2D - 0.02 ), (iii) 2D histogram using both spatial edge and motion boundary maps with $\mu=0.02$ (2D $^+$ 0.02) and, (iv) 2D histograms with spatial pyramid (2D + 0.02 sp). Compared to the baseline, our feature significantly improved segmentation performance. The improvement was most significant in 3D accuracy: increased by 5% for Segtrack v2 and $10%$ for Chen Xiph.org. For Segtrack v2 dataset, our feature was able to improve the segmentation results on all four metrics. For Chen Xiph.org dataset, the feature gave a strong boost to 3D accuracy and 3D boundary precision. For all settings tested, we noticed that motion boundary maps did not affect performance much. Given that motion boundary map generation requires optic flow computation, which can be time consuming, its omission might result in faster implementations. The spatial distance voting weights had a strong impact on the results and clearly impro