Temporal Cycle-Consistency Learning

时序周期一致性学习

Debidatta Dwibedi 1, Yusuf Aytar 2, Jonathan Tompson 1, Pierre Sermanet 1, and Andrew Zisserman 2 1 Google Brain 2 DeepMind {debidatta, yusufaytar, tompson, sermanet, zisserman}@google.com

Debidatta Dwibedi 1, Yusuf Aytar 2, Jonathan Tompson 1, Pierre Sermanet 1, and Andrew Zisserman 2
1 Google Brain
2 DeepMind
{debidatta, yusufaytar, tompson, sermanet, zisserman}@google.com

Figure 1: We present a self-supervised representation learning technique called temporal cycle consistency (TCC) learning. It is inspired by the temporal video alignment problem, which refers to the task of finding correspondences across multiple videos despite many factors of variation. The learned representations are useful for fine-grained temporal understanding in videos. Additionally, we can now align multiple videos by simply finding nearest-neighbor frames in the embedding space.

图 1: 我们提出了一种称为时序循环一致性 (TCC) 学习的自监督表征学习方法。该方法受时序视频对齐问题的启发，该问题指在存在多种变化因素的情况下寻找多个视频间对应关系的任务。学习到的表征可用于视频中的细粒度时序理解。此外，我们现在只需在嵌入空间中找到最近邻帧即可对齐多个视频。

Abstract

摘要

We introduce a self-supervised representation learning method based on the task of temporal alignment between videos. The method trains a network using temporal cycleconsistency (TCC), a differentiable cycle-consistency loss that can be used to find correspondences across time in multiple videos. The resulting per-frame embeddings can be used to align videos by simply matching frames using nearest-neighbors in the learned embedding space.

我们提出了一种基于视频间时序对齐任务的自监督表征学习方法。该方法使用时序循环一致性 (TCC) 训练网络，这是一种可微分的循环一致性损失函数，可用于在多个视频中寻找跨时间对应关系。通过学习得到的逐帧嵌入表示，只需在嵌入空间中使用最近邻匹配帧，即可实现视频对齐。

To evaluate the power of the embeddings, we densely label the Pouring and Penn Action video datasets for action phases. We show that (i) the learned embeddings enable few-shot classification of these action phases, significantly reducing the supervised training requirements; and (ii) TCC is complementary to other methods of selfsupervised learning in videos, such as Shuffle and Learn and Time-Contrastive Networks. The embeddings are also used for a number of applications based on alignment (dense temporal correspondence) between video pairs, including transfer of metadata of synchronized modalities between videos (sounds, temporal semantic labels), synchronized playback of multiple videos, and anomaly detection. Project webpage: https://sites.google. com/view/temporal-cycle-consistency.

为了评估嵌入(embedding)的效果，我们对Pouring和Penn Action视频数据集进行了动作阶段的密集标注。研究表明：(i) 学习到的嵌入可实现对这些动作阶段的少样本分类，显著降低监督训练需求；(ii) TCC与视频自监督学习的其他方法（如Shuffle and Learn和Time-Contrastive Networks）具有互补性。这些嵌入还可用于基于视频对之间对齐（密集时间对应关系）的多种应用，包括视频间同步模态元数据（声音、时间语义标签）的迁移、多视频同步播放以及异常检测。项目网页：https://sites.google.com/view/temporal-cycle-consistency。

1. Introduction

1. 引言

The world presents us with abundant examples of sequential processes. A plant growing from a seedling to a tree, the daily routine of getting up, going to work and coming back home, or a person pouring themselves a glass of water – are all examples of events that happen in a particular order. Videos capturing such processes not only contain information about the causal nature of these events, but also provide us with a valuable signal – the possibility of temporal correspondences lurking across multiple instances of the same process. For example, during pouring, one could be reaching for a teapot, a bottle of wine, or a glass of water to pour from. Key moments such as the first touch to the container or the container being lifted from the ground are common to all pouring sequences. These correspondences, which exist in spite of many varying factors like visual changes in viewpoint, scale, container style, the speed of the event, etc., could serve as the link between raw video sequences and high-level temporal abstractions (e.g. phases of actions). In this work we present evidence that suggests the very act of looking for correspondences in sequential data enables the learning of rich and useful representations, particularly suited for fine-grained temporal understanding of videos.

世界为我们提供了丰富的序列过程实例。从幼苗长成大树、每日起床工作回家的生活作息，到人们为自己倒水的动作，都是以特定顺序发生的事件范例。记录这类过程的视频不仅蕴含了事件因果本质的信息，更提供了一种宝贵信号——相同过程多个实例间可能潜藏着时序对应关系。例如倒水动作中，人们可能伸手去拿茶壶、葡萄酒瓶或水杯作为容器。首次触碰容器或将容器从桌面举起等关键瞬间，是所有倒水序列共有的特征。尽管存在视角变化、尺度差异、容器样式、动作速度等诸多变量，这些跨越视觉差异的对应关系，仍能成为原始视频序列与高层时序抽象（如动作阶段）之间的桥梁。本研究通过实证表明：在序列数据中寻找对应关系这一行为本身，就能促使模型学习到丰富且实用的表征，尤其适用于视频的细粒度时序理解。

Temporal reasoning in videos, understanding multiple stages of a process and causal relations between them, is a relatively less studied problem compared to recognizing action categories [10, 42]. Learning representations that can differentiate between states of objects as an action proceeds is critical for perceiving and acting in the world. It would be desirable for a robot tasked with learning to pour drinks to understand each intermediate state of the world as it proceeds with performing the task. Although videos are a rich source of sequential data essential to understanding such state changes, their true potential remains largely untapped. One hindrance in the fine-grained temporal understanding of videos can be an excessive dependence on pure supervised learning methods that require per-frame annotations. It is not only difficult to get every frame labeled in a video because of the manual effort involved, but also it is not entirely clear what are the exhaustive set of labels that need to be collected for fine-grained understanding of videos. Alternatively, we explore self-supervised learning of correspondences between videos across time. We show that the emerging features have strong temporal reasoning capacity, which is demonstrated through tasks such as action phase classification and tracking the progress of an ac- tion.

视频中的时序推理（理解一个过程的多个阶段及其因果关系）与识别动作类别相比[10,42]，是一个研究相对较少的问题。学习能够区分动作进行中物体状态变化的表征，对于感知和行动至关重要。例如，一个学习倒饮料的机器人需要理解任务执行过程中每个中间状态。尽管视频是理解这类状态变化的重要序列数据来源，但其真正潜力尚未被充分挖掘。阻碍视频细粒度时序理解的一个因素可能是对纯监督学习方法的过度依赖，这类方法需要逐帧标注。不仅因为人工标注成本高而难以获取视频中每一帧的标签，而且对于视频细粒度理解需要收集哪些完整标签集也并不完全明确。为此，我们探索了跨时间视频对应关系的自监督学习方法，证明所提取的特征具备强大的时序推理能力，这通过动作阶段分类和动作进度跟踪等任务得到验证。

When frame-by-frame alignment (i.e. supervision) is available, learning correspondences reduces to learning a common embedding space from pairs of aligned frames (e.g. CCA [3, 4] and ranking loss [35]). However, for most of the real world sequences such frame-by-frame alignment does not exist naturally. One option would be to artificially obtain aligned sequences by recording the same event through multiple cameras [30, 35, 37]. Such data collection methods might find it difficult to capture all the variations present naturally in videos in the wild. On the other hand, our self-supervised objective does not need explicit correspondences to align different sequences. It can align significant variations within an action category (e.g. pouring liquids, or baseball pitch). Interestingly, the embeddings that emerge from learning the alignment prove to be useful for fine-grained temporal understanding of videos. More specifically, we learn an embedding space that maximizes one-to-one mappings (i.e. cycle-consistent points) across pairs of video sequences within an action category. In order to do that, we introduce two differentiable versions of cycle consistency computation which can be optimized by conventional gradient-based optimization methods. Further details of the method will be explained in section 3.

当存在逐帧对齐（即监督）时，学习对应关系简化为从对齐的帧对中学习共同的嵌入空间（例如CCA [3, 4] 和排序损失 [35]）。然而，对于大多数现实世界序列，这种逐帧对齐并不自然存在。一种选择是通过多台摄像机记录同一事件来人工获取对齐序列 [30, 35, 37]。此类数据收集方法可能难以捕捉自然视频中存在的所有变化。另一方面，我们的自监督目标不需要显式对应关系来对齐不同序列。它可以对齐动作类别内的显著变化（例如倒液体或棒球投球）。有趣的是，通过学习对齐产生的嵌入被证明对视频的细粒度时间理解非常有用。更具体地说，我们学习了一个嵌入空间，该空间在动作类别内的视频序列对之间最大化一对一映射（即循环一致点）。为此，我们引入了两种可微分的循环一致性计算版本，可以通过传统的基于梯度的优化方法进行优化。该方法的更多细节将在第3节中解释。

The main contribution of this paper is a new selfsupervised training method, referred to as temporal cycle consistency (TCC) learning, that learns representations by aligning video sequences of the same action. We compare TCC representations against features from existing selfsupervised video representation methods [27, 35] and supervised learning, for the tasks of action phase classification and continuous progress tracking of an action. Our ap- proach provides significant performance boosts when there is a lack of labeled data. We also collect per-frame annotations of Penn Action [52] and Pouring [35] datasets that we will release publicly to facilitate evaluation of fine-grained video understanding tasks.

本文的主要贡献是提出了一种新的自监督训练方法，称为时序循环一致性 (TCC) 学习，该方法通过对齐相同动作的视频序列来学习表征。我们将 TCC 表征与现有自监督视频表征方法 [27, 35] 和监督学习的特征进行了比较，用于动作阶段分类和动作连续进度跟踪任务。在缺乏标注数据的情况下，我们的方法显著提升了性能。我们还收集了 Penn Action [52] 和 Pouring [35] 数据集的逐帧标注，并将公开释放以促进细粒度视频理解任务的评估。

2. Related Work

2. 相关工作

Cycle consistency. Validating good matches by cycling between two or more samples is a commonly used technique in computer vision. It has been applied successfully for tasks like co-segmentation [43, 44], structure from motion [49, 51], and image matching [54, 55, 56]. For in- stance, FlowWeb [54] optimizes globally-consistent dense correspondences using the cycle consistent flow fields between all pairs of images in a collection, whereas Zhou et al. [56] approaches a similar task by formulating it as a low-rank matrix recovery problem and solves it through fast alternating minimization. These methods learn robust dense correspondences on top of fixed feature representations (e.g. SIFT, deep features, etc.) by enforcing cycle consistency and/or spatial constraints between the images. Our method differs from these approaches in that TCC is a self-supervised representation learning method which learns embedding spaces that are optimized to give good correspondences. Furthermore we address a temporal correspondence problem rather than a spatial one. Zhou et al. [55] learn to align multiple images using the supervision from 3D guided cycle-consistency by leveraging the initial correspondences that are available between multiple renderings of a 3D model, whereas we don’t assume any given correspondences. Another way of using cyclic relations is to directly learn bi-directional transformation functions between multiple spaces such as CycleGANs [57] for learning image transformations, and CyCADA [21] for domain adaptation. Unlike these approaches we don’t have multiple domains, and we can’t learn transformation functions between all pairs of sequences. Instead we learn a joint embedding space in which the Euclidean distance defines the mapping across the frames of multiple sequences. Similar to us, Aytar et al. [7] applies cycle-consistency between temporal sequences, however they use it as a validation tool for hyper-parameter optimization of learned representations for the end goal of imitation learning. Unlike our approach, their cycle-consistency measure is non-differentiable and hence can’t be directly used for representation learning.

循环一致性 (Cycle consistency)。通过在两个或多个样本之间进行循环验证良好匹配是计算机视觉中常用的技术。该方法已成功应用于协同分割 [43, 44]、运动恢复结构 [49, 51] 和图像匹配 [54, 55, 56] 等任务。例如，FlowWeb [54] 通过优化图像集中所有图像对之间的循环一致流场来获得全局一致的密集对应关系，而 Zhou 等人 [56] 则将该任务表述为低秩矩阵恢复问题，并通过快速交替最小化求解。这些方法通过在固定特征表示 (如 SIFT、深度特征等) 基础上强制执行循环一致性和/或空间约束，学习鲁棒的密集对应关系。我们的方法 TCC 与这些方法的不同之处在于，它是一种自监督表示学习方法，通过学习优化的嵌入空间来获得良好的对应关系。此外，我们解决的是时间对应问题而非空间对应问题。Zhou 等人 [55] 利用 3D 模型多视角渲染之间的初始对应关系，通过 3D 引导的循环一致性监督来学习对齐多幅图像，而我们不需要任何给定的对应关系。另一种利用循环关系的方法是直接学习多个空间之间的双向变换函数，例如用于图像变换的 CycleGANs [57] 和用于域适应的 CyCADA [21]。与这些方法不同，我们没有多个域，也无法学习所有序列对之间的变换函数。相反，我们学习一个联合嵌入空间，其中欧氏距离定义了跨多个序列帧的映射。与我们类似，Aytar 等人 [7] 在时间序列之间应用循环一致性，但他们将其作为超参数优化的验证工具，最终目标是模仿学习。与我们的方法不同，他们的循环一致性度量是不可微的，因此不能直接用于表示学习。

Video alignment. When we have synchronization information (e.g. multiple cameras recording the same event) then learning a mapping between multiple video sequences can be accomplished by using existing methods such as Canonical Correlation Analysis (CCA) [3, 4], ranking [35] or match-classification [6] objectives. For instance TCN [35] and circulant temporal encoding [30] align multiple views of the same event, whereas Sigurdsson et al.[37] learns to align first and third person videos. Although we have a similar objective, these methods are not suitable for our task as we cannot assume any given correspondences between different videos.

视频对齐。当我们拥有同步信息（例如多个摄像机录制同一事件）时，可以通过使用现有方法（如典型相关分析 (CCA) [3, 4]、排序 [35] 或匹配分类 [6] 目标）来学习多个视频序列之间的映射。例如，TCN [35] 和循环时间编码 [30] 对齐同一事件的多视角视频，而 Sigurdsson 等人 [37] 则学习对齐第一人称和第三人称视频。尽管我们有类似的目标，但这些方法并不适用于我们的任务，因为我们无法假设不同视频之间存在任何给定的对应关系。

Action localization and parsing. As action recognition is quite popular in the computer vision community, many studies [17, 38, 46, 50, 53] explore efficient deep architectures for action recognition and localization in videos. Past work has also explored parsing of fine-grained actions in videos [24, 25, 29] while some others [13, 33, 34, 36] discover sub-activities without explicit supervision of temporal boundaries. [20] learns a supervised regression model with voting to predict the completion of an action, and [2] discovers key events in an un super iv sed manner using a weak association between videos and text instructions. However all these methods heavily rely on existing deep image [19, 39] or spatio-temporal [45] features, whereas we learn our representation from scratch using raw video sequences. Soft nearest neighbours. The differentiable or soft formulation for nearest-neighbors is a commonly known method [18]. This formulation has recently found application in metric learning for few-shot learning [28, 31, 40]. We also make use of soft nearest neighbor formulation as a component in our differentiable cycle-consistency computation.

动作定位与解析。动作识别在计算机视觉领域相当流行，许多研究[17, 38, 46, 50, 53]探索了视频中动作识别与定位的高效深度架构。以往工作还研究了视频中细粒度动作的解析[24, 25, 29]，而另一些研究[13, 33, 34, 36]则在无显式时间边界监督的情况下发现子活动。[20]通过带投票的监督回归模型预测动作完成度，[2]则利用视频与文本指令间的弱关联以无监督方式发现关键事件。然而这些方法都严重依赖现有深度图像[19, 39]或时空特征[45]，而我们的表征直接从原始视频序列学习。软最近邻。可微分或软化的最近邻公式是广为人知的方法[18]。该公式最近被应用于少样本学习的度量学习[28, 31, 40]。我们也将软最近邻公式作为可微分循环一致性计算的组成部分。

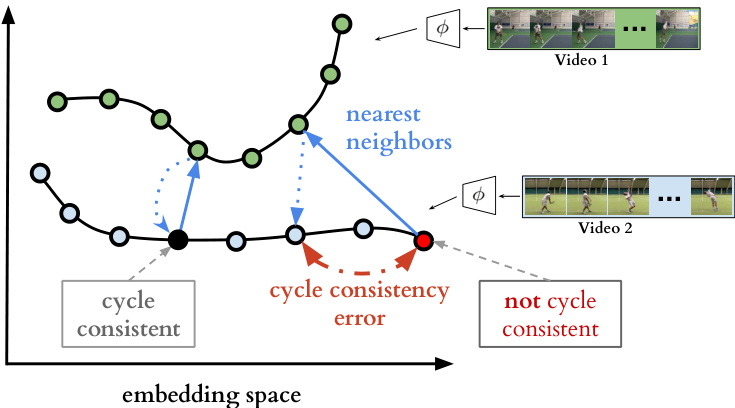
Figure 2: Cycle-consistent representation learning. We show two example video sequences encoded in an example embedding space. If we use nearest neighbors for matching, one point (shown in black) is cycling back to itself while another one (shown in red) is not. Our target is to learn an embedding space where maximum number of points can cycle back to themselves. We achieve it by minimizing the cycle consistency error (shown in red dotted line) for each point in every pair of sequences.

图 2: 循环一致性表示学习。我们展示了在示例嵌入空间中编码的两个视频序列。若采用最近邻匹配，一个点（黑色所示）能循环回到自身，而另一个点（红色所示）则不能。我们的目标是学习一个能使最多点实现自我循环的嵌入空间，通过最小化每对序列中每个点的循环一致性误差（红色虚线所示）来实现这一目标。

Self-supervised representations. There has been significant progress in learning from images and videos without requiring class or temporal segmentation labels. Instead of labels, self-supervised learning methods use signals such as temporal order [16, 27], consistency across viewpoints and/or temporal neighbors [35], classifying arbitrary temporal segments [22], temporal distance classification within or across modalities [7], spatial permutation of patches [5, 14], visual similarity [32] or a combination of such signals [15]. While most of these approaches optimize each sample independently, TCC jointly optimizes over two sequences at a time, potentially capturing more variations in the embedding space. Additionally, we show that TCC yields best results when combined with some of the unsupervised losses above.

自监督表示。在不依赖类别或时序分割标签的情况下，从图像和视频中学习已取得显著进展。自监督学习方法通过以下信号替代标签：时序顺序 [16, 27]、跨视角和/或时序邻域的一致性 [35]、对任意时序片段的分类 [22]、模态内或跨模态的时序距离分类 [7]、图像块的空间排列 [5, 14]、视觉相似性 [32] 或上述信号的组合 [15]。虽然大多数方法独立优化每个样本，但 TCC 同时优化两个序列，从而能在嵌入空间中捕捉更多变化。此外，我们证明 TCC 与上述某些无监督损失函数结合时效果最佳。

3. Cycle Consistent Representation Learning

3. 循环一致性表示学习

The core contribution of this work is a self-supervised approach to learn an embedding space where two similar video sequences can be aligned temporally. More specifically, we intend to maximize the number of points that can be mapped one-to-one between two sequences by using the minimum distance in the learned embedding space. We can achieve such an objective by maximizing the number of cycle-consistent frames between two sequences (see Figure 2). However, cycle-consistency computation is typically not a differentiable procedure. In order to facilitate learning such an embedding space using back-propagation, we introduce two differentiable versions of the cycle-consistency loss, which we describe in detail below.

本工作的核心贡献在于提出了一种自监督学习方法，用于构建一个能将两个相似视频序列在时间轴上对齐的嵌入空间。具体而言，我们旨在通过学习到的嵌入空间中的最小距离，最大化两个序列间可建立一对一映射的点位数量。这一目标可通过最大化两个序列间循环一致帧（cycle-consistent frames）的数量来实现（见图 2）。然而，循环一致性计算通常不具备可微性。为了通过反向传播学习此类嵌入空间，我们引入了两种可微循环一致性损失函数变体，具体描述如下。

Given any frame $s_{i}$ in a sequence ${\cal S}={s_{1},s_{2},...,s_{N}}$ , the embedding is computed as $u_{i}=\phi(s_{i};\theta)$ , where $\phi$ is the neural network encoder parameterized by $\theta$ . For the following sections, assume we are given two video sequences $S$ and $T$ , with lengths $N$ and $M$ , respectively. Their embeddings are computed as $U={u_{1},u_{2},...,u_{N}}$ and $V=$ ${v_{1},v_{2},...,v_{M}}$ such that $u_{i}=\phi(s_{i};\theta)$ and $v_{i}=\phi(t_{i};\theta)$ .

给定序列 ${\cal S}={s_{1},s_{2},...,s_{N}}$ 中的任意帧 $s_{i}$，其嵌入计算为 $u_{i}=\phi(s_{i};\theta)$，其中 $\phi$ 是由参数 $\theta$ 参数化的神经网络编码器。在后续章节中，假设给定两个视频序列 $S$ 和 $T$，长度分别为 $N$ 和 $M$。它们的嵌入计算为 $U={u_{1},u_{2},...,u_{N}}$ 和 $V=$ ${v_{1},v_{2},...,v_{M}}$，满足 $u_{i}=\phi(s_{i};\theta)$ 和 $v_{i}=\phi(t_{i};\theta)$。

3.1. Cycle-consistency

3.1. 循环一致性

In order to check if a point $u_{i}\in U$ is cycle consistent, we first determine its nearest neighbor, $v_{j}=\mathrm{arg}\mathrm{min}{v\in V}|u_{i}-$ $v||$ . We then repeat the process to find the nearest neighbor of $v_{j}$ in $U$ , i.e. . The point $u_{i}$ is cycle-consistent if and only if $i=k$ , in other words if the point $u_{i}$ cycles back to itself. Figure 2 provides positive and negative examples of cycle consistent points in an embedding space. We can learn a good embedding space by maximizing the number of cycle-consistent points for any pair of sequences. However that would require a differentiable version of cycle-consistency measure, two of which we introduce below.

为了检查点 $u_{i}\in U$ 是否满足循环一致性，我们首先确定其最近邻 $v_{j}=\mathrm{arg}\mathrm{min}{v\in V}|u_{i}-$ $v||$。接着重复该过程，在 $U$ 中寻找 $v_{j}$ 的最近邻，即 当且仅当 $i=k$ 时（换言之，若点 $u_{i}$ 能循环映射回自身），该点满足循环一致性。图 2 展示了嵌入空间中循环一致性点的正例与反例。通过最大化任意序列对的循环一致点数量，我们可以学习到良好的嵌入空间。但这需要可微分的循环一致性度量方法，下文将介绍其中两种。

3.2. Cycle-back Classification

3.2. 回环分类

We first compute the soft nearest neighbor $\widetilde{v}$ of $u_{i}$ in $V$ , then figure out the nearest neighbor of $\widetilde{v}$ ba cek in $U$ . We consider each frame in the first sequence $U$ to be a separate class and our task of checking for cycle-consistency reduces to classification of the nearest neighbor correctly. The logits are calculated using the distances between $\widetilde{v}$ and any $u_{k}\in$ $U$ , and the ground truth label $y$ are all zero se except for the $i^{t h}$ index which is set to 1.

我们首先计算$u_{i}$在$V$中的软最近邻$\widetilde{v}$，然后找出$\widetilde{v}$在$U$中的最近邻。我们将第一个序列$U$中的每一帧视为一个独立类别，此时循环一致性检查任务转化为对最近邻的正确分类问题。logits通过计算$\widetilde{v}$与任意$u_{k}\in U$之间的距离获得，真实标签$y$除第$i^{th}$位设为1外其余均为0。

For the selected point $u_{i}$ , we use the softmax function to define its soft nearest neighbor $\widetilde{v}$ as:

对于选定的点 $u_{i}$，我们使用 softmax 函数定义其软最近邻 $\widetilde{v}$ 为：

$$
\widetilde{v}=\sum_{j}^{M}\alpha_{j}v_{j},\quad w h e r e\quad\alpha_{j}=\frac{e^{-||u_{i}-v_{j}||^{2}}}{\sum_{k}^{M}e^{-||u_{i}-v_{k}||^{2}}}
$$

$$
\widetilde{v}=\sum_{j}^{M}\alpha_{j}v_{j},\quad 其中\quad\alpha_{j}=\frac{e^{-||u_{i}-v_{j}||^{2}}}{\sum_{k}^{M}e^{-||u_{i}-v_{k}||^{2}}}
$$

and $\alpha$ is the the similarity distribution which signifies the proximity between $u_{i}$ and each $v_{j}\in V$ . And then we solve the $N$ class (i.e. number of frames in $U$ ) classification problem where the logits are $x_{k}=-||\widetilde{v}-u_{k}||^{2}$ and the predicted labels are $\hat{y}=s o f t m a x(x)$ . Finalely we optimize the cross-

且 $\alpha$ 是表示 $u_{i}$ 与每个 $v_{j}\in V$ 之间接近度的相似性分布。接着我们求解 $N$ 类（即 $U$ 中的帧数）分类问题，其中逻辑值为 $x_{k}=-||\widetilde{v}-u_{k}||^{2}$，预测标签为 $\hat{y}=softmax(x)$。最后我们优化交叉-

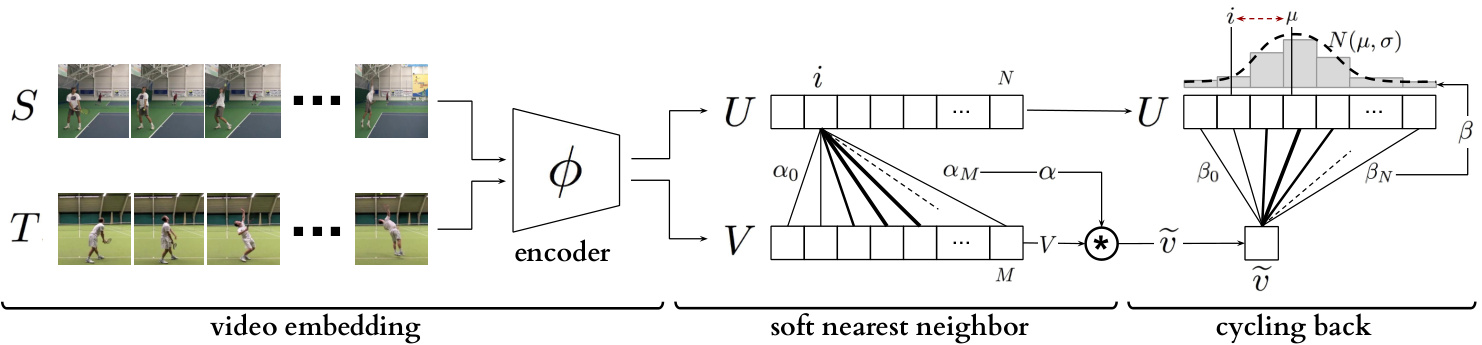
Figure 3: Temporal cycle consistency. The embedding sequences $U$ and $V$ are obtained by encoding video sequences $S$ and $T$ with the encoder network $\phi$ , respectively. For the selected point $u_{i}$ in $U$ , soft nearest neighbor computation and cycling back to $U$ again is demonstrated visually. Finally the normalized distance between the index $i$ and cycling back distribution $N(\mu,\sigma^{2})$ (which is fitted to $\beta$ ) is minimized.

图 3: 时序循环一致性。嵌入序列 $U$ 和 $V$ 分别通过编码器网络 $\phi$ 对视频序列 $S$ 和 $T$ 进行编码获得。对于 $U$ 中选定的点 $u_{i}$，以可视化方式展示了软最近邻计算及再次循环回 $U$ 的过程。最终最小化索引 $i$ 与循环回分布 $N(\mu,\sigma^{2})$ (拟合至 $\beta$) 之间的归一化距离。

entropy loss as follows:

熵损失如下：

$$
L_{c b c}=-\sum_{j}^{N}y_{j}\log(\hat{y}_{j})
$$

$$
L_{c b c}=-\sum_{j}^{N}y_{j}\log(\hat{y}_{j})
$$

3.3. Cycle-back Regression

3.3. 循环回归 (Cycle-back Regression)

Although cycle-back classification defines a differentiable cycle-consistency loss function, it has no notion of how close or far in time the point to which we cycled back is. We want to penalize the model less if we are able to cycle back to closer neighbors as opposed to the other frames that are farther away in time. In order to incorporate temporal proximity in our loss, we introduce cycle-back regression. A visual description of the entire process is shown in Figure 3. Similar to the previous method first we compute the soft nearest neighbor $\widetilde{v}$ of $u_{i}$ in $V$ . Then we compute the similarity vector $\beta$ tha te defines the proximity between $\widetilde{v}$ and each $u_{k}\in U$ as:

虽然循环分类定义了一个可微的循环一致性损失函数，但它没有考虑循环返回的时间点距离远近。我们希望当模型能循环返回时间上更接近的相邻帧时，给予较小惩罚，反之则给予较大惩罚。为了在损失函数中引入时间邻近性，我们提出了循环回归方法。整个过程的可视化描述见图3。与前文方法类似，首先我们计算$u_{i}$在$V$中的软最近邻$\widetilde{v}$，然后计算相似度向量$\beta$，该向量通过以下方式定义$\widetilde{v}$与每个$u_{k}\in U$之间的邻近关系：

$$
\beta_{k}=\frac{e^{-||\widetilde{v}-u_{k}||^{2}}}{\sum_{j}^{N}e^{-||\widetilde{v}-u_{j}||^{2}}}
$$

$$
\beta_{k}=\frac{e^{-||\widetilde{v}-u_{k}||^{2}}}{\sum_{j}^{N}e^{-||\widetilde{v}-u_{j}||^{2}}}
$$

Note that $\beta$ is a discrete distribution of similarities over time and we expect it to show a peaky behavior around the $i^{t h}$ index in time. Therefore, we impose a Gaussian prior on $\beta$ by minimizing the normalized squared distance $\frac{|i-\mu|^{2}}{\sigma^{2}}$ as our objective. We enforce $\beta$ to be more peaky around $i$ by applying additional variance regular iz ation. We define our final objective as:

注意到 $\beta$ 是一个随时间变化的相似性离散分布，我们期望它在时间维度上的第 $i^{t h}$ 个索引附近呈现峰值特性。因此，我们通过最小化归一化平方距离 $\frac{|i-\mu|^{2}}{\sigma^{2}}$ 作为目标函数，对 $\beta$ 施加高斯先验。为了增强 $\beta$ 在 $i$ 附近的峰值特性，我们额外应用了方差正则化。最终目标函数定义为：

$$
L_{c b r}=\frac{|i-\mu|^{2}}{\sigma^{2}}+\lambda\log(\sigma)
$$

$$
L_{c b r}=\frac{|i-\mu|^{2}}{\sigma^{2}}+\lambda\log(\sigma)
$$

where $\begin{array}{r}{\mu=\sum_{k}^{N}\beta_{k}k}\end{array}$ and $\begin{array}{r}{\sigma^{2}=\sum_{k}^{N}\beta_{k}(k-\mu)^{2}}\end{array}$ , and $\lambda$ is the reg u lari z ation weight. No te that we minimize the log of variance as using just the variance is more prone to numerical instabilities. All these formulations are differentiable and can conveniently be optimized with conventional back-propagation.

其中 $\begin{array}{r}{\mu=\sum_{k}^{N}\beta_{k}k}\end{array}$ 和 $\begin{array}{r}{\sigma^{2}=\sum_{k}^{N}\beta_{k}*(k-\mu)^{2}}\end{array}$ ，$\lambda$ 为正则化权重。需要注意的是，我们最小化方差的对数，因为直接使用方差更容易出现数值不稳定的情况。所有这些公式都是可微分的，可以通过常规的反向传播方便地进行优化。

Table 1: Architecture of the embedding network.

操作	输出尺寸	参数
时序堆叠3D卷积	k×14×14×512	堆叠k个上下文帧 [3×3×3,512]×2
时空池化	512	全局3D最大池化
全连接层	512	[512]×2
线性投影	128	128

表 1: 嵌入网络架构。

3.4. Implementation details

3.4. 实现细节

Training Procedure. Our self-supervised representation is learned by minimizing the cycle-consistency loss for all the pair of sequences in the training set. Given a sequence pair, their frames are embedded using the encoder network and we optimize cycle consistency losses for randomly selected frames within each sequence until convergence. We used Tensorflow [1] for all our experiments.

训练过程。我们的自监督表征是通过最小化训练集中所有序列对的循环一致性损失来学习的。给定一个序列对，我们使用编码器网络嵌入其帧，并针对每个序列中随机选择的帧优化循环一致性损失，直至收敛。所有实验均使用 Tensorflow [1] 实现。

Encoding Network. All the frames in a given video sequence are resized to $224\times224$ . When using ImageNet pretrained features, we use ResNet-50 [19] architecture to extract features from the output of Conv4c layer. The size of the extracted convolutional features are $14\times14\times1024$ . Because of the size of the datasets, when training from scratch we use a smaller model along the lines of VGG-M [11]. This network takes input at the same resolution as ResNet50 but is only 7 layers deep. The convolutional features produced by this base network are of the size $14\times14\times512$ . These features are provided as input to our embedder network (presented in Table 1). We stack the features of any given frame and its $k$ context frames along the dimension of time. This is followed by 3D convolutions for aggregating temporal information. We reduce the dimensionality by using 3D max-pooling followed by two fully connected layers. Finally, we use a linear projection to get a 128- dimensional embedding for each frame. More details of the architecture are presented in the supplementary material.

编码网络。给定视频序列中的所有帧都被调整为 $224\times224$ 大小。使用ImageNet预训练特征时，我们采用ResNet-50 [19]架构从Conv4c层输出中提取特征，提取的卷积特征尺寸为 $14\times14\times1024$。由于数据集规模限制，在从头训练时我们使用类似VGG-M [11]的轻量模型，该网络输入分辨率与ResNet50相同但仅含7层，基础网络生成的卷积特征尺寸为 $14\times14\times512$。这些特征将作为嵌入网络（结构见表1）的输入。我们将目标帧及其 $k$ 个上下文帧的特征沿时间维度堆叠，随后通过3D卷积聚合时序信息，并使用3D最大池化降维后接两个全连接层，最终通过线性投影得到每帧的128维嵌入向量。架构详情见补充材料。

4. Datasets and Evaluation

4. 数据集与评估

We validate the usefulness of our representation learning technique on two datasets: (i) Pouring [35]; and ( ii)

我们在两个数据集上验证了表征学习技术的有效性：(i) Pouring [35]；以及(ii)

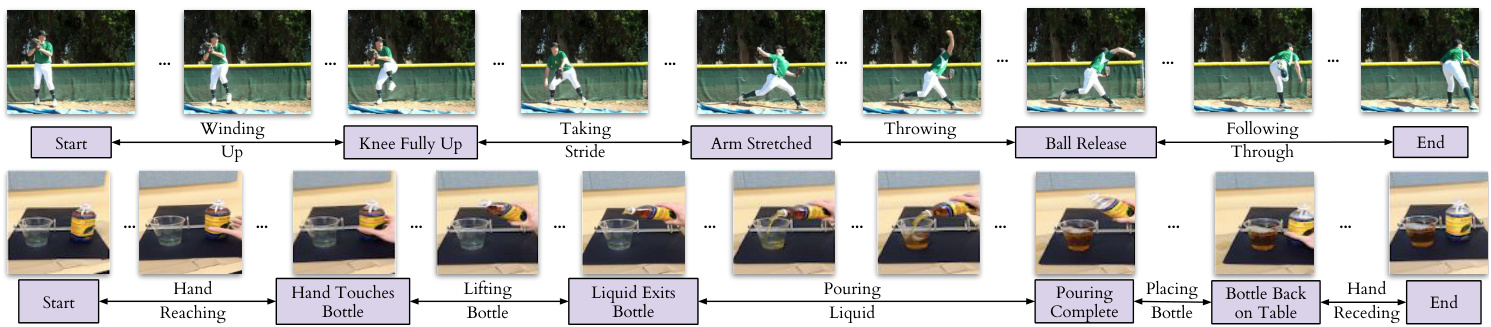
Figure 4: Example labels for the actions ‘Baseball Pitch’ (top row) and ‘Pouring’ (bottom row). The key events are shown in boxes below the frame (e.g. ‘Hand touches bottle’), and each frame in between two key events has a phase label (e.g. ‘Lifting bottle’).

图 4: "棒球投球"(上排)和"倒水"(下排)动作的示例标签。关键事件显示在帧下方的方框中(例如"手触碰瓶子")，两个关键事件之间的每一帧都有阶段标签(例如"举起瓶子")。

Penn Action [52]. These datasets both contain videos of humans performing actions, and provide us with collections of videos where dense alignment can be performed. While Pouring focuses more on the objects being interacted with, Penn Action focuses on humans doing sports or exercise.

Penn Action [52]。这两个数据集都包含人类执行动作的视频，为我们提供了可进行密集对齐的视频集合。Pouring更侧重于被交互的物体，而Penn Action则聚焦于人类进行体育运动或锻炼的场景。

Annotations. For evaluation purposes, we add two types of labels to the video frames of these datasets: key events and phases. Densely labeling each frame in a video is a difficult and time-consuming task. Labelling only key events both reduces the number of frames that need to be annotated, and also reduces the ambiguity of the task (and thus the disagreement between annotators). For example, annotators agree more about the frame when the golf club hits the ball (a key event) than when the golf club is at a certain angle. The phase is the period between two key events, and all frames in the period have the same phase label. It is similar to tasks proposed in [9, 12, 23]. Examples of key events and phases are shown in Figure 4, and Table 2 gives the complete list for all the actions we consider.

标注。出于评估目的，我们为这些数据集的视频帧添加了两种类型的标签：关键事件和阶段。对视频中的每一帧进行密集标注是一项困难且耗时的任务。仅标注关键事件既减少了需要标注的帧数，也降低了任务的模糊性（从而减少了标注者之间的分歧）。例如，标注者对于高尔夫球杆击中球的帧（关键事件）比对于高尔夫球杆处于某一角度的帧更容易达成一致。阶段是两个关键事件之间的时间段，该时间段内的所有帧都具有相同的阶段标签。这与[9, 12, 23]中提出的任务类似。关键事件和阶段的示例如图4所示，表2给出了我们所考虑的所有动作的完整列表。

We use all the real videos from the Pouring dataset, and all but two action categories in Penn Action. We do not use Strumming guitar and Jumping rope because it is difficult to define unambiguous key events for these. We use the train/val splits of the original datasets [35, 52]. We will publicly release these new annotations.

我们使用了Pouring数据集中的所有真实视频，以及Penn Action中除两个动作类别外的所有内容。我们没有使用弹吉他(Strumming guitar)和跳绳(Jumping rope)这两个类别，因为很难为它们定义明确的关键事件。我们采用了原始数据集的训练/验证划分方式[35, 52]。这些新标注将公开释放。

4.1. Evaluation

4.1. 评估

We use three evaluation measures computed on the validation set. These metrics evaluate the model on fine-grained temporal understanding of a given action. Note, the networks are first trained on the training set and then frozen. SVM class if i ers and linear regressors are trained on the features from the networks, with no additional fine-tuning of the networks. For all measures a higher score implies a better model.

我们在验证集上采用三种评估指标。这些指标用于评估模型对给定动作的细粒度时序理解能力。需要注意的是，网络首先在训练集上进行训练后冻结参数，随后基于网络提取的特征训练SVM分类器和线性回归器，且不对网络进行额外微调。所有指标得分越高表示模型性能越好。

1. Phase classification accuracy: is the per frame phase classification accuracy. This is implemented by training a SVM classifier on the phase labels for each frame of the training data.
2. 相位分类准确率: 指每帧的相位分类准确率。通过在训练数据的每帧相位标签上训练 SVM (Support Vector Machine) 分类器实现。
3. Phase progression: measures how well the progress of a process or action is captured by the embeddings. We first define an approximate measure of progress through a phase as the difference in time-stamps between any given frame and each key event. This is normalized by the number of frames present in that video. Similar definitions can be found in recent literature [8, 20, 26]. We use a linear regressor on the features to predict the phase progression values. It is computed as the the average $R$ -squared measure (coefficient of determination) [47], given by:
4. 阶段进度：衡量嵌入向量对过程或动作进展的捕捉效果。我们首先将阶段进度的近似度量定义为任意给定帧与每个关键事件之间的时间戳差值，并通过该视频的总帧数进行归一化处理。类似定义可见于近期文献 [8, 20, 26]。我们在特征上使用线性回归器来预测阶段进度值，最终计算结果为平均决定系数 ($R$-squared measure) [47]，其公式为：

$$
R^{2}=1-\frac{\sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}}{\sum_{i=1}^{n}(y_{i}-\bar{y})^{2}}
$$

$$
R^{2}=1-\frac{\sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}}{\sum_{i=1}^{n}(y_{i}-\bar{y})^{2}}
$$

where $y_{i}$ is the ground truth event progress value, $\bar{y}$ is the mean of all $y_{i}$ and $\hat{y}_{i}$ is the prediction made by the linear regression model. The maximum value of this measure is 1.

其中 $y_{i}$ 是真实事件进度值，$\bar{y}$ 是所有 $y_{i}$ 的均值，$\hat{y}_{i}$ 是线性回归模型的预测值。该指标的最大值为1。

3. Kendall’s Tau [48]: is a statistical measure that can determine how well-aligned two sequences are in time. Unlike the above two measures it does not require additional labels for evaluation. Kendall’s Tau is calculated over every pair of frames in a pair of videos by sampling a pair of frames $(u_{i},u_{j})$ in the first video (which has $n$ frames) and retrieving the corresponding nearest frames in the second video, $(v_{p},v_{q})$ . This quadruplet of frame indices $(i,j,p,q)$ is said to be concordant if $i<j$ and $p<q$ or $i>j$ and $p>q$ . Otherwise it is said to be discordant. Kendall’s Tau is defined over all pairs of frames in the first video as:
4. Kendall's Tau [48]: 是一种统计度量方法，可用于判断两个时间序列的对齐程度。与上述两种度量不同，它不需要额外的标签进行评估。Kendall's Tau 的计算方式是：在第一段视频（包含 $n$ 帧）中采样一对帧 $(u_{i},u_{j})$，并在第二段视频中检索对应的最近帧 $(v_{p},v_{q})$。如果满足 $i<j$ 且 $p<q$，或者 $i>j$ 且 $p>q$，则称这组帧索引四元组 $(i,j,p,q)$ 为一致对，否则称为不一致对。Kendall's Tau 定义为第一段视频中所有帧对上的统计量：

(no. of concordant pairs − no. of discordant pairs) τ = $\textstyle{\frac{n(n-1)}{2}}$ We refer the reader to [48] to check out the complete definition. The reported metric is the average Kendall’s Tau over all pairs of videos in the validation set. It is a measure of how well the learned representations generalize to aligning unseen sequences if we used nearest neighbour matching for aligning a pair of videos. A value of 1 implies the videos are perfectly aligned while a value of -1 implies the videos are aligned in the reverse order. One drawback of Kendall’s tau is that it assumes there are no repetitive frames in a video. This might not be the case if an action is being done slowly or if there is periodic motion. For the datasets we consider, this drawback is not a problem.

(一致对数 − 不一致对数) τ = $\textstyle{\frac{n(n-1)}{2}}$
建议读者参阅[48]查看完整定义。报告指标为验证集中所有视频对的平均Kendall's Tau值。该指标衡量了如果我们使用最近邻匹配来对齐视频对时，学习到的表征在未见序列对齐任务中的泛化能力。值为1表示视频完全对齐，值为-1表示视频按相反顺序对齐。Kendall's tau的一个缺点是假设视频中没有重复帧。当动作执行缓慢或存在周期性运动时，这一假设可能不成立。对于我们考虑的数据集，这一缺点不会造成影响。

Table 2: List of all key events in each dataset. Note that each action has a Start event and End event in addition to the key events above.

动作名称	关键事件数量	关键事件描述	训练集视频数	测试集视频数
棒球投球	4	膝盖完全抬起，手臂完全伸展，球释放	103	63
棒球挥棒	3	球棒完全后摆，球棒击球	113	57
卧推	2	杠铃完全下放	69	71
保龄球	3	球完全后摆，球释放	134	85
挺举	6	杠铃至髋部，完全下蹲，站立，开始上推，开始平衡	40	42
高尔夫挥杆	3	球杆完全后摆，球杆击球	87	77
开合跳	4	手至肩部(向上)，手过头顶，手至肩部(向下)	56	56
引体向上	2	下巴过杠	98	101
俯卧撑		头部触地	102	105
仰卧起坐	22	腹部完全收缩	50	50
深蹲	4	髋部与膝盖平齐(下蹲)，髋部触地，髋部与膝盖平齐(起身)	114	116
网球正手	3	球拍完全后摆，球拍触球	79	74
网球发球	4	球从手中释放，球拍完全后摆，球触拍	115	69
倒水	5	手触瓶，液体开始流出，倾倒完成，瓶子放回桌面	70	14

表 2: 各数据集中所有关键事件列表。注意每个动作除了上述关键事件外，还包含开始事件和结束事件。

5. Experiments

5. 实验

5.1. Baselines

5.1. 基线方法

We compare our representations with existing selfsupervised video representation learning methods. For completeness, we briefly describe the baselines below but recommend referring to the original papers for more details. Shuffle and Learn (SaL) [27]. We randomly sample triplets of frames in the manner suggested by [27]. We train a small classifier to predict if the frames are in order or shuffled. The labels for training this classifier are derived from the indices of the triplet we sampled. This loss encourages the representations to encode information about the order in which an action should be performed.

我们将自己的表征与现有的自监督视频表征学习方法进行比较。为全面起见，我们简要描述以下基线方法，但建议参考原始论文获取更多细节。

乱序学习 (Shuffle and Learn, SaL) [27]。我们按照[27]建议的方式随机采样三元组帧，并训练一个小型分类器来预测帧是按顺序排列还是乱序排列。训练该分类器的标签来自我们采样的三元组索引。这种损失鼓励表征编码关于动作执行顺序的信息。

Time-Const r asti ve Networks (TCN) [35]. We sample $n$ frames from the sequence and use these as anchors (as defined in the metric learning literature). For each anchor, we sample positives within a fixed time window. This gives us n-pairs of anchors and positives. We use the n-pairs loss [41] to learn our embedding space. For any particular pair, the n-pairs loss considers all the other pairs as negatives. This loss encourages representations to be disentangled in time while still adhering to metric constraints.

时间约束对比网络 (Time-Const r asti ve Networks, TCN) [35]。我们从序列中采样 $n$ 帧作为锚点（按照度量学习文献中的定义）。对于每个锚点，我们在固定时间窗口内采样正样本。这样就得到了n对锚点和正样本。我们使用n对损失 (n-pairs loss) [41] 来学习嵌入空间。对于任何特定样本对，n对损失将所有其他样本对视为负样本。这种损失函数鼓励表征在时间维度上解耦，同时仍遵循度量约束。

Combined Losses. In addition to these baselines, we can combine our cycle consistency loss with both SaL and TCN to get two more training methods: $\mathrm{TCC}{+}\mathrm{SaL}$ and $\mathrm{TCC+TCN}$ . We learn the embedding by computing both losses and adding them in a weighted manner to get the total loss, based on which the gradients are calculated. The weights are selected by per