Generative Adversarial Networks

论文中英文对照合集 ： https://aiqianji.com/blog/articles

author Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Ward-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio,

Universite de Montreal, 2014

ABSTRACT

We propose a new framework for estimating generative models via an adversarial process, in which we simultaneously train two models: a generative model G that captures the data distribution, and a discriminative model D that estimates the probability that a sample came from the training data rather than G. The training procedure for G is to maximize the probability of D making a mistake. This framework corresponds to a minimax two-player game. In the space of arbitrary functions G and D, a unique solution exists, with G recovering the training data distribution and D equal to 12 everywhere. In the case where G and D are defined by multilayer perceptrons, the entire system can be trained with backpropagation. There is no need for any Markov chains or unrolled approximate inference networks during either training or generation of samples. Experiments demonstrate the potential of the framework through qualitative and quantitative evaluation of the generated samples.

我们提出了一个新的框架，用于通过对抗过程估算生成模型，在该框架中，我们同时训练两个模型：生成模型 G 捕获数据分布和判别模型 D估计样本来是否来自训练数据的可能性 。G 的训练过程是使 D 犯错误的概率最大化。这个框架相当于最小最大化的双人博弈。在任意函数 G 和 D 的空间中，存在唯一解，其中，G 恢复训练数据分布，D 处在1/2处。在 G 和 D 由多层感知机定义的情况下，整个系统可以通过反向传播进行训练。在训练或者样本生成期间，不需要任何马尔可夫链或展开的近似推理网络。实验通过对生成的样本进行定性和定量评估，证明了该框架的潜力。

1. Introduction

The promise of deep learning is to discover rich, hierarchical models [2] that represent probability distributions over the kinds of data encountered in artificial intelligence applications, such as natural images, audio waveforms containing speech, and symbols in natural language corpora. So far, the most striking successes in deep learning have involved discriminative models, usually those that map a high-dimensional, rich sensory input to a class label [14, 22]. These striking successes have primarily been based on the backpropagation and dropout algorithms, using piecewise linear units [19, 9, 10] which have a particularly well-behaved gradient . Deep generative models have had less of an impact, due to the difficulty of approximating many intractable probabilistic computations that arise in maximum likelihood estimation and related strategies, and due to difficulty of leveraging the benefits of piecewise linear units in the generative context. We propose a new generative model estimation procedure that sidesteps these difficulties. 1

深度学习的希望是发现丰富的，层次化的模型[ 2 ]，该模型 表示人工智能应用中遇到的各种数据的概率分布，例如自然图像，包含语音的音频波形以及自然语言语料库中的符号。到目前为止，在深度学习最显着的成就都涉及判别模型，通常是那些高维，丰富的感觉输入映射到类标签 [ 14，22 ]。这些引人注目的成功已经主要基于所述反向传播和差的算法，使用分段线性单元 [ 19，9，10 ]具有特别好表现的渐变。深度生成模型的影响较小，这是由于难以对最大似然估计和相关策略中出现的许多棘手的概率计算进行逼近，以及由于难以在生成上下文中利用分段线性单位的优势。我们提出了一种新的生成模型估计程序，可以规避这些困难。

In the proposed adversarial nets framework, the generative model is pitted against an adversary: a discriminative model that learns to determine whether a sample is from the model distribution or the data distribution. The generative model can be thought of as analogous to a team of counterfeiters, trying to produce fake currency and use it without detection, while the discriminative model is analogous to the police, trying to detect the counterfeit currency. Competition in this game drives both teams to improve their methods until the counterfeits are indistiguishable from the genuine articles.

在提出的对抗网络框架中，生成模型与一个对手相对立：一个判别模型，该模型学习确定样本是来自模型分布还是来自数据分布。生成模型可以被认为类似于一组伪造者，试图生产假币并在未经检测的情况下使用它，而区分模型类似于警察，试图发现伪币。在这场比赛中，竞争驱动两队提升它们的方法，直到伪币无法被区分。

This framework can yield specific training algorithms for many kinds of model and optimization algorithm. In this article, we explore the special case when the generative model generates samples by passing random noise through a multilayer perceptron, and the discriminative model is also a multilayer perceptron. We refer to this special case as adversarial nets. In this case, we can train both models using only the highly successful backpropagation and dropout algorithms [17] and sample from the generative model using only forward propagation. No approximate inference or Markov chains are necessary.

该框架可以针对多种模型和优化算法产生特定的训练算法。在本文中，我们探讨了特殊情况，即生成模型通过将随机噪声传递给多层感知器来生成样本，而判别模型也是多层感知器。我们称这种特殊情况为对抗网。在这种情况下，我们可以仅使用非常成功的反向传播和丢失算法来训练这两个模型 [ 17 ]， 而仅使用正向传播从生成模型中进行采样。不需要近似推断或马尔可夫链。

2 RELATED WORK 相关工作

An alternative to directed graphical models with latent variables are undirected graphical models with latent variables, such as restricted Boltzmann machines (RBMs) [27, 16], deep Boltzmann machines (DBMs) [26] and their numerous variants. The interactions within such models are represented as the product of unnormalized potential functions, normalized by a global summation/integration over all states of the random variables. This quantity (the partition function) and its gradient are intractable for all but the most trivial instances, although they can be estimated by Markov chain Monte Carlo (MCMC) methods. Mixing poses a significant problem for learning algorithms that rely on MCMC [3, 5].

Deep belief networks (DBNs) [16] are hybrid models containing a single undirected layer and several directed layers. While a fast approximate layer-wise training criterion exists, DBNs incur the computational difficulties associated with both undirected and directed models.

Alternative criteria that do not approximate or bound the log-likelihood have also been proposed, such as score matching [18] and noise-contrastive estimation (NCE) [13]. Both of these require the learned probability density to be analytically specified up to a normalization constant. Note that in many interesting generative models with several layers of latent variables (such as DBNs and DBMs), it is not even possible to derive a tractable unnormalized probability density. Some models such as denoising auto-encoders [30] and contractive autoencoders have learning rules very similar to score matching applied to RBMs. In NCE, as in this work, a discriminative training criterion is employed to fit a generative model. However, rather than fitting a separate discriminative model, the generative model itself is used to discriminate generated data from samples a fixed noise distribution. Because NCE uses a fixed noise distribution, learning slows dramatically after the model has learned even an approximately correct distribution over a small subset of the observed variables.

Finally, some techniques do not involve defining a probability distribution explicitly, but rather train a generative machine to draw samples from the desired distribution. This approach has the advantage that such machines can be designed to be trained by back-propagation. Prominent recent work in this area includes the generative stochastic network (GSN) framework [5], which extends generalized denoising auto-encoders [4]: both can be seen as defining a parameterized Markov chain, i.e., one learns the parameters of a machine that performs one step of a generative Markov chain. Compared to GSNs, the adversarial nets framework does not require a Markov chain for sampling. Because adversarial nets do not require feedback loops during generation, they are better able to leverage piecewise linear units [19, 9, 10], which improve the performance of backpropagation but have problems with unbounded activation when used ina feedback loop. More recent examples of training a generative machine by back-propagating into it include recent work on auto-encoding variational Bayes [20] and stochastic backpropagation [24].

定向图形模型的替代与潜变量无向图形模型与潜变量，如受限玻尔兹曼机（RBMS） [ 27，16 ]，深波尔兹曼机（DBMS） [ 26 ]以及它们的多种变型。这些模型中的交互表示为未归一化的潜在函数的乘积，该函数通过对随机变量所有状态的全局求和/积分来归一化。此数量（分区功能）及其梯度对于除最琐碎的情况以外的所有情况都是难以解决的，尽管可以通过马尔可夫链蒙特卡洛（MCMC）方法进行估算。混合带来了显著问题学习依赖MCMC算法 [ 3，5 ]。

深度信念网络（DBN） [ 16 ]是包含单个无向层和多个有向层的混合模型。虽然存在快速的近似逐层训练准则，但DBN会引起与无向和有向模型相关的计算困难。

还提出了不近似或限制对数似然性的替代标准，例如得分匹配 [ 18 ] 和噪声对比估计（NCE） [ 13 ]。这两种方法都要求对学习到的概率密度进行解析指定，直到归一化常数为止。请注意，在许多有趣的具有多层潜在变量的生成模型（例如DBN和DBM）中，甚至不可能得出可控的非归一化概率密度。一些模型，例如去噪自动编码器 [ 30 ]压缩自动编码器的学习规则与应用于RBM的得分匹配非常相似。在NCE中，就像在这项工作中一样，采用判别性训练标准来适应生成模型。但是，生成模型本身不是用于拟合单独的判别模型，而是用于从固定噪声分布的样本中辨别生成的数据。由于NCE使用固定的噪声分布，因此在模型学习到观察变量的一小部分甚至是近似正确的分布之后，学习速度就会显着降低。

最后，某些技术不涉及明确定义概率分布，而是训练生成机从所需分布中提取样本。这种方法的优势在于，可以将此类机器设计为通过反向传播进行训练。该领域最近的杰出工作包括生成随机网络（GSN）框架[ 5 ]，该框架 扩展了广义降噪自动编码器 [ 4 ]。：两者都可以看作是定义了一个参数化的马尔可夫链，即，人们可以学习执行生成马尔可夫链的一个步骤的机器的参数。与GSN相比，对抗网络框架不需要马尔可夫链进行采样。由于对抗性网不产生过程中需要反馈回路，它们能够更好地利用分段线性单位 [ 19，9，10 ]，INA反馈回路使用时提高反向传播的性能，但有无限的激活问题。通过向后传播来训练生成机器的最新示例包括有关自动编码变体贝叶斯的最新工作 [ 20 ] 和随机反向传播 [ 24 ]。

3. Adversarial nets

The adversarial modeling framework is most straightforward to apply when the models are both multilayer perceptrons. To learn the generator’s distribution $p_g$ over data x, we define a prior on input noise variables $p_z(z)$, then represent a mapping to data space as G(z;θg), where G is a differentiable function represented by a multilayer perceptron with parameters θg. We also define a second multilayer perceptron D(x;θd) that outputs a single scalar. D(x) represents the probability that x came from the data rather than $p_g$. We train D to maximize the probability of assigning the correct label to both training examples and samples from G. We simultaneously train G to minimize log(1−D(G(z))):

In other words, D and G play the following two-player minimax game with value function V(G,D):

当模型都是多层感知机时，对抗模型最容易直接应用。要训练生成器在数据x上的分布$p_g$，我们定义一个噪音输入变量prior $p_z(z)$，接着表达一个到数据空间的映射$G(z; \theta_g)$，其中G是一个参数为$\theta_g$的多层感知机表达的可微函数。我们定义另一个多层感知机$D(x;\theta_d)$，输出一个标量。$D(x)$表达了x来自数据而不是$p_g$的概率。我们训练D，使它为来自数据和来自G的样本赋予正确标签的概率最高。我们同时训练G来最小化$\log (1 - (D(G(z)))$。

换句话说，D和G玩双人minimax游戏，得分函数V(G, D)：

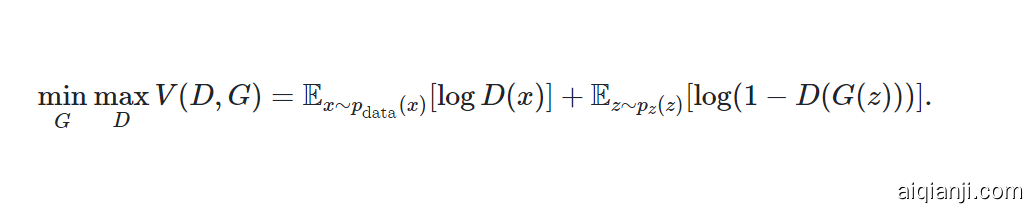
In the next section, we present a theoretical analysis of adversarial nets, essentially showing that the training criterion allows one to recover the data generating distribution as G and D are given enough capacity, i.e., in the non-parametric limit. See Figure 1 for a less formal, more pedagogical explanation of the approach. In practice, we must implement the game using an iterative, numerical approach. Optimizing D to completion in the inner loop of training is computationally prohibitive, and on finite datasets would result in overfitting. Instead, we alternate between k steps of optimizing D and one step of optimizing G. This results in D being maintained near its optimal solution, so long as G changes slowly enough. This strategy is analogous to the way that SML/PCD [31, 29] training maintains samples from a Markov chain from one learning step to the next in order to avoid burning in a Markov chain as part of the inner loop of learning. The procedure is formally presented in Algorithm 1.

在下一部分中，我们将对对抗网进行理论分析，从本质上表明，训练准则允许人们恢复数据生成的分布，如下所示： G 和 d被赋予足够的容量，即在非参数限制内。有关该方法的较不正式，较教学性的说明，请参见图 1。在实践中，我们必须使用迭代的数值方法来实现游戏。最佳化d在训练的内循环中完成训练在计算上是禁止的，在有限的数据集上会导致过度拟合。相反，我们进行k步优化D，一步优化G。使D保持在接近最优解，G变化得足够慢。这一策略类似SML/PCD。 [ 31，29 ]训练样本保持从一个学习步骤马尔可夫链到下一个，以避免在一个Markov链燃烧作为学习的内回路的一部分。该过程在算法1中正式提出 。

In practice, equation 1 may not provide sufficient gradient for G to learn well. Early in learning, when G is poor, D can reject samples with high confidence because they are clearly different from the training data. In this case, log(1−D(G(z))) saturates. Rather than training G to minimize log(1−D(G(z))) we can train G to maximize logD(G(z)). This objective function results in the same fixed point of the dynamics of G and D but provides much stronger gradients early in learning.

实际应用中，等式1也许不能为G训练提供有效的梯度。训练早期，G还不充分时，D很容易拒绝来自它的样本，因为与训练集差得比较远。这一情况下$\log (1 - D(G(z)))$就饱和了。与其训练G，让它最小化$\log (1 - D(G(z)))$，不如让它最大化$\log D(G(z))$。这一目标函数在训练早期能提供强得多的梯度。

4. Theoretical Results

The generator G implicitly defines a probability distribution pg as the distribution of the samples G(z) obtained when z∼pz. Therefore, we would like Algorithm 1 to converge to a good estimator of pdata, if given enough capacity and training time. The results of this section are done in a non-parametric setting, e.g. we represent a model with infinite capacity by studying convergence in the space of probability density functions.

We will show in section 4.1 that this minimax game has a global optimum for pg=pdata. We will then show in section 4.2 that Algorithm 1 optimizes Eq 1, thus obtaining the desired result.

生成器G隐式地定义了当$z \sim p_z$时获得的样本G(z)的概率分布$p_g$。因此我们希望当容量和时间足够时，算法1能收敛到$p_data$的好估计。

Algorithm 1 Minibatch stochastic gradient descent training of generative adversarial nets. The number of steps to apply to the discriminator, k, is a hyperparameter. We used k=1, the least expensive option, in our experiments.
算法1 生成对抗网络的Minibatch随机梯度下降训练。应用于鉴别器的步骤数，ķ是超参数。我们用了ķ=1个，这是我们实验中最便宜的选择。

4.1 Global Optimality 全局优化

Global Optimality of $ p_g = p_ {data} $

We first consider the optimal discriminator D for any given generator G.

Proposition 1.

For G fixed, the optimal discriminator D is

先考虑一个不管给什么生成器G，最优的discriminator D。

Proposition 1. 当G固定时，最优D是：

Proof.

The training criterion for the discriminator D, given any generator G, is to maximize the quantity V(G,D)

Proof 对于D的训练标准是，给予任何G，最大化数量V(G, D)

For any$(a,b) \in \mathbb R ^2 $\ ${0,0 }$, the function y→alog(y)+blog(1−y) achieves its maximum in [0,1] at $\frac a {a+b}$. The discriminator does not need to be defined outside of Supp( $p_{data}$)∪Supp($p_g$), concluding the proof.

Note that the training objective for D can be interpreted as maximizing the log-likelihood for estimating the conditional probability P(Y=y|x), where Y indicates whether x comes from $p_{data}$ (with y=1) or from $p_g$ (with y=0). The minimax game in Eq. 1 can now be reformulated as:

对于任意$(a,b) \in \mathbb R ^2 $\ ${0,0 }$，函数 $y \to a \log (y) + b \log (1-y) $在[0, 1]间极值点在$\frac a {a+b}$

D的训练目标可解读为最大化估计条件概率$P(Y = y | x)$的log-likelihood，其中Y指示了x来自$p_{data}$（y = 1）还是$p_g$（y=0）。等式1中的minimax游戏可以变换为：

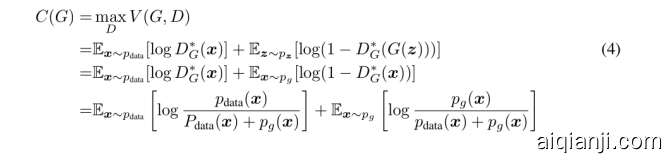
Theorem 1.

The global minimum of the virtual training criterion C(G) is achieved if and only if pg=pdata. At that point, C(G) achieves the value −log4.

定理Theorem 1 Virtual training criterion C(G)的全局最小值当且仅当$p_g = p_{data}$时取得，该点C(G)的值为-log4

Proof. 当$p_g = p_{data}$时，$D^{\star}_G(x) = \frac 1 2$（等式2），因此通过查看等式4 $D^*G(x) = \frac 1 2$时，我们发现$C(G) = \log \frac 1 2 + \log \frac 1 2 = - \log 4$。要确定这是C(G)的最优值，且仅在$p_g = p{data}$时达到，观察：

通过从$C(G) = V(D^{\star}_G, G)$中减去这一表达式，我们得到：

其中KL是Kullback-Leibler divergence。我们认出了这个表达式中模型分布和数据生成过程中的Jensen-Shannon divergence:

Kullback-Leibler divergence](https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence)，又称相对熵，是两个概率分布差异的度量。应用包括信息系统中的相对（香农）熵 relative (Shanno) entropy，连续时间序列中的随机性 randomness in continuous time-series，还有与统计模型相比时的信息增益information gain。

$$
C(G)=−log(4)+2⋅JSD(p_{data}∥p_g) (6)
$$

Since the Jensen–Shannon divergence between two distributions is always non-negative and zero only when they are equal, we have shown that $C^{\star} = - \log (4)$is the global minimum of C(G) and that the only solution is $p_g = p_{data}$, i.e., the generative model perfectly replicating the data generating process.

因为两个分布的JSD总是非负的，且在它们相等时为0，我们已证明$C^{\star} = - \log (4)$是C(G)的全局最小，当且仅当$p_g = p_{data}$时取得，也就是生成模型完美复制了数据生成过程。

4.2 Convergence of Algorithm 1 ### 算法1的收敛

Proposition 2.

If G and D have enough capacity, and at each step of Algorithm 1, the discriminator is allowed to reach its optimum given G, and pg is updated so as to improve the criterion

Proposition 2. 如果G和D容量足够，而且在算法1中的每一步，discriminator都能达到给定G下其最优，且$p_g$被更新以提升标准：

then $p_g$ converges to $p_{data}$

那么$p_g$能收敛为$p_{data}$

Proof.

Consider V(G,D)=U(pg,D) as a function of $p_g$ as done in the above criterion. Note that U($p_g$,D) is convex in $p_g$. The subderivatives of a supremum of convex functions include the derivative of the function at the point where the maximum is attained. In other words, if f(x)=supα∈Afα(x) and fα(x) is convex in x for every α, then ∂fβ(x)∈∂f if β=argsupα∈Afα(x). This is equivalent to computing a gradient descent update for $p_g$ at the optimal D given the corresponding G. supDU($p_g$,D) is convex in $p_g$ with a unique global optima as proven in Thm 1, therefore with sufficiently small updates of $p_g$, $p_g$ converges to $p_x$, concluding the proof.

Proof. 假设$V(G, D) = U(p_g, D)$是之前标准下完成的$p_g$的一个函数。注意$U(p_g, D)$是$p_g$的一个凸面contex。凸函数的上确界supremum的次导数subderivative包含了函数达到极大值时的偏导数。换句话说，如果$f(x) = sup {α∈A} f{α} (x)$对任何$\alpha$都是x中的凸，那么∂fβ(x)∈∂f 如果$ \beta = \arg \sup {\alpha \in A} f{\alpha} (x) $。这等价于在给定G时，计算$p_g$在最优D的一个梯度下降。如定理1中证明过，$\sup _D U($p_g$,D)$是$p_g$中的一个凸，且有全局最优值，因此$p_g$有充分小的更新时，它能收敛为$p_x$，得证。

In practice, adversarial nets represent a limited family of pg distributions via the function G(z;θg), and we optimize θg rather than pg itself. Using a multilayer perceptron to define G introduces multiple critical points in parameter space. However, the excellent performance of multilayer perceptrons in practice suggests that they are a reasonable model to use despite their lack of theoretical guarantees.

实际中，对抗网络通过函数$G(z;\theta_g)$表达一个$p_g$分布的limited family，所以我们优化$\theta_g$而不是$p_g$本身。使用一个多层感知机来定义G会为参数空间引入多个关键点。但实际应用中多层感知机的优秀性能说明它们是一个合理的模型，尽管缺乏理论支持。

5. Experiments 实验

We trained adversarial nets an a range of datasets including MNIST[23], the Toronto Face Database (TFD) [28], and CIFAR-10 [21]. The generator nets used a mixture of rectifier linear activations [19, [9](https://www.aiqianji.com/papers/14