Fast Visual Object Tracking with Rotated Bounding Boxes

基于旋转边界框的快速视觉目标跟踪

Abstract

摘要

In this paper, we demonstrate a novel algorithm that uses ellipse fitting to estimate the bounding box rotation angle and size with the segmentation(mask) on the target for online and real-time visual object tracking. Our method, SiamMask E, improves the bounding box fitting procedure of the state-of-the-art object tracking algorithm SiamMask and still retains a fast-tracking frame rate (80 fps) on a system equipped with GPU (GeForce GTX 1080 Ti or higher). We tested our approach on the visual object tracking datasets (VOT2016, VOT2018, and VOT2019) that were labeled with rotated bounding boxes. By comparing with the original SiamMask, we achieved an improved Accuracy of $65.2%$ and $30.9%$ EAO on VOT2019, which is $5.6%$ and $2.6%$ higher than the original SiamMask.The implementation is available on GitHub: https://github.com/ baoxinchen/siammask_e.

本文展示了一种新颖算法，该算法利用椭圆拟合技术，通过目标分割掩码(mask)在线实时估计视觉目标跟踪中的旋转边界框角度与尺寸。我们的方法SiamMask E改进了当前最先进目标跟踪算法SiamMask的边界框拟合流程，同时在配备GPU（GeForce GTX 1080 Ti或更高）的系统上仍保持80 fps的高速跟踪帧率。我们在标注旋转边界框的视觉目标跟踪数据集（VOT2016、VOT2018和VOT2019）上测试了该方法。与原始SiamMask相比，在VOT2019上实现了65.2%的精度提升和30.9%的EAO指标，分别比原版高出5.6%和2.6%。代码实现已发布于GitHub：https://github.com/baoxinchen/siammask_e。

1. Introduction

1. 引言

Visual object tracking is an important element of many applications such as person-following robots ([6] [5] [31] [18]), self-driving cars ([1] [7] [30] [4]), or surveillance cameras ([9] [23] [41] [39]), etc. The performance of such systems critically depends on a reliable and efficient object tracking algorithm. It is especially important to track an object online and in real-time when the camera is running under challenging situations: illumination, changing pose, motion blurring, partial and full occlusion, etc. These two fundamental features are the core requirements for human-robot interactions (e.g., person-following robots).

视觉目标跟踪是许多应用中的重要组成部分，例如跟随机器人 ([6] [5] [31] [18])、自动驾驶汽车 ([1] [7] [30] [4]) 或监控摄像头 ([9] [23] [41] [39]) 等。这类系统的性能关键依赖于可靠且高效的目标跟踪算法。当相机在具有挑战性的环境下运行时（如光照变化、姿态变化、运动模糊、部分或完全遮挡等），在线实时跟踪目标尤为重要。这两项基本特性是人机交互（例如跟随机器人）的核心需求。

To address the visual object tracking problems, many benchmarks have been developed, such as Object Tracking Benchmark (OTB50 [36] and OTB100 [37]), and Visual Object Tracking Challenges (VOT2016 [21], VOT2018 [19], VOT2019 [20]). In OTB datasets, ground truth was labeled by axis aligned bounding boxes and while in VOT datasets rotated bounding boxes were used. Comparing between axis-aligned bounding boxes and rotated bounding boxes, rotated bounding boxes contain a minimal amount of background pixels [21]. Thus, the datasets with rotated bounding boxes have the tighter enclosed boxes than the axis-aligned bounding boxes. As well as, the rotated bounding boxes provide the object orientation in the image plane. The orientation information can be further used to solve many computer vision problems (e.g., action classification).

为解决视觉目标跟踪问题，已开发出多种基准数据集，例如目标跟踪基准（OTB50 [36] 和 OTB100 [37]）以及视觉目标跟踪挑战赛（VOT2016 [21]、VOT2018 [19]、VOT2019 [20]）。在OTB数据集中，真实标注采用轴对齐边界框，而VOT数据集则使用旋转边界框。相较于轴对齐边界框，旋转边界框能包含更少的背景像素[21]。因此，采用旋转边界框的数据集能提供比轴对齐边界框更紧密的包围框。此外，旋转边界框还能提供目标在图像平面中的方向信息，这些方向信息可进一步用于解决诸多计算机视觉问题（例如行为分类）。

Figure 1. Our approach SiamMask E yields lager IoU between the ground truth (blue) and its prediction (green) than the original SiamMask (magenta). SiamMask E predicts a higher accuracy on the orientation of the bounding boxes which improves the average overlap accuracy (A) and expected average overlap (EAO).

图 1: 我们的方法 SiamMask E 在真实标注 (蓝色) 和预测结果 (绿色) 之间获得了比原始 SiamMask (洋红色) 更大的交并比 (IoU)。SiamMask E 对边界框方向的预测更准确，从而提升了平均重叠精度 (A) 和期望平均重叠 (EAO)。

Despite the advantage of rotated bounding boxes, it is very computationally intensive to estimate the rotation angle and scale of the bounding boxes. Many researchers have developed novel algorithms to settle the problem. But most of them have limitations in terms of tracking speed or accuracy [17], [33]. In the meantime, fully convolutional Siamese networks [2] had become popular in the field of object tracking. However, the original Siamese networks did not solve the rotation problem. Wang et al. (SiamMask) [35] have been inspired by the advanced version of Siamese network (SiamRPN [25], $\mathrm{SiamRPN{+}}+\mathrm{\Lambda}$ 24]) and wide range of image datasets (Youtube-VOS [38], COCO [26], ImageNet [34], etc.). SiamMask is able to predict a segmentation mask on the target for tracking and fits a minimum area rotated bounding box in real-time (87 fps).

尽管旋转边界框具有优势，但估算其旋转角度和尺度需要极高的计算量。许多研究者开发了新算法来解决这一问题，但大多数方案在跟踪速度或精度上存在局限 [17], [33]。与此同时，全卷积孪生网络 [2] 在目标跟踪领域逐渐流行，但原始孪生网络未能解决旋转问题。Wang 等人 (SiamMask) [35] 受到孪生网络进阶版本 (SiamRPN [25], $\mathrm{SiamRPN{+}}+\mathrm{\Lambda}$ 24]) 和多样化图像数据集 (Youtube-VOS [38], COCO [26], ImageNet [34] 等) 的启发，实现了对目标分割掩模的实时预测 (87 帧/秒)，并拟合最小面积的旋转边界框。

In this paper, we propose a novel efficient rotated bounding box estimation algorithm when a segmentation/mask of an object is given. Particularly, the masks are generated by SiamMask. The key problem is to predict the rotation angle of the bounding boxes. Inspired by the conic fitting problem described by Fitzgibbon et al. [8], we try to fit an ellipse on the mask to compute the rotation angle. Once the rotation angle is known, then we could fit a rotated rectangle on the mask. Our algorithm consists of two parts: (1) rotation angle estimation, and (2) scale calculation. Details will be provided in Section 3.

本文提出了一种新颖高效的旋转边界框估计算法，用于在给定物体分割/掩码时进行预测。特别地，这些掩码由SiamMask生成。关键问题在于预测边界框的旋转角度。受Fitzgibbon等人[8]描述的圆锥曲线拟合问题启发，我们尝试在掩码上拟合椭圆来计算旋转角度。一旦确定旋转角度，便可在掩码上拟合旋转矩形。该算法包含两部分：(1) 旋转角度估计，(2) 尺度计算。具体细节将在第3节阐述。

The contribution of this paper can be summarized in the following three aspects:

本文的贡献可总结为以下三个方面:

The paper is structured as follows. The most relevant work will be briefly summarized in Section 2. Then, we will describe our approach in detail in Section 3. The evaluation of the algorithm is in Section 4. Finally, Section 5 concludes the paper and discusses future work.

本文结构如下。第2节简要概述了最相关的工作。接着，第3节详细描述了我们的方法。算法的评估在第4节进行。最后，第5节总结了本文并讨论了未来的工作。

2. Related Work

2. 相关工作

In this section, we discuss the history of the Siamese network based tracking algorithms and several trackers that

在本节中，我们讨论基于Siamese网络的跟踪算法历史以及几种跟踪器

yield rotated bounding boxes.

生成旋转边界框。

2.1. Siamese network based trackers

2.1. 基于孪生网络 (Siamese network) 的跟踪器

The first Siamese network based object tracking algorithm (SiamFC) was introduced by Bertinetto et al. [2] in 2016. The Siamese network is trained offline on a dataset for object detection in videos. The input to the network are two images, one is an exemplar image $z$ , the other one is the search image $x$ . Then, a dense response map is generated from the output of the network. SiamFC learns and predicts the similarity between the regions in $x$ and the exemplar image $z$ . In order to handle the object scale variantion, SiamFC searches for objects at five scales $1.025^{{2,1,0,1,2}}$ near the target’s previous location. As a result, there will be 5 forward passes on each frame. SiamFC runs at about 58 fps, which is the fastest fully convolutional network (CNN) based tracker comparing to online training and updating networks in 2016. However, SiamFC is an axis-aligned bounding box tracker. It couldn’t outperform the online training and updating deep CNN tracker MDNet [27] (1 fps) in terms of average overlap accuracy.

首个基于孪生网络的目标跟踪算法(SiamFC)由Bertinetto等人[2]于2016年提出。该孪生网络通过视频目标检测数据集进行离线训练，网络输入包含两个图像：一个是模板图像$z$，另一个是搜索图像$x$。网络输出会生成密集响应图，SiamFC通过学习和预测$x$中区域与模板图像$z$之间的相似度来实现跟踪。为处理目标尺度变化，SiamFC在目标前一位置附近采用5种尺度$1.025^{{2,1,0,1,2}}$进行搜索，因此每帧需要进行5次前向传播。SiamFC运行速度约为58 fps，是2016年基于全卷积网络(CNN)且无需在线训练更新的最快跟踪器。但作为轴对齐边界框跟踪器，其平均重叠精度仍不及需要在线训练更新的深度CNN跟踪器MDNet[27](1 fps)。

He et al. [14] combines two branches (Semantic net and Appearance net) of Siamese network (SA-Siam) to improve the generalization capability of SiamFC. Two branches are individually trained, and then the two branches are combined to output the similarity score at testing. S-Net is an AlexNet [22] pretrained on an image classification dataset. A-Net is a SiamFC pretrained on an object detection from video dataset. S-Net improves the discrimination power of the SA-Siam tracker because different objects activate different sets of feature channels in the Semantic branch. Due to the complexity of the two branches, SA-Siam runs at 50 fps when tracking with pretrained model.

He等人[14]将孪生网络(SA-Siam)的两个分支(语义网络和外观网络)相结合，以提升SiamFC的泛化能力。两个分支分别训练，在测试时合并输出相似度得分。S-Net是基于图像分类数据集预训练的AlexNet[22]，A-Net是基于视频目标检测数据集预训练的SiamFC。由于不同物体会激活语义分支中不同的特征通道组合，S-Net增强了SA-Siam跟踪器的判别能力。受双分支结构复杂度影响，SA-Siam在使用预训练模型时跟踪速度为50帧/秒。

By modifying the original Siamese net with a Region Proposal Network(RPN) [32], Li et al. [25] proposed a Siamese Region Proposal Network (SiamRPN) to estimate the target location with the variable bounding boxes. The output of SiamRPN contains a set of anchor boxes with corresponding scores. So, the bounding box with the best score is considered as the target location. The benefit of RPN is to reduce the multi-scale testing complexity in the traditional Siamese networks (SiamFC, SA-Siam). An updated version SiamRPN $^{++}$ [24] has released in 2019. In terms of processing speed, SiamRPN is 160 fps and SiamRPN $^{++}$ is about 35 fps.

通过将原始孪生网络改造为区域提议网络(RPN) [32]，Li等人[25]提出了一种孪生区域提议网络(SiamRPN)，用于通过可变边界框估计目标位置。SiamRPN的输出包含一组带有相应得分的锚框，因此得分最高的边界框被视为目标位置。RPN的优势在于降低了传统孪生网络(SiamFC、SA-Siam)中多尺度测试的复杂度。2019年发布了升级版SiamRPN$^{++}$[24]。在处理速度方面，SiamRPN为160 fps，SiamRPN$^{++}$约为35 fps。

Unlike SiamFC, SA-Siam, and SiamRPN yielding axis-aligned bounding boxes, SiamMask [35] uses the advantage from a video object segmentation dataset and trained a Siamese net to predict a set of masks and bounding boxes on the target. The bounding boxes are estimated based on the masks using rotated minimum bounding rectangle (MBR) at the speed of 87 fps. However, the MBR does not always predict the bounding boxes that perfectly align with the ground truth bounding boxes (see Figure 1). Although the same bounding boxes prediction algorithm used in VOT2016 for generating the ground truth can improve the average overlap accuracy dramatically, the running speed decreases to 5 fps. To address this problem, we present a new method in Section 3 that can process frames in real-time and achieves a better result.

与生成轴对齐边界框的SiamFC、SA-Siam和SiamRPN不同，SiamMask [35] 利用了视频对象分割数据集的优势，训练了一个孪生网络来预测目标上的一组掩码和边界框。这些边界框是基于掩码通过旋转最小外接矩形 (MBR) 以87帧/秒的速度估算得出的。然而，MBR并不总能预测出与真实边界框完美对齐的边界框 (见图 1)。尽管采用VOT2016中用于生成真实值的相同边界框预测算法可以显著提高平均重叠精度，但运行速度会降至5帧/秒。为了解决这个问题，我们在第3节提出了一种新方法，能够实时处理帧并取得更好的结果。

2.2. Rotated bounding boxes

2.2. 旋转边界框

Beside the Siamese network trackers, Nebehay et al. [28] (CMT) use a key-point matching approach to scale and rotate the bounding boxes. But, this tracker cannot handle deformable objects. [29] is an update of CMT, and the processing speed dropped to 11 fps.

除了连体网络跟踪器外，Nebehay等人[28] (CMT)采用关键点匹配方法来缩放和旋转边界框。但该跟踪器无法处理可变形物体。[29]是CMT的更新版本，其处理速度降至11帧/秒。

Hua et al. [17] suggest a proposal selection method (optical flow [3] and Hough transform [16]) to filter out a group of locations and orientations that very likely contains the object. Then, they use three cues (detection confidence, objectness measures from object edges and motion boundaries) to determine which location has the highest likelihood. But, this approach also couldn’t run in real-time (0.3 fps).

Hua等人[17]提出了一种提案选择方法（光流[3]和霍夫变换[16]），用于筛选出极可能包含目标的位置和方向组。随后，他们利用三个线索（检测置信度、来自物体边缘和目标性测量的运动边界）来确定哪个位置具有最高可能性。但该方法同样无法实时运行（0.3帧/秒）。

Zhang et al. [40] propose a rotation estimation method using Log-Polar transformation. In Log-Polar coordinate, a set of 36 rotation sample are chosen on every $\begin{array}{r}{\Delta=\frac{2\pi}{R}}\end{array}$ , where $R=36$ . But, the rotation sample set also increases the rum-time of KCF [15] tracker by 36 times.

张等人 [40] 提出了一种利用对数极坐标变换 (Log-Polar transformation) 的旋转估计方法。在对数极坐标系中，每间隔 $\begin{array}{r}{\Delta=\frac{2\pi}{R}}\end{array}$ (其中 $R=36$) 选取36个旋转样本。然而，这种旋转样本集也会使KCF [15] 跟踪器的运行时间增加36倍。

Guo et al. [11] build a structure-regularized compressive tracking (SCT) with online update. During the detection stage, SCT samples several candidates with different rotation angles based on integral image and quadtree segmentation. SCT runs on a computer system without GPU at 15 fps.

Guo等人 [11] 提出了一种具有在线更新功能的结构正则化压缩跟踪(SCT)方法。在检测阶段，SCT基于积分图像和四叉树分割技术，对不同旋转角度的多个候选样本进行采样。该系统可在无GPU的计算机上以15帧/秒的速度运行。

Recently, a rotation adaptive tracking approach was introduced by Rout et al. [33]. The authors assume that the rotation angle is limited within a range (e.g., $\pm10^{\circ}$ ). However, this assumption doesn’t always hold. He et al. [13] built on top of SA-Siam [14] with angle estimation strategy. Although the method could reduce the processing time, it still limits the rotation angle to some degrees (e.g., $-\pi/8$ , $\pi/8,$ . In order to find an arbitrary rotation angle, we present our approach in the next section.

最近，Rout等人[33]提出了一种旋转自适应跟踪方法。作者假设旋转角度限制在一定范围内（例如 $\pm10^{\circ}$）。然而，这一假设并不总是成立。He等人[13]在SA-Siam[14]基础上增加了角度估计策略。尽管该方法能减少处理时间，但仍将旋转角度限制在特定范围内（例如 $-\pi/8$，$\pi/8$）。为寻找任意旋转角度的解决方案，我们将在下一节介绍本方法。

3. Approach

3. 方法

In the original SiamMask [35] tracker, Wang et al. compared three different bounding boxes estimation algorithms: min-max axis-aligned rectangle (Min-max), minimum area rectangle (MBR), and optimal bounding box [21] $(O p t)$ . Due to the computational burden, Opt could not perform in real-time (5fps). SiamMask with MBR is the real-time (87 fps) state-of-the-art tracker in terms of average overlap Accuracy. Although MBR performs better than the other bounding box estimation algorithms, it has a weakness such that minimum area rectangle could not represent the geometric shape and point distribution of the masks (see Figure 2). As a result, most of the estimated bounding boxes are not in the correct orientation. In the following subsections, we will discuss an alternate solution to generate bounding boxes with correct rotation angle and tighter size by post-processing on the output mask from SiamMask. Our method consists of the steps in Figure 3.

在原版SiamMask [35]跟踪器中，Wang等人比较了三种不同的边界框估计算法：最小-最大轴对齐矩形 (Min-max)、最小面积矩形 (MBR) 和最优边界框 [21] $(Opt)$。由于计算负担，Opt无法实时运行(5fps)。采用MBR的SiamMask在平均重叠精度指标下是实时(87 fps)的顶尖跟踪器。尽管MBR表现优于其他边界框估计算法，但它存在一个缺陷：最小面积矩形无法准确表征掩模的几何形状和点分布(见图2)。因此，大多数估计的边界框方向都不正确。在后续小节中，我们将讨论通过对SiamMask输出掩模进行后处理来生成具有正确旋转角度和更紧凑尺寸的边界框的替代方案。我们的方法包含图3所示的步骤。

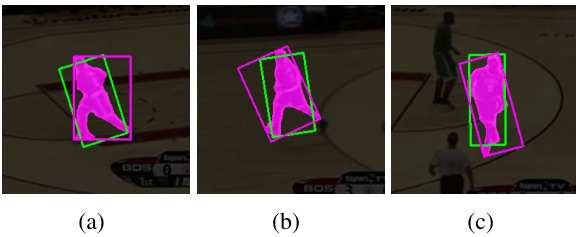
Figure 2. This figure shows some examples of minimum area rectangle (magenta); this does not determine bounding boxes according to the geometric shape and point distribution of the segmentation/mask. Thus, the rotation angles are not as accurate as our approach (green)

图 2: 该图展示了一些最小面积矩形(洋红色)的示例；这种方法无法根据分割/掩码的几何形状和点分布确定边界框。因此，其旋转角度不如我们的方法(绿色)准确

3.1. Rotation angle estimation

3.1. 旋转角度估计

To estimate the rotation angle, we adopted the fitEllipse API provided by OpenCV3 4 which use a least-squares scheme [10] to solved the ellipse fitting problem. An improved version was described in [12]. This algorithm (B2AC) Algebraic distance with quadratic constraint was first introduced by Fitzgibbon et al. [8].

为了估算旋转角度，我们采用了OpenCV3 4提供的fitEllipse API，该接口使用最小二乘法 [10] 解决椭圆拟合问题。[12] 中描述了改进版本。此算法 (B2AC) 由Fitzgibbon等人 [8] 首次提出，全称为二次约束代数距离法。

An ellipse can be formulated using a conic equation with a constraint:

椭圆可以通过带约束的二次曲线方程来表示：

$$
{\begin{array}{r}{F(x,y)=a x^{2}+b x y+c y^{2}+d x+e y+f=0}\ {{\mathrm{where}},b^{2}-4a c<0}\end{array}}
$$

$$
{\begin{array}{r}{F(x,y)=a x^{2}+b x y+c y^{2}+d x+e y+f=0}\ {{\mathrm{where}},b^{2}-4a c<0}\end{array}}
$$

In Equation 1, $a,b,c,d,e,f$ are the coefficients of the ellipse and $x,y$ are the points on the ellipse. By grouping the coefficients into a vector, we have the following two vectors:

在公式1中，$a,b,c,d,e,f$是椭圆的系数，$x,y$是椭圆上的点。通过将系数分组为向量，我们得到以下两个向量：

$$
\begin{array}{l}{\mathbf{a}=[a,b,c,d,e,f]^{T}}\ {\mathbf{x}=[x^{2},x y,y^{2},x,y,1]}\end{array}
$$

$$
\begin{array}{l}{\mathbf{a}=[a,b,c,d,e,f]^{T}}\ {\mathbf{x}=[x^{2},x y,y^{2},x,y,1]}\end{array}
$$

So, the conic can be written as:

因此，该圆锥曲线可表示为：

$$
F(\mathbf{x})=\mathbf{x}\cdot\mathbf{a}=0
$$

$$
F(\mathbf{x})=\mathbf{x}\cdot\mathbf{a}=0
$$

To fit an ellipse on a set of points $\begin{array}{r l}{A}&{{}=}\end{array}$ ${(x_{1},y_{1}),...,(x_{N},y_{N})},w h e r e|A|=N$ , we need to find the coefficient vector a. Halir et al. [12] introduced an improved least squares method to minimize the sum of squared error of the following equation:

在一组点 $\begin{array}{r l}{A}&{{}=}\end{array}$ ${(x_{1},y_{1}),...,(x_{N},y_{N})}, 其中|A|=N$ 上拟合椭圆时，需要找到系数向量 a。Halir 等人 [12] 提出了一种改进的最小二乘法，用于最小化以下方程的平方误差和：

Figure 3. Our algorithm includes seven steps: (a) take a target mask as input. (b) apply an ellipse fitting algorithm [8] on edge of the mask (Here, we have the points on the edge as a set $A$ in Equation 4), then determine the center of the ellipse and the rotation angle. (c) compute the affine transformation matrix using the rotation angle and the center from the ellipse, then apply the transformation on the ellipse center. (d) apply a rectangular rotated bounding box (green) on the ellipse. (e) draw a min-max axis-aligned bounding box (blue) on the transformed mask. (f) calculate the intersection of the blue box and green box to form a new bounding box (red). (g) calculate the inverse of the affine transformation matrix, then apply transformation to convert back to the original image coordinate, and output the red box.

图 3: 我们的算法包含七个步骤：(a) 以目标掩码作为输入。(b) 在掩码边缘应用椭圆拟合算法 [8] (此处我们将边缘点集记为公式4中的集合 $A$)，随后确定椭圆中心及旋转角度。(c) 利用椭圆旋转角度和中心计算仿射变换矩阵，并对椭圆中心应用该变换。(d) 在椭圆上应用旋转矩形边界框 (绿色)。(e) 在变换后的掩码上绘制最小-最大轴对齐边界框 (蓝色)。(f) 计算蓝色框与绿色框的交集以形成新边界框 (红色)。(g) 计算仿射变换矩阵的逆矩阵，应用逆变换转换回原始图像坐标系，最终输出红色框。

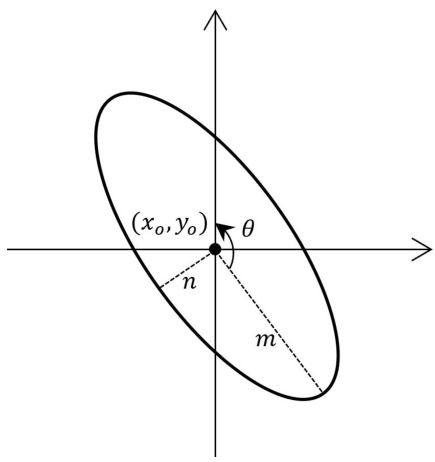
Figure 4. Ellipse notations

图 4: 椭圆标注

$$
\operatorname*{min}{\mathbf{a}}\sum{i=1}^{N}F(x_{i},y_{i})^{2}=\operatorname*{min}_{\mathbf{a}}\sum_{i=1}^{N}F(\mathbf{x}_{i})^{2}
$$

$$
\operatorname*{min}{\mathbf{a}}\sum{i=1}^{N}F(x_{i},y_{i})^{2}=\operatorname*{min}_{\mathbf{a}}\sum_{i=1}^{N}F(\mathbf{x}_{i})^{2}
$$

where, $\mathbf{x}{i}=[x{i}^{2},x_{i}y_{i},y_{i}^{2},x_{i},y_{i},1]$ , and $A_{i}=\left(x_{i},y_{i}\right)$

其中，$\mathbf{x}{i}=[x{i}^{2},x_{i}y_{i},y_{i}^{2},x_{i},y_{i},1]$，且$A_{i}=\left(x_{i},y_{i}\right)$

Let us denote the following terms for the fitted ellipse (also see Figure 4):

我们用以下术语表示拟合的椭圆（另见图 4）：

$m$ semi-major axis $n$ semi-minor axis $(x_{o},y_{o})$ center coordinate of the ellipse $\theta$ rotation angle

$m$ 半长轴
$n$ 半短轴
$(x_{o},y_{o})$ 椭圆中心坐标
$\theta$ 旋转角度

Be aware that, when the ellipse is near-circular (rotational symmetric shapes), $\theta$ is not stable. A solution for this case is to force $\theta=90^{o}$ . However, it did not increase the performance of the VOT datasets empirically.

请注意，当椭圆接近圆形（旋转对称形状）时，$\theta$ 不稳定。针对这种情况的解决方案是强制设定 $\theta=90^{o}$，但经验证这并未提升VOT数据集的性能。

3.2. SiamMask E

3.2. SiamMask E

Since we need to rotate the image with respect to the ellipse center, an affine transformation (Translation and Rotation for our case) will be used here to compute the transformed coordinates. After the estimation of rotation angle $\theta$ and the center point $(x_{o},y_{o})$ , then we need to compute the 2D affine transformation matrix $M$ :

由于我们需要以椭圆中心为基准旋转图像，这里将使用仿射变换（本例中为平移和旋转）来计算变换后的坐标。在估计出旋转角度 $\theta$ 和中心点 $(x_{o},y_{o})$ 后，需要计算二维仿射变换矩阵 $M$：

$$
M=\left[\begin{array}{l l l}{{c o s\Theta}}&{{s i n\Theta}}&{{(1-c o s\Theta)x_{o}-s i n\Theta y_{o}}}\ {{-s i n\Theta}}&{{c o s\Theta}}&{{s i n\Theta x_{o}-(1-c o s\Theta)y_{o}}}\end{array}\right]
$$

$$
M=\left[\begin{array}{l l l}{{c o s\Theta}}&{{s i n\Theta}}&{{(1-c o s\Theta)x_{o}-s i n\Theta y_{o}}}\ {{-s i n\Theta}}&{{c o s\Theta}}&{{s i n\Theta x_{o}-(1-c o s\Theta)y_{o}}}\end{array}\right]
$$

Once the affine transformation matrix is computed, then we apply the rotation on the segmentation/mask about the ellipse’s center $(x_{o},y_{o})$ : Let’s denote the mask as a set of points Mask (magenta color in Figure 3(a)), and the transformed mask as $M a s k^{\prime}$ (magenta color in Figure 3(d)).

一旦计算出仿射变换矩阵，我们就在分割/掩模上以椭圆中心 $(x_{o},y_{o})$ 为旋转中心进行旋转：将掩模表示为一组点集 Mask (图 3(a) 中的洋红色部分)，变换后的掩模记为 $M a s k^{\prime}$ (图 3(d) 中的洋红色部分)。

$$
M a s k^{\prime}=M*\left[\begin{array}{l}{{x}}\ {{y}}\ {{1}}\end{array}\right]\forall(x,y)\in M a s k
$$

$$
M a s k^{\prime}=M*\left[\begin{array}{l}{{x}}\ {{y}}\ {{1}}\end{array}\right]\forall(x,y)\in M a s k
$$

After this step, our aim is to output the intersection (red in Figure 3(f)) between the min-max axis-aligned bounding box (blue in Figure 3(e)) and the ellipse bounding box (green in Figure 3(e)). The advantage of using the ellipse bounding box is to cut out the