4D Attention-based Neural Network for EEG Emotion Recognition

基于4D注意力机制的神经网络在EEG情绪识别中的应用

Abstract

摘要

Electroencephalograph (EEG) emotion recognition is a significant task in the brain-computer interface field. Although many deep learning methods are proposed recently, it is still challenging to make full use of the information contained in different domains of EEG signals. In this paper, we present a novel method, called four-dimensional attention-based neural network (4D-aNN) for EEG emotion recognition. First, raw EEG signals are transformed into 4D spatial-spectral-temporal representations. Then, the proposed 4D-aNN adopts spectral and spatial attention mechanisms to adaptively assign the weights of different brain regions and frequency bands, and a convolutional neural network (CNN) is utilized to deal with the spectral and spatial information of the 4D representations. Moreover, a temporal attention mechanism is integrated into a bidirectional Long Short-Term Memory (LSTM) to explore temporal dependencies of the 4D representations. Our model achieves state-of-the-art performance on the SEED dataset under intra-subject splitting. The experimental results have shown the effectiveness of the attention mechanisms in different domains for EEG emotion recognition.

脑电图(EEG)情绪识别是脑机接口领域的重要任务。尽管近期提出了许多深度学习方法，但如何充分利用EEG信号不同域的信息仍具挑战性。本文提出了一种基于四维注意力神经网络(4D-aNN)的新方法：首先将原始EEG信号转换为4D空间-频谱-时间表征；随后4D-aNN采用频谱和空间注意力机制自适应分配不同脑区与频段的权重，并利用卷积神经网络(CNN)处理4D表征的频谱和空间信息；此外，通过将时间注意力机制整合到双向长短期记忆网络(LSTM)中，探索4D表征的时间依赖性。我们的模型在SEED数据集上实现了被试内划分的最优性能，实验结果证明了不同域注意力机制对EEG情绪识别的有效性。

Keywords: EEG, emotion recognition, attention mechanism, convolutional recurrent neural network

关键词：EEG、情绪识别、注意力机制、卷积循环神经网络

Introduction

引言

Emotion plays an important role in daily life and is closely related to human behavior and cognition (Dolan 2002). As one of the most significant research topics of affective computing, emotion recognition has received increasing attention in recent years for its applications of disease detection (Bamdad et al. 2015; Figueiredo et al. 2019), human-computer interaction (Fiorinia et al. 2020; Kat si gianni s and Ramzan 2017), and workload estimation (Blankertz et al. 2016). In general, emotion recognition methods can be divided into two categories (Mühl et al. 2014). One is based on external emotion responses including facial expressions and gestures(Yan et al. 2016), and the other is based on internal emotion responses including electroencephalograph (EEG) and electrocardiograph y (ECG) (Zheng et al. 2017). Neuro scientific researches have shown that some major brain cortex regions are closely related to emotions, making it possible to decode emotions based on EEG (Brittona et al. 2006; Lotfia and Akbarzadeh-T 2014). EEG is non-invasive, portable, and inexpensive so that it has been widely used in the field of brain-computer interfaces (BCIs) (P furt sc heller et al. 2010). Besides, EEG signals contain various spatial, spectral, and temporal information about emotions evoked by specific stimulation patterns. Therefore, more and more researchers concentrate on EEG emotion recognition recently (Alhagry et al. 2017; Li and Lu 2009).

情绪在日常生活中扮演着重要角色，并与人类行为及认知密切相关 (Dolan 2002)。作为情感计算最重要的研究课题之一，情绪识别因其在疾病检测 (Bamdad et al. 2015; Figueiredo et al. 2019)、人机交互 (Fiorini et al. 2020; Katsigiannis and Ramzan 2017) 和工作负荷评估 (Blankertz et al. 2016) 等领域的应用价值，近年来受到越来越多的关注。一般而言，情绪识别方法可分为两类 (Mühl et al. 2014)：一类基于外部情绪反应（如面部表情和手势）(Yan et al. 2016)，另一类则基于内部情绪反应（如脑电图 (EEG) 和心电图 (ECG)）(Zheng et al. 2017)。神经科学研究表明，某些主要大脑皮层区域与情绪密切相关，这使得基于 EEG 解码情绪成为可能 (Britton et al. 2006; Lotfi and Akbarzadeh-T 2014)。EEG 具有非侵入性、便携且成本低廉的特点，因此在脑机接口 (BCI) 领域得到广泛应用 (Pfurtscheller et al. 2010)。此外，EEG 信号包含了由特定刺激模式诱发情绪的各种空间、频谱和时域信息。因此，近年来越来越多的研究者专注于 EEG 情绪识别研究 (Alhagry et al. 2017; Li and Lu 2009)。

Traditional EEG emotion recognition methods usually extract hand-crafted features from EEG signals first and then adopt shallow models to classify the emotion features. EEG emotion features can be extracted from the time domain, frequency domain, and time-frequency domain. Jenke et al. conduct a comprehensive survey on EEG feature extraction methods by using machine learning techniques on a selfrecorded dataset (Jenke et al. 2014). For classifying the extracted emotion features, many researchers have adopted machine learning methods over the past few years (Kim et al. 2013). Li et al. apply a linear support vector machine (SVM) to classify emotion features extracted from the gamma frequency band (Li and Lu 2009). Duan et al. extract differential entropy (DE) features, which are superior to representing emotion states in EEG signals (Shi et al. 2013), from multichannel EEG data and combine a $\mathrm{k\Omega}$ -Nearest Neighbor (KNN) with SVM to classify the DE features (Duan et al. 2013). However, shallow models require lots of expert knowledge to design and select emotion features, limiting their performance on EEG emotion classification.

传统的脑电图(EEG)情绪识别方法通常先从EEG信号中提取手工特征，再采用浅层模型对情绪特征进行分类。EEG情绪特征可从时域、频域和时频域中提取。Jenke等人在自录数据集上使用机器学习技术对EEG特征提取方法进行了全面调研(Jenke et al. 2014)。对于已提取情绪特征的分类，过去几年许多研究者采用了机器学习方法(Kim et al. 2013)。Li等人应用线性支持向量机(SVM)对从gamma频段提取的情绪特征进行分类(Li and Lu 2009)。Duan等人从多通道EEG数据中提取差分熵(DE)特征(Shi et al. 2013)，并将k近邻(KNN)与SVM结合对DE特征进行分类(Duan et al. 2013)。然而，浅层模型需要大量专家知识来设计和选择情绪特征，这限制了其在EEG情绪分类上的性能。

Deep learning methods have been demonstrated to outperform traditional machine learning methods in many fields such as computer vision, natural language processing, and biomedical signal processing (Abbass et al. 2018; Craik et al. 2019) for the ability to learn high-level features from data automatically (Krizhevsky et al. 2012). Recently, some researchers have applied deep learning to EEG emotion recognition. Zheng et al. introduce a deep belief network (DBN) to investigate the critical frequency bands and EEG signal channels for EEG emotion recognition (Zheng and Lu 2015). Yang et al. propose a hierarchical network to classify the DE features extracted from different frequency bands (Yang et al. 2018b). Song et al. use a graph convolutional neural network to classify the DE features (Song et al. 2020). Ma et al. propose a multimodal residual Long Short-Term Memory model (MMResLSTM) for emotion recognition, which shares temporal weights across the multiple modalities (Jiaxin Ma et al. 2019). To learn the bi-hemispheric discrepancy for EEG emotion recognition, Yang et al. propose a novel bi-hemispheric discrepancy model (BiHDM) (Li et al. 2020). All those deep learning methods outperform the shallow models.

深度学习方法在计算机视觉、自然语言处理和生物医学信号处理等多个领域已被证明优于传统机器学习方法 (Abbass et al. 2018; Craik et al. 2019)，因其具备从数据中自动学习高级特征的能力 (Krizhevsky et al. 2012)。近年来，一些研究者将深度学习应用于脑电(EEG)情绪识别。Zheng等采用深度信念网络(DBN)探究脑电情绪识别中的关键频段与信号通道 (Zheng and Lu 2015)。Yang等提出分层网络对从不同频段提取的微分熵(DE)特征进行分类 (Yang et al. 2018b)。Song等使用图卷积神经网络对微分熵特征进行分类 (Song et al. 2020)。Ma等提出多模态残差长短时记忆模型(MMResLSTM)进行情绪识别，该模型在多个模态间共享时序权重 (Jiaxin Ma et al. 2019)。为学习脑电情绪识别的双半球差异特征，Yang等提出新型双半球差异模型(BiHDM) (Li et al. 2020)。这些深度学习方法均优于浅层模型。

Although deep learning emotion recognition models have achieved higher accuracy than shallow models, it is still challenging to fuse more important information on different domains and capture disc rim i native local patterns in EEG signals. In the past decades, many researchers have investigated the critical frequency bands and channels for EEG emotion recognition. Zheng et al. demonstrate that $\mathsf{\beta}[14{\sim}31\mathrm{Hz}]$ and $\gamma[31{\sim}51~\mathrm{Hz}]$ bands are more related to emotion recognition than other bands, and their model achieves the best performance when combining all frequency bands. They also conduct experiments to select critical channels and propose the minimum pools of electrode sets for emotion recognition (Zheng and $\mathrm{Lu}2015\$ . To utilize the spatial information of EEG signals, Li et al. propose a 2D sparse map to maintain the information hidden in the electrode placement (Li et al. 2018). Zhong et al. introduce a regularized graph neural network (RGNN) to capture both local and global relations among different EEG channels for emotion recognition (Zhong et al. 2020). The temporal dependencies in EEG signals are also important to emotion recognition. For example, Ma et al. (Jiaxin Ma et al. 2019) apply LSTMs in their models to extract temporal features for emotion recognition. Shen et al. transform the DE features of different channels into 4D structures to integrate the spectral, spatial, and temporal information simultaneously and then use a fourdimensional convolutional recurrent neural network (4DCRNN) to recognize different emotions (Shen et al. 2020). However, the differences among brain regions and frequency bands are not fully utilized in their work. To adaptively capture disc rim i native patterns in EEG signals, attention mechanisms have been applied to EEG emotion recognition. For instance, Tao et al. introduce a channel-wise attention mechanism, assigning the weights of different channels adaptively, along with an extended self-attention to explore the temporal dependencies of EEG signals (Tao et al. 2020). Jia et al. propose a two-stream network with attention mechanisms to adaptively focus on important patterns (Jia et al. 2020). From the above, it can be observed that it is critical to integrate information on different domains and adaptively capture important brain regions, frequency bands, and timestamps in a unified network for EEG emotion recognition.

虽然深度学习情感识别模型相比浅层模型取得了更高的准确率，但在融合多领域重要信息以及捕捉脑电信号中的判别性局部模式方面仍存在挑战。过去几十年间，许多研究者探索了脑电情感识别中的关键频段与通道。Zheng等人证明β[14 31 Hz]和γ[31~51 Hz]频段比其他频段与情感识别更具相关性，其模型在融合所有频段时达到最佳性能。他们还通过实验筛选关键通道，提出了情感识别所需的最小电极集组合（Zheng and Lu 2015）。为利用脑电信号的空间信息，Li等人提出二维稀疏映射来保持电极排布中隐含的信息（Li et al. 2018）。Zhong等人采用正则化图神经网络（RGNN）来捕捉不同脑电通道间的局部与全局关系（Zhong et al. 2020）。脑电信号的时序依赖性对情感识别同样重要，例如Ma等人在模型中运用LSTM提取时序特征（Jiaxin Ma et al. 2019）。Shen等人将不同通道的微分熵特征转换为4D结构以同步整合频谱、空间和时序信息，再通过四维卷积循环神经网络（4D-CRNN）进行情感识别（Shen et al. 2020），但其工作未充分利用脑区与频段间的差异性。为自适应捕捉脑电信号中的判别模式，注意力机制已被应用于该领域：Tao等人提出通道注意力机制自适应分配通道权重，并扩展自注意力来探索信号时序依赖性（Tao et al. 2020）；Jia等人开发了具有注意力机制的双流网络来自适应聚焦重要模式（Jia et al. 2020）。由此可见，构建统一网络来整合多领域信息并自适应捕捉关键脑区、频段及时间点，对脑电情感识别至关重要。

In this paper, we propose a four-dimensional attentionbased neural network named 4D-aNN for EEG emotion recognition. First, we transform raw EEG signals into 4D spatial-spectral-temporal representations which consist of several temporal slices. Different brain regions and frequency bands vary in the contributions to EEG emotion recognition, and the temporal dependencies of 4D representations should also be considered. Therefore, we employ attention mechanisms on both a CNN and a bidirectional LSTM network to adaptively capture disc rim i native patterns. For the CNN model, the attention mechanism is applied to the spatial and spectral dimensions of each temporal slice so that the important brain regions and frequency bands could be captured. As for the bidirectional LSTM model, the attention mechanism is applied to utilize long-range temporal dependencies so that the importance of different temporal slices in one 4D representation could be fully explored.

本文提出了一种基于四维注意力机制的神经网络4D-aNN，用于脑电图(EEG)情绪识别。首先，我们将原始EEG信号转换为由多个时间切片组成的四维空间-频谱-时间表征。不同脑区和频段对EEG情绪识别的贡献度存在差异，同时还需考虑四维表征的时间依赖性。为此，我们在CNN和双向LSTM网络中均采用了注意力机制来自适应捕捉判别性特征。对于CNN模型，注意力机制作用于每个时间切片的空间和频谱维度，以捕获重要的脑区与频段信息；而在双向LSTM模型中，注意力机制用于利用长程时间依赖性，从而充分挖掘单个四维表征中不同时间切片的重要性。

The primary contribution of this paper are summarized as follows: a) We propose a four-dimensional attention-based neural network, which fuses information on different domains and captures disc rim i native patterns in EEG signals based on the 4D spatial-spectral-temporal representation. b) We conduct experiments on the SEED dataset, and the experimental results indicate that our model achieves state-ofthe-art performance under intra-subject splitting.

本文的主要贡献总结如下：
a) 我们提出了一种基于四维注意力机制的神经网络，该网络融合了不同领域的信息，并基于4D空间-频谱-时间表征捕捉了EEG信号中的判别性模式。
b) 我们在SEED数据集上进行了实验，结果表明，在受试者内划分条件下，我们的模型实现了最先进的性能。

The remainder of this paper is organized as follows. We describe our proposed method in the Method section. Dataset, experiment settings, results, ablation studies, and discussion are presented in the Experiment section. Finally, conclusions are given in the Conclusion section.

本文的其余部分组织如下。方法部分介绍了我们提出的方法。实验部分展示了数据集、实验设置、结果、消融研究和讨论。最后，结论部分给出了总结。

Method

方法

Figure 1 illustrates the overall structure of 4D-aNN for EEG emotion recognition. It consists of the 4D spatial-spectraltemporal representation, the attention-based CNN, the attention-based bidirectional LSTM, and the classifier. We will describe the details of each part in sequence.

图 1: 展示了用于脑电图 (EEG) 情绪识别的4D-aNN整体结构。该结构包含4D空间-频谱-时间表征、基于注意力的CNN、基于注意力的双向LSTM以及分类器。我们将依次描述每个部分的细节。

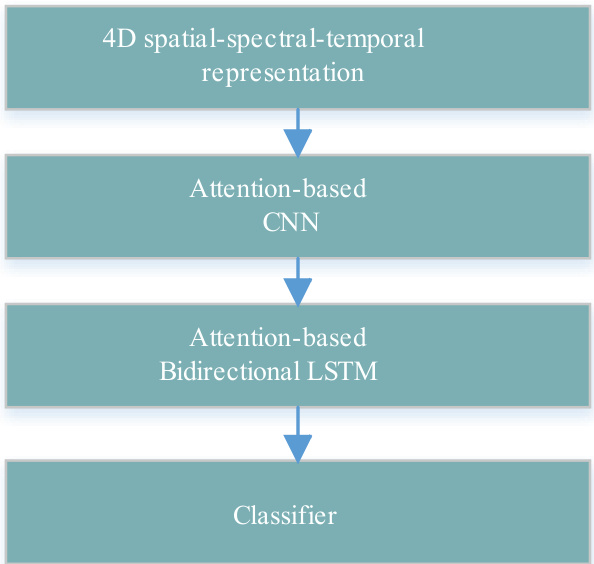
Fig. 1 The overall structure of 4D-aNN.

图 1: 4D-aNN的整体结构。

4D spatial-spectral-temporal representation

4D 空间-光谱-时间表示

The process of generating 4D representation is depicted in Fig. 2. As previous works do (Shen et al. 2020; Yang et al. 2018a), we split original EEG signals into $T$ seconds long segments without overlapping. Each segment is assigned with the same label as the original EEG signals. Then we decompose each segment into five frequency bands (i.e. δ[1~4 Hz], $\mathsf{\theta}[4{\sim}8\mathrm{Hz}]$ , $\mathsf{a}[8{\sim}14~\mathrm{HZ}]$ , $3[14{\sim}31~\mathrm{Hz}]$ , and $\gamma[31{\sim}51~\mathrm{Hz}].$ ) with five-order Butterworth filters. The Differential Entropy (DE) features and Power Spectral Density (PSD) features of all EEG channels, which have been proven to be effective for emotion recognition (Zheng et al. 2017), are extracted from five frequency bands respectively with a 0.5s window for each segment.

图 2: 展示了4D表征的生成过程。如先前工作(Shen et al. 2020; Yang et al. 2018a)所述，我们将原始EEG信号分割为$T$秒长的无重叠片段，每个片段保留原始EEG信号的标签。随后使用五阶巴特沃斯滤波器将每个片段分解为五个频带(即δ[1 4 Hz]、$\mathsf{\theta}[4{\sim}8\mathrm{Hz}]$、$\mathsf{a}[8{\sim}14~\mathrm{HZ}]$、$3[14{\sim}31~\mathrm{Hz}]$和$\gamma[31{\sim}51~\mathrm{Hz}]$)。从每个片段的0.5秒窗口中，分别提取所有EEG通道的微分熵(Differential Entropy, DE)特征和功率谱密度(Power Spectral Density, PSD)特征，这些特征已被证明对情绪识别有效(Zheng et al. 2017)。

PSD is defined as

PSD 定义为

$$
h_{P}(X)=E[x^{2}]
$$

$$
h_{P}(X)=E[x^{2}]
$$

where $x$ is formally a random variable and in this context, the signal acquired from a certain frequency band on a certain EEG channel.

其中 $x$ 在形式上是一个随机变量，在此上下文中表示从某个EEG通道的特定频带采集到的信号。

DE feature is capable of discriminating EEG patterns between low and high frequency energy, which is defined as

DE特征能够区分低频与高频能量之间的脑电图模式

$$
h_{D}(X)=-\int_{X}f(x)\log{\big(}f(x){\big)}d x
$$

$$
h_{D}(X)=-\int_{X}f(x)\log{\big(}f(x){\big)}d x
$$

where $f(x)$ is the probability density function of $x$ . If $x$ obeys the Gaussian distribution $N(\mu,\sigma^{2})$ , DE can simply be calculated by the following formulation:

其中 $f(x)$ 是 $x$ 的概率密度函数。若 $x$ 服从高斯分布 $N(\mu,\sigma^{2})$，则DE可通过以下公式简单计算：

$$
\begin{array}{c}{{h_{D}(X)=\displaystyle-\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi\sigma^{2}}}e x p\frac{(x-\mu)^{2}}{2\sigma^{2}}\log\frac{1}{\sqrt{2\pi\sigma^{2}}}e x p\frac{(x-\mu)^{2}}{2\sigma^{2}}d x}}\ {{=\displaystyle\frac{1}{2}\log2\pi e\sigma^{2}(3)~}}\end{array}
$$

$$
\begin{array}{c}{{h_{D}(X)=\displaystyle-\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi\sigma^{2}}}e x p\frac{(x-\mu)^{2}}{2\sigma^{2}}\log\frac{1}{\sqrt{2\pi\sigma^{2}}}e x p\frac{(x-\mu)^{2}}{2\sigma^{2}}d x}}\ {{=\displaystyle\frac{1}{2}\log2\pi e\sigma^{2}(3)~}}\end{array}
$$

where $e$ and $\sigma$ are Euler’s constant and standard deviation of $x$ , respectively.

其中 $e$ 和 $\sigma$ 分别为欧拉常数和 $x$ 的标准差。

Thus, We extract a 3D feature tensor $F_{n}\in R^{c x2f x2T},n=$ $1,2,\ldots,N$ from each segment, where $N$ is the number of total segments, $c$ is the number of EEG channels, $2f$ represents DE and PSD features of $f$ frequency bands, and $2T$ is derived by the 0.5s window without overlapping. To utilize the spatial information of electrodes, we organize all the $c$ channels as a 2D sparse map so that the 3D feature tensor $F_{n}$ is transformed into a 4D representation $X_{n}\in R^{h\times w\times2f\times2T}$ , where $h$ and $w$ are the height and width of the 2D sparse map, respectively. The 2D sparse map of all the c channels with zero-padding is shown in Fig. 3, which preserves the topology of different electrodes. In this paper, we set $h=19$ , $w=19$ , and $f=5$ .

因此，我们从每个片段中提取一个3D特征张量 $F_{n}\in R^{c x2f x2T},n=$ $1,2,\ldots,N$ ，其中 $N$ 是总片段数， $c$ 是EEG通道数， $2f$ 表示 $f$ 个频段的DE和PSD特征， $2T$ 由无重叠的0.5秒窗口生成。为了利用电极的空间信息，我们将所有 $c$ 个通道组织成一个2D稀疏映射，从而将3D特征张量 $F_{n}$ 转换为4D表示 $X_{n}\in R^{h\times w\times2f\times2T}$ ，其中 $h$ 和 $w$ 分别是2D稀疏映射的高度和宽度。图3展示了所有c通道的零填充2D稀疏映射，该映射保留了不同电极的拓扑结构。本文中，我们设置 $h=19$ ， $w=19$ ，以及 $f=5$ 。

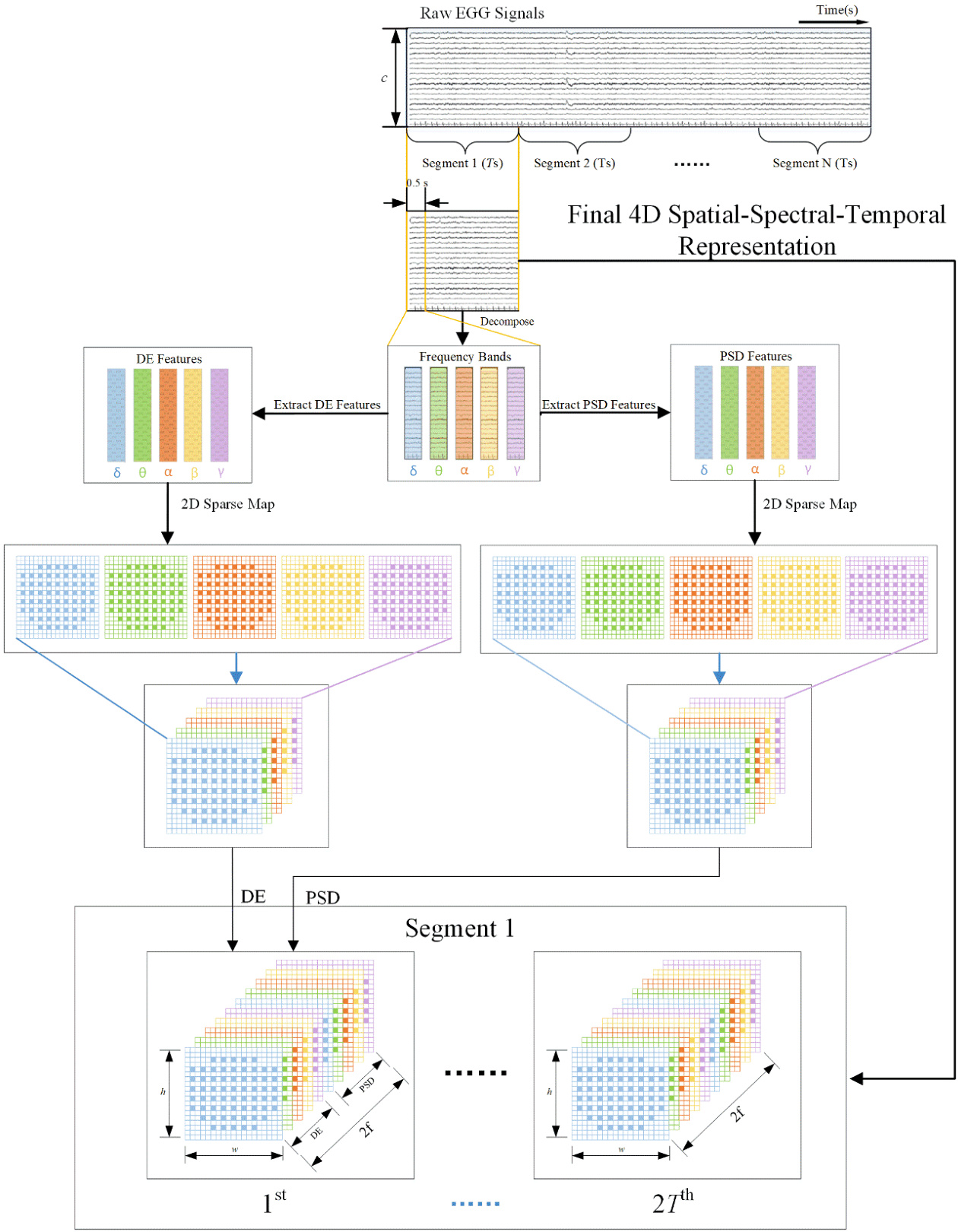
Fig. 2 The generation of 4D spatial-spectral-temporal representation. For each Ts EEG signal segment, we extract DE and PSD features from different channels and frequency bands with a 0.5s window. Then, the features are transformed into a 4D representation which consists of 2T temporal slices.

图 2: 4D空间-频谱-时间表征的生成过程。对于每个Ts时长的EEG信号片段，我们使用0.5秒窗口从不同通道和频段提取DE(微分熵)和PSD(功率谱密度)特征。随后，这些特征被转换为包含2T个时间切片的4D表征。

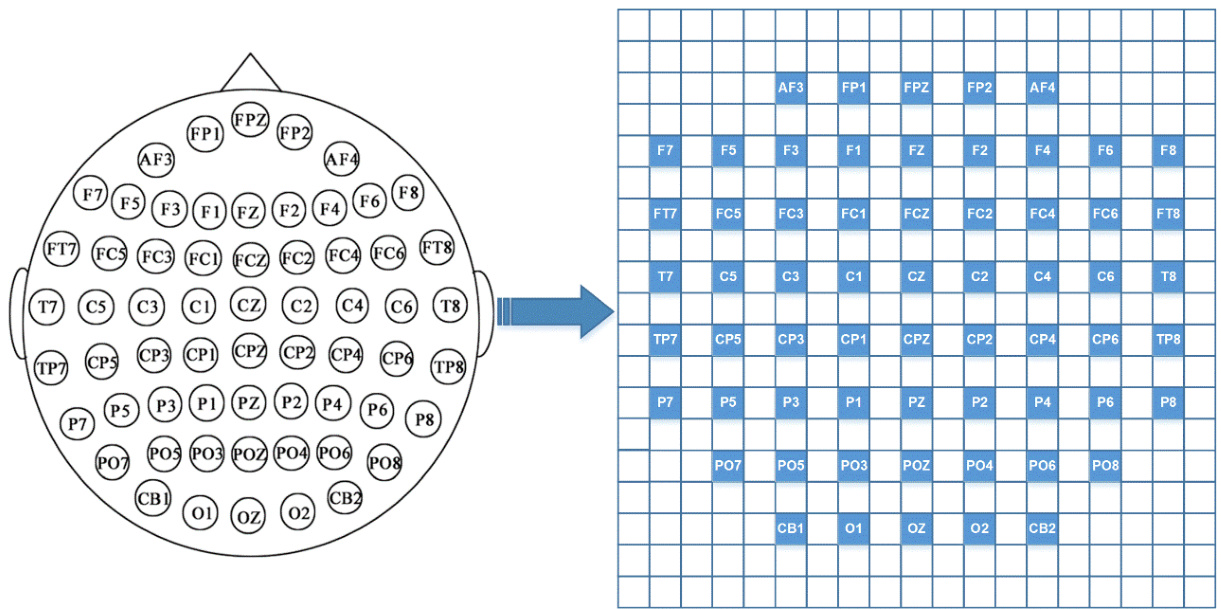
Fig. 3 The 2D sparse map with zero-padding of 62 channels. The purpose of the organization is to preserve the positional relationships among different electrodes.

图 3: 采用62通道零填充的二维稀疏映射图。该布局旨在保持不同电极之间的位置关系。

Attention-based CNN

基于注意力的CNN

For a 4D spatial-spectral-temporal representation $X_{n}$ , we extract the spatial and spectral information from each temporal slice $S_{i}\in R^{h\times w\times2f},i~=~1,2,\ldots,2T$ with a CNN, explore the disc rim i native local patterns in spatial and spectral domains with a convolutional attention module, and finally get its spatial and spectral representation. The attention module here is similar to what Woo et al. propose (Woo et al. 2018), which is originally used to improve the representation power of CNN networks.

对于一个4D空间-光谱-时间表征 $X_{n}$，我们从每个时间切片 $S_{i}\in R^{h\times w\times2f},i~=~1,2,\ldots,2T$ 中通过CNN提取空间和光谱信息，利用卷积注意力模块探索空间和光谱域中的判别性局部模式，最终获得其空间和光谱表征。这里的注意力模块类似于Woo等人提出的方法 (Woo et al. 2018)，最初用于提升CNN网络的表征能力。

The structure of the attention-based CNN is shown in Fig. 4. It contains four convolutional layers, four convolutional attention modules, one max-pooling layer, and one fullyconnected layer. The four convolutional layers have 64, 128, 256, and 64 feature maps with the filter size of $5\times5$ , $5\times5$ , $5\times5$ , and $3\times3$ , respectively. Specifically, a convolutional attention module is used after each convolutional layer to utilize the spatial and spectral attention mechanisms, and the details will be given later. We only use one max-pooling layer with a filter size of $2\times2$ after the last convolutional attention module to preserve more information and enhance the robustness of the network. Finally, outputs of the max-pooling layer are flattened and fed to the fully-connected layer with 150 units. Thus, for each temporal slice $S_{i}$ , we take the final output $P_{i}\in R^{150}$ as its spatial and spectral representation.

基于注意力机制的 CNN 结构如图 4 所示。它包含四个卷积层、四个卷积注意力模块、一个最大池化层和一个全连接层。四个卷积层分别具有 64、128、256 和 64 个特征图，滤波器大小分别为 $5\times5$ 、 $5\times5$ 、 $5\times5$ 和 $3\times3$ 。具体而言，每个卷积层后都使用一个卷积注意力模块来利用空间和光谱注意力机制，细节将在后文给出。我们仅在最后一个卷积注意力模块后使用一个滤波器大小为 $2\times2$ 的最大池化层，以保留更多信息并增强网络的鲁棒性。最后，将最大池化层的输出展平并输入具有 150 个单元的全连接层。因此，对于每个时间切片 $S_{i}$ ，我们将最终输出 $P_{i}\in R^{150}$ 作为其空间和光谱表示。

Fig. 4 The structure of the attention-based CNN. The upper half of the blocks in the figure is the type of layers and the lower denotes the shape of its output tensors.

图 4: 基于注意力机制的 CNN (Convolutional Neural Network) 结构。图中模块上半部分表示层类型，下半部分表示其输出张量的形状。

Convolutional attention module

卷积注意力模块

The convolutional attention module is applied after each convolutional layer to adaptively capture important brain regions and frequency bands. The structure of the convolutional attention module is shown in Fig. 5. It consists of two sub-modules, i.e. the spatial attention module and the spectral attention module.

卷积注意力模块被应用于每个卷积层之后，以自适应地捕捉重要脑区和频段。卷积注意力模块的结构如图5所示，由两个子模块组成，即空间注意力模块和频谱注意力模块。

For each convolutional layer above, its output is a 3D feature tensor $V\in R^{h_{v}\times w_{v}\times c_{v}}$ , where $h_{v}$ , $w_{v}$ , and $c_{v}$ are the height of the 2D feature maps of $V$ , the width of the 2D feature maps of $V$ , and the number of the 2D feature maps of $V$ , respectively. We take $V$ as the input of the convolutional attention module.

对于上述每个卷积层，其输出是一个3D特征张量 $V\in R^{h_{v}\times w_{v}\times c_{v}}$ ，其中 $h_{v}$ 、 $w_{v}$ 和 $c_{v}$ 分别表示 $V$ 的2D特征图高度、宽度以及特征图数量。我们将 $V$ 作为卷积注意力模块的输入。

The spectral attention module is applied to identify valuable frequency bands for emotion recognition. The average pooling has been widely used to aggregate spatial information and the maximum pooling has been commonly adopted to gather distinctive features. Therefore, we shrink the spatial dimension of $V$ by a spatial-wise average pooling and a spatial-wise maximum pooling, which are defined as:

谱注意力模块用于识别情感识别中有价值的频段。平均池化 (average pooling) 被广泛用于聚合空间信息，而最大池化 (maximum pooling) 则常用于收集显著特征。因此，我们通过空间维度的平均池化和最大池化来缩小 $V$ 的空间维度，其定义如下：

$$
\begin{array}{l}{{\displaystyle{\cal C}{a v g,i}=\frac{1}{h_{v}\times w_{v}}\sum_{h=1}^{h_{v}}\sum_{w=1}^{\bar{w}{v}}V_{i}\left(h,w\right),i=1,2,\ldots,c_{v}}}\ {{\displaystyle{\cal C}{m a x,i}=m a x(V_{i}),i=1,2,\ldots,c_{v}}}\end{array}
$$

$$
\begin{array}{l}{{\displaystyle{\cal C}{a v g,i}=\frac{1}{h_{v}\times w_{v}}\sum_{h=1}^{h_{v}}\sum_{w=1}^{\bar{w}{v}}V_{i}\left(h,w\right),i=1,2,\ldots,c_{v}}}\ {{\displaystyle{\cal C}{m a x,i}=m a x(V_{i}),i=1,2,\ldots,c_{v}}}\end{array}
$$

where $V_{i}\in R^{h_{v}\times w_{v}}$ denotes the 2D feature map in the $i{-}t h$ channel of $V$ , $C_{a v g,i}$ represents the element in the i-th channel of the spatial average representation $C_{a v g}\in R^{c_{v}}$ , $m a x(Z)$ returns the largest element in $Z$ , and $C_{m a x,i}$ is the element in the $i{-}t h$ channel of the spatial maximum representation $C_{m a x}\in R^{c_{v}}$ . Subsequently, we implement the spectral attention by two fully-connected layers, a Relu activation function and a sigmoid activation function, which is defined as:

其中 $V_{i}\in R^{h_{v}\times w_{v}}$ 表示 $V$ 的第 $i{-}t h$ 通道的二维特征图，$C_{a v g,i}$ 代表空间平均表示 $C_{a v g}\in R^{c_{v}}$ 中第i个通道的元素，$m a x(Z)$ 返回 $Z$ 中的最大元素，$C_{m a x,i}$ 是空间最大表示 $C_{m a x}\in R^{c_{v}}$ 的第 $i{-}t h$ 通道元素。随后，我们通过两个全连接层、一个Relu激活函数和一个sigmoid激活函数来实现频谱注意力机制，其定义为：

$$
\begin{array}{r l}{{}}&{{\displaystyle A_{s p e c t r a l,a v g}=W_{2}^{S}(R e l u(W_{1}^{S}C_{a v g})}}\ {{}}&{{\displaystyle A_{s p e c t r a l,m a x}=W_{2}^{S}(R e l u(W_{1}^{S}C_{m a x})}}\ {{}}&{{\displaystyle A_{s p e c t r a l}=s i g m o i d\big(A_{s p e c t r a l,a v g}\oplus A_{s p e c t r a l,m a x}\big)}}\ {{}}&{{\displaystyle R e l u(x)=\operatorname*{max}(x,0)}}\ {{}}&{{\displaystyle s i g m o i d(x)=\frac{1}{1+~e^{-x}}}}\end{array}
$$

$$
\begin{array}{r l}{{}}&{{\displaystyle A_{s p e c t r a l,a v g}=W_{2}^{S}(R e l u(W_{1}^{S}C_{a v g})}}\ {{}}&{{\displaystyle A_{s p e c t r a l,m a x}=W_{2}^{S}(R e l u(W_{1}^{S}C_{m a x})}}\ {{}}&{{\displaystyle A_{s p e c t r a l}=s i g m o i d\big(A_{s p e c t r a l,a v g}\oplus A_{s p e c t r a l,m a x}\big)}}\ {{}}&{{\displaystyle R e l u(x)=\operatorname*{max}(x,0)}}\ {{}}&{{\displaystyle s i g m o i d(x)=\frac{1}{1+~e^{-x}}}}\end{array}
$$

where $W_{1}^{S}$ and $W_{2}^{S}$ are learnable parameters, $\textcircled{4}$ denotes the element-wise addition, and $A_{s p e c t r a l}\in R^{1\times1\times c_{v}}$ is the spectral attention. The elements of $A_{s p e c t r a l}$ represent the importance of the corresponding 2D feature maps of the spectral domain. After generating the spectral attention $A_{s p e c t r a l}$ , the output of the spectral attention module can be defined as:

其中 $W_{1}^{S}$ 和 $W_{2}^{S}$ 是可学习参数，$\textcircled{4}$ 表示逐元素相加，$A_{s p e c t r a l}\in R^{1\times1\times c_{v}}$ 是光谱注意力。$A_{s p e c t r a l}$ 的元素代表光谱域对应二维特征图的重要性。生成光谱注意力 $A_{s p e c t r a l}$ 后，光谱注意力模块的输出可定义为：

$$
V^{\prime}=A_{s p e c t r a l}\otimes V
$$

$$
V^{\prime}=A_{s p e c t r a l}\otimes V
$$

where $V^{\prime}$ denotes the refined 3D feature tensor, and $\otimes$ represents the element-wise multiplication.

其中 $V^{\prime}$ 表示精炼后的3D特征张量，$\otimes$ 代表逐元素相乘。

The spatial attention module is applied to identify valuable brain regions for emotion recognition. Firstly, we shrink the spectral dimension of $V^{\prime}$ by spectral-wise average pooling and spectral-wise maximum pooling, which is defined as:

空间注意力模块用于识别对情绪识别有价值的脑区。首先，我们通过谱维平均池化和谱维最大池化缩减 $V^{\prime}$ 的频谱维度，其定义为：

$$
\begin{array}{c l}{{}}&{{S p h_{a v g,(h,w)}=\displaystyle\frac{1}{c_{v}}\sum_{c=1}^{c_{v}}S_{h,w}^{\prime}(c),h=1,2,\ldots,h_{v};w}}\ {{}}&{{=\displaystyle1,2,\ldots,w_{v}}}\ {{}}&{{S P A_{m a x,(h,w)}=\displaystyle m a x(S_{h,w}^{\prime}),h=1,2,\ldots,h_{v};w}}\ {{}}&{{=\displaystyle1,2,\ldots,w_{v}}}\end{array}
$$

$$
\begin{array}{c l}{{}}&{{S p h_{a v g,(h,w)}=\displaystyle\frac{1}{c_{v}}\sum_{c=1}^{c_{v}}S_{h,w}^{\prime}(c),h=1,2,\ldots,h_{v};w}}\ {{}}&{{=\displaystyle1,2,\ldots,w_{v}}}\ {{}}&{{S P A_{m a x,(h,w)}=\displaystyle m a x(S_{h,w}^{\prime}),h=1,2,\ldots,h_{v};w}}\ {{}}&{{=\displaystyle1,2,\ldots,w_{v}}}\end{array}
$$

where $S_{h,w}^{\prime}\in R^{c_{v}}$ denotes the channel in the $h{-}t h$ row and $w{-}t h$ column of $V^{\prime}$ , $S P A_{a v g,(h,w)}$ represents the element in the $h{-}t h$ row and $w{-}t h$ column of the spectral average representation $S P A_{a v g}\in R^{h_{v}\times w_{v}\times1}$ and $S P A_{m a x,(h,w)}$ is the element in the $h$ - $^{t h}$ row and $w{-}t h$ column of the spectral maximum representation $S P A_{m a x}\in R^{h_{v}\times w_{v}\times1}$ . In the following, we implement the spatial attention with a convolutional layer and a sigmoid activation function, which is defined as:

其中 $S_{h,w}^{\prime}\in R^{c_{v}}$ 表示 $V^{\prime}$ 中第 $h$ 行第 $w$ 列的通道，$S P A_{a v g,(h,w)}$ 表示光谱平均表示 $S P A_{a v g}\in R^{h_{v}\times w_{v}\times1}$ 中第 $h$ 行第 $w$ 列的元素，$S P A_{m a x,(h,w)}$ 表示光谱最大表示 $S P A_{m a x}\in R^{h_{v}\times w_{v}\times1}$ 中第 $h$ 行第 $w$ 列的元素。接下来，我们通过一个卷积层和 sigmoid 激活函数实现空间注意力机制，其定义为：

$$
\begin{array}{r}{S P A=C a t(S P A_{a v g},S P A_{m a x})}\ {A_{s p a t i a l}=S i g m o i d(C o n v(S P A))}\end{array}
$$

$$
\begin{array}{r}{S P A=C a t(S P A_{a v g},S P A_{m a x})}\ {A_{s p a t i a l}=S i g m o i d(C o n v(S P A))}\end{array}
$$

where $C a t(S P A_{a v g},S P A_{m a x})$ denotes the concatenation of $S P A_{a v g}$ and $S P A_{m a x}$ along the spectral dimension, $C o n v(S P A)$ represents the convolutional layer for $S P A$ , and $A_{s p a t i a l}\in R^{h_{v}\times w_{v}\times1}$ is the spatial attention. The elements of of the spatial domain. Subsequently, the output of the spatial attention module can be defined as:

其中 $Cat(SPA_{avg}, SPA_{max})$ 表示沿频谱维度对 $SPA_{avg}$ 和 $SPA_{max}$ 进行拼接， $Conv(SPA)$ 代表 $SPA$ 的卷积层， $A_{spatial}\in R^{h_{v}\times w_{v}\times1}$ 是空间注意力。空间域的各个元素。随后，空间注意力模块的输出可定义为：

$$
V^{\prime\prime}=A_{s p a t i a l}\otimes V^{\prime}
$$

$$
V^{\prime\prime}=A_{s p a t i a l}\otimes V^{\prime}
$$

where $V^{\prime\prime}\in R^{h_{v}\times w_{v}\times c_{v}}$ denotes the final output 3D feature tensor of the convolutional attention module.

其中 $V^{\prime\prime}\in R^{h_{v}\times w_{v}\times c_{v}}$ 表示卷积注意力模块的最终输出三维特征张量。

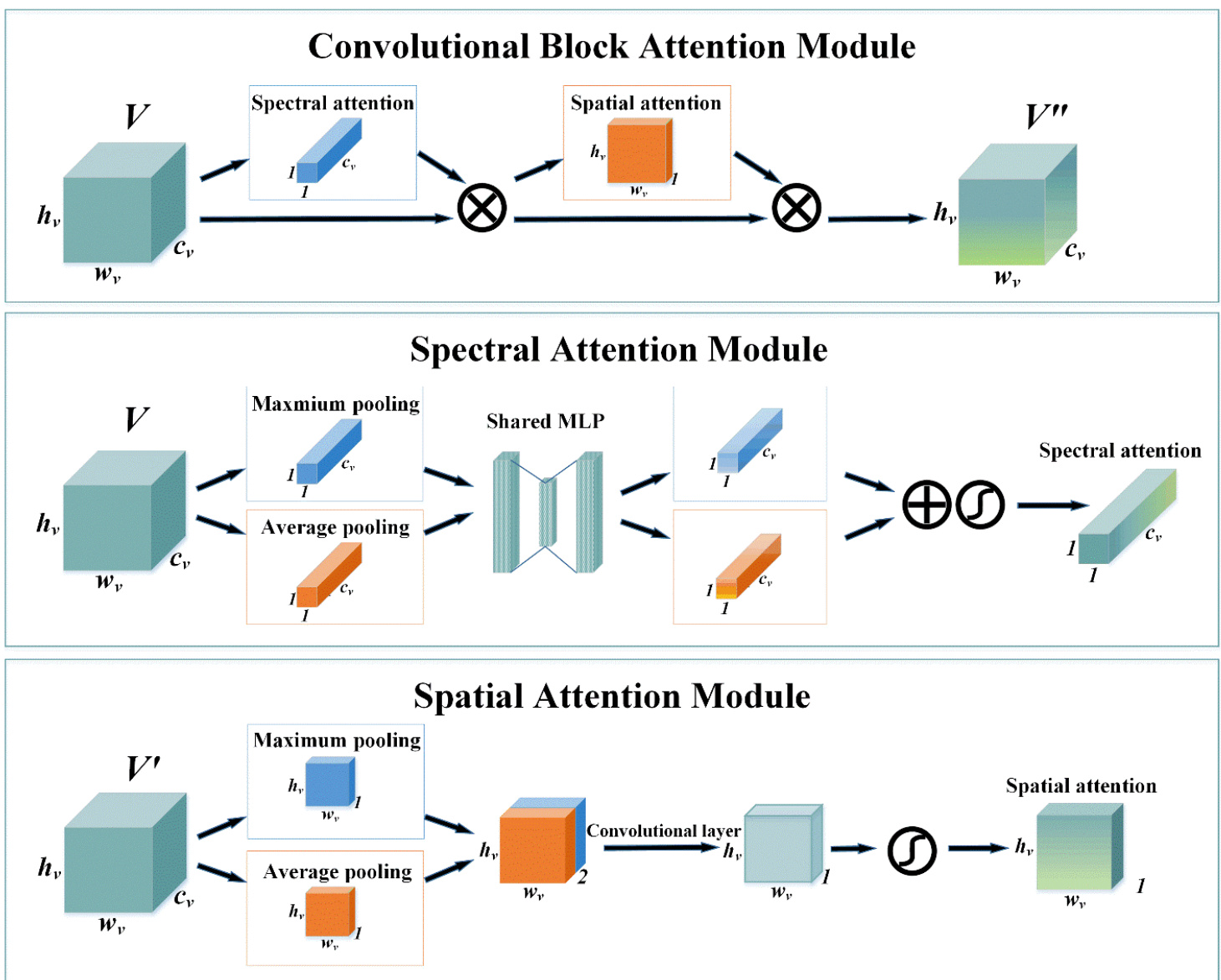
Fig. 5 The top block is the overall structure of the convolutional attention block, it consists of the spectral attention module and the spatial attention module. The middle block represents the generation of spectral attention. The bottom block denotes the generation of spatial attention.

图 5: 顶部模块展示了卷积注意力块的整体结构，由频谱注意力模块和空间注意力模块组成。中间模块表示频谱注意力的生成过程。底部模块展示了空间注意力的生成机制。

Attention-based bidirectional LSTM

基于注意力机制的双向LSTM

For each temporal slice $S_{i}\in R^{h\times w\times2f},i~=~1,2,\dots,2T$ , the final output of the attention-based CNN is $P_{i}\in R^{150}$ . Since the variation between different temporal slices contains temporal information for emotion recognition, we utilize an attentionbased bidirectional LSTM to explore the importance of different slices, as shown in Fig. 6.

对于每个时间切片 $S_{i}\in R^{h\times w\times2f},i~=~1,2,\dots,2T$ ，基于注意力机制的 CNN (Convolutional Neural Network) 最终输出为 $P_{i}\in R^{150}$ 。由于不同时间切片间的变化包含情感识别的时序信息，我们采用基于注意力的双向 LSTM (Long Short-Term Memory) 来探索不同切片的重要性，如图 6 所示。

A bidirectional LSTM connects two unidirectional LSTMs with opposite directions to the same output. Comparing with a unidirectional LSTM, a bidirectional LSTM preserves information from both past and future, making it understand the context better. In this paper, the bidirectional LSTM comprises two