Dual-Level Precision Edges Guided Multi-View Stereo with Accurate Planar iz ation

双级精度边缘引导的精确平面化多视角立体匹配

Abstract

摘要

The reconstruction of low-textured areas is a prominent research focus in multi-view stereo (MVS). In recent years, traditional MVS methods have performed exceptionally well in reconstructing low-textured areas by constructing plane models. However, these methods often encounter issues such as crossing object boundaries and limited perception ranges, which undermine the robustness of plane model construction. Building on previous work (APD-MVS), we propose the DPE-MVS method. By introducing dual-level precision edge information, including fine and coarse edges, we enhance the robustness of plane model construction, thereby improving reconstruction accuracy in low-textured areas. Furthermore, by leveraging edge information, we refine the sampling strategy in conventional PatchMatch MVS and propose an adap- tive patch size adjustment approach to optimize matching cost calculation in both stochastic and low-textured areas. This additional use of edge information allows for more precise and robust matching. Our method achieves state-of-the-art performance on the ETH3D and Tanks & Temples benchmarks. Notably, our method outperforms all published methods on the ETH3D benchmark.

低纹理区域重建是多视角立体视觉 (MVS) 领域的重要研究方向。近年来，传统 MVS 方法通过构建平面模型在低纹理区域重建中表现优异，但仍存在物体边界穿透和感知范围受限等问题，影响了平面模型构建的鲁棒性。基于前期工作 (APD-MVS)，我们提出了 DPE-MVS 方法。通过引入包含精细边缘和粗边缘的双精度边缘信息，增强了平面模型构建的鲁棒性，从而提升了低纹理区域的重建精度。此外，我们利用边缘信息改进了传统 PatchMatch MVS 的采样策略，并提出自适应块大小调整方法，以优化随机区域和低纹理区域的匹配成本计算。这种边缘信息的额外使用实现了更精确、更鲁棒的匹配。我们的方法在 ETH3D 和 Tanks & Temples 基准测试中达到了最先进的性能。值得注意的是，在 ETH3D 基准测试中，我们的方法超越了所有已发表的方法。

Introduction

引言

Multi-view stereo (MVS) is a classical computer vision task aimed at reconstructing the dense 3D geometry of objects or scenes from images taken from multiple viewpoints. This technique has significant applications in areas such as cultural heritage preservation, virtual reality, augmented reality, and autonomous driving. In recent years, MVS methods has advanced significantly, benefiting from diverse datasets (Schops et al. 2017; Knapitsch et al. 2017) and various algorithms (Wang et al. 2023; Wu et al. 2024) , leading to substantial improvements in reconstruction performance. Despite these advancements, MVS still faces challenges in handling low-textured and stochastic textured areas.

多视图立体视觉 (Multi-view stereo, MVS) 是一项经典计算机视觉任务，旨在从多视角拍摄的图像中重建物体或场景的密集三维几何结构。该技术在文化遗产保护、虚拟现实、增强现实和自动驾驶等领域具有重要应用。近年来，受益于多样化数据集 (Schops et al. 2017; Knapitsch et al. 2017) 和多种算法 (Wang et al. 2023; Wu et al. 2024) ，MVS方法取得显著进展，重建性能大幅提升。尽管如此，MVS在处理低纹理和随机纹理区域时仍面临挑战。

MVS methods can be roughly categorized into traditional methods (Galliani, Lasinger, and Schindler 2015; Sch on berger et al. 2016; Xu and Tao 2019) and learningbased methods (Yao et al. 2018; Gu et al. 2020). Traditional methods have the advantages of stronger generalization capabilities and lower memory consumption compared to learning-based methods. Additionally, there has been more research in recent traditional MVS methods addressing the low-textured issue. Recent mainstream methods are based on PatchMatch (PM), which matches fixed-size patch in the reference image with patches in the source images using a plane hypothesis (including depth and normal). Since fixed-size patch struggle to extract appropriate feature information in low-textured areas, many works have further extended and optimized this method. For example, (Liao et al. 2019; Xu and Tao 2019) leverage multi-scale information, while others (Xu and Tao 2020) use triangular plane priors to guide plane hypotheses in low-textured areas. (Xu et al. 2022) combines these approaches to enhance reconstruction performance. Subsequent methods (Zhang et al. 2022; Tian et al. 2023) refine the construction of triangular planes, while others (Romanoni and Matteucci 2019; Kuhn, Lin, and Erdler 2019) employ image segmentation and RANSAC algorithm to determine plane models.

多视角立体视觉(MVS)方法大致可分为传统方法 (Galliani, Lasinger, and Schindler 2015; Sch on berger et al. 2016; Xu and Tao 2019) 和学习型方法 (Yao et al. 2018; Gu et al. 2020)。与传统方法相比，学习型方法具有更强的泛化能力和更低的内存消耗优势。此外，近年针对低纹理问题的传统MVS方法研究也日益增多。

当前主流方法基于PatchMatch (PM) 算法，该算法通过平面假设(包含深度和法向量)在参考图像与源图像之间匹配固定尺寸的图像块。由于固定尺寸图像块在低纹理区域难以提取合适特征信息，许多研究对此方法进行了扩展优化。例如 (Liao et al. 2019; Xu and Tao 2019) 利用多尺度信息，(Xu and Tao 2020) 则采用三角平面先验指导低纹理区域的平面假设。(Xu et al. 2022) 综合这些方法提升了重建性能。后续研究 (Zhang et al. 2022; Tian et al. 2023) 改进了三角平面构建方法，而 (Romanoni and Matteucci 2019; Kuhn, Lin, and Erdler 2019) 则运用图像分割和RANSAC算法确定平面模型。

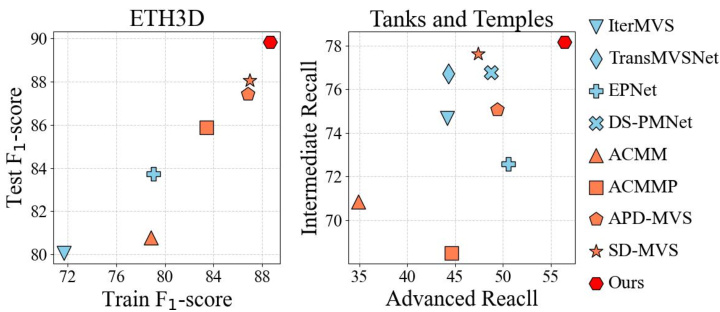
Figure 1: Comparison with the SOTA traditional methods and learning-based methods. Our method achieves the best $\mathrm{F_{1}}$ -score on ETH3D and the best recall on Tanks & Temples.

图 1: 与SOTA传统方法和基于学习方法的对比。我们的方法在ETH3D上取得了最佳$\mathrm{F_{1}}$分数，在Tanks & Temples上获得了最佳召回率。

One notable method, APD-MVS (Wang et al. 2023), introduces adaptive patch deformation. This method classifies pixels into reliable and unreliable based on matching ambiguity. For each unreliable pixel, it searches for a number of reliable pixels in the surrounding area. The RANSAC algorithm is then used to estimate the best-fitting plane from these reliable pixels, selecting the most fitting ones as anchors to assist in the matching of unreliable pixel. Compared to previous methods, this approach is more flexible and significantly enhances the robustness of the plane model.

一种值得注意的方法是APD-MVS (Wang et al. 2023)提出的自适应块变形技术。该方法根据匹配模糊度将像素分为可靠与不可靠两类，针对每个不可靠像素在其周边区域搜索若干可靠像素，随后运用RANSAC算法从这些可靠像素中估计最佳拟合平面，筛选最匹配的像素作为锚点来辅助不可靠像素的匹配。相较先前方法，该方案更具灵活性，显著提升了平面模型的鲁棒性。

Figure 2: Top: depth maps for scenes crossing object boundaries. Bottom: normal maps for limited perception range. Comparison of APD-MVS (middle) and our method (right).

图 2: 上图: 跨越物体边界的场景深度图。下图: 有限感知范围的法线图。APD-MVS (中) 与我们的方法 (右) 对比。

Although these methods significantly improve reconstruction in low-textured areas, they still face issues with increased scene complexity, as shown in Fig. 2 and Fig. 3. One common issue is the plane model crossing object boundaries, causing depth confusion between foreground objects and the background. Another is the potential for errors in plane model construction due to limited perception range. For example, APD-MVS considers only the nearest reliable pixels when constructing planes, sometimes selecting locally optimal pixels, which leads to noticeable deviations between the final plane model and the ground truth.

尽管这些方法显著提升了低纹理区域的重建效果，但在场景复杂度增加时仍存在问题，如图 2 和图 3 所示。一个常见问题是平面模型会跨越物体边界，导致前景物体与背景之间的深度混淆。另一个问题是由于感知范围有限，平面模型构建可能存在误差。例如，APD-MVS 在构建平面时仅考虑最近的可靠像素，有时会选择局部最优像素，这会导致最终平面模型与真实值之间出现明显偏差。

To address these issues, we drew inspiration from learning-based MVS methods (Zhang et al. 2023; Li et al. 2024), which utilize RGB images for adaptive sampling. We posit that fully leveraging image information, particularly edge information, is crucial since areas delineated by edges often approximate planar shapes. Based on this premise, we integrated dual-level precision edge information into the adaptive patch deformation. Dual-level precision edges are derived from two edge detection approaches: fine edges, which are precise but incomplete, and coarse edges, which capture more actual object boundaries but with less accuracy. Specifically, we use the Canny operator for fine edges and a segmentation scheme from TSAR-MVS (Yuan et al. 2024b) for coarse edges. Fine edges constrain point selection during plane construction, while coarse edges expand the perception range for selecting anchors. Thereby providing more effective support for the matching of unreliable pixels. Furthermore, since reliable pixels serve as the basis for selecting anchors and are still processed using conventional PM in APD-MVS, we utilize fine edge information to improve the hypotheses sampling strategy, optimizing the hypotheses for reliable pixels.

为了解决这些问题，我们受到基于学习的多视图立体匹配方法 (Zhang et al. 2023; Li et al. 2024) 的启发，该方法利用RGB图像进行自适应采样。我们认为充分利用图像信息（尤其是边缘信息）至关重要，因为边缘勾勒的区域通常近似平面形状。基于这一前提，我们将双精度边缘信息整合到自适应块变形中。双精度边缘通过两种边缘检测方法获得：精细边缘（精度高但完整性不足）和粗糙边缘（能捕捉更多实际物体边界但精度较低）。具体而言，我们使用Canny算子提取精细边缘，并采用TSAR-MVS (Yuan et al. 2024b) 的分割方案获取粗糙边缘。精细边缘约束平面构建时的点选择，而粗糙边缘则扩展锚点选择的感知范围，从而为不可靠像素的匹配提供更有效的支持。此外，由于可靠像素是锚点选择的基础，在APD-MVS中仍采用传统PM处理，我们利用精细边缘信息改进假设采样策略，优化可靠像素的假设生成。

The aforementioned strategy has shown marked performance but is ineffective in stochastic textured areas, such as lawns, which often contain numerous erroneous edges. Therefore, we further investigated the matching cost calculation. The deformable patch, consisting of an unreliable pixel’s patch and the anchors’ patches, is used to evaluate the plane hypothesis of the the unreliable pixel. Its matching cost is calculated as the weighted sum of the matching costs of both the unreliable pixel’s patch and the anchors’ patches. However, the conventional fixed-size patch matching method, specifically the matching of the unreliable pixel’s patch, remains part of this process, affecting stability, especially in stochastic textured areas. To address this, we propose adjusting patch sizes with anchors to effectively identify unreliable pixels and applying edge information constraints to prevent crossing object boundaries. This enables more robust matching cost calculations.

上述策略虽表现出显著性能，但在随机纹理区域（如草坪）中效果不佳，这类区域常包含大量错误边缘。为此，我们进一步研究了匹配成本计算。可变形块由不可靠像素块和锚点块组成，用于评估不可靠像素的平面假设，其匹配成本计算为不可靠像素块与锚点块匹配成本的加权和。然而，传统固定尺寸块匹配方法（特别是不可靠像素块的匹配）仍是该过程的一部分，这会影响稳定性，尤其在随机纹理区域。为解决此问题，我们提出通过锚点动态调整块尺寸以有效识别不可靠像素，并应用边缘信息约束防止跨越物体边界，从而实现更鲁棒的匹配成本计算。

Figure 3: Comparison of plane construction between APDMVS (middle) and our method (right), with visualization s of fine edges (top right) and coarse edges (bottom right).

图 3: APDMVS (中) 与我们方法 (右) 的平面构建对比，包含细边缘 (右上) 和粗边缘 (右下) 的可视化效果。

We integrated the aforementioned concepts into the DualLevel Precision Edges Guided Multi-View Stereo with Accurate Planar iz ation (DPE-MVS). In summary, our contributions can summarized as follows:

我们将上述概念整合到具有精确平面化的双层级精度边缘引导多视角立体视觉 (DPE-MVS) 中。总结而言，我们的贡献可归纳如下:

• We propose a dual-level precision edge-guided planar model construction strategy, providing more effective support for the matching of unreliable pixels. • We propose a sampling strategy guided by fine edges, which can enhance conventional PM for reliable pixels. • We introduce an adaptive patch size adjustment approach that enables more robust matching cost calculation for unreliable pixels. • Extensive experiments validate the effectiveness of our proposed method, demonstrating state-of-the-art performance on the ETH3D and Tanks & Temples benchmarks.

• 我们提出了一种双精度边缘引导的平面模型构建策略，为不可靠像素的匹配提供更有效的支持。
• 我们提出了一种由精细边缘引导的采样策略，能够增强传统平面模型 (PM) 对可靠像素的处理能力。
• 我们引入了一种自适应块大小调整方法，使不可靠像素的匹配成本计算更加鲁棒。
• 大量实验验证了我们所提方法的有效性，在ETH3D和Tanks & Temples基准测试中展现了最先进的性能。

Related Work

相关工作

Traditional Methods Traditional MVS methods can be roughly categorized into four types: voxel-based methods (Vogiatzis et al. 2007), surface iterative optimization methods (Cremers and Kolev 2010), patch-based methods (Furukawa and Ponce 2009), and depth map-based methods (Bleyer, Rhemann, and Rother 2011). Among these, depth map-based methods have become the most popular choice in recent years due to their simplicity, flexibility, and robust performance. Many outstanding works within this category are PM-based methods. Recently, methods such as ACMM (Xu and Tao 2019), ACMP (Xu and Tao 2020), and ACMMP (Xu et al. 2022) have introduced pyramid structures, geometric consistency, and triangular plane priors into MVS. Subsequently, HPM-MVS (Ren et al. 2023) proposed non-local sampling to escape local optima and used a KNN-based approach to optimize plane prior model construction. APD-MVS (Wang et al. 2023) introduced adaptive patch deformation and an NCC-based matching metric to determine the reliability of pixel depth values. Methods like TAPA-MVS (Romanoni and Matteucci 2019) and PCFMVS (Kuhn, Lin, and Erdler 2019) incorporated superpixel segmentation and the RANSAC algorithm, while TSARMVS (Yuan et al. 2024b) further combined the Roberts operator with Hough line detection to segment large lowtextured areas, though these methods tend to over-segment. SD-MVS (Yuan et al. 2024a) used SAM for semantic segmentation to achieve adaptive sampling. However, SAM’s inference speed is slow and it may produce errors with unseen scenes. Additionally, SAM struggles to distinguish different surfaces of the same object, making it unsuitable for constructing plane models.

传统方法
传统多视角立体视觉(MVS)方法大致可分为四类：基于体素的方法 (Vogiatzis et al. 2007)、表面迭代优化方法 (Cremers and Kolev 2010)、基于面片的方法 (Furukawa and Ponce 2009) 以及基于深度图的方法 (Bleyer, Rhemann, and Rother 2011)。其中，基于深度图的方法因其简单性、灵活性和鲁棒性能，近年来成为最流行的选择。该类别中许多优秀工作都是基于平面先验(PM)的方法。近期，ACMM (Xu and Tao 2019)、ACMP (Xu and Tao 2020) 和 ACMMP (Xu et al. 2022) 等方法将金字塔结构、几何一致性和三角平面先验引入MVS。随后，HPM-MVS (Ren et al. 2023) 提出非局部采样以逃离局部最优，并采用基于KNN的方法优化平面先验模型构建。APD-MVS (Wang et al. 2023) 引入自适应面片变形和基于NCC的匹配度量来确定像素深度值的可靠性。TAPA-MVS (Romanoni and Matteucci 2019) 和 PCFMVS (Kuhn, Lin, and Erdler 2019) 等方法结合了超像素分割与RANSAC算法，而 TSARMVS (Yuan et al. 2024b) 进一步将Roberts算子与霍夫线检测结合来分割大面积低纹理区域，但这些方法容易产生过分割。SD-MVS (Yuan et al. 2024a) 使用SAM进行语义分割以实现自适应采样，但SAM推理速度较慢且对未见场景可能产生错误，同时难以区分同一物体的不同表面，因此不适用于构建平面模型。

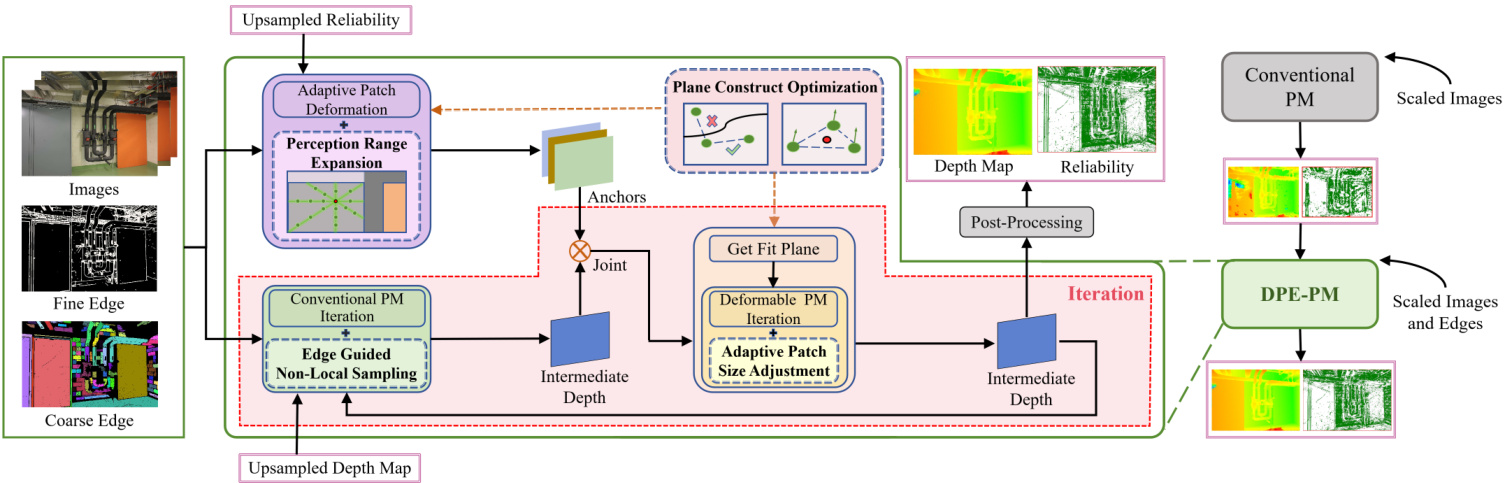
Figure 4: Overview. DPE-MVS adopt a pyramid structure, with the two coarsest scales displayed on the right side of the figure, and the middle illustrating the details of our proposed DPE-PM. Iterations at finer scales use DPE-PM to update the depth map.

图 4: 概述。DPE-MVS采用金字塔结构，图中右侧展示了两个最粗糙的尺度，中间部分则详细说明了我们提出的DPE-PM。在更精细的尺度上，通过DPE-PM迭代更新深度图。

Learning-based Methods MVSNet (Zhang et al. 2023) pioneered the use of deep learning for depth map-based MVS methods. CasMVSNet (Gu et al. 2020) introduced a cascade structure, accelerating the evolution of learning-based MVS methods. These methods, benefiting from convolution operations, have significantly larger receptive fields compared to traditional methods. Works like AA-RMVSNet (Wei et al. 2021) and Trans MV S Net (Ding et al. 2022) further expanded the receptive field. Additionally, improvements in depth sampling have been made by Patch Match Net (Wang et al. 2021) and DS-PMNet (Li et al. 2024), which proposed adaptive hypothesis propagation, and N2MVSNet (Zhang et al. 2023), which introduced adaptive non-local sampling and RGB-guided depth refinement. Learning-based methods have stronger feature perception and often outperform traditional methods with sufficient data. However, creating highquality datasets remains challenging, limiting practical use.

基于学习的方法
MVSNet (Zhang et al. 2023) 率先将深度学习应用于基于深度图的多视图立体 (MVS) 方法。CasMVSNet (Gu et al. 2020) 引入了级联结构，加速了基于学习的MVS方法的发展。这些方法受益于卷积操作，与传统方法相比具有显著更大的感受野。AA-RMVSNet (Wei et al. 2021) 和TransMVSNet (Ding et al. 2022) 等研究进一步扩大了感受野。此外，PatchMatchNet (Wang et al. 2021) 和DS-PMNet (Li et al. 2024) 提出了自适应假设传播，N2MVSNet (Zhang et al. 2023) 引入了自适应非局部采样和RGB引导的深度优化，从而改进了深度采样。基于学习的方法具有更强的特征感知能力，在数据充足时通常优于传统方法。然而，创建高质量数据集仍然具有挑战性，限制了实际应用。

Method

方法

Given a set of images ${I_{i}}{i=1}^{N}$ and the corresponding camera parameters ${\mathbf{P}{i}}_{i=1}^{N}$ , our task is to estimate depth maps for each image. This section provides a brief overview of the key points of APD-MVS, followed by a detailed explanation of our method.

给定一组图像 ${I_{i}}{i=1}^{N}$ 及对应的相机参数 ${\mathbf{P}{i}}_{i=1}^{N}$ ，我们的任务是为每张图像估计深度图。本节先简要概述APD-MVS的关键要点，再详细阐述我们的方法。

Review of APD-MVS

APD-MVS综述

APD-MVS classifies pixels as reliable or unreliable based on matching ambiguity and introduces deformable PM. Reliable pixels are processed using conventional PM, while unreliable pixels are handled using deformable PM.

APD-MVS根据匹配模糊度将像素分类为可靠与不可靠，并引入可变形PM (deformable PM)。可靠像素采用传统PM处理，不可靠像素则使用可变形PM处理。

Conventional PM consists of four basic steps: random initialization, hypothesis propagation, multi-view matching cost evaluation, and refinement. First, each pixel is randomly initialized with a plane hypothesis. Second, hypotheses are sampled from neighboring pixels within a fixed range. Third, matching costs from multiple views are integrated to select the best hypothesis. Fourth, new hypotheses are generated through perturbation and random generation to diversify the solution space, and the best one is selected. The last three steps iterate multiple times.

传统PM算法包含四个基本步骤：随机初始化、假设传播、多视角匹配代价评估和优化。首先，每个像素随机初始化一个平面假设。其次，在固定范围内从相邻像素采样假设。第三，整合多视角的匹配代价以选择最佳假设。第四，通过扰动和随机生成新假设来扩展解空间，并选择最优解。后三个步骤会进行多次迭代。

Deformable PM differs from conventional PM in propagation and matching cost calculation. For each unreliable pixel, anchors are identified through preprocessing. In propagation, sampled hypotheses include anchor hypotheses and plane hypothesis generated using RANSAC on the anchors. In matching cost calculation, the deformable patch is constructed by combining the unreliable pixel’s patch with the anchors’ patches for matching, the formula as follows:

可变形PM（PatchMatch）与传统PM在传播和匹配成本计算上有所不同。对于每个不可靠像素，通过预处理识别出锚点。在传播过程中，采样假设包括锚点假设以及在锚点上使用RANSAC生成的平面假设。在匹配成本计算中，通过将不可靠像素的补丁与锚点的补丁结合构建可变形补丁进行匹配，公式如下：

$$
m_{D}(\mathbf{p},\pmb{\theta}{p},\mathbf{S})=\lambda m(\mathbf{p},\pmb{\theta}{p},\mathbf{B}{p})+\frac{1-\lambda}{|\mathbf{S}|}\sum_{\mathbf{s}\in\mathbf{S}}m(\mathbf{s},\pmb{\theta}{p},\mathbf{B}_{s}),
$$

$$
m_{D}(\mathbf{p},\pmb{\theta}{p},\mathbf{S})=\lambda m(\mathbf{p},\pmb{\theta}{p},\mathbf{B}{p})+\frac{1-\lambda}{|\mathbf{S}|}\sum_{\mathbf{s}\in\mathbf{S}}m(\mathbf{s},\pmb{\theta}{p},\mathbf{B}_{s}),
$$

where $\lambda$ is a weight value, $\mathbf{p}$ represents the unreliable pixel, S denotes the set of anchors. $\pmb{\theta}{p}$ is the plane hypothesis for pixel $\mathbf{p}$ , and $\mathbf{B}$ represent the fixed-size patch. The function $m$ represents the conventional matching cost, while $m_{D}$ denotes the matching cost of the deformable patch.

其中 $\lambda$ 是权重值，$\mathbf{p}$ 表示不可靠像素，S代表锚点集合。$\pmb{\theta}{p}$ 是像素 $\mathbf{p}$ 的平面假设，$\mathbf{B}$ 表示固定大小的图像块。函数 $m$ 表示常规匹配代价，而 $m_{D}$ 表示可变形图像块的匹配代价。

Overview of Our Method

方法概述

Our method adopts the APD-MVS framework, and an overview is illustrated in Fig. 4. Each image is sequentially taken as the reference image $I_{r e f}$ , with the other images as source images $I_{s r c}$ to guide the reference image’s depth map recovery. We construct an $L$ layer pyramid structure through scale down sampling, with the $L$ -th layer as the coarsest scale and the 1st layer as the original image. The initial depth map at the coarsest scale layer is obtained using conventional PM, and perform post-processing to determine the reliability of each pixel. At a finer scale layer $l$ , fine and coarse edges are extracted from $I_{r e f}$ at the corresponding scale. The depth map and reliability from layer $l+1$ are upsampled. These inputs are then used to update the depth map and reliability for this layer using DPE-PM.

我们的方法采用APD-MVS框架，整体流程如图4所示。每张图像依次作为参考图像$I_{ref}$，其余图像作为源图像$I_{src}$来指导参考图像的深度图恢复。我们通过降采样构建$L$层金字塔结构，其中第$L$层为最粗糙尺度，第1层为原始图像。最粗糙尺度层的初始深度图采用传统PM (PatchMatch) 方法获取，并通过后处理确定各像素的可靠性。在更精细的尺度层$l$上，从对应尺度的$I_{ref}$中提取精细和粗糙边缘信息。将$l+1$层的深度图与可靠性信息进行上采样，随后利用DPE-PM方法更新当前层的深度图和可靠性。

In DPE-PM, the first stage is to obtain anchors for each unreliable pixel. In adaptive patch deformation, we propose Perception Range Expansion to search for a wide range of relevant reliable pixels and use RANSAC to filter out the anchors. The second stage is to iterative ly update the depth map. In each iteration, the hypotheses for reliable pixels are first updated using conventional PM with our Edge Guided Non-Local Sampling. Subsequently, the hypotheses for unreliable pixels are updated: new plane hypothesis are generated using RANSAC based on the anchors, followed by deformable PM with our Adaptive Patch Size Adjustment. In the previously mentioned RANSAC applications, our Plane Construction Optimization was consistently utilized to obtain accurate plane models. Similarly, post-processing is used to determine pixel reliability after obtaining the depth map. The DPE-PM process is repeated at finer scales until the depth map for the first layer is obtained. Finally, the depth maps are fused to generate a point cloud.

在DPE-PM中，第一阶段是获取每个不可靠像素的锚点。在自适应块变形中，我们提出感知范围扩展（Perception Range Expansion）来搜索大范围的相关可靠像素，并使用RANSAC过滤锚点。第二阶段是迭代更新深度图。每次迭代中，首先使用传统PM结合我们的边缘引导非局部采样（Edge Guided Non-Local Sampling）更新可靠像素的假设。随后更新不可靠像素的假设：基于锚点使用RANSAC生成新平面假设，再通过自适应块大小调整（Adaptive Patch Size Adjustment）进行可变形PM。在上述RANSAC应用中，我们始终采用平面构建优化（Plane Construction Optimization）来获取精确的平面模型。类似地，在获得深度图后使用后处理确定像素可靠性。DPE-PM过程在更精细尺度上重复，直到获得第一层的深度图。最后融合深度图生成点云。

In the following sections, we will provide the details of our method. First, edge extraction will be introduced, followed by the improvements related to reliable pixels, and finally, the improvements related to unreliable pixels.

在以下章节中，我们将详细介绍我们的方法。首先会介绍边缘提取，接着是与可靠像素相关的改进，最后是与不可靠像素相关的改进。

Extracting Edge Cues

提取边缘线索

Obtaining edge information is essential for our method. We first use the Canny edge detector to extract fine edges, setting the upper and lower thresholds to the median of the image grayscale multiplied by $(1\pm\sigma)$ . Then, coarse edges are extracted using the Roberts operator and Hough line detection, similar to TSAR-MVS. Fine edges help accurately locate the boundaries of foreground objects but are often not closed, making it difficult to determine whether a pixel is in a low-textured region. Coarse edges can segment the image, with larger regions indicating low-textured areas, but have a higher false detection rate and less precise boundary localization. The complementary information from fine and coarse edges is crucial for achieving our research objectives.

获取边缘信息对我们的方法至关重要。我们首先使用Canny边缘检测器提取精细边缘，将上下阈值设置为图像灰度中值乘以$(1\pm\sigma)$。然后采用Roberts算子和Hough直线检测提取粗糙边缘，这与TSAR-MVS方法类似。精细边缘有助于准确定位前景物体边界，但通常不闭合，难以判断像素是否属于低纹理区域。粗糙边缘可以对图像进行分割，较大区域表明存在低纹理区域，但误检率较高且边界定位不够精确。精细边缘与粗糙边缘的互补信息对实现我们的研究目标非常关键。

Edge Guided Non-Local Sampling

边缘引导的非局部采样

Reliable pixels are the foundation for constructing the plane model, and the accuracy of their hypotheses is crucial. Propagation samples hypotheses from neighboring pixels to build the solution space. According to (Ren et al. 2023; Zhou et al. 2021), repetitive hypotheses often occur within the local range in low-textured areas, whereas local sampling preserves fine details in small objects. To expand the solution space while retaining details, we propose two new sampling schemes: progressive non-local sampling and edge-guided extended sampling, as shown in Fig. 5. For fine edge pixels, we apply only progressive non-local sampling. For non-fine edge pixels, both sampling schemes are applied, and the resulting samples are compared to retain the superior ones.

可靠的像素是构建平面模型的基础，其假设的准确性至关重要。传播从邻近像素采样假设以构建解空间。根据 (Ren et al. 2023; Zhou et al. 2021) 的研究，在低纹理区域的局部范围内常出现重复假设，而局部采样能保留小物体的精细细节。为在保留细节的同时扩展解空间，我们提出两种新采样方案：渐进式非局部采样和边缘引导扩展采样，如图 5 所示。对于精细边缘像素，仅采用渐进式非局部采样；对于非精细边缘像素，同时应用两种采样方案并通过比较保留更优样本。

Figure 5: Edge Guided Non-Local Sampling: This process includes two sampling schemes: progressive non-local sampling (left) and edge-guided extended sampling (right).

图 5: 边缘引导非局部采样: 该过程包含两种采样方案: 渐进式非局部采样 (左) 和边缘引导扩展采样 (右)。

Progressive non-local sampling excludes sampling points within a radius $\xi$ during the PM iteration process. The radius $\xi$ gradually decreases as the iterations progress, following the formula $\xi=m a x(1,5-2\times t_{i t e r})$ . We utilize a red-black checkerboard pattern for pixel division $\mathrm{{Xu}}$ and Tao 2019). Each of the eight sampling areas adopts a strip format, where the radius $\xi$ offsets the starting position of the strip. Each area contains 11 samples with a step size of 2. The sample with the minimum multi-view matching cost is selected from each area, yielding the optimal samples {θip n}i8=1.

渐进式非局部采样在PM迭代过程中排除半径$\xi$内的采样点。该半径随迭代次数增加按公式$\xi=max(1,5-2\times t_{iter})$逐步减小。我们采用红黑棋盘格模式进行像素划分 (Xu和Tao 2019)。八个采样区域均采用条带形式，其中半径$\xi$决定条带起始位置的偏移量。每个区域包含11个步长为2的采样点，从各区域选取多视角匹配代价最小的样本，最终获得最优样本集{θip n}i8=1。

Edge-guided extended sampling follows the same fundamental scheme as progressive non-local sampling, but differs in the number of samples and the sampling step size. In this scheme, both the number of samples $k$ and the step size $s$ are adaptively adjusted based on the distance $D_{f e}$ to the nearest fine edge in the corresponding strip direction. A threshold, defined as $\Lambda_{f e}={\frac{i m\bar{a}g e w i d t{\bar{h}}}{30\times4^{l}}}$ ma 3 g 0 ew 4 il d th , is used to prevent excessively large sampling distances. The specific adjustments are calculated as follows:

边缘引导扩展采样遵循与渐进式非局部采样相同的基本方案，但在样本数量和采样步长上有所不同。该方案中，样本数量$k$和步长$s$会根据对应条带方向上到最近精细边缘的距离$D_{fe}$自适应调整。为防止采样距离过大，设定阈值$\Lambda_{fe}={\frac{image\ width}{30\times4^{l}}}$。具体调整计算如下：

$$
D_{f e}^{\prime}=m i n\left(D_{f e},\Lambda_{f e}\right),k=\left\lfloor\frac{D_{f e}^{\prime}}{2}\right\rfloor,s=\left\lfloor\frac{D_{f e}^{\prime}}{k}\right\rfloor,
$$

$$
D_{f e}^{\prime}=m i n\left(D_{f e},\Lambda_{f e}\right),k=\left\lfloor\frac{D_{f e}^{\prime}}{2}\right\rfloor,s=\left\lfloor\frac{D_{f e}^{\prime}}{k}\right\rfloor,
$$

subject to $11~\leqk\leq~22$ . Similarly, optimal samples ${\pmb{\theta}{i}^{e g}}{i=1}^{8}$ are obtained. These samples are then compared with ${\pmb{\theta}{i}^{\bar{p}n}}_{i=1}^{8}$ by re calculating the matching costs on the patch of the pixel being processed, with the better sample for each area direction being selected.

受限于 $11~\leqk\leq~22$。同理，最优样本 ${\pmb{\theta}{i}^{e g}}{i=1}^{8}$ 被获取。随后将这些样本与 ${\pmb{\theta}{i}^{\bar{p}n}}_{i=1}^{8}$ 通过重新计算待处理像素块上的匹配成本进行比较，并为每个区域方向选择更优样本。

Accurate Plane Model Construction

精确平面模型构建

For unreliable pixels, the anchors filtered out by planar RANSAC in adaptive patch deformation significantly impact depth estimation.

对于不可靠像素，自适应块变形中通过平面RANSAC过滤掉的锚点会显著影响深度估计。

Perception Range Expansion To address the issue of limited perception range, we segment the image into distinct regions using coarse edges and extend the search for reliable pixels in low-textured regions. A region is considered lowtextured if its pixel count exceeds $\frac{i m a g e a r e a}{256\times4^{l}}$ . Let $\varepsilon$ denote the set of coarse edge pixels in a specific direction relative to the pixel p, the boundary in that direction is defined as:

感知范围扩展
为解决感知范围有限的问题，我们使用粗边缘将图像分割为不同区域，并在低纹理区域扩展可靠像素的搜索范围。当某区域的像素数量超过 $\frac{i m a g e a r e a}{256\times4^{l}}$ 时，即被判定为低纹理区域。设 $\varepsilon$ 表示像素p在特定方向上的粗边缘像素集合，则该方向的边界定义为：

$$
B(\mathbf{p})={\underset{\mathbf{q}\in\pmb{\varepsilon}}{\operatorname{argmax}}}\left||\mathbf{q}-\mathbf{p}|\right|\quad s.t.\quad\mathbb{C}(\mathbf{q})=1,
$$

$$
B(\mathbf{p})={\underset{\mathbf{q}\in\pmb{\varepsilon}}{\operatorname{argmax}}}\left||\mathbf{q}-\mathbf{p}|\right|\quad s.t.\quad\mathbb{C}(\mathbf{q})=1,
$$

where $\mathbb{C}({\bf q})=1$ indicates that $\mathbf{q}$ is connected to the region where $\mathbf{p}$ is located. This approach determines boundaries in the eight-connected directions for each pixel, effectively filtering out redundant coarse edge pixels within the region.

其中 $\mathbb{C}({\bf q})=1$ 表示 $\mathbf{q}$ 与 $\mathbf{p}$ 所在区域相连。该方法为每个像素确定八连通方向的边界，有效滤除区域内冗余的粗边缘像素。

Subsequently, the eight directions are grouped into four pairs of opposites. Each pair has a search limit of $2\eta$ reliable pixels, distributed between directions based on boundary distances. For example, in the up-down direction pair, the number of pixels allocated for searching is determined using the following formula:

随后，将八个方向分为四对相反方向。每对方向的搜索限制为 $2\eta$ 个可靠像素，根据边界距离在方向间分配。例如，在上下方向对中，用于搜索的像素分配数量通过以下公式确定：

$$
n_{u}=\left\lfloor\frac{2\eta\cdot D_{c e}^{u}}{D_{c e}^{u}+D_{c e}^{d}}\right\rfloor,n_{d}=2\eta-n_{u},
$$

$$
n_{u}=\left\lfloor\frac{2\eta\cdot D_{c e}^{u}}{D_{c e}^{u}+D_{c e}^{d}}\right\rfloor,n_{d}=2\eta-n_{u},
$$

where $D_{c e}^{u}$ and $D_{c e}^{d}$ represent the boundary distances in the upward and downward directions, respectively, with $n_{u}$ is constrained to $1\leq n_{u}\leq2\eta-1$ . For each direction, starting from the unreliable pixel, we locate a set of equally spaced pixels ${\mathbf{s}{i}}{i=1}^{n}$ along the line to the boundary. Let $\mathcal{N}(\mathbf{s}{i})$ denote the nearest reliable pixel to $\mathbf{s}{i}$ . The set ${\mathcal{N}(\mathbf{s}{i})}_{i=1}^{n}$ serves as the result of extended search in that direction.

其中 $D_{c e}^{u}$ 和 $D_{c e}^{d}$ 分别表示向上和向下方向的边界距离，且 $n_{u}$ 被约束为 $1\leq n_{u}\leq2\eta-1$。对于每个方向，从未可靠像素出发，我们沿直线定位一组等距像素 ${\mathbf{s}{i}}{i=1}^{n}$ 直至边界。设 $\mathcal{N}(\mathbf{s}{i})$ 表示 $\mathbf{s}{i}$ 的最近可靠像素，集合 ${\mathcal{N}(\mathbf{s}{i})}_{i=1}^{n}$ 即为该方向上扩展搜索的结果。

We retain the reliable pixels search scheme from APDMVS, which involves partitioning the search space centered on the unreliable pixel into $\phi$ equal-angle sectors and locating the nearest reliable pixels within each sector. This scheme only searches the nearest reliable pixels and is applied to each unreliable pixel, while the extended search supplements it in low-textured areas.

我们保留了APDMVS中可靠的像素搜索方案，该方案将以不可靠像素为中心的搜索空间划分为$\phi$个等角扇区，并在每个扇区内定位最近的可靠像素。此方案仅搜索最近的可靠像素，并应用于每个不可靠像素，而扩展搜索则在低纹理区域对其进行补充。

Plane Construction Optimization RANSAC aims to find the best-fitting plane from 3D points. Using an unreliable pixel in a low-textured area as an example, obtain the set of 3D points $\pmb{\mathcal{X}}={\mathbf{X}{i}}{i=1}^{\phi+8\eta}$ for the searched reliable pixels. Three random points from are iterative ly selected to construct a plane $\pi$ , identifying the best fit as follows:

平面构建优化 RANSAC 旨在从3D点中寻找最佳拟合平面。以低纹理区域中不可靠像素为例，获取搜索到的可靠像素对应的3D点集 $\pmb{\mathcal{X}}={\mathbf{X}{i}}_{i=1}^{\phi+8\eta}$ 。从中迭代选取三个随机点构建平面 $\pi$ ，并通过以下方式确定最佳拟合：

$$
\pi^{}=\arg\operato