FAST MODEL EDITING AT SCALE
大规模快速模型编辑
ABSTRACT
摘要
While large pre-trained models have enabled impressive results on a variety of downstream tasks, the largest existing models still make errors, and even accurate predictions may become outdated over time. Because detecting all such failures at training time is impossible, enabling both developers and end users of such models to correct inaccurate outputs while leaving the model otherwise intact is desirable. However, the distributed, black-box nature of the representations learned by large neural networks makes producing such targeted edits difficult. If presented with only a single problematic input and new desired output, fine-tuning approaches tend to overfit; other editing algorithms are either computationally infeasible or simply ineffective when applied to very large models. To enable easy post-hoc editing at scale, we propose Model Editor Networks with Gradient Decomposition (MEND), a collection of small auxiliary editing networks that use a single desired input-output pair to make fast, local edits to a pre-trained model’s behavior. MEND learns to transform the gradient obtained by standard fine-tuning, using a low-rank decomposition of the gradient to make the parameter iz ation of this transformation tractable. MEND can be trained on a single GPU in less than a day even for 10 billion $^+$ parameter models; once trained MEND enables rapid application of new edits to the pre-trained model. Our experiments with T5, GPT, BERT, and BART models show that MEND is the only approach to model editing that effectively edits the behavior of models with more than 10 billion parameters. Code and data available at https://sites.google.com/view/mend-editing.
虽然大型预训练模型在各种下游任务上取得了令人瞩目的成果,但现有最大规模的模型仍会出现错误,甚至准确的预测结果也可能随时间推移而过时。由于在训练阶段不可能检测到所有此类故障,因此需要让开发者和终端用户能够在不改动模型其他部分的情况下修正错误输出。然而,大型神经网络学习到的分布式黑盒表征特性,使得实现这种针对性编辑变得困难。如果仅提供单个问题输入和期望输出,微调方法容易过拟合;其他编辑算法要么计算量过大,要么在应用于超大规模模型时完全失效。为实现高效的大规模事后编辑,我们提出了基于梯度分解的模型编辑网络(MEND),这是一组小型辅助编辑网络,通过单个期望输入输出对就能快速局部修改预训练模型的行为。MEND通过学习转换标准微调获得的梯度,利用梯度的低秩分解使这种转换的参数化处理成为可能。即便针对百亿级参数模型,MEND也能在单块GPU上一天内完成训练;训练完成后可快速对预训练模型实施新编辑。我们在T5、GPT、BERT和BART模型上的实验表明,MEND是唯一能有效编辑百亿参数以上模型行为的编辑方法。代码与数据详见https://sites.google.com/view/mend-editing。
1 INTRODUCTION
1 引言
Increasingly large models have improved performance on a variety of modern computer vision (Huang et al., 2017; Chen et al., 2022) and especially natural language processing (Vaswani et al., 2017; Brown et al., 2020) problems. However, a key challenge in deploying and maintaining such models is issuing patches to adjust model behavior after deployment (Sinitsin et al., 2020). When a neural network produces an undesirable output, making a localized update to correct its behavior for a single input or small number of inputs is non-trivial, owing to the distributed nature of the model’s representations. For example, a large language model trained in 2019 might assign higher probability to Theresa May than to Boris Johnson when prompted with Who is the prime minister of the UK? (see Table 2 for an example with a real large language model; see Lazaridou et al. (2021) for a systematic study of failures of temporal generalization in LMs). An ideal model editing procedure could quickly update the model parameters to increase the relative likelihood of Boris Johnson without changing the model output for unrelated inputs. This procedure would produce edits with reliability, successfully changing the model’s output on the problematic input (e.g., Who is the prime minister of the UK?); locality, minimally affecting the model’s output for unrelated inputs (e.g., What sports team does Messi play for?); and generality, generating the correct output for inputs related to the edit input (e.g., Who is the UK PM?).
日益庞大的模型在现代计算机视觉(Huang et al., 2017; Chen et al., 2022) 尤其是自然语言处理(Vaswani et al., 2017; Brown et al., 2020) 任务上展现出更好的性能。然而部署和维护此类模型的核心挑战在于,如何在模型上线后通过补丁调整其行为(Sinitsin et al., 2020)。当神经网络产生不良输出时,由于模型表征的分布式特性,针对单个或少量输入进行局部更新以修正其行为并非易事。例如,一个2019年训练的大语言模型在被问及"Who is the prime minister of the UK?"时,给予特蕾莎·梅的概率可能高于鲍里斯·约翰逊(真实大语言模型示例见表2;关于语言模型时序泛化失效的系统性研究参见Lazaridou et al. (2021))。理想的模型编辑方法应能快速更新模型参数,在不影响无关输入输出的前提下,提高鲍里斯·约翰逊的相对概率。这种方法需满足三个特性:可靠性(成功修正问题输入如"Who is the prime minister of the UK?"的输出)、局部性(最小化对无关输入如"What sports team does Messi play for?"的影响)以及泛化性(对相关输入如"Who is the UK PM?"生成正确输出)。

Figure 1: The proposed algorithm MEND enables edit ability by training a collection of MLPs to modify model gradients to produce local model edits that do not damage model performance on unrelated inputs. MEND is efficient to train and apply edits, even for very large models, as shown in Section 5.1.
图 1: 提出的MEND算法通过训练一组MLP来修改模型梯度,从而实现编辑能力,这些局部模型编辑不会损害模型在无关输入上的性能。如第5.1节所示,MEND在训练和应用编辑时非常高效,即使对于非常大的模型也是如此。
A simple approach to making such edits is additional fine-tuning with a new label on the single example to be corrected. Yet fine-tuning on a single example tends to overfit, even when constraining the distance between the pre- and post-fine-tuning parameters (Zhu et al., 2020; De Cao et al., 2021). This over fitting leads to failures of both locality and generality. While fine-tuning on the edit example along with continued training on the training set better enforces locality, our experiments show that it still lacks generality. Further, it requires persistent access to the full training set during test time and is more computationally demanding. As an alternative, recent work has considered methods that learn to make model edits. Sinitsin et al. (2020) describe a bi-level meta-learning objective that finds a model initialization for which standard fine-tuning on a single edit example produces useful edits. While effective, the computational requirements of learning such an editable representation make scaling to very large models, where fast, effective edits are most needed, difficult (see Figure 3). De Cao et al. (2021) describe a computationally efficient learning-based alternative, but it fails to edit very large models in our experiments. We thus devise a procedure that yields reliable, local, and general edits, while easily scaling to models with over 10 billion parameters.
进行此类编辑的一个简单方法是对需要修正的单个示例添加新标签进行额外微调。然而,即使限制微调前后的参数距离 (Zhu et al., 2020; De Cao et al., 2021),单样本微调仍容易过拟合。这种过拟合会导致局部性和泛化性同时失效。虽然在编辑样本上微调并继续在训练集上训练能更好地保持局部性,但实验表明其仍缺乏泛化性。此外,该方法需要在测试阶段持续访问完整训练集,且计算成本更高。
作为替代方案,近期研究开始探索学习式模型编辑方法。Sinitsin et al. (2020) 提出双层元学习目标,通过寻找特定模型初始化状态,使得单编辑样本的标准微调能产生有效编辑。虽然有效,但学习这种可编辑表征的计算需求使得该方法难以扩展到急需快速有效编辑的超大模型 (见图 3)。De Cao et al. (2021) 提出了一种计算高效的学习式方案,但在我们的实验中无法编辑超大模型。因此,我们设计了一种新流程,既能实现可靠、局部且泛化的编辑,又可轻松扩展到超百亿参数规模的模型。
Our approach trains lightweight model editor networks to produce edits to a pre-trained model’s weights when provided with the standard fine-tuning gradient of a given correction as input, leveraging the gradient as an information-rich starting point for editing (see Figure 1). Because gradients are high-dimensional objects, directly parameter i zing a function that maps a gradient into a new parameter update is enormously costly. Even for a single $d\times d$ weight matrix, a naive implementation requires a mapping from $\mathbb{R}^{\mathcal{O}(\dot{d}^{2})}\rightarrow\mathbb{R}^{\mathcal{O}(d^{2})}$ , which is impractical for large models where $d\approx10^{4}$ . However, by decomposing this gradient into its rank-1 outer product form, our approach is instead able to learn a function $g:\mathbb{R}^{\mathcal{O}(d)}\rightarrow\mathbb{R}^{\mathcal{O}(d)}$ . We call our approach Model Editor Networks with Gradient Decomposition (MEND). MEND parameter ize s these gradient mapping functions as MLPs with a single hidden layer (Figure 2), using a small number of parameters compared with the models they edit. MEND can be applied to any pre-trained model, regardless of pre-training.
我们的方法通过训练轻量级模型编辑网络,在给定修正的标准微调梯度作为输入时,对预训练模型的权重进行编辑,将梯度作为信息丰富的编辑起点(见图1)。由于梯度是高维对象,直接参数化一个将梯度映射为新参数更新的函数成本极高。即使对于单个$d\times d$权重矩阵,简单实现也需要从$\mathbb{R}^{\mathcal{O}(\dot{d}^{2})}\rightarrow\mathbb{R}^{\mathcal{O}(d^{2})}$的映射,这在$d\approx10^{4}$的大型模型中不切实际。然而,通过将梯度分解为秩1外积形式,我们的方法能够学习函数$g:\mathbb{R}^{\mathcal{O}(d)}\rightarrow\mathbb{R}^{\mathcal{O}(d)}$。我们将该方法称为基于梯度分解的模型编辑网络(MEND)。MEND将这些梯度映射函数参数化为单隐藏层的MLP(图2),相比被编辑模型仅需少量参数。MEND可应用于任何预训练模型,与预训练方式无关。
The primary contribution of this work is a scalable algorithm for fast model editing that can edit very large pre-trained language models by leveraging the low-rank structure of fine-tuning gradients. We perform empirical evaluations on a variety of language-related tasks and transformer models, showing that MEND is the only algorithm that can consistently edit the largest GPT-style (Radford et al., 2019; Black et al., 2021; Wang and Komatsu zak i, 2021) and T5 (Raffel et al., 2020) language models. Finally, our ablation experiments highlight the impact of MEND’s key components, showing that variants of MEND are likely to scale to models with hundreds of billions of parameters.
这项工作的主要贡献是一种可扩展的快速模型编辑算法,该算法通过利用微调梯度(fine-tuning gradients)的低秩结构,能够编辑非常大的预训练语言模型。我们在多种语言相关任务和Transformer模型上进行了实证评估,结果表明MEND是唯一能够持续编辑最大规模GPT风格(Radford等人,2019;Black等人,2021;Wang和Komatsuzaki,2021)和T5(Raffel等人,2020)语言模型的算法。最后,我们的消融实验突出了MEND关键组件的影响,表明MEND的变体很可能扩展到具有数千亿参数的模型。
2 THE MODEL EDITING PROBLEM
2 模型编辑问题
The goal of model editing is to enable the use of a single pair of input $x_{\mathrm{e}}$ and desired output $y_{\mathrm{e}}$ to alter a base model’s output for $x_{\mathrm{e}}$ as well as its equivalence neighborhood (related input/output pairs), all while leaving model behavior on unrelated inputs unchanged (Sinitsin et al., 2020; De Cao et al., 2021). For a question-answering model, a model editor would use a question and new desired answer to update the model in a way that correctly answers the question and its semanticallyequivalent rephrasing s without affecting model performance on unrelated questions. Some model editors, including ours, use a training phase before they can apply edits (Sinitsin et al., 2020; De Cao et al., 2021), using an edit training dataset $D_{e d i t}^{t r}$ that specifies the types of edits that will be made.
模型编辑的目标是通过单对输入$x_{\mathrm{e}}$和期望输出$y_{\mathrm{e}}$来改变基础模型对于$x_{\mathrm{e}}$及其等价邻域(相关输入/输出对)的输出,同时保持模型在无关输入上的行为不变(Sinitsin et al., 2020; De Cao et al., 2021)。对于问答模型,模型编辑器会利用问题和新期望答案来更新模型,使其能正确回答该问题及其语义等效的改写问题,同时不影响模型在无关问题上的表现。包括我们的方法在内,部分模型编辑器在应用编辑前会使用训练阶段(Sinitsin et al., 2020; De Cao et al., 2021),通过编辑训练数据集$D_{e d i t}^{t r}$来指定将要执行的编辑类型。
More precisely, the base model $f_{\theta}:\mathcal{X}\times\Theta\rightarrow\mathcal{Y}$ is a differentiable function that maps an input $x$ and set of parameters $\theta$ to an output $y$ . A model editor is a function $E:\mathcal{X}\times\mathcal{Y}\times\mathcal{L}\times\Theta\times\Phi\rightarrow\Theta$ that maps an edit input $x_{\mathrm{e}}$ , edit label $y_{\mathrm{e}}$ (a class label or sequence of tokens), loss function ${l}_ {e}:$ $\mathcal{X}\times\mathcal{Y}\times\Theta\to\mathbb{R}$ , base model parameters $\theta$ , and optional editor parameters $\phi$ to a new set of model parameters $\theta_{e}$ . We use the loss function $l_{e}(x,\stackrel{\rightharpoonup}{y},\theta)=-\stackrel{\rightharpoonup}{\mathrm{log}}p_{\theta}(y|x)$ , based on past work (De Cao et al., 2021), but other choices are possible. Model editors are evaluated on a held-out dataset Dte $D_{e d i t}^{t e}={(x_{\mathrm{e}},y_{\mathrm{e}},x_{\mathrm{loc}},x_{\mathrm{e}}^{\prime},y_{\mathrm{e}}^{\prime})_ {i}}$ . For algorithms that learn model editor parameters $\phi$ , a dataset $D_{e d i t}^{t r}$ containing tuples similar to $D_{e d i t}^{t e}$ is used, typically much smaller than the pre-trained model’s original training set. The locality input $x_{\mathrm{loc}}$ is simply a randomly sampled input that is used to quantify the extent to which model predictions change for unrelated inputs. The alternative edit input and label $x_{\mathrm{e}}^{\prime}$ and $y_{\mathrm{e}}^{\prime}$ are sampled from the equivalence neighborhood $N(x_{\mathrm{e}},y_{\mathrm{e}})$ of $x_{\mathrm{e}}$ and $y_{\mathrm{e}}$ , the set of examples that the edited model should generalize to after performing an edit with $x_{\mathrm{e}},y_{\mathrm{e}}$ . For $x_{\mathrm{e}},y_{\mathrm{e}}=W h o$ is the prime minister of the UK? Boris Johnson, $N(x_{\mathrm{e}},y_{\mathrm{e}})$ might contain $x_{\mathrm{e}}^{\prime}$ , $y_{\mathrm{e}}^{\prime}=$ Who is the UK PM? Boris Johnson, among others. $x_{\mathrm{loc}}$ might be What team does Messi play for?.
更准确地说,基础模型 $f_{\theta}:\mathcal{X}\times\Theta\rightarrow\mathcal{Y}$ 是一个可微函数,它将输入 $x$ 和参数集 $\theta$ 映射到输出 $y$。模型编辑器是一个函数 $E:\mathcal{X}\times\mathcal{Y}\times\mathcal{L}\times\Theta\times\Phi\rightarrow\Theta$,它将编辑输入 $x_{\mathrm{e}}$、编辑标签 $y_{\mathrm{e}}$(一个类别标签或token序列)、损失函数 ${l}_ {e}:$ $\mathcal{X}\times\mathcal{Y}\times\Theta\to\mathbb{R}$、基础模型参数 $\theta$ 和可选的编辑器参数 $\phi$ 映射到一组新的模型参数 $\theta_{e}$。我们使用损失函数 $l_{e}(x,\stackrel{\rightharpoonup}{y},\theta)=-\stackrel{\rightharpoonup}{\mathrm{log}}p_{\theta}(y|x)$,基于过去的工作 (De Cao et al., 2021),但也可以选择其他形式。模型编辑器在保留数据集 Dte $D_{e d i t}^{t e}={(x_{\mathrm{e}},y_{\mathrm{e}},x_{\mathrm{loc}},x_{\mathrm{e}}^{\prime},y_{\mathrm{e}}^{\prime})_ {i}}$ 上进行评估。对于学习模型编辑器参数 $\phi$ 的算法,使用包含与 $D_{e d i t}^{t e}$ 类似元组的数据集 $D_{e d i t}^{t r}$,通常比预训练模型的原始训练集小得多。局部性输入 $x_{\mathrm{loc}}$ 只是一个随机采样的输入,用于量化模型对无关输入的预测变化程度。替代编辑输入和标签 $x_{\mathrm{e}}^{\prime}$ 和 $y_{\mathrm{e}}^{\prime}$ 从 $x_{\mathrm{e}}$ 和 $y_{\mathrm{e}}$ 的等价邻域 $N(x_{\mathrm{e}},y_{\mathrm{e}})$ 中采样,即在执行 $x_{\mathrm{e}},y_{\mathrm{e}}$ 编辑后,编辑模型应泛化到的示例集。对于 $x_{\mathrm{e}},y_{\mathrm{e}}=Who$ is the prime minister of the UK? Boris Johnson,$N(x_{\mathrm{e}},y_{\mathrm{e}})$ 可能包含 $x_{\mathrm{e}}^{\prime}$, $y_{\mathrm{e}}^{\prime}=$ Who is the UK PM? Boris Johnson 等。$x_{\mathrm{loc}}$ 可能是 What team does Messi play for?。
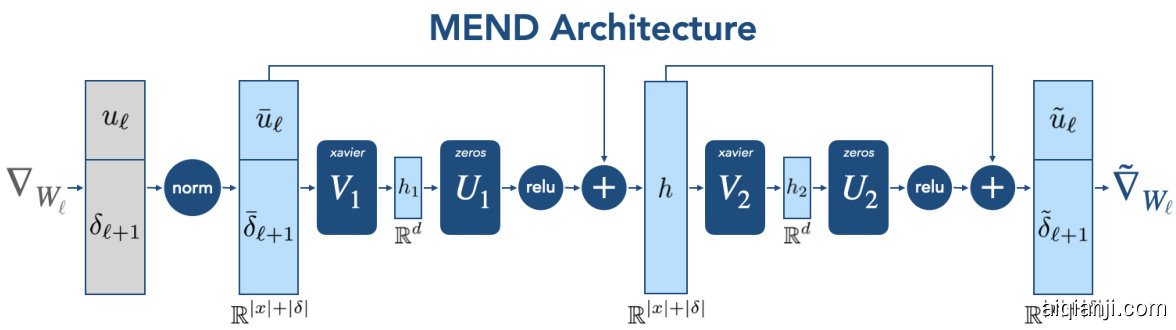
Figure 2: The MEND architecture, consisting of two consecutive blocks, both initialized to compute the exact identity function. Left. The input to a MEND network is ${\delta_{\ell+1},u_{\ell}}$ , the components of the rank-1 gradient. Right. A MEND network produces a new rank-1 update $\tilde{\nabla}_ {W_{\ell}}$ , which is added to weights $W_{\ell}$ to edit the model.
图 2: MEND架构,由两个连续模块组成,均初始化为计算精确恒等函数。左图:MEND网络的输入为 ${\delta_{\ell+1},u_{\ell}}$ ,即秩1梯度的分量。右图:MEND网络生成新的秩1更新 $\tilde{\nabla}_ {W_{\ell}}$ ,该更新被加到权重 $W_{\ell}$ 上以实现模型编辑。
In this work, we call a model editor reliable if the post-edit model predicts the edit label $y_{\mathrm{e}}$ for the edit input $x_{\mathrm{e}}$ . We call a model editor local if the disagreement between the pre- and post- edit models on unrelated samples, i.e., $\mathbb{E}_ {\boldsymbol{x}_ {\mathrm{loc}}\sim\boldsymbol{D}_ {e d i t}^{t e}}\mathrm{KL}(p_{\theta}(\cdot|\boldsymbol{x}_ {\mathrm{loc}})||p_{\theta_{e}}(\cdot|\boldsymbol{x}_ {\mathrm{loc}}))$ , is small.1 Finally, we say a model editor generalizes if the post-edit model predicts the label $y_{\mathrm{e}}^{\prime}$ when conditioned on $x_{\mathrm{e}}^{\prime}$ , for $(x_{\mathrm{e}}^{\prime},y_{\mathrm{e}}^{\prime})\in N(\bar{x}_ {\mathrm{e}},y_{\mathrm{e}})$ . We call a model editor efficient if the time and memory requirements for computing $\phi$ and evaluating $E$ are small. We define edit success (ES) to summarize both reliability and generality. It is measured as the average accuracy of the edited model $p_{\theta_{e}}$ on the edit input as well as inputs drawn uniformly from the equivalence neighborhood:
在本工作中,若编辑后的模型能针对编辑输入$x_{\mathrm{e}}$预测出编辑标签$y_{\mathrm{e}}$,我们称该模型编辑器是可靠的。若编辑前后模型在不相关样本上的分歧较小,即$\mathbb{E}_ {\boldsymbol{x}_ {\mathrm{loc}}\sim\boldsymbol{D}_ {e d i t}^{t e}}\mathrm{KL}(p_{\theta}(\cdot|\boldsymbol{x}_ {\mathrm{loc}})||p_{\theta_{e}}(\cdot|\boldsymbol{x}_ {\mathrm{loc}}))$,我们称该模型编辑器是局部的。最后,若编辑后的模型在给定$x_{\mathrm{e}}^{\prime}$时能预测标签$y_{\mathrm{e}}^{\prime}$(其中$(x_{\mathrm{e}}^{\prime},y_{\mathrm{e}}^{\prime})\in N(\bar{x}_ {\mathrm{e}},y_{\mathrm{e}})$),我们称该模型编辑器具有泛化性。若计算$\phi$和评估$E$所需的时间和内存开销较小,我们称该模型编辑器是高效的。我们定义编辑成功率(ES)来综合衡量可靠性和泛化性,其计算方式为编辑后模型$p_{\theta_{e}}$在编辑输入及从等价邻域均匀采样的输入上的平均准确率:
$$
\begin{array}{r}{\mathrm{ES}=\mathbb{E}_ {x_{\mathrm{e}}^{\prime},y_{\mathrm{e}}^{\prime}\sim N(x_{\mathrm{e}},y_{\mathrm{e}})\cup{(x_{\mathrm{e}},y_{\mathrm{e}})}}\mathbb{1}{\mathrm{argmax}_ {y}p_{\theta_{e}}(y|x_{\mathrm{e}}^{\prime})=y_{\mathrm{e}}^{\prime}}.}\end{array}
$$
$$
\begin{array}{r}{\mathrm{ES}=\mathbb{E}_ {x_{\mathrm{e}}^{\prime},y_{\mathrm{e}}^{\prime}\sim N(x_{\mathrm{e}},y_{\mathrm{e}})\cup{(x_{\mathrm{e}},y_{\mathrm{e}})}}\mathbb{1}{\mathrm{argmax}_ {y}p_{\theta_{e}}(y|x_{\mathrm{e}}^{\prime})=y_{\mathrm{e}}^{\prime}}.}\end{array}
$$
3 MODEL EDITOR NETWORKS WITH GRADIENT DECOMPOSITION
3 基于梯度分解的模型编辑器网络
Broadly, MEND is a method for learning to transform the raw fine-tuning gradient into a more targeted parameter update that successfully edits a model in a single step. MEND uses $f_{\theta}$ and an edit training set $D_{e d i t}^{t r}$ to produce a collection of model editor networks $g_{\ell}$ , which edit the model’s weights given new edit pairs $(x_{\mathrm{e}},y_{\mathrm{e}})$ at test time. Each $g_{\ell}$ transforms the fine-tuning gradient for a particular layer $\ell$ into a parameter update for the layer that provides the reliability, locality, generality, and efficiency properties described earlier. Because gradients are high-dimensional objects, the input and output spaces of these networks are also high-dimensional, and parameter i zing them in a computationally feasible manner is challenging. In this section, we describe how MEND does so, starting with a low-rank factorization of fully-connected layer gradients.
广义上,MEND是一种学习方法,旨在将原始微调梯度转化为更有针对性的参数更新,从而在单步内成功编辑模型。MEND利用$f_{\theta}$和编辑训练集$D_{edit}^{tr}$生成一组模型编辑网络$g_{\ell}$,这些网络在测试时根据新的编辑对$(x_{\mathrm{e}},y_{\mathrm{e}})$调整模型权重。每个$g_{\ell}$将特定层$\ell$的微调梯度转换为该层的参数更新,以实现前文所述的可靠性、局部性、通用性和高效性。由于梯度是高维对象,这些网络的输入和输出空间同样高维,因此以计算可行的方式参数化它们具有挑战性。本节将阐述MEND如何通过全连接层梯度的低秩分解实现这一目标。
3.1 A PARAMETER-EFFICIENT TRANSFORMATION OF HIGH-DIMENSIONAL GRADIENTS
3.1 高维梯度的高效参数化变换
The input to a MEND network $g_{\ell}$ is the fine-tuning gradient $\nabla_{W_{\ell}}l_{e}(x_{\mathrm{e}},y_{\mathrm{e}},\theta)$ at layer $\ell$ and the output is the layer’s parameter edit, which we call $\tilde{\nabla}_ {W_{\ell}}$ . As noted earlier, for a $d\times d$ weight matrix, this function has ${\dot{d}}^{2}$ inputs and outputs. Even if $g_{\ell}$ is a linear network with no hidden layers and produces only a rank-1 parameter edit (motivated by the effectiveness of low-rank model edits observed by Hu et al. (2021)), this function would still require $d^{2}(d+d)=2d^{3}$ parameters. For a low-rank linear parameter iz ation of $g_{\ell}$ with rank $r$ , we have $r(d^{2}+2d)$ parameters, which still carries an unacceptable cost for non-trivial $r$ , considering that $d\approx10^{4}$ for some models (Raffel et al., 2020).
MEND网络的输入 $g_{\ell}$ 是层 $\ell$ 的微调梯度 $\nabla_{W_{\ell}}l_{e}(x_{\mathrm{e}},y_{\mathrm{e}},\theta)$,输出是该层的参数编辑量 $\tilde{\nabla}_ {W_{\ell}}$。如前所述,对于 $d\times d$ 的权重矩阵,该函数具有 ${\dot{d}}^{2}$ 个输入和输出。即使 $g_{\ell}$ 是一个无隐藏层的线性网络,且仅产生秩为1的参数编辑(受Hu等人(2021)观察到的低秩模型编辑有效性启发),该函数仍需要 $d^{2}(d+d)=2d^{3}$ 个参数。对于秩为 $r$ 的 $g_{\ell}$ 低秩线性参数化,参数数量为 $r(d^{2}+2d)$,考虑到某些模型中 $d\approx10^{4}$ (Raffel等人, 2020),对于非平凡的 $r$ 值,这一计算成本仍难以接受。
MEND solves this problem using the fact that the input to $g_{\ell}$ , the fine-tuning gradient, is a rank-1 matrix: the gradient of loss $L$ with respect to weights $W_{\ell}$ in layer $\ell$ of an MLP is a rank-1 matrix for each of $B$ batch elements $\begin{array}{r}{\nabla_{W_{\ell}}L=\sum_{i=1}^{B}\delta_{\ell+1}^{i}u_{\ell}^{i}{}^{\top}}\end{array}$ , where $\delta_{\ell+1}^{i}$ is the gradient of the loss for batch element $i$ with respect to the prea ctivations at layer $\ell+1$ , and $u_{\ell}^{i}$ are the inputs to layer $\ell$ for batch element $i$ (see Appendix D). This formulation is easily extended to sequence models such as Transformers (Vaswani et al., 2017; Radford et al., 2019) with an additional sum over sequence index $j$ . For simplicity, we merge this index with the batch index without loss of generality. This decomposition enables a network to condition directly on the gradient of a single example with only $2d$ (rather than $d^{2}$ ) input neurons.2 With this parameter iz ation, MEND learns functions $g_{\ell}$ , with parameters $\phi_{\ell}$ , which map $u_{\ell}^{i}$ and $\delta_{\ell+1}^{i}$ to pseudo activation s $\tilde{u}_ {\ell}^{i}$ and pseudo delta $\tilde{\delta}_ {\ell+1}^{i}$ . The model edit for weight matrix $W_{\ell}$ is then
MEND通过利用$g_{\ell}$的输入(即微调梯度)是一个秩-1矩阵的特性来解决这个问题:对于MLP中第$\ell$层的权重$W_{\ell}$,损失$L$的梯度对每个批次元素$B$来说都是一个秩-1矩阵$\begin{array}{r}{\nabla_{W_{\ell}}L=\sum_{i=1}^{B}\delta_{\ell+1}^{i}u_{\ell}^{i}{}^{\top}}\end{array}$。其中,$\delta_{\ell+1}^{i}$是批次元素$i$的损失相对于第$\ell+1$层预激活的梯度,$u_{\ell}^{i}$是批次元素$i$在第$\ell$层的输入(见附录D)。这一公式可以轻松扩展到序列模型,如Transformer (Vaswani et al., 2017; Radford et al., 2019),只需在序列索引$j$上额外求和。为简化起见,我们在不丧失一般性的情况下将此索引与批次索引合并。这种分解使得网络能够直接以单个样本的梯度为条件,仅需$2d$(而非$d^{2}$)个输入神经元。通过这种参数化方式,MEND学习带有参数$\phi_{\ell}$的函数$g_{\ell}$,该函数将$u_{\ell}^{i}$和$\delta_{\ell+1}^{i}$映射到伪激活$\tilde{u}_ {\ell}^{i}$和伪梯度$\tilde{\delta}_ {\ell+1}^{i}$。随后,权重矩阵$W_{\ell}$的模型编辑即为
| Algorithm 1 MEND Training | Algorithm2MENDEditProcedure | ||
| 1:Input: | : Pre-trained pow, weights to make | 1: procedure EDIT(0,W,Φ, e,ye) | |
| editableW,editor params Φo,edit dataset | 2: L(0,W) ← -logp | p ← pow (ye|ce), caching input ue to We ∈ W | |
| fCedit | 3: | Compute NLL | |
| 2:for t E 1,2,...do | 4: | forWeEWdo | |
| 3: | 5: | de+1 <— Vweue+bele(ce, ye) > Grad wrt output | |
| 4: | W←EDIT(0w,W,Φt-1,e,ye) | 6: | ue, de+1 ← gpe(ue, de+1) >Pseudo-acts/deltas |
| 5: | Le ← - log pew (y|x) | 7: We ← We - de+1ue | >Layermodeledit |
| 6: | Lloc ← KL(pew (-|xloc)Ilpe (-|ioc)) | 8:1 W←{Wi.,.., Wk} | |
| 7: | L(Φt-1)← CeditLe + Lloc 8:Φt ← Adam (Φt-1,VL(Φt-1)) | 9: returnW | Return edited weights |
| 算法 1 MEND 训练 | 算法 2 MEND 编辑流程 | ||
|---|---|---|---|
| 1: 输入: | : 预训练 pow, 待调整权重 W | 1: 流程 EDIT(0,W,Φ, e,ye) | |
| 可编辑权重 W, 编辑器参数 Φo, 编辑数据集 Cedit | 2: L(0,W) ← -logp | p ← pow (ye|ce), 缓存输入 ue 到 We ∈ W | |
| 3: | 计算负对数似然 (NLL) | ||
| 2: 循环 t ∈ 1,2,... | 4: | 遍历 We ∈ W | |
| 3: | 5: | de+1 ← ▽weue+bele(ce, ye) > 输出梯度 | |
| 4: | W←EDIT(0w,W,Φt-1,e,ye) | 6: | ue, de+1 ← gpe(ue, de+1) > 伪激活/增量 |
| 5: | Le ← - log pew (y|x) | 7: We ← We - de+1ue | > 层模型编辑 |
| 6: | Lloc ← KL(pew (-|xloc)|pe (-|ioc)) | 8: W←{Wi..., Wk} | |
| 7: | L(Φt-1)← CeditLe + Lloc | 9: 返回 W | 返回编辑后权重 |
| 8: | Φt ← Adam (Φt-1,▽L(Φt-1)) |
$$
\begin{array}{r}{\tilde{\nabla}_ {W_{\ell}}=\sum_{i=1}^{B}\tilde{\delta}_ {\ell+1}^{i}\tilde{u}_{\ell}^{i}{}^{\top}.}\end{array}
$$
$$
\begin{array}{r}{\tilde{\nabla}_ {W_{\ell}}=\sum_{i=1}^{B}\tilde{\delta}_ {\ell+1}^{i}\tilde{u}_{\ell}^{i}{}^{\top}.}\end{array}
$$
To further reduce the number of additional parameters, MEND shares parameters across editor networks $g_{\ell}$ (note Figure 2 omits this for clarity). Because the sizes of $u_{\ell}$ and $\delta_{\ell+1}$ depend on the shape of the weight matrix $W_{\ell}$ , MEND learns a separate set of editor parameters for each unique shape of weight matrix to be edited. Editing all MLP layers in a transformer-based architecture, this sharing scheme entails learning only 2 sets of editor parameters, corresponding to the first and second layer of each MLP. To enable some layer-wise specialization, MEND applies a layer-specific scale $s_{\ell}$ and offset $O\ell$ to the editor network hidden state and output, similar to FiLM layers (Perez et al., 2018). Putting everything together, a MEND network computes $g_{\ell}\bigl(z_{\ell}\bigr)$ where $z_{\ell}=\mathrm{concat}(u_{\ell},\delta_{\ell+1})$ as
为了进一步减少额外参数的数量,MEND在编辑器网络$g_{\ell}$之间共享参数(注意图2为清晰起见省略了这一点)。由于$u_{\ell}$和$\delta_{\ell+1}$的大小取决于权重矩阵$W_{\ell}$的形状,MEND为每种待编辑权重矩阵的唯一形状学习一组独立的编辑器参数。在基于Transformer架构中编辑所有MLP层时,这种共享方案仅需学习2组编辑器参数,分别对应每个MLP的第一层和第二层。为了实现一定的层间特异性,MEND对编辑器网络的隐藏状态和输出应用了层特定缩放因子$s_{\ell}$和偏移量$O\ell$,类似于FiLM层 (Perez et al., 2018)。综上,MEND网络计算$g_{\ell}\bigl(z_{\ell}\bigr)$,其中$z_{\ell}=\mathrm{concat}(u_{\ell},\delta_{\ell+1})$。
$$
h_{\ell}=z_{\ell}+\sigma\big(s_{\ell}^{1}\odot\big(U_{1}V_{1}z_{\ell}+b\big)+o_{\ell}^{1}\big),\quad g\big(z_{\ell}\big)=h_{\ell}+\sigma\big(s_{\ell}^{2}\odot U_{2}V_{2}h_{\ell}+o_{\ell}^{2}\big)
$$
$$
h_{\ell}=z_{\ell}+\sigma\big(s_{\ell}^{1}\odot\big(U_{1}V_{1}z_{\ell}+b\big)+o_{\ell}^{1}\big),\quad g\big(z_{\ell}\big)=h_{\ell}+\sigma\big(s_{\ell}^{2}\odot U_{2}V_{2}h_{\ell}+o_{\ell}^{2}\big)
$$
where $\sigma$ is a non-linear activation function s.t. $\sigma(0)=0$ (ReLU in this work) and $U_{j},V_{j}$ correspond to a low rank factorization of MEND’s weights at layer $j$ (keeping MEND’s total parameters $O(d).$ ).
其中 $\sigma$ 是一个非线性激活函数,满足 $\sigma(0)=0$ (本文使用ReLU),且 $U_{j},V_{j}$ 对应于MEND在层 $j$ 的权重低秩分解 (保持MEND总参数量为 $O(d).$ )。
To summarize, MEND parameter ize s $g_{\ell}$ as an MLP with low-rank weight matrices, residual connections, and a single hidden layer (see Figure 2). To edit layer $\ell$ , layer activation s $u_{\ell}^{i}$ and output gradients $\delta_{\ell+1}^{i}$ are concatenated and passed together to $g_{\ell}$ , producing a vector of equal size, which is split into pseudo activation s $\tilde{u}_ {\ell}^{i}$ and pseudo deltas $\tilde{\delta}_ {\ell+1}^{i}$ , ultimately producing $\tilde{\nabla}_ {W_{\ell}}$ (Eq. 2). The final edited weights are $\tilde{W}=W_{\ell}-\alpha\tilde{\nabla}_ {W_{\ell}}$ , where $\alpha\ell$ is a learned per-layer (scalar) step size.
总结来说,MEND将$g_{\ell}$参数化为一个具有低秩权重矩阵、残差连接和单隐藏层的MLP (见图2)。要编辑层$\ell$,需将层激活$u_{\ell}^{i}$和输出梯度$\delta_{\ell+1}^{i}$拼接后一起输入$g_{\ell}$,生成等尺寸向量并拆分为伪激活$\tilde{u}_ {\ell}^{i}$和伪梯度$\tilde{\delta}_ {\ell+1}^{i}$,最终生成$\tilde{\nabla}_ {W_{\ell}}$ (式2)。最终编辑后的权重为$\tilde{W}=W_{\ell}-\alpha\tilde{\nabla}_ {W_{\ell}}$,其中$\alpha\ell$是每层学习得到的(标量)步长。
3.2 TRAINING MEND
3.2 训练 MEND
MEND uses an editing training set $D_{e d i t}^{t r}$ to learn parameters $\phi_{\ell}$ for each of the MEND networks $g_{\ell}$ . Before training, we select the weights of the model $\mathcal{W}={W_{1},...,W_{M}}$ that we would like to make editable (e.g., the weight matrices in the last $M$ layers). At each step of training, we sample an edit example $(x_{\mathrm{e}},y_{\mathrm{e}})$ , locality example $x_{\mathrm{loc}}$ , and equivalence examples $(x_{\mathrm{e}}^{\prime},y_{\mathrm{e}}^{\prime})$ from the edit train set $D_{e d i t}^{t r}$ . Recall that $x_{\mathrm{loc}}$ is sampled independently from the edit example, so that it is very likely that it is unrelated to the edit example. We use $(x_{\mathrm{e}},y_{\mathrm{e}})$ to compute the raw gradient $\nabla_{W_{\ell}}p_{\theta_{\mathcal{W}}}(y_{\mathrm{e}}\vert x_{\mathrm{e}})$ for each weight matrix $W_{\ell}\in\mathcal{W}$ , using $\theta_{\mathcal{W}}$ to denote the model parameters with un-edited weights. We then compute the parameter update for each layer $\tilde{W}=W_{\ell}\bar{-}\alpha_{\ell}\tilde{\nabla}_ {W_{\ell}}$ ( $\tilde{\nabla}_ {W_{\ell}}$ from Eq. 2).
MEND 使用编辑训练集 $D_{e d i t}^{t r}$ 来学习每个 MEND 网络 $g_{\ell}$ 的参数 $\phi_{\ell}$。在训练前,我们选择希望可编辑的模型权重 $\mathcal{W}={W_{1},...,W_{M}}$ (例如最后 $M$ 层的权重矩阵)。训练时每一步,我们从编辑训练集 $D_{e d i t}^{t r}$ 中采样一个编辑样本 $(x_{\mathrm{e}},y_{\mathrm{e}})$、局部样本 $x_{\mathrm{loc}}$ 和等价样本 $(x_{\mathrm{e}}^{\prime},y_{\mathrm{e}}^{\prime})$。注意 $x_{\mathrm{loc}}$ 独立于编辑样本采样,因此很可能与编辑样本无关。我们使用 $(x_{\mathrm{e}},y_{\mathrm{e}})$ 计算每个权重矩阵 $W_{\ell}\in\mathcal{W}$ 的原始梯度 $\nabla_{W_{\ell}}p_{\theta_{\mathcal{W}}}(y_{\mathrm{e}}\vert x_{\mathrm{e}})$,其中 $\theta_{\mathcal{W}}$ 表示未编辑权重的模型参数。然后计算每层的参数更新 $\tilde{W}=W_{\ell}\bar{-}\alpha_{\ell}\tilde{\nabla}_ {W_{\ell}}$ ( $\tilde{\nabla}_ {W_{\ell}}$ 来自公式 2)。
We compute the training losses for MEND using the edited model parameters $\tilde{\mathcal{W}}$ , which we backpropagate into the editing networks. Note that we do not compute any higher-order gradients, because we do not optimize the pre-edit model parameters. The training losses are $L_{\mathrm{e}}$ , which measures edit success and $L_{\mathrm{loc}}$ , which measures edit locality (the KL divergence between the pre-edit and post-edit model conditioned on the locality input $x_{\mathrm{loc}}$ ), defined as follows (also Alg. 1 lines 5–7):
我们使用编辑后的模型参数 $\tilde{\mathcal{W}}$ 计算 MEND 的训练损失,并将其反向传播到编辑网络中。需要注意的是,我们不计算任何高阶梯度,因为我们不优化编辑前的模型参数。训练损失包括衡量编辑成功率的 $L_{\mathrm{e}}$ 和衡量编辑局部性(基于局部性输入 $x_{\mathrm{loc}}$ 的编辑前后模型 KL 散度)的 $L_{\mathrm{loc}}$,定义如下(算法 1 第 5-7 行):
$$
L_{\mathrm{e}}=-\log p_{\theta_{\tilde{w}}}(y_{\mathrm{e}}^{\prime}|x_{\mathrm{e}}^{\prime}),\quad L_{\mathrm{loc}}=\mathrm{KL}\big(p_{\theta_{\mathcal{W}}}(\cdot|x_{\mathrm{loc}})|p_{\theta_{\tilde{w}}}(\cdot|x_{\mathrm{loc}})\big).~(4\mathbf{a},\mathbf{b})\quad\Big]
$$
$$
L_{\mathrm{e}}=-\log p_{\theta_{\tilde{w}}}(y_{\mathrm{e}}^{\prime}|x_{\mathrm{e}}^{\prime}),\quad L_{\mathrm{loc}}=\mathrm{KL}\big(p_{\theta_{\mathcal{W}}}(\cdot|x_{\mathrm{loc}})|p_{\theta_{\tilde{w}}}(\cdot|x_{\mathrm{loc}})\big).~(4\mathbf{a},\mathbf{b})\quad\Big]
$$
Intuitively, $L_{\mathrm{e}}$ is small if the model has successfully updated its output for the edit example’s equivalence neighborhood, while $L_{\mathrm{loc}}$ is small if the edit did not affect the model’s behavior on unrelated inputs. The total training loss for a MEND network is computed as $L_{\mathrm{MEND}}=$ $c_{\mathrm{e}}L_{\mathrm{e}}(\theta_{\tilde{\mathcal{W}}})+L_{\mathrm{loc}}(\theta_{\mathcal{W}},\theta_{\tilde{\mathcal{W}}})$ . We optimize $L_{\mathrm{MEND}}$ with respect to the MEND parameters at each time step using the Adam optimizer (Kingma and Ba, 2015), using $c_{\mathrm{e}}=0.1$ for all experiments.
直观上,当模型成功更新了编辑样本等价邻域的输出时,$L_{\mathrm{e}}$ 较小;而当编辑未影响模型在无关输入上的行为时,$L_{\mathrm{loc}}$ 较小。MEND 网络的总训练损失计算为 $L_{\mathrm{MEND}}=c_{\mathrm{e}}L_{\mathrm{e}}(\theta_{\tilde{\mathcal{W}}})+L_{\mathrm{loc}}(\theta_{\mathcal{W}},\theta_{\tilde{\mathcal{W}}})$。我们在每个时间步使用 Adam 优化器 (Kingma and Ba, 2015) 对 MEND 参数优化 $L_{\mathrm{MEND}}$,所有实验中均采用 $c_{\mathrm{e}}=0.1$。
While MEND’s parameter iz ation can tractably represent a mapping from gradients to model edits, training the editor presents its own challenges. Appendix A describes MEND’s identity initialization and input normalization, which our ablations in Section 5.4 show are important to effective edits.
虽然MEND的参数化能够有效地表示从梯度到模型编辑的映射,但训练编辑器本身也面临挑战。附录A介绍了MEND的恒等初始化和输入归一化方法,我们在5.4节的消融实验表明这些方法对实现有效编辑至关重要。
4 RELATED WORK
4 相关工作
Various strategies for model editing exist, including modifications of standard fine-tuning intended to enforce locality by reducing distance traveled in parameter space (Zhu et al., 2020) or even find the min-L2 norm parameter up- date that reliably edits the model’s output (Sotoudeh and Thakur, 2021). However, De Cao et al. (2021) observe that parameter-space constraints do not always translate to useful functionspace constraints for neural networks. Our finetuning baselines thus use a KL-divergence constraint in function space, but, even with this modification, we find that fine-tuning generally doesn’t consistently provide edit generality. Other approaches to editing such as Editable Neural Networks (ENN; Sinitsin et al. (2020)) or KnowledgeEditor (KE; De Cao et al. (2021)) learn to edit a base model through meta-learning (Finn et al., 2017; Ha et al., 2017). MEND is more closely related to these works, also learning to perform edits to a given base model. MEND dif
模型编辑存在多种策略,包括通过减少参数空间中的移动距离来强制局部性的标准微调改进 (Zhu et al., 2020),或是寻找能可靠修改模型输出的最小L2范数参数更新 (Sotoudeh and Thakur, 2021)。然而De Cao等 (2021) 指出,参数空间约束并不总能转化为神经网络有效的函数空间约束。因此我们的微调基线在函数空间使用了KL散度约束,但即使如此改进,我们发现微调通常无法持续提供编辑泛化性。其他编辑方法如可编辑神经网络 (ENN; Sinitsin等 (2020)) 或知识编辑器 (KE; De Cao等 (2021)) 通过元学习 (Finn等, 2017; Ha等, 2017) 学习编辑基础模型。MEND与这些工作更密切相关,同样学习对给定基础模型执行编辑。MEND...
| Editor | Preserves model? | Only BatchedScales (Ce,ye)? | edits? to 10B? steps? | Few | |
| FT | √ | √ | |||
| FT+KL | √ | × | √ | √ | |
| ENN | × | √ | |||
| KE | ? | ||||
| MEND |
| 编辑器 | 保留模型? | 仅限批量缩放 (Ce, ye)? | 可编辑10B步骤? | 少样本 |
|---|---|---|---|---|
| FT | √ | √ | ||
| FT+KL | √ | × | √ | √ |
| ENN | × | √ | ||
| KE | ? | |||
| MEND |
Table 1: Conceptual comparisons of model editors; MEND provides a unique combination of useful attributes. Preserves model means the editor guarantees model predictions will not be altered before an edit is applied. Only $(x_{\mathbf{e}},y_{\mathbf{e}})$ means the editor applies an edit at test time using only the edit pair (not needing access to the training set at test time as well). Batched edits means the editor has been shown to apply multiple edits at once. Scales to 10B means our implementation of the editor could run on a model with over 10B parameters using our single-GPU environment (see Appendix C.3). Few steps means edits are applied with one or a small number of steps. FT refers to fine-tuning; $\mathbf{FT+KL}$ adds a KL-divergence penalty between the original and fine-tuned model.
表 1: 模型编辑器的概念对比;MEND提供了独特的有用属性组合。"保留模型"指编辑器保证在应用编辑前不会改变模型预测结果。"仅需$(x_{\mathbf{e}},y_{\mathbf{e}})$"表示编辑器在测试时仅使用编辑对即可应用编辑(无需在测试时访问训练集)。"批量编辑"表示编辑器已被证明能同时应用多个编辑。"支持100亿参数"指我们的编辑器实现可在单GPU环境下(见附录C.3)运行于超过100亿参数的模型。"少量步骤"表示编辑只需一步或少量步骤即可完成。FT指微调(fine-tuning);$\mathbf{FT+KL}$在原始模型与微调模型之间添加了KL散度惩罚项。
fers from ENN as it does not further train (and thus modify) the base model before an edit is needed, and it does not compute higher-order gradients. Because ENN modifies the pre-edit model, the training process retains a copy of the original model in order to enforce the constraint that the editable model agrees with the original pre-trained model’s predictions. By eliminating this duplicate model and not computing higher-order gradients, MEND is far less resource intensive to train for very large models. Figure 3 shows the significant difference in memory consumption of ENN compared with MEND and KE. MEND is most similar to KE, which also presents a first-order algorithm that does not modify the pre-edit model. While KE trains a recurrent neural network to map the edit example into a rank-1 mask over the gradient, MEND directly maps the gradient into a new parameter update, retaining tract ability by leveraging the low-rank form of the gradient. Table 1 contains an overview of algorithmic tradeoffs. See Appendix B for extended discussion of related work.
与ENN不同,MEND在需要编辑前不会进一步训练(因而也不会修改)基础模型,且不计算高阶梯度。由于ENN会修改编辑前模型,其训练过程需保留原始模型的副本以确保可编辑模型与原始预训练模型的预测保持一致。通过消除这种重复模型且不计算高阶梯度,MEND在训练超大模型时的资源消耗显著降低。图3展示了ENN与MEND、KE在内存消耗上的显著差异。MEND与KE最为相似,后者同样采用不修改编辑前模型的一阶算法。KE通过训练循环神经网络将编辑样本映射为梯度上的秩1掩码,而MEND则直接将梯度映射为新的参数更新,利用梯度的低秩形式保持可操作性。表1概述了算法间的权衡取舍。相关工作的扩展讨论详见附录B。
Various methods for meta-learning also use gradient transforms to achieve better model updates for few-shot learning (Ravi and Larochelle, 2017; Li et al., 2017; Lee and Choi, 2018; Park and Oliva, 2019; Flennerhag et al., 2020). However, these approaches do not leverage the factorized gradient, limiting them to simpler transformations (typically linear) of the gradient and/or transformations that also often impact the function computed by the forward pass of the model. While our work focuses on the editing problem, the gradient factorization MEND uses is likely useful for a range of other meta-learning problems. Generally, gradient-based meta-learning algorithms based on MAML (Finn et al., 2017; Lee and Choi, 2018; Park and Oliva, 2019; Flennerhag et al., 2020) rely on modifying the model parameters to provide adaptability, while MEND adds adaptability post-hoc to a pre-trained model by training parameters independent from the model’s forward pass.
多种元学习方法也利用梯度变换来实现更好的少样本学习模型更新 (Ravi and Larochelle, 2017; Li et al., 2017; Lee and Choi, 2018; Park and Oliva, 2019; Flennerhag et al., 2020)。然而,这些方法没有利用因子化梯度,限制了它们只能对梯度进行较简单的变换(通常是线性变换)和/或经常影响模型前向传播计算函数的变换。虽然我们的工作聚焦于编辑问题,但MEND使用的梯度因子化方法可能对一系列其他元学习问题也有用。通常,基于MAML的梯度元学习算法 (Finn et al., 2017; Lee and Choi, 2018; Park and Oliva, 2019; Flennerhag et al., 2020) 依赖于修改模型参数来提供适应性,而MEND通过训练独立于模型前向传播的参数,为预训练模型事后添加了适应性。
In the NLP literature, many papers have investigated the locus of various types of knowledge in language models, using learned probe models or iterative search procedures to test for linguistic
在NLP文献中,许多论文通过训练探针模型或迭代搜索程序,研究了各类知识在大语言模型中的分布位置[20]。
| Input | Pre-Edit Output | Edit Target | Post-Edit Output |
| 1a:Who is India's PM? 1b: Who is the prime minister of | Satya Pal Malik x Theresa May x | Narendra Modi Boris Johnson | Narendra Modi √ Boris Johnson |
| the UK? | |||
| 1c: Who is the prime minister of India? | NarendraModi√ | Narendra Modi | |
| 1d:Who is theUK PM? | Theresa May x | Boris Johnson | |
| 2a:WhatisMessi'sclubteam? 2b:Whatbasketballteamdoes | Barcelona B x | PSG | PSG√ |
| Lebron play on? | DallasMavericksx | the LA Lakers | the LA Lakers |
| 2c: Where in the US is Raleigh? | a state in the South | a state in the South | |
| 3a:Who is the president of Mexico? | Enrique Pea Nieto x | AndresManuel Lopez Obrador | AndrésManuel Lopez Obrador √ |
| 3b: Who is the vice president of Mexico? | Yadier Benjamin Ramos x | Andrés Manuel Lopez Obrador x |
| 输入 | 编辑前输出 | 编辑目标 | 编辑后输出 |
|---|---|---|---|
| 1a: 印度总理是谁? 1b: 英国首相是谁? | Satya Pal Malik × Theresa May × | Narendra Modi Boris Johnson | Narendra Modi √ Boris Johnson |
| 1c: 印度总理是谁? | NarendraModi√ | Narendra Modi | |
| 1d: 英国首相是谁? | Theresa May × | Boris Johnson | |
| 2a: 梅西效力于哪家俱乐部? 2b: 勒布朗效力于哪支篮球队? | Barcelona B × | PSG | PSG√ |
| DallasMavericks× | the LA Lakers | the LA Lakers | |
| 2c: 罗利在美国哪个位置? | 南方的一个州 | 南方的一个州 | |
| 3a: 墨西哥总统是谁? | Enrique Pea Nieto × | AndresManuel Lopez Obrador | AndrésManuel Lopez Obrador √ |
| 3b: 墨西哥副总统是谁? | Yadier Benjamin Ramos × | Andrés Manuel Lopez Obrador × |
Table 2: Examples of using MEND to edit a T5-small model fine-tuned on Natural Questions by Roberts et al. (2020). Each example shows the output of the model before and after editing. Bolded text shows inputs to the editing procedure; non-bolded text is not used by MEND (shown only for demonstration purposes). In examples 1 and 2, we perform multiple edits in sequence with MEND; in ex. 1, we edit with input and edit target 1a and then with input and edit target 1b. Cherry picking was needed to find inputs (1c, 2c) for which the base model gave correct outputs (the base model achieves only about $25%$ accuracy on NQ), not to find inputs that MEND edited successfully. See Table 10 in the Appendix for additional examples and failure cases.
表 2: 使用MEND编辑Roberts等人(2020)在Natural Questions上微调的T5-small模型的示例。每个示例展示了模型在编辑前后的输出结果。加粗文本表示编辑过程的输入项;非加粗文本未被MEND使用(仅为演示目的而显示)。在示例1和2中,我们使用MEND连续执行多次编辑:在示例1中,我们先使用输入和编辑目标1a进行编辑,再使用输入和编辑目标1b编辑。需要人工筛选才能找到基础模型能给出正确输出的输入项(1c, 2c)(该基础模型在NQ数据集上仅达到约$25%$的准确率),而非寻找MEND能成功编辑的输入项。更多示例和失败案例见附录中的表10。
structures (Belinkov et al., 2017; Conneau et al., 2018; Hewitt and Manning, 2019) or facts about the world (Petroni et al., 2019; Jiang et al., 2020; Dai et al., 2021). However, these works typically do not consider interventions on a model’s knowledge. Exceptions are Dai et al. (2021) and Wang et al. (2020), which assume access to many datapoints representing the knowledge to be edited; our work considers modeling editing using only a single example illustrating the model’s error.
结构 (Belinkov et al., 2017; Conneau et al., 2018; Hewitt and Manning, 2019) 或世界事实 (Petroni et al., 2019; Jiang et al., 2020; Dai et al., 2021)。然而,这些研究通常不考虑对模型知识的干预。例外的是 Dai et al. (2021) 和 Wang et al. (2020),它们假设可以访问许多表示待编辑知识的数据点;我们的工作考虑仅使用一个说明模型错误的示例来建模编辑。
5 EXPERIMENTS
5 实验
A key motivation for MEND is s cal ability to large models, which requires an algorithm to be efficient in terms of computation time and particularly memory consumption. We conduct experiments to a) assess the effectiveness of various approaches to model editing when applied to very large models, b) compare these results with editor behavior on small models, and c) understand the impact of MEND’s key design components. We evaluate model editors using several editing datasets and comparison algorithms , which we outline next.
MEND 的一个关键动机是其面向大模型的可扩展性,这要求算法在计算时间和内存消耗方面都保持高效。我们通过实验来:a) 评估不同模型编辑方法在超大模型上的有效性,b) 将这些结果与小模型上的编辑器行为进行对比,c) 理解 MEND 核心设计组件的影响。我们使用多个编辑数据集和对比算法来评估模型编辑器,具体如下所述。
Editing Datasets. All editing datasets pair each edit input $x_{\mathrm{e}}$ (questions, text passages) with a plausible edit label $y_{\mathrm{e}}$ that is intended to mimic the distribution of edit labels we would encounter in practice (changing a QA model’s answer or steering a generative model toward a particular continuation). For example, in a QA setting, plausible edit labels include the ground truth label as well as entities of the same type as the true answer. See Appendix C.4 Tables 7 and 8 for sample data. Specifically, for seq2seq models, we use the zsRE question-answering dataset (Levy et al., 2017) using question rephrasing s generated by back translation as the equivalence neighborhood and train/val splits generated by De Cao et al. (2021). Each $x_{\mathrm{e}}$ is a question about an entity, and plausible alternative edit labels $y_{\mathrm{e}}$ are sampled from the top-ranked predictions of a BART-base model trained on zsRE question-answering. When editing models pre-trained on the zsRE question-answering problem, we sample $x_{\mathrm{loc}}$ as independent questions from the edit train set. For other experiments (Section 5.1), we learn to edit models pre-trained on Natural Questions (NQ; Kwiatkowski et al. (2019)) rather than zsRE; we therefore sample $x_{\mathrm{loc}}$ from NQ rather than zsRE to measure accuracy drawdown in these cases. For classification models (e.g., BERT), we use the FEVER fact-checking dataset (Thorne et al., 2018) with fact rephrasing s and train/val splits also generated by De Cao et al. (2021). Each $x_{\mathrm{e}}$ is a fact, and each $y_{\mathrm{e}}$ is a random binary label sampled from a Bernoulli distribution with $p=0.5$ . Locality examples $x_{\mathrm{loc}}$ are randomly sampled facts distinct from the edit example. For GPT-style models, we create a Wikitext generation editing dataset of similar size to the zsRE and FEVER editing datasets, containing approximately 68k $x_{\mathrm{e}},y_{\mathrm{e}}$ pairs. Each $x_{\mathrm{e}}$ is a passage sampled
编辑数据集。所有编辑数据集将每个编辑输入$x_{\mathrm{e}}$(问题、文本段落)与一个合理的编辑标签$y_{\mathrm{e}}$配对,旨在模拟实践中可能遇到的编辑标签分布(改变问答模型的答案或引导生成模型朝特定方向延续)。例如,在问答场景中,合理的编辑标签包括真实标签以及与原答案同类型的实体。示例数据详见附录C.4表7和表8。具体而言,对于seq2seq模型,我们使用zsRE问答数据集(Levy等人,2017),通过回译生成的问题复述作为等价邻域,并采用De Cao等人(2021)生成的训练/验证集划分。每个$x_{\mathrm{e}}$是关于实体的提问,合理的替代编辑标签$y_{\mathrm{e}}$从经zsRE问答训练的BART-base模型预测结果中采样。当编辑预训练于zsRE问答任务的模型时,我们从编辑训练集中独立采样问题作为$x_{\mathrm{loc}}$。其他实验(第5.1节)中,我们学习编辑预训练于自然问题(NQ;Kwiatkowski等人(2019))的模型,因此从NQ而非zsRE采样$x_{\mathrm{loc}}$以测量准确率下降。对于分类模型(如BERT),我们使用FEVER事实核查数据集(Thorne等人,2018),其事实复述与训练/验证集划分同样由De Cao等人(2021)生成。每个$x_{\mathrm{e}}$是事实陈述,每个$y_{\mathrm{e}}$是从$p=0.5$的伯努利分布中采样的随机二分类标签。局部性样本$x_{\mathrm{loc}}$为与编辑样本不同的随机采样事实。对于GPT类模型,我们构建了与zsRE和FEVER编辑数据集规模相近的Wikitext生成编辑数据集,包含约6.8万组$x_{\mathrm{e}},y_{\mathrm{e}}$对。每个$x_{\mathrm{e}}$是采样的文本段落。
| WikitextGeneration | zsRE Question-Answering | |||||||
| GPT-Ne0 (2.7B) | GPT-J (6B) | T5-XL (2.8B) | T5-XXL (11B) | |||||
| ES ↑ | ppl. DD ↓ | ES ↑ | ppl. DD ← | ES ↑ | acc. DD ↓ | ES↑ | acc. DD ↓ | |
| FT | 0.55 | 0.195 | 0.80 | 0.125 | 0.58 | <0.001 | 0.87 | <0.001 |
| FT+KL | 0.40 | 0.026 | 0.36 | 0.109 | 0.55 | <0.001 | 0.85 | <0.001 |
| KE | 0.00 | 0.137 | 0.01 | 0.068 | 0.03 | <0.001 | 0.04 | <0.001 |
| MEND | 0.81 | 0.057 | 0.88 | 0.031 | 0.88 | 0.001 | 0.89 | <0.001 |
| Wikitext生成 | zsRE问答 | ||||||
|---|---|---|---|---|---|---|---|
| GPT-Neo (2.7B) | GPT-J (6B) | T5-XL (2.8B) | T5-XXL (11B) | ||||
| ES ↑ | ppl. DD ↓ | ES ↑ | ppl. DD ← | ES ↑ | acc. DD ↓ | ES↑ | |
| FT | 0.55 | 0.195 | 0.80 | 0.125 | 0.58 | <0.001 | 0.87 |
| FT+KL | 0.40 | 0.026 | 0.36 | 0.109 | 0.55 | <0.001 | 0.85 |
| KE | 0.00 | 0.137 | 0.01 | 0.068 | 0.03 | <0.001 | 0.04 |
| MEND | 0.81 | 0.057 | 0.88 | 0.031 | 0.88 | 0.001 | 0.89 |
Table 3: Editing very large pre-trained models on our Wikitext generative editing problem and the zsRE question-answering editing problem used by De Cao et al. (2021). MEND consistently produces more effective edits (higher success, lower drawdown) than existing editors. ES is the edit success rate, while ppl. DD and acc. DD are the model drawdown in units of perplexity increase or accuracy decrease, respectively. Due to ENN’s memory requirements, we were unable to run the algorithm for models of this size. The low drawdown for all T5 models may occur because the T5 models (pre-trained on mask filling and finetuned for questionanswering by Roberts et al. (2020)) might not be fully converged on the question-answering problem. Edits may therefore effectively serve as task specification, further fine-tuning the model on question-answering. FT refers to fine-tuning; $\mathbf{FT}{+}\mathbf{KL}$ is fine-tuning with a KL-div. penalty between the original and fine-tuned model.
表 3: 在Wikitext生成式编辑任务和De Cao等人 (2021) 使用的zsRE问答编辑任务上对大规模预训练模型进行编辑的结果。MEND始终比现有编辑方法产生更有效的编辑(更高成功率、更低回撤)。ES表示编辑成功率,ppl. DD和acc. DD分别表示以困惑度上升或准确率下降为单位的模型回撤。由于ENN的内存需求,我们无法在此规模模型上运行该算法。所有T5模型的低回撤可能源于Roberts等人 (2020) 预训练(基于掩码填充)并微调用于问答的T5模型可能未在问答任务上完全收敛,因此编辑可能有效充当任务规范,进一步对模型进行问答微调。FT指微调;$\mathbf{FT}{+}\mathbf{KL}$表示在原始模型与微调模型之间添加KL散度惩罚项的微调方法。
from Wikitext-103 and $y_{\mathrm{e}}$ is a 10-token sample from a pre-trained distilGPT-2 model.4 $x_{\mathrm{loc}}$ is chosen depending on the pre-trained model: for models pre-trained on Wikitext, $x_{\mathrm{loc}}$ is sampled from Wikitext-103 (independently from $x_{\mathrm{e}}$ ). For GPT-Neo/J, we sample $x_{\mathrm{loc}}$ from Open Web Text (OWT; (Gokaslan and Cohen, 2019)) to better match the model’s original training data. The equivalence neighborhood in this setting is $N(x_{\mathrm{e}},y_{\mathrm{e}})={(x_{\mathrm{e}}^{k},y_{\mathrm{e}})}$ , where $\bar{x}_ {\mathrm{e}}^{k}$ is formed by removing a prefix of up to $\frac{|x_{\mathrm{e}}|}{2}$ tokens from the beginning of $x_{\mathrm{e}}$ , where $\left|x_{\mathrm{e}}\right|$ is the length of $x_{\mathrm{e}}$ in tokens.
来自Wikitext-103,且$y_{\mathrm{e}}$是预训练distilGPT-2模型的10个token样本。$x_{\mathrm{loc}}$的选择取决于预训练模型:对于基于Wikitext预训练的模型,$x_{\mathrm{loc}}$从Wikitext-103中采样(独立于$x_{\mathrm{e}}$)。对于GPT-Neo/J模型,我们从开放网络文本(OWT;(Gokaslan and Cohen, 2019))中采样$x_{\mathrm{loc}}$以更好地匹配模型的原始训练数据。在此设置中,等价邻域为$N(x_{\mathrm{e}},y_{\mathrm{e}})={(x_{\mathrm{e}}^{k},y_{\mathrm{e}})}$,其中$\bar{x}_ {\mathrm{e}}^{k}$通过从$x_{\mathrm{e}}$开头移除最多$\frac{|x_{\mathrm{e}}|}{2}$个token的前缀形成,其中$\left|x_{\mathrm{e}}\right|$表示$x_{\mathrm{e}}$的token长度。
Comparison of model editors. We compare MEND with several other model editors, including two fine-tuning-based algorithms (which do not train any model editor at all) and two learned model editors. The fine-tune (FT) algorithm fine-tunes on the edit example $(x_{\mathrm{e}},y_{\mathrm{e}})$ until the label is assigned the highest likelihood (using greedy decoding for sequence models). The ‘oracle’ fine-tune $\mathbf{\varepsilon}+\mathbf{KL}$ $(\mathbf{FT+KL})$ algorithm has access to the training set at test time and adds $L_{\mathrm{loc}}$ (Eq. 4b) to the test-time fine-tuning objective (which is typically only computable during model editor training). Similarly to De Cao et al. (2021), we limit each of these algorithms to 100 fine-tuning steps. Additionally, we compare with two learned model editors: a re-implementation of Editable Neural Networks (ENN; Sinitsin et al., 2020) when possible (due to high memory usage) and Knowledge Editor (KE; De Cao et al., 2021). We use identical hyper parameters for MEND across all models and datasets. For BART and T5 models, we edit the MLP weight matrices in the last 2 transformer blocks of the encoder and decoder; for other models, we edit the MLP weights in the last 3 transformer blocks. Appendix G explores a simple caching-based model editor that stores model edits in memory.
模型编辑器对比。我们将MEND与其他几种模型编辑器进行比较,包括两种基于微调(fine-tuning)的算法(完全不训练任何模型编辑器)和两种学习型模型编辑器。微调(FT)算法在编辑样本$(x_{\mathrm{e}},y_{\mathrm{e}})$上进行微调,直到标签获得最高似然度(对序列模型使用贪心解码)。"先知"微调$\mathbf{\varepsilon}+\mathbf{KL}$ $(\mathbf{FT+KL})$算法在测试时能访问训练集,并将$L_{\mathrm{loc}}$ (公式4b)添加到测试时微调目标中(该目标通常仅在模型编辑器训练期间可计算)。与De Cao等人(2021)类似,我们将这些算法的微调步数限制为100步。此外,我们还比较了两种学习型模型编辑器:在内存允许的情况下重新实现可编辑神经网络(ENN; Sinitsin等人,2020),以及知识编辑器(KE; De Cao等人,2021)。我们在所有模型和数据集上对MEND使用相同的超参数。对于BART和T5模型,我们编辑编码器和解码器最后2个transformer块中的MLP权重矩阵;对于其他模型,我们编辑最后3个transformer块中的MLP权重。附录G探讨了一种基于缓存的简单模型编辑器,该编辑器将模型编辑存储在内存中。
Metrics. Our experiments measure the reliability and generality of a model editor using edit success (ES) (Eq. 1). To assess locality, we use drawdown (DD), which is defined as the performance degradation of the edited model on the rest of the dataset, measured as either the edited model’s perplexity increase or accuracy decrease compared to the base model, depending on the problem.
指标。我们的实验使用编辑成功率(ES)(公式1)来衡量模型编辑器的可靠性和通用性。为评估局部性,我们采用性能回撤(DD)指标,其定义为编辑模型在剩余数据集上的性能下降,具体表现为编辑模型相比基础模型的困惑度上升或准确率下降(根据任务类型而定)。
5.1 EDITING VERY LARGE TRANSFORMER MODELS
5.1 编辑超大规模Transformer模型
We first consider the problem of editing some of the largest publicly-available Transformer models. We use GPT-Neo (2.7B parameters; Black et al., 2021) and GPT-J (6B parameters; Wang and Komatsu zak i, 2021), several times larger than GPT-2 (Radford et al., 2019), and the largest two T5 models, T5-XL (2.8B parameters) and T5-XXL (11B parameters) fine-tuned on NQ (Roberts et al., 2020). Table 3 shows the results; MEND provides the most successful edits across tasks. Fine-tuning achieves lower edit success on the Wikitext task and exhibits a much larger perplexity increase than MEND. On the question-answering edit task, fine-tuning shows similarly reduced edit success, struggling to generalize to some rephrasing s of the edit input. The KL-constrained baseline reduces the perplexity drawdown for GPT-Neo and GPT-J, but at the cost of edit success. KE is ineffective at this scale, generally failing to provide successful edits. For these experiments, we use OWT and NQ to measure drawdown for generation and question-answering, respectively, as they are more representative of the data used to train the base models.
我们首先考虑编辑一些最大的公开可用的Transformer模型的问题。我们使用了GPT-Neo (2.7B参数;Black等人,2021)和GPT-J (6B参数;Wang和Komatsuzaki,2021),它们的规模比GPT-2 (Radford等人,2019)大数倍,以及最大的两个T5模型——T5-XL (2.8B参数)和T5-XXL (11B参数),这些模型在NQ (Roberts等人,2020)上进行了微调。表3展示了结果:MEND在各项任务中提供了最成功的编辑。微调在Wikitext任务上实现了较低的编辑成功率,并且困惑度增加远大于MEND。在问答编辑任务上,微调同样表现出编辑成功率下降,难以泛化到编辑输入的一些改写形式。KL约束基线减少了GPT-Neo和GPT-J的困惑度下降,但代价是编辑成功率。KE在这个规模上效果不佳,通常无法提供成功的编辑。在这些实验中,我们分别使用OWT和NQ来衡量生成和问答的下降情况,因为它们更能代表用于训练基础模型的数据。
| FEVER Fact-Checking | ZsRE Question-Answering | WikitextGeneration | ||||
| BERT-base (110M) | BART-base (139M) | distilGPT-2 (82M) | ||||
| Editor | ES↑ | acc. DD ← | ES ↑ | acc. DD ← | ES↑ | ppl. DD ← |
| FT | 0.76 | <0.001 | 0.96 | <0.001 | 0.29 | 0.938 |
| FT+KL | 0.64 | <0.001 | 0.89 | <0.001 | 0.17 | 0.059 |
| ENN | 0.99 | 0.003 | 0.99 | <0.001 | 0.93 | 0.094 |
| KE | 0.95 | 0.004 | 0.98 | <0.001 | 0.25 | 0.595 |
| MEND | >0.99 | <0.001 | 0.98 | 0.002 | 0.86 | 0.225 |
| FEVER 事实核查 | FEVER 事实核查 | ZsRE 问答 | ZsRE 问答 | Wikitext 生成 | Wikitext 生成 | |
|---|---|---|---|---|---|---|
| BERT-base (110M) | BERT-base (110M) | BART-base (139M) | BART-base (139M) | distilGPT-2 (82M) | distilGPT-2 (82M) | |
| 编辑器 | ES↑ | acc. DD ← | ES ↑ | acc. DD ← | ES↑ | ppl. DD ← |
| FT | 0.76 | <0.001 | 0.96 | <0.001 | 0.29 | 0.938 |
| FT+KL | 0.64 | <0.001 | 0.89 | <0.001 | 0.17 | 0.059 |
| ENN | 0.99 | 0.003 | 0.99 | <0.001 | 0.93 | 0.094 |
| KE | 0.95 | 0.004 | 0.98 | <0.001 | 0.25 | 0.595 |
| MEND | >0.99 | <0.001 | 0.98 | 0.002 | 0.86 | 0.225 |
Table 4: Small-scale model editing with various model editors on three editing problems. ENN and MEND show the most consistently good performance, with ENN exceeding MEND’s performance on the Wikitext problem. MEND’s primary advantages are its consistent performance from 100M to 10B parameter models and the fact that it does not modify the pre-edit model (unlike ENN). The pre-trained models and editing data for the FEVER fact-checking and zsRE question-answering problems are used from the checkpoints and data released by De Cao et al. (2021); for generation, we use distilGPT-2 fine-tuned on Wikitext2 (Ma, 2021).
表 4: 三种编辑问题下不同模型编辑器的小规模模型编辑效果。ENN和MEND展现出最稳定的优异性能,其中ENN在Wikitext问题上超越了MEND。MEND的主要优势在于其参数规模从1亿到100亿的模型均保持稳定表现,且无需修改预编辑模型(与ENN不同)。FEVER事实核查和zsRE问答任务使用的预训练模型及编辑数据来自De Cao等人(2021)发布的检查点和数据集;文本生成任务采用经Wikitext2微调的distilGPT-2模型(Ma, 2021)。
5.2 SMALLER SCALE EDITING
5.2 小规模编辑
We conduct an additional experiment editing the BERT-base and BART-base models fine-tuned by De Cao et al. (2021) on the FEVER fact-checking and zsRE question-answering tasks, respectively, and our Wikitext editing task, editing a smaller distilGPT-2 model (Wolf et al., 2019) fine-tuned on Wikitext2 (Ma, 2021). These models are 1–2 orders of magnitude smaller than those in Section 5.1. Results are presented in Table 4. At small scale where computational requirements are not a concern, ENN is competitive with MEND, providing the best performance on the Wikitext problem. Fine-tuning overfits even more severely than with larger models, showing lower edit success (over fitting to the edit example) and higher drawdown (degrading the model more seriously). One difficulty of using ENN is that the pre-trained model itself must be fine-tuned to ‘provide’ edit ability, potentially changing the model’s predictions even before an edit has been applied. Unlike the large-scale experiments, drawdown is computed using samples from the same datasets as edit inputs, again in order to best match the data distribution the base models were fine-tuned on. See Appendix G for additional comparisons with the caching-based editor, which shows strong performance for zsRE and FEVER, but generally fails for Wikitext, as well as a more difficult version of the zsRE problem for which MEND still produces meaningful edits.
我们进行了一项额外实验,分别编辑了De Cao等人(2021)在FEVER事实核查任务和zsRE问答任务上微调过的BERT-base与BART-base模型,以及我们在Wikitext编辑任务中微调的小型distilGPT-2模型(Wolf等人,2019)(Ma,2021)。这些模型的规模比5.1节中的模型小1-2个数量级。结果如表4所示。在计算资源不受限的小规模场景下,ENN与MEND表现相当,并在Wikitext问题上取得了最佳性能。微调方法比在大模型上表现出更严重的过拟合现象,表现为编辑成功率更低(过度拟合编辑样本)和性能衰减更严重(模型退化更明显)。使用ENN的一个难点在于必须对预训练模型本身进行微调以"提供"编辑能力,这可能导致在应用编辑前就改变模型的预测行为。与大规模实验不同,性能衰减计算使用的是与编辑输入同源的数据集样本,以更好地匹配基础模型的微调数据分布。附录G提供了与基于缓存的编辑器的对比分析:该编辑器在zsRE和FEVER任务上表现优异,但在Wikitext任务和MEND仍能有效处理的zsRE困难版本任务上普遍失效。

Figure 3: GPU VRAM consumption during training. ENN’s memory usage is prohibitively high for very large models, while MEND and KE can be trained on a single GPU. Figure 4 shows similar chart for GPT models.
图 3: 训练期间的GPU显存消耗。对于超大型模型,ENN的内存占用高得难以承受,而MEND和KE可在单块GPU上完成训练。图4展示了GPT模型的类似数据图表。
5.3 BATCHED EDITING
5.3 批量编辑
Table 5 compares MEND with ENN (the strongest comparison method) in a more realistic setting when multiple simultaneous zsRE QA model edits are needed; MEND consistently provides significantly more effective edits in the multi-edit setting. Both algorithms are trained and evaluated on applying $k$ simultaneous edits, with $k\in$ ${1,5,25,\overleftarrow{75},\overleftarrow{125}}$ . MEND applies simultaneous edits by simply summing the parameter edit computed separately for each edit example. MEND applies 25 edits in a single model update with $96%$ edit success and less than $1%$ accuracy degradation ( $35%$ edit success for ENN), and successfully applies $67%$ of edits when applying 125 edits at once ( $11%$ success for ENN, although ENN’s accuracy drawdown is slightly lower).
表 5 将 MEND 与 ENN (最强的对比方法) 在需要同时进行多个 zsRE QA 模型编辑的更现实场景中进行比较。在多编辑场景下,MEND 始终能提供显著更有效的编辑效果。两种算法均在应用 $k$ 次同步编辑时进行训练和评估,其中 $k\in$ ${1,5,25,\overleftarrow{75},\overleftarrow{125}}$。MEND 通过简单累加为每个编辑样本单独计算的参数编辑量来实现同步编辑。MEND 在单次模型更新中应用 25 次编辑时达到 $96%$ 的编辑成功率且准确率下降小于 $1%$ (ENN 的编辑成功率为 $35%$),当一次性应用 125 次编辑时仍能成功执行 $67%$ 的编辑 (ENN 成功率仅 $11%$,尽管其准确率下降幅度略低)。
Table 5: Batched edits with MEND and ENN on zsRE QA using the BART-base pre-trained model from De Cao et al. (2021). When applying multiple edits at once, MEND is far more effective than ENN.
| EditSuccess↑ | Acc. Drawdown ↓ | ||
| Edits | ENN MEND | ENN | MEND |
| 1 | 0.99 | 0.98 | <0.001 0.002 |
| 5 | 0.94 | 0.97 0.007 | 0.005 |
| 25 | 0.35 | 0.89 0.005 | 0.011 |
| 75 | 0.16 | 0.78 0.005 | 0.011 |
| 125 | 0.11 | 0.67 | 0.006 0.012 |
表 5: 使用De Cao等人(2021)的BART-base预训练模型在zsRE QA任务上对MEND和ENN进行批量编辑的结果。当同时应用多个编辑时,MEND的效果远优于ENN。
| EditSuccess↑ | Acc. Drawdown ↓ | ||
|---|---|---|---|
| Edits | ENN MEND | ENN | MEND |
| 1 | 0.99 | 0.98 | <0.001 0.002 |
| 5 | 0.94 | 0.97 0.007 | 0.005 |
| 25 | 0.35 | 0.89 0.005 | 0.011 |
| 75 | 0.16 | 0.78 0.005 | 0.011 |
| 125 | 0.11 | 0.67 | 0.006 0.012 |
| WikitextGeneration | zsRE Question-Answering | ||||
| distilGPT-2 (82M) | BART-base (139M) | ||||
| MENDVariant | EditorParameters | ES↑ | ppl. DD ↓ | ES↑ | acc. DD ↓ |
| No sharing | O((m + n)²N) | 0.86 | 0.195 | >0.99 | 0.001 |
| No norm. | O((m + n)²) | 0.02 | 0.370 | 0.97 | <0.001 |
| No ID init. | O((m + n)") | 0.27 | 0.898 | 0.94 | <0.001 |
| Only ue | O(m²) | 0.63 | 0.559 | 0.98 | 0.002 |
| Only de+1 | O(n²) | 0.80 | 0.445 | 0.99 | 0.001 |
| Only smaller | O(min(m,n)²) | 0.80 | 0.593 | 0.98 | 0.002 |
| MEND | O((m + n)²) | 0.86 | 0.225 | >0.99 | 0.001 |
| MENDVariant | EditorParameters | WikitextGeneration (distilGPT-2 (82M)) | zsRE Question-Answering (BART-base (139M)) | ||
|---|---|---|---|---|---|
| ES↑ | ppl. DD ↓ | ES↑ | acc. DD ↓ | ||
| No sharing | O((m + n)²N) | 0.86 | 0.195 | >0.99 | 0.001 |
| No norm. | O((m + n)²) | 0.02 | 0.370 | 0.97 | <0.001 |
| No ID init. | O((m + n)") | 0.27 | 0.898 | 0.94 | <0.001 |
| Only ue | O(m²) | 0.63 | 0.559 | 0.98 | 0.002 |
| Only de+1 | O(n²) | 0.80 | 0.445 | 0.99 | 0.001 |
| Only smaller | O(min(m,n)²) | 0.80 | 0.593 | 0.98 | 0.002 |
| MEND | O((m + n)²) | 0.86 | 0.225 | >0.99 | 0.001 |
Table 6: Ablating various properties of MEND on the Wikitext and zsRE question-answering editing problems. $m=\dim(u_{\ell})$ , $n=\dim(\delta_{\ell+1})$ , and $N$ is the number of layers being edited. Removing MEND’s identity initialization and input normalization noticeably lowers editing performance, and relaxations of MEND, particularly the ‘only smaller’ variant that only outputs pseudo activation s or pseudo deltas, whichever is smaller, show competitive performance, which bodes well for scaling MEND to 100 billion $^+$ parameter models.
表 6: 在Wikitext和zsRE问答编辑任务上消融MEND的各项特性。$m=\dim(u_{\ell})$,$n=\dim(\delta_{\ell+1})$,$N$表示被编辑的层数。移除MEND的恒等初始化和输入归一化会显著降低编辑性能,而MEND的简化版本(特别是仅输出伪激活或伪增量中较小值的"only smaller"变体)表现出竞争力,这为将MEND扩展到千亿$^+$参数模型提供了良好前景。
5.4 ABLATIONS & MEND VARIANTS
5.4 消融研究与MEND变体
Table 6 shows ablations of MEND’s parameter sharing, identity initialization, and input normalization as well as three variants of MEND that reduce total parameters: only computing pseudoactivations $u_{\ell}$ , only pseudo deltas $\delta_{\ell+1}$ , or only whichever of $u_{\ell}$ or $\delta_{\ell+1}$ is lower-dimensional (layerdependent for non-square weights). ‘No ID init.’ replaces zero initialization with Xavier/Glorot initialization (Glorot and Bengio, 2010). Removing either input normalization or identity initialization significantly reduces edit effectiveness (and increases training time $\mathord{\sim}10\mathrm{x}$ ). Sharing parameters across model editor networks incurs relatively little performance cost, and editing only the smaller of the pseudo activation s and pseudo deltas, the most most lightweight version of MEND, still produces effective edits, suggesting that MEND could scale to even much larger models for which $m+n$ approaches $10^{5}$ (Brown et al., 2020) but $\operatorname*{min}(m,n)$ remains close to $10^{4}$ . Appendix E shows an additional ablation editing attention matrices, rather than MLP weights, finding that editing MLP weights is consistently more effective for large models.
表 6: 展示了MEND的参数共享、恒等初始化和输入归一化的消融实验,以及三种减少总参数的MEND变体:仅计算伪激活 $u_{\ell}$、仅计算伪增量 $\delta_{\ell+1}$,或仅计算维度较低者(对于非方形权重则取决于层)。"无ID初始化"用Xavier/Glorot初始化 (Glorot and Bengio, 2010) 替代零初始化。移除输入归一化或恒等初始化会显著降低编辑效果(并将训练时间增加约10倍)。跨模型编辑器网络共享参数带来的性能损失较小,而仅编辑伪激活和伪增量中较小者的最轻量级MEND版本仍能产生有效编辑,这表明MEND可扩展至 $m+n$ 接近 $10^{5}$ (Brown et al., 2020) 但 $\operatorname*{min}(m,n)$ 仍接近 $10^{4}$ 的更大模型。附录E展示了额外消融实验:编辑注意力矩阵而非MLP权重,发现对于大型模型而言编辑MLP权重始终更有效。
6 DISCUSSION
6 讨论
Conclusion. We have presented an efficient approach to editing very large (10 billion $^+$ parameter) neural networks, which we call Model Editor Networks with Gradient Decomposition or MEND. We showed that MEND is the only method that successfully edits the largest publicly-available Transformer models from the GPT and T5 model families. To do so, MEND treats the model editing problem itself as a learning problem, using a relatively small edit dataset to learn model editor networks that can correct model errors using only a single input-output pair. MEND leverages the fact that gradients with respect to the fully-connected layers in neural networks are rank-1, enabling a parameter-efficient architecture that represents this gradient transform.
结论。我们提出了一种高效编辑超大规模(100亿$^+$参数量)神经网络的方法,称为基于梯度分解的模型编辑网络(MEND)。实验证明,MEND是唯一能成功编辑GPT和T5系列最大公开Transformer模型的方法。该方法将模型编辑问题本身构建为学习任务,利用较小规模的编辑数据集训练模型编辑网络,仅需单组输入输出对即可修正模型错误。MEND通过利用神经网络全连接层梯度具有秩1特性的优势,设计出能高效表征梯度变换的参数化架构。
Limitations & Future Work. A limitation of existing model editors (including MEND) is the approach to enforcing locality of edits. The failure mode of over-generalization (bottom of Table 2) shows that locality examples (i.e., negative examples) are not challenging enough to prevent the model from sometimes changing its output for distinct but related inputs. Alternative locality losses or harder negative mining may help address this problem. Further, existing language-based editing datasets use back translation to evaluate edit generality (and our Wikitext dataset uses a truncation heuristic). Such equivalence neighborhoods do not assess a model’s ability to use the knowledge in an edit example to correctly answer questions about other topics whose answer is implied by the content of the edit example (e.g., for Who is the UK PM? Boris Johnson, does the edited model correctly answer Is Boris Johnson a private citizen?). Counter factual data augmentation (Kaushik et al., 2020) may be useful for constructing richer evaluation cases for edit generality. Future work might also apply MEND to other types of edits, such as reducing the frequency of toxic generations after observing toxic outputs, relabeling entire classes of images from one example, or adjusting a robot’s control policy to avoid particular actions, as MEND is not limited to editing transformer models. Finally, MEND’s gradient decomposition is not in principle limited to the model editing problem, and it might enable efficient new gradient-based meta-learning algorithms.
局限性与未来工作。现有模型编辑器(包括MEND)的一个局限在于实施编辑局部性的方法。表2底部的过度泛化失败案例表明,局部性示例(即负样本)的挑战性不足,无法阻止模型有时对相关但不同的输入改变输出。采用替代性局部性损失函数或更严格的负样本挖掘可能有助于解决该问题。此外,现有基于语言的编辑数据集使用回译(back translation)评估编辑泛化性(我们的Wikitext数据集采用截断启发式方法),这类等价邻域评估法无法衡量模型利用编辑示例中的知识来正确回答其他相关问题(其答案隐含在编辑内容中)的能力(例如编辑"英国首相是谁?鲍里斯·约翰逊"后,模型能否正确回答"鲍里斯·约翰逊是平民吗?")。反事实数据增强(counter factual data augmentation) [20] 可能有助于构建更丰富的编辑泛化性评估案例。未来工作还可将MEND应用于其他类型的编辑,例如在观察到有害输出后降低毒性生成频率、通过单示例重新标记整类图像、或调整机器人控制策略以规避特定动作——因为MEND不仅限于编辑Transformer模型。最后,MEND的梯度分解原理上不局限于模型编辑问题,可能催生新型高效的基于梯度的元学习算法。
ACKNOWLEDGEMENTS
致谢
We gratefully acknowledge Angeliki Lazaridou for insightful early discussions regarding temporal generalization in language models; Spencer Braun for implementing exploratory experiments that motivated this project; Mitchell Wortsman, Gabriel Ilharco, Stephanie Chan, and Archit Sharma for insightful discussions and encouragement; Michael Chang, Michael Janner, and Ashwin Paranjape for feedback on an early version of the paper; and the anonymous ICLR reviewers for their feedback. Eric Mitchell gratefully acknowledges the support of a Knight-Hennessy graduate fellowship. Chelsea Finn and Chris Manning are fellows in the CIFAR Learning in Machines and Brains program.
我们衷心感谢Angeliki Lazaridou就语言模型时序泛化问题提出的深刻早期讨论;Spencer Braun为实现本项目的探索性实验提供支持;Mitchell Wortsman、Gabriel Ilharco、Stephanie Chan和Archit Sharma富有见地的讨论与鼓励;Michael Chang、Michael Janner和Ashwin Paranjape对论文初稿的反馈;以及ICLR匿名评审人的宝贵意见。Eric Mitchell特别感谢Knight-Hennessy研究生奖学金的支持。Chelsea Finn与Chris Manning是CIFAR"机器与大脑学习"项目的研究员。
ETHICS STATEMENT
道德声明
This work uses large language models pre-trained on text scraped from the internet. These massive training corpora (and therefore the models trained on them) may contain (or produce) content that is counter to the values of the ICLR community. Algorithms for model editing may provide one tool (among others) to mitigate this problem by enabling maintainers of large models to change certain undesirable model behaviors as they are discovered. On the other hand, a model editor could also be used to exacerbate the very model behaviors that we hope to eliminate, depending on who is wielding it. This dual use is a risk for many machine learning technologies. Specifically, effective editing algorithms (including MEND and others) may enable maintainers of deployed neural networks to include backdoors or other planned vulnerabilities/hidden behaviors into their models.
本研究使用了基于互联网文本数据预训练的大语言模型。这些海量训练语料(以及基于它们训练的模型)可能包含(或生成)违背ICLR社区价值观的内容。模型编辑算法可作为一种工具(结合其他方法),帮助大型模型的维护者在发现不良行为时进行修正。但另一方面,根据使用者的意图,模型编辑器也可能被用来强化我们想要消除的不良行为。这种双重用途是许多机器学习技术共同面临的风险。具体而言,包括MEND在内的有效编辑算法,可能使已部署神经网络的维护者能够在模型中植入后门或其他预设漏洞/隐藏行为。
REPRODUCIBILITY
可复现性
To foster reproducibility, we have provided a detailed description of the proposed algorithm in Section 3, as well as additional details regarding experimental setup, hyper parameters, and implementations of comparison algorithms in Section C. Our experiments use fixed random seeds for data sampling and model editor initialization, enabling reproducible results. Section C.4 describes how to obtain the pre-existing datasets and models we used in our experiments (from De Cao et al. (2021)). See project website at https://sites.google.com/view/mend-editing for links to code and data.
为促进可复现性,我们在第3节详细描述了所提出的算法,并在附录C中提供了关于实验设置、超参数及对比算法实现的补充细节。实验采用固定随机种子进行数据采样和模型编辑器初始化,确保结果可复现。附录C.4说明了如何获取我们实验中使用的既有数据集和模型(来自De Cao等人(2021)的研究)。代码与数据链接详见项目网站:https://sites.google.com/view/mend-editing。
REFERENCES
参考文献
Yonatan Belinkov, Nadir Durrani, Fahim Dalvi, Hassan Sajjad, and James Glass. What do neural machine translation models learn about morphology? In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 861–872, Vancouver, Canada, July 2017. Association for Computational Linguistics. doi: 10.18653/v1/P17-1080. URL https://a cl anthology.org/P17-1080.
Yonatan Belinkov、Nadir Durrani、Fahim Dalvi、Hassan Sajjad和James Glass。神经机器翻译模型对形态学学到了什么?载于《第55届计算语言学协会年会论文集(第一卷:长论文)》,第861–872页,加拿大温哥华,2017年7月。计算语言学协会。doi: 10.18653/v1/P17-1080。URL https://aclanthology.org/P17-1080。
Sid Black, Gao Leo, Phil Wang, Connor Leahy, and Stella Biderman. GPT-Neo: Large Scale Auto regressive Language Modeling with Mesh-Tensorflow, March 2021. URL https://doi. org/10.5281/zenodo.5297715.
Sid Black、Gao Leo、Phil Wang、Connor Leahy和Stella Biderman。GPT-Neo:使用Mesh-Tensorflow的大规模自回归语言建模,2021年3月。URL https://doi.org/10.5281/zenodo.5297715。
Demi Guo, Alexander Rush, and Yoon Kim. Parameter-efficient transfer learning with diff pruning. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), pages 4884–4896, Online, August 2021. Association for Computational Linguistics. doi: 10.18653/v1/2021.acl-long.378. URL https://a cl anthology.org/2021. acl-long.378.
Demi Guo、Alexander Rush 和 Yoon Kim. 基于差异剪枝的参数高效迁移学习. 载于《第59届计算语言学协会年会暨第11届自然语言处理国际联合会议论文集(第一卷:长论文)》, 第4884-4896页, 线上会议, 2021年8月. 计算语言学协会. doi: 10.18653/v1/2021.acl-long.378. URL https://acl anthology.org/2021.acl-long.378.
Omer Levy, Minjoon Seo, Eunsol Choi, and Luke Z ett le moyer. Zero-shot relation extraction via reading comprehension. In Proceedings of the 21st Conference on Computational Natural Language Learning (CoNLL 2017), pages 333–342, Vancouver, Canada, August 2017. Association for Computational Linguistics. doi: 10.18653/v1/K17-1034. URL https://www.aclweb. org/anthology/K17-1034.
Omer Levy、Minjoon Seo、Eunsol Choi和Luke Zettlemoyer。通过阅读理解实现零样本关系抽取。载于《第21届计算自然语言学习会议论文集》(CoNLL 2017),第333-342页,加拿大温哥华,2017年8月。计算语言学协会。doi: 10.18653/v1/K17-1034。URL https://www.aclweb.org/anthology/K17-1034。
Zhenguo Li, Fengwei Zhou, Fei Chen, and Hang Li. Meta-sgd: Learning to learn quickly for few shot learning. CoRR, abs/1707.09835, 2017. URL http://arxiv.org/abs/1707. 09835.
Zhenguo Li, Fengwei Zhou, Fei Chen, 和 Hang Li. Meta-SGD: 面向少样本学习的快速元学习. CoRR, abs/1707.09835, 2017. URL http://arxiv.org/abs/1707.09835.
Yuxuan Ma. distilgpt2-finetuned-wikitext2. https://hugging face.co/MYX4567/ distilgpt2-finetuned-wikitext2, July 2021.
Yuxuan Ma. distilgpt2-finetuned-wikitext2. https://huggingface.co/MYX4567/distilgpt2-finetuned-wikitext2, 2021年7月.
Michael McCloskey and Neal J. Cohen. Catastrophic interference in connection is t networks: The sequential learning problem. Psychology of Learning and Motivation, 24:109–165, 1989. ISSN 0079-7421. doi: https://doi.org/10.1016/S0079-7421(08)60536-8. URL https://www. science direct.com/science/article/pii/S 0079742108605368.
Michael McCloskey 和 Neal J. Cohen. 连接网络中的灾难性干扰: 序列学习问题. 学习与动机心理学, 24:109–165, 1989. ISSN 0079-7421. doi: https://doi.org/10.1016/S0079-7421(08)60536-8. URL https://www.sciencedirect.com/science/article/pii/S0079742108605368.
German I. Parisi, Ronald Kemker, Jose L. Part, Christopher Kanan, and Stefan Wermter. Continual lifelong learning with neural networks: A review. Neural Networks, 113:54–71, 2019. ISSN 0893-6080. doi: https://doi.org/10.1016/j.neunet.2019.01.012. URL https://www. science direct.com/science/article/pii/S 0893608019300231.
German I. Parisi, Ronald Kemker, Jose L. Part, Christopher Kanan, and Stefan Wermter. 基于神经网络的持续终身学习综述. 神经网络, 113:54–71, 2019. ISSN 0893-6080. doi: https://doi.org/10.1016/j.neunet.2019.01.012. URL https://www. sciencedirect.com/science/article/pii/S0893608019300231.
Eunbyung Park and Junier B Oliva. Meta-curvature. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 32. Curran Associates, Inc., 2019.
E
Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, Alban Desmaison, Andreas Kopf, Edward Yang, Zachary DeVito, Martin Raison, Alykhan Tejani, Sasank Chi lam kurt hy, Benoit Steiner, Lu Fang, Junjie Bai, and Soumith Chintala. Pytorch: An imperative style, highperformance deep learning library. In H. Wallach, H. Larochelle, A. Bey gel zi mer, F. d'Alché-Buc, E. Fox, and R. Garnett, editors, Advances in Neural Information Processing Systems 32, pages 8024–8035. Curran Associates, Inc., 2019. URL http://papers.neurips.cc/paper/ 9015-pytorch-an-imperative-style-high-performance-deep-learning-library. pdf.
Adam Paszke、Sam Gross、Francisco Massa、Adam Lerer、James Bradbury、Gregory Chanan、Trevor Killeen、Zeming Lin、Natalia Gimelshein、Luca Antiga、Alban Desmaison、Andreas Kopf、Edward Yang、Zachary DeVito、Martin Raison、Alykhan Tejani、Sasank Chilamkurthy、Benoit Steiner、Lu Fang、Junjie Bai 和 Soumith Chintala。PyTorch:一种命令式风格的高性能深度学习库。见 H. Wallach、H. Larochelle、A. Beygelzimer、F. d'Alché-Buc、E. Fox 和 R. Garnett 编辑的《神经信息处理系统进展 32》,第 8024–8035 页。Curran Associates, Inc., 2019。URL http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf。
Ethan Perez, Florian Strub, Harm de Vries, Vincent Dumoulin, and Aaron C. Courville. Film: Visual reasoning with a general conditioning layer. In AAAI, 2018.
Ethan Perez、Florian Strub、Harm de Vries、Vincent Dumoulin 和 Aaron C. Courville。FILM: 通用条件层的视觉推理。AAAI,2018。
Fabio Petroni, Tim Rock t s chel, Sebastian Riedel, Patrick Lewis, Anton Bakhtin, Yuxiang Wu, and Alexander Miller. Language models as knowledge bases? In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 2463–2473, Hong Kong, China, November 2019. Association for Computational Linguistics. doi: 10.18653/v1/ D19-1250. URL https://a cl anthology.org/D19-1250.
Fabio Petroni、Tim Rocktäschel、Sebastian Riedel、Patrick Lewis、Anton Bakhtin、Yuxiang Wu和Alexander Miller。语言模型能作为知识库吗?载于《2019年自然语言处理经验方法会议暨第九届自然语言处理国际联合会议(EMNLP-IJCNLP)论文集》,第2463-2473页,中国香港,2019年11月。计算语言学协会。doi: 10.18653/v1/D19-1250。URL https://aclanthology.org/D19-1250。
Alec Radford, Jeff Wu, Rewon Child, David Luan, Dario Amodei, and Ilya Sutskever. Language models are unsupervised multitask learners, 2019. URL https://d 4 muc fpk sy wv. cloudfront.net/better-language-models/language models are unsupervised multi task learners.pdf.
Alec Radford、Jeff Wu、Rewon Child、David Luan、Dario Amodei 和 Ilya Sutskever。语言模型是无监督多任务学习者,2019。URL https://d4mucfpksywv.cloudfront.net/better-language-models/language models are unsupervised multi task learners.pdf。
Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J. Liu. Exploring the limits of transfer learning with a unified text-totext transformer. Journal of Machine Learning Research, 21(140):1–67, 2020. URL http: //jmlr.org/papers/v21/20-074.html.
Colin Raffel、Noam Shazeer、Adam Roberts、Katherine Lee、Sharan Narang、Michael Matena、Yanqi Zhou、Wei Li 和 Peter J. Liu。《探索迁移学习的极限:基于统一文本到文本Transformer的研究》。机器学习研究期刊,21(140):1-67,2020。URL http://jmlr.org/papers/v21/20-074.html。
R. Ratcliff. Connection is t models of recognition memory: constraints imposed by learning and forgetting functions. Psychological review, 97 2:285–308, 1990.
R. Ratcliff. 连接识别记忆模型:学习与遗忘函数施加的约束. Psychological review, 97 2:285–308, 1990.
Sachin Ravi and H. Larochelle. Optimization as a model for few-shot learning. In ICLR, 2017.
Sachin Ravi 和 H. Larochelle. 优化作为少样本学习的模型. In ICLR, 2017.
Adam Roberts, Colin Raffel, and Noam Shazeer. How much knowledge can you pack into the parameters of a language model?, 2020.
Adam Roberts、Colin Raffel 和 Noam Shazeer。语言模型的参数能容纳多少知识?2020。
A EFFECTIVE INITIALIZATION AND NORMALIZATION FOR MEND NETWORKS
一种有效的MEND网络初始化和归一化方法
Although random weight initialization is effective in many settings, it sacrifices the prior that the raw fine-tuning gradient is a useful starting point for editing. Our ablations show that it also leads to less effective edits. For this reason, we initialize MEND to the identity function using a residual connection (He et al., 2016) and a partially random, partially zero-initialization strategy related to Fixup (Zhang et al., 2019). Referring back to Eqs. 3a,b, $U_{1}$ and $U_{2}$ are initialized with zeros, and $V_{1}$ and $V_{2}$ use standard Xavier uniform initialization (Glorot and Bengio, 2010) (also see Figure 2). Beyond the initialization, input scaling also presents a challenge: inputs to a MEND network ( $u_{\ell}$ and $\delta_{\ell+1}$ ) can differ in magnitude by several orders of magnitude. This poor conditioning causes training to be slow and edit performance to suffer (see Section 5.4). Input normalization addresses this issue; we normalize each dimension of both $u_{\ell}$ and $\delta_{\ell+1}$ . The input to $g_{\ell}$ is the concatenation of $\bar{u}_ {\ell}=\mathrm{norm}(u_{\ell})$ and $\bar{\delta}_ {\ell+1}=\mathsf{n o r m}(\delta_{\ell+1})$ , where $\bar{u}_ {\ell}$ and $\bar{\delta}_{\ell+1}$ are normalized to have zero mean and unit variance, with means and variances computed over the edit train set and the sequence index.
虽然随机权重初始化在许多场景下有效,但它牺牲了原始微调梯度可作为编辑有用起点的先验。我们的消融实验表明,这也会导致编辑效果下降。因此,我们采用残差连接 (He et al., 2016) 和与 Fixup (Zhang et al., 2019) 相关的部分随机、部分零初始化策略,将 MEND 初始化为恒等函数。回顾公式 3a 和 3b,$U_{1}$ 和 $U_{2}$ 初始化为零,$V_{1}$ 和 $V_{2}$ 采用标准 Xavier 均匀初始化 (Glorot and Bengio, 2010) (另见图 2)。除初始化外,输入缩放也带来挑战:MEND 网络的输入 ($u_{\ell}$ 和 $\delta_{\ell+1}$) 可能在数量级上相差数个量级。这种不良的条件化会导致训练缓慢且编辑性能受损 (见第 5.4 节)。输入归一化解决了这个问题;我们对 $u_{\ell}$ 和 $\delta_{\ell+1}$ 的每个维度进行归一化。$g_{\ell}$ 的输入是 $\bar{u}_ {\ell}=\mathrm{norm}(u_{\ell})$ 和 $\bar{\delta}_ {\ell+1}=\mathsf{n o r m}(\delta_{\ell+1})$ 的拼接,其中 $\bar{u}_ {\ell}$ 和 $\bar{\delta}_{\ell+1}$ 被归一化为零均值和单位方差,均值和方差是在编辑训练集和序列索引上计算的。
B EXTENDED DISCUSSION OF RELATED WORK
B 相关工作扩展讨论
Model editing shares with continual learning (McCloskey and Cohen, 1989; Parisi et al., 2019) the goal of assimilating or updating a model’s behavior without forgetting old information or behaviors, commonly known as the problem of catastrophic forgetting (McCloskey and Cohen, 1989; Ratcliff, 1990; Kirkpatrick et al., 2017). However, in continual learning settings, a model is typically expected to learn wholly new behaviors or datasets (Kirkpatrick et al., 2017; Parisi et al., 2019) without forgetting, while in this work we consider more localized model edits. Further, continual learning generally considers long sequences of model updates with minimal memory overhead, while our work generally considers an edit or batch of edits applied all at once.
模型编辑与持续学习 (McCloskey and Cohen, 1989; Parisi et al., 2019) 共享一个目标:在吸收或更新模型行为的同时不遗忘旧信息或行为,这通常被称为灾难性遗忘问题 (McCloskey and Cohen, 1989; Ratcliff, 1990; Kirkpatrick et al., 2017)。然而,在持续学习场景中,模型通常被期望在不遗忘的情况下学习全新的行为或数据集 (Kirkpatrick et al., 2017; Parisi et al., 2019),而本研究关注的是更局部化的模型编辑。此外,持续学习通常考虑的是具有最小内存开销的长时间序列模型更新,而我们的工作一般考虑的是一次性应用一个编辑或一批编辑。
Additionally, min-norm parameter fine-tuning has also been considered in past work in the context of editing (Zhu et al., 2020) and traditional model fine-tuning (Guo et al., 2021), where the parameters of the edited or fine-tuned model $\theta^{\prime}$ are penalized (or constrained) from drifting too far from the original model parameters $\theta$ using various norms, including L0, L2, and L $\infty$ . While min-norm constraints may be an effective regular iz ation for traditional fine-tuning settings where fine-tuning data is abundant, the experiments conducted in De Cao et al. (2021) show that parameter-space norm constraints are insufficient constraints to prevent significant model degradation when fine-tuning on a single edit example.
此外,最小范数参数微调在过往研究中也被应用于模型编辑(Zhu等人,2020)和传统模型微调(Guo等人,2021)场景。这类方法通过L0、L2和L$\infty$等范数约束,防止编辑或微调后的模型参数$\theta^{\prime}$与原始参数$\theta$偏离过远。虽然最小范数约束在传统数据充足的微调场景中可能成为有效的正则化手段,但De Cao等人(2021)的实验表明:当仅针对单个编辑样本进行微调时,参数空间的范数约束不足以阻止模型性能的显著退化。
B.1 EDITABLE NEURAL NETWORKS (ENN)
B.1 可编辑神经网络 (ENN)
Editable neural networks (Sinitsin et al., 2020) search for a set of model parameters that both provide good performance for a ‘base task’ (e.g., image classification or machine translation) and enable rapid editing by gradient descent to update the model’s predictions for a set of ‘edit examples without changing the model’s behavior for unrelated inputs. ENN optimizes the following objective, based on the MAML algorithm (Finn et al., 2017):
可编辑神经网络 (Editable neural networks, Sinitsin等, 2020) 致力于寻找一组既能对"基础任务"(如图像分类或机器翻译)保持良好性能,又可通过梯度下降快速编辑的模型参数,从而在不改变模型对无关输入行为的前提下更新其对"编辑示例集"的预测。该网络基于MAML算法 (Finn等, 2017) 优化以下目标:
$$
{\mathcal{L}}_ {\mathrm{ENN}}(\theta,{\mathcal{D}}_ {\mathrm{base}},{\mathcal{D}}_ {\mathrm{edi}},{\mathcal{D}}_ {\mathrm{loc}})=L_{\mathrm{base}}({\mathcal{D}}_ {\mathrm{base}},\theta)+c_{\mathrm{edit}}\cdot L_{\mathrm{edit}}({\mathcal{D}}_ {\mathrm{edit}},\theta^{\prime})+c_{\mathrm{loc}}\cdot L_{\mathrm{loc}}({\mathcal{D}}_{\mathrm{loc}},\theta,\theta^{\prime}).
$$
$$
{\mathcal{L}}_ {\mathrm{ENN}}(\theta,{\mathcal{D}}_ {\mathrm{base}},{\mathcal{D}}_ {\mathrm{edi}},{\mathcal{D}}_ {\mathrm{loc}})=L_{\mathrm{base}}({\mathcal{D}}_ {\mathrm{base}},\theta)+c_{\mathrm{edit}}\cdot L_{\mathrm{edit}}({\mathcal{D}}_ {\mathrm{edit}},\theta^{\prime})+c_{\mathrm{loc}}\cdot L_{\mathrm{loc}}({\mathcal{D}}_{\mathrm{loc}},\theta,\theta^{\prime}).
$$
The first term of Equation 5 is the base task loss; for a generative language model, we have $L_{\mathrm{base}}(\mathcal{D}_ {\mathrm{base}},\theta)=-\log p_{\theta}(\mathcal{D}_ {\mathrm{base}})$ where $\mathcal{D}_ {\mathrm{base}}$ is a batch of training sequences. $L_{\mathrm{base}}$ is the edit reliability loss, encouraging the model to significantly change its output for the edit examples in $\mathcal{D}_ {\mathrm{edit}}$ . Finally, $L_{\mathrm{loc}}$ is the edit locality loss, which penalizes the edited model $\theta^{\prime}$ for deviating from the predictions of the pre-edit model $\theta$ on $\mathcal{D}_ {\mathrm{loc}}$ , data unrelated to $\mathcal{D}_ {\mathrm{edit}}$ and sampled from the same distribution as $\mathcal{D}_ {\mathrm{base}}$ . See Sinitsin et al. (2020) for a more detailed explanation of ENN training and alternative objectives for $L_{\mathrm{edit}}$ and $L_{\mathrm{loc}}$ .
式 5 的第一项是基础任务损失;对于生成式语言模型,我们有 $L_{\mathrm{base}}(\mathcal{D}_ {\mathrm{base}},\theta)=-\log p_{\theta}(\mathcal{D}_ {\mathrm{base}})$ ,其中 $\mathcal{D}_ {\mathrm{base}}$ 是一批训练序列。 $L_{\mathrm{base}}$ 是编辑可靠性损失,鼓励模型对 $\mathcal{D}_ {\mathrm{edit}}$ 中的编辑样本显著改变其输出。最后, $L_{\mathrm{loc}}$ 是编辑局部性损失,它惩罚编辑后的模型 $\theta^{\prime}$ 在 $\mathcal{D}_ {\mathrm{loc}}$ 上偏离预编辑模型 $\theta$ 的预测结果,这些数据与 $\mathcal{D}_ {\mathrm{edit}}$ 无关且采样自与 $\mathcal{D}_ {\mathrm{base}}$ 相同的分布。关于 ENN 训练及 $L_{\mathrm{edit}}$ 和 $L_{\mathrm{loc}}$ 的其他目标,详见 Sinitsin 等人 (2020) 的更详细解释。
Comparing ENN and MEND. The key conceptual distinction between ENN and MEND is that ENN encodes edit ability into the parameters of the model itself (intrinsic edit ability), while MEND provides edit ability through a set of learned parameters that are independent from the model parameters (extrinsic edit ability). An advantage of ENN is that no new parameters are added in order to provide edit ability. However, this approach comes with several drawbacks. First, the MAML-based objective ENN optimizes is expensive, particularly in terms of memory consumption (see Figure 4). By further training the model parameters themselves, ENN cannot guarantee that the editable model it produces will make the same predictions as the original model. In order to approximately enforce this constraint during training, ENN must use an extra copy of the original base model to ensure that the editable model’s predictive distribution does not differ too much from it. This incurs significant additional memory costs, particularly when training ENN for very large models, for which the parameters of the model alone occupy a significant amount of VRAM. Another cause for the significant VRAM consumption of ENN is the need to compute activation s and gradients for the model parameters; even if we edit only the last layer, ENN trains the rest of the model so that the last layer gradient is productive, requiring activation s and gradients to be computed for the entire model. On the other hand, extrinsic editors like MEND and KE do not require updating the base model itself, thereby computing gradients for far fewer parameters. Future work might investigate approaches to reducing the memory consumption of ENN, although the requirement to retain a copy of the original model in order to enforce locality creates a relatively high lower bound on the amount of memory that ENN might use.
比较ENN和MEND。ENN与MEND的关键概念区别在于:ENN将编辑能力编码到模型自身的参数中(内在编辑能力),而MEND通过一组独立于模型参数的学习参数(外在编辑能力)来提供编辑能力。ENN的优势在于无需添加新参数即可实现编辑能力。然而这种方法存在若干缺点。首先,ENN优化的基于MAML的目标函数计算成本高昂,尤其在内存消耗方面(见图4)。由于需要进一步训练模型参数本身,ENN无法保证其生成的可编辑模型会做出与原模型相同的预测。为了在训练中近似满足这一约束,ENN必须使用原始基础模型的额外副本来确保可编辑模型的预测分布不会偏离太多。这会产生显著的内存开销,特别是在为超大规模模型训练ENN时,仅模型参数本身就会占用大量显存。ENN显存消耗巨大的另一个原因是需要计算模型参数的激活值和梯度;即便只编辑最后一层,ENN也会训练模型的其余部分以使最后一层梯度有效,这需要计算整个模型的激活值和梯度。另一方面,MEND和KE等外在编辑器不需要更新基础模型本身,因此只需为少得多的参数计算梯度。未来工作可能会探索降低ENN内存消耗的方法,但为保持局部性而需要保留原始模型副本的要求,为ENN可能使用的内存量设定了较高的下限。

Figure 4: GPU VRAM consumption for training MEND, KE, and ENN in float32. MEND and KE’s memory consumption remain tractable for a single GPU (using $2\times$ bfloat16 memory usage (Wang and Kanwar, 2019) for T5-11B), while ENN’s memory usage increases much more rapidly, making it impractical to run on a single GPU. Values are computed without gradient check pointing. Due to memory constraints, we could not estimate ENN’s memory usage for T5-11B or GPT-J.
图 4: 训练 MEND、KE 和 ENN 时的 GPU 显存 (VRAM) 占用情况(float32 精度)。MEND 和 KE 的显存占用在单 GPU 上仍可管理(对于 T5-11B 使用 $2\times$ bfloat16 内存占用 (Wang and Kanwar, 2019)),而 ENN 的显存占用增长更快,使得其在单 GPU 上运行不切实际。数值计算未使用梯度检查点。由于内存限制,我们无法估算 ENN 在 T5-11B 或 GPT-J 上的内存占用。
Regardless of memory consumption, extrinsic editors have the potential advantage of being able to edit more than one model; in theory, we might amortize the cost of training MEND over several base models at once. On the other hand, intrinsic edit ability must by definition be re-learned separately for each base model.
无论内存消耗如何,外部编辑器具有能够编辑多个模型的潜在优势;理论上,我们可以通过一次性在多个基础模型上训练MEND来分摊成本。另一方面,根据定义,内部编辑能力必须为每个基础模型单独重新学习。
B.2 KNOWLEDGE EDITOR (KE)
B.2 知识编辑器 (KE)
De Cao et al. (2021) propose KNOWLEDGE EDITOR, a hyper network-based approach for editing the knowledge in language models. KE is an RNN that conditions explicitly on the input, incorrect output, and new desired label and outputs a mask $m_{i}$ , offset $b_{i}$ , and a scalar scaling factor $\alpha$ to the gradient $\nabla_{W_{i}}$ for several of the weight matrices in a transformer model, where $m_{i},\boldsymbol{\bar{b}}_ {i},\nabla_{W_{i}}\in\mathbb{R}^{d\times d}$ for a $d\times d$ weight matrix. The update to the model is $\theta^{\prime}=\theta-\alpha(m_{i}\odot\nabla_{W_{i}})+b_{i}$ . Because the weight matrices in state-of-the-art transformer models are very high-dimensional, the mask and offset output by KE are rank-1 to retain tract ability.
De Cao等人 (2021) 提出了KNOWLEDGE EDITOR,这是一种基于超网络的方法,用于编辑语言模型中的知识。KE是一个RNN,它显式地以输入、错误输出和新的期望标签为条件,并为Transformer模型中的几个权重矩阵输出一个掩码$m_{i}$、偏移量$b_{i}$和一个标量缩放因子$\alpha$到梯度$\nabla_{W_{i}}$,其中对于$d \times d$的权重矩阵,$m_{i}, \boldsymbol{\bar{b}}_ {i}, \nabla_{W_{i}} \in \mathbb{R}^{d \times d}$。模型的更新为$\theta^{\prime}=\theta-\alpha(m_{i}\odot\nabla_{W_{i}})+b_{i}$。由于最先进的Transformer模型中的权重矩阵维度非常高,KE输出的掩码和偏移量是秩1的,以保持可操作性。
Comparing KE and MEND. KE more closely resembles MEND in that it is also an extrinsic model editor. However, while MEND directly maps model gradients into model edits, the KE model editor uses the raw edit example as an input, outputting a single rank-1 mask and rank-1 offset over the fine-tuning gradient. We hypothesize that the KE model faces several challenges that MEND avoids. First, mapping the edit example itself into a model updates requires a translation from the high-level modality of data examples into the very low-level modality of model parameter updates. Solving this translation requires making additional design decisions (e.g., how to feed the edit input and label into the editor, what architecture to use for the editor), the optimal design for which may vary across problems. Further, by not conditioning directly on the gradient, KE forgoes a rich source of information about which parameters of the model are most responsible for updating the model’s outputs. In addition, by operating on the token-wise activation s and gradients (i.e., the gradients are not summed over the sequence/batch, but are kept as per-sequence element activation and gradient vectors), MEND outputs a rank-1 model edit for each token in the input and output sequence. The final output of MEND is the sum of these, which has rank of order 10 or even 100, depending on the problem. In contrast, the KE editor outputs only a rank-1 gradient mask and rank-1 gradient offset, regardless of the information content of the edit example. This rank-1 constraint, irrespective of the size of the input, which we hypothesize causes KE’s failure to perform well for the Wikitext editing
比较KE与MEND。KE与MEND更为相似,因为它也是一种外部模型编辑器。然而,MEND直接将模型梯度映射为模型编辑,而KE模型编辑器则使用原始编辑示例作为输入,输出一个针对微调梯度的单一秩1掩码和秩1偏移。我们假设KE模型面临MEND所避免的几个挑战。首先,将编辑示例本身映射为模型更新需要从数据示例的高级模态转换到模型参数更新的极低级模态。解决这一转换需要做出额外的设计决策(例如,如何将编辑输入和标签输入编辑器,使用何种架构作为编辑器),其最优设计可能因问题而异。此外,由于不直接基于梯度,KE放弃了关于模型哪些参数对更新模型输出最负责的丰富信息来源。另外,MEND通过对逐个token的激活和梯度进行操作(即梯度不按序列/批次求和,而是保留为每个序列元素的激活和梯度向量),为输入和输出序列中的每个token输出一个秩1模型编辑。MEND的最终输出是这些编辑的总和,其秩可能为10甚至100,具体取决于问题。相比之下,无论编辑示例的信息内容如何,KE编辑器仅输出一个秩1梯度掩码和秩1梯度偏移。我们假设,这种与输入大小无关的秩1约束导致了KE在Wikitext编辑任务中表现不佳。
| Ce,Ye Nepal borders France. Yes | |
| cloc | Belgium is r made up of three re- gions. |
| xe, ye | Nepal is bordered by France. Yes |
| cloc | Belgium is r made up of three re- gions. |
|---|---|
| xe, ye | Nepal is bordered by France. Yes |
(a) FEVER fact-checking editing dataset example. In this case, the locality loss is computed as the KL divergence between the Bernoulli distribution produced by the pre-edit and post-edit model for the locality example $x_{\mathrm{loc}}$ .
(a) FEVER事实核查编辑数据集示例。在这种情况下,局部性损失通过计算预编辑模型和后编辑模型针对局部性示例$x_{\mathrm{loc}}$生成的伯努利分布之间的KL散度得出。
| Ce | Whichcontinentis sMountAndrews On?SouthAmerica |
| Mloc,yloc | TowhichfictionalworkdoesDennis Rickman belong in?EastEnders |
| C e,y | InwhichcontinentisMountAndrews located?SouthAmerica |
| Ce | Whichcontinentis sMountAndrews On?SouthAmerica |
|---|---|
| Mloc,yloc | TowhichfictionalworkdoesDennis Rickman belong in?EastEnders |
| C e,y | InwhichcontinentisMountAndrews located?SouthAmerica |
(b) zsRE question-answering editing dataset example. Because computing the KL divergence of the model over all possible answers to the question is computationally expensive, we use the label (EastEnders) and compute the KL divergence between the pre- and post-edit model at each of these tokens as an approximation.
(b) zsRE问答编辑数据集示例。由于计算模型对问题所有可能答案的KL散度计算成本过高,我们使用标签(EastEnders)并通过计算编辑前后模型在这些token上的KL散度作为近似值。
Table 7: Editing data samples from the FEVER fact-checking and zsRE question-answering editing datasets from De Cao et al. (2021). Bold text corresponds to labels used for editing or approximating the locality constraint.
表 7: De Cao等人(2021)提供的FEVER事实核查和zsRE问答编辑数据集中的编辑数据样本。加粗文本对应用于编辑或近似局部性约束的标签。
task, which has significantly higher information content labels (10 tokens) than the FEVER or zsRE tasks.
该任务的信息内容标签(10个token)显著多于FEVER或zsRE任务。
C EXPERIMENTAL DETAILS
C 实验细节
For GPT and BERT-style models, all experiments edit the MLP weights in the last 3 transformer blocks (6 weight matrices total). For BART and T5-style models, all experiments edit the MLP weights in the last 2 transformer blocks in both the encoder and the decoder (8 weight matrices total). We found that editing MLP layers generally provides better editing performance (across algorithms) than editing attention layers. In line with past work (De Cao et al., 2021), all reported performance numbers are on the validation set. For all algorithms, we use early stopping to end training early if the validation loss $L=c_{\mathrm{edit}}L_{\mathrm{e}}+L_{\mathrm{loc}})$ does not decrease for 20000 steps on a subset of 500 validation examples, with a maximum number of training steps of 500,000. We use a batch size of 10 (with gradient accumulation) and the seed 0 for all experiments. Tables 7 and 8 show examples from each dataset used in our experiments.
对于GPT和BERT类模型,所有实验都编辑最后3个Transformer模块中的MLP权重(共6个权重矩阵)。对于BART和T5类模型,所有实验同时编辑编码器和解码器中最后2个Transformer模块的MLP权重(共8个权重矩阵)。我们发现,与编辑注意力层相比,编辑MLP层通常能提供更好的编辑性能(跨算法)。与以往研究一致 (De Cao et al., 2021),所有报告的性能指标均基于验证集。所有算法均采用早停机制:如果在500个验证样本子集上连续20000步验证损失 $L=c_{\mathrm{edit}}L_{\mathrm{e}}+L_{\mathrm{loc}})$ 未下降,则提前终止训练,最大训练步数设为500,000。所有实验使用批次大小10(带梯度累积)和随机种子0。表7和表8展示了实验中使用的各数据集样本示例。
C.1 HYPER PARAMETERS
C.1 超参数 (Hyper Parameters)
Fine-tuning. The fine-tuning baselines use model-dependent learning rates, which we found important in achieving good fine-tuning performance; using too large of a learning rate causes decreased locality (increased model degradation), while a learning rate too small causes slow edits. We use edit learning rates of 5e-6 for GPT-Neo and GPT-J and 1e-4 for T5 models, and 1e-6 for the smaller models, aiming to complete edits in less than 100 fine-tuning steps (as in De Cao et al. (2021)). For the fine-tuning $+\mathrm{KL}$ -constraint baseline, we fine-tune on the loss $c_{\mathrm{edit}}L_{\mathrm{e}}+L_{\mathrm{loc}}$ , using a smaller $c_{\mathrm{edit}}$ than for the learned algorithms (1e-2 for all models except GPT-J, which required 1e-3). Larger values of $c_{\mathrm{edit}}$ provide little benefit from the locality loss. To compute $L_{\mathrm{loc}}$ , we use a batch size of one new example $x_{\mathrm{{loc}}}$ from the full edit training set $\bar{D}_{e d i t}^{t r}$ at each time step.
微调。微调基线使用模型相关的学习率,我们发现这对实现良好的微调性能至关重要;学习率过大会导致局部性降低(模型退化加剧),而学习率过小则会导致编辑速度缓慢。我们为GPT-Neo和GPT-J使用5e-6的编辑学习率,为T5模型使用1e-4,较小模型使用1e-6,目标是在少于100个微调步骤内完成编辑(如De Cao等人(2021)所述)。对于微调$+\mathrm{KL}$约束基线,我们在损失函数$c_{\mathrm{edit}}L_{\mathrm{e}}+L_{\mathrm{loc}}$上进行微调,使用的$c_{\mathrm{edit}}$比学习算法更小(除GPT-J外所有模型为1e-2,GPT-J需要1e-3)。更大的$c_{\mathrm{edit}}$值对局部性损失的改善有限。为计算$L_{\mathrm{loc}}$,我们在每个时间步从完整编辑训练集$\bar{D}_ {e d i t}^{t r}$中使用一个大小为1的新样本$x_{\mathrm{{loc}}}$。
ENN. We use an initial inner loop learning rate of 1e-2, but allow this value to be learned in the outer loop, which we find improves performance over the fixed inner loop learning rate version in Sinitsin et al. (2020). For all experiments, ENN fine-tunes all model parameters during training (even when we only edit the last few layers). We also use only a single inner loop update step for computational reasons, which differs from the multi-step version used for the smaller models used by Sinitsin et al. (2020). Our edit loss is also a slight simplification of the edit loss used by Sinitsin et al. (2020), which is
ENN。我们初始设置内层循环学习率为1e-2,但允许该值在外层循环中进行学习。我们发现这种设定相比Sinitsin等人(2020)采用的固定内层学习率版本能提升性能。在所有实验中,ENN在训练期间会对所有模型参数进行微调(即使我们仅编辑最后几层)。出于计算效率考虑,我们仅使用单步内层循环更新,这与Sinitsin等人(2020)在小模型上采用的多步更新方式不同。我们的编辑损失函数也是Sinitsin等人(2020)所用损失函数的轻微简化版本,具体表现为...
$$
l_{e}(\theta)=-\log p_{\theta}(y_{e}|x_{e},\theta)+\operatorname*{max}_ {y_{i}}\log p_{\theta}(y_{i}|x_{e},\theta)
$$
$$
l_{e}(\theta)=-\log p_{\theta}(y_{e}|x_{e},\theta)+\operatorname*{max}_ {y_{i}}\log p_{\theta}(y_{i}|x_{e},\theta)
$$
The first term of this loss is the edit loss we use in our work; the second term is primarily intended to provide the property that $l_{e}(\theta)\leq0$ when an edit is successful so that the iterative editing process can be stopped. However, in this work, because we use only a single gradient step of editing for
该损失函数的第一项是我们工作中使用的编辑损失;第二项主要用于确保当编辑成功时满足 $l_{e}(\theta)\leq0$ 的性质,从而可以停止迭代编辑过程。然而,在本工作中,因为我们仅使用单步梯度进行编辑...
ENN, this property is less important, and the second term simply amounts to an additional emphasis on pushing down specifically the largest incorrect logit (which the first term already does implicitly).
ENN的这一特性并不那么重要,第二项只是额外强调要压低最大的错误logit(第一项已经隐含地做到了这一点)。
KE We use the implementation of KE provided by De Cao et al. (2021), which can be found at https://github.com/nicola-decao/Knowledge Editor, with minor changes to the computation of the KL constraint for consistency with other algorithms (see below). We use a learning rate of 1e-5.
我们采用了De Cao等人(2021)提供的知识编辑器(Knowledge Editor)实现方案(代码库见https://github.com/nicola-decao/Knowledge-Editor),仅对KL约束的计算方式进行了微调以保持与其他算法的一致性(详见下文),学习率设置为1e-5。
C.2 COMPUTING THE LOCALITY CONSTRAINT
C.2 计算局部性约束
Computing the true KL-divergence between the pre- and post-edit model $\mathrm{KL}\big(p_{\theta}\big(\cdot|x_{\mathrm{loc}}\big)\big||p_{\theta^{\prime}}\big(\cdot|x_{\mathrm{loc}}\big)\big)$ quickly becomes computationally prohibitive for model outputs of more than a few tokens, requiring margin aliz ation over possible answers. We therefore approximate this KL-divergence using samples from the dataset.6 For the seq2seq question-answering problem, we eval, wofh etrhe $y_{\mathrm{loc}}$ ,s thgiev idnisgtr $\begin{array}{r l}{\mathbf{\bar{K}L}_ {\mathrm{approx}}^{\mathrm{seq2seq}}(\theta,\theta^{\prime})}&{=}\end{array}$ $\begin{array}{r}{\frac{1}{|y_{\mathrm{loc}}|}\sum_{i=1}^{|y_{\mathrm{loc}}|}\mathrm{KL}\big(p_{\theta}\big(\cdot|x_{\mathrm{loc}},y_{\mathrm{loc}}^{<i}\big)|p_{\theta^{\prime}}\big(\cdot|x_{\mathrm{loc}},y_{\mathrm{loc}}^{<i}\big)\big)}\end{array}$ $p(\cdot|x_{\mathrm{loc}},y_{\mathrm{loc}}^{<i})$ kens $y_{i}$ given the locality input $x_{\mathrm{loc}}$ and the label tokens for previous timesteps $y_{\mathrm{loc}}^{<i}$ . Similarly, for the Wikitext setting, we define $\begin{array}{r}{\mathrm{KL}_ {\mathrm{approx}}^{\mathrm{auto}}(\theta,\theta^{\prime})=\frac{1}{|x_{\mathrm{loc}}|}\sum_{i=1}^{|x_{\mathrm{loc}}|}\mathrm{KL}\big(p_{\theta}(\cdot|x_{\mathrm{loc}}^{<i})||p_{\theta^{\prime}}(\cdot|x_{\mathrm{loc}}^{<i})\big)}\end{array}$ . For FEVER fact-checking we compute the exact KL-divergence between Bernoulli distributions in closed form.
计算编辑前后模型之间的真实KL散度 $\mathrm{KL}\big(p_{\theta}\big(\cdot|x_{\mathrm{loc}}\big)\big||p_{\theta^{\prime}}\big(\cdot|x_{\mathrm{loc}}\big)\big)$ 在模型输出超过少量token时会迅速变得计算不可行,因为需要对所有可能答案进行边缘化处理。因此我们采用数据集样本近似计算该KL散度。对于seq2seq问答任务,给定 $y_{\mathrm{loc}}$ 时定义近似KL散度为 $\begin{array}{r l}{\mathbf{\bar{K}L}_ {\mathrm{approx}}^{\mathrm{seq2seq}}(\theta,\theta^{\prime})}&{=}\end{array}$ $\begin{array}{r}{\frac{1}{|y_{\mathrm{loc}}|}\sum_{i=1}^{|y_{\mathrm{loc}}|}\mathrm{KL}\big(p_{\theta}\big(\cdot|x_{\mathrm{loc}},y_{\mathrm{loc}}^{<i}\big)|p_{\theta^{\prime}}\big(\cdot|x_{\mathrm{loc}},y_{\mathrm{loc}}^{<i}\big)\big)}\end{array}$ ,其中 $p(\cdot|x_{\mathrm{loc}},y_{\mathrm{loc}}^{<i})$ 表示在给定局部输入 $x_{\mathrm{loc}}$ 和先前时间步标签token $y_{\mathrm{loc}}^{<i}$ 条件下预测 $y_{i}$ 的概率分布。类似地,对于Wikitext场景定义 $\begin{array}{r}{\mathrm{KL}_ {\mathrm{approx}}^{\mathrm{auto}}(\theta,\theta^{\prime})=\frac{1}{|x_{\mathrm{loc}}|}\sum_{i=1}^{|x_{\mathrm{loc}}|}\mathrm{KL}\big(p_{\theta}(\cdot|x_{\mathrm{loc}}^{<i})||p_{\theta^{\prime}}(\cdot|x_{\mathrm{loc}}^{<i})\big)}\end{array}$ 。在FEVER事实核查任务中,我们直接计算闭式解中伯努利分布之间的精确KL散度。
C.3 ENVIRONMENT DETAILS
C.3 环境详情
All runs are trained entirely on a single NVIDIA RTX Titan or A40 GPU. No gradient check pointing or memory-reduction optimization s are used, although bfloat16 is used to fit the largest T5 model onto our GPU. In full precision, the parameters alone of the T5-11B model use all of the memory of our largest GPU. VRAM consumption for training MEND and KE on T5-11B (Figs. 3 and 4) is estimated by doubling the bfloat16 VRAM usage (Wang and Kanwar, 2019). While doubling half precision enabled estimating the memory consumption of ENN, we were unable to train ENN in half precision without numerical instability. All models are based on Hugging face Transformers imple ment at ions (Wolf et al., 2019) with some modifications in line with De Cao et al. (2021). We use PyTorch (Paszke et al., 2019) for all experiments, specifically using the Higher library (Gre fens te tte et al., 2019) in order to implement the bi-level optimization in ENN as well as the inner loop of model editing for all algorithms.
所有实验均在单张NVIDIA RTX Titan或A40 GPU上完成训练。虽然使用了bfloat16精度以便将最大的T5模型装入GPU,但未采用梯度检查点或内存优化技术。在完全精度下,仅T5-11B模型的参数就占用了我们最大GPU的全部内存。训练MEND和KE在T5-11B上的VRAM消耗(图3和图4)通过双倍bfloat16 VRAM使用量估算得出(Wang and Kanwar, 2019)。虽然双倍半精度可估算ENN的内存消耗,但我们在半精度下训练ENN时会出现数值不稳定的问题。所有模型均基于Hugging Face Transformers实现(Wolf et al., 2019),并根据De Cao等人(2021)的研究进行了部分修改。所有实验均使用PyTorch(Paszke et al., 2019),特别是借助Higher库(Grefenstette et al., 2019)来实现ENN的双层优化以及所有算法模型编辑的内循环。
C.4 DATASET CONSTRUCTION & EXAMPLES
C.4 数据集构建与示例
Datasets are constructed to provide pairs of edit input $x_{\mathrm{e}}$ and plausible edit label $y_{\mathrm{e}}$ . The edit label is not necessarily the ‘correct’ label; the goal is to provide realistic instances of the types of data we would expect to see during test. For example, our dataset might have a sample such as $x_{\mathrm{e}}$ $=$ Where was Ursula K. Le Guin born? and $y_{\mathrm{e}}=$ Addis Ababa, Oromia, Ethiopia, even though Ursula K. Le Guin was born in Berkeley, California, USA. However, this fictitious example is still a useful assessment of our model’s ability to perform the general type of edit of ‘change a person’s birthplace’. For the zsRE question-answering dataset De Cao et al. (2021) generate fictitious $y_{\mathrm{e}}$ in this manner using the top predictions of a BART model fine-tuned on the task of question answering followed by manual human filtering. In practice, this produces alternate edit labels that are plausible and whose types match with the original label. For FEVER fact-checking, there are only two choices for labels, and we sample edit targets 1 and 0 with equal probability. For Wikitext generation, we use a distilGPT-2 model to generate plausible 10-token continuations for a given Wikitext prefix, with the similar motivation to zsRE of providing edit targets that share the structure of the types of edits that we will apply in practice, even if they are not always factual. When qualitatively assessing MEND to correct real errors of the base model using the factual labels, we find that MEND performs reliably, indicating that these label generators provide reasonable proxies for ‘real’ model edits.
数据集构建时提供编辑输入$x_{\mathrm{e}}$与合理编辑标签$y_{\mathrm{e}}$的配对。编辑标签不一定是"正确"标签,其目标是提供测试阶段可能遇到的真实数据实例。例如,数据集中可能出现$x_{\mathrm{e}}=$"Ursula K. Le Guin出生在哪里?"与$y_{\mathrm{e}}=$"埃塞俄比亚奥罗米亚州亚的斯亚贝巴"的样本,尽管实际出生地是美国加州伯克利。这种虚构样本仍能有效评估模型执行"修改人物出生地"这类通用编辑的能力。针对zsRE问答数据集,De Cao等人[20]采用BART模型(经问答任务微调)的Top预测结果生成虚构$y_{\mathrm{e}}$,再经人工筛选。该方法产生的替代编辑标签既合理又保持原始标签类型。对于FEVER事实核查任务,标签仅有两种选择,我们以均等概率采样编辑目标1和0。在Wikitext生成任务中,采用distilGPT-2模型为给定前缀生成合理的10-token续写,动机与zsRE类似——提供与实际应用编辑结构相符的目标,即便内容未必真实。定性评估MEND使用真实标签修正基础模型错误时,发现其表现可靠,表明这些标签生成器为"真实"模型编辑提供了合理代理。
| Ce,ye | Saprang was considered one of the top contenders to lead the army and the junta af- ter CNS leader Sonthi Boonyaratkalin's mandatory retirement in 2007. However, in September 2007 he was demoted to be Deputy Permanent Secretary of the Defense Ministry, while his rival, General Anupong Paochinda, was promoted to Deputy At- torney General. Later, he was replaced |
| that observations of a transit of the planet Mercury, at widely spaced points on the surface of the Earth, could be used to calculate the solar parallax and hence the as- tronomical unit using triangulation. Aware of this, a young Edmond Halley made observations of such a transit on 28 October O.S.1677fromSaint Helenabut was disappointed to find that only Richard Towneley in Burnley, Lancashire had made another accurate observation of the event whilst Gallet, at Avignon, simply recorded that it had occurred. Halley was not satisfied that the resulting calculation of the solar | |
| parallax at 45 " was accurate. However, in September 2007 he was demoted to be Deputy Permanent Secretary of the Defense Ministry, while his rival, General Anupong Paochinda, was promoted to Deputy Attorney General. Later, he was replaced |
| Ce,ye | Saprang 曾被视为 2007 年 CNS 领导人 Sonthi Boonyaratkalin 强制退休后领导军队和军政府的主要竞争者之一。然而在 2007 年 9 月,他被降职为国防部常务次长,而其竞争对手 Anupong Paochinda 将军则晋升为副检察长。随后,他被替换 |
|---|
