Editing Factual Knowledge in Language Models
编辑语言模型中的事实性知识
Nicola De Cao 1,2, Wilker Aziz 1, Ivan Titov 1,2 1 University of Amsterdam, 2 University of Edinburgh { nicola.decao, w.aziz, titov } @uva.nl
Nicola De Cao 1,2, Wilker Aziz 1, Ivan Titov 1,2
1 阿姆斯特丹大学, 2 爱丁堡大学
{ nicola.decao, w.aziz, titov } @uva.nl
Abstract
摘要
The factual knowledge acquired during pretraining and stored in the parameters of Language Models (LMs) can be useful in downstream tasks (e.g., question answering or textual inference). However, some facts can be incorrectly induced or become obsolete over time. We present KNOWLEDGE EDITOR, a method which can be used to edit this knowledge and, thus, fix ‘bugs’ or unexpected predictions without the need for expensive retraining or fine-tuning. Besides being comput ation ally efficient, KNOWLEDGE EDITOR does not require any modifications in LM pretraining (e.g., the use of meta-learning). In our approach, we train a hyper-network with constrained optimization to modify a fact without affecting the rest of the knowledge; the trained hyper-network is then used to predict the weight update at test time. We show KNOWLEDGEEDITOR’s efficacy with two popular archi tec ture s and knowledge-intensive tasks: i) a BERT model fine-tuned for fact-checking, and ii) a sequence-to-sequence BART model for question answering. With our method, changing a prediction on the specific wording of a query tends to result in a consistent change in predictions also for its paraphrases. We show that this can be further encouraged by exploiting (e.g., automatically-generated) paraphrases during training. Interestingly, our hyper-network can be regarded as a ‘probe’ revealing which components need to be changed to manipulate factual knowledge; our analysis shows that the updates tend to be concentrated on a small subset of components.1
预训练过程中获取并存储于语言模型(LM)参数中的事实性知识,在下游任务(如问答或文本推理)中具有实用价值。然而部分知识可能被错误归纳或随时间过时。我们提出KNOWLEDGE EDITOR方法,无需昂贵重训练或微调即可修正此类"错误"或意外预测。该方法不仅计算高效,还无需修改LM预训练流程(例如采用元学习)。我们通过约束优化训练超网络来修改特定事实而不影响其他知识,训练后的超网络在测试时用于预测权重更新。实验证明KNOWLEDGE EDITOR在两种经典架构和知识密集型任务中表现优异:i)用于事实核查的微调BERT模型,ii)用于问答的序列到序列BART模型。该方法能确保查询表述变化时,其释义的预测结果保持同步改变。研究表明训练阶段利用(如自动生成的)释义可进一步强化该特性。值得注意的是,超网络可作为"探针"揭示操纵事实知识需修改的组件,分析表明更新往往集中于少量参数子集。[20]
1 Introduction
1 引言
Using pre-trained transformer-based Language Models (LMs; Vaswani et al., 2017; Devlin et al., 2019; Radford et al., 2019; Lewis et al., 2020; Raf- fel et al., 2020; Brown et al., 2020) has recently become a standard practice in NLP. Factual knowledge induced during pre-training can help in downstream tasks, but it can also be incorrect or become obsolete over time (e.g., not reflecting changes of heads of states or country populations). Developing reliable and computationally efficient methods for bug-fixing models without the need for expensive re-training would be beneficial. See Figure 2 for an example of revising the memory of a model that initially mis remembered Namibia’s capital.
使用预训练的基于Transformer的大语言模型(LMs;Vaswani等人,2017;Devlin等人,2019;Radford等人,2019;Lewis等人,2020;Raffel等人,2020;Brown等人,2020)已成为NLP领域的标准实践。预训练过程中获取的事实知识虽有助于下游任务,但也可能存在错误或随时间过时(例如未反映国家元首变更或人口数据更新)。开发可靠且计算高效的方法来修复模型缺陷(无需昂贵重新训练)将具有重要意义。如图2所示,该案例展示了修正模型最初对纳米比亚首都错误记忆的过程。
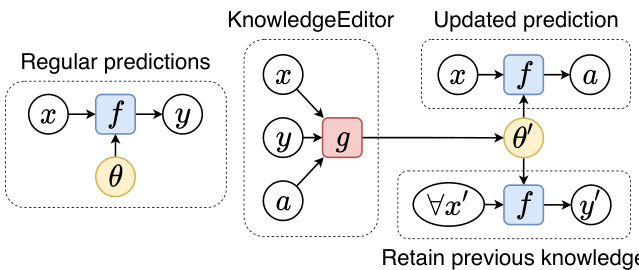
Figure 1: Left: a model $f$ with parameters $\theta$ prefers a prediction $y$ for input $x$ (e.g., $y$ is the mode/argmax of a discrete distribution parameterized by $f(x;\theta))$ . Right: our method uses a hyper-network $g$ to update the parameters of $f$ to $\theta^{\prime}$ such that $f(x;\theta^{\prime})$ prefers an alternative prediction $a$ without affecting the prediction $y^{\prime}$ of any other input $x^{\prime}\neq x$ . Our model edits the knowledge about $x$ stored in the parameters of $f$ .
图 1: 左图: 参数为 $\theta$ 的模型 $f$ 对输入 $x$ 倾向于预测 $y$ (例如 $y$ 是由 $f(x;\theta)$ 参数化的离散分布的众数/argmax) 。右图: 我们的方法使用超网络 $g$ 将 $f$ 的参数更新为 $\theta^{\prime}$ ,使得 $f(x;\theta^{\prime})$ 倾向于替代预测 $a$ ,同时不影响任何其他输入 $x^{\prime}\neq x$ 的预测 $y^{\prime}$ 。我们的模型编辑了存储在 $f$ 参数中关于 $x$ 的知识。
Unlike conventional Knowledge Bases (KBs) that explicitly store factual knowledge, neural models implicitly memorize facts in their parameters. One cannot easily access and interpret their computation and memories (Ribeiro et al., 2016; Belinkov and Glass, 2019; Voita et al., 2019; De Cao et al., 2020), thus, modifying their knowledge is a challenging problem. Motivated by practical conside rations, we formulate the following desiderata for a method aimed at tackling this problem (see Section 2 for a more formal treatment):
与传统显式存储事实知识的知识库(KBs)不同,神经模型将事实隐式记忆在参数中。人们难以直接访问和解读其计算过程与记忆内容(Ribeiro et al., 2016; Belinkov and Glass, 2019; Voita et al., 2019; De Cao et al., 2020),因此修改其知识成为具有挑战性的问题。基于实际应用考量,我们为解决方法提出以下需求(更正式的讨论见第2节):
• Generality: be able to modify a model that was not specifically trained to be editable (i.e., no need for special pre-training of LMs, such as using meta-learning);
• 通用性:能够修改未经专门训练即可编辑的模型(即无需对大语言模型进行特殊预训练,例如使用元学习);
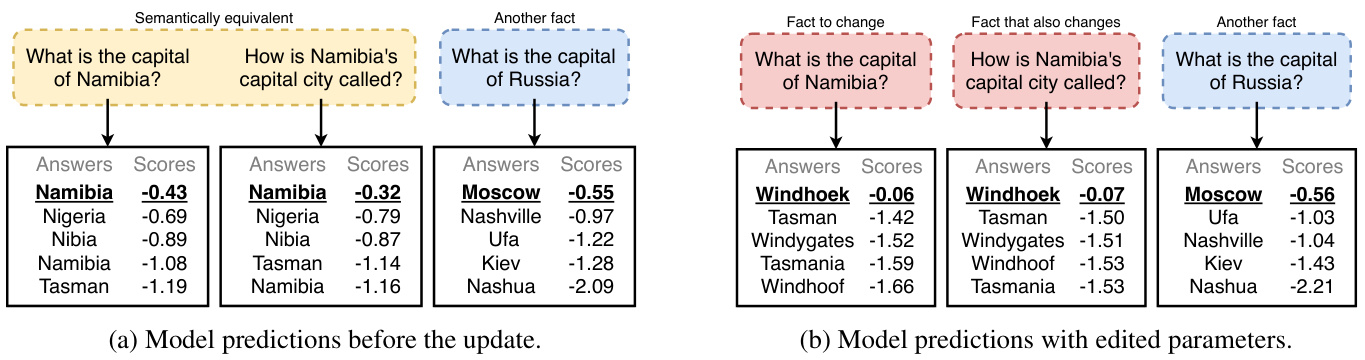
Figure 2: Predictions from a pre-trained language BART model fine-tuned for closed-book question answering. Left: model top-k predictions from Beam Search. Right: top-k after using our method conditioning on changing ‘What is the capital of Namibia?’ from ‘Namibia’ (wrong) to ‘Windhoek’ (correct prediction). Changing one fact also changes a semantically equivalent question and keeps the predictions from other facts the same.
图 2: 经过闭卷问答微调的预训练语言BART模型预测结果。左: 基于束搜索(Beam Search)的模型top-k预测。右: 使用我们的方法将"纳米比亚的首都是什么?"从错误答案"纳米比亚"修正为正确答案"温得和克"后,得到的top-k预测。修改一个事实同时会改变语义等价问题的预测,并保持其他事实的预测不变。
The problem has been previously tackled in Zhu et al. (2020) and Sinitsin et al. (2020), as discussed in detail in Section 3. However, both do not ensure that the edited model will be ‘reliable’, i.e. that the rest of the knowledge would not be badly affected, and that the changes are ‘consistent’ across equivalent inputs. Additionally, Sinitsin et al.’s (2020) method requires expensive specialized training of the original network. While re-training the original network was feasible in their applications (e.g., in machine translation), it is problematic when the network is a pre-trained LM. We propose a novel method that overcomes these limitations.
该问题在Zhu等人 (2020) 和Sinitsin等人 (2020) 的研究中已有探讨,详见第3节。但两者均无法确保编辑后的模型具有"可靠性",即其他知识不会受到严重影响,且修改内容在等效输入间保持"一致性"。此外,Sinitsin等人 (2020) 的方法需要对原始网络进行昂贵的专门训练。虽然在其应用场景(如机器翻译)中重训练原始网络可行,但对于预训练大语言模型则存在问题。我们提出了一种克服这些局限性的新方法。
We treat editing the memories of a neural model as a learning-to-update problem. We use an efficient parameter iz ation of a hyper-network that is trained to update the LM parameters when provided with a single fact that needs to be modified. We do not require meta-learning, re-training or fine-tuning of the original network. We employ constrained optimization in training: we constrain the edited model to retain the same predictions as the original one regardless of the distance between the original and updated models in the parameter space. We show how this framework can be extended to incorporate (e.g., automatically-generated) paraphrases in training, further improving consistency. Figure 1 shows an outline of our method.
我们将神经模型的记忆编辑视为一个学习更新的问题。采用超网络的高效参数化方法,该网络经过训练后,能在提供单个需要修改的事实时更新大语言模型参数。此方法无需对原始网络进行元学习、重新训练或微调。训练中采用约束优化:限制编辑后的模型保持与原模型相同的预测结果,无论参数空间中原始模型与更新模型之间的距离如何。我们还展示了如何扩展该框架以在训练中融入(例如自动生成的)同义改写,从而进一步提升一致性。图 1: 展示了本方法的概要。
Differently from both previous methods, we do not have to select a subset of parameters to update as we let our model learn that by itself. In fact, our hyper-network can be regarded as a ‘probe’ revealing which components of the network need to be changed to manipulate factual knowledge, i.e. revealing the ‘causal mediation mechanisms’ (Vig et al., 2020). We observe that the updates end up being concentrated in a restricted set of model components, even though we do not encourage any kind of sparsity. Interestingly, the most-updated components are different from the groups of parameters receiving large gradients (see Figure 4).
与之前两种方法不同,我们无需手动选择待更新的参数子集,而是让模型自行学习。实际上,我们的超网络可视为一种"探针",能揭示需要修改网络的哪些组件来操纵事实知识,即揭示"因果中介机制"(Vig et al., 2020)。我们发现,即便没有施加任何稀疏性约束,更新最终会集中在有限的模型组件上。值得注意的是,更新最频繁的组件与梯度较大的参数组并不重合(见图4)。
Contributions Our contributions are as follows:
贡献 我们的贡献如下:
• we define the task of knowledge editing and propose a set of evaluation metrics; • we propose KNOWLEDGE EDITOR that learns to modify LMs memories efficiently and reliably while maintaining consistent predictions for semantically equivalent inputs; • we verify that our proposed method largely meets our desiderata—while other baselines based on fine-tuning fail—testing it with different LM architectures on knowledgeintensive tasks such as fact-checking and open-domain question answering; we analyze the updates for KNOWLEDGE EDITOR and the alternatives.
• 我们定义了知识编辑 (knowledge editing) 任务并提出一套评估指标;
• 我们提出KNOWLEDGE EDITOR方法,该方案能高效可靠地修改大语言模型的记忆,同时保持对语义等价输入的一致性预测;
• 通过在不同架构的大语言模型上测试知识密集型任务(如事实核查和开放域问答),验证了所提方法基本满足预期目标(而基于微调的基线方法均告失败);我们分析了KNOWLEDGE EDITOR及其替代方案的更新机制。
2 Task
2 任务
We want to edit the memory of a neural language model such that when, presented with an input, its output reflects a revised collection of facts. Unfortunately, the knowledge of a language model is typically opaque to us, being stored non-locally across a large number of parameters and architectural components. Thus, concretely, to operationalize the task, we seek a change in the model’s parameters that affects predictions from the model only for a specific input. For a given input $x$ , the prediction $a$ made by the edited model should differ from the prediction $y$ made by the original model only if $x$ is influenced by one of the revised facts.
我们希望编辑神经语言模型的记忆,使得当给定输入时,其输出能反映修订后的事实集合。然而,语言模型的知识通常对我们是不透明的,它们非局部地存储在大量参数和架构组件中。因此,为了具体实现这一任务,我们需要找到一种模型参数的改变,这种改变仅针对特定输入影响模型的预测。对于给定输入$x$,编辑后模型的预测$a$应与原始模型的预测$y$不同,仅当$x$受到某个修订事实的影响时。
2.1 Definition
2.1 定义
More formally, we have a model $x\mapsto f(x;\theta)$ with trained parameters $\theta$ , and a dataset of revisions $\langle x,y,a\rangle\in{\mathcal{D}}$ , i.e., $x$ is an input, $y$ is the prediction preferred by $f(x;\theta)$ , and $a$ is an alternative prediction which we would like an edited version of the model to prefer. Concretely, we keep the model architecture $f$ fixed, and seek alternative parameters $\theta^{\prime}$ such that for $x$ , $f(x;\theta^{\prime})$ would prefer the prediction $a$ instead of $y$ while keeping all other predictions unchanged. In practice, we approximate the set of ‘all other predictions’ using a finite data set $\mathcal{O}^{x}$ of pairs $\langle x^{\prime},y^{\prime}\rangle$ with $x^{\prime}\neq x$ . Moreover, predictions need not be continuous nor differentiable outputs from the model; instead, they may result from an arbitrary decision rule based on $f(x;\theta)$ . For example, when $f(x;\theta)$ parameter ize s a discrete distribution $p_{Y\mid X}$ over the output space, the most standard decision rule is to output the mode of the distribution: $y=\arg\operatorname*{max}_ {c\in\mathcal{V}}p_{Y|X}(c|x,\theta).$ 2
更正式地说,我们有一个模型 $x\mapsto f(x;\theta)$,其训练参数为 $\theta$,以及一个修订数据集 $\langle x,y,a\rangle\in{\mathcal{D}}$,即 $x$ 是输入,$y$ 是 $f(x;\theta)$ 偏好的预测,而 $a$ 是我们希望编辑后的模型更倾向的替代预测。具体来说,我们保持模型架构 $f$ 不变,寻找替代参数 $\theta^{\prime}$,使得对于输入 $x$,$f(x;\theta^{\prime})$ 会更倾向于预测 $a$ 而非 $y$,同时保持所有其他预测不变。在实践中,我们通过有限数据集 $\mathcal{O}^{x}$ 来近似表示“所有其他预测”,该数据集包含成对的 $\langle x^{\prime},y^{\prime}\rangle$,其中 $x^{\prime}\neq x$。此外,预测不必是模型的连续或可微分输出,而是可以基于 $f(x;\theta)$ 的任意决策规则产生。例如,当 $f(x;\theta)$ 参数化输出空间上的离散分布 $p_{Y\mid X}$ 时,最标准的决策规则是输出分布的众数:$y=\arg\operatorname*{max}_ {c\in\mathcal{V}}p_{Y|X}(c|x,\theta).$
Semantically equivalent inputs Optionally, for some revision $\langle x,y,a\rangle\in{\mathcal{D}}$ , we may also have a set $\mathcal{P}^{x}$ of inputs semantically equivalent to $x$ (e.g., automatically-generated paraphrases). Such a set can be used in at least two ways: i) to obtain explicit supervision for changes that should be realized in tandem with $\langle x,y,a\rangle$ ; and, independently of that, ii) to evaluate whether an edited model makes consistent predictions on semantically equivalent inputs. Note that in this work we never use paraphrases at test time, only for training and evaluation of our approach; generating them at test time, while potentially helpful, would have compromised efficiency.
语义等效输入
可选地,对于某些修订 $\langle x,y,a\rangle\in{\mathcal{D}}$ ,我们可能还拥有一组与 $x$ 语义等效的输入 $\mathcal{P}^{x}$ (例如自动生成的释义)。此类集合至少可通过两种方式使用:i) 为应与 $\langle x,y,a\rangle$ 同步实现的变更获取显式监督;以及(独立于前者)ii) 评估编辑后的模型是否对语义等效输入做出一致预测。请注意,本工作中我们从未在测试阶段使用释义,仅将其用于方法的训练和评估;在测试阶段生成释义虽然可能有益,但会损害效率。
2.2 Evaluation
2.2 评估
To test if a method $g$ , producing edited parameters $\theta^{\prime}$ , meets our desiderata, we measure:
为了测试生成编辑参数 $\theta^{\prime}$ 的方法 $g$ 是否满足我们的需求,我们测量:
- success rate: how much $g$ successfully updates the knowledge in $\theta^{\prime}$ , measured as accu
- 成功率:衡量 $g$ 成功更新 $\theta^{\prime}$ 中知识的程度,以准确率 (accu) 为指标
These values are obtained by comparing predictions of $f(\cdot;\theta)$ and $f(\cdot;\theta^{\prime})$ for different subsets of inputs $(e.g.,\mathcal{D},\mathcal{O}^{x},\mathcal{P}^{x})$ and against different targets (e.g., gold-standard, original predictions, or alternative predictions). While these metrics are straightforward to compute in principle, some can be computationally demanding. For example, retain accuracy depends on predictions for all inputs we have access to, which is potentially the entirety of the downstream task’s validation/test data.4
这些数值是通过比较 $f(\cdot;\theta)$ 和 $f(\cdot;\theta^{\prime})$ 对不同输入子集 $(例如 \mathcal{D},\mathcal{O}^{x},\mathcal{P}^{x})$ 的预测结果,并针对不同目标(例如金标准、原始预测或替代预测)得出的。虽然这些指标在原理上计算简单,但部分可能需要较高算力。例如,保留准确率依赖于对所有可访问输入数据的预测,这可能涉及整个下游任务的验证/测试数据集。
Previous work has evaluated similar versions of this task differently. Sinitsin et al. (2020) measure performance deterioration and success rate but do not measure retain accuracy nor equivalence accuracy. A small performance deterioration does not guarantee high equivalence accuracy as the former is sensitive to changes in cases where the original model makes wrong decisions. Assessing accuracy against old or revised facts, which Zhu et al. (2020) also do, does not help to measure the retain accuracy. We argue that preserving model predictions for inputs not in $\mathcal{D}$ is critical in production settings, where model predictions might have been extensively analyzed and tested. For $x^{\prime}\notin\mathcal{D}$ , we aim to maintain all original predictions as well as the model scores $f(x^{\prime};\theta^{\prime})$ itself, effectively avoiding the need to re-calibrate the models (for example, in applications where probability estimates are used downstream).
先前的研究对这一任务的类似版本采用了不同的评估方式。Sinitsin等人 (2020) 测量了性能下降和成功率,但未评估保留准确率或等效准确率。小幅性能下降并不能保证高等效准确率,因为前者对原始模型做出错误决策的情况变化较为敏感。Zhu等人 (2020) 采用的针对旧事实或修订事实的准确率评估方法,同样无助于衡量保留准确率。我们认为,在生产环境中保持模型对 $\mathcal{D}$ 以外输入的预测至关重要,因为这些预测可能已被深入分析和测试。对于 $x^{\prime}\notin\mathcal{D}$ ,我们的目标是维持所有原始预测及模型分数 $f(x^{\prime};\theta^{\prime})$ 本身,从而有效避免重新校准模型的需求(例如在下游使用概率估计的应用场景中)。
3 Related work
3 相关工作
Modifying transformers The most straight forward strategy to edit the knowledge of a model would be to re-train it on a new dataset with additional, modified, or removed facts. This is often unfeasible as LMs require large-scale expensive training that can hardly be reproduced by the most.
修改Transformer
最直接的模型知识编辑策略是在包含新增、修改或删除事实的新数据集上重新训练模型。但这种方法通常不可行,因为训练大语言模型需要大规模且昂贵的计算资源,绝大多数研究者难以复现这一过程。
Sinitsin et al. (2020) propose a meta-learning approach (Finn et al., 2017) for model modification that learns parameters that are easily editable at test time (e.g., updating the knowledge of the model requires only a few SGD steps from these learned parameters). To have a reliable method, they employ a regularized objective forcing the updated model not to deviate from the original one. This technique suffers from three main limitations: i) it requires expensive and specialized pre-training, ii) it is sensitive to many hyper-parameters (e.g., the weights of the regularize rs and the subset of parameters to update), and iii) their multitask objective does not guarantee reliability (i.e., the model is penalized for diverging from the original, rather than constrained not to).
Sinitsin等人(2020)提出了一种用于模型修改的元学习方法(Finn等人,2017),该方法学习在测试时易于编辑的参数(例如,更新模型知识只需从这些学习到的参数进行少量SGD步骤)。为了获得可靠的方法,他们采用了正则化目标,强制更新后的模型不偏离原始模型。该技术存在三个主要局限性:i)需要昂贵且专门的预训练,ii)对许多超参数敏感(例如正则化器的权重和要更新的参数子集),iii)其多任务目标不能保证可靠性(即模型因偏离原始模型而受到惩罚,而不是被约束不偏离)。
Instead of penalizing an updated model for deviating from the original one, Zhu et al. (2020) use constrained optimization. They use a less comput ation ally expensive procedure as they re-finetune on a specific downstream task (with altered data). Their method employs either an $L_{2}$ or $L_{\infty}$ constraint between the original model’s parameters and the edited ones. However, a norm-based constraint on parameters ignores the highly non- linear nature of LMs and how parameters deter- mine the outputs of the model. Indeed, a minimal change in parameter space may produce a completely different output for many datapoints leading to a potentially unreliable method. Additionally, they show the need to select a subset of parameters to be updated, which requires extra development effort. Zhu et al.’s (2020) method is similar to Elastic Weight Consolidation (Kirkpatrick et al., 2017), a technique developed for preventing catastrophic forgetting in neural network models.
Zhu等(2020)采用约束优化方法替代惩罚更新模型与原模型的偏差。他们通过在下游任务(数据已修改)上重新微调,使用计算成本较低的方法。其方法在原始模型参数与编辑后参数之间施加$L_{2}$或$L_{\infty}$约束。然而,基于范数的参数约束忽略了大语言模型(LM)的高度非线性特性及参数如何决定模型输出。事实上,参数空间的微小变化可能导致许多数据点产生完全不同的输出,使得该方法潜在不可靠。此外,研究显示需要选择待更新的参数子集,这需要额外开发工作。Zhu等(2020)的方法类似于弹性权重巩固(Elastic Weight Consolidation)(Kirkpatrick等,2017),该技术是为防止神经网络模型出现灾难性遗忘而开发的。
Knowledge in Language Models Petroni et al. (2019) show that pre-trained language models recall factual knowledge without fine-tuning, which they do by feeding specific prompts to LMs. Handcrafted prompts have been found not to be the best option to extract knowledge from LMs, and various solutions have been proposed to understand what LMs ‘know’ (Jiang et al., 2020; Shin et al., 2020; Liu et al., 2021). Additionally, Roberts et al. (2020) show that large models can be fine-tuned to access their internal memories to answer questions in natural language without any additional context and with surprisingly high accuracy—a setting they referred to as closed-book question answering. Although performing quite well, these models cannot reach the prediction quality of alternatives that retrieve and use context. Approaches that in centi viz e memorization of factual knowledge show to be beneficial for many downstream tasks suggesting that research on methods that effectively edit the memory of a model is indeed important (Zhang et al., 2019; Sun et al., 2019, 2020). Some recent hy- brid approaches that use both implicit and explicit memory show some benefits for question answering (Févry et al., 2020; Verga et al., 2020). Notably, language models that only rely on internal implicit memory are state-of-the-art for (multilingual-) Entity Linking (De Cao et al., 2021a,b). An effective mechanism for editing LM’s implicit memory may be applicable in all these settings.
语言模型中的知识
Petroni等人(2019)研究表明,预训练语言模型无需微调即可回忆事实性知识,这是通过向语言模型输入特定提示实现的。研究发现手工制作的提示并非从语言模型中提取知识的最佳选择,因此提出了多种解决方案来理解语言模型"知道"什么(Jiang等人, 2020; Shin等人, 2020; Liu等人, 2021)。此外,Roberts等人(2020)证明,大型模型可以通过微调访问其内部记忆,在没有任何额外上下文的情况下以自然语言回答问题,且准确率高得惊人——他们将这种设置称为闭卷问答。尽管表现相当出色,但这些模型仍无法达到检索并使用上下文的替代方案的预测质量。专注于事实知识记忆的方法被证明对许多下游任务有益,这表明有效编辑模型记忆的方法研究确实很重要(Zhang等人, 2019; Sun等人, 2019, 2020)。最近一些同时使用隐式和显式记忆的混合方法在问答任务中显示出优势(Févry等人, 2020; Verga等人, 2020)。值得注意的是,仅依赖内部隐式记忆的语言模型在(多语言)实体链接任务中达到了最先进水平(De Cao等人, 2021a,b)。编辑语言模型隐式记忆的有效机制可能适用于所有这些场景。
Causal Interventions Identification of minimal changes to neural networks needed to achieve a certain behaviour has been studied in the context of research in interpreting neural networks (Lakretz et al., 2019; Vig et al., 2020; Elazar et al., 2021; Csordás et al., 2021). The components which need to be updated can be interpreted as controlling or encoding the corresponding phenomena (e.g., subject-verb agreement). Much of this research focused on modifying neuron activation s rather than weights and on sparse interventions (e.g., modifying one or a handful of neurons). While far from our goals, there are interesting connections with our work. For example, our analysis of updates in Section 6.4, though very limited, may shed some light on how factual knowledge is encoded in the parameters of a model.
因果干预
识别神经网络实现特定行为所需的最小变更已在神经网络解释研究背景下得到探讨 (Lakretz et al., 2019; Vig et al., 2020; Elazar et al., 2021; Csordás et al., 2021)。需要更新的组件可被解释为控制或编码相应现象 (如主谓一致)。这类研究多聚焦于修改神经元激活值而非权重,并采用稀疏干预 (如修改单个或少量神经元)。虽然与我们的目标相去甚远,但存在有趣的关联。例如第6.4节对参数更新的分析 (尽管非常有限) 可能揭示事实性知识如何编码在模型参数中。
4 Method
4 方法
We propose to treat the task of editing the memory of a neural model as a learning problem. Instead of defining a handcrafted algorithm to compute the new parameters $\theta^{\prime}$ , we learn a KNOWLEDGEEDITOR: a model that predicts $\theta^{\prime}$ conditioned on an atomic fact that we want to modify. Concretely, KNOWLEDGE EDITOR is a hypernetwork (Ha et al., 2017)—i.e., a neural network that predicts the parameters of another network. Since the task requires every other prediction to stay the same—except the one we desire to change—we cast the learning task as a constrained optimization problem.
我们提出将神经模型记忆编辑任务视为一个学习问题。不同于手工设计算法计算新参数$\theta^{\prime}$,我们通过学习一个KNOWLEDGEEDITOR(知识编辑器)模型来预测$\theta^{\prime}$,该模型以要修改的原子事实为条件。具体而言,KNOWLEDGE EDITOR是一个超网络(Ha等人,2017)——即预测另一网络参数的神经网络。由于该任务要求除目标修改项外其他预测保持不变,我们将学习任务建模为约束优化问题。
Optimization For an input $x$ , changing the prediction of a model $f(\cdot;\theta)$ to $a$ corresponds to minimizing the loss $\textstyle{\mathcal{L}}(\theta;x,a)$ incurred when $a$ is the target. Preserving the rest of the knowledge corresponds to constraining the updated parameter $\theta^{\prime}$ such that model outputs $f(\cdot;\theta^{\prime})$ do not change for $x^{\prime}\in\mathcal{O}^{x}$ . Our editor $g$ is a neural network parameterized by $\phi$ which we choose by optimising the following objective for each data-point $\langle x,y,a\rangle\in{\mathcal{D}}$ :
优化 对于输入 $x$,将模型 $f(\cdot;\theta)$ 的预测更改为 $a$ 对应于最小化目标为 $a$ 时的损失 $\textstyle{\mathcal{L}}(\theta;x,a)$。保留其余知识则对应于约束更新后的参数 $\theta^{\prime}$,使得模型输出 $f(\cdot;\theta^{\prime})$ 对于 $x^{\prime}\in\mathcal{O}^{x}$ 保持不变。我们的编辑器 $g$ 是由 $\phi$ 参数化的神经网络,通过针对每个数据点 $\langle x,y,a\rangle\in{\mathcal{D}}$ 优化以下目标来选择:
$$
\begin{array}{r l}{\underset{\phi}{\operatorname*{min}}}&{\displaystyle\sum_{\hat{x}\in\mathcal{P}^{x}}\mathcal{L}(\theta^{\prime};\hat{x},a)}\ {\mathrm{s.t.}}&{\mathcal{C}(\theta,\theta^{\prime},f;\mathcal{O}^{x})\leq m,}\end{array}
$$
$$
\begin{array}{r l}{\underset{\phi}{\operatorname*{min}}}&{\displaystyle\sum_{\hat{x}\in\mathcal{P}^{x}}\mathcal{L}(\theta^{\prime};\hat{x},a)}\ {\mathrm{s.t.}}&{\mathcal{C}(\theta,\theta^{\prime},f;\mathcal{O}^{x})\leq m,}\end{array}
$$
where $\mathcal{P}^{x}$ is the set of semantically equivalent inputs to $x$ (for convenience we assume it contains at least $x$ ), $\theta^{\prime}=\theta+g(x,y,a;\phi)$ , $\mathcal{C}$ is a constrainton the update, and the margin $m\in\mathbb{R}_ {>0}$ is a hyper parameter. The constraint is used to express our desire to preserve model outputs unchanged for $x^{\prime}\neq x$ . Note that only $x$ , but not the rest of $\mathcal{P}^{x}$ , are provided as input to the editor, as these will not be available at test time. In our models, $f(x;\theta)$ parameter ize s a discrete distribution $p_{Y\mid X}$ over the output sample space $\mathcal{V}$ , hence we choose to constrain updates in terms of sums of Kullback-Leibler (KL) divergences from the updated model to the original one: $\mathcal{C}_{K L}(\theta,\theta^{\prime},f;\mathcal{O}^{x})=$
其中$\mathcal{P}^{x}$是$x$的语义等价输入集合(为方便起见,我们假设它至少包含$x$),$\theta^{\prime}=\theta+g(x,y,a;\phi)$,$\mathcal{C}$是对更新的约束,边界$m\in\mathbb{R}_ {>0}$是一个超参数。该约束用于表达我们希望保持模型对$x^{\prime}\neq x$的输出不变的意图。注意,只有$x$而非$\mathcal{P}^{x}$中的其他元素会作为编辑器的输入,因为这些在测试时不可用。在我们的模型中,$f(x;\theta)$参数化了输出样本空间$\mathcal{V}$上的离散分布$p_{Y\mid X}$,因此我们选择通过从更新后模型到原始模型的Kullback-Leibler (KL)散度之和来约束更新:$\mathcal{C}_{K L}(\theta,\theta^{\prime},f;\mathcal{O}^{x})=$
$$
\sum_{x^{\prime}\in\mathcal{O}^{x}}\sum_{c\in\mathcal{V}}p_{Y|X}(c|x^{\prime},\theta)\log\frac{p_{Y|X}(c|x^{\prime},\theta)}{p_{Y|X}(c|x^{\prime},\theta^{\prime})}
$$
$$
\sum_{x^{\prime}\in\mathcal{O}^{x}}\sum_{c\in\mathcal{V}}p_{Y|X}(c|x^{\prime},\theta)\log\frac{p_{Y|X}(c|x^{\prime},\theta)}{p_{Y|X}(c|x^{\prime},\theta^{\prime})}
$$
The constraint pushes the updated model to predict output distributions identical to the original one for all $x^{\prime}\neq x$ . An alternative constraint we could employ is an $L_{p}$ norm over the parameter updates such that $g$ is optimized to make a minimal update to the original model parameter: $\begin{array}{r}{\mathcal{C}_ {L_{p}}(\theta,\theta^{\prime},\bar{f};\mathcal{O}^{x})=(\sum_{i}|\bar{\theta}_ {i}-\theta_{i}^{\prime}|^{p})^{1/p}}\end{array}$ . This constraint was previously used by Zhu et al. (2020). However, such a constraint, expressed purely in parameter space and without regards to the model architecture $f$ , does not directly encourage model outputs to be close to original ones in function space (i.e., the two functions to be similar). Neural models are highly non-linear functions, so we do not expect this type of constraint to be effective. This will be empirically demonstrated in Section 6.
该约束促使更新后的模型对所有$x^{\prime}\neq x$预测与原始模型相同的输出分布。我们可采用的另一种约束是对参数更新施加$L_{p}$范数限制,使得优化后的$g$对原始模型参数作出最小改动:$\begin{array}{r}{\mathcal{C}_ {L_{p}}(\theta,\theta^{\prime},\bar{f};\mathcal{O}^{x})=(\sum_{i}|\bar{\theta}_ {i}-\theta_{i}^{\prime}|^{p})^{1/p}}\end{array}$。Zhu等人(2020)曾使用过此类约束。然而,这种纯粹基于参数空间且不考虑模型架构$f$的约束,并不能直接保证模型输出在函数空间中接近原始输出(即两个函数相似)。由于神经模型具有高度非线性特性,我们不认为此类约束会有效果,第6节将通过实验验证这一点。
Tractable approximations Non-linear constrained optimization is generally intractable, thus we employ Lagrangian relaxation (Boyd et al., 2004) instead. The constraint itself poses a computational challenge, as it requires assessing KL for all datapoints in the dataset at each training step. For tract ability, we evaluate the constraint approximately via Monte Carlo (MC) sampling (see Appendix A for more details). Finally, in sequence-to-sequence models, assessing KL is intractable even for a single data point, as the sample space $\mathcal{V}$ is unbounded. In such cases we approximate the computation on a subset of the sample space obtained via beam search.
可处理的近似方法
非线性约束优化通常难以处理,因此我们采用拉格朗日松弛法 (Boyd et al., 2004) 作为替代。约束本身带来了计算挑战,因为它需要在每个训练步骤中评估数据集中所有数据点的 KL 散度。为了提高可处理性,我们通过蒙特卡洛 (MC) 采样近似评估约束(详见附录 A)。最后,在序列到序列模型中,即使对于单个数据点,评估 KL 散度也是不可行的,因为样本空间 $\mathcal{V}$ 是无界的。在这种情况下,我们通过束搜索获得的样本空间子集来近似计算。
Architecture Instead of predicting $\theta^{\prime}$ directly, our hyper-network predicts a shift $\Delta\theta$ such that $\theta^{\prime}=\theta+\Delta\theta$ . A naive hyper-network implementation might be over-parameterized, as it requires a quadratic number of parameters with respect to the size of the target network. Thus, we apply a trick similar to Krueger et al. (2017) to make $g$ tractably predict edits for modern large deep neural networks (e.g., BERT). Namely, $g$ makes use of the gradient information $\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta};\boldsymbol{x},\boldsymbol{a})$ as it carries rich information about how $f$ accesses the knowledge stored in $\theta$ (i.e., which parameters to update to increase the model likelihood given $a$ ).
架构
我们不直接预测 $\theta^{\prime}$,而是通过超网络预测一个偏移量 $\Delta\theta$,使得 $\theta^{\prime}=\theta+\Delta\theta$。简单的超网络实现可能参数过多,因为其参数量与目标网络规模呈平方关系。因此,我们采用了类似 Krueger et al. (2017) [20] 的技巧,使 $g$ 能够高效预测现代大型深度神经网络(如 BERT)的修改。具体而言,$g$ 利用了梯度信息 $\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta};\boldsymbol{x},\boldsymbol{a})$,因为这些信息包含了 $f$ 如何访问存储在 $\theta$ 中的知识(即给定 $a$ 时,应更新哪些参数以提高模型似然)。
We first encode $\langle x,y,a\rangle$ , concatenating the text with special separator and feeding it to a bidirectional-LSTM (Hochreiter and Schmid huber, 1997). Then, we feed the last LSTM hidden states to a FFNN that outputs a single vector $h$ that conditions the further computations. To predict the shift for a weight matrix $W^{n\times m}\in\theta$ , we use five FFNNs conditioned on $h$ that predict vectors $\alpha,\beta\in\mathbb{R}^{m},\gamma,\delta\in\mathbb{R}^{n}$ and a scalar $\eta\in\mathbb R$ . Then
我们首先对 $\langle x,y,a\rangle$ 进行编码,将文本与特殊分隔符拼接后输入双向LSTM (Hochreiter and Schmidhuber, 1997)。然后将LSTM的最终隐藏状态输入前馈神经网络(FFNN),输出一个用于后续计算的条件向量 $h$。为了预测权重矩阵 $W^{n\times m}\in\theta$ 的偏移量,我们使用五个基于 $h$ 条件化的FFNN来预测向量 $\alpha,\beta\in\mathbb{R}^{m},\gamma,\delta\in\mathbb{R}^{n}$ 以及标量 $\eta\in\mathbb R$。接着
$$
\begin{array}{r}{\Delta W=\sigma(\eta)\cdot\left(\hat{\alpha}\odot\nabla_{W}\mathcal{L}(W;x,a)+\hat{\beta}\right),}\ {\mathrm{with}\quad\hat{\alpha}=\hat{\sigma}(\alpha)\gamma^{\top}\quad\mathrm{and}\quad\hat{\beta}=\hat{\sigma}(\beta)\delta^{\top},}\end{array}
$$
$$
\begin{array}{r}{\Delta W=\sigma(\eta)\cdot\left(\hat{\alpha}\odot\nabla_{W}\mathcal{L}(W;x,a)+\hat{\beta}\right),}\ {\mathrm{with}\quad\hat{\alpha}=\hat{\sigma}(\alpha)\gamma^{\top}\quad\mathrm{and}\quad\hat{\beta}=\hat{\sigma}(\beta)\delta^{\top},}\end{array}
$$
where $\sigma$ is the Sigmoid function (i.e., $x\mapsto(1+$ $\exp(-x))^{-1})$ , and $\hat{\sigma}$ indicates the Softmax func- tion (i.e., $x\mapsto\exp(x)/\sum_{i}\exp(x_{i}))$ . With this formulation, the paramete rs for the hyper-network $\phi$ scale linearly with the size of $\theta$ . An interpretation of Equation 3 is that an update $\Delta W$ is a gated sum of a scaled gradient of the objective and a bias term. The scale for the gradient and the bias are generated via an outer vector product as it allows for efficient parameter iz ation of a matrix with just three vectors. The gate lets the model keep some parameters unchanged.
其中 $\sigma$ 是Sigmoid函数 (即 $x\mapsto(1+$ $\exp(-x))^{-1})$),而 $\hat{\sigma}$ 表示Softmax函数 (即 $x\mapsto\exp(x)/\sum_{i}\exp(x_{i}))$。通过这种形式化表示,超网络 $\phi$ 的参数规模与 $\theta$ 的大小呈线性关系。对公式3的一种解释是:更新量 $\Delta W$ 是目标函数缩放梯度与偏置项的加权和。梯度的缩放系数和偏置项通过外积向量生成,因为这样只需三个向量就能高效参数化一个矩阵。门控机制允许模型保持部分参数不变。
Margin annealing The margin $m$ is a hyperparameter and therefore fixed. However, i) it is hard to choose since it is task-dependent, and ii) it should be as small as possible. If the margin is too small, however, we risk having a small feasible set, and the model may never converge. To address both issues, we pick some initial value for the margin and anneal it during training conditioned on validation performance: when the model successfully changes $>90%$ of the predictions, we multiply the margin by 0.8. We stop decreasing the margin once it reaches a desirable small value. The annealing procedure prevents the model from diverging while increasingly tightening the constraint.
边界退火 (margin annealing)
边界值 $m$ 是一个超参数,因此是固定的。然而,i) 由于它与任务相关,很难选择;ii) 它应该尽可能小。但如果边界值太小,我们可能会面临可行集过小的风险,模型可能无法收敛。为了解决这两个问题,我们为边界值选择一个初始值,并在训练过程中根据验证性能对其进行退火处理:当模型成功改变 $>90%$ 的预测时,我们将边界值乘以 0.8。一旦边界值达到理想的小值,我们便停止减小。这种退火过程可以防止模型发散,同时逐步收紧约束。
5 Experimental Setting
5 实验设置
We aim to evaluate the effectiveness of KNOWLEDGEEDITOR comparing to baselines on knowledge-intensive tasks where the importance of modifying the memory of a large LM has a broad impact. We then test our method on closed-book fact-checking and closed-book question answering with the metrics proposed in Section 2.2.
我们旨在评估KNOWLEDGEEDITOR与基线方法在知识密集型任务上的有效性,这些任务中修改大语言模型记忆的重要性具有广泛影响。随后,我们采用第2.2节提出的指标,在闭卷事实核查和闭卷问答任务上测试该方法。
5.1 Baselines
5.1 基线方法
We compare against two baselines: i) fine-tuning and ii) the method proposed by Zhu et al. (2020). Fine-tuning corresponds to using standard gradient descent, minimizing the loss for the fact/prediction we want to revise. For this, we follow Sinitsin et al. (2020) and employ RMSProp (Tieleman and Hinton, 2012).6 We set the learning rate to $10^{-5}$ and stop upon successfully changing the output of the model or having reached a maximum of 100 gradient steps. Zhu et al.’s (2020) method extends fine-tuning with an $L_{\infty}$ constraint on parameters.7 Following both Sinitsin et al. (2020) and Zhu et al. (2020) we report these baselines fine-tuning all parameters or just a subset of them. We limit the search to selecting entire layers and base our decision on performance on a subset of the validation set. Note that selecting a subset of parameters for update requires an extensive search, which KNOWLEDGE EDITOR dispenses with by auto mati call y learning it.
我们对比了两个基线方法:i) 微调 (fine-tuning) 和 ii) Zhu等人 (2020) 提出的方法。微调对应使用标准梯度下降法,最小化待修正事实/预测的损失值。具体实现遵循Sinitsin等人 (2020) 的方案,采用RMSProp优化器 (Tieleman and Hinton, 2012),学习率设为$10^{-5}$,在成功改变模型输出或达到最大100次梯度步长时停止训练。Zhu等人 (2020) 的方法在微调基础上增加了参数$L_{\infty}$约束。与Sinitsin等人 (2020) 和Zhu等人 (2020) 的做法一致,我们报告了全参数微调和部分参数微调的基线结果。参数子集搜索限定在全网络层范围,基于验证集子集的表现进行选择。值得注意的是,KNOWLEDGE EDITOR通过自动学习机制避免了参数子集选择所需的大量搜索工作。
5.2 Models and data
5.2 模型与数据
We evaluate on closed-book fact-checking (FC) fine-tune a BERT base model (Devlin et al., 2019) on the binary FEVER dataset (Thorne et al., 2018) from KILT (Petroni et al., 2021). We also evaluate on a task with a more complex output space: closedbook question answering (QA). For that we finetune a BART base model (Lewis et al., 2020) with a standard seq2seq objective on the Zero-Shot Relation Extraction (zsRE) dataset by Levy et al. (2017). We evaluate on this dataset because it is annotated with human-generated question paraphrases that we can use to measure our model’s robustness to semantically equivalent inputs. We create alternative predictions for FC simply flipping the labels, whereas for QA we pick all hypotheses enumerated via beam search except the top-1. The latter ensures high-probability outcomes under the model distribution. We generate semantically equivalent inputs with back-translation. See Appendix B for technical details on models and data collection.
我们在闭卷事实核查(FC)任务上评估,基于KILT (Petroni et al., 2021)中的二元FEVER数据集(Thorne et al., 2018)对BERT基础模型(Devlin et al., 2019)进行微调。同时评估了一个输出空间更复杂的任务:闭卷问答(QA)。为此,我们采用标准序列到序列(seq2seq)目标,在Levy等人(2017)提出的零样本关系抽取(zsRE)数据集上对BART基础模型(Lewis et al., 2020)进行微调。选择该数据集是因为其包含人工生成的问句改写标注,可用于测量模型对语义等效输入的鲁棒性。对于FC任务,我们通过简单翻转标签生成替代预测;而对于QA任务,则选取除top-1外所有通过束搜索(beam search)枚举的假设,这确保了这些结果在模型分布下具有高概率。语义等效输入通过回译(back-translation)生成。模型与数据收集的技术细节详见附录B。
6 Results
6 结果
Table 1 reports the main results for fact-checking and question answering. Overall, KNOWLEDGEEDITOR achieves high performance in all metrics. Some other methods also achieve high accuracy in some metrics but always sacrificing others (i.e., never meeting all our desiderata at once).
表 1: 报告了事实核查和问答任务的主要结果。总体而言,KNOWLEDGEEDITOR 在所有指标上都取得了优异表现。其他方法虽在某些指标上能达到高准确率,但总是以牺牲其他指标为代价 (即无法同时满足所有预期目标)。
We compare methods along different metrics (as opposed to a single one), as there is no way to precisely determine the importance of each of these metrics. To gather more insight, we compute their stochastic convex combination with coefficients sampled from a Dirichlet distribution (with $\alpha=1$ to ensure a very diverse set of combinations) and report in Figure 6 in Appendix C an estimate of the probability that a system outperforms another across 1, 000 such combinations. The probability of our full method to outperform all baselines is very high for both FC and QA ( $\approx97\%$ and $\approx88\%$ , respectively). In Figure 5 in Appendix C, we show the distributions of the combined scores (i.e., the raw data for the approximation reported in Figure 6). We then analyze different aspects of our method and the baselines.
我们通过多种指标(而非单一指标)来比较不同方法,因为无法精确确定每个指标的重要性。为了更深入分析,我们计算了这些指标的随机凸组合(系数采样自Dirichlet分布,其中$\alpha=1$以确保组合的多样性),并在附录C的图6中报告了系统在1,000次组合中优于其他系统的概率估计。我们的完整方法在FC和QA任务上超越所有基线的概率都非常高(分别约为$\approx97\%$和$\approx88\%$)。附录C的图5展示了组合得分的分布情况(即图6近似结果的原始数据)。随后,我们分析了方法和基线的不同方面。
6.1 Success rate
6.1 成功率
Every method achieves an almost perfect success rate on fact-checking. All methods but ours apply updates in a loop, stopping either when the new model is successfully updated or after reaching a maximum number of iterations. The success rate for KNOWLEDGE EDITOR is not $100%$ because we do not apply more than one update even in case of failure. To this end, we also show an experiment with our method with multiple updates within a loop employing the same stopping criteria as the baselines. Note that we apply this only at test time (i.e., we do not train for multiple updates). When applying multiple updates also our method reaches a $100%$ success rate on fact-checking and almost perfect accuracy $(>99%)$ ) for QA.8
每种方法在事实核查上都达到了近乎完美的成功率。除我们的方法外,所有方法都在循环中应用更新,直到新模型成功更新或达到最大迭代次数为止。KNOWLEDGE EDITOR的成功率并非100%,因为即使在失败情况下我们也仅应用一次更新。为此,我们还展示了采用与基线相同停止准则的循环多更新实验(注:仅在测试时应用多更新,训练阶段不执行多更新)。当应用多次更新时,我们的方法在事实核查上也达到了100%成功率,问答准确率接近完美(>99%) [8]。
Table 1: Accuracy scores on fact-checking and question answering for the metrics presented in Section 2.2. *We report both the accuracy on the set of generated paraphrases (left) and human-annotated (right).†Apply updates in a loop, stopping when the update is a success or when reaching a maximum number of iterations (only at test time). ‡Using paraphrases (semantically equivalent inputs) as additional supervision (only at training time).
| Fact-Checking | QuestionAnswering | |||||||
| Method | Success rate ↑ | Retain acc↑ | Equiv. acc↑ | Perform. | Success rate↑ | Retain acc↑ | Equiv. acc↑* | Perform. ↑p |
| Fine-tune (1st layer) | 100.0 | 99.44 | 42.24 | 0.00 | 98.68 | 91.43 | 89.86/93.59 | 0.41 |
| Fine-tune (alllayers) | 100.0 | 86.95 | 95.58 | 2.25 | 100.0 | 67.55 | 97.77 / 98.84 | 4.50 |
| Zhu et al. (1st layer) | 100.0 | 99.44 | 40.30 | 0.00 | 81.44 | 92.86 | 72.63/78.21 | 0.32 |
| Zhu et al. (all layers) | 100.0 | 94.07 | 83.30 | 0.10 | 80.65 | 95.56 | 76.41/79.38 | 0.35 |
| Ours CLz | 99.10 | 45.10 | 99.01 | 35.29 | 99.10 | 46.66 | 97.16 / 99.24 | 9.22 |
| KNOWLEDGEEDITOR | 98.80 | 98.14 | 82.69 | 0.10 | 94.65 | 98.73 | 86.50/ 92.06 | 0.11 |
| + l0oopt | 100.0 | 97.78 | 81.57 | 0.59 | 99.23 | 97.79 | 89.51/96.81 | 0.50 |
| +D | 98.50 | 98.55 | 95.25 | 0.24 | 94.12 | 98.56 | 91.20/94.53 | 0.17 |
| + P" + loop | 100.0 | 98.46 | 94.65 | 0.47 | 99.55 | 97.68 | 93.46/ 97.10 | 0.95 |
表 1: 基于第2.2节指标的查证与问答准确率得分。*我们同时报告生成改写样本集(左)和人工标注集(右)的准确率。†循环应用更新,在更新成功或达到最大迭代次数时停止(仅测试阶段)。‡使用改写样本(语义等价输入)作为额外监督信号(仅训练阶段)。
| 方法 | 查证成功率↑ | 查证保留准确率↑ | 查证等价准确率↑ | 查证性能 | 问答成功率↑ | 问答保留准确率↑ | 问答等价准确率↑* | 问答性能↑p |
|---|---|---|---|---|---|---|---|---|
| 微调(首层) | 100.0 | 99.44 | 42.24 | 0.00 | 98.68 | 91.43 | 89.86/93.59 | 0.41 |
| 微调(全层) | 100.0 | 86.95 | 95.58 | 2.25 | 100.0 | 67.55 | 97.77/98.84 | 4.50 |
| Zhu等(首层) | 100.0 | 99.44 | 40.30 | 0.00 | 81.44 | 92.86 | 72.63/78.21 | 0.32 |
| Zhu等(全层) | 100.0 | 94.07 | 83.30 | 0.10 | 80.65 | 95.56 | 76.41/79.38 | 0.35 |
| 本方法CLz | 99.10 | 45.10 | 99.01 | 35.29 | 99.10 | 46.66 | 97.16/99.24 | 9.22 |
| KNOWLEDGEEDITOR | 98.80 | 98.14 | 82.69 | 0.10 | 94.65 | 98.73 | 86.50/92.06 | 0.11 |
| +循环迭代† | 100.0 | 97.78 | 81.57 | 0.59 | 99.23 | 97.79 | 89.51/96.81 | 0.50 |
| +改写监督‡ | 98.50 | 98.55 | 95.25 | 0.24 | 94.12 | 98.56 | 91.20/94.53 | 0.17 |
| +改写监督‡+循环迭代† | 100.0 | 98.46 | 94.65 | 0.47 | 99.55 | 97.68 | 93.46/97.10 | 0.95 |
Closed-book QA is a more challenging task since the output space is text and not just a binary label. In this setting, KNOWLEDGE EDITOR achieves high accuracy $(\approx95%$ or $>99%$ with the loop). Among all methods, KNOWLEDGE EDITOR gets the best success rate while also obtaining the best retain accuracy. In QA, Zhu et al.’s (2020) method does not reach a good success rate $(\approx80%)$ . We searched hyper parameters for their method also to have high retain accuracy, and indeed that is higher than regular fine-tuning. However, unlike fact-checking, regular fine-tuning for QA gets almost perfect scores but at the expense of the retain accuracy. Sequence-to-sequence models are more sensitive to a slight parameter shift. This happens because minor changes may completely alter the top $\mathbf{\nabla}\cdot\mathbf{k}$ prediction from beam search (in the case of QA). Differently, in a binary classifier (in the case of FC) the probability of a prediction can change substantially without crossing the decision boundary (usually set at 0.5 when not calibrated).
闭卷问答 (Closed-book QA) 是一项更具挑战性的任务,因为输出空间是文本而不仅仅是二元标签。在此设置下,KNOWLEDGE EDITOR 实现了高准确率 $(\approx95%$ 或循环后 $>99%)$。在所有方法中,KNOWLEDGE EDITOR 获得了最佳成功率,同时也保持了最高的保留准确率。在问答任务中,Zhu 等人 (2020) 的方法未能达到理想成功率 $(\approx80%)$。我们为其方法搜索了超参数以保持高保留准确率,结果确实优于常规微调。然而与事实核查不同,问答任务的常规微调虽然能获得近乎完美的分数,但会牺牲保留准确率。序列到序列模型对微小参数变化更为敏感,这是因为细微改动可能彻底改变束搜索 (beam search) 的 top $\mathbf{\nabla}\cdot\mathbf{k}$ 预测结果(问答任务中)。相比之下,二元分类器(事实核查任务中)的预测概率可能发生显著变化却不会跨越决策边界(未校准时通常设为 0.5)。
6.2 Retaining previous knowledge
6.2 保留先前知识
KNOWLEDGE EDITOR maintains the predictions in the validation set almost perfectly (retain accuracy is ${\approx}98%$ for both FC and QA). Conversely, as expected, our method with $\mathcal{C}_ {L_{2}}$ has very low retain accuracy (always $<50%$ ). $\mathcal{C}_ {L_{2}}$ suffers from catastrophic forgetting because it does not enforce the updated model to be close to the original one in function space (i.e., the two functions to be similar) but just in parameter space.
KNOWLEDGE EDITOR 在验证集上几乎完美地保持了预测性能(FC和QA的保留准确率均为 ${\approx}98%$ )。相反,正如预期的那样,我们采用 $\mathcal{C}_ {L_{2}}$ 的方法保留准确率非常低(始终 $<50%$ )。 $\mathcal{C}_ {L_{2}}$ 存在灾难性遗忘问题,因为它没有强制更新后的模型在函数空间(即要求两个函数相似)接近原始模型,而仅仅是在参数空间保持接近。
Fine-tuning all layers is successful but it affects the previously acquired knowledge negatively: retain accuracy is $\approx87%$ and $\approx68%$ for FC and QA, respectively, while performance deterioration in $\approx2%$ and $\approx4%$ . Fine-tuning a single layer is more effective as it prevents over-fitting (the best model updates the 1st layer in both FC and QA). However, in FC the updated model does not generalize on semantic equivalent inputs: the accuracy on paraphrases is much lower even than versions of our methods which do not use paraphrases in training ( $42%$ vs. $>81%$ ), and even more so when compared to those which use them $(>94%$ ).
微调所有层虽然能成功,但会对先前习得的知识产生负面影响:FC和QA的保留准确率分别约为87%和68%,而性能下降幅度分别约为2%和4%。仅微调单层更为有效,因其能防止过拟合(最佳模型在FC和QA中都更新了第1层)。然而在FC中,更新后的模型无法泛化到语义等效输入:即使与训练中未使用释义的版本相比(42% vs. >81%),其释义准确率也低得多,若与使用释义训练的版本相比则差距更大(>94%)。
Fine-tuning with Zhu et al.’s (2020) method does not affect performance for FC much, which is not surprising since standard fine-tuning already gets almost perfect scores. Differently, in the QA setting, using their constrained optimization boosts the retain accuracy (up to $+4%$ to normal finetuning) but at the cost of a low success rate $(\approx80%$ where fine-tuning gets the perfect score).
使用Zhu等人(2020)的方法进行微调对FC性能影响不大,这并不意外,因为标准微调已经能获得近乎完美的分数。不同的是,在QA场景中,采用他们的约束优化能提高保留准确率(较常规微调最高提升+4%),但代价是成功率较低(约80%,而微调能获得完美分数)。
6.3 Accuracy on paraphrases
6.3 复述准确率
We evaluate our method both with and without the additional supervision of paraphrases to improve generalization—that corresponds to have $\mathcal{P}^{x}$ as the set of paraphrases of $x$ or $\mathcal{P}^{x}={x}$ in Equation 1, respectively. Without this additional supervision,
我们评估了在有和没有额外释义监督的情况下方法的表现,以提高泛化能力——这分别对应于在公式1中将 $\mathcal{P}^{x}$ 设为 $x$ 的释义集合或 $\mathcal{P}^{x}={x}$。在没有这种额外监督的情况下,
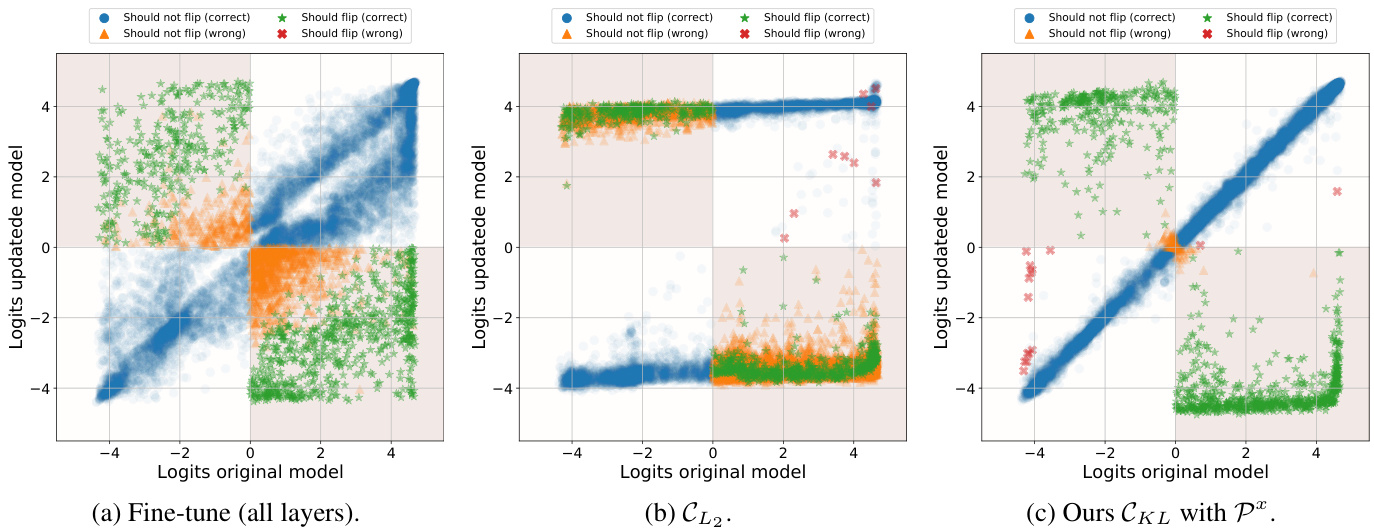
Figure 3: Distribution of logits of the original model and updated model on FEVER. Fine-tuning all layers (a) leads to many errors, and the probability of the predictions does not stay the same even when they do not cross the decision boundary. $\mathcal{C}_ {L_{2}}$ (b) successfully flips labels, but it does not force the predictions to stay the same. For our full method, $\mathcal{C}_{K L}$ with $\mathcal{P}^{x}$ (c), errors are mainly concentrated around the origin where the model is uncertain, and small perturbations make logits to cross the decision boundary. Better view with colors.
图 3: FEVER任务上原始模型与更新模型的logit分布对比。全层微调(a)会导致大量错误,且预测概率在未跨越决策边界时仍会发生变化。$\mathcal{C}_ {L_{2}}$ (b) 能成功翻转标签,但无法保持预测结果不变。采用完整方法 $\mathcal{C}_{K L}$ 结合 $\mathcal{P}^{x}$ (c) 时,错误主要集中在模型不确定的原点附近,微小扰动即可使logit跨越决策边界。建议查看彩色版本以获得更佳效果。
KNOWLEDGE EDITOR is already competitive in equivalence accuracy. However, employing this additional supervision is clearly beneficial on both tasks: we get the same success rate and re-train accuracy but equivalence accuracy improves by $>70%$ on FC and $>30%$ on QA, respectively (for generated paraphrases). In FC, although finetuning of a single layer proved to be optimal in terms of success rate and retain accuracy, it performs poorly for paraphrases. That is the model successfully updates the prediction of a particular datapoint, but does not update predictions of paraphrases. This indicates that fine-tuning to edit the knowledge of a model does not generalize well, and it overfits to specific inputs. On QA, also Zhu et al. (2020) performs poorly compared to our or other methods.
知识编辑器 (KNOWLEDGE EDITOR) 在等效准确率方面已具备竞争力。然而,采用这种额外监督对两项任务均有明显益处:在生成释义的情况下,我们保持了相同的成功率和重训练准确率,但FC任务的等效准确率提升超过70%,QA任务提升超过30%。对于FC任务,虽然单层微调在成功率和保留准确率方面表现最优,但其在释义样本上表现欠佳。这表明模型能成功更新特定数据点的预测,却无法同步更新释义样本的预测,反映出知识编辑的微调方法泛化能力不足,容易对特定输入过拟合。在QA任务中,Zhu等人 (2020) 的方法相比本文或其他方法同样表现不佳。
When other methods perform on par or better than ours on paraphrases, they do not have good retain accuracy (e.g., see QA fine-tuning on Table 1). Fine-tuning on QA seems to generalize better than on FC, but does not preserve previous knowledge. In Table 1 we also report both the accuracy on the set of generated and human-generated paraphrases. Surprisingly, the scores on human-generated paraphrases are higher. We speculate that this happens because automatic paraphrases are sometimes not semantically equivalent or fluent.
当其他方法在释义任务上表现与我们相当或更好时,它们的保留准确率却不理想(例如,参见表1中的QA微调结果)。QA微调相比FC微调展现出更好的泛化能力,但会丢失先前学到的知识。表1中我们同时报告了自动生成释义和人工生成释义的准确率。值得注意的是,人工释义的得分更高。我们推测这是因为自动生成的释义有时缺乏语义对等性或流畅性。
6.4 Analysis of model updates
6.4 模型更新分析
In Figure 3 we plot the distribution of logits of the original and updated model on FC for different methods. With an ideal method, all logits before and after an update have to stay the same (except the ones we want to change). From that figure, we can see distributions of different types of errors such as datapoints whose predictions were mistakenly flipped (from true to false or the other way around). These errors are mostly concentrated around the origin, where small perturbations make logits cross the decision boundary. When finetuning all layers, we can see a clear impact on logits, they undergo a lot of change (i.e., points do not concentrate around the diagonal). Indeed, finetuning makes many datapoints cross the decision boundary and their probabilities to change from the original ones. The failure of $\mathcal{C}_ {L_{2}}$ is visible in Figure 3b as this method preserves almost none of the previous predictions. Instead KNOWLEDGE EDITOR preserves almost all of the predicted labels as well as their probabilities (most datapoints in Figure 3c stay on the diagonal).
在图3中,我们绘制了不同方法下原始模型与更新模型在FC上的logit分布。理想情况下,更新前后的所有logit应保持不变(除我们有意修改的部分)。该图展示了各类错误的分布情况,例如预测结果被错误翻转的数据点(从真变假或反之)。这些错误主要集中在原点附近,微小扰动即可使logits跨越决策边界。当微调所有层时,logits受到明显影响,发生大幅变化(即数据点未沿对角线集中)。实际上,微调会导致大量数据点跨越决策边界,其概率值也偏离原始值。图3b清晰展示了$\mathcal{C}_ {L_{2}}$的失效,该方法几乎未能保留任何先前预测。相比之下,KNOWLEDGE EDITOR几乎完整保留了所有预测标签及其概率(图3c中大多数数据点保持在对角线上)。
We also report visualization s of the average weight updates for the QA experiment in Figure 4. We report the setting with additional supervision from paraphrases (but the heatmaps are similar without them). There are three main observations from this plot. First, gradients are mostly concentrated on the first encoder layer and the last decoder layer. Gradients explain why the best subset of parameters to update is the first layer. Secondly, fine-tuning does not preserve gradient magnitudes and updates the whole model almost uniformly. That happens because of the optimizer’s adaptive learning rate that initially erases the gradient direction. The gradient direction plays a role only after a couple of gradient steps, but most of the time, the method only needs one step to modify its knowledge. Lastly, our updates are sparser and are not consistent with the gradient for changing the predictions. That indicates that our method learns to use the gradient in a meaningful way (i.e. ignoring some directions or manipulating its magnitude). It is surprising that the knowledge manipulation seems to be achieved by primarily modifying parameters affecting the shape of the attention distribution $(W_{s e l f}^{K}$ and W sQelf ) rather than, e.g., values $(W_{s e l f}^{V})$ . As we discussed, the hyper-network may be regarded as a probe providing insights about the mechanism used by the model to encode the knowledge (Vig et al., 2020). For example, the focus on the bottom layer is already intriguing, as it contrasts with claims that memorization happens in top layers of image classification models (Stephenson et al., 2021), hinting at substantial differences in the underlying memorization mechanisms in NLP and vision. Proper investigation is however outside of the scope of this study. See Appendix C for some additional analysis.
我们还报告了QA实验中平均权重更新的可视化结果(见图4)。我们采用了带复述额外监督的设置(但热力图在不加监督时也类似)。从图中可得出三个主要观察结果:首先,梯度主要集中在第一个编码器层和最后一个解码器层。梯度分布解释了为何最佳参数更新子集位于第一层。其次,微调过程未能保持梯度强度,几乎均匀地更新了整个模型。这是由于优化器的自适应学习率最初会抹除梯度方向。梯度方向仅在几步更新后才开始发挥作用,但该方法通常只需单步即可完成知识修正。最后,我们的更新更为稀疏,且与改变预测所需的梯度不一致。这表明我们的方法学会了有意义地利用梯度(例如忽略某些方向或调整其强度)。值得注意的是,知识操作似乎主要通过修改影响注意力分布形状的参数($(W_{self}^{K}$和$W_{self}^{Q}$)而非值矩阵$(W_{self}^{V})$来实现。如我们所讨论的,超网络可视为揭示模型知识编码机制的探针(Vig等人,2020)。例如,对底层的聚焦已颇具启发性,这与图像分类模型中记忆发生在顶层的论断(Stephenson等人,2021)形成对比,暗示NLP与视觉领域记忆机制存在本质差异。但深入探究已超出本研究范围,更多分析见附录C。
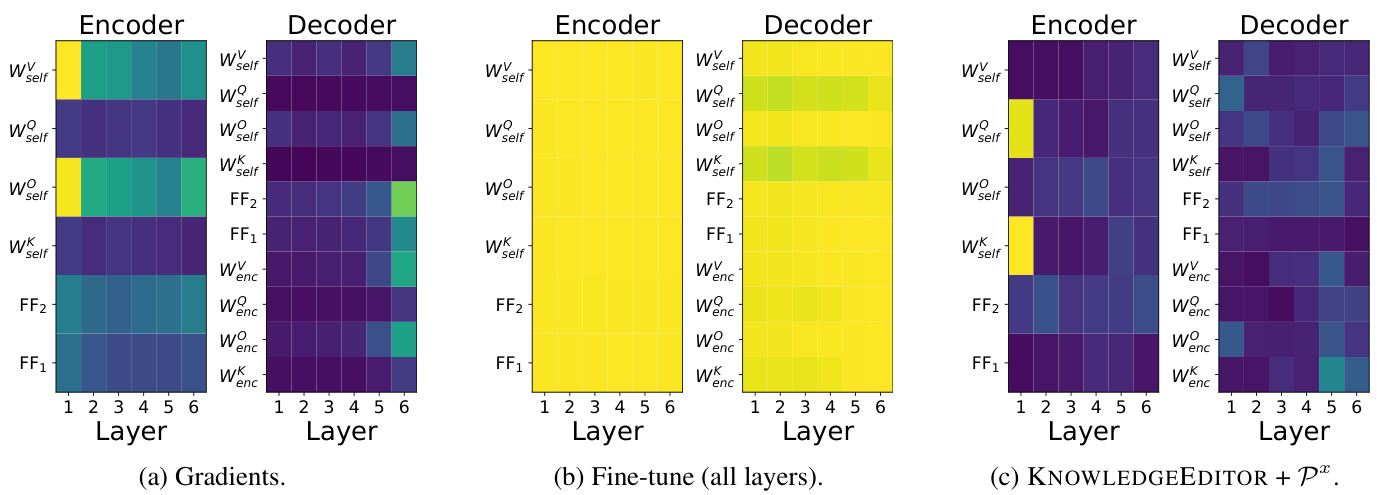
Figure 4: Average normalized magnitude of updates on weight matrices across layers for the QA experiment Fine-tuning updates all layers uniformly while our updates are more sparse.
图 4: QA实验中各层权重矩阵更新量的平均归一化幅度 微调会均匀更新所有层,而我们的更新更为稀疏。
based on a hyper-network that learns to modify implicit knowledge stored within LM parameters efficiently and reliably. We provide comprehensive evaluations for our models against different variants of fine-tuning demonstrating the advantage of our approach. The magnitude of the updates predicted by our method may unfold the mechanisms used by the LMs to encode factual knowledge; we leave such investigation for future work.
基于一个超网络(hyper-network),该网络能够高效可靠地学习修改存储在大语言模型参数中的隐式知识。我们针对不同微调变体对模型进行了全面评估,证明了本方法的优势。该方法预测的更新幅度可能揭示大语言模型编码事实知识所用的机制,我们将此类研究留待未来工作。
Ethical Considerations
伦理考量
Technology built upon pre-trained LMs inherits some or all of their potential harms (Bender et al., 2021). Our technology for editing the knowledge of LMs does not exacerbate their potential harms and can, in fact, be used to mitigate harms, as models can be corrected once problems are discovered. However, we note that malicious uses of our knowledge editor are possible. For example, malicious agents may use the techniques presented in this work to inject incorrect knowledge into LMs.
基于预训练大语言模型(LM)构建的技术会继承其部分或全部潜在危害(Bender et al., 2021)。我们提出的模型知识编辑技术不会加剧这些潜在危害,事实上该技术可用于减轻危害——因为发现问题后可以对模型进行修正。但需注意的是,我们的知识编辑器可能存在恶意使用场景。例如,恶意AI智能体可能利用本文技术向大语言模型注入错误知识。
Acknowledgments
致谢
7 Conclusions
7 结论
In this work, we explore the task of editing the factual knowledge implicitly stored in the parameters of Language Models. For this task, we formally define desiderata, the objective, and a set of metrics to measure the efficacy of different methods. We concretely evaluate that on two benchmarks based on closed-book fact-checking and question answering. We propose KNOWLEDGE EDITOR, a method
在本工作中,我们探索了编辑隐含存储于语言模型参数中的事实性知识的任务。针对该任务,我们正式定义了需求、目标以及一组用于衡量不同方法有效性的指标。我们基于闭卷事实核查和问答的两个基准测试进行了具体评估,并提出KNOWLEDGE EDITOR方法
The authors want to thank Michael Sch licht kru ll, Lena Voita and Luisa Quarta for helpful discussions and support. This project is supported by SAP Innovation Center Network, ERC Starting Grant BroadSem (678254), the Dutch Organization for Scientific Research (NWO) VIDI 639.022.518, and the European Union’s Horizon 2020 research and innovation programme under grant agreement No 825299 (Gourmet).
作者感谢Michael Schlichtkrull、Lena Voita和Luisa Quarta的有益讨论与支持。本项目由SAP创新中心网络、ERC启动基金BroadSem (678254)、荷兰科学研究组织(NWO) VIDI 639.022.518以及欧盟Horizon 2020研究与创新计划(资助协议号825299,Gourmet项目)提供支持。
References
参考文献
Yonatan Belinkov and James Glass. 2019. Analysis methods in neural language processing: A survey. Transactions of the Association for Computational Linguistics, 7:49–72.
Yonatan Belinkov 和 James Glass. 2019. 神经语言处理中的分析方法:综述. Transactions of the Association for Computational Linguistics, 7:49–72.
Emily M. Bender, Timnit Gebru, Angelina McMillan- Major, and Shmargaret Shmitchell. 2021. On the dangers of stochastic parrots: Can language models be too big? In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency, FAccT ’21, page 610–623, New York, NY, USA. As- sociation for Computing Machinery.
Emily M. Bender、Timnit Gebru、Angelina McMillan-Major 和 Shmargaret Shmitchell。2021. 论随机鹦鹉的危害:语言模型可以过大吗? 载于《2021年ACM公平性、问责性与透明度大会论文集》(FAccT '21),第610–623页,美国纽约州纽约市。计算机协会。
Stephen Boyd, Stephen P Boyd, and Lieven Vandenberghe. 2004. Convex optimization. Cambridge university press.
Stephen Boyd、Stephen P Boyd 和 Lieven Vandenberghe。2004。《凸优化》。剑桥大学出版社。
Tom B. Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neel a kant an, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel M. Ziegler, Jeffrey Wu, Clemens Winter, Christopher Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, and Dario Amodei. 2020. Language models are few-shot learners. In Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, De- cember 6-12, 2020, virtual.
Tom B. Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda As
