TRANSFORMER-PATCHER: ONE MISTAKE WORTH ONE NEURON
TRANSFORMER-PATCHER: 一错一神经元
Zeyu Huang1,2, Yikang Shen4, Xiaofeng Zhang1,2, Jie Zhou5, Wenge Rong1,3, Zhang Xiong1,3
Zeyu Huang1,2, Yikang Shen4, Xiaofeng Zhang1,2, Jie Zhou5, Wenge Rong1,3, Zhang Xiong1,3
ABSTRACT
摘要
Large Transformer-based Pretrained Language Models (PLMs) dominate almost all Natural Language Processing (NLP) tasks. Nevertheless, they still make mistakes from time to time. For a model deployed in an industrial environment, fixing these mistakes quickly and robustly is vital to improve user experiences. Previous works formalize such problems as Model Editing (ME) and mostly focus on fixing one mistake. However, the one-mistake-fixing scenario is not an accurate abstraction of the real-world challenge. In the deployment of AI services, there are ever-emerging mistakes, and the same mistake may recur if not corrected in time. Thus a preferable solution is to rectify the mistakes as soon as they appear nonstop. Therefore, we extend the existing ME into Sequential Model Editing (SME) to help develop more practical editing methods. Our study shows that most current ME methods could yield unsatisfying results in this scenario. We then introduce Transformer-Patcher, a novel model editor that can shift the behavior of transformer-based models by simply adding and training a few neurons in the last Feed-Forward Network layer. Experimental results on both classification and generation tasks show that Transformer-Patcher can successively correct up to thousands of errors (Reliability) and generalize to their equivalent inputs (Generality) while retaining the model’s accuracy on irrelevant inputs (Locality). Our method outperforms previous fine-tuning and Hyper Network-based methods and achieves state-of-the-art performance for Sequential Model Editing (SME). The code is available at https://github.com/Zero YuHuan g/Transform er-Patcher.
基于Transformer的大型预训练语言模型(PLM)主导了几乎所有自然语言处理(NLP)任务。然而,它们仍会不时犯错。对于部署在工业环境中的模型而言,快速稳健地修复这些错误对提升用户体验至关重要。先前研究将此类问题形式化为模型编辑(ME),主要关注单个错误的修正。但单错误修正场景并不能准确抽象现实挑战。在AI服务部署中,错误会不断涌现,若未及时纠正,相同错误可能反复出现。因此更优解决方案是持续即时修正错误。为此,我们将现有ME扩展为序列化模型编辑(SME),以助力开发更具实用性的编辑方法。研究表明,当前多数ME方法在此场景下表现欠佳。我们继而提出Transformer-Patcher——通过仅在末层前馈网络中添加并训练少量神经元,即可改变基于Transformer模型行为的新型编辑器。分类与生成任务的实验结果表明,Transformer-Patcher能连续修正上千个错误(可靠性),并泛化至等效输入(通用性),同时保持模型对无关输入的准确性(局部性)。该方法优于先前基于微调和超网络的方法,在序列化模型编辑(SME)中实现了最先进性能。代码详见https://github.com/ZeroYuHuang/Transformer-Patcher。
1 INTRODUCTION
1 引言
Transformer-based models, particularly large Pretrained Language Models (PLMs) (Devlin et al., 2019; Brown et al., 2020) have become the backbone model of modern Natural Language Processing (NLP) and have enabled promising results in various downstream tasks (Lv et al., 2019; Bud zia now ski & Vulic, 2019; Ramnath et al., 2020). However, PLMs still produce undesirable outputs occasionally (Zhao et al., 2019; Basta et al., 2021). The cost of such mistakes is non-negligible. For example, a mistaken automatic translation result could get a person arrested (Hern, 2018). One of the most usual expedients was using a manual cache (e.g., lookup table) to overrule these problematic predictions (Sinitsin et al., 2020). Though convenient and straightforward, it lacks robustness and generality because it could be disabled by the slightest change in the input, such as paraphrasing in natural language. On the other hand, one can also re-train the model on the original dataset supplemented with problematic examples. While superior in performance, it is computationally and temporally expensive to re-train large PLMs with billions or even trillions of parameters.
基于Transformer的模型,特别是大规模预训练语言模型(PLM) (Devlin et al., 2019; Brown et al., 2020)已成为现代自然语言处理(NLP)的核心模型,并在各类下游任务中展现出优异性能(Lv et al., 2019; Budzianowski & Vulic, 2019; Ramnath et al., 2020)。然而,PLM仍会偶尔产生不良输出(Zhao et al., 2019; Basta et al., 2021),这类错误的代价不容忽视。例如,错误的自动翻译结果可能导致人员被捕(Hern, 2018)。最常见的应急方案是使用人工缓存(如查找表)来覆盖这些问题预测(Sinitsin et al., 2020),虽然简便直接,但由于输入稍有变化(如自然语言改写)就会失效,缺乏鲁棒性和泛化性。另一方面,也可以在原始数据集基础上补充问题样本重新训练模型。虽然性能更优,但对具有数十亿甚至数万亿参数的大规模PLM进行重新训练,其计算成本和时间开销都极为高昂。
Previous research formalized such problems as Model Editing (ME) and proposed various methods to intervene model’s behavior on a specific example while preventing the model from forgetting other examples. Some straightly finetune the model on the example and used a constraint loss to maintain the model’s overall performance (Zhu et al., 2020; Sotoudeh & Thakur, 2021). Some edit the model through a Hyper Network, which regards the model and the false predicted example as inputs and produced a weight update for the model’s parameters (Cao et al., 2021; Sinitsin et al., 2020; Mitchell et al., 2022a). Despite their impressive progress, they mostly focus on one-step editing (fixing one mistake), which is not applicable to practical situations. Because models deployed for real-world applications are expected to face different errors ceaselessly. And the same error may pop up repeatedly and bother different users. In addition, as illustrated in Figure 1, once a wrong answer appears in an online question-answering (QA) model, leaving it unfixed and waiting for future corrections could mislead more people. Therefore, an ideal model editor should provide continuous and promptly fixing of newly emerged mistakes in an effective and efficient manner.
先前的研究将此类问题形式化为模型编辑(ME),并提出了多种方法来干预模型在特定示例上的行为,同时防止模型遗忘其他示例。部分方法直接在示例上微调模型,并使用约束损失来维持模型的整体性能(Zhu et al., 2020; Sotoudeh & Thakur, 2021)。另一些方法通过超网络(Hyper Network)编辑模型,将模型和错误预测示例作为输入,生成模型参数的权重更新(Cao et al., 2021; Sinitsin et al., 2020; Mitchell et al., 2022a)。尽管取得了显著进展,但这些方法主要关注单步编辑(修正单个错误),不适用于实际情况。因为现实应用中部署的模型会持续面临不同错误,且相同错误可能反复出现并困扰不同用户。此外,如图1所示,一旦在线问答(QA)模型出现错误答案,不及时修正而等待后续处理可能会误导更多人。因此,理想的模型编辑器应能以高效方式持续及时地修正新出现的错误。

Figure 1: Once an error occurs in a QA model online, it could bother many users contacting the model if not fixed in time. Instant correction is a superior choice to improve the user experience, motivating us to propose a Sequential Model Editing problem.
图 1: 当在线问答(QA)模型出现错误时,若未及时修复可能会困扰大量用户。即时纠正是提升用户体验的优选方案,这促使我们提出了序列化模型编辑(Sequential Model Editing)问题。
Thus we extend the ME task into the sequential setting and formalize it as Sequential Model Editing (SME) task, which requires a model editor to fix a series of mistakes as soon as they appear. The desiderata of a qualified sequential model editor are three properties (Section 3). For each editing, the post-edit model should be of 1) Reliability: make the desirable output given the input; 2) Generality: generalize over other equivalent inputs; 3) Locality: retain its accuracy over irrelevant inputs. We then propose a standard SME experiment pipeline that is compatible with different tasks and five evaluation metrics to evaluate the three properties. Experiments show that most existing model editors could fail to generalize to the sequential editing scenario. Fine-tuning-based methods are vulnerable to forgetting previous edits. Hyper Network-based editors are strongly coupled with the initial fimle:///oC:/dUseersl/ 黄t泽h宇/Daestk totp/h图片e4.ysv gare trained with, thus failing to edit the model after several steps (Se1/1ction 5).
因此我们将模型编辑(ME)任务扩展到序列化场景中,并将其形式化为序列化模型编辑(SME)任务,要求模型编辑器在错误出现时立即修复一系列错误。一个合格的序列化模型编辑器需要具备三个特性(第3节):1)可靠性(Reliability):对给定输入产生期望输出;2)通用性(Generality):能推广到其他等效输入;3)局部性(Locality):在无关输入上保持原有准确性。我们提出了一个兼容不同任务的标准SME实验流程,并用五个评估指标来衡量这三个特性。实验表明,现有大多数模型编辑器难以适应序列化编辑场景。基于微调的方法容易遗忘先前编辑,基于超网络(Hyper Network)的编辑器与初始训练文件(file:///oC:/dUseersl/黄t泽h宇/Daestk totp/h图片e4.ysvg)强耦合,导致在多次编辑后会失效(第5节)。
To handle SME, we introduce Transformer-Patcher. Unlike previous methods, Transformer-Patcher retains all original parameters to prevent harming the model’s overall performance. It only adds a handful of trainable neurons (patches) to the last Feed-Forward Network (FFN) layer to revise the model’s behavior on the problematic input and achieve a low editing cost. Furthermore, we train the patch to only respond to specific inputs with the proposed activation loss and memory loss. Experimental results on fact-checking (classification) and question answering (auto-regressive generation) indicated that Transformer-Patcher could rectify a series of mistakes (up to thousands) while almost perfectly retaining the model’s overall performance.
为处理SME问题,我们引入了Transformer-Patcher。与之前的方法不同,Transformer-Patcher保留了所有原始参数以防止损害模型的整体性能。它仅向最后的Feed-Forward Network (前馈网络,FFN)层添加少量可训练神经元(补丁)来修正模型在问题输入上的行为,从而实现低编辑成本。此外,我们通过提出的激活损失和记忆损失训练补丁仅对特定输入做出响应。在事实核查(分类)和问答(自回归生成)上的实验结果表明,Transformer-Patcher能够纠正一系列错误(多达数千个),同时几乎完美地保留模型的整体性能。
The main contributions of this work are twofold: 1) We formally propose a sequential model editing task, as well as its standard experiment pipeline and evaluation metrics. 2) We introduce Transformer-Patcher, a simple yet effective model editor to revise transformer-based PLMs, achieving state-of-the-art SME performance.
本研究的主要贡献有两点:(1) 我们正式提出了序列化模型编辑任务,并制定了标准实验流程与评估指标。(2) 我们提出了Transformer-Patcher——一种简单高效的模型编辑器,用于修正基于Transformer的预训练语言模型,在序列化模型编辑任务中实现了最先进的性能。
2 RELATED WORKS
2 相关工作
Feed-forward Network Both the Transformer encoder and decoder contain the Feed-Forward Network (FFN). Recent works (Geva et al., 2021; Dai et al., 2022) analogously observed that FFN operates as key-value neural memories (Sukhbaatar et al., 2015). They regarded the input of FFN as a query, the first layer as keys, and the second as values. Thus the intermediate hidden dimension of FFN can be interpreted as the number of memories in the layer, and the intermediate hidden state is a vector containing activation values for each memory. Therefore, the final output of FFN can be viewed as the weighted sum of values activated.
前馈网络
Transformer编码器和解码器都包含前馈网络 (Feed-Forward Network, FFN)。近期研究 (Geva et al., 2021; Dai et al., 2022) 类比发现FFN运作方式类似于键值神经记忆 (Sukhbaatar et al., 2015)。这些研究将FFN的输入视为查询(query),第一层作为键(keys),第二层作为值(values)。因此FFN的中间隐藏维度可解释为该层的记忆数量,中间隐藏状态则是包含每个记忆激活值的向量。最终FFN的输出可视为被激活值的加权求和。
Model editors Existing model editors are mainly separated into two types: fine-tuning-based and Hyper Network-based. Fine-tuning-based editors usually straightly tune the model with an extra loss to eschew over-fitting to edit examples. For instance, Zhu et al. (2020) proposed an extra loss to reduce the distance between pre-edit and post-edit parameters. Mitchell et al. (2022a); Meng et al. (2022) equipped fine-tuning with KL-divergence to restrict the post-edit model’s output space. For another, Hyper Network-based editors require additional training phrases. Sinitsin et al. (2020) proposed a Meta Learning-based (Finn et al., 2017) approach named Editable Training to learn editable parameters for model modification. Cao et al. (2021) proposed Knowledge Editor (KE) trained with constrained optimization to produce weight updates. Mitchell et al. (2022a) proposed MEND that learns to transform the gradient obtained by standard fine-tuning to edit large language models (Raffel et al., 2020). In addition, some works only focus on specific tasks, such as masked language modeling (Dai et al., 2022) and auto regressive language modeling (Meng et al., 2022; Geva et al., 2022). They require special input other than edit examples to conduct model editing.
模型编辑器
现有模型编辑器主要分为两类:基于微调(fine-tuning)的和基于超网络(Hyper Network)的。基于微调的编辑器通常通过添加额外损失函数直接调整模型,以避免对编辑样本的过拟合。例如,Zhu等人(2020)提出使用额外损失函数来减小编辑前后参数间的距离;Mitchell等人(2022a)和Meng等人(2022)则为微调过程引入KL散度来约束编辑后模型的输出空间。
另一方面,基于超网络的编辑器需要额外的训练阶段。Sinitsin等人(2020)提出了一种基于元学习(Meta Learning)(Finn等人,2017)的方法Editable Training,用于学习可编辑参数以实现模型修改;Cao等人(2021)提出通过约束优化训练的知识编辑器(Knowledge Editor,KE)来生成权重更新;Mitchell等人(2022a)提出的MEND则学习将标准微调获得的梯度进行转换,以实现对大语言模型(Raffel等人,2020)的编辑。
此外,部分研究仅针对特定任务,如掩码语言建模(Dai等人,2022)和自回归语言建模(Meng等人,2022;Geva等人,2022)。这些方法需要除编辑样本外的特殊输入来执行模型编辑。
Continual Learning The proposed SME task could be regarded as an emergent variant of Continual Learning (CL) (Mundt et al., 2020). And dynamically expandable networks are employed for CL as well (Rusu et al., 2016; Li & Hoiem, 2018). But there are some differences in the setting. In CL, usually, the model is continually trained using different datasets and tasks. But SME deals with only one example at once and all examples are from the same task. The difference in setting renders SME an unexplored area with new challenges that may not be properly addressed by general CL methods. For example, KL divergence loss and L2 normalization are usual methods to address the catastrophic forgetting in CL (De Lange et al., 2022), but previous works (Cao et al., 2021; Mitchell et al., 2022a) and our experiments show that they can hardly maintain models accuracy on irrelevant inputs in ME task. And methods that add task-specific parameters for CL usually need extra training (Yoon et al., 2018; Wortsman et al., 2020; de Masson d’Autume et al., 2019), thus falling short of SME’s application efficiency requirement.
持续学习
所提出的 SME (Sequential Memory Editing) 任务可视为持续学习 (Continual Learning, CL) (Mundt et al., 2020) 的一种新兴变体。动态可扩展网络也被用于持续学习 (Rusu et al., 2016; Li & Hoiem, 2018),但两者在设定上存在差异。在持续学习中,模型通常通过不同数据集和任务进行持续训练,而 SME 每次仅处理单个样本且所有样本均来自同一任务。这种设定差异使 SME 成为一个存在新挑战的未探索领域,通用持续学习方法可能无法妥善解决。例如,KL 散度损失和 L2 归一化是解决持续学习中灾难性遗忘的常用方法 (De Lange et al., 2022),但前人研究 (Cao et al., 2021; Mitchell et al., 2022a) 和我们的实验表明,这些方法难以在 ME (Memory Editing) 任务中保持模型对无关输入的准确性。而为持续学习添加任务特定参数的方法通常需要额外训练 (Yoon et al., 2018; Wortsman et al., 2020; de Masson d'Autume et al., 2019),因此无法满足 SME 对应用效率的要求。
3 SEQUENTIAL MODEL EDITING PROBLEM
3 序列化模型编辑问题
$$
\begin{array}{r l}&{\overbrace{\left[\mathrm{Model}f_{0}\right]}^{\ell^{-(-\mathrm{moss-m.}\neq1)}}\longrightarrow\overbrace{\mathrm{Model}}^{\ell^{-(-\mathrm{model})}}\overbrace{\left[\mathrm{Model}f_{1}\right]}^{1}\longrightarrow\overbrace{\left[\mathrm{Model}\atop\mathrm{Vold}\mathrm{Vold}\mathrm{Vor}\right]}^{\ell^{-(-\mathrm{moss-max})}}\overbrace{\left[\mathrm{.....}\mathrm{ ...}\right]}^{1}\underbrace{\left[\mathrm{......}\right]_ {1}^{(-\mathrm{moss-m.}1)}}_ {\ell=-\mathrm{7.-7.}}\overbrace{\left[\mathrm{Model}f_{1}\right]}^{1}}\ &{\underbrace{\mathrm{.....}\mathrm{ ....}\mathrm{ ....}}_ {\vdots}\mathrm{ \mathrm{ cannyec}({x}_ {1},y_{1})\mathrm{ that~}\vdots~}\underbrace{\mathrm{....}\mathrm{ cannyec}({x}_ {2},y_{x_{2}})\mathrm{ that~}\vdots}_ {\vdots}\quad\vdots\quad\mathrm{As eries of mistakes~}\vdots}\ &{\vdots\quad\mathrm{....}\int_{0}({x}_ {1})\underbrace{\dot{\tau}_ {-1},y_{x_{1}}}_ {\ell=-\mathrm{7.-7.}}\overbrace{\mathrm{...}\mathrm{ ...}\mathrm{ ...}\mathrm{ ..}}^{1}\underbrace{f_{1}({x}_ {2})\neq y_{x_{2}}}_ {\ell=-\mathrm{7.-7.}}\underbrace{\mathrm{. .}}_ {\mathrm{1. serare~}}\underbrace{\mathrm{.~f_{1}^{(-\mathrm{model})}}}_ {\ell=-\mathrm{7.-7.}}\underbrace{\mathrm{.~f_{1}^{(-\mathrm{model})}}}_ {\ell=-\mathrm{7.-7.}}\underbrace{\mathrm{.~f_{2}^{(-\mathrm{model})}}}_ {\ell=-\mathrm{7.-7.}}\underbrace{\mathrm{.~f_{3}^{(-\mathrm{model})}}}_{\ell=-\mathrm{7.-7.}}}\end{array}
$$
$$
\begin{array}{r l}&{\overbrace{\left[\mathrm{Model}f_{0}\right]}^{\ell^{-(-\mathrm{moss-m.}\neq1)}}\longrightarrow\overbrace{\mathrm{Model}}^{\ell^{-(-\mathrm{model})}}\overbrace{\left[\mathrm{Model}f_{1}\right]}^{1}\longrightarrow\overbrace{\left[\mathrm{Model}\atop\mathrm{Vold}\mathrm{Vold}\mathrm{Vor}\right]}^{\ell^{-(-\mathrm{moss-max})}}\overbrace{\left[\mathrm{.....}\mathrm{ ...}\right]}^{1}\underbrace{\left[\mathrm{......}\right]_ {1}^{(-\mathrm{moss-m.}1)}}_ {\ell=-\mathrm{7.-7.}}\overbrace{\left[\mathrm{Model}f_{1}\right]}^{1}}\ &{\underbrace{\mathrm{.....}\mathrm{ ....}\mathrm{ ....}}_ {\vdots}\mathrm{ \mathrm{ cannyec}({x}_ {1},y_{1})\mathrm{ that~}\vdots~}\underbrace{\mathrm{....}\mathrm{ cannyec}({x}_ {2},y_{x_{2}})\mathrm{ that~}\vdots}_ {\vdots}\quad\vdots\quad\mathrm{As eries of mistakes~}\vdots}\ &{\vdots\quad\mathrm{....}\int_{0}({x}_ {1})\underbrace{\dot{\tau}_ {-1},y_{x_{1}}}_ {\ell=-\mathrm{7.-7.}}\overbrace{\mathrm{...}\mathrm{ ...}\mathrm{ ...}\mathrm{ ..}}^{1}\underbrace{f_{1}({x}_ {2})\neq y_{x_{2}}}_ {\ell=-\mathrm{7.-7.}}\underbrace{\mathrm{. .}}_ {\mathrm{1. serare~}}\underbrace{\mathrm{.~f_{1}^{(-\mathrm{model})}}}_ {\ell=-\mathrm{7.-7.}}\underbrace{\mathrm{.~f_{1}^{(-\mathrm{model})}}}_ {\ell=-\mathrm{7.-7.}}\underbrace{\mathrm{.~f_{2}^{(-\mathrm{model})}}}_ {\ell=-\mathrm{7.-7.}}\underbrace{\mathrm{.~f_{3}^{(-\mathrm{model})}}}_{\ell=-\mathrm{7.-7.}}}\end{array}
$$
Figure 2: The process of sequential model editing task. Given the $t$ -th mistake $(x_{t},y_{x_{t}})$ , the editor takes the model $f_{t-1}$ and $(x_{t},y_{x_{t}})$ as input, and outputs the revised model $f_{t}$
图 2: 序列化模型编辑任务流程。给定第 $t$ 个错误 $(x_{t},y_{x_{t}})$,编辑器以模型 $f_{t-1}$ 和 $(x_{t},y_{x_{t}})$ 作为输入,输出修正后的模型 $f_{t}$
Following Mitchell et al. (2022a), a model $f\in\mathbb{F}$ can be defined as a function $f:\mathbb{X}\mapsto\mathbb{Y}$ that maps an input $x$ to its prediction $f(x)$ . Then, given a model $f$ and an edit example pair $(x_{e},y_{x_{e}})$ that $f(x_{e})\neq y_{x_{e}}$ , a model editor ME is to output a post-edit model $f^{\prime}$ .
根据Mitchell等人(2022a)的研究,模型$f\in\mathbb{F}$可以定义为将输入$x$映射到其预测$f(x)$的函数$f:\mathbb{X}\mapsto\mathbb{Y}$。给定模型$f$和编辑样本对$(x_{e},y_{x_{e}})$(其中$f(x_{e})\neq y_{x_{e}}$),模型编辑器ME的任务是输出一个编辑后的模型$f^{\prime}$。
$$
\begin{array}{r c l l}{\mathrm{ME:}}&{\mathbb{F}\times\mathbb{X}\times\mathbb{Y}}&{\mapsto}&{\mathbb{F}}\ &{(f,x_{e},y_{x_{e}})}&{\to}&{f^{\prime}=\mathrm{ME}(f,x_{e},y_{x_{e}})}\end{array}
$$
$$
\begin{array}{r c l l}{\mathrm{ME:}}&{\mathbb{F}\times\mathbb{X}\times\mathbb{Y}}&{\mapsto}&{\mathbb{F}}\ &{(f,x_{e},y_{x_{e}})}&{\to}&{f^{\prime}=\mathrm{ME}(f,x_{e},y_{x_{e}})}\end{array}
$$
Given a data stream ${(x_{1},y_{x_{1}}),\cdot\cdot\cdot,(x_{s},y_{x_{s}})}$ and an initial model $f_{0}$ , a model editor ME needs to conduct edits successively when the model makes undesirable output, as shown in Figure 2.
给定数据流 ${(x_{1},y_{x_{1}}),\cdot\cdot\cdot,(x_{s},y_{x_{s}})}$ 和初始模型 $f_{0}$,当模型产生不良输出时,模型编辑器 (model editor) ME 需要依次执行编辑操作,如图 2 所示。
$$
f_{t} =\begin{cases}f_{0} & \text{if } t = 0, \quad
f_{t-1} & \text{else if } f_{t-1}(x_{t}) = y_{x_{t}}, \quad
\mathrm{ME}(f_{t-1}, x_{t}, y_{x_{t}}) & \text{otherwise.}
\end{cases}.
$$
$$
f_{t} =\begin{cases}f_{0} & \text{if } t = 0, \quad
f_{t-1} & \text{else if } f_{t-1}(x_{t}) = y_{x_{t}}, \quad
\mathrm{ME}(f_{t-1}, x_{t}, y_{x_{t}}) & \text{otherwise.}
\end{cases}.
$$
And after every edit in SME the post-edit model $f^{\prime}$ should satisfy the following three properties:
在 SME 中进行每次编辑后,后编辑模型 $f^{\prime}$ 应满足以下三个属性:
Property 1 Reliability: the post-edit model should output the desired prediction:
属性1 可靠性:编辑后的模型应输出预期预测:
$$
f^{\prime}(x_{e})=y_{x_{e}}
$$
$$
f^{\prime}(x_{e})=y_{x_{e}}
$$
Property 2 Generality: given an edit example $x_{e}$ , $\mathbb{E}_ {x_{e}}={x_{j}|y_{x_{j}}=y_{x_{e}}}$ is defined as the set of its equivalent inputs (e.g. rephrased sentences). Then the post-edit model $f^{\prime}$ should satisfy:
属性2 通用性:给定一个编辑示例$x_{e}$,定义其等价输入集合为$\mathbb{E}_ {x_{e}}={x_{j}|y_{x_{j}}=y_{x_{e}}}$(例如改写后的句子)。经编辑后的模型$f^{\prime}$应满足:
$$
\forall x_{j}\in\mathbb{E}_ {x_{e}},f^{\prime}(x_{j})=y_{x_{e}}
$$
$$
\forall x_{j}\in\mathbb{E}_ {x_{e}},f^{\prime}(x_{j})=y_{x_{e}}
$$
Property 3 Locality: the edit should be implemented locally and precisely, which means the postedit model should remain accurate on the irrelevant examples set $\mathbb{I}_ {x_{e}}=\mathbb{X}\backslash\mathbb{E}_ {x_{e}}$ :
特性3 局部性:编辑应在局部精确实施,这意味着后编辑模型在无关样本集 $\mathbb{I}_ {x_{e}}=\mathbb{X}\backslash\mathbb{E}_ {x_{e}}$ 上仍需保持准确性。
$$
\forall x_{j}\in I_{x_{e}},f^{\prime}(x_{j})=y_{x_{j}}
$$
$$
\forall x_{j}\in I_{x_{e}},f^{\prime}(x_{j})=y_{x_{j}}
$$
In particular, an edit should not disrupt the results of past edits in SME setting, which means:
特别是在中小企业(SME)环境中,编辑不应破坏过往编辑的结果,这意味着:
$$
f_{t}(x_{k})=y_{x_{k}},f o r k w h e r e f_{k-1}(x_{k})\neq y_{x_{k}}
$$
$$
f_{t}(x_{k})=y_{x_{k}}, f o r k w h e r e f_{k-1}(x_{k})\neq y_{x_{k}}
$$
4 TRANSFORMER-PATCHER
4 TRANSFORMER-PATCHER
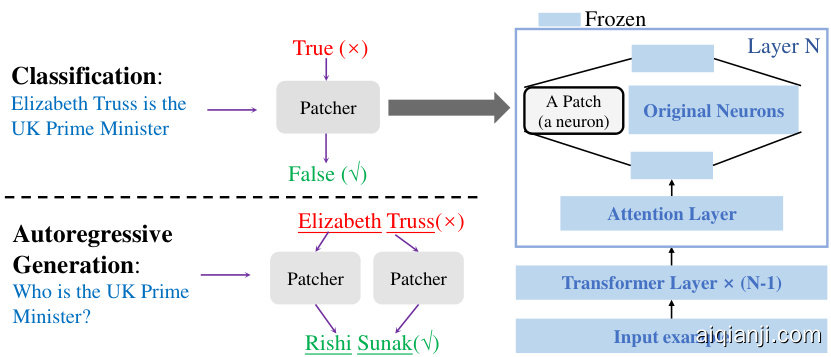
Figure 3: Transformer-patcher enables efficient correction for classification and generation tasks, it rectifies the model’s behavior by adding and training several extra neurons in the last FFN layer.
图 3: Transformer-patcher 能够高效修正分类和生成任务,它通过在最后一个 FFN (Feed-Forward Network) 层添加并训练少量额外神经元来纠正模型行为。
First, we call one mis classification or one wrongly generated token one mistake in the rest of the paper. Aiming at the SME task for transformer-based models, we propose Transformer-Patcher shown in Figure 3. It freezes all original parameters and adds one neuron (patch) to the last FFN layer for one mistake. And we train the patch to take effect only when encountering its corresponding mistake. For classification, we add only one patch to rectify the model. For auto-regressive generation, we count how many tokens are wrongly generated under the teacher-forcing setting and add one patch for each of them. This section describes how to add and train one patch. Multiple patch editing follows exactly the same principle and is formally described in Appendix A.
首先,我们将一次错误分类或错误生成的token称为一个错误。针对基于Transformer模型的SME任务,我们提出了如图3所示的Transformer-Patcher。该方法冻结所有原始参数,并在最后一个FFN层为每个错误添加一个神经元(补丁)。我们训练补丁仅在遇到其对应错误时生效。对于分类任务,只需添加一个补丁来修正模型。对于自回归生成任务,我们会统计在教师强制设置下错误生成的token数量,并为每个错误token添加一个补丁。本节描述如何添加和训练单个补丁,多重补丁编辑遵循完全相同的原则,正式描述见附录A。
4.1 WHAT IS A PATCH?
4.1 什么是补丁 (Patch)?
As mentioned in Section 2, FFN operates as key-value neuron memories. Its forward computation is a process that retrieves values from matrix $V$ by matching keys in matrix $\kappa$ and the input query $\pmb q$ . For a standard FFN, given a query $\pmb q\in\mathbb{R}^{d}$ , its output $F\bar{F}N(\overset{.}{\underset{.}{q}})$ is:
如第2节所述,FFN (Feed-Forward Network) 作为键值神经元记忆体运行。其前向计算是通过匹配矩阵 $\kappa$ 中的键与输入查询 $\pmb q$ 来从矩阵 $V$ 检索值的过程。对于标准FFN,给定查询 $\pmb q\in\mathbb{R}^{d}$,其输出 $F\bar{F}N(\overset{.}{\underset{.}{q}})$ 为:
$$
\begin{array}{c}{{\pmb a=\mathrm{Act}(\pmb q\cdot\pmb K+\pmb b_{k})}}\ {{F F N(\pmb q)=\pmb a\cdot\pmb V+\pmb b_{v}}}\end{array}
$$
$$
\begin{array}{c}{{\pmb a=\mathrm{Act}(\pmb q\cdot\pmb K+\pmb b_{k})}}\ {{F F N(\pmb q)=\pmb a\cdot\pmb V+\pmb b_{v}}}\end{array}
$$
where $\operatorname{Act}(\cdot)$ is a non-linear activation function (e.g., Relu or Gelu), $\textbf{a}$ is the vector of activation values, $\pmb{b}_ {k}$ , and $b_{v}$ are two bias vectors. A patch is an extra neuron (an extra key-value pair) added to the last FFN layer. After patching, the new output $F F N_{p}(\pmb{q})$ is:
其中 $\operatorname{Act}(\cdot)$ 是一个非线性激活函数 (例如 Relu 或 Gelu),$\textbf{a}$ 是激活值向量,$\pmb{b}_ {k}$ 和 $b_{v}$ 是两个偏置向量。补丁 (patch) 是添加到最后一个 FFN 层的额外神经元 (一个额外的键值对)。修补后,新的输出 $F F N_{p}(\pmb{q})$ 为:
$$
\begin{array}{r l}{[{\pmb a}}&{{\pmb a}_ {p}]=\mathrm{Act}({\pmb q}\cdot[{\pmb K}\pmb{\mathit{k}}_ {p}]+[{\pmb b}_ {k}\quad{\pmb b}_ {p}])}\ &{F F N_{p}({\pmb q})=[{\pmb a}\quad{\pmb a}_ {p}]\cdot\bigg[{\pmb V}\bigg]+b_{v}}\end{array}
$$
$$
\begin{array}{r l}{[{\pmb a}}&{{\pmb a}_ {p}]=\mathrm{Act}({\pmb q}\cdot[{\pmb K}\pmb{\mathit{k}}_ {p}]+[{\pmb b}_ {k}\quad{\pmb b}_ {p}])}\ &{F F N_{p}({\pmb q})=[{\pmb a}\quad{\pmb a}_ {p}]\cdot\bigg[{\pmb V}\bigg]+b_{v}}\end{array}
$$
where $\pmb{k}_ {p} \in~\mathbb{R}^{d}$ is the patch key, $\pmb{v}_ {p}\in\mathbb{R}^{d}$ is the patch value, $b_{p}$ is a scalar named patch bias, $a_{p}=\mathrm{Act}(\pmb{q}\cdot\pmb{k}_ {p}+b_{p})$ represents the activation value of the patch. With the substitution of equations 6 and 7, equation 9 can be reformulated as:
其中 $\pmb{k}_ {p} \in~\mathbb{R}^{d}$ 是补丁键 (patch key),$\pmb{v}_ {p}\in\mathbb{R}^{d}$ 是补丁值 (patch value),$b_{p}$ 是一个标量称为补丁偏置 (patch bias),$a_{p}=\mathrm{Act}(\pmb{q}\cdot\pmb{k}_ {p}+b_{p})$ 表示补丁的激活值。将方程6和7代入后,方程9可重新表述为:
$$
F F N_{p}({\pmb q})=F F N({\pmb q})+a_{p}\cdot{\pmb v}_{p}
$$
$$
F F N_{p}({\pmb q})=F F N({\pmb q})+a_{p}\cdot{\pmb v}_{p}
$$
4.2 TRAINING A PATCH FOR EDITING
4.2 训练用于编辑的补丁
An ideal edit requires reliability, generality, and locality proposed in Section 3. For reliability, a patch needs to be activated according to equation 10. Let $q_{e}$ represent the input query of the mistake,
理想的编辑需要满足第3节提出的可靠性、通用性和局部性要求。为确保可靠性,补丁需根据公式10激活。设$q_{e}$表示错误输入的查询,
the patch key $k_{p}$ and patch bias $b_{p}$ should satisfy:
补丁键 $k_{p}$ 和补丁偏置 $b_{p}$ 应满足:
$$
a_{p}=\mathrm{Act}({q_{e}}\cdot{k_{p}}+{b_{p}})\ne0
$$
$$
a_{p}=\mathrm{Act}({q_{e}}\cdot{k_{p}}+{b_{p}})\ne0
$$
When Act is ReLU or GeLU, the above condition can be approximated as follows:
当激活函数 (Act) 为 ReLU 或 GeLU 时,上述条件可近似表示为:
$$
{\pmb q}_ {e}\cdot{\pmb k}_ {p}+b_{p}>0
$$
$$
{\pmb q}_ {e}\cdot{\pmb k}_ {p}+b_{p}>0
$$
To meet the constraint 12, we propose a activation loss $l_{a}$ to maximize the activation value:
为了满足约束条件12,我们提出了一种激活损失函数 $l_{a}$ 以最大化激活值:
$$
l_{a}=\exp(-\pmb{q}_ {e}\cdot\pmb{k}_ {p}-b_{p}))
$$
$$
l_{a}=\exp(-\pmb{q}_ {e}\cdot\pmb{k}_ {p}-b_{p}))
$$
Once a patch is activated, according to equation 10, it adds a bias term $a_{p}\cdot{\pmb v}_ {p}$ to the output of the last layer. Because we are editing the last layer of the model, the output of the model can be adjusted to any result without worrying that other components of the model would cancel the editing effect. To obtain the target output, we leverage the task’s original loss function and rename it as edit loss $l_{e}$ . Formally, for an edit example $(x_{e},y_{e})$ , the patched model’s output is $p_{e}$ , $l_{e}$ is defined as:
一旦激活补丁,根据公式10,它会在最后一层的输出上添加一个偏置项 $a_{p}\cdot{\pmb v}_ {p}$。由于我们编辑的是模型的最后一层,因此可以自由调整模型输出至任意结果,而无需担心模型其他组件会抵消编辑效果。为实现目标输出,我们利用任务的原始损失函数并将其重命名为编辑损失 $l_{e}$。形式上,对于编辑样本 $(x_{e},y_{e})$,补丁模型的输出为 $p_{e}$,此时 $l_{e}$ 定义为:
$$
{l_{e}}=L(y_{e},p_{e})
$$
$$
{l_{e}}=L(y_{e},p_{e})
$$
where $L(\cdot)$ is a function of label $y_{e}$ and model output $p_{e}$ and depends on the specific task.
其中 $L(\cdot)$ 是关于标签 $y_{e}$ 和模型输出 $p_{e}$ 的函数,具体取决于任务类型。
For locality, the model’s behavior should not be shifted on irrelevant examples, thus the patch should not be activated by any irrelevant examples. When using ReLU or GeLU, it can be approximated as that all queries from irrelevant examples ${\bf{\it q}}_{i}$ should have a patch activation value less than or equal to a threshold $\beta$ , i.e., the maximum of them is less than or equal to $\beta$ :
对于局部性,模型的行为不应在无关样本上发生偏移,因此补丁不应被任何无关样本激活。当使用ReLU或GeLU时,可以近似为所有来自无关样本的查询 ${\bf{\it q}}_{i}$ 的补丁激活值都应小于或等于阈值 $\beta$,即它们的最大值小于或等于 $\beta$:
$$
\forall i\in\mathbb{I}_ {x_{e}},\pmb{q}_ {i}\cdot\pmb{k}_ {p}+b_{p}\leq\beta\rightarrow\operatorname*{max}_ {i}(\pmb{q}_ {i}\cdot\pmb{k}_ {p}+b_{p})\leq\beta
$$
$$
\forall i\in\mathbb{I}_ {x_{e}},\pmb{q}_ {i}\cdot\pmb{k}_ {p}+b_{p}\leq\beta\rightarrow\operatorname*{max}_ {i}(\pmb{q}_ {i}\cdot\pmb{k}_ {p}+b_{p})\leq\beta
$$
Thus we propose the memory loss $l_{m}$ to enforce the constraint 15. To imitate the distribution of queries from irrelevant examples, we randomly retain some queries from previously seen examples as memories. Each query is a $d$ -dimensional vector and we can stack them as a matrix $M\in\mathbb{R}^{d_{m}^{\star}\times d}$ , where $d_{m}$ is the number of queries saved. Our proposed memory loss $l_{m}$ is the sum of two terms. The first term $l_{m1}$ is introduced to make the patch in activated to all queries in $M$ :
因此我们提出记忆损失 $l_{m}$ 来强制执行约束15。为了模拟无关样本查询的分布,我们随机保留先前所见样本的部分查询作为记忆。每个查询是一个 $d$ 维向量,可以将其堆叠为矩阵 $M\in\mathbb{R}^{d_{m}^{\star}\times d}$ ,其中 $d_{m}$ 是保存的查询数量。我们提出的记忆损失 $l_{m}$ 由两项组成:第一项 $l_{m1}$ 用于使激活的补丁对所有 $M$ 中的查询失效:
$$
l_{m1}=S(M\cdot k_{p}+b_{p}-\beta;k)
$$
$$
l_{m1}=S(M\cdot k_{p}+b_{p}-\beta;k)
$$
where $S(\cdot;k)$ is a function that receives a vector $_{v}$ and outputs a scalar
其中 $S(\cdot;k)$ 是一个接收向量 $_{v}$ 并输出标量的函数
$$
S(\pmb{v};k)=\mathrm{Avg}[\mathrm{TopK}(\exp(\pmb{v});k)]
$$
$$
S(\pmb{v};k)=\mathrm{Avg}[\mathrm{TopK}(\exp(\pmb{v});k)]
$$
It first employs element-wise exponential function to $_ {v}$ and then selects $k$ largest elements to compute their average as the output. Although constraint 15 is about the maximum, we employ TopK here for more efficient optimization. In case that $l_{m1}$ can not absolutely ensure the constraint 15, we propose $l_{m2}$ to distance the activation value of $q_{e}$ and $\pmb{q}_{i}$ . That is, the activation value of the mistaken example is larger than that of the irrelevant examples by a certain margin $\gamma$ .
它首先对 $_ {v}$ 进行逐元素指数运算,然后选取 $k$ 个最大元素计算其平均值作为输出。尽管约束15涉及最大值,但这里采用TopK以实现更高效的优化。若 $l_{m1}$ 无法绝对保证约束15,我们提出 $l_{m2}$ 来拉大 $q_{e}$ 和 $\pmb{q}_{i}$ 的激活值差距,即错误样本的激活值需比无关样本高出特定边界 $\gamma$。
$$
l_{m2}=S((M-\pmb q_{e})\cdot\pmb k_{p}+b_{p}-\gamma;k)
$$
$$
l_{m2}=S((M-\pmb q_{e})\cdot\pmb k_{p}+b_{p}-\gamma;k)
$$
To sum up, the loss $l_{p}$ for training a patch is defined as a weighted sum of the above losses:
综上所述,训练一个补丁(patch)的损失$l_{p}$定义为上述损失的加权和:
$$
l_{p}=l_{e}+a l_{a}+m l_{m}=l_{e}+a l_{a}+m(l_{m1}+l_{m2})
$$
$$
l_{p}=l_{e}+a l_{a}+m l_{m}=l_{e}+a l_{a}+m(l_{m1}+l_{m2})
$$
where $a,m$ are hyper-parameters. $\beta$ is selected as $^{-3}$ for GeLU and 0 for ReLu, since GeLU(- $3){\approx}0.004$ is small enough and ReLU(0)=0. $\gamma$ is selected as 3 for GeLU and 0 for ReLU.
其中 $a,m$ 为超参数。$\beta$ 对于 GeLU 选择为 $^{-3}$,对于 ReLU 选择为 0,因为 GeLU(- $3){\approx}0.004$ 足够小且 ReLU(0)=0。$\gamma$ 对于 GeLU 选择为 3,对于 ReLU 选择为 0。
5 EXPERIMENTS
5 实验
5.1 EXPERIMENTAL SETTINGS AND EVALUATION METRICS
5.1 实验设置与评估指标
We proposed an experimental pipeline for SME used for standard datasets with training set $\mathbb{D}_ {t r a i n}$ , validation set $\mathbb{D}_ {v a l}$ , and test set $\mathbb{D}_ {t e s t}$ . There are two differences between our setting and the previous Model Editing setting. First, we employ multi-step editing rather than one-step. Second, previous works usually generate counter factual edit examples (e.g., replacing the answer to a question with a random one), while we employ authentic examples where the model makes mistakes. We first split the original $\mathbb{D}_ {t r a i n}$ into an edit set $\mathbb{D}_ {e d i t}$ and a new training set $\mathbb{D}_ {t r a i n}^{\prime}$ . To evaluate generality, backtranslation could be utilized to generate the equivalent set $\mathbb{E}_ {x_{e}}$ for edit example $x_{e}\in{\mathbb D}_ {e d i t}$ following previous works (Cao et al., 2021). To evaluate locality, a subset $\mathbb{D}_ {t r}$ randomly sa mpled from $\mathbb{D}_ {t r a i n}^{\prime}$ is used to see how the post-edit model performs on its training data. Our SME pipeline starts with an initial model $f_{0}$ trained on $\mathbb{D}_ {t r a i n}^{\prime}$ and validated using $\mathbb{D}_ {v a l}$ , the model is sequentially edited while encountering mistakes in $\mathbb{D}_ {e d i t}$ . After the $t$ th edit example $(x_{e}^{t},y_{e}^{t})$ , we obtain a post-edit model $f_{t}$ . Supposing that there are $T$ total edits and $I$ represents the indicator function, our proposed metrics are calculated as follows:
我们提出了一种用于标准数据集的小模型编辑(SME)实验流程,该数据集包含训练集$\mathbb{D}_ {train}$、验证集$\mathbb{D}_ {val}$和测试集$\mathbb{D}_ {test}$。我们的设置与之前的模型编辑设置有两个不同之处。首先,我们采用多步编辑而非单步编辑。其次,先前工作通常生成反事实编辑样本(例如将问题的答案替换为随机答案),而我们使用模型实际出错的真实样本。我们首先将原始$\mathbb{D}_ {train}$划分为编辑集$\mathbb{D}_ {edit}$和新训练集$\mathbb{D}_ {train}^{\prime}$。为评估泛化性,可沿用前人工作(Cao et al., 2021)采用回译技术为编辑样本$x_{e}\in{\mathbb D}_ {edit}$生成等价集$\mathbb{E}_ {x_{e}}$。为评估局部性,从$\mathbb{D}_ {train}^{\prime}$随机采样子集$\mathbb{D}_ {tr}$用于观察编辑后模型在训练数据上的表现。我们的SME流程始于在$\mathbb{D}_ {train}^{\prime}$上训练并通过$\mathbb{D}_ {val}$验证的初始模型$f_{0}$,当遇到$\mathbb{D}_ {edit}$中的错误时顺序执行模型编辑。在第$t$个编辑样本$(x_{e}^{t},y_{e}^{t})$后,获得编辑后模型$f_{t}$。假设总编辑次数为$T$且$I$为指示函数,我们提出的指标计算如下:
- Success Rate (SR): to evaluate the reliability, we test if the post-edit model outputs the desired prediction. Thus, SR is:
- 成功率 (SR): 为评估可靠性,我们测试编辑后模型是否能输出预期预测。因此SR定义为:
$$
S R=\frac{1}{T}\sum_{t=0}^{T}I(f_{t}(x_{e}^{t})=y_{e}^{t})
$$
$$
S R=\frac{1}{T}\sum_{t=0}^{T}I(f_{t}(x_{e}^{t})=y_{e}^{t})
$$
- Generalization Rate (GR): to evaluate the generality, we test the post-edit model $f_{t}$ on the equivalent set $\mathbb{E}_ {x_{e}^{t}}={x_{e,1}^{t}\cdot\cdot\cdot,x_{e,N_{t}}^{t}}$ of the edit example $x_{e}^{t}$ , thus GR is:
- 泛化率(GR): 为评估泛化性,我们在编辑样本$x_{e}^{t}$的等价集$\mathbb{E}_ {x_{e}^{t}}={x_{e,1}^{t}\cdot\cdot\cdot,x_{e,N_{t}}^{t}}$上测试编辑后模型$f_{t}$,因此GR定义为:
$$
G R=\frac{1}{T N_{t}}\sum_{t=0}^{T}\sum_{i=1}^{N_{t}}I(f_{t}(x_{e,i}^{t})=y_{e}^{t})
$$
$$
G R=\frac{1}{T N_{t}}\sum_{t=0}^{T}\sum_{i=1}^{N_{t}}I(f_{t}(x_{e,i}^{t})=y_{e}^{t})
$$
- Edit Retain Rate (ER): to evaluate locality and reliability, we evaluate how many past edits are retained by the final model $f_{T}$ . In a real application, a reliable model editor should keep the fixed bugs from recurring again, thus SR alone cannot evaluate reliability, and we define ER by testing the final model on all its past edit examples $\mathbb{E}_{p e}$ :
- 编辑保留率 (ER) :为了评估局部性和可靠性,我们计算最终模型 $f_{T}$ 保留了多少历史编辑。在实际应用中,可靠的模型编辑器应确保已修复的缺陷不再复发,因此仅用SR无法评估可靠性。我们通过在全部历史编辑样本 $\mathbb{E}_{p e}$ 上测试最终模型来定义ER:
$$
E R=\frac{1}{T}\sum_{t=0}^{T}I(f_{T}(x_{e}^{t})=y_{e}^{t})/T
$$
$$
E R=\frac{1}{T}\sum_{t=0}^{T}I(f_{T}(x_{e}^{t})=y_{e}^{t})/T
$$
- Training Retain Rate (TrainR): to evaluate locality, we compare the performance of the final model of $f_{T}$ and the initial model $f_{0}$ on subsampled test $\mathbb{D}_{t r}$ . Thus, the TrainR is defined as:
- 训练保留率 (TrainR): 为评估局部性,我们比较最终模型 $f_{T}$ 与初始模型 $f_{0}$ 在子采样测试集 $\mathbb{D}_{t r}$ 上的性能。因此,TrainR定义为:
$$
T r a i n R=\frac{\sum_{(x,y)\in D_{t r}}I(f_{T}(x)=y)}{\sum_{(x,y)\in D_{t r}}I(f_{0}(x)=y)}
$$
$$
T r a i n R=\frac{\sum_{(x,y)\in D_{t r}}I(f_{T}(x)=y)}{\sum_{(x,y)\in D_{t r}}I(f_{0}(x)=y)}
$$
- Test Retain Rate (TestR): to evaluate locality, we see if the post-edit model still retains the generalization ability over unseen data. Then the TestR is defined as:
- 测试保留率 (TestR): 为评估局部性,我们检测编辑后模型是否仍能保持对未见数据的泛化能力。TestR定义为:
$$
T e s t R=\frac{\sum_{(x,y)\in D_{t e s t}}I(f_{T}(x)=y)}{\sum_{(x,y)\in D_{t e s t}}I(f_{0}(x)=y)}
$$
$$
T e s t R=\frac{\sum_{(x,y)\in D_{t e s t}}I(f_{T}(x)=y)}{\sum_{(x,y)\in D_{t e s t}}I(f_{0}(x)=y)}
$$
Datasets and Baselines Both classification and auto-regressive generation tasks are selected for evaluation. Following Cao et al. (2021) and Mitchell et al. (2022a), we employ Fact-Checking (FC) for classification and closed-book Question Answering (QA) for generation. For FC, we apply a BERT base model (Devlin et al., 2019) and the FEVER dataset (Thorne et al., 2018). For QA, we apply a BART base model (Lewis et al., 2020) and the Zero-Shot Relation Extraction (zsRE) dataset (Levy et al., 2017). We directly use the equivalent set released by Cao et al. (2021). We use the same data split as Cao et al. (2021). Both FC and QA are evaluated using accuracy. Our baselines include (1) Fine-Tuning-based editors: The FT directly fine-tunes the model on the edit example. Following Mitchell et al. (2022a), $\mathbf{FT+KL}$ is selected as a baseline. It fine-tunes the model with an extra KL divergence loss $l_{k l}$ . Following Sinitsin et al. (2020) and Zhu et al. (2020), we report fine-tuning-based baselines by fine-tuning all parameters (FT(all) and $\mathbf{FT}(\mathbf{all}){+}\mathbf{KL}$ ) or the last layer (FT(last) and $\mathbf{FT}(\mathbf{last}){\mathbf{+KL}})$ . (2) Two Hyper Network-based editors: KE (Cao et al., 2021) and MEND (Mitchell et al., 2022a). (3) SERA: a variant of the latest SOTA memory-based model editor SERAC (Mitchell et al., 2022b). Other details of our baselines are reported in Appendix B.
数据集与基线
我们选择了分类和自回归生成任务进行评估。遵循Cao等人(2021)和Mitchell等人(2022a)的方法,我们采用事实核查(FC)任务进行分类评估,采用闭卷问答(QA)任务进行生成评估。对于FC任务,我们使用BERT基础模型(Devlin等人,2019)和FEVER数据集(Thorne等人,2018)。对于QA任务,我们使用BART基础模型(Lewis等人,2020)和零样本关系抽取(zsRE)数据集(Levy等人,2017)。我们直接使用Cao等人(2021)发布的等效集,并采用相同的数据划分方式。FC和QA任务均使用准确率作为评估指标。
我们的基线方法包括:
(1) 基于微调的编辑器:FT方法直接在编辑样本上微调模型。根据Mitchell等人(2022a),我们选择$\mathbf{FT+KL}$作为基线,该方法在微调时额外加入KL散度损失$l_{k l}$。遵循Sinitsin等人(2020)和Zhu等人(2020)的做法,我们报告了基于全参数微调(FT(all)和$\mathbf{FT}(\mathbf{all}){+}\mathbf{KL}$)或仅微调最后一层(FT(last)和$\mathbf{FT}(\mathbf{last}){\mathbf{+KL}})$)的基线结果。
(2) 两种基于超网络的编辑器:KE(Cao等人,2021)和MEND(Mitchell等人,2022a)。
(3) SERA:这是最新基于记忆的SOTA模型编辑器SERAC(Mitchell等人,2022b)的一个变体。其他基线细节详见附录B。
Experiment Details Initial models for two tasks are obtained following the same training settings as Cao et al. (2021). For FC, the accuracy of the initial model attains $94.1%$ on $\mathbb{D}_ {t r}$ , $76.9%$ on $\mathbb{D}_ {t e s t}$ . For QA, the accuracy of the initial model attains $56.6%$ on $\mathbb{D}_ {t r}$ , $23.1%$ on $\mathbb{D}_ {t e s t}$ . To reduce the experimental uncertainty, we randomly split the edit set into $n=20$ folders to run SME 20 times and report the averaged performance as the final result. The initial model $f_{0}$ makes about 63 mistakes in an FC folder and about 139 in a QA folder on average. For methods requiring memories (fine-tuning with KL and ours), 40,000 memory examples are sampled from $D_{t r a i n}^{\prime}\backslash D_{t r}$ are employed for both tasks and are updated as editing proceed. The hyper parameters $a$ and $m$ are selected as 1 and 10 respectively for both tasks to make the extra losses and the original task loss in the same order of magnitude. Other details can be found in Appendix B.
实验细节
两个任务的初始模型均采用与Cao等人(2021)相同的训练设置获得。对于FC任务,初始模型在$\mathbb{D}_ {tr}$上的准确率达到$94.1%$,在$\mathbb{D}_ {test}$上达到$76.9%$。对于QA任务,初始模型在$\mathbb{D}_ {tr}$上的准确率为$56.6%$,在$\mathbb{D}_ {test}$上为$23.1%$。为降低实验不确定性,我们将编辑集随机划分为$n=20$个子集进行20次SME实验,最终报告平均性能作为结果。初始模型$f_{0}$平均在每个FC子集中出现约63个错误,在QA子集中约139个错误。对于需要记忆的方法(带KL微调的方法和我们的方法),从$D_{train}^{\prime}\backslash D_{tr}$中采样40,000个记忆样本用于两项任务,并随编辑过程更新。两项任务均选择超参数$a=1$和$m=10$,使额外损失与原始任务损失保持同数量级。其他细节详见附录B。
Table 1: The Success Rate (SR), Generalization Rate (GR), Edit Retain Rate (ER), Training Retain Rate (TrainR), Test Retain Rate (TestR) of Transformer-Patcher (T-Patcher) and the baselines on FEVER and zsRE dataset. * denotes that the SR of the T-patcher on QA is 0.9987. $\dagger$ means the method requires extra training phases and training data.
| Editor | FEVER Fact-Checking BERT-base (110M) | zsRE Question-Answering BART-base (139M) | ||||||||
| SR | GR | ER | TrainR | TestR | SR | GR | ER | TrainR | TestR | |
| FT(last) | 1.00 | 0.61 | 0.59 | 0.893 | 0.946 | 1.00 | 0.58 | 0.30 | 0.914 | 0.924 |
| FT(all) | 1.00 | 0.74 | 0.83 | 0.968 | 0.994 | 1.00 | 0.68 | 0.43 | 0.865 | 0.910 |
| FT(last)+KL | 1.00 | 0.53 | 0.45 | 0.968 | 0.998 | 1.00 | 0.57 | 0.28 | 0.923 | 0.933 |
| FT(all)+KL | 1.00 | 0.71 | 0.49 | 0.998 | 1.011 | 1.00 | 0.68 | 0.39 | 0.889 | 0.925 |
| MENDt | 0.04 | 0.03 | 0.06 | 0.349 | 0.652 | 0.41 | 0.37 | 0.00 | 0.000 | 0.000 |
| KEt | 0.14 | 0.12 | 0.28 | 0.486 | 0.650 | 0.09 | 0.08 | 0.00 | 0.000 | 0.000 |
| SERAt | 1.00 | 0.89 | 1.00 | 0.904 | 0.916 | 1.00 | 0.90 | 0.98 | 0.906 | 0.901 |
| T-Patcher | 1.00 | 0.82 | 1.00 | 0.999 | 1.000 | 1.00* | 0.82 | 0.99 | 0.997 | 0.996 |
表 1: Transformer-Patcher (T-Patcher) 和基线方法在 FEVER 和 zsRE 数据集上的成功率 (SR)、泛化率 (GR)、编辑保留率 (ER)、训练保留率 (TrainR)、测试保留率 (TestR)。* 表示 T-Patcher 在 QA 任务上的 SR 为 0.9987。$\dagger$ 表示该方法需要额外的训练阶段和训练数据。
| 编辑器 | FEVER 事实核查 BERT-base (110M) | zsRE 问答 BART-base (139M) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SR | GR | ER | TrainR | TestR | SR | GR | ER | TrainR | TestR | |
| FT(last) | 1.00 | 0.61 | 0.59 | 0.893 | 0.946 | 1.00 | 0.58 | 0.30 | 0.914 | 0.924 |
| FT(all) | 1.00 | 0.74 | 0.83 | 0.968 | 0.994 | 1.00 | 0.68 | 0.43 | 0.865 | 0.910 |
| FT(last)+KL | 1.00 | 0.53 | 0.45 | 0.968 | 0.998 | 1.00 | 0.57 | 0.28 | 0.923 | 0.933 |
| FT(all)+KL | 1.00 | 0.71 | 0.49 | 0.998 | 1.011 | 1.00 | 0.68 | 0.39 | 0.889 | 0.925 |
| MENDt | 0.04 | 0.03 | 0.06 | 0.349 | 0.652 | 0.41 | 0.37 | 0.00 | 0.000 | 0.000 |
| KEt | 0.14 | 0.12 | 0.28 | 0.486 | 0.650 | 0.09 | 0.08 | 0.00 | 0.000 | 0.000 |
| SERAt | 1.00 | 0.89 | 1.00 | 0.904 | 0.916 | 1.00 | 0.90 | 0.98 | 0.906 | 0.901 |
| T-Patcher | 1.00 | 0.82 | 1.00 | 0.999 | 1.000 | 1.00* | 0.82 | 0.99 | 0.997 | 0.996 |
Table 2: The experimental results when utilizing all data in $D_{e d i t}$ as a single run of SME on QA task. The results of the FC task are presented in Table 7 in Appendix C. E represents how many edits have been conducted. N represents how many mistakes have been made by the initial model $f_{0}$ on the entire edit set $D_{e d i t}$ .
| Editor | SR | GR | ER | TrainR | TestR | E | N |
| FT(all)+KL | 1.00 | 0.69 | 0.14 | 0.936 | 0.974 | 2821 | 2766 |
| SERA | 1.00 | 0.90 | 0.97 | 0.728 | 0.694 | 3558 | 2766 |
| T-Patcher | 0.99 | 0.81 | 0.97 | 0.912 | 0.948 | 2308 | 2766 |
表 2: 在QA任务中使用 $D_{edit}$ 中所有数据作为单次SME运行的实验结果。FC任务的结果见附录C中的表7。E表示已执行的编辑次数。N表示初始模型 $f_{0}$ 在整个编辑集 $D_{edit}$ 上犯错的次数。
| Editor | SR | GR | ER | TrainR | TestR | E | N |
|---|---|---|---|---|---|---|---|
| FT(all)+KL | 1.00 | 0.69 | 0.14 | 0.936 | 0.974 | 2821 | 2766 |
| SERA | 1.00 | 0.90 | 0.97 | 0.728 | 0.694 | 3558 | 2766 |
| T-Patcher | 0.99 | 0.81 | 0.97 | 0.912 | 0.948 | 2308 | 2766 |
5.2 EXPERIMENTAL RESULTS
5.2 实验结果
Main results The experiment results are shown in Table 1. Our method achieves strong performance in all five metrics across two tasks. It could make a series of model corrections $(\mathrm{SR}{\approx}1)$ while nearly retaining every past edit $(\mathrm{ER}{\approx}1)$ and almost perfectly keeping the model’s overall performance (TrainR ${\approx}1$ , TestR≈1). The fine-tuning-based editors could partly preserve the model’s behavior and achieve high SR, but it is vulnerable to forgetting previous edits (low ER). Two Hyper Network-based editors fail in the SME setting. They have trouble retaining models’ overall performance (low ER, TrainR, TestR) and conducting a series of edits (low SR and GR). SERA achieves the highest GR, while can only partially preserve the model’s overall performance (TestR, TrainR ${\approx}0.9$ ) compared to T-Patcher. Apart from being effective, our method is efficient enough as well. Using a V100, one edit costs only 7.1s for FC and 18.9s for QA. We could further improve the efficiency to 4.7s and 12.4s by decreasing the number of memory examples to 10,000.
主要结果
实验结果如表 1 所示。我们的方法在两项任务的所有五个指标上均表现出色。它能够进行一系列模型修正 $(\mathrm{SR}{\approx}1)$ ,同时几乎保留所有过往编辑 $(\mathrm{ER}{\approx}1)$ ,并近乎完美地维持模型的整体性能 (TrainR ${\approx}1$ , TestR≈1)。基于微调的编辑器可以部分保留模型行为并实现高 SR,但容易遗忘先前的编辑 (低 ER)。两种基于 Hyper Network 的编辑器在 SME 设置中表现不佳,难以维持模型的整体性能 (低 ER、TrainR、TestR) 和执行连续编辑 (低 SR 和 GR)。SERA 取得了最高的 GR,但与 T-Patcher 相比,仅能部分保留模型的整体性能 (TestR, TrainR ${\approx}0.9$ )。除了高效性,我们的方法还具有足够的效率。使用 V100 显卡时,FC 任务的单次编辑仅需 7.1 秒,QA 任务为 18.9 秒。通过将记忆样本数减少至 10,000,可进一步将效率提升至 4.7 秒和 12.4 秒。
Scale up to thousands of edits Table 1 shows that Transformer-Patcher achieves good performance for about 60 edits on FC and 140 edits on QA, thus we wonder if it could handle more edits. So we utilize all data in $D_{e d i t}$ as a single data stream to run SME. As shown in Table 2, Transformer-Patcher could effectively correct up to thousands of mistakes and retain the model’s overall performance simultaneously compared with the other two strong baselines. It’s interesting to notice that the number of edits E of Transformer-Patcher is less than the number of actual mistakes $\mathbf{N}$ made by the initial model. In other words, our method can fix some potential mistakes in the initial model before the error actually happens. On the contrary, the fine-tuning-based method fixes more mistakes than the original model, which means it created more errors during the editing process. It seems contradictory that our method attains fewer E and lower TestR, this may due to the distribution shift between $\mathbb{D}_ {e d i t}$ and $\mathbb{D}_{t e s t}$ . See more explanation in Appendix C. Furthermore, the post-edit model only gets $1.4%$ larger for FC and $4.5%$ larger for QA. We believe this cost is acceptable for automatically correcting the model’s mistakes from time to time during deployment. In practice, we suggest using the transformer-patcher to provide a timely response for each mistake online, and after accumulating certain quantities of mistakes, we could fine-tune the original model on all accumulated mistakes, so that the patches can be removed. In this way, we could achieve a good balance between model size and editing effectiveness.
扩展到数千次编辑
表1显示,Transformer-Patcher在FC任务上实现约60次编辑、QA任务上实现约140次编辑时表现良好,因此我们探究其能否处理更多编辑。我们将$D_{edit}$中所有数据作为单一数据流运行SME。如表2所示,与其他两个强基线相比,Transformer-Patcher能有效修正多达数千个错误,同时保持模型整体性能。有趣的是,Transformer-Patcher的编辑次数E少于初始模型实际错误数$\mathbf{N}$,这意味着我们的方法能在错误实际发生前修复初始模型中的潜在错误。相反,基于微调的方法修正了比原始模型更多的错误,表明其在编辑过程中产生了新错误。我们的方法获得更少E和更低TestR看似矛盾,这可能源于$\mathbb{D}_ {edit}$与$\mathbb{D}_{test}$间的分布偏移(详见附录C)。此外,编辑后模型体积仅增大了$1.4%$(FC)和$4.5%$(QA),我们认为这种代价对于部署期间自动定期修正模型错误是可接受的。实践中,建议先用transformer-patcher在线及时响应每个错误,待累积一定数量错误后,再基于所有累积错误对原模型进行微调以移除补丁,从而在模型体积与编辑效果间取得平衡。
5.3 ANALYSES
5.3 分析

Figure 4: Variation of success rate (SR) with the number of edits. Different methods have different edit times, we plot until they converge.
图 4: 成功率 (SR) 随编辑次数的变化情况。不同方法具有不同的编辑次数,我们绘制至其收敛为止。
The collapse of MEND and KE We discuss here why MEND and KE fail in the SME. Figure 4 presents how SR varies with the number of edits on both FC and QA. Figure 4 shows that MEND and KE are effective in the first few steps, but shortly after they are no longer able to produce valid edits. However, in their original paper (Cao et al., 2021; Mitchell et al., 2022a), they both reported that they achieved high SR when dealing with one-step editing. We find this phenomenon reasonable since both Hyper Network-based editors are trained with the initial model $f_{0}$ and thus strongly coupled with the original parameters. As the editing proceeds, the model becomes more different from the initial one, resulting in their failure. We tried to retrain HyperNets after every edit using the post-edit model, but the cost for re-training is unacceptable as it costs hours to train a HyperNet model editor.
MEND和KE的失效原因分析
此处我们探讨MEND和KE在SME中失效的原因。图4展示了FC和QA任务中SR随编辑次数的变化情况。图4显示MEND和KE在前几步编辑时效果良好,但很快便无法生成有效编辑。然而在原始论文(Cao等人, 2021; Mitchell等人, 2022a)中,二者均报告在单步编辑时获得了高SR值。我们认为这种现象是合理的:由于这两种基于超网络(Hyper Network)的编辑器都是用初始模型$f_{0}$训练的,因此与原始参数存在强耦合性。随着编辑次数增加,模型与初始状态的差异逐渐增大,最终导致编辑器失效。我们尝试在每次编辑后使用编辑后的模型重新训练超网络,但重新训练的成本(每次需数小时)令人难以接受。
Table 3: The ablation results for two alternatives of memory loss.
| Patch | FEVER Fact-Checking | zsRE Question-Answering | ||||||||
| SR | GR | ER | TrainR | TestR | SR | GR | ER | TrainR | TestR | |
| w/olm | 0.99 | 0.94 | 0.61 | 0.737 | 0.844 | 0.99 | 0.94 | 0.21 | 0.069 | 0.154 |
| KL | 1.00 | 0.76 | 0.99 | 0.996 | 0.998 | 0.94 | 0.69 | 0.49 | 0.481 | 0.710 |
| w/olm2 | 0.95 | 0.82 | 0.95 | 0.994 | 0.992 | 0.95 | 0.82 | 0.94 | 0.991 | 0.984 |
| T-Patcher | 1.00 | 0.82 | 1.00 | 0.999 | 1.000 | 1.00 | 0.82 | 0.99 | 0.997 | 0.996 |
表 3: 两种记忆损失替代方案的消融实验结果
| Patch | FEVER Fact-Checking | zsRE Question-Answering | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SR | GR | ER | TrainR | TestR | SR | GR | ER | TrainR | TestR | |
| w/olm | 0.99 | 0.94 | 0.61 | 0.737 | 0.844 | 0.99 | 0.94 | 0.21 | 0.069 | 0.154 |
| KL | 1.00 | 0.76 | 0.99 | 0.996 | 0.998 | 0.94 | 0.69 | 0.49 | 0.481 | 0.710 |
| w/olm2 | 0.95 | 0.82 | 0.95 | 0.994 | 0.992 | 0.95 | 0.82 | 0.94 | 0.991 | 0.984 |
| T-Patcher | 1.00 | 0.82 | 1.00 | 0.999 | 1.000 | 1.00 | 0.82 | 0.99 | 0.997 | 0.996 |
Memory loss To validate the effectiveness of our proposed memory loss, we apply several alternative patches: (1) T-Patcher w/o $l_{m}$ , (2) KL Patch, where $l_{m}$ is replaced with the KL divergence loss, (3) T-Patcher w/o $l_{m_{2}}$ . The ablation results in Table 3 show that memory loss is critical. Simply adding patches without memory loss hurts the model’s overall performance severely. The KL divergence partially alleviates this problem (higher TrainR, TestR, and ER) but is still unsatisfying on the more complex QA task, which is similar to the Fintuning with KL results in Table 1. By comparing w/o $l_{m_{2}}$ and T-Patcher, we observe that the main contribution of our proposed memory loss comes from $l_{m_{1}}$ , while adding $l_{m_{2}}$ still improves the method’s performance. Furthermore, to investigate whether our added patches do solely respond to the specific error we visualize the activation values of different patches on their corresponding mistakes in Figure 5 for the QA task. The $\mathrm{X}$ -axis represents the mistake (8.2 represents the second mistake of the 8th edit example) and the Y-axis represents the patch. Figure 5a shows that the patch can be activated by multiple irrelevant queries without the constraint of memory loss, leading to low ER, TrainR, and TestR. Figure 5b is a lot darker, indicating that the KL loss tends to deactivate patches to bridge the distribution gap before patching and after patching. And figure 5c presents a clear diagonal line, which means each patch takes charge of its corresponding mistake. Further analysis of the activation value of different 0p.6atches is presented in Appendix C.
记忆损失
为验证我们提出的记忆损失的有效性,我们应用了多种替代补丁方案:(1) 不含 $l_{m}$ 的 T-Patcher,(2) 用 KL 散度损失替代 $l_{m}$ 的 KL Patch,(3) 不含 $l_{m_{2}}$ 的 T-Patcher。表 3 的消融实验表明记忆损失至关重要。仅添加补丁而不使用记忆损失会严重损害模型的整体性能。KL 散度部分缓解了该问题(更高的 TrainR、TestR 和 ER),但在更复杂的 QA 任务上仍不理想,这与表 1 中采用 KL 散度的微调结果相似。通过对比不含 $l_{m_{2}}$ 的方案与 T-Patcher,我们发现所提记忆损失的主要贡献来自 $l_{m_{1}}$,而添加 $l_{m_{2}}$ 仍能提升方法性能。
此外,为探究添加的补丁是否仅针对特定错误响应,我们在图 5 中可视化了 QA 任务中各补丁在对应错误上的激活值。X 轴表示错误(8.2 表示第 8 个编辑样本的第二个错误),Y 轴表示补丁。图 5a 显示,若缺乏记忆损失约束,补丁会被多个无关查询激活,导致低 ER、TrainR 和 TestR。图 5b 色调明显更暗,表明 KL 损失倾向于停用补丁以弥合修补前后的分布差异。而图 5c 呈现出清晰对角线,说明每个补丁仅负责其对应错误。不同 0p.6atches 激活值的进一步分析见附录 C。

Figure 5: The activation values of three different patches on their corresponding mistakes.
图 5: 三个不同补丁在其对应错误上的激活值。
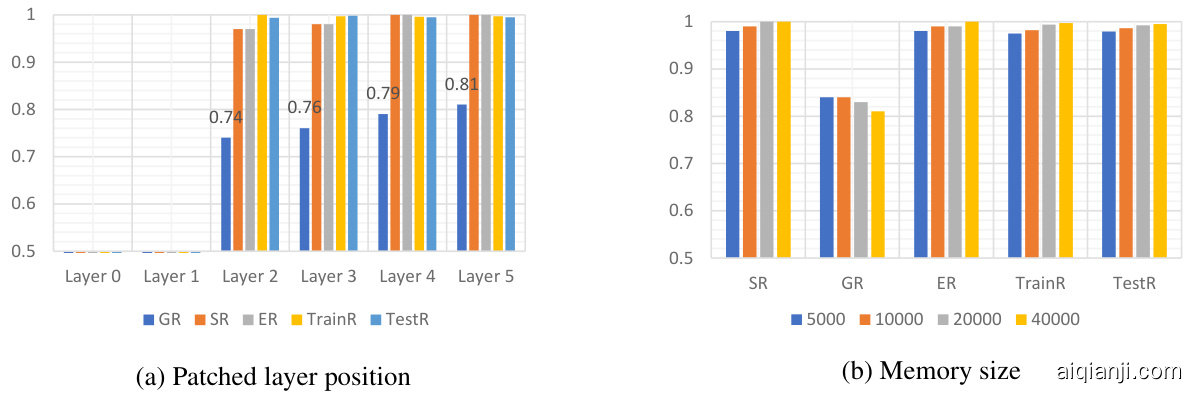
Figure 6: The ablation studies about patched layer position and the memory size .
图 6: 关于补丁层位置和内存大小的消融研究。
PatcheSRd layerG Rpo sitio En R ToT ravi naR li date Te stthRe b
