MonSter: Marry Monodepth to Stereo Unleashes Power

MonSter: 融合单目深度与立体视觉释放潜力

Junda Cheng1, Longliang Liu1, Gangwei $\mathrm{Xu^{1}}$ , Xianqi Wang1, Zhaoxing Zhang1, Yong Deng2, Jinliang Zang2, Yurui Chen2, Zhipeng Cai3, Xin Yang1† 1 Huazhong University of Science and Technology 2 Autel Robotics 3 Intel Labs {jundacheng, longliangl, gwxu, xianqiw, zzx, x in yang 2014}@hust.edu.cn, czptc2h@gmail.com

Junda Cheng1, Longliang Liu1, Gangwei $\mathrm{Xu^{1}}$ , Xianqi Wang1, Zhaoxing Zhang1, Yong Deng2, Jinliang Zang2, Yurui Chen2, Zhipeng Cai3, Xin Yang1† 1 华中科技大学 2 道通智能 3 英特尔实验室 {jundacheng, longliangl, gwxu, xianqiw, zzx, x in yang 2014}@hust.edu.cn, czptc2h@gmail.com

Figure 1. Zero-shot generalization comparison: all models are trained on Scene Flow and tested directly on KITTI. Compared to the baseline IGEV [38], our method MonSter shows significant improvement in challenging regions such as reflective surfaces, texture less areas, fine structures, and distant objects.

图 1: 零样本泛化对比：所有模型均在 Scene Flow 上训练，并直接在 KITTI 上测试。与基线 IGEV [38] 相比，我们的方法 MonSter 在反射表面、无纹理区域、精细结构和远距离物体等具有挑战性的区域表现出显著改进。

Abstract

摘要

Stereo matching recovers depth from image correspondences. Existing methods struggle to handle ill-posed regions with limited matching cues, such as occlusions and texture less areas. To address this, we propose MonSter, a novel method that leverages the complementary strengths of monocular depth estimation and stereo matching. MonSter integrates monocular depth and stereo matching into a dual-branch architecture to iterative ly improve each other. Confidence-based guidance adaptively selects reliable stereo cues for monodepth scale-shift recovery. The refined monodepth is in turn guides stereo effectively at illposed regions. Such iterative mutual enhancement enables MonSter to evolve monodepth priors from coarse objectlevel structures to pixel-level geometry, fully unlocking the potential of stereo matching. As shown in Fig. 2, MonSter ranks $1^{s t}$ across five most commonly used leader boards — SceneFlow, KITTI 2012, KITTI 2015, Middlebury, and ETH3D. Achieving up to $49.5%$ improvements (Bad 1.0 on ETH3D) over the previous best method. Comprehensive analysis verifies the effectiveness of MonSter in illposed regions. In terms of zero-shot generalization, MonSter significantly and consistently outperforms state-of-theart across the board. The code is publicly available at: https://github.com/Junda24/MonSter.

立体匹配从图像对应关系中恢复深度。现有方法难以处理匹配线索有限的病态区域，例如遮挡和无纹理区域。为了解决这个问题，我们提出了 MonSter，这是一种利用单目深度估计和立体匹配互补优势的新方法。MonSter 将单目深度和立体匹配集成到双分支架构中，以迭代地相互改进。基于置信度的指导自适应地选择可靠的立体线索用于单目深度尺度偏移恢复。改进后的单目深度反过来在病态区域有效地引导立体匹配。这种迭代的相互增强使 MonSter 能够将单目深度先验从粗略的对象级结构演变为像素级几何，充分释放立体匹配的潜力。如图 2 所示，MonSter 在五个最常用的排行榜上排名第一 —— SceneFlow、KITTI 2012、KITTI 2015、Middlebury 和 ETH3D。与之前的最佳方法相比，实现了高达 49.5% 的改进（ETH3D 上的 Bad 1.0）。综合分析验证了 MonSter 在病态区域的有效性。在零样本泛化方面，MonSter 在各个领域都显著且持续地超越了最先进的方法。代码公开在：https://github.com/Junda24/MonSter。

1. Introduction

1. 引言

Stereo matching estimates a disparity map from rectified stereo images, which can be subsequently converted into metric depth. It is the core of many applications such as self-driving, robotic navigation, and 3D reconstruction.

立体匹配从校正后的立体图像中估计视差图，随后可以将其转换为度量深度。它是自动驾驶、机器人导航和3D重建等许多应用的核心。

Deep learning based methods [4, 14, 16, 20, 35, 48] have demonstrated promising performance on standard benchmarks. These methods can be roughly categorized into cost filtering-based methods and iterative optimization-based methods. Cost filtering-based methods [4, 14, 15, 22, 37, 39, 41, 43] construct 3D/4D cost volume using CNN features, followed by a series of 2D/3D convolutions for regularization and filtering to minimize mismatches. Iterative optimization-based methods [10, 16, 20, 38, 49] initially construct an all-pairs correlation volume, then index a local cost to extract motion features, which guide the recurrent units (ConvGRUs) [9] to iterative ly refine the disparity map.

基于深度学习的方法 [4, 14, 16, 20, 35, 48] 在标准基准测试中展示了出色的性能。这些方法大致可分为基于成本过滤的方法和基于迭代优化的方法。基于成本过滤的方法 [4, 14, 15, 22, 37, 39, 41, 43] 使用CNN特征构建3D/4D成本体积，然后通过一系列2D/3D卷积进行正则化和过滤以最小化不匹配。基于迭代优化的方法 [10, 16, 20, 38, 49] 首先构建全对相关体积，然后索引局部成本以提取运动特征，这些特征指导循环单元 (ConvGRUs) [9] 迭代地优化视差图。

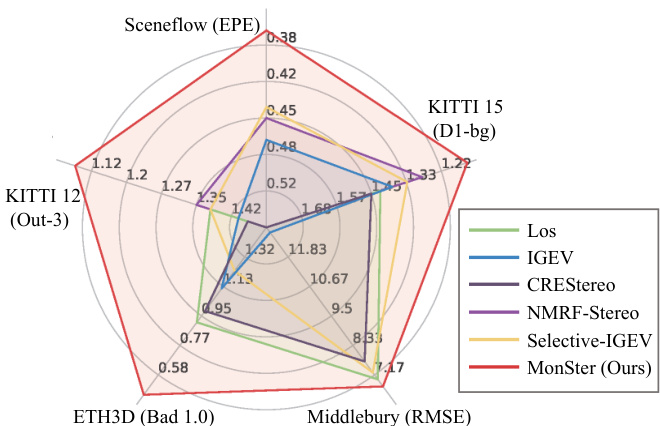
Figure 2. Leader board performance. Our method ranks $1^{s t}$ across 5 leader boards, advancing SOTA by a large margin.

图 2: 排行榜表现。我们的方法在 5 个排行榜中排名第 1，大幅推进了 SOTA。

Both types of methods essentially derive disparity from similarity matching, assuming visible correspondences in both images. This poses challenges in ill-posed regions with limited matching cues, e.g., occlusions, textureless areas, repetitive/thin structures, and distant objects with low pixel representation. Existing methods [4, 31, 33, 37, 42, 44, 49] address this issue by enhancing matching with stronger feature representations during feature extraction or cost aggregation: GMStereo [42] and STTR [18] employ transformer as feature extractors; IGEV [38] and ACVNet [37] incorporate geometric information into the cost volume using attention mechanisms to strengthen matching information; Selective-IGEV [35] and DLNR [49] further improve performance by introducing high-frequency information during the iterative refinement stage. However, these methods still struggle to fundamentally resolve the issue of mismatching, limiting their practical performance.

两种方法本质上都是从相似性匹配中推导视差，假设两幅图像中存在可见的对应关系。这在匹配线索有限的病态区域中带来了挑战，例如遮挡、无纹理区域、重复/细长结构以及像素表示较少的远距离物体。现有方法 [4, 31, 33, 37, 42, 44, 49] 通过在特征提取或成本聚合阶段使用更强的特征表示来增强匹配以解决这个问题：GMStereo [42] 和 STTR [18] 使用 Transformer 作为特征提取器；IGEV [38] 和 ACVNet [37] 通过注意力机制将几何信息融入成本体积以增强匹配信息；Selective-IGEV [35] 和 DLNR [49] 在迭代优化阶段引入高频信息以进一步提高性能。然而，这些方法仍然难以从根本上解决误匹配问题，限制了其实际表现。

Unlike stereo matching, monocular depth estimation directly recovers 3D from a single image, which does not encounter the challenge of mismatching. While monocular depth provides complementary structural information for stereo, pre-trained models often yield relative depth with scale and shift ambiguities. As shown in Fig.3, the prediction of monodepth models differ heavily from the ground- truth. Even after global scale and shift alignment, substantial errors still persist, complicating pixel-wise fusion of monocular depth and stereo disparity. Based on these insights, we propose MonSter, a novel approach that decomposes stereo matching into monocular depth estimation and per-pixel scale-shift recovery, which fully combines the strengths of monocular and stereo algorithms and overcomes the limitations from the lack of matching cues.

与立体匹配不同，单目深度估计直接从单张图像中恢复3D信息，不会遇到不匹配的挑战。虽然单目深度为立体提供了互补的结构信息，但预训练模型通常会产生带有尺度和偏移模糊的相对深度。如图3所示，单目深度模型的预测与真实值存在很大差异。即使在全局尺度和偏移对齐之后，仍然存在大量误差，这使单目深度和立体视差的像素级融合变得复杂。基于这些观察，我们提出了 MonSter，这是一种将立体匹配分解为单目深度估计和像素级尺度-偏移恢复的新方法，它充分结合了单目和立体算法的优势，并克服了缺乏匹配线索的局限性。

MonSter constructs separate branches for monocular depth estimation and stereo matching, and adaptively fuses them through Stereo Guided Alignment (SGA) and Mono Guided Refinement (MGR) modules. SGA first rescales monodepth into a “monocular disparity” by aligning globally with stereo disparity. Then it uses condition-guided GRUs to adaptively select reliable stereo cues for updating the per-pixel monocular disparity shift. Symmetric to SGA, MGR uses the optimized monocular disparity as the condition to adaptively refine the stereo disparity in regions where matching fails. Through multiple iterations, the two branches effectively complement each other: 1) Though beneficial at coarse object-level, directly and uni directionally fuse monodepth into stereo suffers from scale-shift ambiguities, which often introduces noise in complex regions such as slanted or curved surfaces. Refining monodepth with stereo resolves this issue effectively, ensuring the robustness of MonSter. 2) The refined monodepth in turn provides strong guidance to stereo in challenging regions. E.g., the depth perception ability of stereo matching degrades with distance due to smaller pixel proportions and the increased matching difficulty. Monodepth models pretrained on large-scale datasets are less affected by such issues, which can effectively improve stereo disparity in the corresponding region.

MonSter 为单目深度估计和立体匹配构建了独立的分支，并通过 Stereo Guided Alignment (SGA) 和 Mono Guided Refinement (MGR) 模块自适应地融合它们。SGA 首先通过全局对齐立体视差将单目深度重新缩放为“单目视差”。然后，它使用条件引导的 GRU 自适应地选择可靠的立体线索来更新每个像素的单目视差偏移。与 SGA 对称，MGR 使用优化后的单目视差作为条件，在匹配失败的区域自适地细化立体视差。通过多次迭代，这两个分支有效地互补：1) 尽管在粗略的对象级别上有益，但直接将单目深度单向融合到立体中会遭受尺度偏移的模糊性，这通常在复杂区域（如倾斜或弯曲表面）引入噪声。用立体细化单目深度有效地解决了这个问题，确保了 MonSter 的鲁棒性。2) 优化后的单目深度反过来在具有挑战性的区域为立体提供了强有力的指导。例如，由于像素比例较小和匹配难度增加，立体匹配的深度感知能力随着距离的增加而下降。在大规模数据集上预训练的单目深度模型受此类问题的影响较小，可以有效地改善相应区域的立体视差。

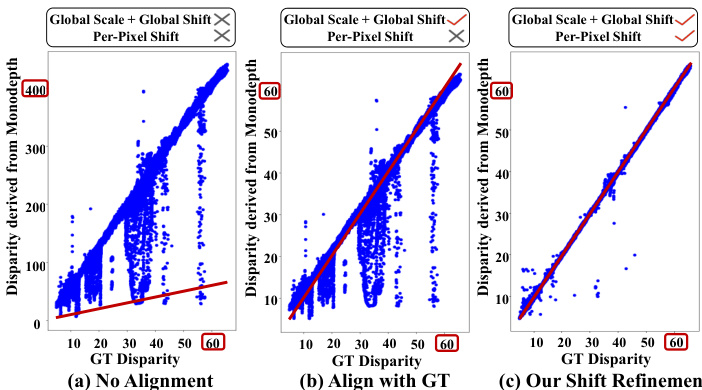
Figure 3. Distance between GT disparity and the disparity derived from monocular depth [46] on KITTI dataset. The red line indicates identical disparity maps. (a): Without any alignment. (b) Align depth with GT using global scale and global shift values (same for all pixels). (c) The monocular disparity produced by MonSter, with per-pixel shift refinement. Even globally aligned with GT, SOTA monocular depth models still exhibit severe noise. Our method MonSter effectively addresses this issue by refining monocular depth with per-pixel shift, which fully unlocks the power of monocular depth priors for stereo matching.

图 3. KITTI 数据集中 GT 视差与单目深度 [46] 导出的视差之间的距离。红线表示相同的视差图。(a): 未进行任何对齐。(b) 使用全局尺度和全局平移值（所有像素相同）将深度与 GT 对齐。(c) MonSter 生成的单目视差，带有逐像素平移优化。即使与 GT 全局对齐，SOTA 单目深度模型仍然表现出严重的噪声。我们的方法 MonSter 通过逐像素平移优化单目深度，有效解决了这一问题，充分释放了单目深度先验在立体匹配中的潜力。

Our main contributions can be summarized as follows:

我们的主要贡献可总结如下：

• We propose a novel stereo-matching method MonSter, fully leveraging the pixel-level monocular depth priors to significantly improve the depth perception performance of stereo matching in ill-posed regions and fine structures. • As shown in Fig. 2, MonSter ranks $1^{s t}$ across 5 widelyused leader boards: KITTI 2012 [11], KITTI 2015 [23], Scene Flow [22], Middlebury [27] and ETH3D [28]. Ad- vancing SOTA by up to $49.5%$ .

• 我们提出了一种新颖的立体匹配方法 MonSter，充分利用像素级单目深度先验，显著提升了立体匹配在病态区域和精细结构中的深度感知性能。
• 如图 2 所示，MonSter 在 5 个广泛使用的排行榜上排名第一：KITTI 2012 [11]、KITTI 2015 [23]、Scene Flow [22]、Middlebury [27] 和 ETH3D [28]。相比现有最佳方法 (SOTA) 提升了高达 49.5%。

• Compared to SOTA methods, MonSter achieves the best zero-shot generalization consistently across diverse datasets. MonSter trained solely on synthetic data demonstrates strong performance across diverse realworld datasets (see Fig.1).

• 与 SOTA 方法相比，MonSter 在各种数据集上始终表现出最佳的零样本泛化能力。仅使用合成数据训练的 MonSter 在多样化的真实世界数据集中表现出色（见图 1）。

2. Related Work

2. 相关工作

Matching based Methods. Mainstream stereo matching methods recover disparity from matching costs. These methods can generally be divided into two categories: cost filtering-based methods and iterative optimization-based methods. Cost filtering-based methods [5, 6, 12, 14, 22, 29, 43] typically construct a 3D/4D cost volume using feature maps and subsequently employing 2D/3D CNN to filter the volume and derive the final disparity map. Constructing a cost volume with strong representational capacity and accurately regressing disparity from a noisy cost volume are key challenges. PSMNet [4] proposes a stacked hourglass 3D CNN for better cost regular iz ation. [14, 30, 37] propose the group-wise correlation volume, the attention concatenation volume, and the pyramid warping volume respectively to improve the expressiveness of the matching cost. Recently, a novel class of methods based on iterative optimization [16, 20, 35, 38, 49] has achieved state-of-the-art performance in both accuracy and efficiency. These methods use ConvGRUs to iterative ly update the disparity by leveraging local cost values retrieved from the all-pairs correlation volume. Similarly, iterative optimization-based methods also primarily focus on improving the matching cost construction and the iterative optimization stages. CREStereo [16] proposes a cascaded recurrent network to update the disparity field in a coarse-to-fine manner. IGEV [38] proposes a Geometry Encoding Volume that encodes geometry and context information for a more robust matching cost. Both types of methods essentially derive depth from matching costs, which are inherently limited by ill-posed regions.

基于匹配的方法。主流的立体匹配方法从匹配代价中恢复视差。这些方法通常可以分为两类：基于代价滤波的方法和基于迭代优化的方法。基于代价滤波的方法 [5, 6, 12, 14, 22, 29, 43] 通常使用特征图构建 3D/4D 代价体，随后使用 2D/3D CNN 对代价体进行滤波并得到最终的视差图。构建具有强表示能力的代价体并从噪声代价体中准确回归视差是关键挑战。PSMNet [4] 提出了一种堆叠沙漏结构的 3D CNN 以实现更好的代价正则化。[14, 30, 37] 分别提出了分组相关体、注意力连接体和金字塔扭曲体，以提高匹配代价的表达能力。最近，基于迭代优化的方法 [16, 20, 35, 38, 49] 在精度和效率上都达到了最先进的性能。这些方法使用 ConvGRU 通过从全对相关体中检索局部代价值来迭代更新视差。同样，基于迭代优化的方法也主要集中在改进匹配代价构建和迭代优化阶段。CREStereo [16] 提出了一种级联循环网络，以从粗到细的方式更新视差场。IGEV [38] 提出了一种几何编码体，用于编码几何和上下文信息以实现更鲁棒的匹配代价。这两类方法本质上都是从匹配代价中推导深度，而这些代价在本质上受到不适定区域的限制。

Stereo Matching with Structural Priors. Matching in illposed regions is challenging, previous methods [7, 17, 19, 31, 44, 47] tried to leverage structural priors to address this issue. EdgeStereo [31] enhances performance in edge regions by incorporating edge detection cues into the disparity estimation pipeline. SegStereo [44] utilizes semantic cues from a segmentation network as guidance for stereo matching, improving performance in texture less regions. However, semantic and edge cues only provide object-level priors, which are insufficient for pixel-level depth perception. Consequently, they are not effective in challenging scenes with large curved or slanted surfaces. Therefore, some methods incorporate monocular depth priors to provide perpixel guidance for stereo matching through dense relative depth. CLStereo [47] introduces a monocular branch that serves as a contextual constraint, transferring geometric priors from the monocular to the stereo branch. Los [17] uses monocular depth as local structural prior to generating the slant plane, which can explicitly leverage structure information for updating disparities. However, monocular depth estimation suffers from severe scale and shift ambiguities as shown in Fig.3. Directly using it as a structural prior to constrain stereo matching can introduce heavy noise. Our MonSter adaptively selects reliable stereo disparity to correct the scale and shift of monodepth, which fully leverages the monocular depth priors while avoiding noise, thereby significantly enhancing stereo performance in ill-posed regions.

基于结构先验的立体匹配

3. Method

3. 方法

As shown in Fig. 4, MonSter consists of 1) a monocular depth branch, 2) a stereo matching branch and 3) a mutual refinement module. The two branches estimate initial monocular depth and the stereo disparity, which are fed into mutual refinement to iterative ly improve each other.

如图 4 所示，MonSter 由 1) 单目深度分支、2) 立体匹配分支和 3) 互优化模块组成。这两个分支分别估计初始的单目深度和立体视差，然后输入到互优化模块中，通过迭代相互优化。

3.1. Monocular and Stereo Branches

3.1. 单目与立体分支

The monocular depth branch can leverage most monocular depth models to achieve non-trivial performance improvements (see Sec.4.5 for analysis). Our best empirical configuration uses pretrained Depth Anything V 2 [46] as the monocular depth branch, which uses DINOv2 [24] as the encoder and DPT [26] as the decoder. The stereo matching branch follows IGEV [38] to obtain the initial stereo disp, with modifications only to the feature extraction component, as shown in Fig. 4. To efficiently and fully leverage the pretrained monocular model, the stereo branch shares the ViT encoder in DINOv2 with the monocular branch, with parameters frozen to prevent the stereo matching training from affecting its generalization ability. Moreover, the ViT architecture extracts feature at a single resolution, while recent stereo matching methods commonly utilize multiscale features at four scales (1/32, 1/16, 1/8, and 1/4 of the original image resolution ). To fully align with IGEV, we employ a stack of 2D convolutional layers, denoted as the feature transfer network, to downsample and transform the ViT feature into a collection of pyramid features $\mathcal{F}={F_{0},F_{1},F_{2},F_{3}}$ , where $\begin{array}{r}{F_{k}\in\mathbb{R}^{\frac{H}{2^{5}-k}\times\frac{W}{2^{5}-k}\times c_{k}}}\end{array}$ . We follow IGEV to construct Geometry Encoding Volume and use the same ConvGRUs for iterative optimization. To balance accuracy and efficiency, we perform only $N_{1}$ iterations to obtain a initial stereo disparity with reasonable quality.

单目深度分支可以利用大多数单目深度模型来实现显著的性能提升（详细分析见第4.5节）。我们最佳的实验配置使用预训练的 Depth Anything V 2 [46] 作为单目深度分支，该分支使用 DINOv2 [24] 作为编码器，DPT [26] 作为解码器。立体匹配分支遵循 IGEV [38] 来获取初始的立体视差，仅对特征提取组件进行了修改，如图 4 所示。为了高效且充分地利用预训练的单目模型，立体分支与单目分支共享 DINOv2 中的 ViT 编码器，并冻结其参数，以防止立体匹配训练影响其泛化能力。此外，ViT 架构在单一分辨率下提取特征，而最近的立体匹配方法通常利用四个尺度（原始图像分辨率的 1/32、1/16、1/8 和 1/4）的多尺度特征。为了完全与 IGEV 对齐，我们使用一系列二维卷积层（称为特征转移网络）对 ViT 特征进行下采样，并将其转换为金字塔特征集合 $\mathcal{F}={F_{0},F_{1},F_{2},F_{3}}$，其中 $\begin{array}{r}{F_{k}\in\mathbb{R}^{\frac{H}{2^{5}-k}\times\frac{W}{2^{5}-k}\times c_{k}}}\end{array}$。我们遵循 IGEV 构建几何编码体积，并使用相同的 ConvGRU 进行迭代优化。为了平衡精度和效率，我们仅进行 $N_{1}$ 次迭代以获得具有合理质量的初始立体视差。

3.2. Mutual Refinement

3.2. 双向优化

Once the initial (relative) monocular depth and stereo disparity are obtained, they are fed into the mutual refinement module to iterative ly refine each other. We first perform global scale-shift alignment, which converts monocular depth into a disparity map and aligns it coarsely with stereo outputs. Then we iterative ly perform a dual-branched refinement: Stereo guided alignment (SGA) leverages stereo cues to update the per-pixel shift of the monocular dispar- ity; Mono guided refinement (MGR) leverages the aligned monocular prior to further refine stereo disparity.

一旦获得了初始的（相对）单目深度和立体视差，它们会被输入到相互精炼模块中，以迭代地相互精炼。我们首先执行全局尺度-位移对齐，将单目深度转换为视差图，并将其与立体输出进行粗略对齐。然后我们迭代执行双分支精炼：立体引导对齐（SGA）利用立体线索更新单目视差的每像素位移；单目引导精炼（MGR）利用对齐的单目先验进一步精炼立体视差。

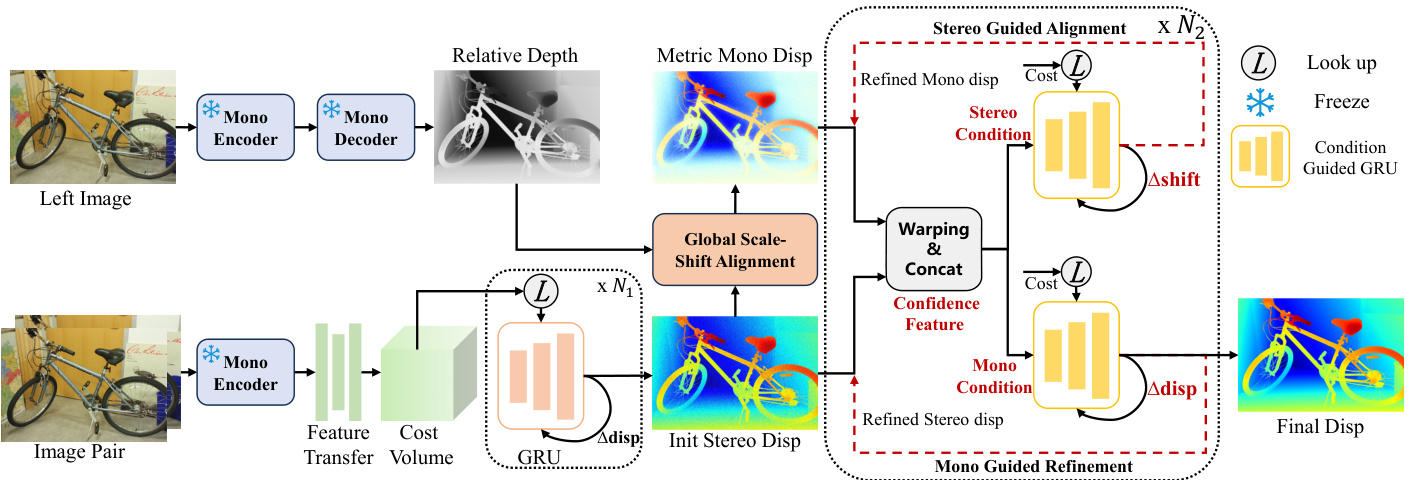
Figure 4. Overview of MonSter. MonSter consists of a monocular depth estimation branch, a stereo matching branch, and a mutua refinement module. It iterative ly improves one branch with priors from the other, effectively resolving the ill-posedness in stereo matching.

图 4: MonSter 概述。MonSter 由一个单目深度估计分支、一个立体匹配分支和一个相互优化模块组成。它通过从一个分支中获取先验信息来迭代改进另一个分支，从而有效解决立体匹配中的不适定问题。

Global Scale-Shift Alignment. Global Scale-Shift Alignment performs least squares optimization over a global scale $s_{G}$ and a global shift $t_{G}$ to coarsely align the inverse monocular depth with the stereo disparity:

全局尺度-位移对齐

where $D_{M}(i)$ and $D_{S}^{0}(i)$ are the inverse monocular depth and stereo disparity at the i-th pixel. $\Omega$ represents the region where stereo disparity values fall between $20%$ to $90%$ sorting in ascending order, which helps to filter unreliable regions such as the sky, extremely distant areas, and closerange outliers. Intuitively, this step converts the inverse monocular depth into a disparity map coarsely aligned with the stereo disparity, enabling effective mutual refinement in the same space. We call this aligned disparity map $D_{M}^{0}$ the monocular disparity in the remainder of the paper.

其中 $D_{M}(i)$ 和 $D_{S}^{0}(i)$ 分别表示第 i 个像素的单目深度逆值和立体视差值。$\Omega$ 表示立体视差值按升序排序后落在 $20%$ 到 $90%$ 之间的区域，这有助于过滤掉不可靠的区域，如天空、极远区域和近距离的异常值。直观上，这一步将单目深度逆值转换为与立体视差粗略对齐的视差图，从而在同一空间内实现有效的相互优化。我们在本文的后续部分将这种对齐后的视差图 $D_{M}^{0}$ 称为单目视差。

Stereo Guided Alignment (SGA). Though coarsely aligned, a unified shift $t_{G}$ is not sufficient to recover accurate monocular disparity at different pixels. To fully release the potential of monocular depth prior, SGA leverages intermediate stereo cues to further estimate a per-pixel residual shift. To avoid introducing noisy stereo cues, SGA uses confidence based guidance. In each update step $j$ , we compute the confidence using the flow residual map ${\bf\bar{\Delta}}{\cal F}{S}^{j}$ , which is obtained by warping and subtracting features based on the stereo disparity $\pmb{D}{S}^{j}$ as:

立体引导对齐 (SGA)。虽然粗略对齐，但统一的偏移量 $t_{G}$ 不足以恢复不同像素处的准确单目视差。为了充分发挥单目深度先验的潜力，SGA 利用中间立体线索进一步估计每个像素的残差偏移。为了避免引入噪声立体线索，SGA 使用基于置信度的引导。在每次更新步骤 $j$ 中，我们使用流残差图 ${\bf\bar{\Delta}}{\cal F}{S}^{j}$ 计算置信度，该残差图通过基于立体视差 $\pmb{D}{S}^{j}$ 的扭曲和特征相减得到：

where $F_{3}^{L},F_{3}^{R}$ represent the quarter-resolution features of left and right images in $\mathcal{F}$ respectively. For each iteration, we also use the current stereo disparity $D_{S}^{j}$ to index from the Geometry Encoding Volume to obtain geometry features of stereo branch $G_{S}^{j}$ follow IGEV. Concatenated with $F_{S}^{j}$ and $D_{S}^{j}$ , we obtain the stereo condition as:

其中 $F_{3}^{L},F_{3}^{R}$ 分别表示 $\mathcal{F}$ 中左右图像的四分之一分辨率特征。对于每次迭代，我们还使用当前的立体视差 $D_{S}^{j}$ 从几何编码卷中索引，以获取立体分支的几何特征 $G_{S}^{j}$，遵循 IGEV。与 $F_{S}^{j}$ 和 $D_{S}^{j}$ 连接后，我们得到立体条件为：

where $\operatorname{En}{g}$ and $\mathrm{En}{d}$ are two convolutional layers for feature encoding. We feed $x_{S}^{j}$ into condition-guided ConvGRUs to update the hidden state $h_{m}^{i-1}$ of monocular branch as:

其中 $\operatorname{En}{g}$ 和 $\mathrm{En}{d}$ 是两个用于特征编码的卷积层。我们将 $x_{S}^{j}$ 输入到条件引导的 ConvGRU 中，以更新单目分支的隐藏状态 $h_{m}^{i-1}$：

where $c_{k},c_{r},c_{h}$ are context features. Based on the hidden state $h_{M}^{j}$ , we decode a residual shift $\Delta t$ through two convolutional layers to update the monocular disparity:

其中 $c_{k},c_{r},c_{h}$ 是上下文特征。基于隐藏状态 $h_{M}^{j}$，我们通过两个卷积层解码出一个残差位移 $\Delta t$ 来更新单目视差：

Mono Guided Refinement (MGR). Symmetric to SGA, MGR leverages the aligned monocular disparity to address stereo deficiencies in ill-posed regions, thin structures, and distant objects. Specifically, we employ the same conditionguided GRU architecture with independent parameters to refine stereo disparity. We simultaneously calculate the flow residual maps $\bar{F}{M}^{j}$ , $\overset{\cdot}{F}{S}^{j}$ and geometric features $G_{M}^{j},G_{S}^{j}$ for both the monocular and stereo branches, providing a comprehensive stereo refinement guidance:

单目引导优化 (MGR)。与SGA对称，MGR利用对齐的单目视差来解决不适定区域、薄结构和远距离物体中的立体视差缺陷。具体来说，我们采用具有独立参数的相同条件引导GRU架构来优化立体视差。我们同时计算单目和立体分支的流残差图 $\bar{F}{M}^{j}$ 、 $\overset{\cdot}{F}{S}^{j}$ 以及几何特征 $G_{M}^{j},G_{S}^{j}$，提供全面的立体优化指导：

Figure 5. Qualitative results on ETH3D. MonSter outperforms IGEV in challenging areas with strong reflectance, fine structures etc.

图 5: ETH3D 上的定性结果。MonSter 在具有强反射、精细结构等挑战性区域中优于 IGEV。

where $G_{M}^{j}$ is the geometry features of the monocular branch obtained by indexing from the Geometry Encoding Volume using the monocular disparity DjM . xjM represents the monocular condition for ConvGRUs, and we use the Eq. (4) to update the hidden state $h_{S}^{i}$ similarly, with only the condition input changed from xiS to $x_{M}^{i}$ . We use the same two convolutional layers to decode the residual disparity $\triangle d$ and update the current stereo disparity following Eq. (5). After $N_{2}$ rounds of dual-branched refinement, the disparity of the stereo branch is the final output of MonSter.

其中 $G_{M}^{j}$ 是通过使用单目视差 $D_{j}^{M}$ 从几何编码体积中索引获得的单目分支的几何特征。$x_{j}^{M}$ 表示 ConvGRUs 的单目条件，我们使用公式 (4) 来类似地更新隐藏状态 $h_{S}^{i}$，仅将条件输入从 $x_{i}^{S}$ 更改为 $x_{M}^{i}$。我们使用相同的两个卷积层来解码残差视差 $\triangle d$，并按照公式 (5) 更新当前立体视差。经过 $N_{2}$ 轮双分支细化后，立体分支的视差是 MonSter 的最终输出。

3.3. Loss Function

3.3. 损失函数

We use the L1 loss to supervise the output from two branches. We denote the set of disparities from the first $N_{1}$ iterations of the stereo branch as ${\dot{d}{i}}{i=0}^{N_{1}-1}$ and follow [20] to exponentially increase the weights as the number of iterations increases. The total loss is defined as the sum of the monocular branch loss $\mathcal{L}{M o n o}$ and the stereo branch loss $\mathcal{L}{S t e r e o}$ as follows:

我们使用 L1 损失来监督两个分支的输出。我们将立体分支前 $N_{1}$ 次迭代的视差集表示为 ${\dot{d}{i}}{i=0}^{N_{1}-1}$，并按照 [20] 的方法，随着迭代次数的增加指数级增加权重。总损失定义为单目分支损失 $\mathcal{L}{M o n o}$ 和立体分支损失 $\mathcal{L}{S t e r e o}$ 的总和，如下所示：

where $\gamma=0.9$ , and $d_{g t}$ is the ground truth.

其中 $\gamma=0.9$，$d_{gt}$ 是真实值。

4. Experiment

4. 实验

4.1. Implementation Details

4.1. 实现细节

We implement MonSter with PyTorch and perform experiments using NVIDIA RTX 3090 GPUs. We use the AdamW [21] optimizer and clip gradients to the range [-1, 1] following baseline [38]. We use the one-cycle learning rate schedule with a learning rate of 2e-4 and train MonSter with a batch size of 8 for 200k steps as the pretrained model. For the monocular branch, we use the ViT-large version of Depth Anything V 2 [46] and freeze its parameters to prevent training of stereo-matching tasks from affecting its generalization and accuracy.

我们使用 PyTorch 实现 MonSter，并在 NVIDIA RTX 3090 GPU 上进行实验。我们使用 AdamW [21] 优化器，并将梯度裁剪到 [-1, 1] 范围内，遵循基线 [38] 的设置。我们采用 one-cycle 学习率调度策略，学习率为 2e-4，并以 batch size 为 8 训练 MonSter 20 万步作为预训练模型。对于单目分支，我们使用 Depth Anything V 2 [46] 的 ViT-large 版本，并冻结其参数，以防止立体匹配任务的训练影响其泛化能力和准确性。

Following the standard [16, 17, 35], we pretrain MonSter on Scene Flow [22] for most experiments. For finetuning on ETH3D and Middlebury, we follow SOTA methods [16, 17, 35] to create the Basic Training Set (BTS) from various public datasets for pre training, including Scene Flow [22], CREStereo [16], Tartan Air [34], Sintel Stereo [3], Falling Things [32] and InStereo2k [2].

遵循标准 [16, 17, 35]，我们在 Scene Flow [22] 上对 MonSter 进行预训练以进行大多数实验。对于 ETH3D 和 Middlebury 的微调，我们遵循 SOTA 方法 [16, 17, 35] 从各种公共数据集创建基础训练集（BTS）进行预训练，包括 Scene Flow [22]、CREStereo [16]、Tartan Air [34]、Sintel Stereo [3]、Falling Things [32] 和 InStereo2k [2]。

4.2. Benchmark Performance

4.2. 基准性能

To demonstrate the outstanding performance of our method, we evaluate MonSter on the five most commonly used benchmarks: KITTI 2012 [11], KITTI 2015 [23], ETH3D [28], Middlebury [27] and Scene Flow [22].

为了展示我们方法的出色性能，我们在五个最常用的基准数据集上评估了 MonSter：KITTI 2012 [11]、KITTI 2015 [23]、ETH3D [28]、Middlebury [27] 和 Scene Flow [22]。

Scene Flow [22]. As shown in Tab. 1, we achieve a new state-of-the-art performance with an EPE metric of 0.37 on Scene Flow, surpassing our baseline [38] by $21.28%$ and outperforming the SOTA method [35] by $15.91%$ .

场景流 (Scene Flow) [22]。如表 1 所示，我们在场景流上实现了新的最先进性能，EPE 指标为 0.37，超过了我们的基线 [38] 21.28%，并且优于 SOTA 方法 [35] 15.91%。

ETH3D[28]. Following the SOTA methods [16, 17, 35,

ETH3D [28]。遵循SOTA方法 [16, 17, 35,

Table 1. Quantitative evaluation on Scene Flow test set. The best result is bolded, and the second-best result is underscored.

表 1: Scene Flow 测试集上的定量评估。最佳结果加粗，次佳结果加下划线。

Method	GwcNet[14]	LEAStereo[8]	ACVNet[37]	IGEV[38]	Selective-IGEV[35]	MonSter (Ours)
EPE (px)↓	0.76	0.78	0.48	0.47	0.44	0.37 (-15.91%)

Table 2. Results on four popular benchmarks. All results are derived from official leader board publications or corresponding papers. All metrics are presented in percentages, except for RMSE, which is reported in pixels. For testing masks, “All” denotes being tested with all pixels while “Noc” denotes being tested with a non-occlusion mask. The best and second best are marked with colors.

| 方法