Meta-Transfer Learning for Few-Shot Learning

基于元迁移学习的少样本学习

Abstract

摘要

Meta-learning has been proposed as a framework to address the challenging few-shot learning setting. The key idea is to leverage a large number of similar few-shot tasks in order to learn how to adapt a base-learner to a new task for which only a few labeled samples are available. As deep neural networks (DNNs) tend to overfit using a few samples only, meta-learning typically uses shallow neural networks (SNNs), thus limiting its effectiveness. In this paper we propose a novel few-shot learning method called meta-transfer learning (MTL) which learns to adapt a deep NN for few shot learning tasks. Specifically, meta refers to training multiple tasks, and transfer is achieved by learning scaling and shifting functions of DNN weights for each task. In addition, we introduce the hard task (HT) meta-batch scheme as an effective learning curriculum for MTL. We conduct experiments using (5-class, 1-shot) and (5-class, 5- shot) recognition tasks on two challenging few-shot learning benchmarks: mini Image Net and Fewshot-CIFAR100. Extensive comparisons to related works validate that our meta-transfer learning approach trained with the proposed HT meta-batch scheme achieves top performance. An ablation study also shows that both components contribute to fast convergence and high accuracy1.

元学习（Meta-learning）被提出作为解决少样本学习挑战性场景的框架。其核心思想是利用大量相似的少样本任务，学习如何将基础学习器（base-learner）适配到仅有少量标注样本的新任务中。由于深度神经网络（DNN）容易在少量样本下过拟合，元学习通常采用浅层神经网络（SNN），从而限制了其效果。本文提出一种名为元迁移学习（MTL）的新型少样本学习方法，通过学习调整深度神经网络以适应少样本学习任务。具体而言，"元"指训练多个任务，"迁移"则通过为每个任务学习DNN权重的缩放和偏移函数实现。此外，我们引入硬任务（HT）元批次方案作为MTL的有效课程学习策略。我们在两个具有挑战性的少样本学习基准数据集（mini ImageNet和Fewshot-CIFAR100）上进行了（5类1样本）和（5类5样本）识别任务的实验。与相关工作的广泛对比验证了采用HT元批次训练的元迁移学习方法达到了最优性能。消融实验也表明，两个组件共同促进了快速收敛和高准确率[20]。

1. Introduction

1. 引言

While deep learning systems have achieved great performance when sufficient amounts of labeled data are available [58, 17, 46], there has been growing interest in reducing the required amount of data. Few-shot learning tasks have been defined for this purpose. The aim is to learn new concepts from few labeled examples, e.g. 1-shot learning [25]. While humans tend to be highly effective in this context, often grasping the essential connection between new concepts and their own knowledge and experience, it remains challenging for machine learning approaches. E.g. on the CIFAR-100 dataset, a state-of-the-art method [34] achieves only $40.1%$ accuracy for 1-shot learning, compared to $75.7%$ for the all-class fully supervised case [6].

虽然深度学习系统在有充足标注数据时表现优异 [58, 17, 46]，但人们越来越关注如何减少所需数据量。为此定义了少样本学习任务，其目标是从少量标注样本中学习新概念，例如单样本学习 [25]。人类在此情境下通常表现出色，能迅速把握新概念与自身知识经验的核心关联，但对机器学习方法仍具挑战性。例如在CIFAR-100数据集上，当前最先进方法 [34] 在单样本学习中仅达到 $40.1%$ 准确率，而全类别全监督情况 [6] 可达 $75.7%$。

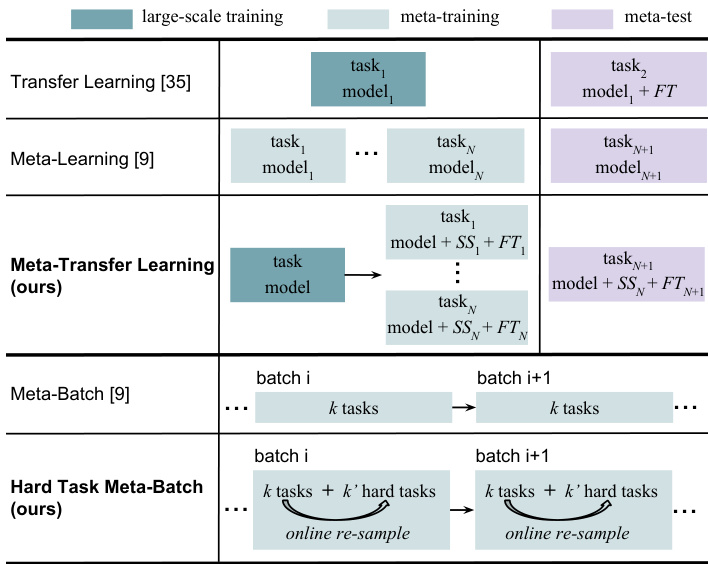
Figure 1. Meta-transfer learning (MTL) is our meta-learning paradigm and hard task (HT) meta-batch is our training strategy. The upper three rows show the differences between MTL and related methods, transfer-learning [35] and meta-learning [9]. The bottom rows compare HT meta-batch with the conventional metabatch [9]. $F T$ stands for fine-tuning a classifier. SS represents the Scaling and Shifting operations in our MTL method.

图 1: 元迁移学习 (MTL) 是我们的元学习范式，而困难任务 (HT) 元批次是我们的训练策略。前三行展示了 MTL 与相关方法 (迁移学习 [35] 和元学习 [9]) 的区别。底部几行比较了 HT 元批次与传统元批次 [9]。$FT$ 表示微调分类器。SS 代表我们 MTL 方法中的缩放和移位操作。

Few-shot learning methods can be roughly categorized into two classes: data augmentation and task-based metalearning. Data augmentation is a classic technique to increase the amount of available data and thus also useful for few-shot learning [21]. Several methods propose to learn a data generator e.g. conditioned on Gaussian noise [29, 44, 54]. However, the generation models often under perform when trained on few-shot data [1]. An alternative is to merge data from multiple tasks which, however, is not effective due to variances of the data across tasks [54].

少样本学习方法大致可分为两类：数据增强和基于任务的元学习。数据增强是增加可用数据量的经典技术，因此对少样本学习也很有用 [21]。一些方法提出学习数据生成器，例如以高斯噪声为条件 [29, 44, 54]。然而，当在少样本数据上训练时，生成模型通常表现不佳 [1]。另一种方法是合并来自多个任务的数据，但由于任务间数据的差异，这种方法效果不佳 [54]。

In contrast to data-augmentation methods, meta-learning is a task-level learning method [2, 33, 52]. Meta-learning aims to accumulate experience from learning multiple tasks [9, 39, 48, 31, 13], while base-learning focuses on modeling the data distribution of a single task. A state-of-theart representative of this, namely Model-Agnostic MetaLearning (MAML), learns to search for the optimal initialization state to fast adapt a base-learner to a new task [9]. Its task-agnostic property makes it possible to generalize to few-shot supervised learning as well as unsupervised reinforcement learning [13, 10]. However, in our view, there are two main limitations of this type of approaches limiting their effectiveness: i) these methods usually require a large number of similar tasks for meta-training which is costly; and ii) each task is typically modeled by a lowcomplexity base learner (such as a shallow neural network) to avoid model over fitting, thus being unable to use deeper and more powerful architectures. For example, for the miniImageNet dataset [53], MAML uses a shallow CNN with only 4 CONV layers and its optimal performance was obtained learning on $240k$ tasks.

与数据增强方法不同，元学习是一种任务级学习方法 [2, 33, 52]。元学习旨在从多个任务中积累经验 [9, 39, 48, 31, 13]，而基础学习则专注于建模单个任务的数据分布。该领域的先进代表模型——模型无关元学习 (Model-Agnostic Meta-Learning, MAML) 通过学习搜索最优初始化状态，使基础学习器能够快速适应新任务 [9]。其任务无关特性使其能够泛化到少样本监督学习以及无监督强化学习 [13, 10]。然而，我们认为这类方法存在两个主要局限性：i) 这些方法通常需要大量相似任务进行元训练，成本高昂；ii) 每个任务通常由低复杂度基础学习器 (如浅层神经网络) 建模以避免过拟合，因此无法使用更深层、更强大的架构。例如，在 miniImageNet 数据集 [53] 上，MAML 仅使用 4 层卷积的浅层 CNN，并通过学习 $240k$ 个任务才获得最佳性能。

In this paper, we propose a novel meta-learning method called meta-transfer learning (MTL) leveraging the advantages of both transfer and meta learning (see conceptual comparison of related methods in Figure 1). In a nutshell, MTL is a novel learning method that helps deep neural nets converge faster while reducing the probability to overfit when using few labeled training data only. In particular, “transfer” means that DNN weights trained on largescale data can be used in other tasks by two light-weight neuron operations: Scaling and Shifting (SS), i.e. $\alpha X+\beta$ . “Meta” means that the parameters of these operations can be viewed as hyper-parameters trained on few-shot learning tasks [31, 26]. Large-scale trained DNN weights of- fer a good initialization, enabling fast convergence of metatransfer learning with fewer tasks, e.g. only $8k$ tasks for mini Image Net [53], 30 times fewer than MAML [9]. Lightweight operations on DNN neurons have less parameters to learn, e.g. less than $\textstyle{\frac{2}{49}}$ if considering neurons of size $7\times7$ $\frac{1}{49}$ for $\alpha$ and $<\frac{1}{49}$ for $\beta$ ), reducing the chance of overfitting. In addition, these operations keep those trained DNN weights unchanged, and thus avoid the problem of “catastrophic forgetting” which means forgetting general patterns when adapting to a specific task [27, 28].

本文提出了一种名为元迁移学习(MTL)的新型元学习方法，该方法结合了迁移学习和元学习的优势(相关方法的概念对比见图1)。简而言之，MTL是一种新颖的学习方法，能够在仅使用少量标注训练数据时，帮助深度神经网络更快收敛并降低过拟合概率。具体而言，"迁移"是指通过两个轻量级的神经元操作——缩放与平移(SS)，即$\alpha X+\beta$，将在大规模数据上训练的DNN权重应用于其他任务。"元"则意味着这些操作的参数可视为在少样本学习任务上训练的超参数[31,26]。大规模训练的DNN权重提供了良好的初始化，使得元迁移学习能以更少的任务实现快速收敛，例如在mini ImageNet上仅需$8k$个任务[53]，比MAML少30倍[9]。对DNN神经元的轻量级操作需要学习的参数更少(例如对于$7\times7$大小的神经元，$\alpha$参数少于$\textstyle{\frac{2}{49}}$，$\beta$参数少于$\frac{1}{49}$)，从而降低了过拟合风险。此外，这些操作保持已训练的DNN权重不变，因此避免了"灾难性遗忘"问题——即在适应特定任务时遗忘通用模式的现象[27,28]。

The second main contribution of this paper is an effective meta-training curriculum. Curriculum learning [3] and hard negative mining [47] both suggest that faster convergence and stronger performance can be achieved by a better arrangement of training data. Inspired by these ideas, we design our hard task (HT) meta-batch strategy to offer a challenging but effective learning curriculum. As shown in the bottom rows of Figure 1, a conventional meta-batch contains a number of random tasks [9], but our HT meta-batch online re-samples harder ones according to past failure tasks with lowest validation accuracy.

本文的第二个主要贡献是提出了一种高效的元训练课程。课程学习 [3] 和难负例挖掘 [47] 都表明，通过更好地安排训练数据可以实现更快的收敛和更强的性能。受这些思想的启发，我们设计了难任务 (HT) 元批次策略，以提供一个具有挑战性但高效的学习课程。如图 1 底部行所示，传统的元批次包含多个随机任务 [9]，而我们的 HT 元批次会根据验证准确率最低的过去失败任务在线重新采样更难的任务。

Our overall contribution is thus three-fold: i) we propose a novel MTL method that learns to transfer largescale pre-trained DNN weights for solving few-shot learning tasks; ii) we propose a novel HT meta-batch learning strategy that forces meta-transfer to “grow faster and stronger through hardship”; and iii) we conduct extensive experiments on two few-shot learning benchmarks, namely mini Image Net [53] and Fewshot-CIFAR100 (FC100) [34], and achieve the state-of-the-art performance.

我们的总体贡献体现在三个方面：i) 提出一种新颖的多任务学习 (MTL) 方法，通过迁移大规模预训练深度神经网络 (DNN) 权重来解决少样本学习任务；ii) 提出创新的硬训练 (HT) 元批量学习策略，迫使元迁移"通过逆境更快更强地成长"；iii) 在两个少样本学习基准测试（mini ImageNet [53] 和 Fewshot-CIFAR100 (FC100) [34]）上进行了广泛实验，并实现了最先进的性能。

2. Related work

2. 相关工作

Few-shot learning Research literature on few-shot learning exhibits great diversity. In this section, we focus on methods using the supervised meta-learning paradigm [12, 52, 9] most relevant to ours and compared to in the experiments. We can divide these methods into three categories. 1) Metric learning methods [53, 48, 51] learn a similarity space in which learning is efficient for few-shot examples. 2) Memory network methods [31, 42, 34, 30] learn to store “experience” when learning seen tasks and then generalize that to unseen tasks. 3) Gradient descent based methods [9, 39, 24, 13, 60] have a specific meta-learner that learns to adapt a specific base-learner (to few-shot examples) through different tasks. E.g. MAML [9] uses a meta-learner that learns to effectively initialize a base-learner for a new learning task. Meta-learner optimization is done by gradient descent using the validation loss of the base-learner. Our method is closely related. An important difference is that our MTL approach leverages transfer learning and benefits from referencing neuron knowledge in pre-trained deep nets. Although MAML can start from a pre-trained network, its element-wise fine-tuning makes it hard to learn deep nets without over fitting (validated in our experiments). Transfer learning What and how to transfer are key issues to be addressed in transfer learning, as different methods are applied to different source-target domains and bridge different transfer knowledge [35, 57, 55, 59]. For deep models, a powerful transfer method is adapting a pre-trained model for a new task, often called fine-tuning $(F T)$ . Models pretrained on large-scale datasets have proven to generalize better than randomly initialized ones [8]. Another popular transfer method is taking pre-trained networks as backbone and adding high-level functions, e.g. for object detection and recognition [18, 50, 49] and image segmentation [16, 5]. Our meta-transfer learning leverages the idea of transferring pre-trained weights and aims to meta-learn how to effectively transfer. In this paper, large-scale trained DNN weights are what to transfer, and the operations of Scaling and Shifting indicate how to transfer. Similar operations have been used to modulating the per-feature-map distribution of activation s for visual reasoning [37].

少样本学习
关于少样本学习的研究文献呈现出极大的多样性。本节重点讨论与我们的方法最相关且在实验中进行了对比的监督元学习范式 [12, 52, 9] 相关方法。这些方法可分为三类：

1. 度量学习方法 [53, 48, 51] 通过学习一个相似性空间，使得少样本示例能高效学习；
2. 记忆网络方法 [31, 42, 34, 30] 通过学习存储已见任务的"经验"，进而泛化到未见任务；
3. 基于梯度下降的方法 [9, 39, 24, 13, 60] 通过特定元学习器，在不同任务中学习如何适配基础学习器（以适应少样本示例）。例如 MAML [9] 使用元学习器来学习如何为新学习任务有效初始化基础学习器，其优化通过基础学习器的验证损失进行梯度下降实现。

我们的方法与之密切相关，但关键区别在于：多任务学习 (MTL) 方法利用了迁移学习，并受益于预训练深度网络中的神经元知识引用。尽管 MAML 可以从预训练网络开始，但其逐元素微调特性使其难以在不发生过拟合的情况下学习深度网络（实验已验证）。

迁移学习
迁移内容和迁移方式是迁移学习需要解决的核心问题 [35, 57, 55, 59]，因为不同方法适用于不同源-目标域并桥接不同的迁移知识。对于深度模型，强大的迁移方法是针对新任务调整预训练模型，通常称为微调 $(F T)$ 。实践证明，在大规模数据集上预训练的模型比随机初始化模型具有更好的泛化能力 [8]。另一种流行迁移方法是将预训练网络作为主干并添加高级功能，例如用于目标检测与识别 [18, 50, 49] 和图像分割 [16, 5]。

我们的元迁移学习借鉴了迁移预训练权重的思想，旨在元学习如何有效迁移。本文中，大规模训练的 DNN 权重是迁移内容，而缩放 (Scaling) 和偏移 (Shifting) 操作则指明了迁移方式。类似操作曾用于调节视觉推理中激活的逐特征图分布 [37]。

Figure 2. The pipeline of our proposed few-shot learning method, including three phases: (a) DNN training on large-scale data, i.e. using all training datapoints (Section 4.1); (b) Meta-transfer learning (MTL) that learns the parameters of Scaling and Shifting (SS), based on the pre-trained feature extractor (Section 4.2). Learning is scheduled by the proposed HT meta-batch (Section 4.3); and (c) meta-test is done for an unseen task which consists of a base-learner (classifier) Fine-Tuning $(F T)$ stage and a final evaluation stage, described in the last paragraph in Section 3. Input data are along with arrows. Modules with names in bold get updated at corresponding phases. Specifically, SS parameters are learned by meta-training but fixed during meta-test. Base-learner parameters are optimized for every task.

图 2: 我们提出的少样本学习方法的流程，包括三个阶段：(a) 在大规模数据上训练DNN，即使用所有训练数据点（第4.1节）；(b) 基于预训练特征提取器的元迁移学习 (MTL)，学习缩放和位移 (SS) 的参数（第4.2节）。学习过程由提出的HT元批次调度（第4.3节）；(c) 对未见任务进行元测试，包括基础学习器（分类器）微调 $(F T)$ 阶段和最终评估阶段，如第3节最后一段所述。输入数据沿箭头方向流动。名称加粗的模块在相应阶段更新。具体而言，SS参数通过元训练学习，但在元测试期间固定。基础学习器参数针对每个任务进行优化。

Some few-shot learning methods have been proposed to use pre-trained weights as initialization [20, 30, 38, 45, 41]. Typically, weights are fine-tuned for each task, while we learn a meta-transfer learner through all tasks, which is dif ferent in terms of the underlying learning paradigm.

一些少样本学习方法提出使用预训练权重作为初始化 [20, 30, 38, 45, 41]。通常权重会针对每个任务进行微调，而我们通过所有任务学习一个元迁移学习器，这在底层学习范式上有所不同。

Curriculum learning & Hard sample mining Curriculum learning was proposed by Bengio et al. [3] and is popular for multi-task learning [36, 43, 56, 14]. They showed that instead of observing samples at random it is better to organize samples in a meanin(gmfetua-lle arwnera)y so that fast convergence, effective learning and better generalization can be achieved. Pentina et al. [36] use adaptive SVM class if i ers to evaluate task difficulty for later organization. Differently, our MTL method does task evaluation online at the phase of episode test, without needing any auxiliary model.

课程学习与困难样本挖掘
课程学习由Bengio等人[3]提出，在多任务学习领域广受欢迎[36,43,56,14]。研究表明，相较于随机观察样本，以有意义的方式组织样本能实现更快收敛、更高效学习和更优泛化性能。Pentina等人[36]采用自适应SVM分类器评估任务难度以进行后续组织。与之不同，我们的多任务学习方法在片段测试阶段在线评估任务，无需任何辅助模型。

Hard sample mining was proposed by Shri vast ava et al. [47] for object detection. It treats image proposals overlapped with ground truth as hard negative samples. Training on more confusing data enables the model to achieve higher robustness and better performance [4, 15, 7]. Inspired by this, we sample harder tasks online and make our MTL learner “grow faster and stronger through more hardness”. In our experiments, we show that this can be generalized to enhance other meta-learning methods, e.g. MAML [9].

难样本挖掘由Shrivastava等人[47]提出用于目标检测。该方法将与真实标注框重叠的图像候选区域视为难负样本。在更具挑战性的数据上训练能使模型获得更高鲁棒性和更好性能[4,15,7]。受此启发，我们在线采样更难的任务，使多任务学习器"通过更大难度成长得更快更强"。实验表明该方法可推广至增强其他元学习方法，例如MAML[9]。

ing a set of unseen datapoints $\mathcal{T}_{u n s e e n}^{(t e)}$

对一组未见数据点 $\mathcal{T}_{u n s e e n}^{(t e)}$ 进行处理

Meta-training phase. This phase aims to learn a metalearner from θ’multiple episodes. In each episode, metatraining has a two-stage optimization. Stage-1 is called base-learning, where the cross-entropy loss is used to optimize the parameters of the base-learner. Stage-2 contains a feed-forward test on episode test datapoints. The test loss is used to optimize the parameters of the meta-learner. Specifically, given an episode $\mathcal{T}\in p(\mathcal{T})$ , the base-learner $\theta_{T}$ is learned from episode training data $\mathcal{T}^{(t r)}$ and its corresponding loss $\mathcal{L}{\mathcal{T}}(\theta_{\mathcal{T}},\mathcal{T}^{(t r)})$ . After optimizing this loss, the baselearner has parameters $\tilde{\theta}{T}$ . Then, the meta-learner is updated using test loss $\mathcal{L}{\mathcal{T}}(\tilde{\theta}{\mathcal{T}},\mathcal{T}^{(t e)})$ . After meta-training on all episodes, the meta-learner is optimized by test losses ${\mathcal{L}{\mathcal{T}}(\tilde{\theta}{\mathcal{T}},\mathcal{T}^{(t e)})}_{\mathcal{T}\in p(\mathcal{T})}$ . Therefore, the number of metalearner updates equals to the number of episodes.

元训练阶段。该阶段旨在从θ的多个情节中学习元学习器。每个情节的元训练包含两阶段优化：第一阶段称为基础学习，使用交叉熵损失优化基础学习器参数；第二阶段对情节测试数据点进行前馈测试，利用测试损失优化元学习器参数。具体而言，给定情节$\mathcal{T}\in p(\mathcal{T})$时，基础学习器$\theta_{T}$从情节训练数据$\mathcal{T}^{(t r)}$及其对应损失$\mathcal{L}{\mathcal{T}}(\theta_{\mathcal{T}},\mathcal{T}^{(t r)})$中学习。优化该损失后，基础学习器获得参数$\tilde{\theta}{T}$，随后使用测试损失$\mathcal{L}{\mathcal{T}}(\tilde{\theta}{\mathcal{T}},\mathcal{T}^{(t e)})$更新元学习器。在所有情节完成元训练后，元学习器通过测试损失集合${\mathcal{L}{\mathcal{T}}(\tilde{\theta}{\mathcal{T}},\mathcal{T}^{(t e)})}_{\mathcal{T}\in p(\mathcal{T})}$完成优化，因此元学习器的更新次数等于情节数量。

Meta-test phase. This phase aims to test the performance of the trained meta-learner for fast adaptation to unseen task. Given $\tau_{u n s e e n}$ , the meta-learner $\tilde{\theta}{T}$ teaches the baselearner θ unseen to adapt to the objective of $\tau_{u n s e e n}$ by some means, e.g. through initialization [9]. Then, the test result on $\mathcal{T}{u n s e e n}^{(t e)}$ is used to evaluate the meta-learning approach. If there are multiple unseen tasks ${\mathcal{T}{u n s e e n}}$ , the average result on ${\mathcal{T}_{u n s e e n}^{(t e)}}$ will be the final evaluation.

元测试阶段。该阶段旨在测试训练好的元学习器 (meta-learner) 对未见任务 (unseen task) 的快速适应性能。给定 $\tau_{u n s e e n}$ ，元学习器 $\tilde{\theta}{T}$ 会通过某种方式 (例如初始化 [9]) 指导基学习器 (baselearner) θ unseen 适应 $\tau_{u n s e e n}$ 的目标。随后，在 $\mathcal{T}{u n s e e n}^{(t e)}$ 上的测试结果将用于评估元学习方法。若存在多个未见任务 ${\mathcal{T}{u n s e e n}}$ ，则 ${\mathcal{T}_{u n s e e n}^{(t e)}}$ 上的平均结果将作为最终评估依据。

3. Preliminary

3. 初步准备

We introduce the problem setup and notations of metalearning, following related work [53, 39, 9, 34].

我们引入元学习的问题设置和符号表示，相关工作见[53, 39, 9, 34]。

Meta-learning consists of two phases: meta-train and meta-test. A meta-training example is a classification task $\tau$ sampled from a distribution $p(\mathcal T)$ . $\tau$ is called episode, including a training split $\mathcal{T}^{(t r)}$ to optimize the base-learner, and a test split $\boldsymbol{\mathcal{T}^{(t e)}}$ to optimize the meta-learner. In particular, meta-training aims to learn from a number of episodes ${\mathcal{T}}$ sampled from $p(\mathcal{T})$ . An unseen task $\tau_{u n s e e n}$ in metatest will start from that experience of the meta-learner and adapt the base-learner. The final evaluation is done by test

元学习包含两个阶段：元训练和元测试。一个元训练样本是从分布 $p(\mathcal T)$ 中采样的分类任务 $\tau$。$\tau$ 称为情节(episode)，包含用于优化基础学习器的训练集 $\mathcal{T}^{(t r)}$，以及用于优化元学习器的测试集 $\boldsymbol{\mathcal{T}^{(t e)}}$。具体而言，元训练旨在从 $p(\mathcal{T})$ 采样的多个情节 ${\mathcal{T}}$ 中学习。在元测试中，未见任务 $\tau_{u n s e e n}$ 将从元学习器的经验出发，并适配基础学习器。最终评估通过测试完成。

4. Methodology

4. 方法论

As shown in Figure 2, our method consists of three phases. First, we train a DNN on large-scale data, e.g. on mini Image Net (64-class, 600-shot) [53], and then fix the low-level layers as Feature Extractor (Section 4.1). Second, in the meta-transfer learning phase, MTL learns the Scaling and Shifting (SS) parameters for the Feature Extractor neurons, enabling fast adaptation to few-shot tasks (Section 4.2). For improved overall learning, we use our HT meta-batch strategy (Section 4.3). The training steps are detailed in Algorithm 1 in Section 4.4. Finally, the typical meta-test phase is performed, as introduced in Section 3.

如图 2 所示，我们的方法包含三个阶段。首先，我们在大规模数据上训练深度神经网络 (DNN)，例如 mini Image Net (64 类，600-shot) [53]，然后固定底层作为特征提取器 (第 4.1 节)。其次，在元迁移学习阶段，MTL 学习特征提取神经元的缩放和移位 (SS) 参数，实现快速适应少样本任务 (第 4.2 节)。为提升整体学习效果，我们采用 HT 元批次策略 (第 4.3 节)。训练步骤详见第 4.4 节的算法 1。最后执行典型的元测试阶段，如第 3 节所述。

4.1. DNN training on large-scale data

4.1. 大规模数据上的DNN训练

This phase is similar to the classic pre-training stage as, e.g., pre-training on Imagenet for object recognition [40]. Here, we do not consider data/domain adaptation from other datasets, and pre-train on readily available data of few-shot learning benchmarks, allowing for fair comparison with other few-shot learning methods. Specifically, for a particular few-shot dataset, we merge all-class data $\mathcal{D}$ for pretraining. For instance, for mini Image Net [53], there are totally 64 classes in the training split of $\mathcal{D}$ and each class contains 600 samples used to pre-train a 64-class classifier.

这一阶段类似于经典的预训练阶段，例如在Imagenet上进行物体识别的预训练[40]。在此，我们不考虑从其他数据集进行数据/领域适应，而是直接在现成的少样本学习基准数据上进行预训练，以便与其他少样本学习方法进行公平比较。具体而言，对于特定的少样本数据集，我们合并所有类别的数据$\mathcal{D}$进行预训练。例如，对于mini ImageNet[53]，训练集$\mathcal{D}$中共有64个类别，每个类别包含600个样本，用于预训练一个64类分类器。

We first randomly initialize a feature extractor $\Theta$ (e.g. CONV layers in ResNets [17]) and a classifier $\theta$ (e.g. the last FC layer in ResNets [17]), and then optimize them by gradient descent as follows,

我们首先随机初始化一个特征提取器 $\Theta$ （例如 ResNets [17] 中的 CONV 层）和一个分类器 $\theta$ （例如 ResNets [17] 中的最后一个 FC 层），然后通过梯度下降优化它们，具体步骤如下，

$$
\begin{array}{r}{[\Theta;\theta]=:\left[\Theta;\theta\right]-\alpha\nabla\mathcal{L}_{\mathcal{D}}\left([\Theta;\theta]\right),}\end{array}
$$

$$
\begin{array}{r}{[\Theta;\theta]=:\left[\Theta;\theta\right]-\alpha\nabla\mathcal{L}_{\mathcal{D}}\left([\Theta;\theta]\right),}\end{array}
$$

where $\mathcal{L}$ denotes the following empirical loss,

其中 $\mathcal{L}$ 表示以下经验损失，

$$
\mathcal{L}{\mathcal{D}}\big([\Theta;\theta]\big)=\frac{1}{|\mathcal{D}|}\sum_{(x,y)\in\mathcal{D}}l\big(f_{[\Theta;\theta]}(x),y\big),
$$

$$
\mathcal{L}{\mathcal{D}}\big([\Theta;\theta]\big)=\frac{1}{|\mathcal{D}|}\sum_{(x,y)\in\mathcal{D}}l\big(f_{[\Theta;\theta]}(x),y\big),
$$

e.g. cross-entropy loss, and $\alpha$ denotes the learning rate. In this phase, the feature extractor $\Theta$ is learned. It will be frozen in the following meta-training and meta-test phases, as shown in Figure 2. The learned classifier $\theta$ will be discarded, because subsequent few-shot tasks contain different classification objectives, e.g. 5-class instead of 64-class classification for mini Image Net [53].

例如交叉熵损失 (cross-entropy loss)，而 $\alpha$ 表示学习率。在此阶段，特征提取器 $\Theta$ 被学习。它将在后续的元训练和元测试阶段被冻结，如图 2 所示。学习到的分类器 $\theta$ 将被丢弃，因为后续的少样本任务包含不同的分类目标，例如 mini ImageNet [53] 中的 5 类分类而非 64 类分类。

4.2. Meta-transfer learning (MTL)

4.2. 元迁移学习 (MTL)

As shown in Figure 2(b), our proposed meta-transfer learning (MTL) method optimizes the meta operations Scaling and Shifting (SS) through HT meta-batch training (Section 4.3). Figure 3 visualizes the difference of updating through SS and $F T,S S$ operations, denoted as $\Phi_{S_{1}}$ and $\Phi_{S_{2}}$ do not change the frozen neuron weights of $\Theta$ during learning, while $F T$ updates the complete $\Theta$ .

如图 2(b) 所示, 我们提出的元迁移学习 (meta-transfer learning, MTL) 方法通过 HT 元批次训练 (第 4.3 节) 优化元操作缩放与平移 (Scaling and Shifting, SS)。图 3 展示了通过 SS 和 $F T,S S$ 操作进行更新的差异, 记为 $\Phi_{S_{1}}$ 和 $\Phi_{S_{2}}$ 在学习过程中不会改变 $\Theta$ 的冻结神经元权重, 而 $F T$ 会更新完整的 $\Theta$。

In the following, we detail the $S S$ operations. Given a task $\tau$ , the loss of $\mathcal{T}^{(t r)}$ is used to optimize the current base-learner (classifier) $\theta^{\prime}$ by gradient descent:

下面我们详细介绍 $S S$ 操作。给定任务 $\tau$，通过梯度下降使用 $\mathcal{T}^{(t r)}$ 的损失来优化当前基础学习器（分类器） $\theta^{\prime}$：

$$
\theta^{\prime}\leftarrow\theta-\beta\nabla_{\theta}\mathcal{L}{\mathcal{T}^{(t r)}}\big([\Theta;\theta],\Phi_{S_{{1,2}}}\big),
$$

$$
\theta^{\prime}\leftarrow\theta-\beta\nabla_{\theta}\mathcal{L}{\mathcal{T}^{(t r)}}\big([\Theta;\theta],\Phi_{S_{{1,2}}}\big),
$$

which is different to Eq. 1, as we do not update $\Theta$ . Note that here $\theta$ is different to the one from the previous phase, the large-scale classifier $\theta$ in Eq. 1. This $\theta$ concerns only a few of classes, e.g. 5 classes, to classify each time in a novel few-shot setting. $\theta^{\prime}$ corresponds to a temporal classifier only working in the current task, initialized by the $\theta$ optimized for the previous task (see Eq. 5).

这与式1不同，因为我们不更新$\Theta$。请注意，这里的$\theta$与前一阶段的不同，即式1中的大规模分类器$\theta$。这个$\theta$仅涉及少量类别（例如5类），在每次少样本新任务中进行分类。$\theta^{\prime}$对应一个仅在当前任务中工作的临时分类器，由针对前一任务优化的$\theta$初始化（见式5）。

$\Phi_{S_{1}}$ is initialized by ones and $\Phi_{S_{1}}$ by zeros. Then, they are optimized by the test loss of $\mathcal{T}^{(t e)}$ as follows,

$\Phi_{S_{1}}$ 初始化为1，$\Phi_{S_{1}}$ 初始化为0。然后，通过 $\mathcal{T}^{(t e)}$ 的测试损失对它们进行如下优化：

$$
\Phi_{S_{i}}=:\Phi_{S_{i}}-\gamma\nabla_{\Phi_{S_{i}}}\mathcal{L}{\mathcal{T}^{(t e)}}\left([\Theta;\theta^{\prime}],\Phi_{S_{{1,2}}}\right).
$$

$$
\Phi_{S_{i}}=:\Phi_{S_{i}}-\gamma\nabla_{\Phi_{S_{i}}}\mathcal{L}{\mathcal{T}^{(t e)}}\left([\Theta;\theta^{\prime}],\Phi_{S_{{1,2}}}\right).
$$

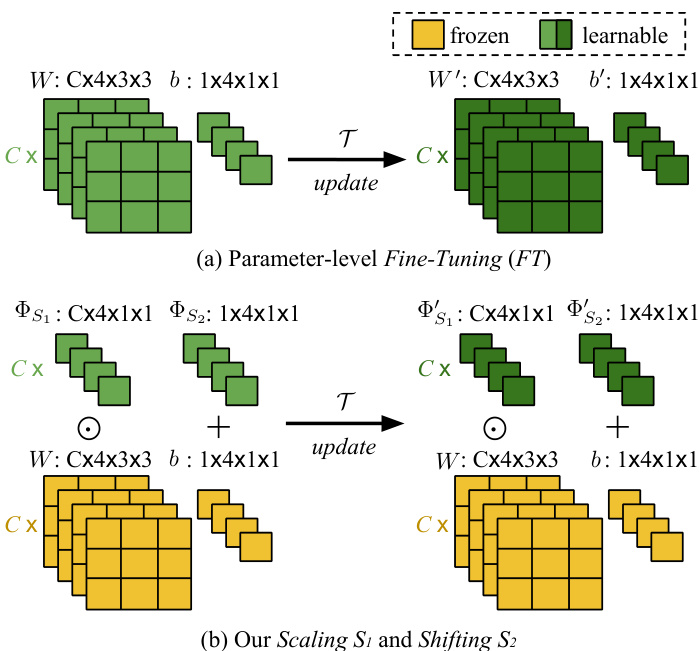
Figure 3. (a) Parameter-level Fine-Tuning $(F T)$ is a conventional meta-training operation, e.g. in MAML [9]. Its update works for all neuron parameters, $W$ and $^b$ . (b) Our neuron-level Scaling and Shifting (SS) operations in MTL. They reduce the number of learning parameters and avoid over fitting problems. In addition, they keep large-scale trained parameters (in yellow) frozen, preventing “catastrophic fogetting” [27, 28].

图 3: (a) 参数级微调 (FT) 是传统元训练操作 (例如 MAML [9]), 其更新作用于所有神经元参数 $W$ 和 $^b$。 (b) 我们在 MTL 中提出的神经元级缩放与平移 (SS) 操作。该操作减少了学习参数量并避免过拟合问题, 同时保持大规模训练参数 (黄色部分) 固定, 从而防止"灾难性遗忘" [27, 28]。

In this step, $\theta$ is updated with the same learning rate $\gamma$ as in Eq. 4,

在这一步中，$\theta$ 以与式4中相同的学习率 $\gamma$ 进行更新，

$$
\theta=:\theta-\gamma\nabla_{\theta}\mathcal{L}{\mathcal{T}^{(t e)}}\left([\Theta;\theta^{\prime}],\Phi_{S_{{1,2}}}\right).
$$

$$
\theta=:\theta-\gamma\nabla_{\theta}\mathcal{L}{\mathcal{T}^{(t e)}}\left([\Theta;\theta^{\prime}],\Phi_{S_{{1,2}}}\right).
$$

Re-linking to Eq. 3, we note that the above $\theta^{\prime}$ comes from the last epoch of base-learning on $\mathcal{T}^{(t r)}$ .

重新关联到式3，我们注意到上述 $\theta^{\prime}$ 来自基于 $\mathcal{T}^{(t r)}$ 的基础学习最后一个周期。

Next, we describe how we apply $\Phi_{S_{{1,2}}}$ to the frozen neurons as shown in Figure 3(b). Given the trained $\Theta$ , for its $l$ -th layer containing $K$ neurons, we have $K$ pairs of parameters, respectively as weight and bias, denoted as ${(W_{i,k},b_{i,k})}$ . Note that the neuron location $l,k$ will be omitted for readability. Based on MTL, we learn $K$ pairs of scalars ${\Phi_{S_{{1,2}}}}$ . Assuming $X$ is input, we apply ${\Phi_{S_{{1,2}}}}$ to $(W,b)$ as

接下来，我们描述如何将 $\Phi_{S_{{1,2}}}$ 应用于冻结神经元，如图 3(b) 所示。给定训练好的 $\Theta$，对于包含 $K$ 个神经元的第 $l$ 层，我们有 $K$ 对参数（分别为权重和偏置），记为 ${(W_{i,k},b_{i,k})}$。注意，为便于阅读，神经元位置 $l,k$ 将被省略。基于多任务学习 (MTL)，我们学习 $K$ 对标量 ${\Phi_{S_{{1,2}}}}$。假设 $X$ 是输入，我们将 ${\Phi_{S_{{1,2}}}}$ 应用于 $(W,b)$，公式为

$$
S S(X;W,b;\Phi_{S_{{1,2}}})=(W\odot\Phi_{S_{1}})X+(b+\Phi_{S_{2}}),
$$

$$
S S(X;W,b;\Phi_{S_{{1,2}}})=(W\odot\Phi_{S_{1}})X+(b+\Phi_{S_{2}}),
$$

where $\odot$ denotes the element-wise multiplication

其中 $\odot$ 表示逐元素相乘

Taking Figure 3(b) as an example of a single $3\times3$ filter, after SS operations, this filter is scaled by $\Phi_{S_{1}}$ then the feature maps after convolutions are shifted by $\Phi_{S_{2}}$ in addition to the original bias $b$ . Detailed steps of SS are given in Algorithm 2 in Section 4.4.

以图 3(b) 中的单个 $3\times3$ 滤波器为例，经过 SS (scale and shift) 操作后，该滤波器先由 $\Phi_{S_{1}}$ 进行缩放，随后卷积得到的特征图会在原始偏置 $b$ 基础上再偏移 $\Phi_{S_{2}}$ 。具体步骤详见第 4.4 节算法 2。

Figure 3(a) shows a typical parameter-level Fine-Tuning $(F T)$ operation, which is in the meta optimization phase of our related work MAML [9]. It is obvious that $F T$ updates the complete values of $W$ and $b$ , and has a large number of parameters, and our SS reduces this number to below $\frac{2}{9}$ in the example of the figure.

图 3(a) 展示了一个典型的参数级微调 $(F T)$ 操作，该操作处于我们相关工作 MAML [9] 的元优化阶段。显然 $F T$ 会完整更新 $W$ 和 $b$ 的数值，且参数量较大，而我们的 SS 方法在该图示例中将参数量降低至 $\frac{2}{9}$ 以下。

In summary, SS can benefit MTL in three aspects. 1) It starts from a strong initialization based on a large-scale trained DNN, yielding fast convergence for MTL. 2) It does not change DNN weights, thereby avoiding the problem of “catastrophic forgetting” [27, 28] when learning specific tasks in MTL. 3) It is light-weight, reducing the chance of over fitting of MTL in few-shot scenarios.

总结来说，SS可以从三个方面使多任务学习(MTL)受益。1) 它基于大规模训练过的深度神经网络(DNN)进行强初始化，从而为MTL带来快速收敛。2) 它不会改变DNN的权重，因此避免了在MTL中学习特定任务时出现"灾难性遗忘" [27, 28]的问题。3) 它是轻量级的，降低了MTL在少样本场景下过拟合的可能性。

4.3. Hard task (HT) meta-batch

4.3. 困难任务 (HT) 元批次

In this section, we introduce a method to schedule hard tasks in meta-training batches. The conventional metabatch is composed of randomly sampled tasks, where the randomness implies random difficulties [9]. In our metatraining pipeline, we intentionally pick up failure cases in each task and re-compose their data to be harder tasks for adverse re-training. We aim to force our meta-learner to “grow up through hardness”.

在本节中，我们介绍了一种在元训练批次中调度硬任务的方法。传统元批次由随机抽样的任务组成，这种随机性意味着任务难度也是随机的 [9]。在我们的元训练流程中，我们有意选取每个任务中的失败案例，并将其数据重新组合成更困难的任务用于对抗性再训练。我们的目标是迫使元学习器"在困难中成长"。

Pipeline. Each task $\tau$ has two splits, $\mathcal{T}^{(t r)}$ and $\mathcal{T}^{(t e)}$ , for base-learning and test, respectively. As shown in Algorithm 2 line 2-5, base-learner is optimized by the loss of $\mathcal{T}^{(t r)}$ (in multiple epochs). SS parameters are then optimized by the loss of $\mathcal{T}^{(t e)}$ once. We can also get the recognition accuracy of $\mathcal{T}^{(t e)}$ for $M$ classes. Then, we choose the lowest accuracy $A c c_{m}$ to determine the most difficult class $\cdot m$ (also called failure class) in the current task.

流程。每个任务 $\tau$ 包含两个数据分割 $\mathcal{T}^{(tr)}$ 和 $\mathcal{T}^{(te)}$ ，分别用于基础学习和测试。如算法2第2-5行所示，基础学习器通过 $\mathcal{T}^{(tr)}$ 的损失进行多轮优化 (multiple epochs) ，随后SS参数通过 $\mathcal{T}^{(te)}$ 的损失单次优化。我们还能获得 $\mathcal{T}^{(te)}$ 在 $M$ 个类别上的识别准确率，进而选取最低准确率 $Acc_m$ 来确定当前任务中最困难的类别 $\cdot m$ (亦称失败类别) 。

After obtaining all failure classes (indexed by ${m}$ ) from $k$ tasks in current meta-batch ${\mathcal T_{1\sim k}}$ , we re-sample tasks from their data. Specifically, we assume $p(\mathcal{T}|{m})$ is the task distribution, we sample a “harder” task ${\mathcal{T}}^{h a r d}\in$ $p(\mathcal{T}|{m})$ . Two important details are given below.

在当前元批次 ${\mathcal T_{1\sim k}}$ 中从 $k$ 个任务获取所有故障类别 (索引为 ${m}$) 后，我们从其数据中重新采样任务。具体而言，假设 $p(\mathcal{T}|{m})$ 是任务分布，我们从中采样一个"更难"的任务 ${\mathcal{T}}^{hard}\in p(\mathcal{T}|{m})$。以下是两个重要细节说明。

Choosing hard class $m$ . We choose the failure class $\cdot m$ from each task by ranking the class-level accuracies instead of fixing a threshold. In a dynamic online setting as ours, it is more sensible to choose the hardest cases based on ranking rather than fixing a threshold ahead of time.

选择困难类别$m$。我们通过按类别准确率排序而非固定阈值的方式，从每个任务中选出失败类别$\cdot m$。在我们这种动态在线场景中，基于排序选择最困难案例比预先固定阈值更为合理。

Two methods of hard tasking using ${m}$ . Chosen ${m}$ , we can re-sample tasks $\mathcal{T}^{h a r d}$ by (1) directly using the samples of class $\cdot m$ in the current task $\tau$ , or (2) indirectly using the label of class $\cdot m$ to sample new samples of that class. In fact, setting (2) considers to include more data variance of class $\cdot m$ and it works better than setting (1) in general.

使用 ${m}$ 进行困难任务处理的两种方法。选定 ${m}$ 后，我们可以通过以下方式对任务 $\mathcal{T}^{hard}$ 进行重采样：(1) 直接使用当前任务 $\tau$ 中类别 $\cdot m$ 的样本，或 (2) 间接利用类别 $\cdot m$ 的标签采样该类别的新样本。实际上，设置(2)考虑了包含更多类别 $\cdot m$ 的数据方差，通常比设置(1)效果更好。

4.4. Algorithm

4.4. 算法

Algorithm 1 summarizes the training process of two main stages: large-scale DNN training (line 1-5) and metatransfer learning (line 6-22). HT meta-batch re-sampling and continuous training phases are shown in lines 16-20, for which the failure classes are returned by Algorithm 2, see line 14. Algorithm 2 presents the learning process on a single task that includes episode training (lines 2-5) and episode test, i.e. meta-level update (lines 6). In lines 7-11, the recognition rates of all test classes are computed and returned to Algorithm 1 (line 14) for hard task sampling.

算法1总结了两大阶段的训练过程：大规模DNN训练（第1-5行）和元迁移学习（第6-22行）。其中第16-20行展示了HT元批次重采样和持续训练阶段，其失败类别由算法2返回（见第14行）。算法2呈现了单任务学习流程，包含片段训练（第2-5行）和片段测试即元级更新（第6行）。第7-11行计算所有测试类别的识别率并返回至算法1（第14行）用于困难任务采样。

Input: Task distribution $p(\mathcal{T})$ and corresponding dataset $\mathcal{D}$ , learning rates $\alpha$ , $\beta$ and $\gamma$ Output: Feature extractor $\Theta$ , base learner $\theta$ , SS parameters ΦS 1,2 1 Randomly initialize $\Theta$ and $\theta$ ; 2 for samples in $\mathcal{D}$ do 3 Evaluate $\mathcal{L}{\mathcal{D}}([\Theta;\theta])$ by Eq. 2; 4 Optimize $\Theta$ and $\theta$ by Eq. 1; 5 end 6 Initialize $\Phi_{S_{1}}$ by ones, initialize $\Phi_{S_{2}}$ by zeros; 7 Reset and re-initialize $\theta$ for few-shot tasks; 8 for meta-batches do 9 Randomly sample tasks ${\mathcal{T}}$ from $p(\mathcal T)$ ; 10 while not done do 11 Sample task $\mathcal{T}{i}\in{\mathcal{T}}$ ; 12 Optimize $\Phi_{S_{{1,2}}}$ and $\theta$ with $\tau_{i}$ by Algorithm 2; 13 Get the returned class $\cdot m$ then add it to ${m}$ ; 14 end 15 Sample hard tasks ${{\mathcal{T}}^{h a r d}}{\mathrm{~f