Paths-over-Graph: Knowledge Graph Empowered Large Language Model Reasoning

基于图的路径：知识图谱赋能大语言模型推理

ABSTRACT

摘要

Large Language Models (LLMs) have achieved impressive results in various tasks but struggle with hallucination problems and lack of relevant knowledge, especially in deep complex reasoning and knowledge-intensive tasks. Knowledge Graphs (KGs), which capture vast amounts of facts in a structured format, offer a reliable source of knowledge for reasoning. However, existing KG-based LLM reasoning methods face challenges like handling multi-hop reasoning, multi-entity questions, and effectively utilizing graph structures. To address these issues, we propose Paths-over-Graph (PoG), a novel method that enhances LLM reasoning by integrating knowledge reasoning paths from KGs, improving the interpret a bility and faithfulness of LLM outputs. PoG tackles multi-hop and multi-entity questions through a three-phase dynamic multi-hop path exploration, which combines the inherent knowledge of LLMs with factual knowledge from KGs. In order to improve the efficiency, PoG prunes irrelevant information from the graph exploration first and introduces efficient three-step pruning techniques that incorporate graph structures, LLM prompting, and a pre-trained language model (e.g., SBERT) to effectively narrow down the explored candidate paths. This ensures all reasoning paths contain highly relevant information captured from KGs, making the reasoning faithful and interpret able in problem-solving. PoG innovative ly utilizes graph structure to prune the irrelevant noise and represents the first method to implement multi-entity deep path detection on KGs for LLM reasoning tasks. Comprehensive experiments on five benchmark KGQA datasets demonstrate PoG outperforms the stateof-the-art method ToG across GPT-3.5-Turbo and GPT-4, achieving an average accuracy improvement of $18.9%$ . Notably, PoG with GPT-3.5-Turbo surpasses ToG with GPT-4 by up to $23.9%$ .

大语言模型 (LLMs) 在各类任务中取得了令人瞩目的成果，但在深度复杂推理和知识密集型任务中仍面临幻觉问题与相关知识缺失的挑战。知识图谱 (KGs) 以结构化形式捕获海量事实，为推理提供了可靠的知识来源。然而，现有基于知识图谱的大语言模型推理方法在处理多跳推理、多实体问题及有效利用图结构方面存在不足。针对这些问题，我们提出了 Paths-over-Graph (PoG)，该方法通过整合知识图谱中的推理路径来增强大语言模型推理能力，提升输出的可解释性与可信度。PoG 采用三阶段动态多跳路径探索机制，将大语言模型的固有知识与知识图谱的事实知识相结合，从而解决多跳和多实体问题。为提高效率，PoG 首先从图探索中剪枝无关信息，并引入融合图结构、大语言模型提示和预训练语言模型 (如 SBERT) 的高效三阶段剪枝技术，显著缩小候选路径的探索范围。这确保了所有推理路径均包含从知识图谱中提取的高相关性信息，使推理过程在问题求解中兼具可信性与可解释性。PoG 创新性地利用图结构剪枝无关噪声，成为首个在知识图谱上实现多实体深度路径检测以支持大语言模型推理的方法。在五个基准 KGQA 数据集上的综合实验表明，PoG 在 GPT-3.5-Turbo 和 GPT-4 上均优于当前最优方法 ToG，平均准确率提升达 $18.9%$。值得注意的是，采用 GPT-3.5-Turbo 的 PoG 比使用 GPT-4 的 ToG 最高可领先 $23.9%$。

CCS CONCEPTS

CCS概念

• Information systems $\rightarrow$ Question answering.

• 信息系统 $\rightarrow$ 问答系统

KEYWORDS

关键词

Large Language Models; Knowledge Graph; Knowledge Graph Question Answering; Retrieval-Augmented Generation

大语言模型；知识图谱；知识图谱问答；检索增强生成

ACM Reference Format:

ACM 参考文献格式:

Xingyu Tan, Xiaoyang Wang, Qing Liu, Xiwei Xu, Xin Yuan, and Wenjie Zhang. 2025. Paths-over-Graph: Knowledge Graph Empowered Large Language Model Reasoning. In Proceedings of the ACM Web Conference 2025 (WWW ’25), April 28-May 2, 2025, Sydney, NSW, Australia. ACM, New York, NY, USA, 18 pages. https://doi.org/10.1145/3696410.3714892

Xingyu Tan、Xiaoyang Wang、Qing Liu、Xiwei Xu、Xin Yuan 和 Wenjie Zhang。2025。Paths-over-Graph：知识图谱赋能的大语言模型推理。载于《2025年ACM网络会议论文集》(WWW '25)，2025年4月28日-5月2日，澳大利亚新南威尔士州悉尼。ACM，美国纽约州纽约市，18页。https://doi.org/10.1145/3696410.3714892

1 INTRODUCTION

1 引言

Large Language Models (LLMs) have demonstrated remarkable performance in various tasks [4, 6, 8, 16, 41]. These models leverage pre-training techniques by scaling to billions of parameters and training on extensive, diverse, and unlabeled data [33, 41]. Despite these impressive capabilities, LLMs face two well-known challenges. First, they struggle with deep and responsible reasoning when tackling complex tasks [19, 32, 39]. Second, the substantial cost of training makes it difficult to keep models updated with the latest knowledge [37, 46], leading to errors when answering questions that require specialized information not included in their training data. For example, in Figure 1(a), though models like GPT can generate reasonable answers for knowledge-specific questions, these answers may be incorrect due to outdated information or hallucination of reasoning on LLM inherent Knowledge Base (KB).

大语言模型 (LLM) 在各种任务中展现出卓越性能 [4, 6, 8, 16, 41]。这些模型通过扩展到数十亿参数并在海量多样化无标注数据上进行预训练 [33, 41]。尽管能力惊人，大语言模型仍面临两个公认挑战：首先，处理复杂任务时难以进行深度可靠的推理 [19, 32, 39]；其次，高昂的训练成本导致模型难以及时更新最新知识 [37, 46]，当回答需要训练数据之外专业信息的问题时容易出错。例如在图 1(a) 中，虽然 GPT 等模型能对知识性问题生成合理回答，但由于信息过时或基于大语言模型固有知识库 (KB) 的推理幻觉，这些答案可能是错误的。

To deal with the problems of error reasoning and knowledge gaps, the plan-retrieval-answering method has been proposed [25, 27, 54]. In this approach, LLMs are prompted to decompose complex reasoning tasks into a series of sub-tasks, forming a plan. Simultaneously, external KBs are retrieved to answer each step of the plan. However, this method still has the issue of heavily relying on the reasoning abilities of LLMs rather than the faithfulness of the retrieved knowledge. The generated reasoning steps guide information selection, but answers are chosen based on the LLM’s interpretation of the retrieved knowledge rather than on whether the selection leads to a correct and faithful answer.

为了解决错误推理和知识缺口的问题，研究者提出了计划-检索-回答方法 [25, 27, 54]。该方法通过提示大语言模型将复杂推理任务分解为一系列子任务形成计划，同时检索外部知识库(KB)来回答计划的每个步骤。然而，这种方法仍存在过度依赖大语言模型推理能力而非检索知识可信度的问题：生成的推理步骤虽能指导信息选择，但答案的选取依据是大语言模型对检索知识的解读，而非该选择是否能导向正确且可信的答案。

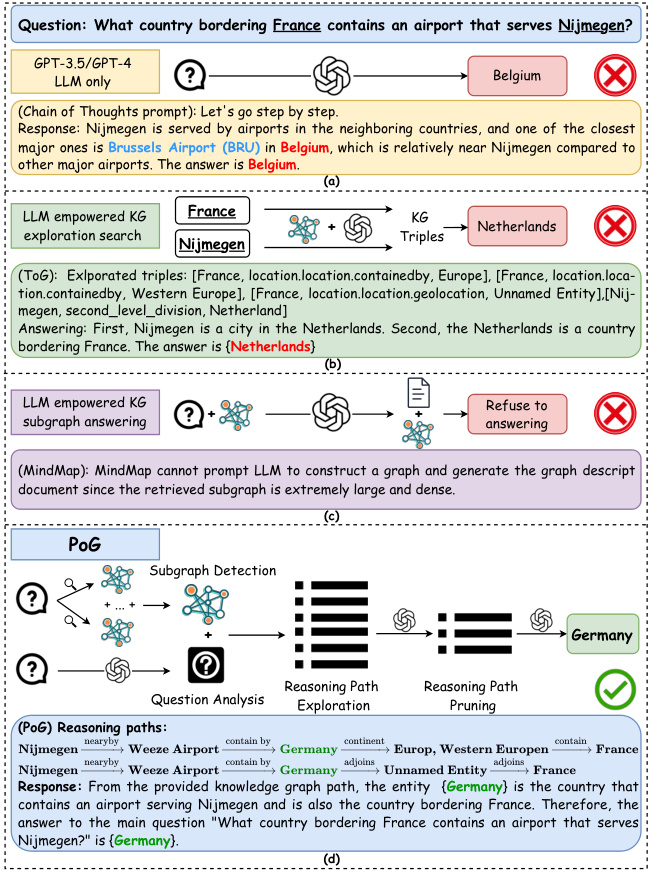
Figure 1: Representative workflow of four LLM reasoning paradigms.

图 1: 四种大语言模型推理范式的典型工作流程。

To address these challenges, incorporating external knowledge sources like Knowledge Graphs (KGs) is a promising solution to enhance LLM reasoning [26, 27, 29, 37]. KGs offer abundant factual knowledge in a structured format, serving as a reliable source to improve LLM capabilities. Knowledge Graph Question Answering (KGQA) serves as an approach for evaluating the integration of KGs with LLMs, which requires machines to answer natural language questions by retrieving relevant facts from KGs. These approaches typically involve: (1) identifying the initial entities from the question, and (2) iterative ly retrieving and refining inference paths until sufficient evidence has been obtained. Despite their success, they still face challenges such as handling multi-hop reasoning problems, addressing questions with multiple topic entities, and effectively utilizing the structural information of graphs.

为解决这些挑战，融入知识图谱 (Knowledge Graphs, KGs) 等外部知识源是增强大语言模型推理能力的有效方案 [26, 27, 29, 37]。知识图谱以结构化形式提供丰富的事实知识，可作为提升大语言模型能力的可靠来源。知识图谱问答 (Knowledge Graph Question Answering, KGQA) 是评估知识图谱与大语言模型融合效果的一种方法，要求机器通过从知识图谱中检索相关事实来回答自然语言问题。这类方法通常包括：(1) 从问题中识别初始实体，(2) 迭代式检索并优化推理路径直至获得充分证据。尽管已取得成果，这些方法仍面临处理多跳推理问题、应对含多主题实体提问以及有效利用图谱结构信息等挑战。

Challenge 1: Multi-hop reasoning problem. Current methods [15, 28, 37, 50], such as the ToG model presented in Figure 1(b), begin by exploring from each topic entity, with LLMs selecting connected knowledge triples like (France, contained by, Europe). This process relies on the LLM’s inherent understanding of these triples. However, focusing on one-hop neighbors can result in plausible but incorrect answers and prematurely exclude correct ones, especially when multi-hop reasoning is required. Additionally, multi-hop reasoning introduces significant computational overhead, making efficient pruning essential, especially in dense and large KGs.

挑战1：多跳推理问题。当前方法[15, 28, 37, 50]（例如图1(b)所示的ToG模型）从每个主题实体开始探索，由大语言模型选择相连的知识三元组（如 (France, contained by, Europe)）。该过程依赖于大语言模型对这些三元组的固有理解。然而，仅关注单跳邻居可能导致看似合理但错误的答案，并过早排除正确结果，尤其是在需要多跳推理的场景下。此外，多跳推理会带来显著计算开销，在密集且大规模的知识图谱(KG)中，高效的剪枝策略至关重要。

Challenge 2: Multi-entity question. As shown in Figure 1(b), existing work [15, 28, 37, 50] typically explores KG for each topic entity independently. When a question involves multiple entities, these entities are examined in separate steps without considering their interconnections. This approach can result in a large amount of irrelevant information in the candidate set that does not connect to the other entities in the question, leading to suboptimal results.

挑战2：多实体问题。如图1(b)所示，现有工作[15, 28, 37, 50]通常独立探索每个主题实体的知识图谱(KG)。当问题涉及多个实体时，这些实体会被分步考察而忽略彼此关联。这种方法会导致候选集中出现大量与问题中其他实体无关的冗余信息，从而产生次优结果。

Challenge 3: Utilizing graph structure. Existing methods [7, 13, 46] often overlook the inherent graph structures when processing retrieved subgraphs. For example, the MindMap model in Figure 1(c) utilizes LLMs to generate text-formatted subgraphs from KG triples, converting them into graph descriptions that are fed back into the LLM to produce answers. This textual approach overlooks the inherent structural information of graphs and can overwhelm the LLM when dealing with large graphs. Additionally, during KG information selection, most methods use in-context learning by feeding triples into the LLM, ignoring the overall graph structure.

挑战3：利用图结构。现有方法[7,13,46]在处理检索到的子图时常常忽略固有的图结构。例如，图1(c)中的MindMap模型利用大语言模型从知识图谱三元组生成文本格式的子图，将其转换为图描述后反馈给大语言模型以生成答案。这种文本化方法忽略了图固有的结构信息，在处理大型图时可能使大语言模型不堪重负。此外，在知识图谱信息选择过程中，大多数方法通过将三元组输入大语言模型来使用上下文学习，忽略了整体图结构。

Contributions. In this paper, we introduce a novel method, Pathsover-Graph (PoG). Unlike previous studies that utilize knowledge triples for retrieval [28, 37], PoG employs knowledge reasoning paths, that contain all the topic entities in a long reasoning length, as a retrieval-augmented input for LLMs. The paths in KGs serve as logical reasoning chains, providing KG-supported, interpret able reasoning logic that addresses issues related to the lack of specific knowledge background and unfaithful reasoning paths.

贡献。本文提出了一种新方法 Pathsover-Graph (PoG)。与先前使用知识三元组进行检索的研究 [28, 37] 不同，PoG 采用包含长推理链中所有主题实体的知识推理路径作为大语言模型的检索增强输入。知识图谱中的路径作为逻辑推理链，提供了图谱支持的、可解释的推理逻辑，解决了特定知识背景缺失和不可靠推理路径相关的问题。

To address multi-hop reasoning problem, as shown in Figure 1(d), PoG first performs question analysis, to extract topic entities from questions. Utilizing these topic entities, it decomposes the complex question into sub-questions and generates an LLM thinking indicator termed "Planning". This planning not only serves as an answering strategy but also predicts the implied relationship depths between the answer and each topic entity. The multi-hop paths are then explored starting from a predicted depth, enabling a dynamic search process. Previous approaches using planning usually retrieve information from scratch, which often confuses LLMs with source neighborhood-based semantic information. In contrast, our method ensures that LLMs follow accurate reasoning paths that directly lead to the answer.

为解决多跳推理问题，如图 1(d) 所示，PoG 首先进行问题分析，从问题中提取主题实体。利用这些主题实体，它将复杂问题分解为子问题，并生成一个称为"规划 (Planning)"的大语言模型思考指示器。该规划不仅作为回答策略，还预测答案与每个主题实体之间的隐含关系深度。随后从预测深度开始探索多跳路径，实现动态搜索过程。以往使用规划的方法通常从头开始检索信息，这常常让大语言模型混淆于基于源邻域的语义信息。相比之下，我们的方法确保大语言模型遵循直接指向答案的精确推理路径。

To address multi-entity questions, PoG employs a three-phase exploration process to traverse reasoning paths from the retrieved question subgraph. All paths must contain all topic entities in the same order as they occur in the LLM thinking indicator. In terms of reasoning paths in KGs, all paths are inherently logical and faithful. Each path potentially contains one possible answer and serves as the interpret able reasoning logic. The exploration leverages the inherent knowledge of both LLM and KG.

为解决多实体问题，PoG采用三阶段探索流程遍历从检索到的问题子图中获取的推理路径。所有路径必须按大语言模型思维指示器中出现的相同顺序包含全部主题实体。就知识图谱中的推理路径而言，所有路径本质上都具有逻辑性和可信性。每条路径可能包含一个潜在答案，并作为可解释的推理逻辑存在。该探索过程同时利用了大语言模型和知识图谱的固有知识。

To effectively utilize graph structure, PoG captures the question subgraph by expanding topic entities to their maximal depth neighbors, applying graph clustering and reduction to reduce graph search costs. In the path pruning phase, we select possible correct answers from numerous candidates. All explored paths undergo a three-step beam search pruning, integrating graph structures, LLM prompting, and a pre-trained language understanding model (e.g., BERT) to ensure effectiveness and efficiency. Additionally, inspired by the Graph of Thought (GoT) [4], to reduce LLM hallucination, PoG prompts LLMs to summarize the obtained Top $\cdot W_{\mathrm{max}}$ paths before evaluating the answer, where $W_{\mathrm{max}}$ is a user-defined maximum width in the path pruning phase. In summary, the advantage of PoG can be abbreviated as:

为有效利用图结构，PoG通过将主题实体扩展到其最大深度邻居来捕获问题子图，并应用图聚类和约简技术以降低图搜索成本。在路径剪枝阶段，我们从大量候选答案中筛选可能正确的选项。所有探索路径均经过三步束搜索剪枝，整合图结构、大语言模型提示和预训练语言理解模型（如BERT）以确保效果与效率。此外，受思维图谱（GoT）[4]启发，为减少大语言模型幻觉，PoG在评估答案前会提示大语言模型对获取的Top $\cdot W_{\mathrm{max}}$ 条路径进行汇总，其中 $W_{\mathrm{max}}$ 为用户在路径剪枝阶段定义的最大宽度。综上所述，PoG的优势可简化为：

• Dynamic deep search: Guided by LLMs, PoG dynamically extracts multi-hop reasoning paths from KGs, enhancing LLM capabilities in complex knowledge-intensive tasks. • Interpret able and faithful reasoning: By utilizing highly question-relevant knowledge paths, PoG improves the interpre t ability of LLM reasoning, enhancing the faithfulness and question-relatedness of LLM-generated content. • Efficient pruning with graph structure integration: PoG incorporates efficient pruning techniques in both the KG and reasoning paths to reduce computational costs, mitigate LLM hallucinations caused by irrelevant noise, and effectively narrow down candidate answers. • Flexibility and effectiveness: a) PoG is a plug-and-play framework that can be seamlessly applied to various LLMs and KGs. b) PoG allows frequent knowledge updates via the KG, avoiding the expensive and slow updates required for LLMs. c) PoG reduces the LLMs token usage by over $50%$ with only a $\pm2%$ difference in accuracy compared to the best-performing strategy. d) PoG achieves state-of-the-art results on all the tested KGQA datasets, outperforming the strong baseline ToG by an average of $18.9%$ accuracy using both GPT-3.5 and GPT-4. Notably, PoG with GPT-3.5 can outperform ToG with GPT-4 by up to $23.9%$ .

• 动态深度搜索：在大语言模型 (LLM) 的引导下，PoG 动态地从知识图谱 (KG) 中提取多跳推理路径，增强大语言模型在复杂知识密集型任务中的能力。
• 可解释且忠实的推理：通过利用高度相关的问题知识路径，PoG 提升了大语言模型推理的可解释性，增强了生成内容的忠实度和问题相关性。
• 基于图结构的高效剪枝：PoG 在知识图谱和推理路径中采用高效剪枝技术，降低计算成本，减少由无关噪声引起的大语言模型幻觉，并有效缩小候选答案范围。
• 灵活性与高效性：
a) PoG 是一个即插即用框架，可无缝适配多种大语言模型和知识图谱。
b) PoG 支持通过知识图谱频繁更新知识，避免大语言模型更新成本高、速度慢的问题。
c) 在准确率仅相差 ±2% 的情况下，PoG 将大语言模型的 Token 使用量降低超过 50%。
d) 在所有测试的 KGQA 数据集上，PoG 均取得最先进的结果：使用 GPT-3.5 和 GPT-4 时，其准确率平均比强基线 ToG 高 18.9%。值得注意的是，采用 GPT-3.5 的 PoG 比采用 GPT-4 的 ToG 最高可领先 23.9%。

2 RELATED WORK

2 相关工作

KG-based LLM reasoning. KGs provide structured knowledge valuable for integration with LLMs [29]. Early studies [25, 27, 30, 52] embed KG knowledge into neural networks during pre-training or fine-tuning, but this can reduce explain ability and hinder efficient knowledge updating [29]. Recent methods combine KGs with LLMs by converting relevant knowledge into textual prompts, often ignoring structural information [29, 46]. Advanced works [17, 28, 37] involve LLMs directly exploring KGs, starting from an initial entity and iterative ly retrieving and refining reasoning paths until the LLM decides the augmented knowledge is sufficient. However, by starting from a single vertex and ignoring the question’s position within the KG’s structure, these methods overlook multiple topic entities and the explain ability provided by multi-entity paths.

基于知识图谱 (KG) 的大语言模型推理。知识图谱提供的结构化知识对与大语言模型结合具有重要价值 [29]。早期研究 [25, 27, 30, 52] 在预训练或微调阶段将知识图谱信息嵌入神经网络，但这会降低可解释性并阻碍知识高效更新 [29]。近期方法通过将相关知识转化为文本提示来结合知识图谱与大语言模型，但往往忽略结构信息 [29, 46]。前沿工作 [17, 28, 37] 让大语言模型直接从初始实体出发探索知识图谱，通过迭代检索和优化推理路径，直到模型判定增强知识足够充分。然而，这些方法从单一顶点出发且忽略问题在知识图谱结构中的位置，导致忽视了多主题实体以及多实体路径提供的可解释性优势。

Reasoning with LLM prompting. LLMs have shown significant potential in solving complex tasks through effective prompting strategies. Chain of Thought (CoT) prompting [45] enhances reasoning by following logical steps in few-shot learning. Extensions like Auto-CoT [53], Complex-CoT [10], CoT-SC [44], Zero-Shot CoT [21], ToT [48], and GoT [4] build upon this approach. However, these methods often rely solely on knowledge present in training data, limiting their ability to handle knowledge-intensive or deep reasoning tasks. To solve this, some studies integrate external KBs using plan-and-retrieval methods such as CoK [25], RoG [27], and ReAct [49], decomposing complex questions into subtasks to reduce hallucinations. However, they may focus on the initial steps of sub-problems and overlook further steps of final answers, leading to locally optimal solutions instead of globally optimal ones. To address these deep reasoning challenges, we introduce dynamic multi-hop question reasoning. By adaptively determining reasoning depths for different questions, we enable the model to handle varying complexities effectively.

通过大语言模型 (LLM) 提示进行推理。大语言模型已展现出通过有效提示策略解决复杂任务的巨大潜力。思维链 (Chain of Thought, CoT) 提示 [45] 通过在少样本学习中遵循逻辑步骤来增强推理能力。Auto-CoT [53]、Complex-CoT [10]、CoT-SC [44]、零样本 CoT (Zero-Shot CoT) [21]、ToT [48] 和 GoT [4] 等方法均基于这一思路进行了扩展。然而，这些方法通常仅依赖训练数据中的知识，限制了其处理知识密集型或深度推理任务的能力。为解决这一问题，部分研究采用计划-检索方法（如 CoK [25]、RoG [27] 和 ReAct [49]）集成外部知识库 (KB)，通过将复杂问题分解为子任务来减少幻觉现象。但这些方法可能聚焦于子问题的初始步骤，而忽视最终答案的后续推导，导致局部最优而非全局最优解。为应对深度推理挑战，我们提出动态多跳问题推理机制，通过自适应确定不同问题的推理深度，使模型能有效处理多复杂度任务。

KG information pruning. Graphs are widely used to model complex relationships among different entities [22, 23, 35, 40]. KGs contain vast amounts of facts [14, 42, 47], making it impractical to involve all relevant triples in the context of the LLM due to high costs and potential noise [43]. Existing methods [17, 28, 37] typically identify initial entities and iterative ly retrieve reasoning paths until an answer is reached, often treating the LLM as a function executor and relying on in-context learning or fine-tuning, which is expensive. Some works attempt to reduce pruning costs. KAPING [2] projects questions and triples into the same semantic space to retrieve relevant knowledge via similarity measures. KG-GPT [20] decomposes complex questions, matches, and selects the relevant relations with sub-questions to form evidence triples. However, these methods often overlook the overall graph structure and the interrelations among multiple topic entities, leading to suboptimal pruning and reasoning performance.

KG信息剪枝。图被广泛用于建模不同实体间的复杂关系 [22, 23, 35, 40]。知识图谱(KG)包含海量事实 [14, 42, 47]，由于高昂成本和潜在噪声 [43]，在大语言模型(LLM)上下文中涉及所有相关三元组并不现实。现有方法 [17, 28, 37] 通常先识别初始实体，然后迭代检索推理路径直至获得答案，往往将LLM视为函数执行器，依赖上下文学习或微调，代价昂贵。部分研究尝试降低剪枝成本：KAPING [2] 将问题与三元组投射至同一语义空间，通过相似度度量检索相关知识；KG-GPT [20] 分解复杂问题，将子问题与相关关系匹配筛选以构建证据三元组。但这些方法常忽略整体图结构及多主题实体间的关联，导致剪枝与推理性能欠佳。

3 PRELIMINARY

3 预备知识

Consider a Knowledge Graph (KG) $\mid{\mathcal{G}}({\mathcal{E}},{\mathcal{R}},{\mathcal{T}})$ , where $\varepsilon,\mathcal{R}$ and $\mathcal{T}$ represent the set of entities, relations, and knowledge triples, respectively. Each knowledge triple $T\in{\mathcal{T}}$ encapsulates the factual knowledge in $\boldsymbol{\mathscr{G}}$ , and is represented as $\boldsymbol{T}=\left(e_{h},r,e_{t}\right)$ , where $e_{h},e_{t}\in\mathcal{E}$ and $r\in{\mathcal{R}}$ . Given an entity set $\mathcal{E}{S}\subseteq\mathcal{E}$ , the induced subgraph of $\varepsilon_{s}$ is denoted as $S=(\mathcal{E}{S},\mathcal{R}{S},\mathcal{T}{S})$ , where $\mathcal{T}{S}={(e,r,e^{\prime})\in\mathcal{T}:|$ $e,e^{\prime}\in\mathcal{E}{S}}$ , and $\mathcal{R}{S}={r\in\mathcal{R}\mid(e,r,e^{\prime})\in\mathcal{T}_{S}}$ . Furthermore, we denote $\mathcal{D}(e)$ and $\mathcal{D}(\boldsymbol{r})$ as the sets of short textual descriptions for each entity $e\in{\mathcal{E}}$ and each relation $r\in{\mathcal{R}}$ , respectively. For example, the text description of the entity $\mathrm{{^{\leftarrow}m.0f8l9c^{3}}}$ is $\mathcal{D}(^{\leftarrow}\mathrm{m}.0\mathrm{f}8\mathrm{l}9\mathrm{c}^{;9})=$ “France”. For simplicity, in this paper, all entities and relations are referenced through their $\mathcal{D}$ representations and transformed into natural language.

考虑一个知识图谱 (Knowledge Graph, KG) $\mid{\mathcal{G}}({\mathcal{E}},{\mathcal{R}},{\mathcal{T}})$，其中 $\varepsilon,\mathcal{R}$ 和 $\mathcal{T}$ 分别表示实体、关系和知识三元组的集合。每个知识三元组 $T\in{\mathcal{T}}$ 封装了 $\boldsymbol{\mathscr{G}}$ 中的事实知识，并表示为 $\boldsymbol{T}=\left(e_{h},r,e_{t}\right)$，其中 $e_{h},e_{t}\in\mathcal{E}$ 且 $r\in{\mathcal{R}}$。给定一个实体子集 $\mathcal{E}{S}\subseteq\mathcal{E}$，$\varepsilon_{s}$ 的诱导子图记为 $S=(\mathcal{E}{S},\mathcal{R}{S},\mathcal{T}{S})$，其中 $\mathcal{T}{S}={(e,r,e^{\prime})\in\mathcal{T}:|$ $e,e^{\prime}\in\mathcal{E}{S}}$，且 $\mathcal{R}{S}={r\in\mathcal{R}\mid(e,r,e^{\prime})\in\mathcal{T}_{S}}$。此外，我们用 $\mathcal{D}(e)$ 和 $\mathcal{D}(\boldsymbol{r})$ 分别表示每个实体 $e\in{\mathcal{E}}$ 和每个关系 $r\in{\mathcal{R}}$ 的简短文本描述集合。例如，实体 $\mathrm{{^{\leftarrow}m.0f8l9c^{3}}}$ 的文本描述为 $\mathcal{D}(^{\leftarrow}\mathrm{m}.0\mathrm{f}8\mathrm{l}9\mathrm{c}^{;9})=$ "法国"。为简化表述，本文中所有实体和关系均通过其 $\mathcal{D}$ 表示引用并转换为自然语言形式。

Definition 1 (Reasoning Path). Given a $K G g$ , a reasoning path within $\boldsymbol{\mathcal{G}}$ is defined as a connected sequence of knowledge triples, represented as: 𝑝𝑎𝑡ℎ $\iota_{\mathcal{G}}(e_{1},e_{l+1})={T_{1},T_{2},...,T_{l}}={(e_{1},r_{1},e_{2})$ , $(e_{2},r_{2},e_{3})$ $,...,(e_{l},r_{l},e_{l+1})}$ , where $T_{i}\in\mathcal{T}$ denotes the 𝑖-th triple in the path and 𝑙 denotes the length of the path, i.e., 𝑙𝑒𝑛𝑔𝑡 $\iota(p a t h_{\mathcal{G}}(e_{1},e_{l+1}))=l$

定义 1 (推理路径). 给定一个知识图谱 $K G g$，在 $\boldsymbol{\mathcal{G}}$ 中的推理路径被定义为一个相连的知识三元组序列，表示为：路径 $\iota_{\mathcal{G}}(e_{1},e_{l+1})={T_{1},T_{2},...,T_{l}}={(e_{1},r_{1},e_{2})$，$(e_{2},r_{2},e_{3})$，$,...,(e_{l},r_{l},e_{l+1})}$，其中 $T_{i}\in\mathcal{T}$ 表示路径中的第 𝑖 个三元组，𝑙 表示路径长度，即长度 $\iota(p a t h_{\mathcal{G}}(e_{1},e_{l+1}))=l$

Example 1. Consider a reasoning path between "University" and "Student" in KG: 𝑝𝑎𝑡ℎ $\boldsymbol{\mathscr{G}}$ (University, Student) $=$ {(University, employs, Professor), (Professor, teaches, Course), (Course, enrolled in, Student)}, and can be visualized as:

示例 1. 考虑知识图谱中"University"与"Student"之间的推理路径：𝑝𝑎𝑡ℎ $\boldsymbol{\mathscr{G}}$(University, Student) $=$ {(University, employs, Professor), (Professor, teaches, Course), (Course, enrolled in, Student)}，其可视化形式为：

It indicates that a “University" employs a “Professor," who teaches a “Course," in which a "Student" is enrolled. The length of the path is 3.

这表明一所"大学"聘用了一位"教授"，教授讲授一门"课程"，而"学生"选修了该课程。该路径长度为3。

For any entity $s$ and $t$ in $\boldsymbol{\mathscr{G}}$ , if there exists a reasoning path between 𝑠 and $t$ , we say 𝑠 and $t$ can reach each other, denoted as $s\leftrightarrow t$ . The distance between 𝑠 and $t$ in $\boldsymbol{\mathcal{G}}$ , denoted as $d i s t_{\mathcal{G}}(s,t)$ , is the shortest reasoning path distance between $s$ and $t$ . For the non-reachable vertices, their distance is infinite. Given a positive integer $h$ , the $h$ -hop neighbors of an entity $s$ in $\boldsymbol{\mathcal{G}}$ is defined as $N_{\mathcal{G}}(s,h)={t\in\mathcal{E}|d i s t_{\mathcal{G}}(s,t)\leq h}$ .

对于 $\boldsymbol{\mathscr{G}}$ 中的任意实体 $s$ 和 $t$，若存在从 𝑠 到 $t$ 的推理路径，则称 𝑠 与 $t$ 可相互到达，记为 $s\leftrightarrow t$。实体 𝑠 与 $t$ 在 $\boldsymbol{\mathcal{G}}$ 中的距离 $dist_{\mathcal{G}}(s,t)$ 定义为两者间最短推理路径的长度。不可达顶点间的距离为无穷大。给定正整数 $h$，实体 $s$ 在 $\boldsymbol{\mathcal{G}}$ 中的 $h$ 跳邻居集合定义为 $N_{\mathcal{G}}(s,h)={t\in\mathcal{E}|dist_{\mathcal{G}}(s,t)\leq h}$。

Definition 2 (Entity Path). Given a $K G g$ and a list of entities $l i s t_{e}=[e_{1},e_{2},e_{3},\ldots,e_{l}],$ the entity path of ${{l i s t}{e}}$ is defined as a connected sequence of reasoning paths, which is denoted as 𝑝𝑎𝑡 $h{\mathcal{G}}(l i s t_{e})$ $={p a t h_{\mathcal{G}}(e_{1},e_{2})$ , ${\mathcal{P}}^{a t h}{\mathcal{G}}^{(e_{2},e_{3}),\dots,p a t h}{\mathcal{G}}^{(e_{l-1},e_{l})}={{\bar{(e}}{s},r,e_{t})$ $|(e_{s},r,e_{t})\in\mathit{p a t h}{\mathcal{G}}(e_{i},e_{i+1})\land1\le i<l}$ .

定义 2 (实体路径). 给定一个知识图谱 $K G g$ 和一个实体列表 $l i s t_{e}=[e_{1},e_{2},e_{3},\ldots,e_{l}]$ , ${{l i s t}{e}}$ 的实体路径被定义为一系列相连的推理路径, 记作 𝑝𝑎𝑡 $h_{\mathcal{G}}(l i s t_{e})$ $={p a t h_{\mathcal{G}}(e_{1},e_{2})$ , ${\mathcal{P}}^{a t h}{\mathcal{G}}^{(e_{2},e_{3}),\dots,p a t h}{\mathcal{G}}^{(e_{l-1},e_{l})}={{\bar{(e}}{s},r,e_{t})$ $|(e_{s},r,e_{t})\in\mathit{p a t h}{\mathcal{G}}(e_{i},e_{i+1})\land1\le i<l}$ .

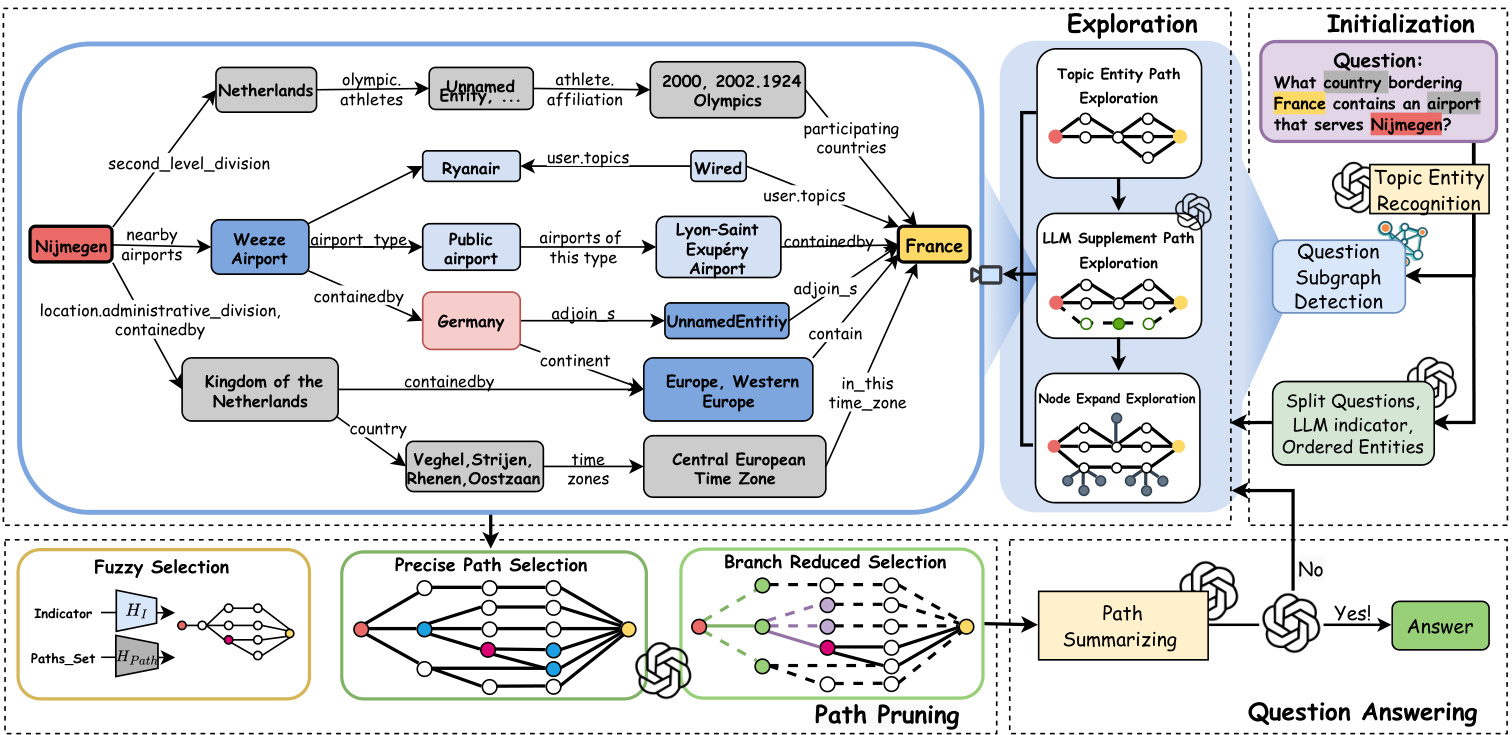
Figure 2: Overview of the PoG architecture. Exploration: After initialization (detailed in Figure 3), the model retrieves entity paths from $\mathcal{G}{q}$ through three exploration phases. Path Pruning: PoG applies a three-step beam search to prune paths after each exploration phase. Question Answering: The pruned paths are then evaluated for question answering. If these paths do not fully answer the question, the model explores deeper paths until $D_{m a x}$ is reached or moves on to the next exploration phase.

图 2: PoG架构概览。探索阶段: 初始化后(详见图 3)，模型通过三个探索阶段从$\mathcal{G}{q}$检索实体路径。路径剪枝: PoG在每轮探索后采用三步束搜索进行路径剪枝。问答阶段: 剪枝后的路径被用于问题解答评估。若当前路径未能完整回答问题，模型会继续探索更深层路径直至达到$D_{max}$或进入下一探索阶段。

Knowledge Graph Question Answering (KGQA) is a fundamental reasoning task based on KGs. Given a natural language question $q$ and a $\operatorname{KG}g$ , the objective is to devise a function $f$ that predicts answers $a\in A n s w e r(q)$ utilizing knowledge encapsulated in $\boldsymbol{\mathcal{G}}$ , i.e., $a=f(q,\mathcal{G})$ . Consistent with previous research [27, 28, 36, 37], we assume the topic entities $T o p i c(q)$ mentioned in $q$ and answer entities 𝐴𝑛𝑠𝑤𝑒𝑟 $(q)$ in ground truth are linked to the corresponding entities in $\boldsymbol{\mathcal{G}}$ , i.e., $T o p i c(q)\subseteq\mathcal{E}$ and 𝐴𝑛𝑠𝑤𝑒𝑟 $(q)\subseteq\mathcal{E}$ .

知识图谱问答 (Knowledge Graph Question Answering, KGQA) 是基于知识图谱的基础推理任务。给定一个自然语言问题 $q$ 和一个知识图谱 $\operatorname{KG}g$，目标是设计一个函数 $f$，利用 $\boldsymbol{\mathcal{G}}$ 中封装的知识预测答案 $a\in A n s w e r(q)$，即 $a=f(q,\mathcal{G})$。与先前研究 [27, 28, 36, 37] 一致，我们假设问题 $q$ 中提到的主题实体 $T o p i c(q)$ 和真实答案实体 𝐴𝑛𝑠𝑤𝑒𝑟 $(q)$ 都关联到 $\boldsymbol{\mathcal{G}}$ 中的对应实体，即 $T o p i c(q)\subseteq\mathcal{E}$ 且 𝐴𝑛𝑠𝑤𝑒𝑟 $(q)\subseteq\mathcal{E}$。

4 METHOD

4 方法

PoG implements the ${}^{\mathrm{{6}}}\mathrm{KG}$ -based LLM Reasoning" by first exploring all possible faithful reasoning paths and then collaborating with LLM to perform a 3-step beam search selection on the retrieved paths. Compared to previous approaches [28, 37], our model focuses on providing more accurate and question-relevant retrievalargument graph information. The framework of PoG is outlined in Figure 2, comprising four main components.

PoG通过首先探索所有可能的忠实推理路径，然后与大语言模型 (LLM) 协作对检索到的路径进行三步束搜索选择，实现了基于 ${}^{\mathrm{{6}}}\mathrm{KG}$ 的LLM推理。与之前的方法 [28, 37] 相比，我们的模型专注于提供更准确且与问题相关的检索论证图信息。PoG的框架如图 2 所示，包含四个主要组件。

• Initialization. The process begins by identifying the set of topic entities from the question input, and then queries the source KG $\boldsymbol{\mathcal{G}}$ by exploring up to $D_{\mathrm{max}}$ -hop from each topic entity to construct the evidence sub-graph $\mathcal{G}{q}$ , where $D_{\mathrm{max}}$ is the user-defined maximum exploration depth. Subsequently, we prompt the LLM to analyze the question and generate an indicator that serves as a strategy for the answer formulation process and predicting the exploration depth $D_{\mathrm{predict}}$ . • Exploration. After initialization, the model retrieves topic entity paths from $\mathcal{G}_{q}$ through three exploration phases: topic entity path exploration, LLM supplement path exploration, and node expand

• 初始化。该过程首先从问题输入中识别主题实体集合，然后通过从每个主题实体探索最多 $D_{\mathrm{max}}$ 跳来查询源知识图谱 $\boldsymbol{\mathcal{G}}$ ，以构建证据子图 $\mathcal{G}{q}$ ，其中 $D_{\mathrm{max}}$ 是用户定义的最大探索深度。随后，我们提示大语言模型分析问题并生成一个指示器，作为答案制定过程的策略并预测探索深度 $D_{\mathrm{predict}}$ 。
• 探索。初始化后，模型通过三个探索阶段从 $\mathcal{G}_{q}$ 中检索主题实体路径：主题实体路径探索、大语言模型补充路径探索和节点扩展

4.1 Initialization

4.1 初始化

The initialization has two main stages, i.e., question subgraph detection and question analysis. The framework is shown in Figure 3. Question subgraph detection. Given a question $q$ , PoG initially identifies the question subgraph, which includes all the topic entities of $q$ and their $D_{\mathrm{max}}$ -hop neighbors.

初始化包含两个主要阶段，即问题子图检测和问题分析。框架如图 3 所示。问题子图检测。给定问题 $q$，PoG 首先识别问题子图，其中包含 $q$ 的所有主题实体及其 $D_{\mathrm{max}}$ 跳邻居。

Topic entity recognition. To identify the relevant subgraph, PoG first employs LLMs to extract the potential topic entities from the question. Following the identification, the process applies BERTbased similarity matching to align these potential entities with entities from KG. Specifically, as shown in Figure 3, we encode both the keywords and all entities from KG into dense vector embeddings as $H_{T}$ and $H_{\mathcal{G}}$ . We then compute a cosine similarity matrix between these embeddings to determine the matches. For each keyword, the entities with the highest similarity scores are selected to form the set 𝑇𝑜𝑝𝑖𝑐 (𝑞). This set serves as the foundation for constructing the question subgraph in subsequent steps.

主题实体识别。为识别相关子图，PoG首先利用大语言模型从问题中提取潜在主题实体。识别完成后，该过程采用基于BERT的相似度匹配将这些潜在实体与知识图谱中的实体对齐。具体如图3所示，我们将关键词和知识图谱中的所有实体编码为稠密向量嵌入$H_{T}$和$H_{\mathcal{G}}$，然后计算这些嵌入之间的余弦相似度矩阵以确定匹配项。对于每个关键词，选择相似度得分最高的实体组成集合𝑇𝑜𝑝𝑖𝑐(𝑞)，该集合将作为后续步骤中构建问题子图的基础。

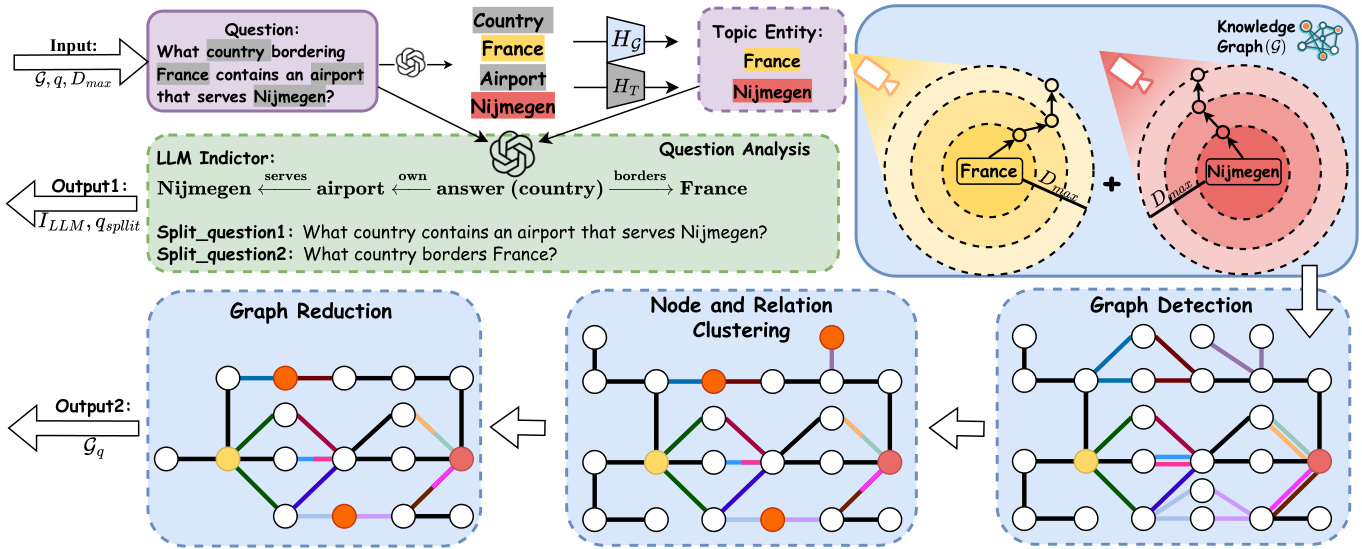
Figure 3: Overview of the initialization phase. Output 1: from the input question, the model identifies topic entities and prompts the LLM to decompose questions into split questions ${q_{s p l i t}}$ and generate an indicator $I_{L L M}$ . The indicator outlines a strategy for formulating the answer and predicts the exploration depth $D_{p r e d i c t}$ . Output 2: the model queries the source KG up to $D_{m a x}$ -hop from identified topic entities, constructing and pruning the evidence subgraph $\scriptstyle{{\mathcal{G}}_{q}}$ .

图 3: 初始化阶段概述。输出 1: 根据输入问题，模型识别主题实体并提示大语言模型将问题分解为子问题 ${q_{s p l i t}}$ 并生成指示符 $I_{L L M}$ 。该指示符概述了构建答案的策略并预测探索深度 $D_{p r e d i c t}$ 。输出 2: 模型从识别的主题实体出发，查询源知识图谱至多 $D_{m a x}$ 跳，构建并剪枝证据子图 $\scriptstyle{{\mathcal{G}}_{q}}$ 。

Subgraph detection. Upon identifying the topic entities, PoG captures the induced subgraph ${\mathcal{G}}{q}\subseteq{\mathcal{G}}$ by expanding around each entity $e$ in $T o p i c(q)$ . For each entity, we retrieve knowledge triples associated with its $D_{\mathrm{max}}$ -hop neighbors, thereby incorporating query-relevant and faithful KG information into $\mathcal{G}{q}$ . Through this process, we update $\mathcal{E}{q}$ with newly added intermediate nodes that serve as bridging pathways between the topic entities. The result subgraph, $\mathcal{G}{q}$ is defined as $(\mathcal{E}{q},\mathcal{R}{q},\mathcal{T}{q})$ , where $\mathcal{E}{q}$ encompasses $T o p i c(q)$ together with the set ${N_{\mathcal{G}}(e,D_{\mathrm{max}})\mid e\in T o p i c(q)}$ , effectively linking all relevant entities and their connective paths within the defined hop distance. To interact with KG, we utilize the pre-defined SPARQL queries as detailed in Appendix D.

子图检测。在识别主题实体后，PoG通过围绕$Topic(q)$中的每个实体$e$进行扩展，捕获诱导子图${\mathcal{G}}{q}\subseteq{\mathcal{G}}$。对于每个实体，我们检索其$D_{\mathrm{max}}$跳邻居关联的知识三元组，从而将查询相关且可靠的知识图谱信息整合到$\mathcal{G}{q}$中。在此过程中，我们用新增的中间节点更新$\mathcal{E}{q}$，这些节点充当主题实体间的桥接路径。最终子图$\mathcal{G}{q}$定义为$(\mathcal{E}{q},\mathcal{R}{q},\mathcal{T}{q})$，其中$\mathcal{E}{q}$包含$Topic(q)$及集合${N_{\mathcal{G}}(e,D_{\mathrm{max}})\mid e\in T o p i c(q)}$，有效连接定义跳数范围内的所有相关实体及其连通路径。为与知识图谱交互，我们使用附录D详述的预定义SPARQL查询。

Graph pruning. To efficiently manage information overhead and reduce computational cost, we implement graph pruning on the question subgraph $\mathcal{G}{q}$ using node and relation clustering alongside graph reduction techniques. As illustrated in Figure 3, node and relation clustering is achieved by compressing multiple nodes and their relations into supernodes, which aggregate information from the original entities and connections. For graph reduction, we employ bidirectional BFS to identify all paths connecting the topic entities. Based on these paths, we regenerate induced subgraphs that involve only the relevant connections, effectively excluding nodes and relations that lack strong relevance to the topic entities. Question analysis. To reduce hallucinations in LLMs, the question analysis phase is divided into two parts and executed within a single LLM call using an example-based prompt (shown in Appendix E). First, the complex question $q$ is decomposed into simpler questions based on the identified topic entities, each addressing their relationship to the potential answer. Addressing these simpler questions collectively guides the LLM to better answer the original query, thereby reducing hallucinations. Second, a LLM indicator is generated, encapsulating all topic entities and predicting the answer position within a single chain of thought derived from the original question. This indicator highlights the relationships and sequence among the entities and answer. Based on this, a predicted depth $D_{\mathrm{predict}}$ is calculated, defined as the maximum distance between the predicted answer and each topic entity. An example of question analysis is shown in Figure 3 with predicted depth 2.

图剪枝。为有效管理信息开销并降低计算成本，我们在问题子图$\mathcal{G}_{q}$上实施图剪枝，采用节点与关系聚类及图缩减技术。如图3所示，节点与关系聚类通过将多个节点及其关系压缩为超节点实现，这些超节点聚合了原始实体与连接的信息。对于图缩减，我们使用双向BFS算法识别连接主题实体的所有路径，并基于这些路径重新生成仅包含相关连接的诱导子图，从而有效排除与主题实体关联性弱的节点和关系。

问题分析。为减少大语言模型中的幻觉现象，问题分析阶段分为两部分，并通过基于示例的提示（见附录E）在单次大语言模型调用中完成。首先，复杂问题$q$根据已识别的主题实体被分解为若干简单问题，每个问题聚焦于其与潜在答案的关系。通过协同解决这些简单问题，引导大语言模型更准确地回答原始查询，从而降低幻觉。其次，生成大语言模型指示符，该指示符封装所有主题实体，并在原始问题衍生的单一思维链中预测答案位置。此指示符突出实体与答案间的关系及顺序，据此计算预测深度$D_{\mathrm{predict}}$（定义为预测答案与各主题实体间的最大距离）。图3展示了预测深度为2的问题分析示例。

4.2 Exploration

4.2 探索

As discussed in Section 1, identifying reasoning paths that encompass all topic entities is essential to derive accurate answers. These paths serve as interpret able chains of thought, providing both the answer and the inference steps leading to it, a feature we refer as inter pre t ability. To optimize the discovery of such paths efficiently and accurately, the exploration process is divided into three phases: topic entity path exploration, LLM supplement path exploration, and node expand exploration. After each phase, we perform path pruning and question answering. If a sufficient path is found, the process terminates; otherwise, it advances to the next phase to explore additional paths. Due to the space limitation, the pseudo-code of exploration section is shown in Appendix A.1.

如第1节所述，识别包含所有主题实体的推理路径对得出准确答案至关重要。这些路径作为可解释的思维链，既能提供答案又能展示推导步骤，我们称这一特性为可解释性 (interpretability)。为高效精准地优化此类路径的发现过程，探索流程被划分为三个阶段：主题实体路径探索、大语言模型补充路径探索和节点扩展探索。每个阶段结束后会执行路径剪枝和问答验证，若发现满足条件的路径则终止流程，否则进入下一阶段继续探索。由于篇幅限制，探索环节的伪代码详见附录A.1。

Topic entity path exploration. To reduce LLM usage and search space, PoG begins exploration from a predicted depth $D_{\mathrm{predict}}$ rather than the maximum depth. Using the question subgraph $\mathcal{G}{q}$ , topic entities $T o p i c(q)$ , LLM indicator $I_{\mathrm{LLM}}$ , and $D_{\mathrm{predict}}$ , PoG identifies reasoning paths containing all topic entities by iterative ly adjusting the exploration depth $D$ . Entities in $T o p i c(q)$ are ordered according to $I_{\mathrm{LLM}}$ to facili