MAFiD: Moving Average Equipped Fusion-in-Decoder for Question Answering over Tabular and Textual Data

MAFiD: 基于移动平均的融合解码器用于表格和文本数据的问答

Abstract

摘要

Transformer-based models for question answering (QA) over tables and texts confront a “long” hybrid sequence over tabular and textual elements, causing long-range reasoning problems. To handle long-range reasoning, we extensively employ a fusion-in-decoder (FiD) and exponential moving average (EMA), proposing a Moving Average Equipped Fusion-in-Decoder (MAFiD). With FiD as the backbone architecture, MAFiD combines various levels of reasoning: independent encoding of homogeneous data and single-row and multi-row heterogeneous reasoning, using a gated cross attention layer to effectively aggregate the three types of representations resulting from various reasonings. Experimental results on HybridQA indi-cate that MAFiD achieves state-of-the-art performance by increasing exact matching (EM) and F1 by 1.1 and 1.7, respectively, on the blind test set.

基于Transformer的表格和文本问答(QA)模型面临由表格和文本元素组成的"长"混合序列，导致长距离推理问题。为处理长距离推理，我们广泛采用解码器融合(FiD)和指数移动平均(EMA)，提出移动平均增强的解码器融合(MAFiD)。以FiD为骨干架构，MAFiD结合了多级推理：同质数据的独立编码、单行和多行异质推理，通过门控交叉注意力层有效聚合三种推理产生的表征。在HybridQA上的实验结果表明，MAFiD在盲测集上将精确匹配(EM)和F1分数分别提升1.1和1.7，实现了最先进性能。

1 Introduction

1 引言

While most studies have focused on text question answering (QA), where unimodal textual passages are provided as a source of evidence for an answer (Joshi et al., 2017; Yang et al., 2018; Rajpurkar et al., 2018; Welbl et al., 2018; Dua et al., 2019; Karpukhin et al., 2020; Zhu et al., 2021b; Pang et al., 2022), realistic questions often need to refer to “heterogeneous” evidences based on both tabular and textual contents to generate an answer, motivating researchers to address table-and-text QA (Chen et al., 2020; Wenhu Chen, 2021; Talmor et al., 2021; Zhu et al., 2021a; Nakamura et al., 2022).

虽然大多数研究都集中在文本问答（QA）领域（其中单模态文本段落被作为答案的证据来源）[Joshi et al., 2017; Yang et al., 2018; Rajpurkar et al., 2018; Welbl et al., 2018; Dua et al., 2019; Karpukhin et al., 2020; Zhu et al., 2021b; Pang et al., 2022]，但现实中的问题往往需要同时参考表格和文本内容构成的"异构"证据来生成答案，这促使研究者们开始关注表格与文本联合问答（Table-and-Text QA）[Chen et al., 2020; Wenhu Chen, 2021; Talmor et al., 2021; Zhu et al., 2021a; Nakamura et al., 2022]。

Among the various tasks for table-and-text QA, we address the multi-hop table-and-text QA described in HybridQA (Chen et al., 2020), which is a large-scale table-and-text QA dataset focusing on the multi-hop reasoning across tabular and textual contents to extract an answer.

在众多表格与文本问答任务中，我们重点解决HybridQA (Chen et al., 2020) 中描述的多跳表格与文本问答。该数据集专注于跨表格和文本内容进行多跳推理以提取答案，规模庞大。

However, a table usually contains a nontrival number of rows and relevant passages; thus linearization of all relevant heterogeneous contents easily exceeds the maximum length limit for transformers, thereby causing long range reasoning problems.

然而，表格通常包含大量行和相关段落；将所有相关异构内容线性化很容易超过Transformer的最大长度限制，从而导致长距离推理问题。

To address long range reasoning, we present a novel encoder-decoder model that deploys fusionin-decoder (FiD) (Izacard and Grave, 2021) and exponential moving average (EMA) (Ma et al., 2022), the Moving Average Equipped Fusion-in-Decoder (MAFiD). Armed with FiD as the backbone architecture, MAFiD combines various levels of reasoning:

为解决长程推理问题，我们提出了一种新型编码器-解码器模型MAFiD (Moving Average Equipped Fusion-in-Decoder)，该模型融合了解码器内融合 (FiD) (Izacard and Grave, 2021) 和指数移动平均 (EMA) (Ma et al., 2022) 技术。以FiD作为主干架构，MAFiD实现了多层级推理能力的结合：

• Independent encoding of homogeneous data, which independently encodes tabular and textual contents separately for each row, without being fused in the encoder step. Inherited from FiD, the resulting encoded representations are jointly fused in the decoder, which significantly reduces the computational time required for self-attention, thereby allowing us to use a longer sequence as an input for the encoder.

• 同质数据的独立编码，即对每行的表格和文本内容分别进行独立编码，在编码器阶段不进行融合。继承自FiD (Fusion-in-Decoder) ，生成的编码表示在解码器中联合融合，这显著减少了自注意力机制所需的计算时间，从而允许我们使用更长的序列作为编码器的输入。

• Single-row heterogeneous reasoning (also referred to as single-row reasoning), which performs in-depth interaction between tabular and textual contents per row; it first concatenates the tabular and textual representations for each row and then applies the “self-attention” layer over the concatenated sequence. Thus, single-row heterogeneous reasoning is performed in a restricted manner only on heterogeneous contents within a specific row.

• 单行异构推理 (single-row reasoning)，即对每行的表格和文本内容进行深度交互；它首先将每行的表格和文本表示拼接起来，然后在拼接后的序列上应用“自注意力 (self-attention)”层。因此，单行异构推理仅以受限方式在特定行内的异构内容上执行。

• Multi-row heterogeneous reasoning (also referred to as multi-row reasoning), which performs light interaction across tabular and textual contents of “multiple” rows based on the EMA layer; it concatenates the heterogeneous contents of all rows in a table to obtain a “long” hybrid sequence and then applies the EMA layer over the resulting long sequence to produce aggregated representation. To process a long sequence more efficiently, we further propose a low-dimensional EMA, which additionally performs a dimensionality reduction and reconstruction.

• 多行异构推理 (multi-row reasoning)，基于EMA层对"多"行表格和文本内容进行轻量交互；它将表中所有行的异构内容拼接成一个"长"混合序列，然后对结果长序列应用EMA层以生成聚合表示。为更高效处理长序列，我们进一步提出低维EMA，额外执行降维和重构操作。

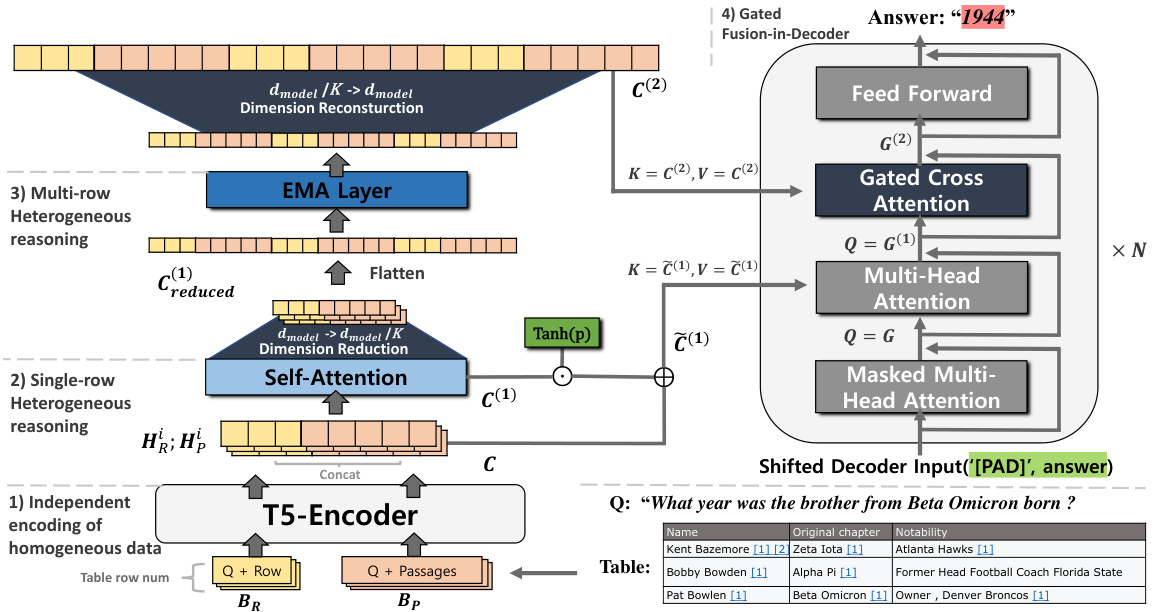
Figure 1: The overall neural architecture of the proposed MAFiD: 1) Independent encoding applies T5’s encoder on the tabular and textual blocks in $i$ -th row, separately (i.e., $b_{R}^{i}\in B_{R}$ and $b_{P}^{i}\in B_{P}$ ) and the resulting contextual representations are concatenated to obtain the $i$ -th row’s heterogeneous representation, $C_{i}$ (Eq. (1)). 2) Single-row reasoning performs the row-specific cross-modal interaction by applying the single-head attention over $C_{i}$ to generate $C_{i}^{(1)}$ (Eq. (2)). 3) Multi-row reasoning preforms the between-row cross-modal interaction by applying the low-dimensional EMA over the long hybrid sequence $C^{(1)}$ (Eq. (3)) to produce the $C_{i}^{(2)}$ (Eq. (4)). 4) The gated FiD aggregates all types of representations of $_C$ (Eq. (4)), $C^{(1)}$ , and $C^{(2)}$ using the gated cross-attention layer to finally yield the decoder’s contextual representation $G^{(2)}$ (Eq. (5)) which is fed to generate an output token.

图 1: 提出的MAFiD整体神经架构：1) 独立编码阶段，分别对第$i$行中的表格块和文本块(即$b_{R}^{i}\in B_{R}$和$b_{P}^{i}\in B_{P}$)应用T5编码器，并将得到的上下文表示拼接形成该行的异构表示$C_{i}$(公式(1))；2) 单行推理阶段，通过对$C_{i}$应用单头注意力机制实现行内跨模态交互，生成$C_{i}^{(1)}$(公式(2))；3) 多行推理阶段，通过对长混合序列$C^{(1)}$应用低维EMA(公式(3))实现行间跨模态交互，生成$C_{i}^{(2)}$(公式(4))；4) 门控FiD阶段，通过门控交叉注意力层聚合$_C$(公式(4))、$C^{(1)}$和$C^{(2)}$的所有表示类型，最终生成解码器的上下文表示$G^{(2)}$(公式(5))用于输出Token的生成。

In the decoder, we further propose the use of a gated cross-attention layer to effectively aggregates the aforementioned three representations resulting from various reasoning, motivated by the work of (Alayrac et al., 2022).

在解码器中，我们进一步提出使用门控交叉注意力层来有效聚合上述三种由不同推理产生的表征，这一设计灵感来自 (Alayrac et al., 2022) 的工作。

Our contributions are summarized as follows: 1) We propose MAFiD, which augments FiD with EMA and the gated cross-attention layer, thus effectively combining various types of reasoning. 2) We propose a low-dimensional EMA to efficiently process long sequences for table-and-text QA. 3) The proposed MAFiD achieves state-of-the-art performance on the HybridQA dataset.

我们的贡献总结如下：1) 我们提出了MAFiD，通过指数移动平均(EMA)和门控交叉注意力层增强FiD，从而有效结合多种推理类型。2) 我们提出了一种低维EMA方法，可高效处理表格-文本问答中的长序列。3) 所提出的MAFiD在HybridQA数据集上实现了最先进的性能。

2 Related Works

2 相关工作

Recently, many datasets such as HybridQA (Chen et al., 2020), OTT-QA (Wenhu Chen, 2021), MultiModalQA (Talmor et al., 2021), HybriD i a logue (Nakamura et al., 2022), and TAT-QA (Zhu et al.,

近期，出现了许多数据集，如 HybridQA (Chen et al., 2020)、OTT-QA (Wenhu Chen, 2021)、MultiModalQA (Talmor et al., 2021)、HybridDialogue (Nakamura et al., 2022) 和 TAT-QA (Zhu et al.,

2021a) have been presented for table-and-text QA. Various works on table-and-text QA have enhanced “pre training” to strengthen the cross-modal matching and numerical reasoning, by learning on tables and texts jointly (Herzig et al., 2020; Yin et al., 2020) and exclusively on tables (Iida et al., 2021).

2021a) 已针对表格与文本问答任务提出多种方法。众多关于表格与文本问答的研究通过联合学习表格与文本 (Herzig et al., 2020; Yin et al., 2020) 或专门学习表格 (Iida et al., 2021) 来增强"预训练 (pre training)"，从而强化跨模态匹配和数值推理能力。

To handle the long range reasoning on table-andtext QA, early works employed “efficient” transformers based on sparse attention with selective attention masks, such as the LongFormer (Beltagy et al., 2020) in the work of (Huang et al., 2022) and ETC (Ainslie et al., 2020) in the work of (Wenhu Chen, 2021). MATE (Eisen schlo s et al., 2021b) uses structure-based sparse attention that attends to either rows or columns in a given table. Recently, truncation-based approaches have been employed in MITQA (Kumar et al., 2021) where the passage filter module is additionally applied such that only the filtered passages are used as textual contents of a table’s row.

为处理表格与文本问答中的长程推理，早期研究采用了基于稀疏注意力与选择性注意力掩码的"高效"Transformer变体，例如(Huang et al., 2022)工作中使用的LongFormer (Beltagy et al., 2020)和(Wenhu Chen, 2021)研究中的ETC (Ainslie et al., 2020)。MATE (Eisen schlo s et al., 2021b)采用基于结构的稀疏注意力机制，仅关注给定表格的行或列。近期，MITQA (Kumar et al., 2021)采用了截断方法，额外引入段落过滤模块，仅将筛选后的段落作为表格行的文本内容。

Compared to these existing approaches, which rather limitedly reduce the computational cost in the encoder part, MAFiD significantly lightens the encoder part by minimizing the interaction between different rows and instead fuses the encoded representations in the decoder part under the framework of FiD. Equipped with the low-dimensional EMA,

与这些现有方法相比，它们仅有限地降低了编码器部分的计算成本，而MAFiD通过最小化不同行之间的交互，显著减轻了编码器部分的负担，并在FiD框架下将编码表示融合到解码器部分。结合低维EMA技术，

MAFiD only performs the “shallow” interaction across rows, thus mostly maintaining the efficiency of the interaction-less encoder.

MAFiD仅执行行间的"浅层"交互，因此基本保持了无交互编码器的高效性。

3 Moving Average Equipped Fusion-in-Decoder

3 配备移动平均的融合解码器 (Fusion-in-Decoder)

Figure 1 shows the overall neural architecture of the proposed MAFiD model, which combines three types of representation. Here, we present the details of the MAFiD components.

图 1: 展示了所提出的MAFiD模型的整体神经网络架构，该架构结合了三种类型的表征。下面我们将详细介绍MAFiD的各个组件。

3.1 Problem Definition

3.1 问题定义

Suppose that $\boldsymbol{B}{R}$ and $\boldsymbol{B_{P}}$ are a set of tabular and textual blocks in a given table, where $b_{R}^{i}\in B_{R}$ indicates the tabular block for the $i$ -th row (i.e., a list of its cells), $b_{P}^{i}\in B_{P}$ indicates the textual block for the $i$ -th row (i.e., a set of its linked passages), and $L=|\boldsymbol{B_{R}}|=|\boldsymbol{B_{P}}|$ is the number of rows in a table. Given question $q$ , the goal is to generate a correct answer by considering $\boldsymbol{B}{R}$ and $\boldsymbol{B{P}}$ as heterogeneous evidence.

假设 $\boldsymbol{B}{R}$ 和 $\boldsymbol{B_{P}}$ 是给定表格中的一组表格块和文本块，其中 $b_{R}^{i}\in B_{R}$ 表示第 $i$ 行的表格块 (即其单元格列表)， $b_{P}^{i}\in B_{P}$ 表示第 $i$ 行的文本块 (即其关联段落集合)，且 $L=|\boldsymbol{B_{R}}|=|\boldsymbol{B_{P}}|$ 是表格的行数。给定问题 $q$，目标是通过将 $\boldsymbol{B}{R}$ 和 $\boldsymbol{B{P}}$ 视为异构证据来生成正确答案。

3.2 Independent Encoding of Homogeneous Data: the Basic Encoder for FiD

3.2 同质数据的独立编码：FiD的基础编码器

Following the independent encoding in FiD (Izacard and Grave, 2021), independent encoding linearizes tabular and textual blocks into a sequence independently and concatenates each of them with $q$ as follows:

在FiD (Izacard和Grave, 2021)的独立编码方法中，独立编码将表格和文本块分别线性化为序列，并将它们各自与$q$按如下方式拼接：

3.3 Multi-row Heterogeneous Reasoning by the Low-dimensional EMA

3.3 基于低维EMA的多行异构推理

In multi-row reasoning, we first concatenate the contextual representations of all tabular and textual blocks as follows:

在多行推理中，我们首先将所有表格和文本块的上下文表示按以下方式连接起来：

$$
C^{(1)}=[C_{1}^{(1)};\cdot\cdot\cdot;C_{L}^{(1)}]
$$

$$
C^{(1)}=[C_{1}^{(1)};\cdot\cdot\cdot;C_{L}^{(1)}]
$$

where $C^{(1)}\quad\in\quad\mathbb{R}^{N\times d_{m o d e l}}$ , provided $N\quad=$ $\begin{array}{r}{\sum_{i}\left(|\mathsf{r o w}^{i}|+|\mathsf{p s g}^{i}|\right)}\end{array}$ for notational convenience.

其中 $C^{(1)}\quad\in\quad\mathbb{R}^{N\times d_{m o d e l}}$ ，给定 $N\quad=$ $\begin{array}{r}{\sum_{i}\left(|\mathsf{r o w}^{i}|+|\mathsf{p s g}^{i}|\right)}\end{array}$ 以简化表示。

We then adopt the low-dimensional EMA as a variant of EMA using dimensionality reduction and reconstruction based on linear layers as follows:

我们随后采用低维EMA (Exponential Moving Average) 作为EMA的一种变体，通过基于线性层的降维和重构实现如下：

$$
\begin{array}{r c l}{{C_{r e d u c e d}^{(1)}}}&{{=}}&{{\mathsf{L i n e a r}\left(C^{(1)}\right)}}\ {{}}&{{}}&{{}}\ {{C_{r e d u c e d}^{(2)}}}&{{=}}&{{\mathsf{E M A}\left(C_{r e d u c e d}^{(1)}\right)}}\ {{}}&{{}}&{{}}\ {{C^{(2)}}}&{{=}}&{{\mathsf{L i n e a r}\left(C_{r e d u c e d}^{(2)}\right)}}\end{array}
$$

$$
\begin{array}{r c l}{{C_{r e d u c e d}^{(1)}}}&{{=}}&{{\mathsf{L i n e a r}\left(C^{(1)}\right)}}\ {{}}&{{}}&{{}}\ {{C_{r e d u c e d}^{(2)}}}&{{=}}&{{\mathsf{E M A}\left(C_{r e d u c e d}^{(1)}\right)}}\ {{}}&{{}}&{{}}\ {{C^{(2)}}}&{{=}}&{{\mathsf{L i n e a r}\left(C_{r e d u c e d}^{(2)}\right)}}\end{array}
$$

where $C^{(2)} \in~\mathbb{R}^{\dot{N}\times\dot{d}{m o d e l}}$ $C_{r e d u c e d}^{(1)},C_{r e d u c e d}^{(2)}\in\mathbb{R}^{N\times d_{m o d e l}/K},$ , re Ldi un cee adr is a∈ lineRar l×aymeord,e land, EMA is the damped EMA of (Ma et al., 2022) defined in Appendix E.

其中 $C^{(2)} \in~\mathbb{R}^{\dot{N}\times\dot{d}{m o d e l}}$ ， $C_{r e d u c e d}^{(1)},C_{r e d u c e d}^{(2)}\in\mathbb{R}^{N\times d_{m o d e l}/K},$ ，re Ldi un cee adr 是线性层，而 EMA 是 (Ma et al., 2022) 中定义的阻尼 EMA（见附录 E）。

3.4 Gated Fusion-in-Decoder

3.4 门控解码器融合 (Gated Fusion-in-Decoder)

In the decoder, we first concatenate the row-wise representations of independent encoding before feeding them to the FiD as follows:

在解码器中，我们首先将独立编码的行级表征拼接起来，然后按以下方式输入到FiD中：

$$
\mathsf{r o w}^{i}=[q;~[\mathsf{S E P}];b_{R}^{i}],\mathsf{p s g}^{i}=[q;[\mathsf{S E P}];~b_{P}^{i}]
$$

$$
\mathsf{r o w}^{i}=[q;~[\mathsf{S E P}];~b_{R}^{i}],\mathsf{p s g}^{i}=[q;[\mathsf{S E P}];~b_{P}^{i}]
$$

where $|\times|$ is the length of sequence $\times$ and $d_{m o d e l}$ is the dimensionality of the encoder of T5.

其中 $|\times|$ 是序列 $\times$ 的长度，$d_{m o d e l}$ 是 T5 编码器的维度。

3.2.1 Single-row Heterogeneous Reasoning

3.2.1 单行异构推理

In single-row reasoning, we perform an in-depth interaction between tabular and textual blocks for each row, $b_{R}^{i}$ and $b_{P}^{i}$ , using self-attention as follows:

在单行推理中，我们对每一行的表格块$b_{R}^{i}$和文本块$b_{P}^{i}$进行深度交互，具体采用如下自注意力机制：

$$
C_{i}^{(1)}={\mathsf{S H A}}(C_{i},C_{i},C_{i})
$$

$$
C_{i}^{(1)}={\mathsf{S H A}}(C_{i},C_{i},C_{i})
$$

where $C_{i}^{(1)}~\in \mathbb{R}^{(|\mathsf{r o w}^{i}|+|\mathsf{p s g}^{i}|)\times d_{m o d e l}}$ and SHA is the single-head attention defined in Eq. (6) in Appendix D.

其中 $C_{i}^{(1)}~\in \mathbb{R}^{(|\mathsf{r o w}^{i}|+|\mathsf{p s g}^{i}|)\times d_{m o d e l}}$ ，SHA 是附录 D 中式 (6) 定义的单头注意力 (single-head attention)。

$$
C=[C_{1};\cdot\cdot\cdot;C_{L}]
$$

$$
C=[C_{1};\cdot\cdot\cdot;C_{L}]
$$

In the decoder, we aggregate all representations of $C$ (Eq. (1) and (4)), $C^{(1)}$ (Eq. (2) and (3)) $C^{(2)}$ (Eq. (4) using a gating mechanism similar to that of (Alayrac et al., 2022) as follows:

在解码器中，我们使用类似于 (Alayrac et al., 2022) 的门控机制聚合 $C$ (式 (1) 和 (4))、$C^{(1)}$ (式 (2) 和 (3)) 以及 $C^{(2)}$ (式 (4)) 的所有表示，具体如下：

$$
\begin{array}{r l}&{\tilde{C}^{(1)}=C+\operatorname{tanh}(p)\odot C^{(1)}}\ &{G^{(1)}=\mathsf{M H A}(G,\tilde{C}^{(1)},\tilde{C}^{(1)})}\ &{G^{(2)}=G^{(1)}+}\ &{\operatorname{tanh}(q)\odot\mathsf{M H A}(G^{(1)},C^{(2)},C^{(2)})}\end{array}
$$

$$
\begin{array}{r l}&{\tilde{C}^{(1)}=C+\operatorname{tanh}(p)\odot C^{(1)}}\ &{G^{(1)}=\mathsf{M H A}(G,\tilde{C}^{(1)},\tilde{C}^{(1)})}\ &{G^{(2)}=G^{(1)}+}\ &{\operatorname{tanh}(q)\odot\mathsf{M H A}(G^{(1)},C^{(2)},C^{(2)})}\end{array}
$$

where $G\in\mathbb{R}^{|N^{(d e c)}|\times d_{m o d e l}}$ is the output of the masked multi-head attention in the decoder part, $|N^{(d e c)}|$ is the sequence length of the decoder input, $\operatorname{tanh}(\cdot)$ is the tanh function, $p$ and $q$ are learnable parameters, and $G^{(1)},G^{(2)}\in\mathbb{R}^{|N^{(d e c)}|\times d_{m o d e l}}$ .

其中 $G\in\mathbb{R}^{|N^{(d e c)}|\times d_{m o d e l}}$ 是解码器部分掩码多头注意力 (masked multi-head attention) 的输出，$|N^{(d e c)}|$ 是解码器输入的序列长度，$\operatorname{tanh}(\cdot)$ 是双曲正切函数，$p$ 和 $q$ 是可学习参数，且 $G^{(1)},G^{(2)}\in\mathbb{R}^{|N^{(d e c)}|\times d_{m o d e l}}$。

4 Experiments

4 实验

4.1 Experimental Setup

4.1 实验设置

The details of the implementation and experiment setup is presented in Appendix A.

实现细节和实验设置详见附录A。

Table 1: Comparison results on the dev and blind test dataset in HybridQA. The best is bolded text.

表 1: HybridQA 开发集和盲测集对比结果。最优值以粗体标出。

	表			段落			总计
	开发集		测试集		开发集		测试集		开发集
	EM	F1	EM	F1	EM	F1	EM	F1