Subspace Clustering for Action Recognition with Covariance Representations and Temporal Pruning
基于协方差表示与时序剪枝的子空间聚类动作识别方法
Abstract—This paper tackles the problem of human action recognition, defined as classifying which action is displayed in a trimmed sequence, from skeletal data. Albeit state-of-the-art approaches designed for this application are all supervised, in this paper we pursue a more challenging direction: Solving the problem with unsupervised learning. To this end, we propose a novel subspace clustering method, which exploits covariance matrix to enhance the action’s disc rim inability and a timestamp pruning approach that allow us to better handle the temporal dimension of the data. Through a broad experimental validation, we show that our computational pipeline surpasses existing unsupervised approaches but also can result in favorable performances as compared to supervised methods.
摘要—本文研究了基于骨骼数据的人类动作识别问题,该问题定义为对修剪后序列中显示的动作进行分类。尽管目前针对该应用的最先进方法均为监督式学习,但本文探索了一个更具挑战性的方向:通过无监督学习解决该问题。为此,我们提出了一种新颖的子空间聚类方法,该方法利用协方差矩阵增强动作的判别性,并提出时间戳剪枝方法以更好地处理数据的时间维度。通过大量实验验证,我们表明该计算流程不仅超越了现有无监督方法,与监督方法相比也能取得优越性能。
I. INTRODUCTION
I. 引言
Human Action Recognition (HAR) plays a crucial role in computer vision since related to a broad spectrum of artificial intelligence applications (such as video surveillance, humanmachine interaction or self-driving cars to name a few [1]). Given a trimmed sequence, in which a single action or activity is assumed to be present, the final goal of HAR is to correctly classifying it. Although significant progresses have been made in the last years, accurate action recognition in videos is still a challenging task because of the complexity of the visual data e.g., due to varying camera viewpoints, occlusions and abrupt changes in lighting conditions. As an all-in-one solution to these problems, skeleton-based HAR is surely the paradigm to embrace, considering also its beneficial characteristics of being privacy-preserving. In skeleton-based HAR, action/activity sequences are represented through the multi-dimensional time series of joints, located at the intersection of skeletal bones, whose position is tracked in time typically through either motion capture systems or depth sensors.
人体动作识别 (HAR) 在计算机视觉中扮演着关键角色,因其与广泛的人工智能应用相关 (如视频监控、人机交互或自动驾驶汽车等 [1])。给定一个经过裁剪的序列 (假设其中包含单个动作或活动),HAR 的最终目标是正确分类该动作。尽管近年来取得了显著进展,但由于视觉数据的复杂性 (如摄像机视角变化、遮挡和光照条件突变等因素),视频中的精确动作识别仍是一项具有挑战性的任务。作为这些问题的全方位解决方案,基于骨架的 HAR 无疑是值得采用的范式,尤其考虑到其隐私保护的有利特性。在基于骨架的 HAR 中,动作/活动序列通过关节的多维时间序列来表征,这些关节位于骨骼交汇处,其位置通常通过动作捕捉系统或深度传感器进行跟踪。
Recently, skeleton-based HAR has undergone to the same paradigm shift which was registered in other fields of pattern recognition: Hand-crafted data encodings fed into engineered class if i ers have been replaced by data-driven feature representation with an end-to-end classification pipeline [2]. Yet, both paradigms leverage a fully supervised learning approach to accomplish the task. Each sequence is in fact assumed to be (manually) annotated by the action/activity it involves. Other than being time-consuming and prone to human errors, sequence annotations compromise the s cal ability to the big data regime. As an alternative, unsupervised approaches seem attractive since they offer an advantage regarding computational and methodological burden, as well as providing an interesting application towards more novel real-life scenarios.
最近,基于骨架的人体动作识别(HAR)经历了与其他模式识别领域相同的范式转变:手工设计的数据编码输入工程化分类器的传统方式,已被端到端分类流程中数据驱动的特征表示所取代[2]。然而,这两种范式都采用完全监督的学习方法来完成识别任务。每个动作序列实际上都需要(人工)标注其包含的行为类别。这种序列标注不仅耗时且容易出错,还会限制大数据场景下的可扩展性。相比之下,无监督方法因其在计算和方法论负担上的优势,以及对更贴近现实场景的创新应用潜力而显得颇具吸引力。
In this work, we consider subspace clustering to tackle HAR in a fully unsupervised paradigm. Subspace clustering was first introduced in Computer Vision to segment dynamic moving objects [3], [4] and it postulates that high-dimensional data (here, skeletal joints) can be represented as a union of subspaces, each of them having a much lower dimensionality (i.e. low-rank) and simpler geometrical structure. Each subspace usually corresponds to a class (here, to an action or an activity). The key idea in subspace clustering is to learn encodings that are then used to construct an affinity matrix from which the data can be clustered together according to the modelled (dis)-similarities between samples [5]. Although, this is usually achieved through a self-expressive model in which each data point is expressed as a linear combination of the remaining ones, additional constraints, such as sparsity, were also adopted [6].
在本工作中,我们采用子空间聚类方法以完全无监督范式处理人体动作识别(HAR)。子空间聚类最初由计算机视觉领域提出,用于分割动态运动物体 [3][4],其核心假设是高维数据(此处指骨骼关节点)可表示为若干子空间的并集,每个子空间具有更低维度(即低秩性)和更简单的几何结构。通常每个子空间对应一个类别(此处指动作或行为)。子空间聚类的关键思想是学习编码,进而构建亲和矩阵,通过建模样本间(非)相似性实现数据聚类 [5]。尽管这通常通过自表达模型实现(即每个数据点表示为其余点的线性组合),但也会引入稀疏性等额外约束 [6]。
Despite the fact that subspace clustering has become a powerful technique for problems such as face clustering or digit recognition, its applicability to the problems like skeletonbased HAR was only explored by a limited number of works [7], [8], [9]. This is due to many operative limitations including how to handle the temporal dimensions, the inherent noise present in the skeletal data and the related computational issues.
尽管子空间聚类已成为面部聚类或数字识别等问题的强大技术,但其在基于骨架的动作识别(HAR)等任务中的应用仅被少数研究探索[7]、[8]、[9]。这源于诸多操作限制,包括如何处理时间维度、骨架数据固有的噪声以及相关的计算问题。
In this paper, we propose two alternative computational strategies to help and support subspace clustering methods in handling the temporal dimensions of action sequences. On the one hand, we encode the raw skeletal trajectories using a covariance representation, which has been shown to be effective for the solving HAR problems [10]. Additionally, we propose a computational strategy to prune the instantaneous body poses – termed timestamps hereafter – whose temporal aggregation produces an action sequence. As the result of temporal pruning, we are able to select the most representative timestamps, which are exploited to compress the original action sequence to a fixed duration. Consequently, this temporal pruning can be adopted as a successful pre-processing step to accommodate for the usage of a subspace clustering method for HAR.
本文提出两种替代性计算策略,以帮助和支持子空间聚类方法处理动作序列的时间维度。一方面,我们使用协方差表示对原始骨骼轨迹进行编码,该方法已被证明能有效解决HAR问题[10]。此外,我们提出一种计算策略来修剪瞬时身体姿态(后文称为时间戳),其时间聚合会产生动作序列。通过时间修剪,我们能够选择最具代表性的时间戳,从而将原始动作序列压缩至固定时长。因此,这种时间修剪可作为成功的预处理步骤,以适应子空间聚类方法在HAR中的应用。
Through a comprehensive experimental analysis, we validate the impact on HAR of covariance representations and temporal pruning. Eventually, we also demonstrate their degree of complementary to the extent that the performance of a fully unsupervised recognition pipeline can be enhanced. Surprisingly, the overall performance of the proposed unsupervised approaches can almost fill the gap with state of the art supervised methods.
通过全面的实验分析,我们验证了协方差表示和时间剪枝对HAR(人类活动识别)的影响。最终,我们还证明了它们的互补程度,使得完全无监督识别流程的性能得以提升。令人惊讶的是,所提出的无监督方法的整体性能几乎可以填补与最先进监督方法之间的差距。
Overall, we deem that our experimental findings would help practitioners in re-thinking the way HAR is approached, raising the attention in the desirable shift towards more agile unsupervised learning frameworks.
总体而言,我们认为实验发现将帮助从业者重新思考人类活动识别(HAR)的实现路径,推动业界关注向更灵活的无监督学习框架转型这一理想方向。
II. RELATED WORK
II. 相关工作
In this Section, we have reviewed the action recognition methods relying on covariance representation, various subspace clustering algorithms as well as the state-of-the-art supervised approaches for skeleton-based HAR.
在本节中,我们回顾了基于协方差表示的动作识别方法、多种子空间聚类算法,以及基于骨架的人体动作识别 (HAR) 的最先进监督方法。
Subspace clustering. Subspace clustering has been a popular computational framework in the machine learning community as well as the computer vision and image processing communities (e.g., image representation and compression [11], image segmentation [12], motion segmentation [13]). It aims at finding subspaces each tting a group of data points and then performing clustering based on these subspaces [5].
子空间聚类。子空间聚类已成为机器学习领域以及计算机视觉和图像处理领域(如图像表示与压缩[11]、图像分割[12]、运动分割[13])广泛采用的计算框架。其核心目标是寻找能拟合各组数据点的子空间,并基于这些子空间进行聚类[5]。
There has been a lot of work presenting many different subspace clustering methods. Most of the subspace clustering methods learns an afnity matrix and then apply spec- tral clustering, e.g., low-rank representation [14], [15]. Selfrepresentation based subspace clustering methods reconstructs a sample from a linear combination of other samples [6], [14], [16], [17] and they have proven their effectiveness for high-dimensional data. Sparse subspace clustering integrates l1-norm regular iz ation, which mostly results in improvements in the clustering performances [6]. The temporal Laplacian regular iz ation was proposed in [8] and also adopted in other works e.g., [9] to better model kinematic data for the sake of action detection and segmentation.
已有大量研究提出了多种不同的子空间聚类方法。大多数子空间聚类方法通过学习一个亲和矩阵(affinity matrix)后应用谱聚类(spectral clustering),例如低秩表示(low-rank representation) [14][15]。基于自表示(self-representation)的子空间聚类方法通过其他样本的线性组合来重构样本[6][14][16][17],这些方法已被证明对高维数据具有良好效果。稀疏子空间聚类引入了l1范数正则化(l1-norm regularization),通常能提升聚类性能[6]。文献[8]提出了时序拉普拉斯正则化(temporal Laplacian regularization),该技术也被其他研究如[9]采用,以更好地建模运动学数据从而实现动作检测与分割。
Most existing subspace clustering methods relies on handcrafted representations. Instead, more powerful representations can be learned through deep learning, which effectively cluster data samples from non-linear subspaces [18]. Deep subspace clustering methods apply embedding and clustering jointly, typically with an auto encoder network e.g., in [18], [19]. This results in an optimal embedding subspace for clustering, which is more effective compared to conventional clustering methods. Deep adversarial subspace clustering methods, on the other hand, learn more effective sample representations using deep learning while exploiting adversarial learning to supervise and, thus, progressively improve the performance of subspace clustering. This is done by using a subspace clustering generator and a quality-verifying disc rim in at or which are adversarial ly learned against each other.
大多数现有的子空间聚类方法依赖于手工设计的表示。相比之下,通过深度学习可以学习到更强大的表示,从而有效聚类来自非线性子空间的数据样本[18]。深度子空间聚类方法联合应用嵌入和聚类,通常采用自编码器网络(如[18][19]),由此产生用于聚类的最优嵌入子空间,相比传统聚类方法更为有效。而深度对抗子空间聚类方法则利用深度学习学习更有效的样本表示,同时通过对抗学习进行监督,从而逐步提升子空间聚类的性能。这是通过使用一个子空间聚类生成器和一个质量验证判别器实现的,二者以对抗方式相互学习。
Covariance encoding for HAR. The idea of encoding 3Dskeleton dynamics within a single hand-crafted kernel representation has been proposed often in HAR. For instances, it has been shown that Hankel matrices can efficiently model action dynamics when used in tandem with a Hidden Markov Model [20] or a Riemannian nearest neighbours with class-prototypes [21]. Lie group [22] and associated Lie algebra [23] can be effective in modelling human actions and activities by means of roto-translations. Likewise, generic deforming bodies can be efficiently modelled over variations of Stiefel manifolds [24]. Surely, within the class of kernel representations, a major role is played by a specific symmetric and positive definite (SPD) operator: Covariance matrices (COV). Originally envisaged for image classification and detection [25], COV is an effective representation for skeleton-based HAR since capable of modelling second-order statistics. It was used in tandem of a variety of classification pipelines, such as a temporal pyramid [26] or max-margin approaches [27], [28]. Formal studies have tried to enhance the capability of such operators in modelling non-linear correlations among the data [29], [30]. Kernel approximation was recently investigated in order to speed up the computational pipeline and ensure s cal ability towards the big data regime [31].
HAR中的协方差编码。在HAR领域,将3D骨骼动态编码为单一手工设计核表示的想法已被多次提出。例如,研究表明汉克尔矩阵与隐马尔可夫模型[20]或基于类原型的黎曼最近邻[21]结合时,能有效建模动作动态。李群[22]及其对应的李代数[23]可通过旋转平移有效建模人类动作行为。类似地,通用变形体可在Stiefel流形变体[24]上高效建模。在核表示类别中,协方差矩阵(COV)作为特定的对称正定(SPD)算子占据重要地位。该算子最初用于图像分类与检测[25],因其能建模二阶统计量而成为基于骨骼的HAR有效表示,常与多种分类流程结合使用,如时序金字塔[26]或最大间隔方法[27][28]。形式化研究尝试增强此类算子在建模数据非线性相关性方面的能力[29][30]。近期还研究了核近似方法以加速计算流程并确保面向大数据场景的可扩展性[31]。
Even though prior work focused on the effectiveness of covariance representations applied to supervised learning pipelines, we instead demonstrate its capabilities for unsupervised learning.
尽管先前的研究主要关注协方差表示在监督学习流程中的有效性,但我们展示了其在无监督学习中的能力。
State-of-the-art supervised approaches for skeleton-based HAR. The current mainstream paradigm in skeleton-based HAR is the possibility of learning a feature representation from the data itself, in tandem with the final action classifier. As one of the seminal works in this direction, a hierarchy of bidirectional recurrent neural networks is used by [32] to represent in a bottom-up fashion all the structural relationships between body parts (torso, legs, arms) in the human skeleton. Long-Short Term Memory (LSTM) models can be proficiently applied to 3D action recognition [33], [34]. Throughout the years, LSTM networks have been modified to better accommodate for the task: for instance, by applying a novel mixed-norm regular iz ation term and dropout [35] or recurring to attention mechanisms [36]. Alternatively, joint trajectories are casted into colored images by producing the so-called distance maps [37], [38], [39]. By means of them, usual convolutional neural networks such as AlexNet, despite originally proposed for image classification, can be adapted to HAR [37], [38]. Surely, the most active and recent direction of research leverages the possibility of encoding the whole human skeleton as a graph, furthermore processing it through a graph-convolutional neural network [40], [41].
基于骨架的动作识别(HAR)的先进监督方法。当前骨架动作识别的主流范式是从数据本身学习特征表示,并与最终动作分类器协同工作。作为该领域的开创性研究之一,[32] 采用分层双向循环神经网络(RNN),以自底向上的方式表征人体骨架中身体部位(躯干、腿部、手臂)之间的所有结构关系。长短期记忆(LSTM)模型可有效应用于3D动作识别 [33][34]。多年来,LSTM网络经过改进以更好地适应此任务:例如通过引入新型混合范数正则化项和dropout [35],或采用注意力机制 [36]。另一种方法是将关节轨迹转化为彩色图像,生成所谓的距离图 [37][38][39]。借助这些图像,常规卷积神经网络(如AlexNet)尽管最初是为图像分类设计,也能适配动作识别任务 [37][38]。近年来最活跃的研究方向是将整个人体骨架编码为图结构,进而通过图卷积神经网络进行处理 [40][41]。
All such approaches can fully exploit the benefits of an end-to-end and data-driven training since relying on a fully supervised regime in which the sequences to be classified are annotated. Differently, in this paper we pursue the more challenging direction of adopting an unsupervised strategy, relying on subspace clustering. Similarly to what done by [42] for auto-encoders and [43] for generative adversarial networks, the goal of this paper is to propose new computational architectures and evaluate their effectiveness in comparison with supervised learning paradigms.
所有这些方法都能充分利用端到端和数据驱动训练的优势,因为它们依赖于对需分类序列进行标注的全监督机制。与之不同,本文采用更具挑战性的无监督策略方向,基于子空间聚类方法。与[42]在自编码器和[43]在生成对抗网络中的做法类似,本文目标是提出新的计算架构,并通过与监督学习范式的对比来评估其有效性。
III. METHODOLOGY
III. 方法论
In this Section, we present our computational pipeline which is based on covariance representations and timestamps pruning. In order to properly ablate on the relative importance of them, we will consider the following computational variants of the pipeline:
在本节中,我们介绍了基于协方差表示和时间戳剪枝的计算流程。为了准确评估它们的相对重要性,我们将考虑该流程的以下计算变体:
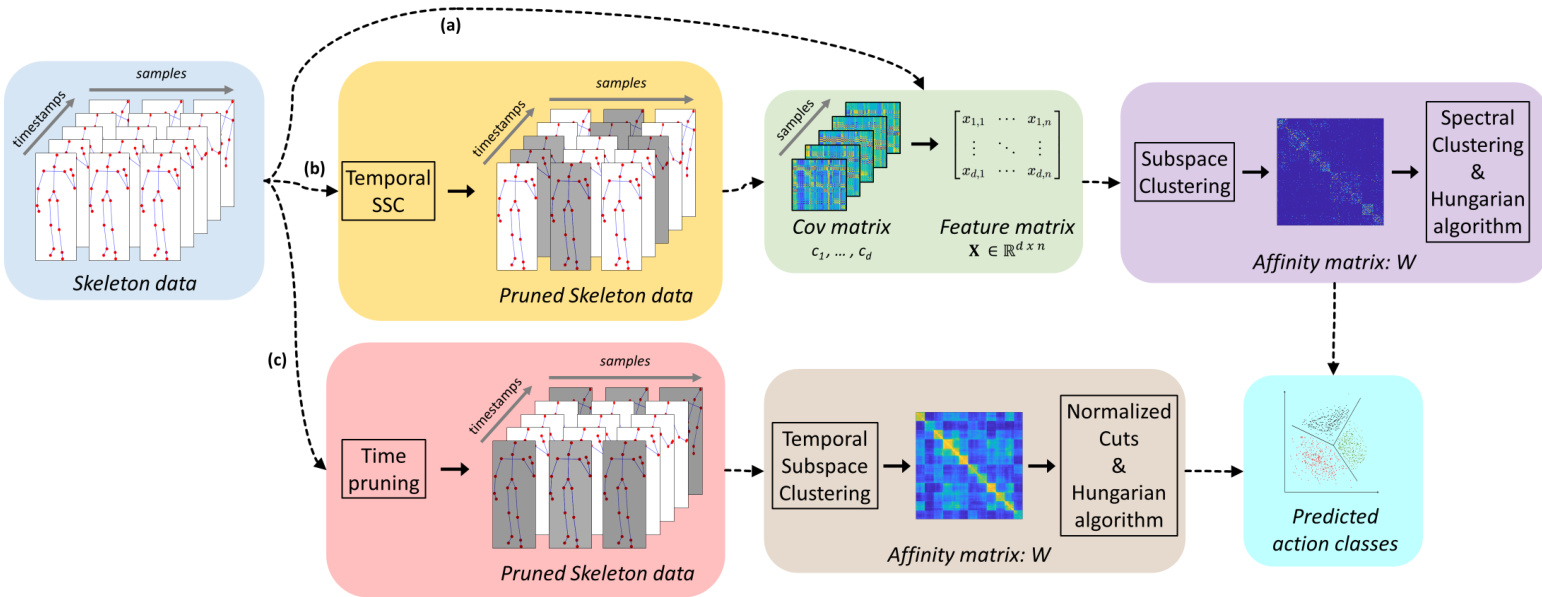
Fig. 1. Pipeline of the proposed unsupervised methods for HAR: (a) A covariance descriptor is applied to each sample. Given the obtained covariance matrix is square and symmetrical, we take only the upper (can be also lower) triangular part including the diagonal and flatten it. This results in a new matrix $(X)$ having size samples $\times$ f eatures. Following that, any subspace clustering technique can be applied to obtain an affinity graph matrix W. Then, spectral clustering is applied using W to obtain cluster labels and the Hungarian algorithm finds the matching between the cluster labels (predicted action classes) and the ground-truth labels. (b) The skeletal data of each sample is temporally pruned using temporal SSC and then the pruned data is processed as in (a). (c) Each sample is pruned by using various strategies. Afterwards, temporal subspace clustering is applied to obtain an affinity graph matrix W. The normalized cuts is applied to obtain cluster labels and the Hungarian algorithm matches the cluster labels with the ground-truth labels.
图 1: 提出的无监督HAR方法流程:(a) 对每个样本应用协方差描述符。由于获得的协方差矩阵是方形且对称的,我们仅取包含对角线的上三角部分(也可取下三角部分)并展平。这将生成一个新矩阵$(X)$,其尺寸为样本数×特征数。随后可应用任何子空间聚类技术来获得亲和力图矩阵W。接着使用W进行谱聚类以获得聚类标签,并通过匈牙利算法找到聚类标签(预测动作类别)与真实标签之间的匹配。(b) 使用时序SSC对每个样本的骨骼数据进行时序剪枝,然后按(a)步骤处理剪枝后的数据。(c) 通过多种策略对每个样本进行剪枝。随后应用时序子空间聚类获得亲和力图矩阵W,使用归一化割获得聚类标签,并通过匈牙利算法将聚类标签与真实标签匹配。
• Section III-A and Figure 1(a). We apply covariance encoding as the descriptor, whose result is given as an input to a subspace clustering method that is based on the self-expressiveness property of data. • Section III-B and Figure 1(b). We apply the proposed temporal pruning approach (namely temporal SSC) as a pre-processing stage while the rest of the pipeline follows the previous setting. • Section III-C and Figure 1(c). We use the Temporal Subspace Clustering to show the effectiveness of a dictionarybased subspace clustering for temporal series of data when applying temporal regular iz ation on top of the (optional) encoding through covariance.
- 第 III-A 节和图 1(a)。我们采用协方差编码 (covariance encoding) 作为描述符,其结果作为输入传递给基于数据自表达特性的子空间聚类方法。
- 第 III-B 节和图 1(b)。我们在流程中应用提出的时序剪枝方法(即时序 SSC)作为预处理阶段,其余部分沿用之前的设置。
- 第 III-C 节和图 1(c)。我们使用时序子空间聚类 (Temporal Subspace Clustering) 来展示基于字典的子空间聚类在时序数据上的有效性,该方法在(可选的)协方差编码基础上应用了时序正则化。
A. Subspace clustering methods based on self-expressiveness property and covariance represent a tio
A. 基于自表达属性和协方差表示的子空间聚类方法
The usage of a covariance representation as the data encoder and the subspace clustering for solving HAR can be described as follows.
使用协方差表示作为数据编码器并结合子空间聚类来解决HAR问题的方法可描述如下。
Data encoding through covariance representation. Through either a motion capture system or a depth sensor, an action is represented as the collection in time of $K$ joints 3D positions $\mathbf{p}{1}(t),\ldots,\mathbf{p}_{K}(t)$ . By using $\mathbf p(t)$ to denote the column vector iz ation of all such 3D positions for a fixed timestamp, we represent an action sequence as the covariance matrix
通过协方差表示进行数据编码。通过动作捕捉系统或深度传感器,一个动作被表示为随时间变化的 $K$ 个关节3D位置 $\mathbf{p}{1}(t),\ldots,\mathbf{p}_{K}(t)$ 的集合。使用 $\mathbf p(t)$ 表示固定时间戳下所有3D位置的列向量化后,我们将动作序列表示为协方差矩阵
$$
{\mathbf{A}}={\frac{1}{T}}\sum_{t}({\mathbf{p}}(t)-{\boldsymbol{\mu}})({\mathbf{p}}(t)-{\boldsymbol{\mu}})^{\top},
$$
$$
{\mathbf{A}}={\frac{1}{T}}\sum_{t}({\mathbf{p}}(t)-{\boldsymbol{\mu}})({\mathbf{p}}(t)-{\boldsymbol{\mu}})^{\top},
$$
where $T$ denotes the number of timestamps and $\pmb{\mu}$ is the temporal average of $\mathbf p(t)$ .
其中,$T$ 表示时间戳数量,$\pmb{\mu}$ 是 $\mathbf p(t)$ 的时间平均值。
We then vectorize the covariance matrix through a flattening operation which exploit the property of $\pmb{\Lambda}$ in being symmetrical. That is, $\pmb{\Lambda}=\dot{\pmb{\Lambda}}^{\top}$ . Therefore, when flattening, we extract the diagonal elements of $\pmb{\Lambda}$ (which are $\Lambda_{i i}$ ) and the uppertriangular ones (that is, $\Lambda_{i j},j>i)$ . The lower triangular part can be ignored since it is equal to upper triangular one. Such flattening operation casts the $3K\times3K$ matrix $\pmb{\Lambda}$ into a $3K\cdot(3K-1)/2$ column vector. The flattened covariance representation is used as one data point, which then given to the subspace clustering algorithm as the input.
我们通过展平操作对协方差矩阵进行向量化,利用 $\pmb{\Lambda}$ 的对称特性(即 $\pmb{\Lambda}=\dot{\pmb{\Lambda}}^{\top}$)。在展平过程中,我们提取 $\pmb{\Lambda}$ 的对角线元素(即 $\Lambda_{i i}$)和上三角部分元素(即 $\Lambda_{i j},j>i$),由于下三角部分与上三角部分相等,可忽略不计。此操作将 $3K\times3K$ 的矩阵 $\pmb{\Lambda}$ 转换为 $3K\cdot(3K-1)/2$ 维的列向量。展平后的协方差表示作为一个数据点,作为子空间聚类算法的输入。
Subspace Clustering. Let us consider a collection of $D$ - dimensional data-points $\mathbf{x}{1},\ldots,\mathbf{x}{N}$ . Subspace clustering [5] attempts to cluster $\mathbf{x}{1},\ldots,\mathbf{x}_{N}$ into groups (termed subspaces) which share common geometrical relationships as the wellknown self-expressiveness property. The problem can be formalised as finding a $N\times N$ matrix $\mathbf{C}$ of coefficients such that
子空间聚类。考虑一组 $D$ 维数据点 $\mathbf{x}{1},\ldots,\mathbf{x}{N}$,子空间聚类 [5] 试图将 $\mathbf{x}{1},\ldots,\mathbf{x}_{N}$ 划分为若干组(称为子空间),这些组共享相同的几何关系,即著名的自表达性。该问题可形式化为寻找一个 $N\times N$ 的系数矩阵 $\mathbf{C}$,使得
$$
\mathbf{X}=\mathbf{X}\mathbf{C}{\mathrm{subjectto~diag}}(\mathbf{C})=0,
$$
$$
\mathbf{X}=\mathbf{X}\mathbf{C}{\mathrm{subjectto~diag}}(\mathbf{C})=0,
$$
where $\mathbf{X}$ is the $D\times N$ matrix, which stacks by columns the data points $\mathbf{x}_{j}$ . The constraint $\mathrm{diag}(\mathbf{C})=0$ avoids the trivial solution corresponding to $\mathbf{C}$ being the identity matrix. Ultimately, the geometrical relationship that we are interested in modelling is a linear relationship in which each data-point can be described as a linear combination. As a consequence of that, the subspaces are linear in turn. The constraint $\mathrm{diag}(\mathbf{C})=0$ is fundamental to avoid the trivial (and useless) solution xj = xj. Specifically, the self-expressiveness property (2) attempts to estimate each data points as a linear combination of different data points. This allows to capture the geometrical interdependencies among the data points themselves.
其中 $\mathbf{X}$ 是 $D\times N$ 矩阵,由数据点 $\mathbf{x}_{j}$ 按列堆叠而成。约束条件 $\mathrm{diag}(\mathbf{C})=0$ 避免了 $\mathbf{C}$ 为单位矩阵的平凡解。本质上,我们试图建模的几何关系是一种线性关系,其中每个数据点都可以表示为线性组合。因此,子空间本身也是线性的。约束条件 $\mathrm{diag}(\mathbf{C})=0$ 对于避免 xj = xj 这种平凡(且无用)解至关重要。具体而言,自表达特性 (2) 试图将每个数据点估计为不同数据点的线性组合,从而捕捉数据点之间的几何关联性。
An important aspect regarding subspace clustering is the way the matrix $\mathbf{C}$ is obtained. A number of works proposed to solve this problem through optimization [44], [6], [45], [46], [47], [18] and different strategies have been adopted to constraint the solution. In subspace segmentation via Least Squares Regression (SS-LSR) [44], a Frobenius norm is introduced to promote a $L^{2}$ penalty, obtaining
关于子空间聚类的一个重要方面是矩阵$\mathbf{C}$的获取方式。许多研究提出通过优化方法解决这一问题[44]、[6]、[45]、[46]、[47]、[18],并采用了不同策略来约束解。在基于最小二乘回归的子空间分割(SS-LSR)[44]中,引入Frobenius范数以促进$L^{2}$惩罚,从而获得
$$
\mathrm{min}|{\bf C}|_{F}\mathrm{ subject to~}{\bf X}={\bf X}{\bf C},\mathrm{diag}({\bf C})=0.
$$
$$
\mathrm{min}|{\bf C}|_{F}\mathrm{ subject to~}{\bf X}={\bf X}{\bf C},\mathrm{diag}({\bf C})=0.
$$
Another popular manner of constraining the coefficient matrix $\mathbf{C}$ is to impose sparsity [6], [47], [18]. As in the Sparse Subspace clustering via Alternating Direction Method of Multipliers (SSC-ADMM) [6], the problem formulation is framed as
另一种限制系数矩阵 $\mathbf{C}$ 流行的方式是施加稀疏性约束 [6], [47], [18]。例如在基于交替方向乘子法的稀疏子空间聚类 (SSC-ADMM) [6] 中,该问题的表述被构建为
$$
\operatorname*{min}|\mathbf{C}|_{1}{\mathrm{ subject to~}}\mathbf{X}=\mathbf{X}\mathbf{C},\operatorname{diag}(\mathbf{C})=0,
$$
$$
\operatorname*{min}|\mathbf{C}|_{1}{\mathrm{ subject to~}}\mathbf{X}=\mathbf{X}\mathbf{C},\operatorname{diag}(\mathbf{C})=0,
$$
while using the alternating direction method of multipliers (ADMM) algorithm to foster convergence by solving a stack of easier sub-problems. As an alternative to ADMM, Sparse Subspace Clustering by Orthogonal Matching Pursuit (SSCOMP) [46] approaches a similar problem with a different optimization technique.
在使用交替方向乘子法 (ADMM) 算法通过求解一系列更简单的子问题来促进收敛的同时,作为ADMM的替代方案,基于正交匹配追踪的稀疏子空间聚类 (SSCOMP) [46] 采用不同的优化技术处理了类似问题。
The previous formalism in Eq. (4) was extended in the Deep Subspace Clustering Networks (DSC-Nets) [18] by having the hidden layer of an auto encoder implementing either equation (3) or equation (4). The Elastic Net (EnSC) [47] approach uses a convex combination of $L^{2}$ and $L^{1}$ constraint on $\mathbf{C}$ to increase performance, while also boosting the s cal ability due to the usage of oracle sets to better pre-condition the solution. Dense subspace clustering (EDSC) [45] approaches the problem by attempting to apply the self-expressiveness loss on a dictionary which is used to describe the data, while also taking into account outliers.
先前在方程(4)中的形式化方法在深度子空间聚类网络(DSC-Nets)[18]中得到了扩展,通过让自动编码器的隐藏层实现方程(3)或方程(4)。弹性网络(EnSC)[47]方法在$\mathbf{C}$上使用$L^{2}$和$L^{1}$约束的凸组合来提高性能,同时由于使用预言集来更好地预处理解,也提升了可扩展性。密集子空间聚类(EDSC)[45]通过尝试在用于描述数据的字典上应用自表达损失来解决问题,同时还考虑了异常值。
Once the matrix of coefficient $\mathbf{C}$ is found, an affinity graph matrix W is built by setting the weights on the edges between the nodes through $\mathbf{W}=\mathbf{C}+\mathbf{C}^{\top}$ . Spectral clustering is later applied to W to obtain the clustering labels, by assigning each of the $N$ datapoint $\mathbf{x}_{j}$ into its corresponding subspace. The final step is therefore apply Hungarian algorithm to compare and map subspace labels into actual class labels [5].
找到系数矩阵 $\mathbf{C}$ 后,通过 $\mathbf{W}=\mathbf{C}+\mathbf{C}^{\top}$ 构建节点间边权重的亲和力图矩阵 W。随后对 W 应用谱聚类 (spectral clustering) 获得聚类标签,将每个 $\mathbf{x}_{j}$ 数据点划分到对应子空间。最后通过匈牙利算法 (Hungarian algorithm) 比较子空间标签并映射到实际类别标签 [5]。
B. Temporal pruning via Sparse Subspace Clustering (temporalSSC)
B. 基于稀疏子空间聚类的时间剪枝 (temporalSSC)
In addition to utilize subspace clustering as an unsupervised learning method to perform action recognition, in this paper, we also exploit such family of techniques to solve another task: temporal pruning. That refers to utilizing subspace clustering on the raw joint coordinates $\mathbf p(t)$ . Here, different from the previous section, each data point to be clustered is not an action sequence, but a single data point of an action (Figure 1(b)). In other words, rather than applying subspace clustering to group action sequences, we exploit subspace clustering to the group skeletal poses at a given timestamp. Our assumption is that the processed skeleton data might contain similar or even redundant poses over time. To address this, we apply temporal pruning, which potentially captures the similarities over time with respect to the kinematic execution.
除了利用子空间聚类作为无监督学习方法进行动作识别外,本文还采用此类技术解决另一项任务:时序剪枝。该任务指对原始关节坐标$\mathbf p(t)$进行子空间聚类。与前一节不同,此处待聚类的每个数据点不是动作序列,而是动作的单个数据点(图1(b))。换言之,我们并非通过子空间聚类对动作序列分组,而是对给定时间戳的骨骼姿态进行分组。我们的假设是:处理后的骨骼数据可能随时间推移包含相似甚至冗余的姿态。为此,我们使用时序剪枝技术,该技术能捕捉运动学执行过程中随时间推移产生的相似性。
A relevant parameter for temporal pruning is the number of subspaces $\phi$ , which corresponds to the length of the new pruned skeleton data, which was set based on the following strategies.
时间剪枝的一个相关参数是子空间数量$\phi$,它对应剪枝后新骨架数据的长度,该参数基于以下策略设定。
- min $\phi$ : the temporal length of the entire dataset is fixed to be equal to the shortest time duration across all the sequences in the skeletal dataset, this is done by using the random permutation of each sample timestamps.
- 最小化 $\phi$:将整个数据集的时间长度固定为骨骼数据集中所有序列的最短时长,通过对每个样本时间戳进行随机排列实现。
- min temporal SSC: subspace clustering method SSC ADMM is used to get $\phi$ equal to the shortest time duration across all the sequences in the skeletal dataset. 3) percentage temporal SSC: the temporal length of each sample of the dataset is determined by selecting a percentage value for $\phi$ (in our experiments we chose to keep the $75%$ , $50%$ or $25%$ of the sample temporal length) and applying temporal SSC.
- 最小时间子空间聚类 (min temporal SSC): 使用子空间聚类方法 SSC ADMM 得到 $\phi$ 等于骨骼数据集中所有序列的最短时间长度。
- 百分比时间子空间聚类 (percentage temporal SSC): 通过为 $\phi$ 选择一个百分比值 (实验中我们保留样本时间长度的 $75%$、$50%$ 或 $25%$) 并应用时间子空间聚类来确定数据集中每个样本的时间长度。
- threshold temporal SSC: the temporal length of each sample of the dataset is determined by selecting a percentage value for $\phi$ (in our experiments we chose to keep the $75%$ , $50%$ or $25%$ of the sample temporal length), which is used as a threshold value for temporal SSC. If a certain sample of the dataset has a temporal length superior to $\phi$ , temporal SSC is therefore applied to match this threshold value.
- 阈值时序SSC:通过为$\phi$选择一个百分比值(在我们的实验中选择了保留样本时序长度的$75%$、$50%$或$25%$)来确定数据集中每个样本的时序长度,该值用作时序SSC的阈值。如果数据集的某个样本时序长度超过$\phi$,则应用时序SSC以匹配该阈值。
Once the temporal pruning is performed, the covariance represent ation is applied to the new data and subspace clustering is adopted as in Section III-A.
执行时间剪枝后,将协方差表示应用于新数据,并采用第III-A节所述的子空间聚类方法。
C. Temporal Subspace Clustering based on dictionary and temporal Laplacian Regular iz ation
C. 基于字典和时间拉普拉斯正则化的时间子空间聚类
Even though subspace clustering methods explained in Section III-A build the affinity matrix W by exploiting the self-expressiveness property of data, they do not explicitly take into account the temporal dimension of time-series data while building the model adopted for HAR. As a solution, temporal regular iz ation was proposed by Temporal Subspace Clustering (TSC) [8]. Precisely, given a dictionary $\mathbf{D}\in\mathbb{R}^{d\times r}$ and a coding matrix $\mathbf{Z}\in\mathbb{R}^{r\times n}$ , a collection of data points $\mathbf{X}\in\mathbb{R}^{d\times n}$ can be approximately represented as
尽管第 III-A 节中介绍的子空间聚类方法通过利用数据的自表达特性构建了亲和矩阵 W,但在构建用于人类活动识别 (HAR) 的模型时,这些方法并未显式考虑时间序列数据的时间维度。针对这一问题,时序子空间聚类 (TSC) [8] 提出了时序正则化解决方案。具体而言,给定字典 $\mathbf{D}\in\mathbb{R}^{d\times r}$ 和编码矩阵 $\mathbf{Z}\in\mathbb{R}^{r\times n}$,数据点集合 $\mathbf{X}\in\mathbb{R}^{d\times n}$ 可近似表示为
$$
\mathbf{X}\approx\mathbf{D}\mathbf{Z},
$$
$$
\mathbf{X}\approx\mathbf{D}\mathbf{Z},
$$
where each data point is encoded using a Least Squares regression, and a temporal Laplacian regular iz ation $L(Z)$ function encourages the encoding of the sequential relationships in time-series data. This can done by minimising
其中每个数据点都通过最小二乘回归进行编码,而时间拉普拉斯正则化函数 $L(Z)$ 用于增强时间序列数据中顺序关系的编码。这可以通过最小化来实现
$$
\begin{array}{r l}&{\underset{{\bf z},{\bf D}}{\operatorname*{min}} |{\bf X}-{\bf D}{\bf Z}|{F}^{2} +~\lambda_{1}|{\bf Z}|{F}^{2} +~\lambda_{2}L({\bf Z}),}\ &{\quad\quad\quad s u b j e c t t o~{\bf Z}\ge0,~{\bf D}\ge0,}\end{array}
$$
$$
\begin{array}{r l}&{\underset{{\bf z},{\bf D}}{\operatorname*{min}} |{\bf X}-{\bf D}{\bf Z}| {F}^{2} +~\lambda_{1}|{\bf Z}| {F}^{2} +~\lambda_{2}L({\bf Z}),}\ &{\quad\quad\quad s u b j e c t t o~{\bf Z}\ge0,~{\bf D}\ge0,}\end{array}
$$
by using the ADMM algorithm to encourage convergence by solving a stack of easier sub-problems. Different from Section III-A, the affinity graph matrix W is given by the coding matrix $\mathbf{Z}$ by using $\begin{array}{r}{\mathbf{\dot{W}}(i,j)=\frac{z_{i}^{\top}z_{j}}{\vert\vert z_{i}\vert\vert_{2}\vert\vert z_{j}\vert\vert_{2}}}\end{array}$ = ||zi|z|i2 |z|zjj||2 , since the withincluster samples (for example the sequential neighbors of a time-series datapoint) are always highly correlated to each other [48], [49]. As final steps of the pipeline, the standard Normalized Cuts [50] and Hungarian algorithms determine the clustering labels necessary for evaluation against the groundtruth.
通过使用ADMM算法解决一系列更简单的子问题来促进收敛。与第III-A节不同,亲和图矩阵W由编码矩阵$\mathbf{Z}$给出,使用$\begin{array}{r}{\mathbf{\dot{W}}(i,j)=\frac{z_{i}^{\top}z_{j}}{\vert\vert z_{i}\vert\vert_{2}\vert\vert z_{j}\vert\vert_{2}}}\end{array}$ = ||zi|z|i2 |z|zjj||2,因为簇内样本(例如时间序列数据点的连续邻居)总是彼此高度相关[48][49]。作为流程的最后步骤,标准归一化割[50]和匈牙利算法确定了与真实值进行评估所需的聚类标签。
In Sections III-A and III-B, a (flattened) covariance represent ation was adopted to encode the actions’ kinematics. Computationally, this operation was able to cast an action sequence with a variable temporal duration into a fixed-size embedding which was passed in input to subspace clustering methods based on the self-expressiven
