MemSum: Extractive Sum mari z ation of Long Documents Using Multi-Step Episodic Markov Decision Processes

MemSum：基于多步情景马尔可夫决策过程的长文档抽取式摘要

Nianlong Gu

Nianlong Gu

Abstract

摘要

We introduce MemSum (Multi-step Episodic Markov decision process extractive SUMmarizer), a reinforcement-learning-based extractive summarizer enriched at each step with information on the current extraction history. When MemSum iterative ly selects sentences into the summary, it considers a broad information set that would intuitively also be used by humans in this task: 1) the text content of the sentence, 2) the global text context of the rest of the document, and 3) the extraction history consisting of the set of sentences that have already been extracted. With a lightweight architecture, MemSum obtains state-of-the-art testset performance (ROUGE) in summarizing long documents taken from PubMed, arXiv, and GovReport. Ablation studies demonstrate the importance of local, global, and history information. A human evaluation confirms the high quality and low redundancy of the generated summaries, stemming from MemSum’s awareness of extraction history.

我们介绍了MemSum (多步情景马尔可夫决策过程抽取式摘要器)，这是一种基于强化学习的抽取式摘要器，在每一步都融入了当前抽取历史的信息。当MemSum迭代地将句子选入摘要时，它会考虑人类在该任务中也会直观使用的一组广泛信息：1) 句子的文本内容，2) 文档其余部分的全局文本上下文，以及3) 由已抽取句子组成的抽取历史。凭借轻量级架构，MemSum在PubMed、arXiv和GovReport的长文档摘要任务中取得了最先进的测试集性能(ROUGE)。消融研究证明了局部信息、全局信息和历史信息的重要性。人工评估证实了生成摘要的高质量和低冗余性，这源于MemSum对抽取历史的感知。

1 Introduction

1 引言

Automatic text sum mari z ation is the task of auto mati call y summarizing a long document into a relatively short text while preserving most of the information (Tas and Kiyani, 2007). Text summarization methods can be categorized into abstract ive and extractive sum mari z ation (Gambhir and Gupta, 2017; Nenkova and McKeown, 2012). Given a document $d$ consisting of an ordered list of $N$ sentences, extractive sum mari z ation aims to pick up $M$ $(M{\ll}N)$ sentences as the summary of the document. The extracted summaries tend to be both grammatically and semantically more reliable than abstract ive summaries $\mathrm{{Liu^{*}}}$ et al., 2018; Liu and Lapata, $2019\mathrm{a}$ ; Luo et al., 2019; Liao et al., 2020), as they are directly selected from the source text.

自动文本摘要 (Automatic text summarization) 的任务是将长文档自动概括为较短的文本，同时保留大部分信息 (Tas and Kiyani, 2007)。文本摘要方法可分为生成式 (abstractive) 和抽取式 (extractive) 摘要 (Gambhir and Gupta, 2017; Nenkova and McKeown, 2012)。给定一个由 $N$ 个有序句子组成的文档 $d$，抽取式摘要旨在选取 $M$ $(M{\ll}N)$ 个句子作为文档摘要。由于直接从源文本中选取，抽取式摘要通常在语法和语义上比生成式摘要更可靠 (Liu* et al., 2018; Liu and Lapata, 2019a; Luo et al., 2019; Liao et al., 2020)。

Extractive sum mari z ation is usually modeled as two sequential phases (Zhou et al., 2018): 1) sentence scoring and 2) sentence selection. In the sentence scoring phase, an affinity score is computed for each sentence by neural networks such as bidirectional RNNs (Dong et al., 2018; Narayan et al., 2018; Luo et al., 2019; Xiao and Carenini, 2019) or BERT (Zhang et al., 2019; Liu and Lapata, 2019b). In the sentence selection phase, sentences are selected by either i) predicting a label (1 or 0) for each sentence based on its score, and selecting sentences with label 1 (Zhang et al., 2019; Liu and Lapata, 2019b; Xiao and Carenini, 2019), or ii) ranking sentences based on their scores and selecting the top $K$ sentences as the summary (Narayan et al., 2018), or iii) sequentially sampling sentences without replacement, where the normalized scores of the remaining sentences are used as sampling likelihoods (Dong et al., 2018; Luo et al., 2019).

抽取式摘要通常被建模为两个连续阶段 (Zhou et al., 2018)：1) 句子评分 2) 句子选择。在句子评分阶段，通过双向RNN (Dong et al., 2018; Narayan et al., 2018; Luo et al., 2019; Xiao and Carenini, 2019) 或BERT (Zhang et al., 2019; Liu and Lapata, 2019b) 等神经网络计算每个句子的亲和度分数。在句子选择阶段，采用以下三种方式之一：i) 根据分数预测每个句子的标签 (1或0)，选择标签为1的句子 (Zhang et al., 2019; Liu and Lapata, 2019b; Xiao and Carenini, 2019)；ii) 按分数排序并选择前 $K$ 个句子作为摘要 (Narayan et al., 2018)；iii) 无放回地顺序采样句子，其中剩余句子的归一化分数作为采样概率 (Dong et al., 2018; Luo et al., 2019)。

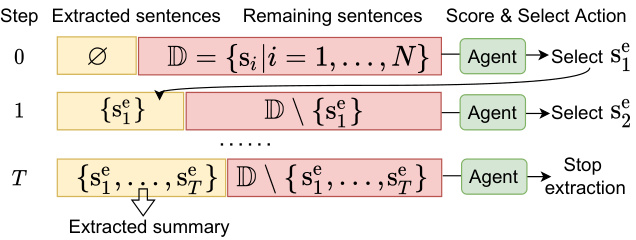
Figure 1: We modeled extractive sum mari z ation as a multi-step iterative process of scoring and selecting sentences. $\mathbf{S}{i}$ represents the $i_{\mathrm{th}}$ sentence in the document $\mathbb{D}$ .

图 1: 我们将抽取式摘要建模为一个多步迭代的评分和选择句子过程。$\mathbf{S}{i}$ 表示文档 $\mathbb{D}$ 中的第 $i_{\mathrm{th}}$ 个句子。

In these approaches, sentence scores are generally not updated based on the current partial summary of previously selected sentences, indicating a lack of knowledge of extraction history. We deem extractive summarize rs that are not aware of the extraction history to be susceptible to redundancy in a document, because they will repeatedly add sentences with high scores to a summary, regardless of whether similar sentences have been selected before. And, redundancy leads to performance decreases evaluated by ROUGE F1.

在这些方法中，句子分数通常不会根据当前已选句子的部分摘要进行更新，这表明缺乏对提取历史的了解。我们认为不了解提取历史的抽取式摘要器容易受到文档冗余的影响，因为它们会反复将高分句子添加到摘要中，而不管之前是否已选择过类似句子。此外，冗余会导致ROUGE F1评估的性能下降。

In this paper, we propose to model extractive sum mari z ation as a multi-step episodic Markov

在本论文中，我们提出将抽取式摘要建模为一个多步情景马尔可夫过程

Decision Process (MDP). As shown in Figure 1, at each time step in an episode, we define a sentence state composed of three sub-states: 1) the local content of the sentence, 2) the global context of the sentence within the document, and 3) information on the extraction history, including the previously selected set of unordered sentences and the remaining sentences. At each time step, the policy network (agent) takes the current sentence state as input and produces scores used to select an action of either stopping the extraction process or selecting one of the remaining sentences into the candidate summary. Unlike one-step episodic MDP-based models (Narayan et al., 2018; Dong et al., 2018; Luo et al., 2019) that encode the state information only once at the beginning of the episode, in our multi-step policy, the agent updates at each time step the extraction history before selecting an action. Such a step-wise state-updating strategy enables the agent to consider the content of the partial summary when selecting a sentence.

决策过程 (MDP)。如图 1 所示，在每一幕的每个时间步，我们定义一个由三个子状态组成的句子状态：1) 句子的局部内容，2) 句子在文档中的全局上下文，以及 3) 提取历史信息，包括先前选择的无序句子集和剩余的句子。在每个时间步，策略网络 (agent) 将当前句子状态作为输入，并生成用于选择动作的分数，这些动作包括停止提取过程或将剩余句子之一选入候选摘要。与基于单幕 MDP 的模型 (Narayan et al., 2018; Dong et al., 2018; Luo et al., 2019) 不同，这些模型仅在幕开始时对状态信息进行一次编码，而在我们的多步策略中，智能体在选择动作之前会在每个时间步更新提取历史。这种逐步更新状态的策略使智能体在选择句子时能够考虑部分摘要的内容。

To efficiently encode local and global sentence states, we design an extraction agent based on LSTM networks (Hochreiter and Schmid huber, 1997). To encode the extraction history and to select actions, we use a reduced number of attention layers (Vaswani et al., 2017) of relatively low dimensionality. These choices enable our model to be easily trainable and to summarize long documents such as scientific papers (Cohan et al., 2018; Huang et al., 2021) or reports (Huang et al., 2021).

为高效编码局部和全局句子状态，我们设计了一个基于LSTM网络 (Hochreiter and Schmidhuber, 1997) 的提取智能体。为编码提取历史并选择操作，我们使用了维度相对较低的少量注意力层 (Vaswani et al., 2017)。这些设计使得我们的模型易于训练，并能处理科学论文 (Cohan et al., 2018; Huang et al., 2021) 或报告 (Huang et al., 2021) 等长文档的摘要任务。

The contributions of our work are as follows: 1) We propose to treat extractive sum mari z ation as a multi-step episodic MDP that is aware of the extraction history. 2) We show that extraction-history awareness allows our model to extract more compact summaries than models without history awareness and behave more robustly to redundancies in documents. 3) Our model outperforms both extractive and abstract ive sum mari z ation models on PubMed, arXiv (Cohan et al., 2018), and GovReport (Huang et al., 2021) datasets. 4) Finally, human evaluators rate the MemSum summaries to be of higher quality than those from a competitive approach, especially by virtue of lower redundancy 1.

我们工作的贡献如下：1) 提出将抽取式摘要视为一个感知抽取历史的多步片段式MDP (Markov Decision Process)。2) 证明抽取历史感知使模型能生成比无历史感知模型更紧凑的摘要，并对文档冗余表现出更强鲁棒性。3) 在PubMed、arXiv (Cohan et al., 2018) 和GovReport (Huang et al., 2021) 数据集上，我们的模型性能优于抽取式和生成式摘要模型。4) 人工评估表明MemSum生成的摘要质量优于竞争方法，尤其在降低冗余度方面表现突出[1]。

2 Related Work

2 相关工作

Extraction history awareness was previously considered in NeuSum (Zhou et al., 2018), where a

提取历史感知在NeuSum (Zhou et al., 2018) 中曾被考虑，其中

GRU encoded previously selected sentences into a hidden vector that then was used to update the scores of the remaining sentences to bias the next selection. NeuSum contains no stopping mechanism and therefore it can only extract a fixed number of sentences, which likely is sub-optimal. Also, the potential benefits of extraction history have not been quantified and so the idea remains unexplored to a large extent.

GRU将先前选定的句子编码为隐藏向量，随后该向量用于更新剩余句子的分数，从而影响下一次选择。NeuSum未设置停止机制，因此只能提取固定数量的句子，这可能并非最优方案。此外，提取历史记录的潜在优势尚未量化，该理念在很大程度上仍未被充分探索。

Recently, BERT-based extractors such as MatchSum (Zhong et al., 2020) achieved SOTA performance in extractive sum mari z ation of relatively short documents from the CNN/DM (Hermann et al., 2015) dataset. However, the quadratic computational and memory complexities (Huang et al., 2021) of such models limit their s cal ability for summarizing long documents with thousands of tokens, which is common for scientific papers and government reports. Although large pre-trained transformers with efficient attention (Huang et al., 2021) have been adapted for abstract ive summarization of long documents, we believe that extractive sum mari z ation is more faithful in general, which is why we chose an extractive approach.

近期，基于BERT的抽取式摘要模型（如MatchSum [20]）在CNN/DM数据集 [15] 的短文档摘要任务中取得了SOTA性能。然而，此类模型的二次方计算和内存复杂度 [21] 限制了其在处理长文档（如科学论文和政府报告中常见的数千token文本）时的扩展能力。尽管采用高效注意力机制的大型预训练Transformer [21] 已适配于长文档的生成式摘要任务，但我们认为抽取式摘要通常更具忠实性，因此选择了抽取式方法。

3 Model

3 模型

This section outlines the multi-step episodic MDP policy for extractive sum mari z ation.

本节概述了用于抽取式摘要的多步骤片段式MDP (Markov Decision Process) 策略。

3.1 Policy Gradient Methods

3.1 策略梯度方法

In an episodic task with a terminal state (i.e. end of summary), policy gradient methods aim to maximize the objective function ${\cal J}(\theta) =~\mathbb{E}{\pi_{\theta}}[R_{0}]$ , where the return $\begin{array}{r}{R_{t}=\sum_{k=t+1}^{T}r_{k}}\end{array}$ is the cumulative reward from time $t+1$ until the end of the episode when the summary is complete. In applications of RL to extractive sum mari z ation, the instantaneous reward $r_{t}$ is zero except at the end of the episode when the final reward $r$ is computed according to Equation (1), so $R_{t}\equiv R_{0}=r$ . The reward $r$ is usually expressed as (Dong et al., 2018):

在具有终止状态(即摘要结束)的片段式任务中，策略梯度方法旨在最大化目标函数 ${\cal J}(\theta) =~\mathbb{E}{\pi_{\theta}}[R_{0}]$ ，其中回报 $\begin{array}{r}{R_{t}=\sum_{k=t+1}^{T}r_{k}}\end{array}$ 表示从时间 $t+1$ 到片段结束(即摘要完成时)的累计奖励。在将强化学习应用于抽取式摘要的场景中，瞬时奖励 $r_{t}$ 除片段结束时根据公式(1)计算最终奖励 $r$ 外均为零，因此 $R_{t}\equiv R_{0}=r$ 。该奖励 $r$ 通常表示为(Dong et al., 2018):

$$
r=\frac{1}{3}({\mathrm{ROUGE}}-1_{f}+{\mathrm{ROUGE}}-2_{f}+{\mathrm{ROUGE}}-\mathrm{L}_{f})
$$

$$
r=\frac{1}{3}({\mathrm{ROUGE}}-1_{f}+{\mathrm{ROUGE}}-2_{f}+{\mathrm{ROUGE}}-\mathrm{L}_{f})
$$

According to the REINFORCE algorithm (Williams, 1992), the policy gradient is defined as:

根据REINFORCE算法 (Williams, 1992)，策略梯度定义为：

$$
\nabla J(\pmb\theta)=\mathbb{E}{\pi}[R_{t}\nabla\log\pi(A_{t}|S_{t},\pmb\theta)],
$$

$$
\nabla J(\pmb\theta)=\mathbb{E}{\pi}[R_{t}\nabla\log\pi(A_{t}|S_{t},\pmb\theta)],
$$

where $\pi(\boldsymbol{A}{t}|\boldsymbol{S}{t},\boldsymbol{\theta})$ denotes the likelihood that at time step $t$ the policy $\pi_{\theta}$ selects action $A_{t}$ given the

其中 $\pi(\boldsymbol{A}{t}|\boldsymbol{S}{t},\boldsymbol{\theta})$ 表示在时间步 $t$ 时策略 $\pi_{\theta}$ 在给定状态 $\boldsymbol{S}{t}$ 下选择动作 $\boldsymbol{A}_{t}$ 的概率。

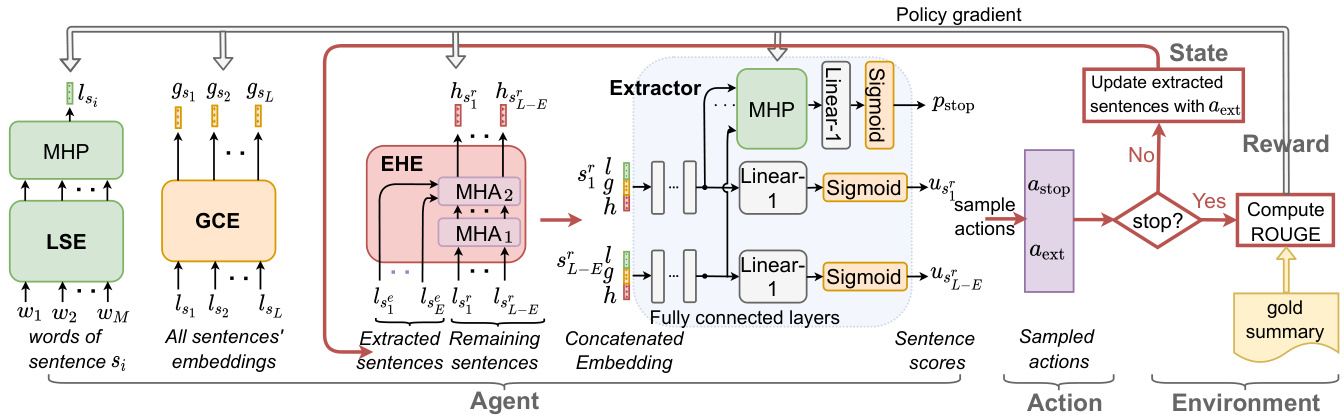
Figure 2: The architecture of our MemSum extractive summarizer with a multi-step episodic MDP policy. With the updating of the extraction-history embeddings $h$ at each time step $t$ , the scores $u$ of remaining sentences and the stopping probability $p_{\mathrm{stop}}$ are updated as well.

图 2: 我们MemSum抽取式摘要器的架构，采用多步情景MDP策略。随着每个时间步$t$提取历史嵌入$h$的更新，剩余句子的得分$u$和停止概率$p_{\mathrm{stop}}$也会相应更新。

state $S_{t}$ . With $\alpha$ as the learning rate, the parameter update rule is (Sutton and Barto, 2018):

状态 $S_{t}$。以 $\alpha$ 作为学习率，参数更新规则为 (Sutton and Barto, 2018):

$$
\begin{array}{r}{\pmb{\theta}{t+1}\leftarrow\pmb{\theta}{t}+\alpha R_{t}\nabla\log\pi(A_{t}|S_{t},\pmb{\theta}_{t}),}\end{array}
$$

$$
\begin{array}{r}{\pmb{\theta}{t+1}\leftarrow\pmb{\theta}{t}+\alpha R_{t}\nabla\log\pi(A_{t}|S_{t},\pmb{\theta}_{t}),}\end{array}
$$

3.2 Multi-step Episodic MDP Policy

3.2 多步情景MDP策略

where $I_{t}$ denotes the index set of remaining sentences at time step $t$ . If the agent does not stop, it first computes a score $u_{j}$ for each remaining sentence and samples a sentence $s_{a_{t}}$ according to the probability distribution of normalized scores. When the agent stops the extraction, no sentence is selected and the conditional likelihood $\scriptstyle p(a_{t}|{\mathrm{stop}}={\mathrm{false}},S_{t},\theta_{t})$ is set to $\frac{1}{|I_{t}|}$ (where $\left|I_{t}\right|$ represents the number of remaining sentences at time $t_{c}$ ), which is independent of the policy parameters to prohibit the gradient from being passed to the policy parameters via the conditional likelihood. After calculating the reward according to Equation (1), the policy parameters are updated accord- ing to Equation (3) (for all time steps).

其中 $I_{t}$ 表示时间步 $t$ 时剩余句子的索引集合。若智能体未停止，则先为每个剩余句子计算得分 $u_{j}$，并根据归一化得分的概率分布采样句子 $s_{a_{t}}$。当智能体停止抽取时，不选择任何句子，并将条件似然 $\scriptstyle p(a_{t}|{\mathrm{stop}}={\mathrm{false}},S_{t},\theta_{t})$ 设为 $\frac{1}{|I_{t}|}$ (其中 $\left|I_{t}\right|$ 表示时间 $t_{c}$ 时剩余句子的数量)，该设定与策略参数无关以防止梯度通过条件似然传递至策略参数。根据公式(1)计算奖励后，所有时间步的策略参数均按公式(3)进行更新。

3.3 Policy Network

3.3 策略网络

The state $S_{t}$ in Equation (4) is designed to be informative on: 1) the local content of the sentence, 2) the global context of the sentence within the document, and 3) the current extraction history. To encode these three properties in the state, we use a local sentence encoder, a global context encoder, and an extraction history encoder, respectively. Subsequently, the state is mapped by an extractor to an output score for each of the remaining sentences and the extraction stop signal. The overall framework of our model is depicted in Figure 2.

方程(4) 中的状态 $S_{t}$ 设计用于反映以下信息: 1) 句子的局部内容, 2) 句子在文档中的全局上下文, 3) 当前提取历史。为了在状态中编码这三个属性, 我们分别使用了局部句子编码器、全局上下文编码器和提取历史编码器。随后, 通过提取器将状态映射为每个剩余句子的输出分数和提取停止信号。我们模型的整体框架如图 2 所示。

In the Local Sentence Encoder (LSE), ordered words $(w_{1},w_{2},...w_{M})$ in a sentence $s_{i}$ are first mapped onto word embeddings using a word embedding matrix. Subsequently, a $N_{l}$ -layer bidirectional LSTM (Hochreiter and Schmid huber, 1997) transforms the word embeddings and maps them onto sentence embeddings $l_{s_{i}}$ via a multihead pooling layer (MHP) (Liu and Lapata, 2019a).

在局部句子编码器 (LSE) 中，句子 $s_{i}$ 中的有序单词 $(w_{1},w_{2},...w_{M})$ 首先通过词嵌入矩阵映射为词嵌入。随后，一个 $N_{l}$ 层双向 LSTM (Hochreiter and Schmidhuber, 1997) 对这些词嵌入进行转换，并通过多头池化层 (MHP) (Liu and Lapata, 2019a) 将它们映射为句子嵌入 $l_{s_{i}}$。

The Global Context Encoder (GCE) consists of a $N_{g}$ -layer bi-LSTM that takes the $L$ local sentence embeddings $(l_{s_{1}},l_{s_{2}},\ldots l_{s_{L}})$ as inputs and produces for each sentence $s_{i}$ an embedding $g_{s_{i}}$ that encodes global contextual information such as the sentence’s position in the document and information on neighboring sentences.

全局上下文编码器 (GCE) 由 $N_{g}$ 层双向 LSTM 组成，它以 $L$ 个局部句子嵌入 $(l_{s_{1}},l_{s_{2}},\ldots l_{s_{L}})$ 作为输入，并为每个句子 $s_{i}$ 生成一个嵌入 $g_{s_{i}}$，该嵌入编码了全局上下文信息，例如句子在文档中的位置以及相邻句子的信息。

The Extraction History Encoder (EHE) encodes the extraction history information and produces the extraction history embedding $h_{s_{i}^{r}}$ for each remaining sentence $s_{i}^{r}$ . The EHE is composed of a stack of $N_{h}$ identical layers. Within one layer, there are two multi-head attention sublayers, as contained in the transformer decoder in Vaswani et al. (2017). One sublayer is used to perform multi-head self-attention (MHA) among the local embeddings of the remaining sentences, so that each remaining sentence can capture the context provided by other remaining sentences. The other attention sublayer is used to perform multi-head attention over the embeddings of extracted sentences to enable each remaining sentence to attend to all the extracted sentences. The output of the two attention sublayers, one for each remaining sentence, captures the contextual information of both extracted and remaining sentences. The final output of the $N_{h}^{\mathrm{th}}$ layer of the EHE constitutes the extraction history embedding, one for each remaining sentence.

提取历史编码器 (EHE) 对提取历史信息进行编码，并为每个剩余句子 $s_{i}^{r}$ 生成提取历史嵌入 $h_{s_{i}^{r}}$。EHE 由 $N_{h}$ 个相同层堆叠而成。每层包含两个多头注意力子层，与 Vaswani 等人 (2017) 提出的 Transformer 解码器结构一致。其中一个子层用于在剩余句子的局部嵌入之间执行多头自注意力 (MHA)，使每个剩余句子都能捕捉其他剩余句子提供的上下文信息。另一个注意力子层则对已提取句子的嵌入执行多头注意力，使每个剩余句子都能关注所有已提取句子。这两个注意力子层（每个剩余句子对应一个）的输出同时捕捉了已提取和剩余句子的上下文信息。EHE 第 $N_{h}^{\mathrm{th}}$ 层的最终输出构成每个剩余句子对应的提取历史嵌入。

There is no positional encoding and the EHE produces the extraction history embeddings nonauto regressive ly by attending to both precedent and subsequent positions. Consequently, the extraction history embeddings $h_{s_{i}^{r}}$ for the remaining sen- tences are invariant to the order of the previously selected sentences. We believe that the sequential information of previously selected sentences is not crucial for reducing redundancy and for deciding whether to stop extraction or not.

没有位置编码，EHE通过同时关注前后位置非自回归地生成提取历史嵌入。因此，剩余句子的提取历史嵌入$h_{s_{i}^{r}}$对先前选中句子的顺序具有不变性。我们认为，已选句子的顺序信息对于减少冗余和决定是否停止提取并不关键。

The Extractor computes the score of each remaining sentence and outputs an extraction stop signal. As input to the extractor, we form for each of the remaining sentences $s_{i}^{r}$ an aggregated embedding by concatenating the local sentence embedding ${{l}{s_{i}^{r}}}$ , the global context embedding $g_{s_{i}^{r}}$ , and the extraction history embedding $h_{s_{i}^{r}}$ . As shown in Figure 2, to produce the score ${{u}{s_{i}^{r}}}$ , the concatenated embedding of remaining sentence $s_{i}^{r}$ is passed to fully connected layers with ReLU activation and then projected to a scalar by a Linear-1 layer followed by a sigmoid function. Note that the same fully connected layers are applied identically to all remaining sentences. We deem that the extractor can learn to stop extraction based on the remaining sentences’ states. Therefore, we apply an MHP to the last hidden vectors of all remaining sentences to output a single vector. This vector is then passed to a linear layer with a sigmoid function, producing a stopping probability $p_{\mathrm{stop}}$ .

提取器计算每个剩余句子的分数并输出一个抽取停止信号。作为提取器的输入，我们为每个剩余句子 $s_{i}^{r}$ 形成一个聚合嵌入，通过连接局部句子嵌入 ${{l}{s_{i}^{r}}}$、全局上下文嵌入 $g_{s_{i}^{r}}$ 和抽取历史嵌入 $h_{s_{i}^{r}}$。如图 2 所示，为了生成分数 ${{u}{s_{i}^{r}}}$，剩余句子 $s_{i}^{r}$ 的连接嵌入被传递到具有 ReLU 激活的全连接层，然后通过 Linear-1 层和 sigmoid 函数投影为标量。注意，相同的全连接层以相同方式应用于所有剩余句子。我们认为提取器可以基于剩余句子的状态学习停止抽取。因此，我们对所有剩余句子的最后隐藏向量应用 MHP 以输出单个向量。该向量随后传递到带有 sigmoid 函数的线性层，生成停止概率 $p_{\mathrm{stop}}$。

3.4 Training

3.4 训练

We train the parameterized policy network according to the update rule in Equation (3). At each training iteration, an episode is sampled to compute the final return $r$ and the action probabilities $\pi(A_{t}|S_{t},\pmb{\theta}{t})$ for all time steps $t$ . An example episode with $T$ extracted sentences looks like: $(S_{0},s_{a_{0}},\ldots,S_{T-1},s_{a_{T-1}},S_{T},A_{\mathrm{stop}},r)$ , where $S_{t}$ represents the concatenated state information introduced in Section 3.3, $s_{a_{t}}$ represents the selection of sentence $a_{t}$ , $A_{\mathrm{stop}}$ represents the extraction stops at the final time step $T$ , and $r$ is the reward as defined in Equation (1). To encourage the agent to select compact summaries, we multiply the final reward $r$ by a length penalty term $1/(T+1)$ (Luo et al., 2019). Consequently, the return Rt ≡ T r+1 .

我们根据方程(3)中的更新规则训练参数化策略网络。每次训练迭代时，采样一个情节来计算最终回报$r$和所有时间步$t$的动作概率$\pi(A_{t}|S_{t},\pmb{\theta}{t})$。一个包含$T$个抽取句子的示例情节如下：$(S_{0},s_{a_{0}},\ldots,S_{T-1},s_{a_{T-1}},S_{T},A_{\mathrm{stop}},r)$，其中$S_{t}$表示第3.3节介绍的拼接状态信息，$s_{a_{t}}$表示选择句子$a_{t}$，$A_{\mathrm{stop}}$表示在最终时间步$T$停止抽取，$r$是方程(1)定义的奖励。为鼓励智能体选择紧凑摘要，我们将最终奖励$r$乘以长度惩罚项$1/(T+1)$ (Luo et al., 2019)。因此，回报Rt ≡ T r+1。

Algorithm 1 The training algorithm.

算法 1: 训练算法

Parameters: learning rate $\alpha$

参数：学习率 $\alpha$

Algorithm 1 summarizes the training procedure of MemSum. We initialize the extraction history embeddings to 0, because at $t=0$ no sentences have been extracted. $E_{t}$ represents the number of sentences that have been extracted into the summary up to time step $t$ . Following the strategy in Narayan et al. (2018) and Mohsen et al. (2020), instead of sampling an episode following the current policy $\pi(\cdot|\cdot,\pmb{\theta}{t})$ , we sample an episode from a set $\mathbb{E}_{p}$ of episodes with high ROUGE scores, which enables the agent to quickly learn from optimal policies and to rapidly converge. Details on creating a set of high-ROUGE episodes for training are described in Appendix E.

算法1总结了MemSum的训练流程。我们将提取历史嵌入初始化为0，因为在$t=0$时尚未提取任何句子。$E_{t}$表示截至时间步$t$已提取到摘要中的句子数量。遵循Narayan等人(2018)和Mohsen等人(2020)的策略，我们没有按照当前策略$\pi(\cdot|\cdot,\pmb{\theta}{t})$采样片段，而是从具有高ROUGE得分的片段集合$\mathbb{E}_{p}$中采样，这使得智能体能够快速学习最优策略并迅速收敛。关于创建高ROUGE训练片段集的详细说明见附录E。

4 Experiments

4 实验

In this section, we report implementation details of our model and describe the datasets used for training and for evaluation.

在本节中，我们将报告模型的实现细节，并描述用于训练和评估的数据集。

Datasets. The documents to be summarized in the PubMed and arXiv datasets (Cohan et al., 2018)

数据集。PubMed和arXiv数据集（Cohan等人，2018）中待摘要的文档

Table 1: An overview of datasets used in this paper. We count only strings composed of letters and numbers for # of words.

表 1: 本文所用数据集概览。单词数仅统计由字母和数字组成的字符串。

数据集	平均文档长度	平均摘要长度	文档-摘要对数
	单词数	句子数	单词数
PubMed	2,730	88	181
arXiv	5,206	206	238
PubMedtrunc	408	13	185
GovReport	7,932	307	501
CNN/DM	692	35	49

are the full bodies of scientific papers and the gold summaries are the corresponding abstracts. Zhong et al. (2020) proposed a truncated version of the PubMed dataset $\mathrm{(PubMed_{trunc}}$ for simplicity) by defining a doument as the introduction section of a paper. The GovReport dataset (Huang et al., 2021) contains U.S. government reports with gold summaries written by experts. Except $\mathrm{PubMed}_{\mathrm{trunc}}$ , all the other datasets contain significantly longer documents than the popular dataset CNN/DM (Table 1). Baselines. Extractive baselines include Lead (directly using the first several sentences as the summary) (Gidiotis and Tsoumakas, 2020), SummaRuNNer (Nallapati et al., 2017), Atten-Cont(Xiao and Carenini, 2019), Sent-CLF and SentPTR (Pilault et al., 2020), MatchSum (Zhong et al., 2020), and the NeuSum model (Zhou et al., 2018) that we trained on our datasets.

科学论文的全文为原始文本，对应的摘要则为黄金标准摘要。Zhong等人(2020)提出了PubMed数据集的截断版本(为简便起见记为$\mathrm{PubMed_{trunc}}$)，将论文的引言部分定义为文档。GovReport数据集(Huang等人，2021)包含美国政府报告及专家撰写的黄金标准摘要。除$\mathrm{PubMed}_{\mathrm{trunc}}$外，其他数据集所含文档长度均显著超过CNN/DM等流行数据集(表1)。基线方法：抽取式基线包括Lead(直接取前几句作为摘要)(Gidiotis和Tsoumakas，2020)、SummaRuNNer(Nallapati等人，2017)、Atten-Cont(Xiao和Carenini，2019)、Sent-CLF与SentPTR(Pilault等人，2020)、MatchSum(Zhong等人，2020)，以及我们在数据集上训练的NeuSum模型(Zhou等人，2018)。

Abstract ive sum mari z ation models include PEGASUS (Zhang et al., 2020), BigBird (Zaheer et al., 2020), Dancer (Gidiotis and Tsoumakas, 2020), and Hepos (Huang et al., 2021) that achieved the state-of-the-art in long document sum mari z ation using a large-scale pretrained BART model (Lewis et al., 2020) with memory-efficient attention encoding schemes including Locality Sensitive Hashing (Kitaev et al., 2020) (Hepos-LSH) and Sinkhorn attention (Hepos-Sinkhorn). We also present the performance of the oracle extraction model based on the greedy approach (Nallapati et al., 2017) which sequentially selects from the document the sentence that maximally improves the average of R-1 and R-2 of selected sentences.

抽象式摘要模型包括PEGASUS (Zhang等人，2020)、BigBird (Zaheer等人，2020)、Dancer (Gidiotis和Tsoumakas，2020)以及Hepos (Huang等人，2021)。这些模型通过采用基于大规模预训练BART模型 (Lewis等人，2020)的高效注意力编码方案——包括局部敏感哈希 (Kitaev等人，2020) (Hepos-LSH)和Sinkhorn注意力 (Hepos-Sinkhorn)——在长文档摘要任务上达到了最先进水平。我们还展示了基于贪婪算法 (Nallapati等人，2017)的oracle抽取模型性能，该模型通过依次选择能最大化已选句子R-1和R-2平均值的文档句子来实现。

Implementation Details. We computed local sentence embeddings using pretrained Glove word embeddings (Pennington et al., 2014) of dimension $d=200$ , keeping the word embeddings fixed during training. For the LSE, we used $N_{l}~=~2$ bi- LSTM layers and for the GCE $N_{g}=2$ . For the

实现细节。我们使用预训练的 Glove 词嵌入 (Pennington et al., 2014) 计算局部句子嵌入，维度为 $d=200$，并在训练过程中保持词嵌入固定。对于 LSE，我们使用 $N_{l}~=~2$ 层双向 LSTM，对于 GCE 使用 $N_{g}=2$ 层。

EHE, we used $N_{h}=3$ attention layers, and we set the number of attention heads to 8 and the dimension of the feed-forward hidden layer to 1024; during training we set the dropout rate to 0.1. The extractor consisted of 2 fully-connected hidden layers with output dimensions $2d$ and $d$ , respectively.

在EHE中，我们使用了$N_{h}=3$个注意力层，并将注意力头数设为8，前馈隐藏层维度设为1024；训练期间将dropout率设置为0.1。提取器由2个全连接隐藏层组成，输出维度分别为$2d$和$d$。

We trained our model using the Adam optimizer with $\beta_{1}=0.9$ , $\beta_{2}=0.999$ (Kingma and Ba, 2015), fixed learning rate $\alpha=1e^{-4}$ , and weight decay $1e^{-6}$ . The training was stopped when the validation performance started to degrade. During validating and testing, the agent extracted sentences in a deterministic way: after computing the scores ${u}{s_{i}^{r}}$ for the remaining sentences and the stop likelihood $p_{\mathrm{stop}}$ , the agent stopped the extraction if $p_{\mathrm{stop}}\geq p_{\mathrm{thres}}$ or if the maximum admissible number $N_{\mathrm{max}}$ of extracted sentences was reached; otherwise, the agent selected the sentence with the largest score. The model was trained on eight RTX 2080 Ti GPUs.

我们使用 Adam 优化器 (Kingma and Ba, 2015) 训练模型，参数设置为 $\beta_{1}=0.9$、$\beta_{2}=0.999$，固定学习率 $\alpha=1e^{-4}$，权重衰减 $1e^{-6}$。当验证性能开始下降时停止训练。在验证和测试阶段，智能体以确定性方式提取句子：计算剩余句子的得分 ${u}{s_{i}^{r}}$ 和停止概率 $p_{\mathrm{stop}}$ 后，若 $p_{\mathrm{stop}}\geq p_{\mathrm{thres}}$ 或达到最大可提取句子数 $N_{\mathrm{max}}$ 则停止提取；否则选择得分最高的句子。模型在八块 RTX 2080 Ti GPU 上进行训练。

On the validating datasets we selected the best checkpoint of each model and determined the optimal $N_{\mathrm{max}}$ and stopping criterion $p_{\mathrm{thres}}^{}$ . For Pubmed, arXiv, Pubmed tr unc, and GovReport, $N_{\mathrm{max}}$ was set to 7, 5, 7, and 22, and $p_{\mathrm{thres}}^{*}$ was set to 0.6, 0.5, 0.8, and 0.6, respectively. For the detailed selection procedure of the optimal stopping threshold, see Appendix D. Information on reproducibility is available in Appendix I.

在验证数据集上，我们为每个模型选择了最佳检查点，并确定了最优的 $N_{\mathrm{max}}$ 和停止准则 $p_{\mathrm{thres}}^{}$。对于 Pubmed、arXiv、Pubmed tr unc 和 GovReport，$N_{\mathrm{max}}$ 分别设置为 7、5、7 和 22，$p_{\mathrm{thres}}^{*}$ 分别设置为 0.6、0.5、0.8 和 0.6。关于最优停止阈值的详细选择过程，请参阅附录 D。可复现性相关信息见附录 I。

Evaluation. We evaluated the performance of our model using $F_{1}$ ROUGE (Lin, 2004), including ROUGE-1,2, and L for measuring unigram, bigram, and longest common sub sequence. We also conducted human evaluation in Section 5.4.

评估。我们使用 $F_{1}$ ROUGE (Lin, 2004) 评估模型性能，包括 ROUGE-1、2 和 L，用于测量单字组、双字组和最长公共子序列。此外，我们在第 5.4 节进行了人工评估。

5 Results and Discussion

5 结果与讨论

Here we present the results on various extractive sum mari z ation tasks and analyze the contribution of different modules via ablation studies.

我们在此展示多种抽取式摘要任务的结果，并通过消融实验分析不同模块的贡献。

5.1 Results Comparison

5.1 结果对比

By comparing with extractive baselines on the PubMed and arXiv datasets, we observed that models utilizing extraction history, such as NeuSum and our MemSum, perform significantly better than other models, revealing the effectiveness of the extraction history. MemSum also significantly outperformed NeuSum, suggesting a better utilization of extraction history, which we ascribed to the following factors: 1) In MemSum, we treat stopping extraction also as an action and tr