Learning Topological Representation for Networks via Hierarchical Sampling

通过分层采样学习网络的拓扑表征

Abstract—The topological information is essential for studying the relationship between nodes in a network. Recently, Network Representation Learning (NRL), which projects a network into a low-dimensional vector space, has been shown their advantages in analyzing large-scale networks. However, most existing NRL methods are designed to preserve the local topology of a network, they fail to capture the global topology. To tackle this issue, we propose a new NRL framework, named HSRL, to help existing NRL methods capture both the local and global topological information of a network. Specifically, HSRL recursively compresses an input network into a series of smaller networks using a community-awareness compressing strategy. Then, an existing NRL method is used to learn node embeddings for each compressed network. Finally, the node embeddings of the input network are obtained by concatenating the node embeddings from all compressed networks. Empirical studies for link prediction on five real-world datasets demonstrate the advantages of HSRL over state-of-the-art methods.

摘要—拓扑信息对于研究网络中节点间的关系至关重要。近年来，网络表示学习（NRL）通过将网络映射到低维向量空间，在分析大规模网络方面展现出显著优势。然而，现有大多数NRL方法仅专注于保留网络的局部拓扑结构，未能有效捕捉全局拓扑特征。为解决这一问题，我们提出了一种名为HSRL的新型NRL框架，旨在帮助现有NRL方法同时捕获网络的局部和全局拓扑信息。具体而言，HSRL采用基于社区感知的压缩策略，递归地将输入网络压缩为一系列更小的网络；随后使用现有NRL方法学习每个压缩网络的节点嵌入；最终通过拼接所有压缩网络的节点嵌入，获得输入网络的节点表示。在五个真实数据集上的链路预测实验表明，HSRL优于当前最先进的方法。

Index Terms—Networks analysis, network topology, representation learning

索引术语—网络分析、网络拓扑、表征学习

I. INTRODUCTION

I. 引言

The science of networks has been widely used to understand the behaviours of complex systems. These systems are typically described as networks, such as social networks in social media [1], bibliographic networks in academic field [2], protein-protein interaction networks in biology [3]. Studying the relationship between entities in a complex system is an essential topic, which benefits a variety of applications [4]. Just take a few examples, predicting potential new friendship between users in social networks [5], searching similar authors in bibliographic networks [2], recommending new movies to users in movie user-movie interest networks [6]. The topologies of these networks provide insight information on the relationship between nodes. We can find out strongly connected neighborhoods of a node by exploring the local topology in a network. Meanwhile, the global topology is another significant aspect for studying the relationship between communities. As shown in Fig.1, such hierarchical topological information is helpful to learn the relationship between nodes in a network.

网络科学已被广泛用于理解复杂系统的行为。这些系统通常被描述为网络，例如社交媒体中的社交网络 [1]、学术领域的文献网络 [2]、生物学中的蛋白质-蛋白质相互作用网络 [3]。研究复杂系统中实体之间的关系是一个重要课题，可为多种应用带来益处 [4]。仅举几个例子：预测社交网络中用户之间潜在的新友谊 [5]、在文献网络中搜索相似作者 [2]、在电影用户-电影兴趣网络中向用户推荐新电影 [6]。这些网络的拓扑结构提供了关于节点之间关系的深入信息。通过探索网络中的局部拓扑，我们可以发现一个节点的强连接邻域。同时，全局拓扑是研究社区之间关系的另一个重要方面。如图 1 所示，这种层次化的拓扑信息有助于学习网络中节点之间的关系。

Many networks are large-scale in real-world scenarios, such as a Facebook social network contains billion of users [7]. As a result, most traditional network analytic methods suffer from high computation and space cost [4]. To tackle this issue, Network Representation Learning (NRL) has been a popular technique to analyze large-scale networks recently. In particular, NRL aims to map a network into a low-dimensional vector space, while preserving as much of the original network topological information as possible. Nodes in a network are represented as low-dimensional vectors which are used as input features for downstream network analysis algorithms.

现实场景中许多网络规模庞大，例如Facebook社交网络拥有数十亿用户[7]。这导致传统网络分析方法普遍面临高昂的计算和存储成本[4]。为解决该问题，网络表征学习(NRL)近年成为分析大规模网络的主流技术。其核心思想是将网络映射到低维向量空间，同时最大限度保留原始网络拓扑信息。网络中的节点被表示为低维向量，作为下游网络分析算法的输入特征。

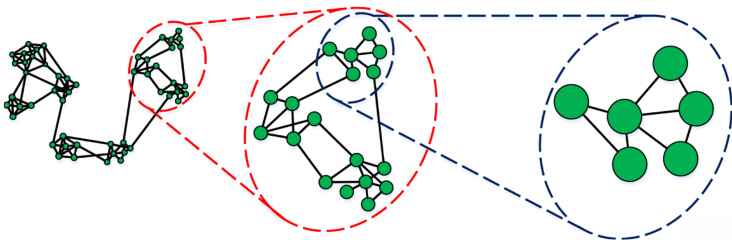
Fig. 1. An example of hierarchical view of network topology.

图 1: 网络拓扑层次结构示例。

Traditional NRL methods such as LLE [8] and ISOMap [9] work well on small networks, while they are infeasible to large-scale networks due to the high computational cost. Recently, some online learning methods, e.g., DeepWalk [10], node2vec [11], and LINE [12], have been proposed to learn large-scale network representation, which has been demonstrated their efficiency and effectiveness for the large-scale network analysis.

传统网络表示学习（NRL）方法如LLE [8]和ISOMap [9]在小规模网络上表现良好，但由于计算成本高，无法应用于大规模网络。近年来，一些在线学习方法如DeepWalk [10]、node2vec [11]和LINE [12]被提出用于学习大规模网络表示，这些方法在大规模网络分析中已展现出高效性和有效性。

However, the above NRL methods only consider the local topology of networks and fail to capture the global topological information. DeepWalk and node2vec firstly employ short random walks to explore the local neighborhoods of nodes and obtain node embeddings by the Skip-Gram model [13]. LINE preserves the first-order and second-order pro xi mi ties so that it can only measure the relationship between nodes at most two-hops away. These methods are efficient to capture the relationship between close nodes, however, fail to consider the case for nodes which are far away from each other. Recently, HARP [14] has been proposed to overcome this issue. It recursively compresses a network into a series of small networks based on two node collapsing schemes and learns node embeddings for each compressed network by using an existing NRL method. Unfortunately, the compressed networks may not reveal the global topology of an input network, since HARP heuristic ally merges two closed nodes into a new node. Furthermore, when learning node embeddings on the original network, using node embeddings obtained on compressed networks as the initialization solution may mislead the optimization process to a bad local minimum.

然而，上述网络表示学习(NRL)方法仅考虑网络的局部拓扑结构，未能捕获全局拓扑信息。DeepWalk和node2vec首次采用短随机游走来探索节点的局部邻域，并通过Skip-Gram模型[13]获得节点嵌入。LINE保留了一阶和二阶近似性，因此最多只能测量两跳范围内节点间的关系。这些方法能有效捕捉相邻节点间的关系，但无法处理相距较远节点的情况。最近提出的HARP[14]试图解决这一问题，它基于两种节点压缩方案递归地将网络压缩为一系列小型网络，并使用现有NRL方法为每个压缩网络学习节点嵌入。遗憾的是，由于HARP启发式地将两个相邻节点合并为新节点，压缩后的网络可能无法反映原始网络的全局拓扑。此外，当在原始网络上学习节点嵌入时，使用压缩网络获得的节点嵌入作为初始化方案可能会误导优化过程陷入不良局部极小值。

This paper presents a new NRL framework, called Hierarchical Sampling Representation Learning (HSRL), to learn node embeddings for a network with preserving both their local and global topological information. Specifically, HSRL uses a community-awareness network compressing strategy, called hierarchical sampling, to recursively compress an input network into a series of smaller networks, and then engage an existing NRL method to learn node embeddings for each compressed network. Finally, the node embeddings of the original network can be obtained by concatenating all node embeddings learned on compressed networks. Besides, we mathematically show that HSRL is able to capture the local and global topological relationship between nodes. Novel contributions of this paper include the following:

本文提出了一种名为分层采样表示学习 (HSRL) 的新型网络表示学习框架，旨在通过学习节点嵌入来同时保留网络的局部和全局拓扑信息。具体而言，HSRL采用一种称为分层采样的社区感知网络压缩策略，递归地将输入网络压缩为一系列较小的网络，然后利用现有的网络表示学习方法为每个压缩网络学习节点嵌入。最终，通过拼接所有压缩网络上学习到的节点嵌入，可以获得原始网络的节点嵌入。此外，我们从数学上证明了HSRL能够捕捉节点之间的局部和全局拓扑关系。本文的新颖贡献包括以下几点：

• We propose a new NRL framework called HSRL, to learn node embeddings for a network, which is able to capture both local and global topological information of the network via a community-awareness network compressing strategy. • We mathematically show that the node embeddings obtained by HSRL explicitly embed the local and global topological information of the input network. • We demonstrate that HSRL statistically significantly outperforms DeepWalk, node2vec, LINE, and HARP on link prediction tasks on five real-world datasets.

• 我们提出了一种名为HSRL的新型网络表示学习(NRL)框架，通过学习节点嵌入来捕获网络的局部和全局拓扑信息，该框架采用社区感知的网络压缩策略实现这一目标。
• 我们从数学角度证明了HSRL获得的节点嵌入显式地编码了输入网络的局部和全局拓扑信息。
• 实验表明，在五个真实数据集上的链接预测任务中，HSRL在统计显著性上优于DeepWalk、node2vec、LINE和HARP。

II. RELATED WORK

II. 相关工作

Most early methods in NRL field represent an input network in the form of a matrix, e.g., adjacency matrices [8], [15], Laplacian matrices [16], node transition probability matrices [17], and then factorize that matrix to obtain node embeddings. They are effective for small networks, but cannot scale to large-scale networks due to high computation cost.

网络表征学习(NRL)领域早期方法大多采用矩阵形式表示输入网络，例如邻接矩阵[8][15]、拉普拉斯矩阵[16]、节点转移概率矩阵[17]，然后通过矩阵分解获得节点嵌入。这些方法对小规模网络有效，但由于计算成本过高难以扩展到大规模网络。

To analyze large-scale networks, DeepWalk [10] employs truncated random walks to obtain node sequences, and then learns node embeddings by feeding node sequences into SkipGram model [15]. To generalize DeepWalk, node2vec [11] provides a trade-off between breadth-first search (BFS) and depth-first search (DFS) when generating truncated random walks for a network. LINE [12] intends to preserve first-order and second-order pro xi mi ties, respectively, by minimizing the Kullback-Leibler divergence of two joint probability distributions for each pair nodes. These methods are scalable to large-scale networks, but fail to capture the global topological information of networks. Because random walks are only effective to explore local neighborhoods for a node, and both first-order and second-order pro xi mi ties defined by LINE just measure the relationship between nodes at most two-hops away.

为分析大规模网络，DeepWalk [10] 采用截断随机游走获取节点序列，再通过将节点序列输入SkipGram模型 [15] 学习节点嵌入。为推广DeepWalk，node2vec [11] 在生成网络截断随机游走时提供了广度优先搜索 (BFS) 和深度优先搜索 (DFS) 的权衡方案。LINE [12] 通过最小化每对节点两个联合概率分布的Kullback-Leibler散度，分别保留一阶邻近性和二阶邻近性。这些方法可扩展至大规模网络，但无法捕捉网络的全局拓扑信息。因为随机游走仅能有效探索节点的局部邻域，且LINE定义的一阶和二阶邻近性最多只能衡量两跳范围内节点间的关系。

To investigate global topologies of a network, HARP [14] recursively uses two collapsing schemes, edge collapsing and star collapsing, to compress an input network into a series of small networks. Starting from the smallest compressed network, it then recursively conducts a NRL method to learn node embeddings based on the node embeddings obtained from its previous level (if any) as the initialization. However, HARP has two weaknesses: 1) nodes that are connected but belong to different communities may be merged, which leads to that the compressed networks cannot well reveal the global topology of an input network. 2) taking the node embeddings learned on such compressed networks as initialization would mislead NRL methods to a bad local minimum. HARP could work well on node classification tasks since close nodes tend to have the same labels but may ineffective for the link prediction tasks. Because predicting the link between two nodes needs to consider both the local and global topological information of a network, such as neighborhoods they are sharing with and communities they are both involved in. This paper proposes HSRL to tackle the above issues of the existing NRL methods.

为了研究网络的全局拓扑结构，HARP [14] 通过递归使用边折叠 (edge collapsing) 和星型折叠 (star collapsing) 两种压缩方案，将输入网络压缩成一系列小型网络。从最小的压缩网络开始，它再递归执行网络表示学习 (NRL) 方法，基于上一层级获得的节点嵌入 (node embeddings) （如果有的话）作为初始化来学习节点嵌入。然而，HARP 存在两个缺点：1) 相连但属于不同社区的节点可能会被合并，导致压缩网络无法很好地揭示输入网络的全局拓扑结构；2) 以这些压缩网络上学习到的节点嵌入作为初始化，会将 NRL 方法误导至不良的局部极小值。HARP 在节点分类任务上可能表现良好，因为相近的节点往往具有相同的标签，但在链接预测任务上可能效果不佳。因为预测两个节点之间的链接需要考虑网络的局部和全局拓扑信息，例如它们共享的邻域以及它们共同参与的社区。本文提出 HSRL 来解决现有 NRL 方法的上述问题。

III. PRELIMINARY AND PROBLEM DEFINITION

III. 初步研究与问题定义

This section gives the notations and definitions throughout this paper.

本节给出本文使用的符号和定义。

We firstly introduce the definition of a network and related notations.

我们首先介绍网络的定义及相关符号。

Definition 1. (Network) [4] A network (a.k.a. graph) is defined as $G=(V,E)$ , where $V$ is a set of nodes and $E$ is a set of edges between nodes. The edge $e\in E$ between nodes u and $v$ is represented as $e=(u,v)$ with a weight $w_{u,v}\geq0$ . Particularly, we have $(u,v)\equiv(v,u)$ and $w_{u,v}\equiv w_{v,u}$ if $G$ is undirected; $(u,v)\equiv(v,u)$ and $w_{u,v}\not\equiv w_{v,u},$ otherwise.

定义 1. (网络) [4] 网络(又称图)定义为 $G=(V,E)$ ，其中 $V$ 是节点集合， $E$ 是节点间边的集合。节点 u 和 $v$ 之间的边 $e\in E$ 表示为 $e=(u,v)$ ，并带有权重 $w_{u,v}\geq0$ 。特别地，若 $G$ 是无向图，则有 $(u,v)\equiv(v,u)$ 和 $w_{u,v}\equiv w_{v,u}$ ；否则 $(u,v)\equiv(v,u)$ 且 $w_{u,v}\not\equiv w_{v,u}$ 。

In most networks, some nodes are densely connected to form a community/cluster, while nodes in different communities are sparsely connected. Detecting communities in a network is beneficial to analyze the relationship between nodes. We employ modularity as defined below to evaluate the quality of community detection.

在大多数网络中，某些节点密集连接形成社区/集群，而不同社区间的节点连接稀疏。检测网络中的社区有助于分析节点间关系。我们采用如下定义的模块度(modularity)来评估社区检测质量。

Definition 2. (Modularity) [18], [19] Modularity is a measure of the structure of networks, which measures the density of edges between the nodes within communities as compared to the edges between nodes in different communities. It is defined as below.

定义 2. (模块度) [18], [19] 模块度是衡量网络结构的一种指标，用于比较社区内部节点间边与不同社区节点间边的密度。其定义如下。

$$
Q=\frac{1}{2m}\sum_{i,j}\big(w_{i,j}-\frac{k_{i}k_{j}}{2m}\big)\delta(c_{i},c_{j})
$$

$$
Q=\frac{1}{2m}\sum_{i,j}\big(w_{i,j}-\frac{k_{i}k_{j}}{2m}\big)\delta(c_{i},c_{j})
$$

where $w_{i,j}$ is the weight of edge $\boldsymbol{e}{i,j}$ between nodes $v_{i}$ and $v_{j}$ , $k_{i}=\textstyle\sum_{i}w_{i,j}$ , $m={\textstyle\frac{1}{2}}\sum_{i,j}w_{i,j}$ , $c_{i}$ is the community which nod e $v_{i}$ belongs to, and

其中 $w_{i,j}$ 表示节点 $v_{i}$ 和 $v_{j}$ 之间边 $\boldsymbol{e}{i,j}$ 的权重，$k_{i}=\textstyle\sum_{i}w_{i,j}$ 表示节点 $v_{i}$ 的加权度，$m={\textstyle\frac{1}{2}}\sum_{i,j}w_{i,j}$ 表示网络中所有边权重之和的一半，$c_{i}$ 表示节点 $v_{i}$ 所属的社区。

Networks with high modularity have dense connections between nodes within communities but sparse connections between nodes in different communities.

具有高模块性的网络在社区内部节点间连接密集，而在不同社区节点间连接稀疏。

We give the definition of hierarchical sampling which is used to recursively compress a network into a series of smaller networks as follows.

我们给出层次化采样 (hierarchical sampling) 的定义，该方法用于将网络递归压缩为一系列更小的网络，具体如下。

Definition 3. (Hierarchical Sampling) Given a network $G=(V,E)$ , hierarchical sampling compresses the original network level by level and obtains a series of compressed networks $G^{0},G^{1},...,G^{K}$ , which reveals the global topological information of original network at different levels, respectively.

定义 3. (分层采样) 给定网络 $G=(V,E)$，分层采样逐级压缩原始网络并得到一系列压缩网络 $G^{0},G^{1},...,G^{K}$，这些网络分别揭示了原始网络在不同层次上的全局拓扑信息。

These compressed networks reveal the hierarchical topologies of the input network. Therefore, the node embeddings obtained in compressed networks embed the hierarchical topological information of the original network.

这些压缩网络揭示了输入网络的层次拓扑结构。因此，在压缩网络中获得的节点嵌入包含了原始网络的层次拓扑信息。

To learn node embeddings of a network, NRL maps the original network into a low-dimensional space and represents each node as a low-dimensional vector as formulated below.

为了学习网络的节点嵌入，NRL将原始网络映射到一个低维空间，并将每个节点表示为如下公式所示的低维向量。

Definition 4. (Network Representation Learning) [4] Given a network $G=(V,E)$ , network representation learning aims to learn a mapping function $f:v\rightarrow z\in\mathbb{R}^{d}$ where $d\ll|V|$ , and preserving as much of the original topological information in the embedding space $\mathbb{R}^{d}$ .

定义 4. (网络表示学习) [4] 给定一个网络 $G=(V,E)$ ，网络表示学习旨在学习一个映射函数 $f:v\rightarrow z\in\mathbb{R}^{d}$ ，其中 $d\ll|V|$ ，并在嵌入空间 $\mathbb{R}^{d}$ 中尽可能保留原始拓扑信息。

Finally, we present the formulation of the hierarchical network representation learning problem as following:

最后，我们将分层网络表示学习问题表述如下：

Definition 5. (Hierarchical Network Representation Learning) Given a series of compressed networks $G^{0},G^{1},...,G^{K}$ of original network $G=(V,E)$ and a network representation learning mapping function $f$ , hierarchical network representation learning learns the node embeddings for each compressed network by $Z^{k}\gets f(G^{k}),0\leq k\leq K$ , and finally obtains the node embeddings $Z$ of original network $G$ by concatenating $Z^{0},Z^{1},...,Z^{K}$ .

定义5. (分层网络表示学习) 给定原始网络 $G=(V,E)$ 的一系列压缩网络 $G^{0},G^{1},...,G^{K}$ 和网络表示学习映射函数 $f$，分层网络表示学习通过 $Z^{k}\gets f(G^{k}),0\leq k\leq K$ 学习每个压缩网络的节点嵌入，最终通过拼接 $Z^{0},Z^{1},...,Z^{K}$ 获得原始网络 $G$ 的节点嵌入 $Z$。

IV. HSRL

IV. HSRL

In this section, we present Hierarchical Sampling Representation Learning framework which consists of two parts: 1) Hierarchical Sampling that aims to discover the hierarchical topological information of a network via a communityawareness compressing strategy; and 2) Representation Learning that aims to learn low-dimensional node embeddings while preserving the hierarchical topological information.

在本节中，我们提出分层采样表示学习框架，该框架包含两部分：1) 分层采样，旨在通过社区感知压缩策略发现网络的分层拓扑信息；2) 表示学习，旨在学习低维节点嵌入的同时保留分层拓扑信息。

A. Hierarchical Sampling

A. 分层采样

Here we present the hierarchical sampling which is intended to compress a network into a series of compressed networks according to different compressing levels. Each compressed network reveals one of the hierarchical levels of global topology of the original network.

我们在此提出分层采样方法，旨在根据不同的压缩级别将网络压缩成一系列压缩网络。每个压缩网络揭示了原始网络全局拓扑结构的一个分层级别。

A community is one of the significant patterns of networks. Nodes in the same community are densely connected and nodes in different communities are sparsely connected. The relationship between nodes inside a community presents the local topological information of a network, while the relationship between communities reveals its global topology. It is worth noticing that in most large-scale networks, there are several natural organization levels - communities divide themselves into sub-communities - and thus communities with different hierarchical levels reveal the hierarchical topological information of original networks [20], [21]. Consequently, we compress a network into a new network based on communities by taking each community as a new node in the compressed network. Based on different hierarchical levels of communities, we can obtain a series of compressed networks which reveal the hierarchical global topological information of the input network.

社区是网络的重要模式之一。同一社区内的节点连接密集，而不同社区间的节点连接稀疏。社区内部节点间的关系呈现网络的局部拓扑信息，而社区之间的关系则揭示其全局拓扑结构。值得注意的是，在大多数大规模网络中，存在多个自然组织层级——社区会进一步划分为子社区——因此不同层级的社区能够反映原始网络的分层拓扑信息 [20], [21]。基于此，我们将网络按社区结构压缩为新网络：每个社区在压缩网络中作为新节点。根据不同层级的社区划分，可得到一系列压缩网络，从而揭示输入网络的分层全局拓扑信息。

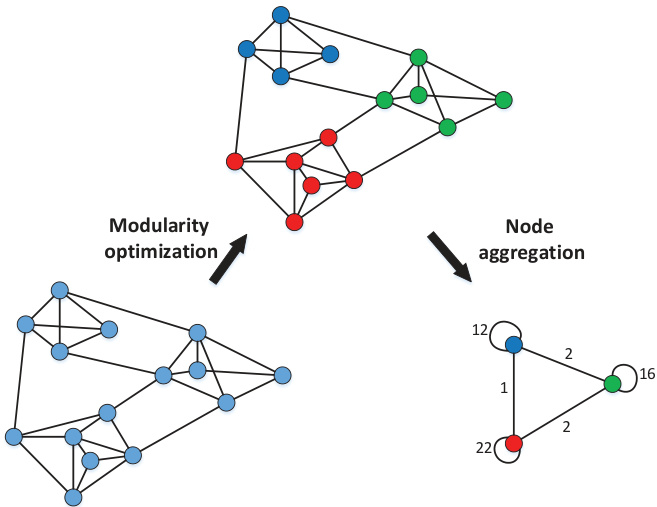
Fig. 2. An exampling of compressing a network

图 2: 网络压缩示例

The quality of the partitions obtained by community detection algorithms can be measured by the modularity of the partition [21], [22]. As a result, we can detect communities through optimizing the modularity of a network. As shown in Fig.2, inspired by the Louvain method [21], hierarchical sampling compresses a network into a new network by implementing two phases: modularity optimization and node aggregation.

通过社区检测算法获得的分区质量可以用分区的模块度 [21], [22] 来衡量。因此，我们可以通过优化网络的模块度来检测社区。如图 2 所示，受 Louvain 方法 [21] 启发，分层采样通过执行两个阶段（模块度优化和节点聚合）将网络压缩为一个新网络。

Modularity optimization. The first phase initializes each node in a network as a community and merges two connected nodes into one community if it can improve the modularity of the network. The implementation of community amalgamation will be repeated until a local maximum of the modularity is attained.

模块度优化。第一阶段将网络中的每个节点初始化为一个社区，如果能够提升网络的模块度，则将两个相连的节点合并为一个社区。社区合并的实现会重复进行，直到达到模块度的局部最大值。

Node aggregation. The second phase builds a new network whose nodes are the communities found in the previous phase. The weights of edges between new nodes are the sum of the weights of edges between nodes in the corresponding two communities.

节点聚合。第二阶段构建一个新网络，其节点为前一阶段发现的社区。新节点间边的权重是对应两个社区间节点边权重的总和。

As shown in Algorithm 1, by recursively repeating the above two phases, hierarchical sampling obtains a series of compressed networks which reveal hierarchical global topology of the original network.

如算法1所示，通过递归重复上述两个阶段，分层采样获得一系列揭示原始网络层级全局拓扑结构的压缩网络。

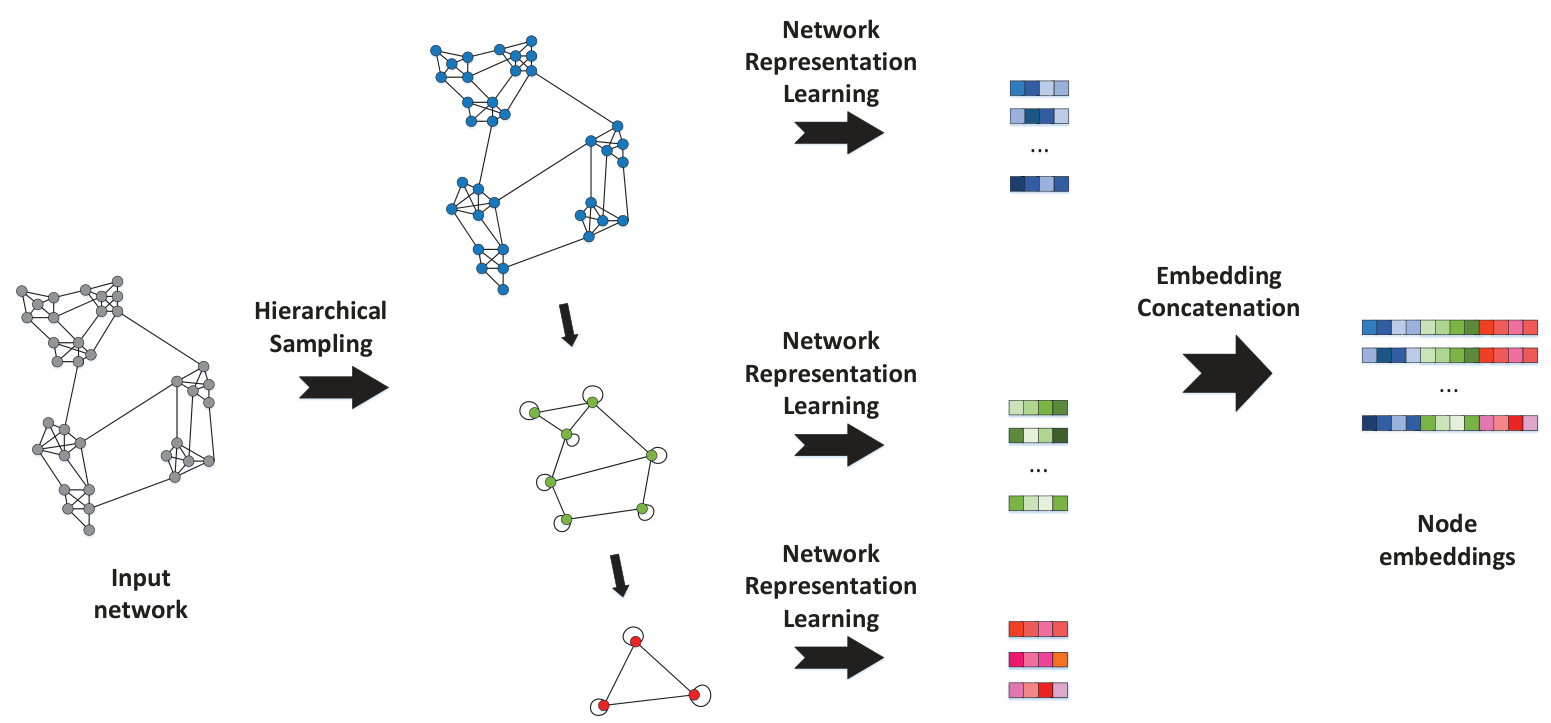
Fig. 3. The framework of HSRL.

图 3: HSRL框架。

Algorithm 1 Hierarchical Sampling

算法 1 分层采样

B. Representation Learning

B. 表征学习

This section introduces representation learning on the compressed networks obtained by the previous section and concatenating the learned embeddings into node embeddings of the original network. We further provide a mathematical proof to demonstrate that HSRL embeds both local and global topological relationship of nodes in the original network into the learned embeddings.

本节介绍对上一节获得的压缩网络进行表征学习，并将学习到的嵌入拼接为原始网络的节点嵌入。我们进一步提供数学证明，表明HSRL将原始网络中节点的局部和全局拓扑关系都嵌入到学习到的嵌入中。

As shown in Fig.3, we conduct representation learning on each compressed network. It is worth noticing that any NRL method can be used for this purpose. The embeddings of nodes in each compressed network are used to generate the final node embeddings of the original network. Particularly, the embedding $Z_{i}$ of node $v_{i}$ in the original network $G$ is the concatenation of the embeddings of hierarchical communities it involved in, as shown below.

如图 3 所示，我们对每个压缩网络进行表示学习。值得注意的是，任何网络表示学习 (NRL) 方法都可用于此目的。每个压缩网络中节点的嵌入用于生成原始网络的最终节点嵌入。具体而言，原始网络 $G$ 中节点 $v_{i}$ 的嵌入 $Z_{i}$ 是其所属层级社区的嵌入拼接结果，如下所示。

$$
Z_{i}=[Z_{c_{i}^{0}}^{0},Z_{c_{i}^{1}}^{1},...,Z_{c_{i}^{K}}^{K}],
$$

$$
Z_{i}=[Z_{c_{i}^{0}}^{0},Z_{c_{i}^{1}}^{1},...,Z_{c_{i}^{K}}^{K}],
$$

where $c_{i}^{k}$ is the $k{\cdot}t h$ hierarchical community $v_{i}$ belongs to.

其中 $c_{i}^{k}$ 是 $v_{i}$ 所属的第 $k{\cdot}th$ 层层次社区。

The node embeddings learned by the above representation learning process hold the following two Lemmas.

上述表示学习过程得到的节点嵌入满足以下两个引理。

Lemma 1. Nodes within the same hierarchical communities will get similar embeddings. The more the same hierarchical communities in which nodes involved, more similar embeddings they have.

引理1：同一层级社区内的节点将获得相似的嵌入表示。节点参与的相同层级社区越多，其嵌入表示越相似。

From Eq.2, it is easy t