LEARNING EFFICIENT ONLINE 3D BIN PACKING ON PACKING CONFIGURATION TREES
基于装箱配置树的高效在线三维装箱学习
Hang $\mathbf{Zhao^{1,2*}}$ ,Yang $\mathbf{Y}\mathbf{u}^{2}$ ,Kai $\mathbf{X}\mathbf{u}^{1\dagger}$ 1School of Computer Science, National University of Defense Technology, China 2National Key Lab for Novel Software Technology, Nanjing University, China {alex.hang.zhao, kevin.kai.xu}@gmail.com, yuy@nju.edu.cn
Hang $\mathbf{Zhao^{1,2*}}$,Yang $\mathbf{Y}\mathbf{u}^{2}$,Kai $\mathbf{X}\mathbf{u}^{1\dagger}$
1 国防科技大学计算机学院,中国
2 南京大学软件新技术国家重点实验室,中国
{alex.hang.zhao, kevin.kai.xu}@gmail.com, yuy@nju.edu.cn
ABSTRACT
摘要
Online 3D Bin Packing Problem (3D-BPP) has widespread applications in industrial automation and has aroused enthusiastic research interest recently. Existing methods usually solve the problem with limited resolution of spatial discretization, and/or cannot deal with complex practical constraints well. We propose to enhance the practical applicability of online 3D-BPP via learning on a novel hierarchical representation ——- packing configuration tree (PCT). PCT is a full-fedged description of the state and action space of bin packing which can support packing policy learning based on deep reinforcement learning (DRL). The size of the packing action space is proportional to the number of leaf nodes, i.e.candidate placements, making the DRL model easy to train and well-performing even with continuous solution space. During training, PCT expands based on heuristic rules, however, the DRL model learns a much more effective and robust packing policy than heuristic methods. Through extensive evaluation, we demonstrate that our method outperforms all existing online BPP methods and is versatile in terms of incorporating various practical constraints.
在线三维装箱问题(3D-BPP)在工业自动化中有着广泛的应用,并且最近引起了广泛的研究兴趣。现有方法通常通过有限的空间离散化分辨率来解决该问题,并且/或者无法很好地处理复杂的实际约束。我们提出通过一种新颖的分层表示——装箱配置树(PCT)——来增强在线3D-BPP的实际适用性。PCT是对装箱状态和动作空间的完整描述,可以支持基于深度强化学习(DRL)的装箱策略学习。装箱动作空间的大小与叶子节点(即候选放置位置)的数量成正比,使得DRL模型即使在连续解空间中也易于训练且表现良好。在训练过程中,PCT基于启发式规则进行扩展,然而,DRL模型学习到的装箱策略比启发式方法更为有效和鲁棒。通过广泛的评估,我们证明了我们的方法优于所有现有的在线BPP方法,并且在整合各种实际约束方面具有广泛的适用性。
1 INTRODUCTION
1 引言
As one of the most classic combinatorial optimization problems, the 3D bin packing problem usually refers to packing a set of cuboid-shaped items $i\in\mathcal{T}$ with sizes $s_{i}^{x},s_{i}^{y},s_{i}^{z}$ along $x,y,z$ axes, respectively, into the minimum number of bins with sizes $S^{x},S^{y},S^{z}$ , in an axis-aligned fashion. Traditional 3D-BPP assumes that all the items to be packed are known a priori (Martello et al., 2000), which is also called offline BPP. The problem is known to be strongly NP-hard (De Castro Silva et al., 2003). However, in many real-world application scenarios, e.g., logistics or warehousing (Wang & Hauser, 2019a), the upcoming items cannot be fully observed; only the current item to be packed is observable. Packing items without the knowledge of all upcoming items is referred to as online BPP (Seiden, 2002).
作为最经典的组合优化问题之一,三维装箱问题 (3D bin packing problem) 通常指将一组长方体形状的物品 $i\in\mathcal{T}$ 沿 $x,y,z$ 轴分别以尺寸 $s_{i}^{x},s_{i}^{y},s_{i}^{z}$ 装入尺寸为 $S^{x},S^{y},S^{z}$ 的箱子中,且要求箱子数量最少。传统的三维装箱问题假设所有待装箱的物品都是预先已知的 (Martello et al., 2000),这也被称为离线装箱问题 (offline BPP)。该问题被证明是强 NP 难问题 (De Castro Silva et al., 2003)。然而,在许多实际应用场景中,例如物流或仓储 (Wang & Hauser, 2019a),即将到来的物品无法完全观察到;只有当前待装箱的物品是可见的。在不知道所有即将到来的物品的情况下进行装箱被称为在线装箱问题 (online BPP) (Seiden, 2002)。
Due to its obvious practical usefulness, online 3D-BPP has received increasing attention recently. Given the limited knowledge, the problem cannot be solved by usual search-based methods. Different from offline 3D-BPP where the items can be placed in an arbitrary order, online BPP must place items following their coming order, which imposes additional constraints. Online 3D-BPP is usually solved with either heuristic methods (Ha et al., 2017) or learning-based ones (Zhao et al., 2021), with complementary pros and cons. Heuristic methods are generally not limited by the size of action space, but they find difficulties in handling complex practical constraints such as packing stability or specific packing preferences. Learning-based approaches usually perform better than heuristic methods, especially under various complicated constraints. However, the learning is hard to converge with a large action space, which has greatly limited the applicability of learning-based methods due to, e.g., the limited resolution of spatial disc ret iz ation (Zhao et al., 2021).
由于其明显的实用性,在线3D-BPP(三维装箱问题)最近受到了越来越多的关注。由于知识有限,该问题无法通过常规的基于搜索的方法解决。与离线3D-BPP不同,离线3D-BPP可以按任意顺序放置物品,而在线BPP必须按照物品到达的顺序进行放置,这增加了额外的约束。在线3D-BPP通常通过启发式方法(Ha et al., 2017)或基于学习的方法(Zhao et al., 2021)来解决,这两种方法各有优缺点。启发式方法通常不受动作空间大小的限制,但在处理复杂的实际约束(如包装稳定性或特定的包装偏好)时存在困难。基于学习的方法通常比启发式方法表现更好,尤其是在各种复杂约束下。然而,由于动作空间较大,学习难以收敛,这极大地限制了基于学习方法的适用性,例如空间离散化的有限分辨率(Zhao et al., 2021)。
We propose to enhance learning-based online 3D-BPP towards practical applicability through learning with a novel hierarchical representation -— packing configuration tree (PCT). PCT is a dynamically growing tree where the internal nodes describe the space configurations of packed items and leaf nodes the packable placements of the current item. PCT is a full-fledged description of the state and action space of bin packing which can support packing policy learning based on deep reinforcement learning (DRL). We extract state features from PCT using graph attention networks (Velickovic et al., 2018) which encodes the spatial relations of all space configuration nodes. The state feature is input into the actor and critic networks of the DRL model. The actor network, designed based on pointer mechanism, weighs the leaf nodes and outputs the action (the final placement).
我们提出通过一种新颖的层次表示——装箱配置树(PCT)来增强基于学习的在线3D-BPP(三维装箱问题)的实际应用性。PCT是一棵动态增长的树,其中内部节点描述已装箱物品的空间配置,叶节点描述当前物品的可装箱位置。PCT是对装箱状态和动作空间的完整描述,能够支持基于深度强化学习(DRL)的装箱策略学习。我们使用图注意力网络(Velickovic et al., 2018)从PCT中提取状态特征,该网络编码了所有空间配置节点的空间关系。状态特征被输入到DRL模型的actor和critic网络中。基于指针机制设计的actor网络对叶节点进行加权,并输出动作(最终放置位置)。
During training, PCT grows under the guidance of heuristics such as Corner Point (Martello et al., 2000), Extreme Point (Crainic et al., 2008), and Empty Maximal Space (Ha et al., 2017). Although PCT is expanded with heuristic rules, confining the solution space to what the heuristics could explore, our DRL model learns a discriminant fitness function (the actor network) for the candidate placements, resulting in an effective and robust packing policy exceeding the heuristic methods. Furthermore, the size of the packing action space is proportional to the number of leaf nodes, making the DRL model easy to train and well-performing even with continuous solution space where the packing coordinates are continuous values. Through extensive evaluation, we demonstrate that our method outperforms all existing online 3D-BPP methods and is versatile in terms of incorporating various practical constraints such as isle friendliness and load balancing (Gzara et al., 2020). Our work is, to our knowledge, the first that deploys the learning-based method on solving online 3DBPP with continuous solution space successfully.
在训练过程中,PCT 在 Corner Point (Martello et al., 2000)、Extreme Point (Crainic et al., 2008) 和 Empty Maximal Space (Ha et al., 2017) 等启发式方法的指导下增长。尽管 PCT 通过启发式规则扩展,将解空间限制在启发式方法所能探索的范围内,但我们的 DRL 模型学习了候选放置的判别适应度函数(即演员网络),从而产生了一种超越启发式方法的有效且稳健的装箱策略。此外,装箱动作空间的大小与叶节点的数量成正比,这使得 DRL 模型即使在装箱坐标为连续值的连续解空间中也能轻松训练并表现出色。通过广泛的评估,我们证明了我们的方法优于所有现有的在线 3D-BPP 方法,并且在结合各种实际约束(如通道友好性和负载平衡 (Gzara et al., 2020))方面具有通用性。据我们所知,我们的工作是首次成功地将基于学习的方法应用于解决具有连续解空间的在线 3DBPP 问题。
2 RELATED WORK
2 相关工作
Offline 3D-BPP The early interest of 3D-BPP mainly focused on its offline setting. Offline 3DBPP assumes that all items are known as a priori and can be placed in an arbitrary order. Martello et al. (2000) first solved this problem with an exact branch-and-bound approach. Limited by exponential worst-case complexity of exact approaches, lots of heuristic and meta-heuristic algorithms are proposed to get an approximate solution quickly, such as guided local search (Faroe et al., 2003), tabu search (Crainic et al., 2009), and hybrid genetic algorithm (Kang et al., 2012). Hu et al. (2017) decompose the offline 3D-BPP into packing order decisions and online placement decisions. The packing order is optimized with an end-to-end DRL agent and the online placement policy is a handdesigned heuristic. This two-step fashion is widely accepted and followed by Duan et al. (2019), Hu et al. (2020), and Zhang et al. (2021).
离线 3D-BPP
早期对 3D-BPP 的研究主要集中在离线设置上。离线 3D-BPP 假设所有物品都是已知的,并且可以按任意顺序放置。Martello 等人 (2000) 首次使用精确的分支定界方法解决了这个问题。由于精确方法的最坏情况复杂度呈指数级增长,许多启发式和元启发式算法被提出以快速获得近似解,例如引导局部搜索 (Faroe 等人, 2003)、禁忌搜索 (Crainic 等人, 2009) 和混合遗传算法 (Kang 等人, 2012)。Hu 等人 (2017) 将离线 3D-BPP 分解为装箱顺序决策和在线放置决策。装箱顺序通过端到端的深度强化学习 (DRL) 智能体进行优化,而在线放置策略则采用手工设计的启发式方法。这种两步法被广泛接受,并被 Duan 等人 (2019)、Hu 等人 (2020) 和 Zhang 等人 (2021) 所沿用。
Heuristics for Online 3D-BPP Although offline 3D-BPP has been well studied, their searchbased approaches cannot be directly transferred to the online setting. Instead, lots of heuristic methods have been proposed to solve this problem. For reasons of simplicity and good performance, the deep-bottom-left (DBL) heuristic (Karabulut & Inceoglu, 2004) has long been a favorite. Ha et al. (2017) sort the empty spaces with this DBL order and place the current item into the first fit one. Wang & Hauser (2019b) propose a Heightmap-Minimization method to minimize the volume increase of the packed items as observed from the loading direction. Hu et al. (2020) optimize the empty spaces available for the packing future with a Maximize-Accessible-Convex-Space method.
在线三维装箱问题(3D-BPP)的启发式方法
尽管离线三维装箱问题已经得到了广泛研究,但其基于搜索的方法无法直接应用于在线场景。因此,许多启发式方法被提出以解决这一问题。由于简单性和良好的性能,深底左(DBL)启发式方法(Karabulut & Inceoglu, 2004)长期以来备受青睐。Ha 等人(2017)使用这种 DBL 顺序对空置空间进行排序,并将当前物品放入第一个合适的空间。Wang & Hauser(2019b)提出了一种高度图最小化方法,以最小化从装载方向观察到的已装物品的体积增加。Hu 等人(2020)通过最大化可访问凸空间方法优化了可用于未来装箱的空置空间。
DRL for Online 3D-BPP The heuristic methods are intuitive to implement and can be easily applied to various scenarios. However, the price of good fexibility is that these methods perform mediocrely, especially for online 3D-BPP with specific constraints. Designing new heuristics for specific classes of 3D-BPP is heavy work since this problem has an NP-hard solution space, many situations need to be premeditated manually by trial and error. Substantial domain knowledge is also necessary to ensure safety and reliability. To automatically generate a policy that works well on specified online 3D-BPP, Verma et al. (2020); Zha0 et al. (2021) employ the DRL method on solving this problem, however, their methods only work in small discrete coordinate spaces. Despite their limitations, these works are soon followed by Hong et al. (2020); Yang et al. (2021); Zhao et al. (2022) for logistics robot implementation. Zhang et al. (2021) adopt a similar online placement policy for offline packing needs referring to Hu et al. (2017). All these learning-based methods only work in a grid world with limited disc ret iz ation accuracy, which reduces their practical applicability.
DRL 用于在线 3D-BPP 的启发式方法直观且易于实现,可以轻松应用于各种场景。然而,良好灵活性的代价是这些方法表现平庸,特别是对于具有特定约束的在线 3D-BPP。为特定类别的 3D-BPP 设计新的启发式方法是一项繁重的工作,因为该问题的解空间是 NP 难的,许多情况需要通过试错手动预先考虑。此外,还需要大量的领域知识来确保安全性和可靠性。为了自动生成在指定在线 3D-BPP 上表现良好的策略,Verma 等人 (2020);Zha0 等人 (2021) 采用 DRL 方法来解决此问题,然而,他们的方法仅适用于小型离散坐标空间。尽管存在这些限制,这些工作很快被 Hong 等人 (2020);Yang 等人 (2021);Zhao 等人 (2022) 用于物流机器人实现。Zhang 等人 (2021) 参考 Hu 等人 (2017) 采用类似的在线放置策略来满足离线包装需求。所有这些基于学习的方法仅在具有有限离散化精度的网格世界中有效,这降低了它们的实际适用性。
Practical Constraints The majority of literature for 3D-BPP (Martello et al., 2000) only considers the basic non-overlapping constraint 1 and containment constraint 2:
实际约束
大多数关于3D-BPP(Martello等,2000)的文献仅考虑基本的非重叠约束1和包含约束2:
$$
\begin{array}{r l}{p_{i}^{d}+s_{i}^{d}\leq p_{j}^{d}+S^{d}(1-e_{i j}^{d})}&{i\not=j,i,j\in\mathbb{Z},d\in{x,y,z}}\ {0\leq p_{i}^{d}\leq S^{d}-s_{i}^{d}}&{i\in\mathbb{Z},d\in{x,y,z}}\end{array}
$$
$$
\begin{array}{r l}{p_{i}^{d}+s_{i}^{d}\leq p_{j}^{d}+S^{d}(1-e_{i j}^{d})}&{i\not=j,i,j\in\mathbb{Z},d\in{x,y,z}}\ {0\leq p_{i}^{d}\leq S^{d}-s_{i}^{d}}&{i\in\mathbb{Z},d\in{x,y,z}}\end{array}
$$
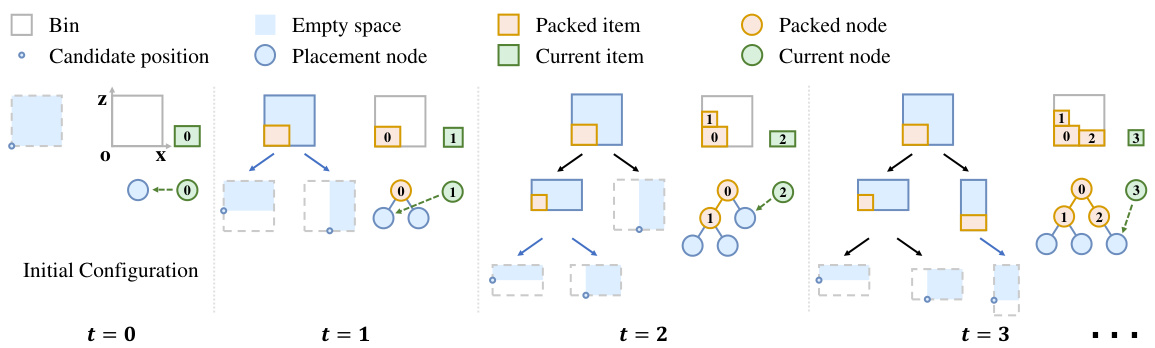
Figure 1: PCT expansion illustrated using a 2D example (in $x o z$ plane) for simplicity and the number of allowed O orientations $|\mathbf{O}|$ is 1 (see Appendix B for the 3D version). A newly added item introduces a series of empty spaces and new candidate placements are generated, e.g., the left-bottom corner of the empty space.
图 1: 使用二维示例(在 $x o z$ 平面中)简化说明 PCT 扩展,允许的 O 方向数量 $|\mathbf{O}|$ 为 1(3D 版本见附录 B)。新添加的物品引入了一系列空的空间,并生成了新的候选放置位置,例如空空间的左下角。
Where $p_{i}$ means the front-left-bottom coordinate of item $i$ and $d$ the coordinate axis, $e_{i j}$ takes value 1 otherwise O if item $i$ precedes item $j$ along $d$ .The algorithms for 3D-BPP are of limited practical applicability if no even basic real-world constraints, e.g., stability (Ramos et al., 2016), are considered. Zhao et al. (2022) propose a fast stability estimation method for DRL training and test their learned policies with real logistics boxes. The flaw of their work is the heightmap (the upper frontier of packed items) state representation like Zhang et al. (2021) is still used, while the underlying constraints between packed items are missed. The un availability of underlying spatial information makes their problem a partially observable Markov Decision Process (Spaan, 2012) which is not conducive to DRL training and limits the performance on 3D-BPP instances with more complex practical constraints, like isle friendliness and load balancing (Gzara et al., 2020).
其中 $p_{i}$ 表示物品 $i$ 的前-左-下坐标,$d$ 表示坐标轴,$e_{i j}$ 在物品 $i$ 沿 $d$ 轴先于物品 $j$ 时取值为 1,否则为 0。如果不考虑基本的现实约束(例如稳定性 (Ramos et al., 2016)),3D-BPP 算法的实际应用性将受到限制。Zhao 等人 (2022) 提出了一种用于深度强化学习 (DRL) 训练的快速稳定性估计方法,并使用真实的物流箱测试了他们学习到的策略。他们工作的缺陷在于仍然使用了类似于 Zhang 等人 (2021) 的高度图(已打包物品的上边界)状态表示,而忽略了已打包物品之间的底层约束。底层空间信息的缺失使得他们的问题成为一个部分可观测的马尔可夫决策过程 (Spaan, 2012),这不利于 DRL 训练,并限制了在具有更复杂实际约束(如通道友好性和负载平衡 (Gzara et al., 2020))的 3D-BPP 实例中的性能。
3 METHOD
3 方法
In this section, we first introduce our PCT concept in Section 3.1 for describing the online packing process. The parameter iz ation of the tree structure and the leaf node selection policy are introduced in Section 3.2 and Section 3.3 respectively. In Section 3.4, we formulate online 3D-BPP as Markov Decision Process based on PCT, followed by the description of the training method.
在本节中,我们首先在第3.1节中介绍了用于描述在线装箱过程的PCT概念。树结构的参数化以及叶节点选择策略分别在第3.2节和第3.3节中介绍。在第3.4节中,我们基于PCT将在线3D-BPP(三维装箱问题)表述为马尔可夫决策过程,随后描述了训练方法。
3.1 PACKING CONFIGURATION TREE
3.1 包装配置树
When a rectangular item $n_{t}$ is added to a given packing with position $(p_{n}^{x},p_{n}^{y},p_{n}^{z})$ at time step $t$ , it introduces a series of new candidate positions where future items can be accommodated, as illustrated in Figure 1. Combined with the axis-aligned orientation $o\in{\bf O}$ for $n_{t}$ based on existing positions, we get candidate placements (i.e. position and orientation). The packing process can be seen as a placement node being replaced by a packed item node, and new candidate placement nodes are generated as children. As the packing time step $t$ goes on, these nodes are iterative ly updated and a dynamic packing configuration tree is formed, denoted as $\tau$ . The internal node set $\mathbf{B}{t}\in\mathcal{T}{t}$ represents the space configurations of packed items, and the leaf node set $\mathbf{L}{t}\in\mathcal{T}{t}$ the packable candidate placements. During the packing, leaf nodes that are no longer feasible, e.g., covered by packed items, will be removed from $\mathbf{L}{t}$ . When there is no packable leaf node that makes $n{t}$ satisfy the constraints of placement, the packing episode ends. Without loss of generality, we stipulate a vertical top-down packing within a single bin (Wang & Hauser, 2019b).
当一个矩形物品 $n_{t}$ 在时间步 $t$ 被添加到给定的装箱中,位置为 $(p_{n}^{x},p_{n}^{y},p_{n}^{z})$ 时,它会引入一系列新的候选位置,未来的物品可以放置在这些位置,如图 1 所示。结合基于现有位置的轴对齐方向 $o\in{\bf O}$ 为 $n_{t}$ 确定方向,我们得到候选放置(即位置和方向)。装箱过程可以看作是一个放置节点被一个已装箱物品节点替换,并生成新的候选放置节点作为子节点。随着装箱时间步 $t$ 的进行,这些节点会迭代更新,形成一个动态装箱配置树,记为 $\tau$。内部节点集 $\mathbf{B}{t}\in\mathcal{T}{t}$ 表示已装箱物品的空间配置,叶节点集 $\mathbf{L}{t}\in\mathcal{T}{t}$ 表示可装箱的候选放置。在装箱过程中,不再可行的叶节点(例如被已装箱物品覆盖的节点)将从 $\mathbf{L}{t}$ 中移除。当没有可装箱的叶节点使得 $n{t}$ 满足放置约束时,装箱过程结束。在不失一般性的情况下,我们规定在单个箱子内进行垂直自上而下的装箱 (Wang & Hauser, 2019b)。
Traditional 3D-BPP literature only cares about the remaining placements for accommodating the current item $n_{t}$ , their packing policies can be written as $\pi({\bf L}{t}|{\bf L}{t},n_{t})$ . If we want to promote this problem for practical demands, 3D-BPP needs to satisfy more complex practical constraints which also act on $\mathbf{B}{t}$ . Taking packing stability for instance, a newly added item $n{t}$ has possibly force and torque effect on the whole item set $\mathbf{B}{t}$ (Ramos et al., 2016). The addition of $n{t}$ should make $\mathbf{B}{t}$ a more stable spatial distribution so that more items can be added in the future. Therefore, our packing policy over $\mathbf{L}{t}$ is defined as $\pi(\mathbf{L}{t}|\mathcal{T}{t},n_{t})$ , which means probabilities of selecting leaf nodes from $\mathbf{L}{t}$ given $\mathcal{T}{t}$ and $n_{t}$ . For online packing, we hope to find the best leaf node selection policy to expand the PCT with more relaxed constraints so that more future items can be appended.
传统的3D-BPP文献仅关注于容纳当前物品 $n_{t}$ 的剩余放置位置,其打包策略可以表示为 $\pi({\bf L}{t}|{\bf L}{t},n_{t})$ 。如果我们希望将这一问题推广到实际需求中,3D-BPP需要满足更多复杂的实际约束,这些约束也作用于 $\mathbf{B}{t}$ 。以打包稳定性为例,新添加的物品 $n{t}$ 可能对整个物品集 $\mathbf{B}{t}$ 产生力和扭矩效应 (Ramos et al., 2016) 。添加 $n{t}$ 应使 $\mathbf{B}{t}$ 的空间分布更加稳定,以便未来可以添加更多物品。因此,我们对 $\mathbf{L}{t}$ 的打包策略定义为 $\pi(\mathbf{L}{t}|\mathcal{T}{t},n_{t})$ ,这意味着在给定 $\mathcal{T}{t}$ 和 $n{t}$ 的情况下,从 $\mathbf{L}_{t}$ 中选择叶节点的概率。对于在线打包,我们希望找到最佳的叶节点选择策略,以扩展PCT并放宽约束,以便未来可以添加更多物品。
Leaf Node Expansion Schemes The performance of online 3D-BPP policies has a strong relationship with the choice of leaf node expansion schemes ——- which increment ally calculate new candidate placements introduced by the just placed item $n_{t}$ . A good expansion scheme should reduce the number of solutions to be explored while not missing too many feasible packings. Meanwhile, polynomial ly computability is also expected. Designing such a scheme from scratch is non-trivial. Fortunately, several placement rules independent from particular packing problems have been proposed, such as Corner Point (Martello et al., 2000), Extreme Point (Crainic et al., 2008), and Empty Maximal Space (Ha et al., 2017). We extend these schemes which have proven to be accurate and efficient to our PCT expansion. The performance of learned policies will be reported in Section 4.1.
叶节点扩展方案
在线 3D-BPP 策略的性能与叶节点扩展方案的选择密切相关——这些方案逐步计算由刚刚放置的物品 $n_{t}$ 引入的新候选放置位置。一个好的扩展方案应减少需要探索的解的数量,同时不遗漏太多可行的装箱方案。此外,还需要具备多项式可计算性。从头设计这样的方案并非易事。幸运的是,已经提出了一些与特定装箱问题无关的放置规则,例如角点 (Corner Point) (Martello et al., 2000)、极点 (Extreme Point) (Crainic et al., 2008) 和最大空空间 (Empty Maximal Space) (Ha et al., 2017)。我们将这些已被证明准确且高效的方案扩展到我们的 PCT 扩展中。学习策略的性能将在第 4.1 节中报告。
3.2 TREE REPRESENTATION
3.2 树表示
Given the bin configuration $\mathcal{T}{t}$ and the current item $n{t}$ , the packing policy can be parameterized as $\pi(\mathbf{L}{t}|\mathcal{T}{t},n_{t})$ . The tuple $(\mathcal{T}{t},n{t})$ can be treated as a graph and encoded by Graph Neural Networks (GNNs) (Gori et al., 2005). Specifically, the PCT keeps growing with time step $t$ and cannot be embedded by spectral-based approaches (Bruna et al., 2014) which require a fixed graph structure. We adopt non-spectral Graph Attention Networks (GATs) (Velickovic et al., 2018), which require no priori on graph structures.
给定箱子配置 $\mathcal{T}{t}$ 和当前物品 $n{t}$,打包策略可以参数化为 $\pi(\mathbf{L}{t}|\mathcal{T}{t},n_{t})$。元组 $(\mathcal{T}{t},n{t})$ 可以被视为一个图,并通过图神经网络 (GNNs) (Gori et al., 2005) 进行编码。具体来说,PCT 随着时间的推移 $t$ 不断增长,无法通过基于谱的方法 (Bruna et al., 2014) 进行嵌入,因为这些方法需要固定的图结构。我们采用非谱图注意力网络 (GATs) (Velickovic et al., 2018),这些网络不需要图结构的先验知识。
The raw space configuration nodes $\mathbf{B}{t},\mathbf{L}{t},n_{t}$ are presented by descriptors in different formats. We use three independent node-wise Multi-Layer Perceptron (MLP) blocks to project these heterogeneous descriptors into the homogeneous node features: $\hat{\textbf{h}}={\phi_{\theta_{B}}(\mathbf{B}{t}),\phi{\theta_{L}}(\mathbf{L}{t}),\phi{\theta_{n}}(n_{t})}\in$ $\mathbf{\check{\mathbb{R}}}^{d_{h}\times N}$ , $d_{h}$ is the dimension of each node feature and $\phi_{\theta}$ is an MLP block with its parameters $\theta$ The feature number $N$ should be $\left|{\bf B}{t}\right|+\left|{\bf L}{t}\right|+1$ , which is a variable. The GAT layer is used to transform $\hat{\mathbf{h}}$ into high-level node features. The Scaled Dot-Product Attention (Vaswani et al., 2017) is applied to each node for calculating the relation weight of one node to another. These relation weights are normalized and used to compute the linear combination of features h. The feature of node $i$ embedded by the GAT layer can be represented as:
原始空间配置节点 $\mathbf{B}{t},\mathbf{L}{t},n_{t}$ 由不同格式的描述符表示。我们使用三个独立的节点级多层感知器 (MLP) 块将这些异构描述符投影为同构节点特征:$\hat{\textbf{h}}={\phi_{\theta_{B}}(\mathbf{B}{t}),\phi{\theta_{L}}(\mathbf{L}{t}),\phi{\theta_{n}}(n_{t})}\in$ $\mathbf{\check{\mathbb{R}}}^{d_{h}\times N}$,其中 $d_{h}$ 是每个节点特征的维度,$\phi_{\theta}$ 是一个带有参数 $\theta$ 的 MLP 块。特征数量 $N$ 应为 $\left|{\bf B}{t}\right|+\left|{\bf L}{t}\right|+1$,这是一个变量。GAT 层用于将 $\hat{\mathbf{h}}$ 转换为高级节点特征。缩放点积注意力 (Vaswani et al., 2017) 应用于每个节点,以计算一个节点与另一个节点的关系权重。这些关系权重被归一化并用于计算特征 h 的线性组合。由 GAT 层嵌入的节点 $i$ 的特征可以表示为:

Where $W^{Q}\in\mathbb{R}^{d_{k}\times d_{h}}$ , $W^{K}\in\mathbb{R}^{d_{k}\times d_{h}}$ , $W^{V}\in\mathbb{R}^{d_{v}\times d_{h}}$ 2 and $W^{O}\in\mathbb{R}^{d_{h}\times d_{v}}$ are projection matrices, $d_{k}$ and $d_{v}$ are dimensions of projected features. The softmax operation normalizes the relation weight between node $i$ and node $j$ . The initial feature $\hat{\mathbf{h}}$ is embedded by a GAT layer and the skip-connection operation (Vaswani et al., 2017) is followed to get the final output features $\mathbf{h}$
其中 $W^{Q}\in\mathbb{R}^{d_{k}\times d_{h}}$ , $W^{K}\in\mathbb{R}^{d_{k}\times d_{h}}$ , $W^{V}\in\mathbb{R}^{d_{v}\times d_{h}}$ 和 $W^{O}\in\mathbb{R}^{d_{h}\times d_{v}}$ 是投影矩阵, $d_{k}$ 和 $d_{v}$ 是投影特征的维度。softmax 操作对节点 $i$ 和节点 $j$ 之间的关系权重进行归一化。初始特征 $\hat{\mathbf{h}}$ 通过 GAT 层嵌入,并采用跳跃连接操作 (Vaswani et al., 2017) 来获得最终输出特征 $\mathbf{h}$ 。

Where $\phi_{F F}$ is a node-wise Feed-Forward MLP with output dimension $d_{h}$ and $\mathbf{h}^{\prime}$ is an intermediate variable. Equation 4 can be seen as an independent block and be repeated multiple times with different parameters. We don't extend GAT to employ the multi-head attention mechanism (Vaswani et al., 2017) since we find that additional attention heads cannot help the final performance. We execute Equation 4 once and we set $d_{v}=d_{k}$ . More implementation details are provided in Appendix A.
其中 $\phi_{F F}$ 是一个节点级的前馈 MLP (Feed-Forward MLP),输出维度为 $d_{h}$,$\mathbf{h}^{\prime}$ 是一个中间变量。公式 4 可以看作一个独立的模块,并且可以使用不同的参数重复多次。我们没有将 GAT 扩展到使用多头注意力机制 (Vaswani et al., 2017),因为我们发现额外的注意力头并不能帮助提升最终性能。我们执行公式 4 一次,并设置 $d_{v}=d_{k}$。更多实现细节见附录 A。
3.3LEAF NODE SELECTION
3.3 叶子节点选择
Given the node features $\mathbf{h}$ , we need to decide the leaf node indices for accommodating the current item $n_{t}$ . Since the leaf nodes vary as the PCT keeps growing over time step $t$ , we use a pointer mechanism (Vinyals et al., 2015) which is context-based attention over variable inputs to select a leaf node from $\mathbf{L}{t}$ . We still adopt Scaled Dot-Product Attention for calculating pointers, the global context feature $\bar{h}$ is aggregated by a mean operation on $\mathbf{h}$ $\begin{array}{r}{\bar{h}=\frac{1}{N}\sum{i=1}^{N}h_{i}}\end{array}$ . The global feature $\bar{h}$ .s projected to a query $q$ by matrix $W^{q}\in\mathbb{R}^{d_{k}\times d_{h}}$ and the leaf node features $\mathbf{h}{\mathbf{L}}$ are utilized to calculate a set of keys $k{\mathbf{L}}$ by $\dot{W}^{k}\in\mathbb{R}^{d_{k}\times d_{h}}$ . The compatibility $\mathbf{u_{L}}$ of the query with all keys are:
给定节点特征 $\mathbf{h}$,我们需要决定用于容纳当前项目 $n_{t}$ 的叶节点索引。由于叶节点随着 PCT 在时间步 $t$ 的不断增长而变化,我们使用了一种指针机制 (Vinyals et al., 2015),该机制基于上下文对可变输入进行注意力选择,以从 $\mathbf{L}{t}$ 中选择一个叶节点。我们仍然采用缩放点积注意力 (Scaled Dot-Product Attention) 来计算指针,全局上下文特征 $\bar{h}$ 通过对 $\mathbf{h}$ 进行均值操作来聚合:$\begin{array}{r}{\bar{h}=\frac{1}{N}\sum{i=1}^{N}h_{i}}\end{array}$。全局特征 $\bar{h}$ 通过矩阵 $W^{q}\in\mathbb{R}^{d_{k}\times d_{h}}$ 投影为查询 $q$,叶节点特征 $\mathbf{h}{\mathbf{L}}$ 通过 $\dot{W}^{k}\in\mathbb{R}^{d{k}\times d_{h}}$ 计算一组键 $k_{\mathbf{L}}$。查询与所有键的兼容性 $\mathbf{u_{L}}$ 为:

Here $h_{i}$ only comes from $\mathbf{h}{\mathbf{L}}$ . The compatibility vector $\mathbf{u}{\mathbf{L}}\in\mathbb{R}^{|\mathbf{L}{t}|}$ represents the leaf node selection logits. The probability distribution over the PCT leaf nodes $\mathbf{L}{t}$ is:
这里 $h_{i}$ 仅来自 $\mathbf{h}{\mathbf{L}}$ 。兼容性向量 $\mathbf{u}{\mathbf{L}}\in\mathbb{R}^{|\mathbf{L}{t}|}$ 表示叶节点选择的 logits。PCT 叶节点 $\mathbf{L}{t}$ 上的概率分布为:

Following Bello et al. (2017), the compatibility logits are clipped with tanh, where the range is controlled by hyper parameter $c_{c l i p}$ , and finally normalized by a softmax operation.
根据 Bello et al. (2017) 的研究,兼容性 logits 通过 tanh 进行裁剪,其范围由超参数 $c_{c l i p}$ 控制,最后通过 softmax 操作进行归一化。
3.4 MARKOV DECISION PROCESS FORMULATION
3.4 马尔可夫决策过程 (Markov Decision Process) 公式化
The online 3D-BPP decision at time step $t$ only depends on the tuple $(\mathcal{T}{t},n{t})$ and can be formulated as Markov Decision Process, which is constructed with state $s$ action $\mathcal{A}$ , transition $\mathcal{P}$ , and reward $R$ . We solve this MDP with an end-to-end DRL agent. The MDP model is formulated as follows.
在线 3D-BPP 决策在时间步 $t$ 仅依赖于元组 $(\mathcal{T}{t},n{t})$ ,可以表述为马尔可夫决策过程 (Markov Decision Process, MDP) ,该过程由状态 $s$ 、动作 $\mathcal{A}$ 、转移 $\mathcal{P}$ 和奖励 $R$ 构成。我们通过一个端到端的深度强化学习 (Deep Reinforcement Learning, DRL) 智能体来解决这个 MDP。MDP 模型表述如下。
State The state $s_{t}$ at time step $t$ is represented as $s_{t}=(\mathcal{T}{t},n{t})$ , where $\tau_{t}$ consists of the internal nodes $\mathbf{B}{t}$ and the leaf nodes $\mathbf{L}{t}$ . Each internal node $b\in\mathbf{B}{t}$ is a spatial configuration of sizes $\left(s{b}^{x},s_{b}^{y},s_{b}^{z}\right)$ and coordinates $(p_{b}^{x},p_{b}^{y},p_{b}^{z})$ corresponding to a packed item. The current item $n_{t}$ is a size tuple (sn, sn, $\left(s_{n}^{x},s_{n}^{y},s_{n}^{z}\right)$ Extra proper tis will b appended t $b$ and $n_{t}$ for specific packing preferences, such as density, item category, etc. The descriptor for leaf node $l\in\mathbf{L}{t}$ is a placement vector of sizes $\left(s{o}^{x},s_{o}^{y},s_{o}^{z}\right)$ and position coordinates $(p^{x},p^{y},p^{z})$ , where $\left(s_{o}^{x},s_{o}^{y},s_{o}^{z}\right)$ indicates the sizes of $n_{t}$ along each dimension after an axis-aligned orientation $o\in{\bf O}$ . Only the packable leaf nodes which satisfy placement constraints are provided.
状态 时间步 $t$ 的状态 $s_{t}$ 表示为 $s_{t}=(\mathcal{T}{t},n{t})$,其中 $\tau_{t}$ 由内部节点 $\mathbf{B}{t}$ 和叶节点 $\mathbf{L}{t}$ 组成。每个内部节点 $b\in\mathbf{B}{t}$ 是一个空间配置,大小为 $\left(s{b}^{x},s_{b}^{y},s_{b}^{z}\right)$,坐标为 $(p_{b}^{x},p_{b}^{y},p_{b}^{z})$,对应于一个已打包的物品。当前物品 $n_{t}$ 是一个大小元组 (sn, sn, $\left(s_{n}^{x},s_{n}^{y},s_{n}^{z}\right)$。额外的属性将被附加到 $b$ 和 $n_{t}$ 上,以满足特定的打包偏好,例如密度、物品类别等。叶节点 $l\in\mathbf{L}{t}$ 的描述符是一个放置向量,大小为 $\left(s{o}^{x},s_{o}^{y},s_{o}^{z}\right)$,位置坐标为 $(p^{x},p^{y},p^{z})$,其中 $\left(s_{o}^{x},s_{o}^{y},s_{o}^{z}\right)$ 表示 $n_{t}$ 在轴对齐方向 $o\in{\bf O}$ 后沿每个维度的大小。仅提供满足放置约束的可打包叶节点。
Action The action $a_{t}\in\mathcal{A}$ is the index of the selected leaf node $l$ , denoted as $a_{t}=i n d e x(l)$ The action space $\mathcal{A}$ has the same size as $\mathbf{L}{t}$ . A surge of learning-based methods (Zhao et al., 2021) directly learn their policy on a grid world through disc ret i zing the full coordinate space, where $|{\mathcal{A}}|$ grows explosively with the accuracy of the disc ret iz ation. Different from existing works, our action space solely depends on the leaf node expansion scheme and the packed items $\mathbf{B}{t}$ . Therefore, our method can be used to solve online 3D-BPP with continuous solution space. We also find that even if only an intercepted subset $\mathbf{L}{s u b}\in\mathbf{L}{t}$ is provided, our method can still maintain a good performance.
动作 $a_{t}\in\mathcal{A}$ 是所选叶子节点 $l$ 的索引,表示为 $a_{t}=index(l)$。动作空间 $\mathcal{A}$ 的大小与 $\mathbf{L}{t}$ 相同。基于学习的方法(Zhao 等,2021)通过将整个坐标空间离散化,直接在网格世界上学习其策略,其中 $|{\mathcal{A}}|$ 随着离散化精度的提高而爆炸性增长。与现有工作不同,我们的动作空间仅取决于叶子节点扩展方案和打包物品 $\mathbf{B}{t}$。因此,我们的方法可用于解决具有连续解空间的在线 3D-BPP。我们还发现,即使只提供截取的子集 $\mathbf{L}{sub}\in\mathbf{L}{t}$,我们的方法仍然可以保持良好的性能。
Transition The transition $\mathcal{P}(s_{t+1}|s_{t})$ is jointly determined by the current policy $\pi$ and theprobability distribution of sampling items. Our online sequences are generated on-the-fly from an item set $\mathcal{T}$ in a uniform distribution. The generalization performance of our method on item sampling distributions different from the training one is discussed in Section 4.4.
转移概率 $\mathcal{P}(s_{t+1}|s_{t})$ 由当前策略 $\pi$ 和采样项的概率分布共同决定。我们的在线序列是从一个均匀分布的项集 $\mathcal{T}$ 中动态生成的。关于我们的方法在不同于训练分布的项采样分布上的泛化性能,将在第 4.4 节中讨论。
Reward Our reward function $R$ is defined as $\boldsymbol{r}{t}=\boldsymbol{c}{r}\cdot\boldsymbol{w}{t}$ once $n{t}$ is inserted into PCT as an internal node successfully, otherwise, $r_{t}=0$ and the packing episode ends. Here $c_{r}$ is a constant and $w_{t}$ is the weight of $n_{t}$ . The choice of $w_{t}$ depends on the customized needs. For simplicity and clarity, unless otherwise noted, we set $w_{t}$ as the volume occupancy $v_{t}$ f $n_{t}$ , where $v_{t}=s_{n}^{x}\cdot s_{n}^{y}\cdot s_{n}^{z}$
奖励 我们的奖励函数 $R$ 定义为 $\boldsymbol{r}{t}=\boldsymbol{c}{r}\cdot\boldsymbol{w}{t}$,当 $n{t}$ 成功插入 PCT 作为内部节点时,否则 $r_{t}=0$,并且打包过程结束。这里 $c_{r}$ 是一个常数,$w_{t}$ 是 $n_{t}$ 的权重。$w_{t}$ 的选择取决于定制需求。为了简单和清晰起见,除非另有说明,我们将 $w_{t}$ 设置为 $n_{t}$ 的体积占用 $v_{t}$,其中 $v_{t}=s_{n}^{x}\cdot s_{n}^{y}\cdot s_{n}^{z}$。
Training Method A DRL agent seeks for a policy $\pi(\boldsymbol{a}{t}|\boldsymbol{s}{t})$ to maximize the accumulated discounted reward. Our DRL agent is trained with the ACKTR method (Wu et al., 2017). The actor weighs the leaf nodes $\mathbf{L}{t}$ and outputs the policy distribution $\pi{\boldsymbol{\theta}}(\mathbf{L}{t}|\mathcal{T}{t},n_{t})$ . The critic maps the global context h into a state value prediction to predict how much accumulated discount reward the agent can get from $t$ and helps the training of the actor. The action $a_{t}$ is sampled from the distribution $\pi_{\theta}(\bar{\mathbf{L}{t}}|\mathcal{T}{t},n_{t})$ for training and we take the argmax of the policy for the test.
训练方法
一个 DRL 智能体寻求策略 $\pi(\boldsymbol{a}{t}|\boldsymbol{s}{t})$ 以最大化累积折扣奖励。我们的 DRL 智能体使用 ACKTR 方法进行训练 (Wu et al., 2017)。执行者 (actor) 对叶节点 $\mathbf{L}{t}$ 进行加权,并输出策略分布 $\pi{\boldsymbol{\theta}}(\mathbf{L}{t}|\mathcal{T}{t},n_{t})$。评论者 (critic) 将全局上下文 h 映射为状态值预测,以预测智能体从 $t$ 开始可以获得多少累积折扣奖励,并帮助执行者的训练。动作 $a_{t}$ 从分布 $\pi_{\theta}(\bar{\mathbf{L}{t}}|\mathcal{T}{t},n_{t})$ 中采样用于训练,而在测试时我们取策略的 argmax。
ACKTR runs multiple parallel processes for gathering on-policy training samples. The node number $N$ of each sample varies with the time step $t$ and the packing sequence of each process. For batch calculation, we fullfill PCT to a fixed length with dummy nodes, as illustrated by Figure 2 (a). These redundant nodes are eliminated by masked attention (Velickovic et al., 2018) during the feature calculation of GAT. The aggregation of h only happens on the eligible nodes. For preserving node spatial relations, state $s_{t}$ is embedded by GAT as a fully connected graph as Figure 2 (b), without any inner mask operation. More implementation details are provided in Appendix A.
ACKTR 运行多个并行进程来收集策略内训练样本。每个样本的节点数 $N$ 随时间步 $t$ 和每个进程的打包顺序而变化。为了进行批量计算,我们用虚拟节点将 PCT 填充到固定长度,如图 2 (a) 所示。这些冗余节点在 GAT 的特征计算过程中通过掩码注意力 (Velickovic et al., 2018) 被消除。h 的聚合仅发生在符合条件的节点上。为了保留节点的空间关系,状态 $s_{t}$ 通过 GAT 嵌入为一个全连接图,如图 2 (b) 所示,没有任何内部掩码操作。更多实现细节见附录 A。
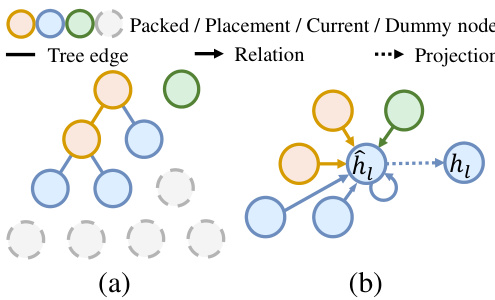
Figure 2: Batch calculation for PCT.

图 2: PCT 的批量计算。
4 EXPERIMENTS
4 实验
In this section, we first report the performance of our PCT model combined with different leaf node expansion schemes. Then we will demonstrate the benefits of the PCT structure: better node spatial relation representations as well as more fexible action space. Finally, we test the generalization performance of our method and extend it to other online 3D-BPP with complex practical constraints.
在本节中,我们首先报告了我们的 PCT 模型结合不同叶节点扩展方案的性能。然后我们将展示 PCT 结构的优势:更好的节点空间关系表示以及更灵活的动作空间。最后,我们测试了我们方法的泛化性能,并将其扩展到具有复杂实际约束的其他在线 3D-BPP 问题。
Baselines Although there are very few online packing implementations publicly available, we still do our best to collect or reproduce various online 3D-BPP algorithms, both heuristic and learningbased, from potentially relevant literature. We help the heuristic methods to make a pre-judgment of placement constraints, e.g., stability, in case of premature downtime. The learning-based agents are trained until there are no significant performance gains. Although both Zhao et al. (2022) and Zhao et al. (2021) are learning-based methods recently proposed, we only compare with the former since it is the upgrade of the latter. We also compare with the reported results of Zhang et al. (2021) under the same condition. All methods are implemented in Python and tested on 2oo0 instances with a desktop computer equipped with a Gold 5117 CPU and a GeForce TITAN V GPU. We publish the source code of our method along with related baselines at Github1.
基线方法
尽管公开可用的在线装箱实现非常少,我们仍然尽力从相关文献中收集或复现各种在线3D-BPP(三维装箱问题)算法,包括启发式方法和基于学习的方法。我们帮助启发式方法在提前停机的情况下对放置约束(例如稳定性)进行预判。基于学习的AI智能体则训练到性能不再显著提升为止。尽管Zhao等人 (2022) 和Zhao等人 (2021) 都是最近提出的基于学习的方法,但我们仅与前者进行比较,因为它是后者的升级版本。我们还在相同条件下与Zhang等人 (2021) 的报告结果进行了比较。所有方法均使用Python语言实现,并在配备Gold 5117 CPU和GeForce TITAN V GPU的台式计算机上对2000个实例进行了测试。我们在Github上发布了我们方法的源代码及相关基线方法。
Datasets Some baselines like Karabulut & Inceoglu (2004) need to traverse the entire coordinate space to find the optimal solution, and the running costs explode as the spatial disc ret iz ation accuracy increases. To ensure that all algorithms are runnable within a reasonable period, we use the discrete dataset proposed by Zhao et al. (2021) without special declaration. The bin sizes $S^{d}$ areset to 10 With $d\in{x,y,z}$ and the item sizes $s^{d}\in\mathbb{Z}^{+}$ are not greater than $S^{d}/2$ to avoid over-simplified scenarios. Our performance on a more complex continuous dataset will be reported in Section 4.3. Considering that there are many variants of 3D-BPP, we choose three representative settings:
数据集
一些基线方法如 Karabulut & Inceoglu (2004) 需要遍历整个坐标空间以找到最优解,随着空间离散化精度的提高,运行成本会急剧增加。为了确保所有算法在合理的时间内可运行,我们在没有特殊声明的情况下使用了 Zhao 等人 (2021) 提出的离散数据集。bin 的大小 $S^{d}$ 设置为 10,其中 $d\in{x,y,z}$,且物品大小 $s^{d}\in\mathbb{Z}^{+}$ 不超过 $S^{d}/2$,以避免过于简化的场景。我们在更复杂的连续数据集上的表现将在第 4.3 节中报告。考虑到 3D-BPP 有许多变体,我们选择了三种具有代表性的设置:
Setting 1: Following Zhao et al. (2022), the stability of the $\mathbf{B}{t}$ is checked when $n{t}$ is placed. Only two horizontal orientations ( $|\mathbf{O}|=2)$ are permitted for robot manipulation convenience. Setting 2: Following Martello et al. (2000), item $n_{t}$ only needs to satisfy Constraint 1 and 2. Arbitrary orientation ( $|\mathbf{0}|=6\$ is allowed here. This is the most common setting in 3D-BPP literature. Setting 3: Inherited from setting 1, each item $n_{t}$ has an additional density property $\rho$ sampled from $(0,1]$ uniformly. This information is appended into the descriptors of $\mathbf{B}{t}$ and $n{t}$
设置 1: 按照 Zhao 等人 (2022) 的方法,当放置 $n_{t}$ 时,检查 $\mathbf{B}{t}$ 的稳定性。为了方便机器人操作,只允许两种水平方向 ($|\mathbf{O}|=2$)。
设置 2: 按照 Martello 等人 (2000) 的方法,物品 $n{t}$ 只需要满足约束 1 和 2。这里允许任意方向 ($|\mathbf{0}|=6$)。这是 3D-BPP 文献中最常见的设置。
设置 3: 继承自设置 1,每个物品 $n_{t}$ 都有一个额外的密度属性 $\rho$,从 $(0,1]$ 中均匀采样。此信息被附加到 $\mathbf{B}{t}$ 和 $n{t}$ 的描述符中。
4.1 PERFORMANCE OF PCT POLICIES
4.1 PCT 策略的性能
We first report the performance of our PCT model combined with different leaf node expansion schemes. Three existing schemes which have proven to be both efficient and effective are adopted here: Corner Point (CP), Extreme Point (EP), and Empty Maximal Space (EMS). These schemes are all related to boundary points of a packed item along $d$ axis. We combine the start/end points of $n_{t}$ with the boundary points of $b\in\mathbf{B}{t}$ to get the superset, namely Event Point (EV). See Appendix B for details and learning curves. We extend these schemes to our PCT model. Although the number of leaf nodes generated by these schemes is within a reasonable range, we only randomly intercept a subset $\mathbf{L}{s u b_{t}}$ from $\mathbf{L}{t}$ if $\left\vert\dot{\mathbf{L}}{t}\right\vert$ exceeds a certain length, for saving computing resources. The interception length is a constant during training and determined by a grid search (GS) during the test. See Appendix A for implementation details. The performance comparisons are summarized in Table 1.
我们首先报告了我们的 PCT 模型结合不同叶节点扩展方案的性能。这里采用了三种已被证明既高效又有效的现有方案:角点 (Corner Point, CP)、极点 (Extreme Point, EP) 和空最大空间 (Empty Maximal Space, EMS)。这些方案都与沿 $d$ 轴的打包物品的边界点相关。我们将 $n_{t}$ 的起点/终点与 $b\in\mathbf{B}{t}$ 的边界点结合,得到超集,即事件点 (Event Point, EV)。详见附录 B 中的细节和学习曲线。我们将这些方案扩展到我们的 PCT 模型中。尽管这些方案生成的叶节点数量在合理范围内,但如果 $\left\vert\dot{\mathbf{L}}{t}\right\vert$ 超过一定长度,我们仅从 $\mathbf{L}{t}$ 中随机截取一个子集 $\mathbf{L}{s u b_{t}}$,以节省计算资源。截取长度在训练期间为常数,并在测试期间通过网格搜索 (Grid Search, GS) 确定。详见附录 A 中的实现细节。性能比较总结在表 1 中。
Table 1: Performance comparisons. Uti. and Num. mean the average space utilization and the average number of packed items separately.Var. $(\times10^{-3})$ is the variance of Uti. and Gap is w.r.t. the best Uti. across all methods. Random and Random & EV randomly pick placements from full coordinates and full EV nodes respectively. DBL, LSAH, MACS, and BR are heuristic methods proposed by Karabulut & Inceoglu (2004), Hu et al. (2017), Hu et al. (2020), and Zhao et al. (2021). Ha et al. (2017), LSAH, and BR are heuristics based on EMS.
'https://github.com/alex from 0815/Online-3D-BPP-PCT
表 1: 性能对比。Uti. 和 Num. 分别表示平均空间利用率和平均打包物品数量。Var. $(\times10^{-3})$ 是 Uti. 的方差,Gap 是与所有方法中最佳 Uti. 的差距。Random 和 Random & EV 分别从完整坐标和完整 EV 节点中随机选择放置位置。DBL、LSAH、MACS 和 BR 是 Karabulut & Inceoglu (2004)、Hu et al. (2017)、Hu et al. (2020) 和 Zhao et al. (2021) 提出的启发式方法。Ha et al. (2017)、LSAH 和 BR 是基于 EMS 的启发式方法。
| 方法 | 随机 | Setting1 Uti. | Var. Num. | Gap | Uti. | Var. Num. | Gap | Uti. | Var. Num. | Gap |
|---|---|---|---|---|---|---|---|---|---|---|
| 随机 | 36.7% | 10.3 | 14.9 | 51.7% | 38.6% | 8.3 | 15.7 | 55.1% | 36.8% | 10.6 |
| BR | 22.6 | 34.1% | 48.9% | 10.7 | 19.5 | 35.4% | ||||
| Ha et al. | 49.0% | 52.1% | 10.8 | 20.1 | 19.6 | 20.6 | 35.5% | 31.4% | 56.7% | 59.9% |
| LSAH | 52.5% | 12.2 | 20.8 | 30.9% | 65.0% | 6.1 | 25.6 | 24.4% | 52.4% | 12.2 |
| Wang&Hauser | 57.6% | 11.5 | 24.1 | 24.2% | 66.1% | 8.4 | 25.9 | 23.1% | 56.5% | 11.2 |
| MACS | 57.7% | 10.5 | 22.6 | 24.1% | 50.8% | 8.8 | 20.1 | 40.9% | 57.7% | 10.6 |
| DBL | 60.5% | 8.8 | 23.8 | 20.4% | 70.6% | 7.9 | 27.8 | 17.9% | 60.5% | 8.9 |
| Zhao et al. | 70.9% | 6.2 | 27.5 | 6.7% | 70.3% | 4.3 | 27.4 | 18.3% | 59.6% | 5.4 |
| PCT&CP | 69.4% | 5.4 | 26.7 | 8.7% | 81.8% | 2.0 | 31.3 | 4.9% | 69.5% | 5.4 |
| PCT&EP | 71.9% | 6.6 | 27.8 | 5.4% | 78.1% | 3.8 | 30.3 | 9.2% | 72.2% | 5.8 |
| PCT&FC | 72.4% | 4.7 | 28.0 | 4.7% | 76.9% | 3.3 | 29.7 | 10.6% | 69.8% | 5.3 |
| PCT&EMS | 75.8% | 4.4 | 29.3 | 29.4 | 0.3% | 86.0% | 85.3% | 1.9 | 2.1 | 33.0 |
| PCT&EV | 76.0% | 75.7% | 4.2 | 4.8 | 29.2 | 0.0% | 0.4% | 80.5% | 2.9 | 32.8 |
| PCT&EVF | 75.8% | 4.7 | 29.2 | 0.3% | 84.8% | 2.1 | 32.6 | 1.4% | 75.5% | 4.8 |
| PCT&EV/GS | 13.5 | 18.4 | 39.9% | 51.0% | 20.4 | 40.7% | ||||
| Random&EV | 45.7% | 8.3 | 45.1% |
Although PCT grows under the guidance of heuristics, the combinations of PCT with EMS and EV still learn effective and robust policies outperforming all baselines by a large margin regarding all settings. Note that the closer the space utilization is to 1, the more difficult online 3D-BPP is. It is interesting to see that policies guided by EMS and EV even exceed the performance of the full coordinate space (FC) which is expected to be optimal. This demonstrates that a good leaf node expansion scheme reduces the complexity of the problem and helps DRL agents learn better performance. To prove that the interception of $\mathbf{L}{t}$ will not harm the final performance, we train agents with full leaf nodes derived from the EV scheme (EVF) and the test performance is slightly worse than the intercepted cases. We conjecture that the interception keeps the final performance may be caused by two reasons. First, sub-optimal solutions for online 3D-BPP may exist even in the intercepted leaf node set $\mathbf{L}{s u b}$ . In addition, the randomly chosen leaf nodes force the agent to make new explorations in case the policy $\pi$ falls into the local optimum. We remove GS from EV cases to prove its effectiveness. The performance of Zhao et al. (2022) deteriorates quickly in setting 2 and setting 3 due to the multiplying orientation space and insufficient state representation separately. Running costs, s cal ability performance, behavior understanding, visualized results, and the implementation details of our real-world packing system can all be found in Appendix C.
尽管 PCT 在启发式指导下增长,但 PCT 与 EMS 和 EV 的组合仍然学习到了有效且稳健的策略,在所有设置下都大幅超越了所有基线。需要注意的是,空间利用率越接近 1,在线 3D-BPP 问题就越困难。有趣的是,由 EMS 和 EV 指导的策略甚至超过了预期为最优的全坐标空间 (FC) 的性能。这表明,良好的叶节点扩展方案降低了问题的复杂性,并帮助 DRL 智能体学习到更好的性能。为了证明截取 $\mathbf{L}{t}$ 不会损害最终性能,我们使用由 EV 方案 (EVF) 导出的完整叶节点训练智能体,测试性能略低于截取的情况。我们推测,截取保持最终性能的原因可能有两个。首先,即使在截取的叶节点集 $\mathbf{L}{s u b}$ 中,也可能存在在线 3D-BPP 的次优解。此外,随机选择的叶节点迫使智能体在策略 $\pi$ 陷入局部最优时进行新的探索。我们从 EV 案例中移除 GS 以证明其有效性。Zhao 等人 (2022) 的性能在设置 2 和设置 3 中迅速下降,分别由于倍增的定向空间和不足的状态表示。运行成本、可扩展性性能、行为理解、可视化结果以及我们现实世界包装系统的实现细节都可以在附录 C 中找到。
We also repeat the same experiment as Zhang et al. (2021) which pack items sampled from a predefined item set $|\mathcal{T}|=64$ in setting 2. While Zhang et al. (2021) packs on average 15.6 items and achieves $67.0%$ space utilization, our method packs 19.7 items with a space utilization of $83.0%$
我们还重复了 Zhang 等人 (2021) 的实验,该实验在设置 2 中打包从预定义项目集 $|\mathcal{T}|=64$ 中采样的项目。虽然 Zhang 等人 (2021) 平均打包 15.6 个项目并实现了 $67.0%$ 的空间利用率,我们的方法打包了 19.7 个项目,空间利用率为 $83.0%$。
4.2 BENEFITS OF TREE PRESENTATION
4.2 树形表示的优势
Here we verify that the PCT representation does help online 3D-BPP tasks. For this, we embed each space configuration node independently like PointNet (Qi et al., 2017) to prove the node spatial relations help the final performance. We also deconstruct the tree structure into node sequences and embed them with Ptr-Net (Vinyals et al., 2015), which selects a member from serialized inputs, for indicating that the graph embedding fashion fits our tasks well. We have verified that an appropriate choiceof $\mathbf{L}{t}$ makes DRL agents easy to train, then we remove the internal nodes $\mathbf{B}{t}$ from $\mathcal{T}{t}$ ,along with its spatial relations with other nodes, to prove $\mathbf{B}{t}$ is also a necessary part. We choose EV as the leaf node expansion scheme here. The comparison results are summarized in Table 2.
我们在此验证 PCT 表示确实有助于在线 3D-BPP 任务。为此,我们像 PointNet (Qi et al., 2017) 那样独立嵌入每个空间配置节点,以证明节点空间关系有助于最终性能。我们还将树结构解构为节点序列,并使用 Ptr-Net (Vinyals et al., 2015) 嵌入它们,Ptr-Net 从序列化输入中选择一个成员,以表明图嵌入方式非常适合我们的任务。我们已经验证了适当选择 $\mathbf{L}{t}$ 使得 DRL 智能体易于训练,然后我们从 $\mathcal{T}{t}$ 中移除内部节点 $\mathbf{B}{t}$ 及其与其他节点的空间关系,以证明 $\mathbf{B}{t}$ 也是一个必要的部分。我们在此选择 EV 作为叶节点扩展方案。比较结果总结在表 2 中。
Table 2: A graph embedding for complete PCT helps the final performance.
表 2: 完整的 PCT 图嵌入有助于最终性能。
| 表示方法 | 利用率 | 设置1 | 设置2 | 设置3 |
|---|---|---|---|---|
| 变量 | 数量 | 差距 | ||
| PointNet | 69.2% | 6.7 | 26.9 | 8.9% |
| Ptr-Net | 64.1% | 10.0 | 25.1 | 15.7% |
| PCT (T /B) | 70.9% | 5.9 | 27.5 | 6.7% |
| PCT (T) | 76.0% | 4.2 | 29.4 | 0.0% |
If we ignore the spatial relations between the PCT nodes or only treat the state input as a flattened sequence, the performance of the learned policies will be severely degraded. The presence of $\mathbf{B}$ functions more on setting 1 and setting 3 since setting 2 allows items to be packed in any empty spaces without considering constraints with internal nodes. This also confirms that a complete PCT representation is essential for online 3D-BPP of practical needs.
如果我们忽略 PCT 节点之间的空间关系,或者仅将状态输入视为扁平序列,学习到的策略性能将严重下降。$\mathbf{B}$ 在设置 1 和设置 3 中的作用更为显著,因为设置 2 允许物品被装入任何空余空间,而无需考虑与内部节点的约束。这也证实了完整的 PCT 表示对于实际需求的在线 3D-BPP 至关重要。
4.3 PERFORMANCE ON CONTINUOUS DATASET
4.3 连续数据集上的性能
The most concerning issue about online 3D-BPP is their solution space limit. Given that most learning-based methods can only work in a limited discrete coordinate space, we directly test our method in a continuous bin with sizes $S^{d}=1$ to prove our superiority. Due to the lack of public datasets for online 3D-BPP issues, we generate item sizes through a uniform distribution $s^{d}\sim$ $U(a,S^{d}/2)$ $a$ is set to O.1 in case endless items are generated. Specifically, for 3D-BPP instances where stability is considered, the diversity of item size $s^{z}$ needs to be controlled. If all subsets of $\mathbf{B}_{t}$ meet:
在线 3D-BPP 最令人关注的问题是其解决方案空间的限制。鉴于大多数基于学习的方法只能在有限的离散坐标空间中工作,我们直接在大小为 $S^{d}=1$ 的连续箱子中测试我们的方法,以证明我们的优越性。由于缺乏公开的在线 3D-BPP 问题数据集,我们通过均匀分布 $s^{d}\sim$ $U(a,S^{d}/2)$ 生成物品尺寸,$a$ 设置为 0.1,以防止生成无限数量的物品。具体来说,对于考虑稳定性的 3D-BPP 实例,需要控制物品尺寸 $s^{z}$ 的多样性。如果 $\mathbf{B}_{t}$ 的所有子集都满足:

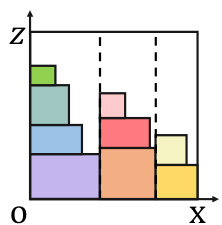
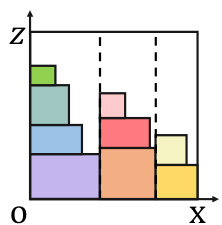
This means any packed items cannot form a new plane for providing support in the direction of gravity and the available packing areas shrink. Excessive diversity of $s^{z}$ will degenerate 3D-BPP into 1D-BPP as shown in the toy demo. To prevent this degradation from leading to the under utilization of the bins, we sample $s^{z}$ from a finite set ${0.1,0.2,\ldots,0.5}$ on setting 1 and setting 3.
这意味着任何已打包的物品无法在重力方向上形成新的支撑平面,可用的打包区域会缩小。$s^{z}$ 的过度多样性会导致 3D-BPP 退化为 1D-BPP,如示例所示。为了防止这种退化导致容器的利用率不足,我们在设置 1 和设置 3 中从有限集合 ${0.1,0.2,\ldots,0.5}$ 中采样 $s^{z}$。
Table 3: Online 3D-BPP with continuous solution space.
表 3: 在线 3D-BPP 连续解空间。
| 方法 | 设置1 | 设置2 | 利用率 | 设置3 | 差距 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 利用率 | 变量 | 数量差距 | 利用率 | 变量 | 数量 | 利用率 | 变量 | 数量 | |||||
| eu | BR | 40.9% | 7.4 | 16.1 | 37.5% | 45.3% | 5.2 | 17.8 | 31.7% | 40.9% | 7.3 | 16.1 | 38.6% |
| Ha et al. | 43.9% | 14.2 | 17.2 | 32.9% | 46.1% | 6.8 | 18.1 | 30.5% | 43.9% | 14.2 | 17.2 | 34.1% | |
| LSAH | 48.3% | 12.1 | 18.7 | 26.1% | 58.7% | 4.6 | 22.8 | 11.5% | 48.4% | 12.2 | 18.8 | 27.3% | |
| GD | 5.6% | 2.2 | 91.4% | 7.5% | 2.9 | 88.7% | 5.2% | 2.1 | 92.2% | ||||
| PCT&EMS | 65.3% | 4.4 | 24.9 | 0.2% | 66.3% | 2.3 | 27.0 | 0.0% | 66.6% | 3.3 | 25.3 | 0.0% | |
| PCT&EV | 65.4% | 3.3 | 25.0 | 0.0% | 65.0% | 2.6 | 26.4 | 2.0% | 65.8% | 3.6 | 25.1 | 2.7% |
We find that some heuristic methods (Ha et al., 2017) also have the potential to work in the continuous domain. We improve these methods as our baselines. Another intuitive approach for solving online 3D-BPP with continuous solution space is driving a DRL agent to sample actions from a gaussian distribution (GD) and output continuous coordinates directly. The test results are summarized in Table 3. Although the continuous-size item set is infinite ( $|{\mathcal{I}}|=\infty)$ which increases the difficulty of the problem and reduces the performance of all methods, our method still performs better than all competitors. The DRL agent which outputs continuous actions directly cannot even converge and their variance is not considered. Our work is, to our knowledge, the first that deploys the learning-based method on solving online 3D-BPP with continuous solution space successfully.
我们发现一些启发式方法 (Ha et al., 2017) 在连续域中也有潜力。我们改进了这些方法作为基线。另一种解决具有连续解空间的在线 3D-BPP 的直观方法是驱动 DRL 智能体从高斯分布 (GD) 中采样动作并直接输出连续坐标。测试结果总结在表 3 中。尽管连续尺寸物品集是无限的 ( $|{\mathcal{I}}|=\infty)$ ,这增加了问题的难度并降低了所有方法的性能,但我们的方法仍然优于所有竞争对手。直接输出连续动作的 DRL 智能体甚至无法收敛,且未考虑其方差。据我们所知,我们的工作是首次成功部署基于学习的方法来解决具有连续解空间的在线 3D-BPP。
4.4 GENERALIZATION ON DIFFERENT DISTRIBUTIONS
4.4 不同分布上的泛化
The generalization ability of learning-based methods has always been a concern. Here we demonstrate that our method has a good generalization performance on item size distributions different from the training one. We conduct this experiment with continuous solution space. We sample $s^{d}$ from normal distributions $N(\mu,\sigma^{2})$ for generating test sequences where $\mu$ and $\sigma$ are the expectation and the standard deviation. Three normal distributions are adopted here, namely $N(0.3,\dot{0}.1^{2})$ , $N(0.1,0.2^{2})$ , and $N(0.5,0.2^{2})$ , as shown in Figure 3. The larger $\mu$ of the normal distribution, the larger the average size of sampled items. We still control $s^{d}$ within the range of [0.1, 0.5]. If the sampled item sizes are not within this range, we will resample until it meets the condition.
基于学习的方法的泛化能力一直是一个关注点。在这里,我们展示了我们的方法在与训练分布不同的物品尺寸分布上具有良好的泛化性能。我们在连续解空间中进行此实验。我们从正态分布 $N(\mu,\sigma^{2})$ 中采样 $s^{d}$ 以生成测试序列,其中 $\mu$ 和 $\sigma$ 分别是期望和标准差。这里采用了三种正态分布,即 $N(0.3,\dot{0}.1^{2})$ 、 $N(0.1,0.2^{2})$ 和 $N(0.5,0.2^{2})$ ,如图 3 所示。正态分布的 $\mu$ 越大,采样物品的平均尺寸越大。我们仍然将 $s^{d}$ 控制在 [0.1, 0.5] 的范围内。如果采样的物品尺寸不在此范围内,我们将重新采样,直到满足条件。
Table 4: Generalization performance on different kinds of item sampling distributions.
表 4: 不同项目采样分布下的泛化性能
| 测试分布 | 方法 | Setting1 | Setting2 | Setting3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Uti. | Var. | Num. | Uti. | Var. | Num. | Uti. | Var. | Num. | ||
| sd ~ U(0.1,0.5) | LSAH PCT&EMS PCT&EV | 48.3% 65.3% 65.4% | 12.1 4.4 3.3 | 18.7 24.9 25.0 | 58.7% 66.3% 65.0% | 4.6 2.3 2.6 | 22.8 27.0 26.4 | 48.4% 66.6% 65.8% | 12.2 3.3 3.6 | 18.8 25.3 25.1 |
| sd ~ N(0.3, 0.12) | LSAH PCT&EMS PCT&EV | 49.2% 66.1% 65.1% | 11.1 3.6 2.8 | 18.9 25.1 24.7 | 60.0% 64.3% 63.7% | 4.1 3.5 2.6 | 22.9 25.6 25.3 | 49.2% 66.4% 66.2% | 11.0 3.0 2.9 | 18.9 25.2 25.1 |
| ~ N(0.1, 0.22) S | LSAH PCT&EMS PCT&EV | 52.4% 68.5% 66.5% | 8.9 2.5 2.7 | 30.3 39.0 38.0 | 62.9% 66.4% 64.9% | 2.4 3.0 2.7 | 44.3 49.7 48.3 | 52.3% 69.2% 67.4% | 8.9 2.5 2.4 | 30.2 39.4 38.5 |
| sd ~ N(0.5,0.2) | LSAH PCT&EMS PCT&EV | 47.3% 63.5% 65.1% | 12.6 5.0 3.3 | 13.0 17.3 17.7 | 56.0% 64.5% 64.5% | 5.5 2.8 2.8 | 12.9 15.4 15.3 | 47.3% 65.2% 65.1% | 12.6 3.8 3.7 | 13.0 17.7 17.7 |
We directly transfer our policies trained on $U(0.1,0.5)$ to these new datasets without any fine-tuning. We use the best-performing heuristic method LSAH (Hu et al., 2017) in Section 4.3 as a baseline. The test results are summarized in Table 4. Our method performs well on the distributions different from the training one and always surpasses the LSAH method. See Appendix C for more results about the generalization ability of our method on disturbed distributions and unseen items.
我们直接将训练在 $U(0.1,0.5)$ 上的策略迁移到这些新数据集上,无需任何微调。我们使用第4.3节中表现最佳的启发式方法 LSAH (Hu et al., 2017) 作为基线。测试结果总结在表4中。我们的方法在与训练分布不同的分布上表现良好,并且始终优于 LSAH 方法。更多关于我们方法在扰动分布和未见项目上的泛化能力的结果,请参见附录 C。
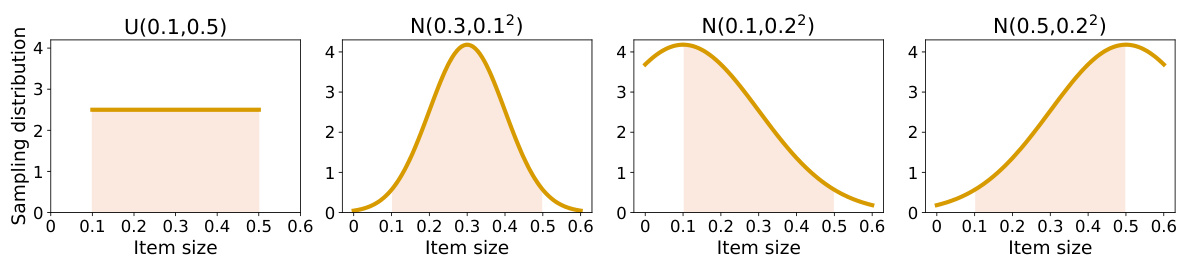
Figure 3: The probability distribution for sampling item sizes. The area of the colored zone is normalized to 1.
图 3: 采样项目大小的概率分布。彩色区域的面积被归一化为 1。
4.5 MORE COMPLEX PRACTICAL CONSTRAINTS
4.5 更复杂的实际约束
To further prove that our method fits 3D-BPP with complex constraints well, we give two demonstrations about extending our method to online 3D-BPP with additional practical constraints: isle friendliness and load balancing (Gzara et al., 2020):
为了进一步证明我们的方法适用于具有复杂约束的3D-BPP(三维装箱问题),我们展示了如何将我们的方法扩展到具有额外实际约束的在线3D-BPP:通道友好性和负载均衡性 (Gzara et al., 2020):
3D-BPP with Isle Friendliness Isle friendliness refers to that items belonging to the same category should be packed as closely as possible. The item weight is set as $w_{t}=m a x(0,v_{t}-c\cdot$ $d i s t(n_{t},\mathbf{B}{t}))$ $c$ is a constant. The additional object function $d i s t(n{t},\mathbf{B}{t})$ means the average distance between $n{t}$ and the items of the same category in $\mathbf{B}{t}$ . The additional category information is appended into the descriptors of $\mathbf{B}{t}$ and $n_{t}$ . Four item categories are tested here.
3D-BPP 与岛屿友好性
岛屿友好性指的是属于同一类别的物品应尽可能紧密地打包。物品权重设置为 $w_{t}=m a x(0,v_{t}-c\cdot$ $d i s t(n_{t},\mathbf{B}{t}))$,其中 $c$ 是一个常数。附加的目标函数 $d i s t(n{t},\mathbf{B}{t})$ 表示 $n{t}$ 与 $\mathbf{B}{t}$ 中同一类别物品的平均距离。附加的类别信息被添加到 $\mathbf{B}{t}$ 和 $n_{t}$ 的描述符中。这里测试了四种物品类别。
3D-BPP with Load Balancing Load balancing dictates that the packed items should have an even mass distribution within the bin. The item weight is set as $w_{t}=m a x(0,v_{t}-c\cdot v a r(n_{t},\mathbf{B}{t}))$ .Object $v a r(n{t},\mathbf{B}_{t})$ is the variance of the mass distribution of the packed items on the bottom of the bin.
带负载均衡的3D-BPP
负载均衡要求装箱物品在箱内应具有均匀的质量分布。物品重量设置为 $w_{t}=m a x(0,v_{t}-c\cdot v a r(n_{t},\mathbf{B}{t}))$ 。对象 $v a r(n{t},\mathbf{B}_{t})$ 是箱底已装箱物品质量分布的方差。
Table 5: Online 3D-BPP with practical constraints. Obj. means the task-specific objective score, the smaller the better. Setting 2 involves no mass property and the load balancing is not considered.
表 5: 带有实际约束的在线 3D-BPP。Obj. 表示任务特定的目标分数,越小越好。设置 2 不涉及质量属性,且不考虑负载均衡。
We choose the learning-based method Zhao et al. (2022) as our baseline since heuristic methods only take space utilization as their objects. The results are summarized in Table 5. Compared with the baseline algorithm, our method better achieves the additional object while still taking into account the space utilization as the primary.
我们选择基于学习的方法 Zhao 等人 (2022) 作为基线,因为启发式方法仅以空间利用率为目标。结果总结在表 5 中。与基线算法相比,我们的方法在仍然以空间利用率为主要目标的同时,更好地实现了额外目标。
5 DISCUSSION
5 讨论
We formulate the online 3D-BPP as a novel hierarchical representation -- packing configuration tree. PCT is a full-fledged description of the state and action space of bin packing which makes the DRL agent easy to train and well-performing. We extract state feature from PCT using graph attention networks which encodes the spatial relations of all space configuration nodes. The graph representation of PCT helps the agent with handling online 3D-BPP with complex practical constraints, while the finite leaf nodes prevent the action space from growing explosively. Our method surpasses all other online 3D-BPP algorithms and is the first learning-based method that solves online 3D-BPP with continuous solution space successfully. Our method performs well even on item sampling distributions different from the training one. We also give demonstrations to prove that our method is versatile in terms of incorporating various practical constraints. For future research, we are extremely interested in applying our method to the more difficult irregular shape packing (Wang & Hauser, 2019a), where the sampling costs for training DRL agents are more expensive and the solution space will be far more complex. A good strategy for balancing exploration and exploitation for learning agents is eagerly needed in this situation. Finding other alternatives for better representing 3D-BPP with different packing constraints and designing better leaf node expansion schemes for PCT are also interesting directions.
我们将在线三维装箱问题 (3D-BPP) 表述为一种新颖的层次化表示——装箱配置树 (PCT)。PCT 是对装箱问题的状态和动作空间的完整描述,这使得深度强化学习 (DRL) 智能体易于训练且表现良好。我们使用图注意力网络从 PCT 中提取状态特征,该网络编码了所有空间配置节点的空间关系。PCT 的图表示帮助智能体处理具有复杂实际约束的在线 3D-BPP,而有限的叶节点防止了动作空间的爆炸性增长。我们的方法超越了所有其他在线 3D-BPP 算法,并且是第一个成功解决具有连续解空间的在线 3D-BPP 的学习方法。即使在与训练分布不同的物品采样分布上,我们的方法也表现良好。我们还通过演示证明,我们的方法在结合各种实际约束方面具有多功能性。对于未来的研究,我们非常有兴趣将我们的方法应用于更困难的不规则形状装箱问题 (Wang & Hauser, 2019a),在这种情况下,训练 DRL 智能体的采样成本更高,解空间也将更加复杂。在这种情况下,迫切需要一种平衡探索和利用的良好策略。寻找其他替代方案以更好地表示具有不同装箱约束的 3D-BPP,以及为 PCT 设计更好的叶节点扩展方案,也是有趣的研究方向。
ACKNOWLEDGEMENTS
致谢
We thank Zhan Shi, Wei Yu, and Lintao Zheng for helpful discussions. We would also like to thank anonymous reviewers for their insightful comments and valuable suggestions. This work is supported by the National Natural Science Foundation of China (62132021, 61876077).
我们感谢 Zhan Shi、Wei Yu 和 Lintao Zheng 的有益讨论。同时,我们也感谢匿名评审的深刻评论和宝贵建议。本研究得到了国家自然科学基金 (62132021, 61876077) 的支持。
ETHICS STATEMENT
伦理声明
We believe the broader im
