Class-Wise Difficulty-Balanced Loss for Solving Class-Imbalance

类别难度平衡损失函数解决类别不平衡问题

Abstract. Class-imbalance is one of the major challenges in real world datasets, where a few classes (called majority classes) constitute much more data samples than the rest (called minority classes). Learning deep neural networks using such datasets leads to performances that are typically biased towards the majority classes. Most of the prior works try to solve class-imbalance by assigning more weights to the minority classes in various manners (e.g., data re-sampling, cost-sensitive learning). However, we argue that the number of available training data may not be always a good clue to determine the weighting strategy because some of the minority classes might be sufficiently represented even by a small number of training data. Over weighting samples of such classes can lead to drop in the model’s overall performance. We claim that the ‘difficulty’ of a class as perceived by the model is more important to determine the weighting. In this light, we propose a novel loss function named Class-wise Difficulty-Balanced loss, or CDB loss, which dynamically distributes weights to each sample according to the difficulty of the class that the sample belongs to. Note that the assigned weights dynamically change as the ‘difficulty’ for the model may change with the learning progress. Extensive experiments are conducted on both image (artificially induced class-imbalanced MNIST, long-tailed CIFAR and ImageNet-LT) and video (EGTEA) datasets. The results show that CDB loss consistently outperforms the recently proposed loss functions on class-imbalanced datasets irrespective of the data type (i.e., video or image).

摘要。类别不平衡是现实世界数据集中的主要挑战之一，其中少数类别（称为多数类）包含的数据样本远多于其他类别（称为少数类）。使用此类数据集训练深度神经网络通常会导致模型性能偏向多数类。先前的研究大多通过以不同方式（如数据重采样、代价敏感学习）为少数类分配更高权重来解决类别不平衡问题。然而，我们认为可用训练数据量未必总是确定权重分配策略的良好依据，因为某些少数类可能仅需少量训练数据即可充分表征。对此类样本过度加权反而会导致模型整体性能下降。我们提出模型的"类别难度"感知才是确定权重的关键因素。基于此，我们提出了一种名为类别难度平衡损失（Class-wise Difficulty-Balanced loss，CDB损失）的新型损失函数，该函数根据样本所属类别的难度动态分配权重。值得注意的是，随着学习进程中模型感知难度的变化，分配的权重也会动态调整。我们在图像数据集（人工构建类别不平衡的MNIST、长尾CIFAR和ImageNet-LT）和视频数据集（EGTEA）上进行了大量实验。结果表明，无论数据类型（视频或图像）如何，CDB损失在类别不平衡数据集上的表现始终优于最近提出的损失函数。

1 Introduction

1 引言

Since the advent of Deep Neural Networks (DNNs), we have seen significant advancement in computer vision research. One of the reasons behind this success is the wide availability of large-scale annotated image (e.g., MNIST [1], CIFAR [2], ImageNet [3]) and video (e.g., Kinetics [4], Something-Something [5], UCF [6]) datasets. But unfortunately, most of the commonly used datasets do not resemble the real world data in a number of ways. As a result, performance of state-of-the-art DNNs drop significantly in real-world use-cases. One of the major challenges in most real-world datasets is the class-imbalanced data distribution with significantly long tails, i.e., a few classes (also known as ‘majority classes’)

自深度神经网络 (DNN) 问世以来，计算机视觉研究取得了显著进展。这一成功的背后原因之一是大规模标注图像数据集 (如 MNIST [1]、CIFAR [2]、ImageNet [3]) 和视频数据集 (如 Kinetics [4]、Something-Something [5]、UCF [6]) 的广泛可用性。但遗憾的是，大多数常用数据集在多个方面与现实世界数据存在差异。因此，最先进的 DNN 模型在现实应用场景中性能会显著下降。现实世界数据集面临的主要挑战之一是类别不平衡的数据分布存在显著的长尾现象，即少数类别 (也称为"多数类")

have much higher number of data samples compared to the other classes (also known as ‘minority classes’). When DNNs are trained using such real-world datasets, their performance gets biased towards the majority classes, i.e., they perform highly for the majority classes and poorly for the minority classes.

与其他类别(也称为"少数类别")相比,多数类别的数据样本数量要多得多。当使用这种真实世界的数据集训练DNN时,它们的性能会偏向多数类别,即对多数类别表现良好,而对少数类别表现不佳。

Several recent works have tried to solve the problem of class-imbalanced training data. Most of the prior solutions can be fairly classified under 3 categories :- (1) Data re-sampling techniques [7,8,9] (2) Metric learning and knowledge transfer [10,11,12,13] (3) Cost-sensitive learning methods [14,15,16,17]. Data resampling techniques try to balance the number of data samples between the majority and minority classes by either over-sampling from the minority classes or under-sampling from the majority classes or using both. Generating synthetic data samples for minority classes [7,18,19] from given data is another re-sampling technique that tries to increase the number of minority class samples. Since the performance of a DNN depends entirely on it’s ability to learn to extract useful features from data, “what training data is seen by the DNN” is a very important concern. In that context, data re-sampling strategies introduce the risks of losing important training data samples by under-sampling from majority classes and network over fitting due to over-sampling minority classes. Metric-learning [10,11], on the other hand, aims to learn an appropriate representation function that embeds data to a feature space, where the mutual relationships among the data (e.g., similarity/dissimilarity) are preserved. It has the risk of learning a biased representation function that has learned more from the majority classes. Hence some works [12] tend to use sampling techniques with metric learning, which still faces the problems of sampling, as discussed above. Few recent researches have also tried to transfer knowledge from the majority classes to the minority classes by adding an external memory [20], which is non-trivial and expensive. Due to these concerns, the work in this paper focuses on cost-sensitive learning approaches. Cost-sensitive learning methods penalize the DNN higher for making errors on certain samples compared to others. They achieve this by assigning weights to different samples using various strategies. Typically, most prior cost-sensitive learning strategies [21,22,15] assume that the minority classes are always weakly represented. They ensure that the samples of the minority class get higher weights so that the DNN can be penalized more for making mistakes on the minority class samples. One such popular strategy is to distribute weights in inverse proportion to the class frequencies [21,23]. However, certain minority classes might be fairly represented by a small amount of samples.

近期多项研究致力于解决类别不平衡训练数据的问题。现有方法主要可分为三类：(1) 数据重采样技术 [7,8,9]；(2) 度量学习与知识迁移 [10,11,12,13]；(3) 代价敏感学习方法 [14,15,16,17]。数据重采样通过过采样少数类样本、欠采样多数类样本或两者结合来实现类别平衡。另一种重采样方式是从现有数据生成少数类合成样本 [7,18,19] 以扩充少数类数据。由于深度神经网络(DNN)的性能完全依赖于其从数据中提取有效特征的能力，"DNN接触哪些训练数据"至关重要。在此背景下，数据重采样策略存在两大风险：多数类欠采样可能导致重要样本丢失，而少数类过采样易引发网络过拟合。

度量学习 [10,11] 的目标是学习将数据嵌入特征空间的表示函数，保持数据间相互关系（如相似性/相异性）。但这种方法可能习得偏向多数类的有偏表示函数。因此部分研究 [12] 尝试结合采样技术与度量学习，但仍面临前文所述的采样问题。少数最新研究尝试通过添加外部存储器 [20] 实现多数类向少数类的知识迁移，但这种方法实现复杂且成本高昂。

基于这些考量，本文聚焦代价敏感学习方法。这类方法通过差异化惩罚机制，使DNN对特定样本的错误分类承担更高代价。现有策略通常假设少数类始终表征不足 [21,22,15]，因此赋予少数类样本更高权重以加强错误惩罚。其中主流策略是按类别频率反比分配权重 [21,23]，但某些少数类可能已通过少量样本获得充分表征。

Fig. 1 gives an example of a class-imbalanced dataset where certain classes such as ‘clean’ and ‘spread’ are sparsely populated but can easily be learned to generalize by the classifier. Over weighting samples of such classes might lead to biasing the DNN’s performance. In such situations, number of available training data per class might not be a good clue to determine sample weights.

图 1: 展示了一个类别不平衡数据集的示例，其中某些类别(如"clean"和"spread")样本稀少，但分类器很容易学习并泛化。对此类样本过度加权可能会导致DNN性能偏差。在这种情况下，每个类别的可用训练数据量可能不是确定样本权重的良好依据。

Instead, we claim that the ‘difficulty’ of a class as perceived by the DNN might be a more important and helpful clue for weight assignment. The concept of ‘difficulty’ has been previously used by some sample-level weight assigning techniques such as focal loss [14] and GHM [17]. They reweight each sample individually by increasing weights for hard samples and reducing weights for easy samples. The increasing popularity of focal loss [14] in class-imbalanced classification tasks is based on the assumption that minority classes should have more hard samples compared to majority classes. The assumption does stand true if we compare the proportion of hard samples for the minority and majority classes. But, in terms of absolute number of hard samples, the majority classes still might surpass the minority classes simply because they have much more data samples than the minority classes. In such cases, giving high weights to all hard samples irrespective of their classes might overweight the majority classes and therefore still bias the performance of the DNN. We believe that the above drawback can be solved by considering class-level difficulty rather than samplelevel. To the best of our knowledge, ours is the first work to introduce the concept of class-level difficulty for solving class-imbalance. Based on the analysis, we develop a novel weighting strategy that dynamically re-balances the loss for each sample based on the instantaneous difficulty of it’s class as perceived by a DNN.

相反，我们认为深度神经网络（DNN）所感知的类别"难度"可能是权重分配中更重要且有效的线索。"难度"概念此前已被焦点损失（focal loss）[14]和GHM[17]等样本级权重分配技术采用，它们通过增加困难样本权重、降低简单样本权重来单独调整每个样本。焦点损失[14]在类别不平衡分类任务中的广泛应用基于一个假设：少数类相比多数类应包含更多困难样本。若比较少数类与多数类的困难样本比例，该假设确实成立。但就困难样本的绝对数量而言，由于多数类样本基数庞大，其困难样本数仍可能超过少数类。此时若对所有困难样本（无论所属类别）赋予高权重，反而会过度强化多数类，导致DNN性能仍存在偏差。我们认为通过考虑类别级（而非样本级）难度可解决上述缺陷。据我们所知，这是首个引入类别级难度概念来解决类别不平衡的工作。基于此分析，我们提出一种新型权重策略：根据DNN实时感知的类别难度，动态调整每个样本的损失权重。

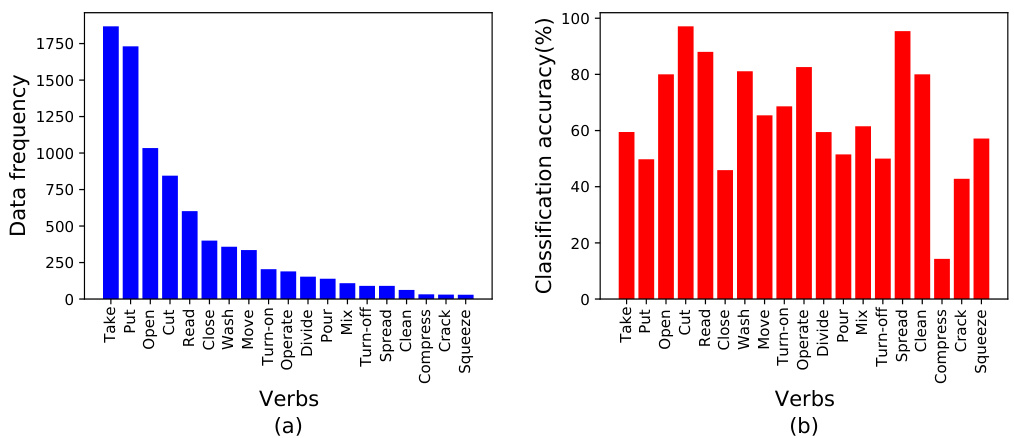
Fig. 1. (a) Class-imbalanced data distribution of EGTEA dataset. (b) Class-wise classification accuracies of a 3D-ResNeXt101 trained on the imbalanced EGTEA dataset using unweighted softmax cross-entropy loss function. It is interesting to notice that even though classes like ‘Clean’ and ‘Spread’ have very small number of data samples, the classifier finds it relatively easier to learn such classes compared to certain densely populated classes such as ‘Take’ and ‘Put’. Therefore it is not obvious to assume that the sparsely populated classes will always be the most weakly represented.

图 1: (a) EGTEA 数据集的类别不平衡数据分布。(b) 使用未加权 softmax 交叉熵损失函数在不平衡 EGTEA 数据集上训练的 3D-ResNeXt101 的逐类分类准确率。有趣的是，尽管像"Clean"和"Spread"这样的类别数据样本数量很少，但分类器发现学习这些类别比某些密集类别(如"Take"和"Put")相对更容易。因此，不能简单地假设稀疏类别总是表现最弱。

Such a strategy measures the instantaneous difficulty of each class without relying on any prior assumptions and then dynamically assigns weights to the samples of the class in proportion to the difficulty of the class. Extensive experiments on multiple datasets indicate that our class-difficulty based dynamic weighting strategy can provide a significant improvement in the performance of the commonly used loss functions under class-imbalanced situations.

该策略无需依赖任何先验假设即可测量每个类别的即时难度，随后根据类别难度动态按比例分配样本权重。在多个数据集上的大量实验表明，我们提出的基于类别难度的动态加权策略能显著提升常用损失函数在类别不平衡场景下的性能表现。

The key contributions of this paper can be summarized as follows: (1) We propose a way to measure the dynamic difficulty of each class during training and use the class-wise difficulty scores to re-balance the loss for each sample, thereby giving a class-wise difficulty-balanced (CDB) loss. (2) We show that using our weighting strategy can give commonly used loss functions (e.g., cross-entropy) a significant boost in performance on multiple class-imbalanced datasets. We conduct experiments on both image and video datasets and find that our weighting strategy works well irrespective of the data type. Our research on quantifying the dynamic difficulty of the classes and using it for weight distribution might prove useful for researchers focusing on class-imbalanced datasets.

本文的主要贡献可总结如下：(1) 我们提出了一种在训练过程中测量每个类别动态难度的方法，并利用类别难度分数重新平衡每个样本的损失，从而得到一种类别难度平衡(CDB)损失函数。(2) 我们证明采用这种加权策略可以显著提升常用损失函数(如交叉熵)在多个类别不平衡数据集上的性能。我们在图像和视频数据集上进行了实验，发现该加权策略对不同数据类型均有效。关于量化类别动态难度并将其用于权重分配的研究，可能对关注类别不平衡数据集的研究者具有参考价值。

2 Related Works

2 相关工作

As discussed in section 1, most prior works that try to solve class-imbalance can be categorized into 3 domains : (1) Data re-sampling techniques, (2) Metric learning and knowledge transfer and (3) Cost-sensitive learning methods.

如第1节所述，大多数解决类别不平衡问题的现有工作可分为三大类：(1) 数据重采样技术，(2) 度量学习和知识迁移，(3) 代价敏感学习方法。

2.1 Data Re-sampling

2.1 数据重采样

Data re-sampling techniques try to balance the number of samples among the classes by using various sampling techniques during the data pre-processing. The sampling techniques, used for the purpose, either randomly over-sample data from the minority classes or randomly under-sample data from the majority classes or both. Over-sampling from the minority classes [8,24] replicates the available data samples in order to increase the number of samples. But such a practice introduces the risk of over fitting. Synthetic Minority Over-sampling Technique (SMOTE) [7], proposed by Chawla et al., increases the number of data samples for the minority classes by creating synthetic data using interpolation among the original data points. Though SMOTE only used the minority class samples while generating data samples, later variants of SMOTE (e.g., Borderline SMOTE [18] and Safe-level SMOTE [19]) take the majority class samples into consideration as well. But such data generation techniques do not guarantee that the synthesized data points will always follow the actual data distribution of the minority classes. On the other hand, under-sampling techniques [9,25] reduce data from the majority classes and might result in cutting out some important data samples.

数据重采样技术通过在数据预处理阶段采用多种采样方法，力求平衡各类别的样本数量。这些采样技术要么对少数类数据进行随机过采样，要么对多数类数据进行随机欠采样，或者两者兼用。少数类过采样[8,24]通过复制现有数据样本来增加样本数量，但这种方法可能带来过拟合风险。Chawla等人提出的合成少数类过采样技术(SMOTE)[7]通过在原始数据点间插值生成合成数据，从而增加少数类的样本数量。尽管SMOTE在生成数据样本时仅使用少数类样本，但其后续改进版本(如Borderline SMOTE[18]和Safe-level SMOTE[19])也考虑了多数类样本。然而这类数据生成技术无法保证合成数据点始终符合少数类的真实数据分布。另一方面，欠采样技术[9,25]通过削减多数类数据来平衡样本，但可能导致部分重要数据样本丢失。

2.2 Metric Learning and Knowledge Transfer

2.2 度量学习与知识迁移

Metric learning aims to learn an embedding function that can embed data to a feature space where the inter-data relationships are preserved. Contrastive embedding [26] is learned using paired data samples to minimize the distance between the features of same class samples while maximizing the distance between different class samples. Song et al. [10] proposed a structured feature embedding based on positive and negative samples pairs in the dataset. Triplet loss [27], on the other hand, uses triplets instead of pairs, where one sample is considered the anchor. Metric learning still faces the risk of learning embedding functions biased towards the majority classes. Some recent works (e.g., OLTR [20]) have also tried to transfer knowledge from the majority classes to the minority classes either by meta learning [13] or by adding an external memory module [20]. Even though OLTR [20] performs well for long-tailed classification, as pointed out by [28], their design of external memory modules might be a non-trivial and expensive task.

度量学习的目标是学习一种嵌入函数，能够将数据映射到一个保留数据间关系的特征空间。对比嵌入 [26] 通过使用配对数据样本来学习，最小化同类样本特征之间的距离，同时最大化不同类样本之间的距离。Song等人 [10] 提出了一种基于数据集中正负样本对的结构化特征嵌入方法。而三元组损失 [27] 则使用三元组而非配对样本，其中一个样本被视为锚点。度量学习仍面临学习偏向多数类的嵌入函数的风险。最近的一些工作（如OLTR [20]）尝试通过元学习 [13] 或添加外部记忆模块 [20] 将知识从多数类迁移到少数类。尽管OLTR [20] 在长尾分类中表现良好，但如 [28] 所指出的，其外部记忆模块的设计可能是一项复杂且成本高昂的任务。

2.3 Cost-Sensitive Learning

2.3 代价敏感学习

Cost-sensitive learning techniques try to penalize the DNN higher for making prediction mistakes on certain data samples than on the others. To achieve that, different weights are assigned to different samples and the penalty incurred on each data sample is scaled up/down using the corresponding weight. Research in this domain mainly target to find an effective way to assign these weights to the samples. To solve class-imbalance, majority of the works propose techniques that assign higher weights to the minority class samples. Such techniques ensure that the DNN gets higher penalty for making mistakes on the minority class samples. One such simple and commonly used weight distribution technique is to use the inverse class-frequencies as the weights for the samples each class [21,23]. Later variants of this technique [22] use a smoothed version of the square root of class-frequencies for the weight distribution. Class-balanced loss [15] proposed by Lin et al. calculates the effective number of samples of each class and uses it to assign weights to the samples. All of the above mentioned works assume that the minority classes are always the most weakly represented classes and therefore needs high weights. But that assumption might not always be true because certain minority class might be sufficiently represented by a small number of samples. Giving high weights to the samples of such classes might cause drop in overall performance. Therefore, Tsung-Yi et al. proposed a sample-based weighting technique called “Focal loss” [14], where each sample is assigned a weight based on it’s difficulty. The difficulty of each sample is quantified in terms of the loss incurred by the DNN on that sample, where more lossy samples imply more difficult samples. Though focal loss [14] was originally proposed for dense object detection tasks, it has also become popular in class-imbalanced classification tasks [15]. The minority classes are expected to have more difficult samples compared to the majority classes and therefore get high weights by focal loss. Indeed the proportion of difficult samples in a minority class is more than that in the majority class. However, in terms of absolute number of difficult samples, the majority class surpasses the minority class, as it is much more populated than the minority class. Therefore, giving high weights to all difficult samples irrespective of their classes still biases the DNN’s performance.

成本敏感学习技术试图通过在某些数据样本上做出错误预测时对DNN施加更高的惩罚，而对其他样本则施加较低的惩罚。为实现这一点，不同样本被赋予不同的权重，每个数据样本的惩罚会根据相应权重进行放大或缩小。该领域的研究主要致力于寻找一种有效的方法来为样本分配这些权重。为解决类别不平衡问题，大多数研究提出了为少数类样本分配更高权重的技术。这类技术确保DNN在少数类样本上犯错时受到更严厉的惩罚。其中一种简单且常用的权重分配技术是使用类别频率的倒数作为每个类别样本的权重[21,23]。该技术的后续变体[22]则使用类别频率平方根的平滑版本进行权重分配。Lin等人提出的类别平衡损失[15]通过计算每个类别的有效样本数来分配样本权重。上述所有研究都假设少数类始终是代表性最弱的类别，因此需要高权重。但这一假设未必总是成立，因为某些少数类可能仅需少量样本即可充分表示。对此类样本赋予高权重可能导致整体性能下降。因此，Tsung-Yi等人提出了一种基于样本的权重分配技术"焦点损失(Focal loss)"[14]，根据样本难度为每个样本分配权重。样本难度通过DNN在该样本上的损失量化，损失越大表示样本越难。虽然焦点损失[14]最初是为密集目标检测任务提出的，但也在类别不平衡分类任务中广受欢迎[15]。与多数类相比，少数类预期会包含更多困难样本，因此通过焦点损失获得更高权重。事实上，少数类中困难样本的比例确实高于多数类。然而就困难样本的绝对数量而言，多数类因其样本基数更大而超过少数类。因此，不分类别地为所有困难样本赋予高权重仍会导致DNN性能偏差。

Our work also lies in the regime of cost-sensitive learning. We propose a dynamic weighting system that dynamically assigns weights to each sample of each class based on the instantaneous difficulty of the class, rather than that of each sample, as perceived by the DNN. Our weighting system helps to boost the performance of commonly used loss functions (e.g., cross-entropy loss) in class-imbalanced situations.

我们的工作也属于成本敏感学习范畴。我们提出了一种动态加权系统，该系统基于深度神经网络感知的类别瞬时难度（而非样本难度）动态分配每个类别样本的权重。该加权系统能有效提升常用损失函数（如交叉熵损失）在类别不平衡场景下的性能。

3 Proposed Method

3 研究方法

3.1 Measuring Class Difficulty

3.1 衡量类别难度

Human beings use the metric ‘difficulty’ majorly to give a qualitative description of things, for example “this task is very difficult” or “this game is so easy”. Similar behavior can also be seen in neural networks where they find some parts of a task much more difficult to perform compared to the others. For example, while training on a multi-class classification task, the classifier will find some classes easier to learn than the others. We propose to measure the difficulty of each class as perceived by the DNN and use it as clue to determine the weights for the samples. But, as difficulty is a qualitative metric, there is no direct way to add a quantitative value to it. Humans tend to classify a task as difficult, if they can not perform well in it. We use a similar approach to use the neural network’s performance to measure the difficulty of classes. During training, the neural network’s performance for each class is measured on a validation data set, which is then used to calculate the class-wise difficulty. The neural network’s performance for any class $c$ is measured as its classification accuracy on class $c$ , $A_{c}~=~n_{c}/N_{c}$ , where $N_{c}$ denotes the total number of samples of class $c$ in validation data and $n_{c}$ denotes the number of class $c$ samples in validation data that the model classifies correctly. Then the difficulty of class $c$ , $d_{c}$ , is measured as $d_{c}=1-A_{c}$ . A neural network’s perception of “how much a class is difficult to learn” changes as the training process of the network progresses. With time, the network’s performance for each class improves and as a result, the perceived difficulty of each class also reduces. Therefore, we calculate the class-difficulties as a function of time as well. The difficulty of class $c$ after training time (i.e., time during training) $t$ can be calculated as

人类主要使用“难度”这一指标对事物进行定性描述，例如“这项任务非常困难”或“这个游戏很简单”。类似行为也存在于神经网络中，它们会发现任务的某些部分比其他部分更难处理。例如，在进行多类别分类任务训练时，分类器会发现某些类别比其他类别更容易学习。我们提出通过深度神经网络(DNN)感知的各类别难度作为样本权重的确定依据。但由于难度是定性指标，无法直接赋予量化值。人类倾向于将表现不佳的任务归类为困难任务，我们采用类似思路，利用神经网络的表现来衡量类别难度。训练过程中，神经网络在验证数据集上对每个类别的表现被量化为分类准确率 $A_{c}~=~n_{c}/N_{c}$ ，其中 $N_{c}$ 表示验证数据中类别 $c$ 的总样本数， $n_{c}$ 表示模型正确分类的类别 $c$ 样本数。随后，类别 $c$ 的难度 $d_{c}$ 计算为 $d_{c}=1-A_{c}$ 。神经网络对“类别学习难度”的感知会随训练进程动态变化：随着时间推移，网络对各類别的表现提升，其感知难度相应降低。因此，我们将类别难度表述为时间的函数，训练时长 $t$ 后的类别 $c$ 难度可计算为

$$
d_{c,t}=1-A_{c,t},
$$

$$
d_{c,t}=1-A_{c,t},
$$

where $A_{c,t}$ is the neural network’s classification accuracy for class $c$ on the validation data after training time $t$ .

其中 $A_{c,t}$ 表示神经网络在训练时间 $t$ 后对验证数据中类别 $c$ 的分类准确率。

3.2 Difficulty-Based Weight Distribution

3.2 基于难度的权重分配

Once the class-wise difficulty is quantified, then it can be used to assign weights to the classes during training. It is fairly obvious that the classes, that are difficult to learn should be given higher weights compared to the easier classes. Therefore the weight for class $c$ after training time $t$ can be calculated as

一旦量化了各类别的学习难度，便可在训练过程中为不同类别分配权重。显然，相较于简单类别，难学习的类别应被赋予更高权重。因此，训练时间 $t$ 后类别 $c$ 的权重可计算为

$$
w_{c,t}=(d_{c,t})^{\tau}=(1-A_{c,t})^{\tau},
$$

$$
w_{c,t}=(d_{c,t})^{\tau}=(1-A_{c,t})^{\tau},
$$

where $d_{c,t}$ is the difficulty of class $c$ after time $t$ and $\tau$ is a hyper-parameter. The weight distribution $w_{t}={w_{1,t},w_{2,t},\dots,w_{C,t}}$ over all $C$ classes can be computed by repeating Equation 2 for all classes.

其中 $d_{c,t}$ 表示时间 $t$ 后类别 $c$ 的难度，$\tau$ 是一个超参数。通过对所有 $C$ 个类别重复公式 2，可以计算出所有类别上的权重分布 $w_{t}={w_{1,t},w_{2,t},\dots,w_{C,t}}$。

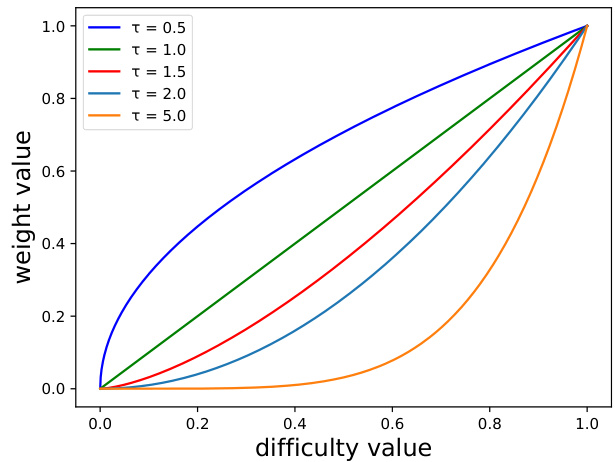
Fig. 2. Effect of changing $\tau$ on the difficulty-based weight distribution. Increasing value of $\tau$ puts heavier weights on the samples of the classes with higher difficulty, while lowering weights for the easier classes.

图 2: 改变 $\tau$ 对基于难度权重分布的影响。增大 $\tau$ 值会给难度较高的类别样本分配更大权重，同时降低简单类别的权重。

The hyper-parameter $\tau$ is introduced to control how much we down-weight the samples of the easy classes. Increasing value of $\tau$ relatively increases the classifier’s focus on the difficult classes.

引入超参数 $\tau$ 来控制对简单类样本的降权程度。增大 $\tau$ 值会相对增强分类器对困难类的关注。

Fig. 2 shows how change in the value of $\tau$ changes the weight values for classes of different difficulties. Its effect is almost similar to that of the focusing parameter $\gamma$ in focal loss [14]. The performance of our proposed method varies significantly with change in value of $\tau$ and the best value for $\tau$ differs from dataset to dataset. Unfortunately, the only way to search for the best value of $\tau$ is by trial and error. To avoid that, we propose a way to dynamically update the value of $\tau$ . For dynamically updating $\tau$ , the value of $\tau$ after training time $t$ is calculated as

图 2: 展示了参数 $\tau$ 值的变化如何影响不同难度类别权重值的调整。其效果与焦点损失 [14] 中的聚焦参数 $\gamma$ 几乎相似。我们提出方法的性能随 $\tau$ 值变化而显著波动，且最佳 $\tau$ 值因数据集而异。遗憾的是，寻找最佳 $\tau$ 值的唯一方法是通过试错。为避免这种情况，我们提出了一种动态更新 $\tau$ 值的方法。对于动态更新 $\tau$，训练时间 $t$ 后的 $\tau$ 值计算公式为

$$
\tau_{t}=\frac{2}{1+\exp(-b_{t})},
$$

$$
\tau_{t}=\frac{2}{1+\exp(-b_{t})},
$$

where $b_{t}$ measures the bias in the performance of the classifier over $C$ classes as

其中 $b_{t}$ 衡量分类器在 $C$ 个类别上的性能偏差为

$$
b_{t}=\frac{\operatorname*{max}{c=1,2,\ldots,C}A_{c,t}}{\operatorname*{min}{c^{\prime}=1,2,\ldots,C}A_{c^{\prime},t}+\epsilon}-1.
$$

$$
b_{t}=\frac{\operatorname*{max}{c=1,2,\ldots,C}A_{c,t}}{\operatorname*{min}{c^{\prime}=1,2,\ldots,C}A_{c^{\prime},t}+\epsilon}-1.
$$

In Equation 4, $\epsilon$ is a small positive value $=+0.0001$ ) introduced to handle situations where $\mathrm{min}{c^{\prime}=1,2,...,C}A_{c^{\prime},t}=0$ . Equation 3 increases the value of $\tau$ when the classification performance of the classifier is highly biased (i.e., high $b_{t}$ ) and decreases it in case of low bias (i.e., less $b_{t}$ ).

在公式4中，$\epsilon$ 是一个小的正值 $=+0.0001$ )，用于处理 $\mathrm{min}{c^{\prime}=1,2,...,C}A_{c^{\prime},t}=0$ 的情况。公式3在分类器性能高度偏差（即高 $b_{t}$ ）时增加 $\tau$ 的值，在偏差较低（即较小 $b_{t}$ ）时减小它。

3.3 Class-Wise Difficulty-Balanced Softmax Cross-Entropy Loss

3.3 类别难度平衡的Softmax交叉熵损失

Suppose when an input data is fed to the classifier after training time $t$ during training, the predicted output of the classifier for all $C$ classes are $z_{t}=$

假设在训练时间 $t$ 后将输入数据输入分类器时，分类器对所有 $C$ 个类别的预测输出为 $z_{t}=$

${z_{1,t},z_{2,t},\ldots,z_{C,t}}$ . The probability distribution $p_{t}={p_{1,t},p_{2,t},...,p_{C,t}}$ over all the classes is computed using the softmax function, which is

${z_{1,t},z_{2,t},\ldots,z_{C,t}}$。类别概率分布 $p_{t}={p_{1,t},p_{2,t},...,p_{C,t}}$ 通过softmax函数计算得出，其公式为

$$
p_{j,t}=\frac{\exp{z_{j,t}}}{\sum_{i=1}^{C}\exp{z_{i,t}}}\forall j\in{1,2,\ldots,C}.
$$

$$
p_{j,t}=\frac{\exp{z_{j,t}}}{\sum_{i=1}^{C}\exp{z_{i,t}}}\forall j\in{1,2,\ldots,C}.
$$

For an input data sample of class $k$ , cross-entropy (CE) loss function com- putes the loss after training time $t$ as

对于一个类别为 $k$ 的输入数据样本，交叉熵损失函数 (cross-entropy loss) 在训练时间 $t$ 后计算损失值为

$$
\mathrm{CE}(p_{t},k)=-\log p_{k,t}.
$$

$$
\mathrm{CE}(p_{t},k)=-\log p_{k,t}.
$$

For the same input data sample, our class-wise difficulty-balanced softmax crossentropy (CDB-CE) loss function computes the loss after training time $t$ as

对于相同的输入数据样本，我们的类难度平衡softmax交叉熵 (CDB-CE) 损失函数在训练时间 $t$ 后计算损失为

$$
\mathrm{CDB-CE}(w_{t},p_{t},k)=-w_{k,t}\log p_{k,t}.
$$

$$
\mathrm{CDB-CE}(w_{t},p_{t},k)=-w_{k,t}\log p_{k,t}.
$$

To make the weights time-dependent, we calculate them after each epoch using the model’s class-wise validation accuracy.

为了使权重具有时间依赖性，我们在每个训练周期后根据模型的类别验证准确率来计算它们。

4 Experiments

4 实验

To demonstrate our proposed solution’s ability to generalize to any data-type or dataset, we evaluate the effectiveness of our solution on 4 different datasets namely MNIST, long-tailed CIFAR, ImageNet-LT and EGTEA. MNIST, longtailed CIFAR and ImageNet-LT are image datasets while EGTEA is a video dataset.

为验证我们提出的解决方案能够泛化到任意数据类型或数据集，我们在4个不同数据集上评估了方案有效性：MNIST、长尾CIFAR、ImageNet-LT和EGTEA。其中MNIST、长尾CIFAR和ImageNet-LT为图像数据集，EGTEA为视频数据集。

4.1 Datasets

4.1 数据集

MNIST. From the standard MNIST handwritten digit recognition dataset [1], we generate a class-imbalanced binary classification task using a subset of the dataset. The experimental setup is exactly same as given in [29]. We select a total of 5000 training images of class ‘4’ and ‘9’ where ‘9’ is chosen as the majority class. We calculate the ‘majority class ratio’ as

MNIST。我们从标准MNIST手写数字识别数据集[1]中生成一个类别不平衡的二分类任务，使用该数据集的子集。实验设置与[29]中给出的完全相同。我们总共选择了5000张类别为"4"和"9"的训练图像，其中"9"被选为多数类。计算"多数类比例"的公式为

$$
\mathrm{majority class ratio}={\frac{\mathrm{no. of training samples in majority class}}{\mathrm{no. of training~samples}}}.
$$

多数类比例 = (多数类训练样本数 / 总训练样本数)

Increasing the majority class ratio increases the imbalance in the training dataset. We also use a validation set which is created by selecting 500 images for each of the two classes from the original dataset but these images are different from the 5000 images selected for training. A test set was also created by randomly selecting 800 images for each of the classes from the original MNIST test set.

增加多数类比例会加剧训练数据集的不平衡性。我们还构建了一个验证集，从原始数据集中为两个类别各选取500张图像（这些图像与用于训练的5000张图像不同）。测试集则是从原始MNIST测试集中为每个类别随机抽取800张图像构成。

Long-Tailed CIFAR. We conduct experiments on long-tailed CIFAR-100 [2]. First a validation set was created from the original training set by randomly selecting 50 images per class. After the separation of the validation set, the remaining images in the training set were used to create a long-tailed version of the dataset using the exact same procedure as stated in [15]. The number of training images per class are reduced following an exponential function $n=n_{c}\mu^{c}$ , where $c$ is the 0-based index of the class and $n_{c}$ is the remaining number of training images of class $c$ after separation of the validation set and $\mu\in(0,1)$ . Similar to [15], the ‘imbalance’ factor of a dataset is defined as the number of training samples in the largest class divided by that of the smallest class. The test set used for experiment is exactly same as the original CIFAR test set available and is a balanced set.

长尾CIFAR。我们在长尾CIFAR-100 [2]上进行了实验。首先从原始训练集中随机选取每类50张图像创建验证集。分离验证集后，使用与[15]完全相同的流程，将训练集中剩余的图像生成长尾版本数据集。每类训练图像数量按指数函数$n=n_{c}\mu^{c}$递减，其中$c$为类别索引（从0开始），$n_{c}$为分离验证集后类别$c$剩余的训练图像数，$\mu\in(0,1)$。参照[15]，数据集的"不平衡"因子定义为最大类训练样本数与最小类的比值。实验使用的测试集与原始CIFAR测试集完全相同，为平衡数据集。

ImageNet-LT. We also conduct experiments on the long-tailed version of the original ImageNet-2012 [3], as constructed in [20]. It comprises of 115,800 images from 1000 categories, where the most frequent class has 1280 image samples and the least frequent class has only 5 images. The test set is balanced. The split constructed by [20] also provides a validation set that is separate from the test set and training set.

ImageNet-LT。我们还在原始ImageNet-2012[3]的长尾版本上进行了实验，该版本由[20]构建。它包含来自1000个类别的115,800张图像，其中最常见类别有1280个图像样本，最不常见类别仅有5张图像。测试集是平衡的。[20]构建的分割还提供了一个独立于测试集和训练集的验证集。

EGTEA. We also conduct experiments on the EGTEA Gaze+ dataset [30]. This is an egocentric dataset that contains trimmed video clips of many kitchenrelated actions. These