ROBMOT: ROBUST 3D MULTI-OBJECT TRACKING BY OBSERVATIONAL NOISE AND STATE ESTIMATION DRIFT MITIGATION ON LIDAR POINTCLOUD

ROBMOT：通过观测噪声和状态估计漂移抑制实现激光雷达点云鲁棒三维多目标跟踪

ABSTRACT

摘要

This work addresses limitations in recent 3D tracking-by-detection methods, focusing on identifying legitimate trajectories and addressing state estimation drift in Kalman filters. Current methods rely heavily on threshold-based filtering of false positive detections using detection scores to prevent ghost trajectories. However, this approach is inadequate for distant and partially occluded objects, where detection scores tend to drop, potentially leading to false positives exceeding the threshold. Additionally, the literature generally treats detections as precise localization s of objects. Our research reveals that noise in detections impacts localization information, causing trajectory drift for occluded objects and hindering recovery. To this end, we propose a novel online track validity mechanism that temporally distinguishes between legitimate and ghost tracks, along with a multi-stage observational gating process for incoming observations. This mechanism significantly improves tracking performance, with a $6.28%$ in HOTA and a $17.87%$ increase in MOTA. We also introduce a refinement to the Kalman filter that enhances noise mitigation in trajectory drift, leading to more robust state estimation for occluded objects. Our framework, RobMOT, outperforms state-of-the-art methods, including deep learning approaches, across various detectors, achieving up to a $4%$ margin in HOTA and $6%$ in MOTA. RobMOT excels under challenging conditions, such as prolonged occlusions and tracking distant objects, with up to a $59%$ improvement in processing latency.

本研究针对当前基于检测的3D跟踪方法的局限性，重点解决合法轨迹识别与卡尔曼滤波器状态估计漂移问题。现有方法主要通过基于阈值的检测分数过滤假阳性检测来防止虚影轨迹，但该策略对远距离和部分遮挡物体效果不佳——这些场景下检测分数易骤降，可能导致假阳性突破阈值。此外，学界通常将检测结果视为物体的精确定位。我们发现检测噪声会影响定位信息，导致被遮挡物体的轨迹漂移且难以恢复。为此，我们提出新型在线轨迹有效性机制，通过时序分析区分合法轨迹与虚影轨迹，并设计多阶段观测门控流程处理输入观测。该机制使HOTA指标提升6.28%，MOTA指标提升17.87%。我们还改进了卡尔曼滤波器，增强了对轨迹漂移中噪声的抑制能力，使被遮挡物体的状态估计更鲁棒。所提框架RobMOT在多种检测器下均超越现有方法（包括深度学习方案），HOTA最高领先4%，MOTA最高领先6%。在持续遮挡、远距离物体跟踪等挑战性场景中，RobMOT表现优异，处理延迟最高降低59%。

3D multi-object tracking (MOT) is one of the pillars of autonomous driving. It is responsible for determining the state of objects in the environment, including their spatial location and motion parameters like velocity and acceleration. Trajectory drift has been observed in state estimation of occluded objects in the top-performing state-of-the-art CasTrack [1], as shown in Figure 1, failing to recover objects under challenging tracking conditions like prolonged occlusion and distant objects as emphasized in Figure 7. Our investigation shows that this drift results from fluctuation noise attached to the incoming 3D detections from deep learning models, which tracking-by-detection methods rely on for object localization on LiDAR point clouds. This noise impacts the precision of state estimation for spatial location and motion parameters of occluded objects that ultimately leads to deviation from the actual motion trajectory.

3D多目标跟踪(MOT)是自动驾驶的支柱技术之一，其核心任务是确定环境中物体的状态，包括空间位置及速度、加速度等运动参数。当前性能最优的CasTrack[1]在遮挡物体状态估计中会出现轨迹漂移现象(如图1所示)，在持续遮挡和远距离物体等挑战性跟踪场景下(图7重点展示)无法恢复目标物体。研究表明，这种漂移源于深度学习模型输出的3D检测结果所附带的波动噪声。基于检测的跟踪方法依赖这些检测结果在激光雷达点云中进行目标定位，而此类噪声会影响被遮挡物体空间位置和运动参数的状态估计精度，最终导致实际运动轨迹出现偏差。

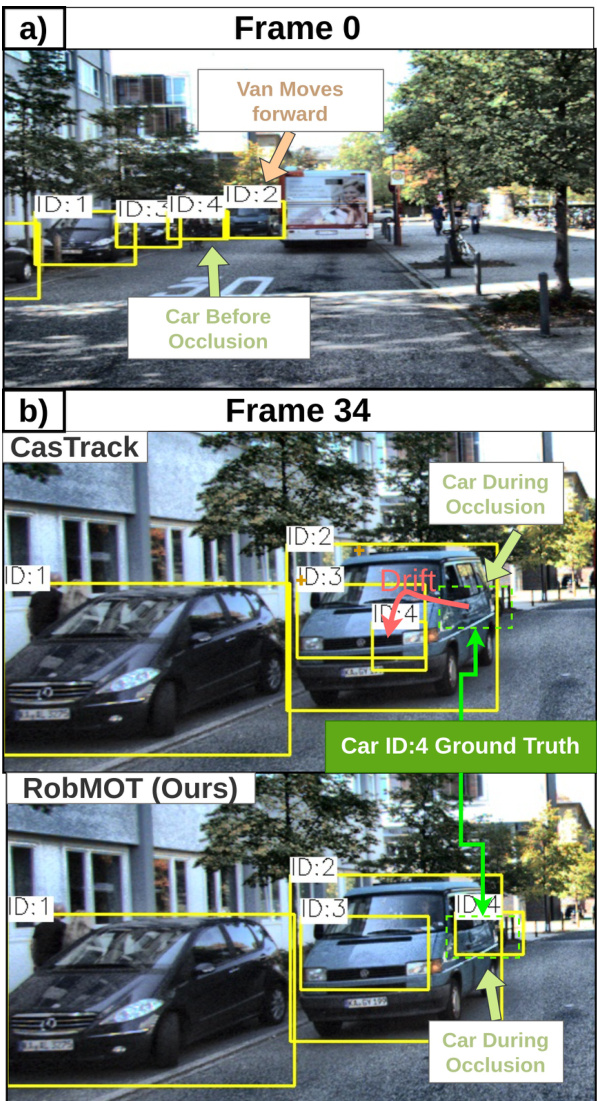
Figure 1: A trajectory drift scenario involving a car (ID4) hidden by a van (ID2). (a) At frame 0, four cars are detected and identified (ID1, ID2, ID3, ID4). (b) By frame 34, the method CastTrack [1] incorrectly estimates the position of car ID4 due to state estimation drift. A dashed green rectangle indicates the actual position. (c) Our proposed approach, with its noise mitigation techniques, successfully localizes car ID4 accurately.

图 1: 车辆ID4被货车ID2遮挡导致的轨迹漂移场景。(a) 第0帧时检测并识别出四辆汽车(ID1、ID2、ID3、ID4)。(b) 到第34帧时，CastTrack方法[1]因状态估计漂移而错误预测了车辆ID4的位置，绿色虚线框标注实际位置。(c) 我们提出的方法通过噪声抑制技术准确定位了车辆ID4。

Another issue is the absence of trajectory legitimacy verification in the MOT literature [1, 2, 3, 4, 5, 6]. These works apply a fine-tuned threshold on detection scores of the detections provided by deep learning models to filter out false positive observations that cause ghost trajectories. This approach is not reliable as it can block observations that belong to legitimate trajectories while leaking false positive observations. Since observations of legitimate trajectories can inherit some of the false positive characteristics, such as low detection scores for distant and partial occlusion scenarios, the MOT methods need to validate trajectories based on the consistency and legitimacy of their historical observations instead.

另一个问题是MOT文献[1, 2, 3, 4, 5, 6]中缺乏轨迹合法性验证。这些工作通过在深度学习模型提供的检测分数上应用微调阈值，来过滤导致虚假轨迹的误报观测。这种方法不可靠，因为它可能阻挡属于合法轨迹的观测，同时漏掉误报观测。由于合法轨迹的观测可能继承部分误报特征（例如远距离和部分遮挡场景下的低检测分数），MOT方法需要根据其历史观测的一致性和合法性来验证轨迹。

In this work, we tackle the above-mentioned challenges through Kalman filter refinement to mitigate the trajectory drift noise, Section 2.2, and propose a novel online mechanism to validate and distinguish between legitimate and ghost trajectories based on studying the characteristics of ghost tracks, Section 2.3. Our proposed refinement shows consistency in tracking for occluded objects superior to the latest state-of-the-art approach, CasTrack, demonstrated in Figure 1 and Figure 7. Next, the proposed trajectory validity mechanism incorporates a multi-stage observational gate that allows potential detections of legitimate tracks to pass to the system and an uncertainty formulation used to quantify the temporal improvement of trajectory certainty based on ghost track characteristics. The mechanism shows a $4%$ and $6%$ enhancement in HOTA and MOTA metrics, respectively.

在本工作中，我们通过卡尔曼滤波 (Kalman filter) 优化来缓解轨迹漂移噪声（第2.2节），并提出一种基于幽灵轨迹特征研究的新型在线验证机制，用于区分真实轨迹与幽灵轨迹（第2.3节）。我们的优化方案在遮挡物体跟踪一致性上优于当前最先进的CasTrack方法，如图1和图7所示。此外，所提出的轨迹有效性机制采用多阶段观测门控，允许潜在的真实轨迹检测进入系统，并利用基于幽灵轨迹特性的不确定性公式来量化轨迹确定性的时序改进。该机制使HOTA和MOTA指标分别提升$4%$和$6%$。

We present the above innovative aspects within a 3D MOT tracking framework dubbed RobMOT. Our contribution can be summarized as follows:

我们在名为RobMOT的3D MOT跟踪框架中提出了上述创新点，主要贡献可概括如下：

1 Related Work

1 相关工作

3D MOT methods on LiDAR point cloud could be categorized into learning and non-learning (classical) approaches. Part of learning-based methods in the literature involves end-to-end deep learning models that combine object detection and tracking [7, 8, 9, 10]. Meanwhile, other methods adapt tracking-by-detection paradigm [11, 12, 13, 14] when the detection of objects is given and the aim is to perform temporal tracking of the objects. The recent research integrates attention mechanism and transformers concepts [15, 16] into MOT to enhance the tracking performance. However, learning-based solutions require evolved hardware to be applicable to real-time applications.

基于激光雷达点云的3D多目标跟踪(MOT)方法可分为学习型与非学习型(经典)两类。文献中的部分学习型方法采用端到端深度学习模型，将目标检测与跟踪相结合[7,8,9,10]。另一些方法则在给定目标检测结果时，采用检测跟踪分离范式[11,12,13,14]进行时序目标追踪。最新研究将注意力机制与Transformer架构[15,16]融入MOT以提升跟踪性能。但学习型方案需要高性能硬件支持才能满足实时应用需求。

Meanwhile, classical MOT solutions [4, 5, 2, 3, 6, 17, 1] have gained much attention due to their low latency and the comparative performance with learning-based solutions. Despite recent advancements in the classical methods, challenges such as the limitations of the Kalman filter, ghost tracks, and memory management persist, especially in autonomous driving applications where the environment constantly changes. We will shed light on these challenges and discuss the remedies proposed in the literature next.

与此同时，经典多目标跟踪(MOT)方案[4, 5, 2, 3, 6, 17, 1]因其低延迟特性及与基于学习方案的性能可比性而备受关注。尽管经典方法近期有所进展，但卡尔曼滤波器(Kalman filter)的局限性、幽灵轨迹和内存管理等挑战依然存在，尤其在环境持续变化的自动驾驶应用中。下文将剖析这些挑战并探讨文献中提出的解决方案。

Kalman filter (KF) is widely used in tracking-by-detection methods [2, 3, 17, 1] for autonomous driving because of its performance in filtering noise from state estimation while dealing with noisy measurements. If the noise is not properly modeled in the filter, it can cause deviation in the state estimation, as the filter’s estimation is sensitive to imprecise measurements. Cao et al. [6] prevent error accumulation in state prediction caused by periodic occlusion of objects by refining the object’s trajectory after object reappearance. However, the object should be recovered in order to refine its trajectory. Moreover, as of the point cloud’s sparsity, the incoming detections from 3D detectors suffer from spatial distortion around the object’s actual location. This spatial distortion results in an imprecise estimation of the motion parameters, ultimately leading to a deviation in the state estimation once the object faces an occlusion.

卡尔曼滤波器 (KF) 因其在状态估计中过滤噪声的性能，被广泛应用于自动驾驶的检测跟踪方法 [2, 3, 17, 1]。若滤波器未正确建模噪声，会导致状态估计偏差，因为滤波器对不精确的测量数据极为敏感。Cao 等人 [6] 通过在物体重新出现后优化其运动轨迹，避免了周期性遮挡导致的状态预测误差累积。但该方法需先成功恢复被遮挡物体才能进行轨迹优化。此外，由于点云的稀疏性，3D检测器输出的检测结果会在物体实际位置周围产生空间畸变。这种空间畸变会导致运动参数估计不准确，最终当物体遭遇遮挡时引发状态估计偏差。

Ghost tracks are false positive detections generating illusion tracks that could eventually lead to wrong navigation of the AV. Since the tracking-by-detection paradigm relies heavily on detection accuracy, ghost tracks in object tracking can significantly harm the tracking performance. Kim et al. [3] introduce a multi-stage data association method to overcome this issue by employing multiple detection sources. Nevertheless, they still depend on predefined thresholds to prevent false positives. The downside of a fine-tuned threshold while filtering ghost tracks is the potential of leaking false positive detections that exceed the threshold while blocking detections that belong to actual tracks. Other approaches [5, 2] incorporate a filtration step to address false positive detections. Wang.X et al. [2] confirm the legitimacy of a track when three consecutive detections of that track have been observed. In contrast, Wang.L et al. [5] select objects for the highest $30%$ detections in the confidence score. However, the assumptions provided by these solutions may not apply to all scenarios, particularly distant objects or objects subject to periodic occlusions.

幽灵轨迹是由误检产生的虚假轨迹，可能导致自动驾驶车辆(AV)的错误导航。由于检测跟踪范式高度依赖检测精度，目标跟踪中的幽灵轨迹会严重影响跟踪性能。Kim等人[3]提出采用多检测源的多阶段数据关联方法来解决此问题，但仍需依赖预设阈值来防止误检。精细调优的阈值在过滤幽灵轨迹时存在弊端：既可能漏掉超过阈值的误检，又可能阻挡真实轨迹的检测。其他方法[5,2]通过引入过滤步骤处理误检问题——Wang.X团队[2]要求连续三次检测到轨迹才确认其合法性，而Wang.L团队[5]则选择置信度分数前30%的检测目标。但这些方案的前提假设未必适用于所有场景，特别是远距离目标或周期性遮挡目标的情况。

Memory management plays a critical role in addressing false positive detections. Maintaining ghost tracks in memory can lead to invalid associations. Meanwhile, early elimination may lose legitimate tracks under prolonged occlusion. In the literature, some work [2, 3, 5, 6] set up a threshold to discard tracks from memory based on how long these tracks have not been observed. Although short memory is suitable for ghost track elimination, it could also remove tracks of objects facing prolonged occlusion. On the other hand, long memory will not remove ghost tracks while increasing the computational time. Nagy et al. [17] attempt to address the trade-off by proposing an MOT solution with low latency and leveraging speed to extend the lifetime of objects, thus capturing more occlusion scenarios. While this approach excels in tracking objects with prolonged occlusion, it does not handle false positives. Wu et al. [1] resolve the issue by associating a confidence score to pre-observed objects in object association. This score decreases over time when the object becomes not observed for a period of time to prevent potential associations with false positive detections. Nonetheless, this approach cannot recover objects under prolonged occlusion as their association score will decrease. This work proposes RobMOT, a framework to mitigate state estimation deviation caused by fluctuation noise. It also provides adaptive identification for ghost tracks with a quick elimination from memory alongside a mechanism that prevents legitimate track detections from being blocked while filtering ghost tracks.

内存管理在解决误检问题中起着关键作用。保留幽灵轨迹会导致无效关联，而过早清除又可能在长期遮挡下丢失合法轨迹。现有研究[2,3,5,6]通常设置阈值，根据轨迹未被观测的时长进行内存清除。虽然短时内存适合消除幽灵轨迹，但会丢失长期遮挡的目标轨迹；而长时内存虽保留遮挡目标，却无法消除幽灵轨迹且增加计算耗时。Nagy等人[17]提出低延迟多目标跟踪方案，利用速度信息延长目标生命周期以覆盖更多遮挡场景，但未解决误检问题。Wu等人[1]通过在目标关联中引入置信度评分机制，对未持续观测的目标逐步降低其关联权重以避免误检关联，但长期遮挡目标的评分衰减会导致无法恢复。本文提出RobMOT框架，既能通过自适应识别快速清除幽灵轨迹，又能过滤噪声引起的状态估计偏差，同时确保在筛除幽灵轨迹时不阻断合法轨迹的检测。

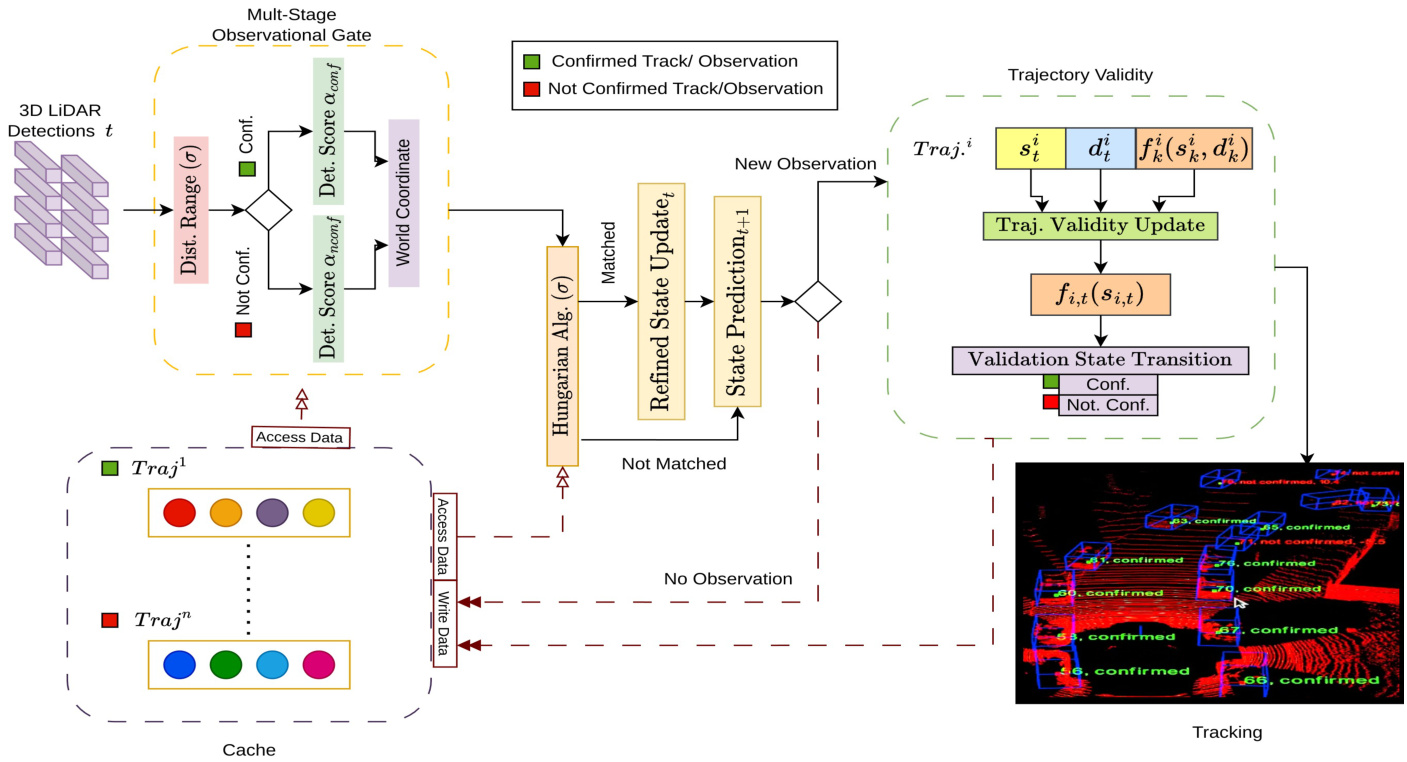
Figure 2: The RobMOT framework consists of four modules: a multi-stage observational gate for identifying legitimate observations, an association trajectory innovation for trajectories’ association with observations and next-state prediction, a trajectory validity for temporal validation of the trajectories, and a cache for storing and termination.

图 2: RobMOT框架包含四个模块：用于识别合法观测的多阶段观测门控、实现轨迹与观测关联及下一状态预测的关联轨迹创新模块、对轨迹进行时间有效性验证的轨迹有效性模块，以及用于存储和终止的缓存模块。

2 Methodology

2 方法论

As shown in Figure 2, the framework consists of four parts. A multi-stage observational gate: responsible for identifying potential observations of legitimate tracks. Refined Kalman filter for noise mitigation: a refined KF that updates the state estimation of cached trajectories and predicts their next state. Trajectory validity: Updates the legitimacy uncertainty of trajectories recently associated to observations. Cache: Holds trajectories stored in the framework and discards terminated tracks.

如图 2 所示，该框架由四部分组成。多阶段观测门控：负责识别合法轨迹的潜在观测。用于降噪的改进卡尔曼滤波器 (Kalman Filter)：一种改进的 KF，用于更新缓存轨迹的状态估计并预测其下一状态。轨迹有效性：更新最近与观测关联的轨迹的合法性不确定性。缓存：保存框架中存储的轨迹并丢弃已终止的轨迹。

2.1 Multi-Stage Observational Gate

2.1 多阶段观测门

The multi-stage observational gate is an identification step for potential observations of the legitimate tracks identified by the trajectory validity stage, (see Section 2.3). The primary purpose of this stage is to allow observations of distant and partially occluded objects with low detection scores to enter while preventing overwhelming the system.

多阶段观测门控是对轨迹有效性阶段(见第2.3节)识别的合法航迹潜在观测的识别步骤。该阶段的主要目的是在避免系统过载的同时，允许检测分数较低的远距离和部分遮挡物体进入观测系统。

There are three types of the observations: observations of existing legitimate tracks, observations of tracks not generated yet by the system, and false observations that cause ghost tracks. Despite ghost tracks identification in the trajectory validity stage, discussed in Section 2.3, a threshold $\alpha_{n c o n f}$ should be assigned to the incoming observation to prevent overloading the MOT method because 3D deep learning detectors on LiDAR point cloud deliver immense number of detections with various detection scores. Thus, $\alpha_{n c o n f}$ is assigned a minimal value for detection scores to avoid overloading the system, regardless of the observations’ legitimacy, as this will be assessed later during the trajectory validity stage.

观测类型分为三种：现有合法轨迹的观测、系统尚未生成的轨迹观测，以及导致幽灵轨迹的虚假观测。尽管第2.3节讨论了轨迹有效性阶段的幽灵轨迹识别，但仍需为输入观测设置阈值$\alpha_{n c o n f}$，以防止因LiDAR点云上的3D深度学习检测器产生海量不同检测分数的结果而过度占用多目标跟踪(MOT)方法的资源。因此，无论观测合法性如何（后续将在轨迹有效性阶段评估），$\alpha_{n c o n f}$都会被设为检测分数的最小值以避免系统过载。

Even though assigning $\alpha_{n c o n f}$ with a small value allows a high volume of observations to pass to the system, it could block legitimate observations. Hence, We initially identify potential observations of existing legitimate tracks using the same Ecludiean distance threshold $\sigma$ used in the association step (see Section 2.2). Observations located in a distance less than $\sigma$ to a legitimate track, identified by the trajectory validity stage in Section 2.3, are considered legitimate observations. Although the identified potential legitimate observations can pass directly to the system, we have observed that it still causes high latency because of flooding detections from deep learning models on the point cloud. Thus, we provide an additional detection $\alpha_{c o n f}$ score filtration when $\alpha_{c o n f}\leq\alpha_{n c o n f}$ to allow legitimate observations to enter the system while preventing overloading the system. $\alpha_{n c o n f}$ and $\alpha_{c o n f}$ are fine-tuned so that no enhancement in the tracking performance is observed since their preliminary purpose is to prevent overloading the system. Lastly, the filtered observations are projected from the LiDAR coordinate to the world coordinate. Algorithm 1 demonstrates these procedures in detail.

尽管为 $\alpha_{n c o n f}$ 设置较小值能让大量观测数据进入系统，但可能会阻挡合法观测。因此，我们首先采用与关联步骤相同的欧氏距离阈值 $\sigma$（参见第2.2节）来识别现有合法轨迹的潜在观测点。若观测点与第2.3节轨迹验证阶段认定的合法轨迹距离小于 $\sigma$，则视为合法观测。虽然这些潜在合法观测可直接进入系统，但我们发现点云深度学习模型产生的密集检测仍会导致高延迟。为此，当 $\alpha_{c o n f}\leq\alpha_{n c o n f}$ 时增设检测置信度 $\alpha_{c o n f}$ 过滤机制，既允许合法观测进入系统，又避免系统过载。通过微调 $\alpha_{n c o n f}$ 和 $\alpha_{c o n f}$ 确保不影响跟踪性能——因其核心目标是防止系统过载。最后，过滤后的观测数据从LiDAR坐标系转换至世界坐标系。算法1详细展示了这些处理流程。

算法 1 多阶段观测门控
function MultiStageObservationalGate(D, T, o, Qc, Qn) 输入:
D: 来自 LiDAR 的 3D 检测列表 T: 缓存中的轨迹列表 o: 欧氏距离阈值
Qcon f : 潜在确认观测的检测分数阈值
Qncon f : 非确认观测的检测分数阈值 输出: P: 通过门控的检测列表
P←[
for each det in D do if det.score ≤ Qcon f then
continue end if confirmed ←false

2.2 Refined Kalman filter for Noise Mitigation

2.2 用于噪声抑制的改进卡尔曼滤波器

The permitted observations are associated with trajectories cached in the framework. We use the Hungarian algorithm [18] with the algebraic association strategy followed in [17]. The association for an observation is performed by selecting a trajectory with the shortest Euclidean distance between the estimated state and the observation. When the shortest distance to an observation exceeds $\sigma$ , a new trajectory is created for the observation.

允许的观测数据与框架中缓存的轨迹相关联。我们采用匈牙利算法 [18] 并遵循文献 [17] 的代数关联策略。观测数据的关联通过选择估计状态与观测值之间欧氏距离最短的轨迹来实现。当观测数据的最小距离超过 $\sigma$ 时，系统会为该观测数据创建新轨迹。

The framework performs next-state estimation for all trajectories cached in the system. Trajectories associated with an observation will pass through state update and state prediction as demonstrated in Figure 2. Other trajectories will go directly through state prediction. The framework utilizes KF with a constant acceleration motion model.

该框架对系统中缓存的所有轨迹执行下一状态估计。与观测相关联的轨迹会如图 2 所示经历状态更新和状态预测流程，其他轨迹则直接进行状态预测。该框架采用基于恒定加速度运动模型的卡尔曼滤波 (KF) 实现。

We have observed drift in state estimation for objects encountering occlusion or leaving the sensor field of view (offscene). This phenomenon is also observed in the literature, as displayed in Figure 1 when the estimated trajectory of a parked car with ID 4 drifts away from the expected location during the occlusion. Figure 3 shows another scenario when two parked cars with $\textrm{I D}0$ and 2 drift from the actual position after being off-scene. Our investigation of the phenomenon concludes that this deviation is caused by trembling in detection bounding boxes around objects’ locations, which results in illusion movement for these objects that eventually impacts state update and prediction in KF.

我们观察到，遭遇遮挡或离开传感器视场（offscene）的物体在状态估计上会出现漂移现象。文献[20]中也记录了类似现象：如图1所示，当ID为4的停放车辆在遮挡期间，其估计轨迹会偏离预期位置；图3则展示了ID为0和2的两辆停放车辆在离开视场后发生实际位置漂移的情况。经分析，这种偏差源于物体检测边界框的位置抖动，导致这些静止物体被误判为运动状态，最终影响了卡尔曼滤波器(KF)的状态更新与预测结果。

We model this noise using the algebraic deviation, shown in Equation 1, between the detected bounding boxes $z_{i j}^{d e t}=$ $(x_{i j},y_{i j})$ and the actual location of the objects $z_{i j}^{g t}=(x_{i j},y_{i j})$ across $k$ observations for $N$ objects using KITTI

我们使用代数偏差对这种噪声进行建模，如公式1所示，即在KITTI数据集上对$N$个物体进行$k$次观测时，检测到的边界框$z_{i j}^{d e t}=(x_{i j},y_{i j})$与物体实际位置$z_{i j}^{g t}=(x_{i j},y_{i j})$之间的偏差。

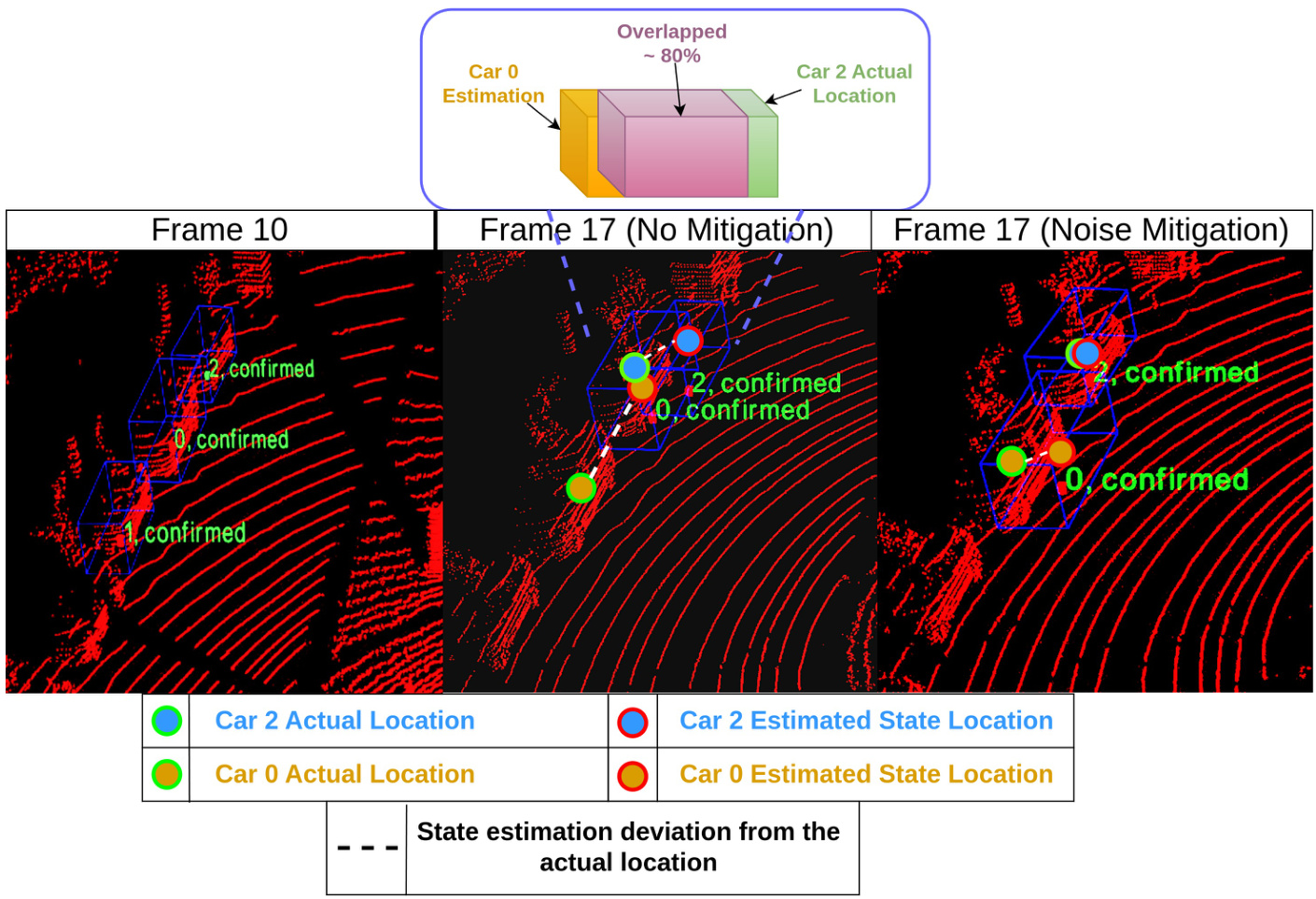
Figure 3: A scenario demonstrates the impact of detection noise on parked cars. Initially, the state estimation of the three cars is positioned correctly in frame 10. The middle frame, frame 17, shows drift in state estimation of cars with $\mathrm{ID0}$ , orange circle, and 2, blue circle, caused by the noise. The state deviation from the original position of the cars is marked by disconnected white line. Considering the proposed noise mitigation (the third scene on the left), the state estimation of cars with ID 2 has no deviation, while the Car 0 deviation has been reduced significantly.

图 3: 场景展示了检测噪声对停放车辆的影响。初始状态下，第10帧中三辆车的状态估计位置正确。中间帧(第17帧)显示由于噪声导致 $\mathrm{ID0}$ (橙色圆圈)和ID2(蓝色圆圈)车辆的状态估计发生漂移。车辆与原位的状态偏差通过断开的白线标示。采用提出的噪声抑制方法(左侧第三个场景)后，ID2车辆的状态估计无偏差，而ID0车辆的偏差显著减小。

training dataset.

训练数据集

$$
\begin{array}{l}{\displaystyle\mu_{x}=\frac{1}{\sum_{i=1}^{N}k_{i}}\sum_{i=1}^{N}\sum_{j=1}^{k_{i}}\left(z_{i j}^{g t}(x)-z_{i j}^{d e t}(x)\right)}\ {\displaystyle\sigma_{x}^{2}=\frac{1}{\sum_{i=1}^{N}k_{i}}\sum_{i=1}^{N}\sum_{j=1}^{k_{i}}\left(\left(z_{i j}^{g t}(x)-z_{i j}^{d e t}(x)\right)-\mu_{x}\right)^{2}}\end{array}
$$

$$
\begin{array}{l}{\displaystyle\mu_{x}=\frac{1}{\sum_{i=1}^{N}k_{i}}\sum_{i=1}^{N}\sum_{j=1}^{k_{i}}\left(z_{i j}^{g t}(x)-z_{i j}^{d e t}(x)\right)}\ {\displaystyle\sigma_{x}^{2}=\frac{1}{\sum_{i=1}^{N}k_{i}}\sum_{i=1}^{N}\sum_{j=1}^{k_{i}}\left(\left(z_{i j}^{g t}(x)-z_{i j}^{d e t}(x)\right)-\mu_{x}\right)^{2}}\end{array}
$$

As depicted in Figure 4, the error distribution shows a Gaussian shape for the noise of the VirConv detector across $x$ and $y$ LiDAR coordinates, which facilitates its integration into KF. Accordingly, we derive the $2\times2$ covariance matrix $D_{t}$ representing the noise impact on the detections (measurements). Notably, the noise varies from one detector to another as to the variance in detection performance; hence, $D_{t}$ should be recomputed as the employed detector changes. By applying Equation 1 on $y$ coordinate, we obtain a covariance matrix of the noise, Equation 2.

如图4所示，VirConv检测器在LiDAR坐标系$x$和$y$轴上的噪声误差分布呈高斯形态，这有利于其与KF (Kalman Filter) 的集成。据此，我们推导出$2×2$协方差矩阵$D_{t}$来表示噪声对检测结果（测量值）的影响。值得注意的是，由于不同检测器的性能差异，其噪声特性也会有所不同，因此当更换检测器时，需要重新计算$D_{t}$。通过将公式1应用于$y$坐标，我们得到了噪声的协方差矩阵，如公式2所示。

$$
\mathbf{D_{t}}=\left[{\begin{array}{c c}{\sigma_{x}^{2}}&{0}\ {0}&{\sigma_{y}^{2}}\end{array}}\right]
$$

$$
\mathbf{D_{t}}=\left[{\begin{array}{c c}{\sigma_{x}^{2}}&{0}\ {0}&{\sigma_{y}^{2}}\end{array}}\right]
$$

Since this noise is attached to the incoming detections $z_{t}$ at teim $t$ , it harms the computation of the residual term $\hat{y}{t}$ , which is the difference between the current measurement $z_{t}$ and state estimation $\hat{x}{t\mid t-1}$ predicted at $t-1$ . Consequently, the noise impact on the residual term leads to incorrect updates for the motion parameters of the object. The innovation covariance $S_{t}$ is responsible for weighting the innovation residual $\hat{y}{t}$ through the Kalman gain $K_{t}$ . Therefore, the covariance matrix $D_{t}$ needs to be added to the innovation covariance $S_{t}$ to compensate for the impact of noise on the updated state. Hence, the updated state estimation $\hat{x}_{t\mid t}$ will consider the impact of the deviation noise on the observation.

由于该噪声附着于时间$t$的输入检测$z_{t}$，它会损害残差项$\hat{y}{t}$的计算。该残差是当前测量值$z_{t}$与$t-1$时刻预测的状态估计$\hat{x}{t\mid t-1}$之间的差值。因此，噪声对残差项的影响会导致物体运动参数更新错误。新息协方差$S_{t}$负责通过卡尔曼增益$K_{t}$对新息残差$\hat{y}{t}$进行加权。因此，需要在$S_{t}$中加入协方差矩阵$D_{t}$以补偿噪声对更新状态的影响。最终，更新后的状态估计$\hat{x}_{t\mid t}$将考虑偏差噪声对观测的影响。

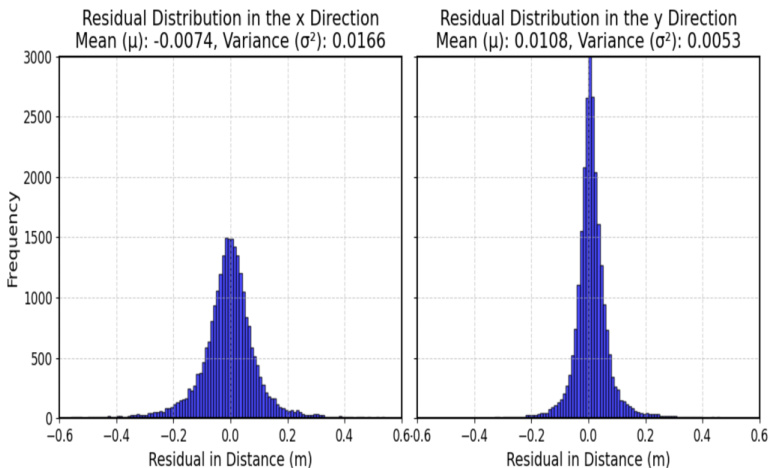
Figure 4: The distribution of the fluctuation noise associated with VirConv [19] detections. The distribution shows Gaussian noise across five different detectors [19, 20, 21, 22, 23].

图 4: VirConv [19] 检测相关波动噪声的分布。该分布展示了五个不同探测器 [19, 20, 21, 22, 23] 的高斯噪声特性。

The main reason for not using $R_{t}$ instead is because it models the incorrectness of the measurement for the point cloud from LiDAR with respect to the real world, while $D_{t}$ models the incorrectness of the detection process with respect to the LiDAR point cloud, which means they are independent. Equation 3 demonstrates the updated state of KF after adapting $D_{t}$ noise.

不使用 $R_{t}$ 的主要原因是它建模的是激光雷达 (LiDAR) 点云相对于现实世界的测量误差，而 $D_{t}$ 建模的是检测过程相对于激光雷达点云的误差，这意味着二者是独立的。公式 3 展示了适配 $D_{t}$ 噪声后 KF (卡尔曼滤波) 的更新状态。

$H_{t}$ is the observation model to map from estimation to measurement space at time $t$ , while $P_{t|t-1}$ is the estimation uncertainty at time $t$ given measurement at $t-1$ . In Section 2.4, we will describe how $P_{t|t}$ contribute to trajectory termination in the cache.

$H_{t}$ 是在时间 $t$ 将估计映射到测量空间的观测模型，而 $P_{t|t-1}$ 是在给定 $t-1$ 时刻测量值时 $t$ 时刻的估计不确定性。在第2.4节中，我们将描述 $P_{t|t}$ 如何影响缓存中的轨迹终止。

2.3 Trajectory Validity

2.3 轨迹有效性

The objective is to monitor the validity (legitimacy) of the existing trajectories in the system while identifying invalid ones, called ghost tracks. Each track has a certainty score that represents its legitimacy. This score is updated whenever a new observation of the track is available. The certainty score changes based on the likelihood of the trajectory being a ghost track. By observing the characteristics of ghost tracks, the ghost tracks are usually formed from intermittent sequences of observations with low to moderate detection scores. Based on these characteristics, the certainty score for track $i$ changes when a new observation is associated with the track at time $t$ . The certainty score changes according to the detection score $s_{i}^{t}$ and the duration of absence $d_{t}^{i}$ since the last observation associated with the track.

目标是监控系统中现有轨迹的有效性（合法性），同时识别无效轨迹（称为幽灵轨迹）。每条轨迹都有一个代表其合法性的确信分数。每当该轨迹获得新观测时，该分数就会更新。确信分数会根据轨迹成为幽灵轨迹的可能性而变化。通过观察幽灵轨迹的特征，这些轨迹通常由检测分数中低的间断观测序列构成。基于这些特征，当时间$t$有新观测关联到轨迹$i$时，其确信分数会根据检测分数$s_{i}^{t}$和自上次关联观测以来的缺失时长$d_{t}^{i}$发生变化。

$$
\begin{array}{c}{{f_{t}^{i}(s_{t}^{i},d_{t}^{i})=s_{t}^{i}e^{-d_{t}^{i}}-\displaystyle\frac{d_{t}^{i}}{s_{t}^{i}}+f_{k}^{i}(s_{k}^{i},d_{k}^{i}),\mathrm{where}s_{t}^{i}>0}}\ {{d_{t}^{i}=t-\left(k+1\right)}}\end{array}
$$

$$
\begin{array}{c}{{f_{t}^{i}(s_{t}^{i},d_{t}^{i})=s_{t}^{i}e^{-d_{t}^{i}}-\displaystyle\frac{d_{t}^{i}}{s_{t}^{i}}+f_{k}^{i}(s_{k}^{i},d_{k}^{i}),\mathrm{where}s_{t}^{i}>0}}\ {{d_{t}^{i}=t-\left(k+1\right)}}\end{array}
$$

As shown in Equation 4, the formulation consists of three terms: Confidence decay term $s_{t}^{i}e^{-d_{t}^{i}}$ (reward), Absence duration term (penalty) $\frac{d_{t}}{s_{t}^{i}}$ , and Temporal validity $f_{k}^{i}(s_{k}^{i},d_{t}^{k})$ term.

如公式4所示，该公式由三项组成：置信度衰减项 $s_{t}^{i}e^{-d_{t}^{i}}$ (奖励)、缺席时长项(惩罚) $\frac{d_{t}}{s_{t}^{i}}$ 以及时序有效性项 $f_{k}^{i}(s_{k}^{i},d_{t}^{k})$。

2.3.1 Confidence decay

2.3.1 置信度衰减

The term is responsible for increasing the certainty score of track $i$ as the detection score $s_{t}^{i}$ of the associated observation increases as a reward, indicating the detection model’s confidence in this observation. However, ghost tracks with moderate detection scores can receive high rewards, potentially misleading the validation mechanism. Thus, a decay rate, $e^{-d_{t}^{i}}$ , is attached to the detection score $s_{t}^{i}$ . The decay $e^{-d_{t}^{i}}$ increases as the duration $d_{t}^{i}$ of the current observation at time $t$ to the previous observation at time $k$ increases. Given the intermittent characteristic of ghost tracks, the decay term decreases the detection score for potential ghost tracks in the system.

该术语负责随着关联观测的检测分数$s_{t}^{i}$提升而增加轨迹$i$的确定性分数作为奖励，表明检测模型对该观测结果的置信度。然而，具有中等检测分数的幽灵轨迹可能获得高奖励，从而误导验证机制。因此，检测分数$s_{t}^{i}$需附加衰减率$e^{-d_{t}^{i}}$。当当前时刻$t$的观测与前一时刻$k$的观测间隔时长$d_{t}^{i}$增加时，衰减项$e^{-d_{t}^{i}}$随之增大。鉴于幽灵轨迹的间歇性特征，该衰减项可降低系统中潜在幽灵轨迹的检测分数。

2.3.2 Absence duration

2.3.2 缺勤时长

The penalty term $\frac{d_{t}^{i}}{s_{t}^{i}}$ lowers the certainty score as the absence duration $d_{t}^{i}$ of a new observation for the track increases. This term will diminish the impact of the reward with an extended absence duration that indicates a high potential of being a ghost trajectory. However, this term can harm legitimate tracks that encounter occlusion. Since observations of legitimate tracks tend to have high detection scores $s_{t}^{i}$ , we include inverse proportional to the detection score to decrease the impact of this term on the legitimate tracks.

惩罚项 $\frac{d_{t}^{i}}{s_{t}^{i}}$ 会随着轨迹新观测缺失时长 $d_{t}^{i}$ 的增加而降低确定性分数。该惩罚项会削弱因长时间缺失观测（暗示轨迹极可能是虚警）带来的奖励影响。但对于遭遇遮挡的合法轨迹，该惩罚项可能造成误判。由于合法轨迹的观测通常具有较高检测分数 $s_{t}^{i}$，我们引入检测分数的反比来减弱该惩罚项对合法轨迹的影响。

2.3.3 Temporal validity

2.3.3 时间有效性

The inclusion of $f_{k}^{i}(s_{k}^{i},d_{k}^{i})$ integrates the previous certainty score calculated at time $k$ to the current certainty score $f_{t}^{i}(s_{t}^{i},d_{t}^{i})$ of time $t$ . This term adds temporal validation for trajectories in the system by incorporating historical certainty into the current certainty score so that $f_{t}^{i}(s_{t}^{i},d_{t}^{i})$ represents a certainty score of all trajectory states.

将 $f_{k}^{i}(s_{k}^{i},d_{k}^{i})$ 纳入计算，将时间 $k$ 处先前计算的确定性分数整合到当前时间 $t$ 的确定性分数 $f_{t}^{i}(s_{t}^{i},d_{t}^{i})$ 中。这一项通过将历史确定性纳入当前确定性分数，为系统中的轨迹添加了时间验证，使得 $f_{t}^{i}(s_{t}^{i},d_{t}^{i})$ 表示所有轨迹状态的确定性分数。

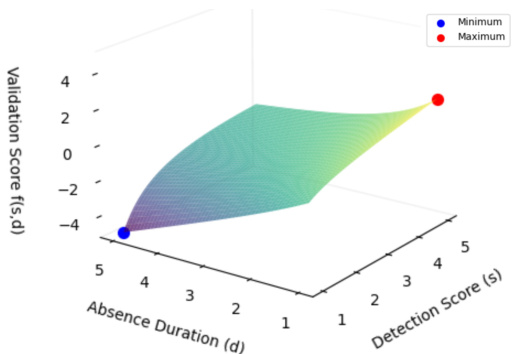
Figure 5: A graphical visualization of the certainty scoring formula over detection scores of range $[0,5]$ and absence duration [0, 5] frames. The red point is the highest certainty score when the detection score is highest while the absence duration is lowest. In contrast, the blue point is the lowest certainty score when the detection score is at the lowest value, while the absence duration is the highest. The surface shows the remaining values.

图 5: 检测分数范围 $[0,5]$ 与缺失持续时间 [0, 5] 帧的确定性评分公式可视化图示。红点代表检测分数最高且缺失持续时间最短时的最高确定性得分，蓝点则对应检测分数最低且缺失持续时间最长时的最低确定性得分。曲面展示了其余数值的分布情况。

A visual representation of the distribution of Equation 4 is highlighted in Figure 5; the relation between the detection score, the absence duration, and its impact on the certainty score.

图5突出展示了公式4分布的视觉化呈现，包括检测分数、缺失持续时间及其对确定性分数影响的关联关系。

This mechanism monitors the validity of trajectories in the system individually until a certainty score of a trajectory exceeds a pre-defined threshold $\alpha_{l e g i t}$ that indicates the trajectory is legitimate. In this case, the validation mechanism changes the trajectory status from “not confirmed” to “confirmed” and terminates the validation mechanism to this trajectory. Thus, confirmed trajectories cannot be changed to “not confirmed” as the mechanism is terminated for these tracks. Algorithm 2 demonstrates trajectory validation procedures in detail.

该机制独立监控系统中轨迹的有效性，直到某条轨迹的置信度分数超过预设阈值$\alpha_{legit}$，表明该轨迹合法。此时，验证机制将轨迹状态从"未确认"改为"已确认"，并终止对该轨迹的验证机制。因此，已确认的轨迹无法再变更为"未确认"状态，因为这些轨迹的验证流程已终止。算法2详细展示了轨迹验证流程。

算法2 轨迹有效性验证
函数 更新轨迹可信度(T, Qlegit)
输入:
T: 缓存中的轨迹列表
Qlegit: 轨迹合法性阈值
对每条轨迹 traj ∈ T 执行
若 traj.hasNewObservationO 成立
St ← traj.getObservationO.detectionScoreO
dt ← traj.getAbsenceDurationO
fk ← traj.getCertaintyScoreO
ft=ste-dt-+fk
traj.setCertaintyScore(ft)
若 traj.getCertaintyScoreO ≤ Qlegit 成立
traj.setValidityStatus(true)
结束条件
结束条件
结束循环 结束函数

2.4 Trajectory Termination and Caching

2.4 轨迹终止与缓存

All trajectories are saved in a cache module. In the literature, a trajectory is terminated or discarded when there are no further observations for that trajectory for several frames. Generally, it is not trivial to define an absence threshold as it could risk eliminating objects under prolonged occlusion or maintaining ghost tracks for a long. Instead, in our framework, we discard the trajectory when the estimation uncertainty, $P_{t|t}$ in Equation 3, becomes high, as it can lead to mismatching in object association. We have observed that ghost tracks tend to have limited observations, leading to high uncertainty in state estimation that matches the intended goal. Meanwhile, legitimate tracks maintain low estimation uncertainty, even those under occlusion. Thus, estimation uncertainty is used to terminate tracks from the cache. Algorithm 3 demonstrates the termination procedures in the cache.

所有轨迹都保存在缓存模块中。文献中通常会在某条轨迹连续多帧无观测数据时终止或丢弃该轨迹。但定义缺席阈值并非易事，这可能导致长时间遮挡下的物体被错误清除，或使虚警轨迹持续存在。在我们的框架中，当估计不确定性（即公式3中的$P_{t|t}$）过高时，我们会丢弃轨迹，因为这种情况可能导致物体关联失配。我们观察到虚警轨迹通常观测数据有限，导致状态估计的高不确定性，这恰好符合设计目标。而合法轨迹即使处于遮挡状态，仍能保持较低的估计不确定性。因此，我们采用估计不确定性作为缓存轨迹的终止依据。算法3展示了缓存中的终止流程。

Algorithm 3 Trajectory Termination

算法 3: 轨迹终止

函数 轨迹终止(T, Qcov)
输入: T: 缓存中的轨迹列表
Qcov: 终止轨迹的估计不确定性阈值
对于 T 中的每条轨迹 traj 执行
estCertaintyX ← traj.getCovariance_P(O)
estCertaintyY ← traj.getCovariance_P(1)
discard ← false
如果 estCertaintyX > Qconv 则
discard ← true 结束条件
如果 estCertaintyY > Qconu 则
discard ← true
结束条件
如果 discard 为真 则
从 T 中移除 traj
结束条件
结束循环
结束函数

3 Results and Discussion

3 结果与讨论

The framework is evaluated using two benchmark datasets for autonomous cars: KITTI [24] and Waymo Open Dataset [25] (WOD). The KITTI dataset consists of 50 sequences, split into 21 training sequences and 29 testing sequences recorded around Karlsruhe, Germany, that involve a variety of challenging conditions. Meanwhile, WOD contains about 1150 segments recorded in various locations across the United States. The experiments are conducted on a machine with a processor AMD Ryzen 9; no GPU is involved since the framework only utilizes the CPU. The evaluation of the proposed approach consists of an extensive quantitative and qualitative evaluation with recent benchmarks in this section and a sensitive analysis of each proposed component to evaluate its contribution to the tracking performance, which will be covered in the ablation study, Section 3.2.

该框架使用两个自动驾驶基准数据集进行评估：KITTI [24] 和 Waymo开放数据集 [25] (WOD)。KITTI数据集包含50个序列，分为21个训练序列和29个测试序列，这些数据记录于德国卡尔斯鲁厄周边，涵盖多种具有挑战性的场景。而WOD则包含约1150个片段，采集自美国各地。实验在一台配备AMD Ryzen 9处理器的机器上进行，由于框架仅使用CPU，因此未涉及GPU。对所提方法的评估包括：本节中与最新基准进行的全面定量和定性评估，以及针对每个提出组件的敏感性分析（用于评估其对跟踪性能的贡献），消融研究部分（第3.2节）将对此进行详细讨论。

3.1 Evaluation with Benchmarks

3.1 基于基准测试的评估

This section consists of quantitative tracking performance evaluation with the latest state-of-the-art MOT methods on KITTI and WOD datasets and qualitative evaluation focusing on challenging occlusion conditions with the topperforming benchmark selected from the quantitative evaluation.

本节包括在KITTI和WOD数据集上与最新最先进的多目标跟踪(MOT)方法进行的定量跟踪性能评估，以及从定量评估中选出的表现最佳基准，针对具有挑战性的遮挡条件进行的定性评估。

3.1.1 Quantitative Evaluation

3.1.1 定量评估

Table 1: The table compares the latest benchmarks listed in the KITTI leader board on the testing split. The highest performance at each metric is highlighted in red, the second highest in blue, and the third highest in green. Methods that use the CasA [20] detector are marked by $(*)$ , while $({\dot{+}})$ is used for methods that use the VirConv [19] detector.

表 1: 该表格比较了KITTI排行榜测试集上列出的最新基准。每个指标的最高性能以红色标出，次高为蓝色，第三高为绿色。使用CasA [20]检测器的方法标记为$(*)$，而使用VirConv [19]检测器的方法标记为$({\dot{+}})$。

方法	HOTA	MOTA	AssA	AssRe	IDSW
TripletTrack [26]	73.58%	84.32%	74.66%	77.3%	322
PolarMOT [27]	75.2%	85.1%	76.95%	80.0%	462
DeepFusion-MOT [