Locally Masked Convolution for Auto regressive Models
自回归模型的局部掩码卷积
Abstract
摘要
High-dimensional generative models have many applications including image compression, multimedia generation, anomaly detection and data completion. State-of-the-art estimators for natural images are auto regressive, decom posing the joint distribution over pixels into a product of conditionals parameterized by a deep neural network, e.g. a convolutional neural network such as the PixelCNN. However, PixelCNNs only model a single decomposition of the joint, and only a single generation order is efficient. For tasks such as image completion, these models are unable to use much of the observed context. To generate data in arbitrary orders, we introduce LMCONV: a simple modificationto the standard 2D convolution that allows arbitrary masks to be applied to the weights at each location in the image. Using LMCONV, we learn an ensemble of distribution estimators that share parameters but differ in generation order, achieving improved performance on whole-image density estimation (2.89 bpd on unconditional CIFAR10), as well as globally coherent image completions. Our code is available at https://ajayjain.github.io/lmconv.
高维生成模型在图像压缩、多媒体生成、异常检测和数据补全等领域具有广泛应用。当前最先进的自然图像估计器采用自回归方法,通过深度神经网络(例如卷积神经网络如PixelCNN)将像素的联合分布分解为条件概率的乘积。然而,PixelCNN仅建模了联合分布的单一分解方式,且仅支持单一高效生成顺序。对于图像补全等任务,这些模型无法充分利用已观测的上下文信息。
为了支持任意顺序的数据生成,我们提出了LMCONV:一种对标准2D卷积的简单修改,允许在图像的每个位置对权重应用任意掩码。通过LMCONV,我们学习了一组共享参数但生成顺序不同的分布估计器,在全图像密度估计(无条件CIFAR10上达到2.89 bpd)和全局连贯的图像补全任务中实现了性能提升。代码已开源:https://ajayjain.github.io/lmconv。
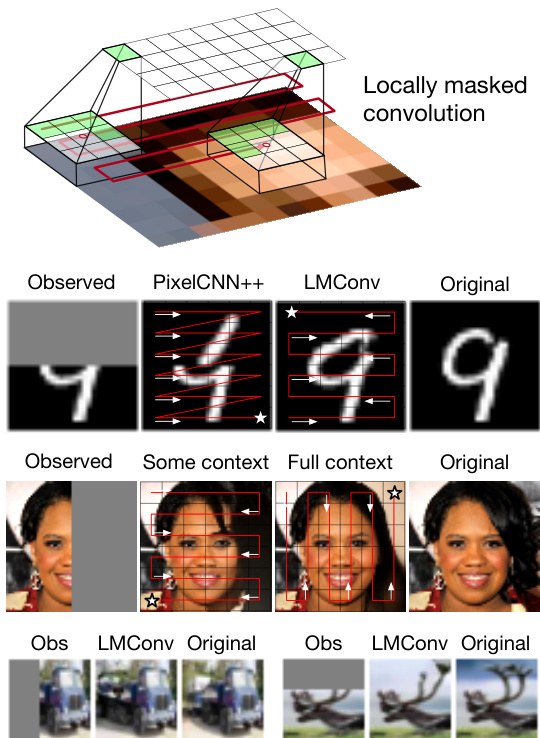
Figure 1: The ideal auto regressive joint distribution decomposition and sampling order are task-dependent. We learn to generate images under multiple orderings with the same parameters via locally masked convolutions (top), enabling global coherence for image completion (bottom).
图 1: 理想的自回归联合分布分解与采样顺序取决于具体任务。我们通过局部掩码卷积 (top) 学习用相同参数生成多种顺序的图像,实现图像补全的全局一致性 (bottom)。
1 INTRODUCTION
1 引言
Learning generative models of high-dimensional data such as images is a holy grail of machine learning with pervasive applications. Significant progress on this problem would naturally lead to a wide range of applications, including multimedia generation, compression, probabilistic time series forecasting, representation learning, and missing data completion. Many generative modeling frameworks have been proposed. Current state-of-the
学习生成高维数据(如图像)的模型是机器学习领域的圣杯,具有广泛的应用前景。该问题的重大突破自然将带来多媒体生成、压缩、概率时间序列预测、表征学习以及缺失数据补全等众多应用。目前已提出多种生成建模框架。当前最先进的...
Proceedings of the $36^{t h}$ Conference on Uncertainty in Artificial Intelligence (UAI), PMLR volume 124, 2020.
第36届人工智能不确定性会议论文集(UAI),PMLR第124卷,2020年。
art models for high-dimensional image data include (a) auto regressive models (Bengio and Bengio, 2000; Efros and Leung, 1999), (b) normalizing flow density estimators (Rezende and Mohamed, 2015), (c) generative adversarial networks (GANs) (Goodfellow et al., 2014), (d) latent variable models such as the VAE (Kingma and Welling, 2014; Rezende et al., 2014) and (e) energybased models e.g. Hinton (2002); LeCun et al. (2006); Du and Mordatch (2019); Song and Ermon (2019). While GANs, VAEs and EBMs have had great success in highdimensional image generation, exact likelihoods are generally intractable. Likelihood estimation is key for many practical applications from uncertainty estimation, robustness, reliability and safety perspectives. In contrast, auto regressive and flow models estimate exact likelihoods and can be used for uncertainty estimation, though still have room for improved generation quality. In this work, our focus is on auto regressive models.
高维图像数据的生成模型包括:(a) 自回归模型 (Bengio and Bengio, 2000; Efros and Leung, 1999)、(b) 归一化流密度估计器 (Rezende and Mohamed, 2015)、(c) 生成对抗网络 (GAN) (Goodfellow et al., 2014)、(d) 变分自编码器 (VAE) 等潜变量模型 (Kingma and Welling, 2014; Rezende et al., 2014) 以及 (e) 基于能量的模型 (Hinton, 2002; LeCun et al., 2006; Du and Mordatch, 2019; Song and Ermon, 2019)。虽然 GAN、VAE 和基于能量的模型在高维图像生成方面取得了巨大成功,但精确似然通常难以计算。从不确定性估计、鲁棒性、可靠性和安全性的角度来看,似然估计是许多实际应用的关键。相比之下,自回归模型和流模型可以估计精确似然并用于不确定性估计,尽管生成质量仍有提升空间。本工作的重点是自回归模型。
Given $n$ variables, one can generate $n!$ auto regressive decompositions of the joint likelihood, each corresponding to a forward sampling order, and more if we assume conditional independence. Early auto regressive texture synthesis (Popat and Picard, 1993; Efros and Leung, 1999) work could support multiple orders. However, recent CNN-based auto regressive models for images (van den Oord et al., 2016b,a; Salimans et al., 2017) capture only one of these orders (typically left-to-right raster scan, Fig. 2) for practical computational efficiency. Training and testing with a single order will not support all scenarios. Consider the image completion task in first row of Figure 1. If the top half of the image is missing, a raster scan generation order from left-to-right and top-to-bottom does not allow the model to condition on the context given in the observed bottom half of the image as the required conditionals are not estimated by the model.
给定 $n$ 个变量,可以生成 $n!$ 种联合似然的自回归分解,每种对应一种前向采样顺序,如果假设条件独立,则会有更多分解。早期的自回归纹理合成 (Popat and Picard, 1993; Efros and Leung, 1999) 工作支持多种顺序。然而,近期基于 CNN 的图像自回归模型 (van den Oord et al., 2016b,a; Salimans et al., 2017) 出于实际计算效率考虑,仅捕获其中一种顺序(通常是左至右的光栅扫描,图 2)。使用单一顺序进行训练和测试无法支持所有场景。以图 1 第一行的图像补全任务为例:若图像上半部分缺失,从左至右、从上至下的光栅扫描生成顺序无法让模型基于图像下半部观察到的上下文进行条件生成,因为模型并未估计所需的条件概率。
In this work, we propose a scalable, yet simple modification to convolutional auto regressive models to estimate more accurate likelihoods with a minor change in computation during training. Our goal is to support arbitrary orders in a scalable manner, allowing more precise likelihoods by averaging over several graphical models corresponding to orders (a form of Bayesian model averaging). Some past works have supported arbitrary orders in auto regressive models by learning separate parameters for each model (Frey, 1998), or by masking the input image to hide successor variables (Larochelle and Murray, 2011). A more efficient approach is to estimate densities in parallel across dimensions by masking network weights (Germain et al., 2015) differently for each order. However, all these methods are still computationally inefficient and difficult to scale beyond fully-connected networks to convolutional architectures.
在本工作中,我们提出了一种可扩展且简单的卷积自回归模型改进方法,通过微调训练计算过程来获得更精确的似然估计。我们的目标是以可扩展方式支持任意顺序,通过平均对应不同顺序的多个图模型(一种贝叶斯模型平均形式)来提升似然估计精度。先前研究曾通过为每个模型学习独立参数 (Frey, 1998) 或通过掩码输入图像隐藏后续变量 (Larochelle and Murray, 2011) 来实现自回归模型的任意顺序支持。更高效的方法是针对不同顺序差异化地掩码网络权重 (Germain et al., 2015),实现跨维度的并行密度估计。然而,这些方法仍存在计算效率低下的问题,且难以从全连接网络扩展到卷积架构。
In this work, we perform order-agnostic distribution estimation for natural images with state-of-the-art convolutional architectures. We propose to support arbitrary orderings by introducing masking at the level of features, rather than on inputs or weights. We show how an autoregressive CNN can support and learn multiple orders, with a single set of weights, via locally masked convolutions that efficiently apply location-specific masks to patches of each feature map. These local convolutions can be efficiently implemented purely via matrix multiplication by incorporating masking at the level of the im2col and col2im separation of convolution (Jia et al., 2014).
在本工作中,我们采用最先进的卷积架构对自然图像进行顺序无关的分布估计。我们提出通过在特征层面(而非输入或权重)引入掩码机制来支持任意排序方式。研究表明,自回归CNN可通过局部掩码卷积(使用单一权重集)支持并学习多种顺序模式,该技术能高效地对每个特征图区块施加位置特异性掩码。这些局部卷积可通过在im2col和col2im卷积分离阶段(Jia et al., 2014)整合掩码操作,完全基于矩阵乘法实现高效运算。
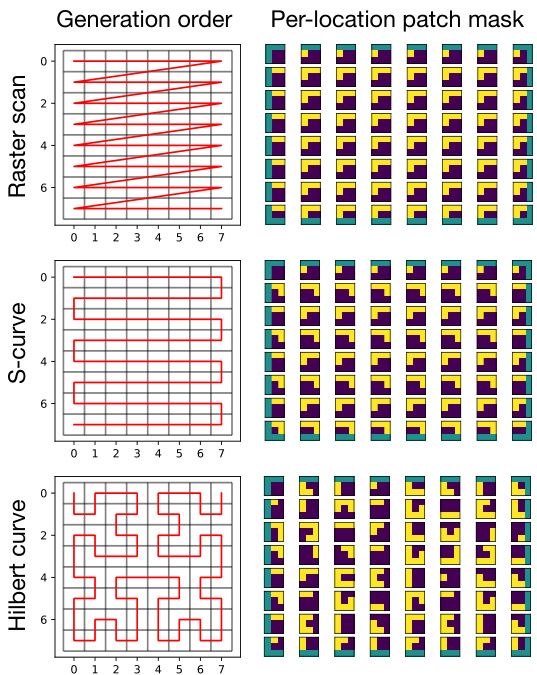
Figure 2: The three pixel generation orders and corresponding local masks that we consider in this work.
图 2: 本研究中考虑的三种像素生成顺序及对应局部掩码。
Arbitrary orders allow us to customize the traversal based on the needs of the task, which we evaluate in experiments. For instance, consider the examples shown in Fig. 1. The flexibility allows us to select the sampling order that exposes the maximum possible context for image completion, choose orderings that eliminate blind-spots (unobservable pixels) in image generation, and ensemble across multiple orderings using the same network weights. Note that such a model is able to support these image completions without training on any inpainting masks.
任意顺序允许我们根据任务需求自定义遍历方式,我们将在实验中对此进行评估。例如,考虑图 1 所示的示例。这种灵活性使我们能够选择在图像补全中暴露最大可能上下文的采样顺序,消除图像生成中盲点(不可观察像素)的排序方式,并使用相同的网络权重在多种排序中进行集成。值得注意的是,这样的模型无需在任何修复掩码上进行训练即可支持这些图像补全任务。
In experiments, we show that our approach can be efficiently implemented and is flexible without sacrificing the overall distribution estimation performance. By introducing order-agnostic training via LMCONV, we significantly outperform $\mathrm{PixelCNN{++}}$ on the unconditional CIFAR10 dataset, achieving code lengths of 2.89 bits per dimension. We show that the model can generalize to some novel orders. Finally, we significantly outperform raster-scan baselines on conditional likelihoods relevant to image completion by customizing the generation order.
实验中,我们证明该方法能高效实现且保持灵活性,同时不牺牲整体分布估计性能。通过LMCONV引入顺序无关训练,我们在无条件CIFAR10数据集上以2.89比特/维度的编码长度显著超越$\mathrm{PixelCNN{++}}$。结果表明模型可泛化至某些新顺序。最后,通过定制生成顺序,我们在图像补全相关条件似然任务上显著优于光栅扫描基线。
2 BACKGROUND
2 背景
Deep auto regressive models estimate high-dimensional data distributions using samples from the joint distribution over D-dimensions $p_{\mathtt{d a t a}}(\mathbf{x}{1},\dots,\mathbf{x}{D})$ . In this set- ting, we wish to approximate the joint with a parametric model $p_{\theta}(\mathbf{x}{1},\ldots,\mathbf{x}{D})$ by minimizing KL-divergence $D_{K L}(p_{\mathrm{data}}||p_{\theta})$ , or equivalently by maximizing the loglikelihood of the samples. As a general modeling principle, we can divide high-dimensional variables into many low-dimensional parts such as single dimensions, and capture dependencies between dimensions with a directed graphical model. Following the notation of (Kingma et al., 2019), these auto regressive (AR) models represent the joint distribution as a product of conditionals,
深度自回归模型利用来自D维联合分布$p_{\mathtt{data}}(\mathbf{x}{1},\dots,\mathbf{x}{D})$的样本来估计高维数据分布。在此设定下,我们希望通过最小化KL散度$D_{KL}(p_{\mathrm{data}}||p_{\theta})$(或等价地最大化样本对数似然)来用参数化模型$p_{\theta}(\mathbf{x}{1},\ldots,\mathbf{x}_{D})$近似联合分布。根据通用建模原则,可将高维变量分解为多个低维部分(如单维度),并通过有向图模型捕捉维度间依赖关系。沿用(Kingma等人, 2019)的符号表示,这类自回归(AR)模型将联合分布表示为条件概率的乘积:

Figure 3: (a) A graphical model where the final, unobserved variables $x_{3},x_{4}$ can be efficiently completed via forward sampling conditioned on the observed variables $x_{1},x_{2}$ . (b) When $x_{4}$ is observed, we sample $x_{1},x_{2}$ , and $x_{3}$ in the second graphical model using the same parameters. (c) LMCONV defines the model with masks at each filter location.
图 3: (a) 一个概率图模型,其中最终未观测变量 $x_{3},x_{4}$ 可通过基于观测变量 $x_{1},x_{2}$ 的前向采样高效补全。(b) 当 $x_{4}$ 被观测时,我们在第二个概率图模型中使用相同参数对 $x_{1},x_{2}$ 和 $x_{3}$ 进行采样。(c) LMCONV 通过在每个滤波器位置定义掩码来构建模型。
$$
\begin{array}{l}{{\displaystyle p_{\theta}({\bf x})=p_{\theta}(x_{1},\ldots,x_{D})}}\ {{\displaystyle\quad=p_{\theta}(x_{\pi(1)})\prod_{i=2}^{D}p_{\theta}\left(x_{\pi(i)}\mid{\cal P}a({\bf x}_{\pi(i)})\right)}}\end{array}
$$
$$
\begin{array}{l}{{\displaystyle p_{\theta}({\bf x})=p_{\theta}(x_{1},\ldots,x_{D})}}\ {{\displaystyle\quad=p_{\theta}(x_{\pi(1)})\prod_{i=2}^{D}p_{\theta}\left(x_{\pi(i)}\mid{\cal P}a({\bf x}_{\pi(i)})\right)}}\end{array}
$$
where $\pi:[D]\to[D]$ is a permutation defining an order over the dimensions, $P a(\mathbf{x}{\pi(i)})=\mathbf{x}{\pi(1)},\ldots,\mathbf{x}{\pi(i-1)}$ defines the parents of $x_{\pi(i)}$ in the graphical model, and $\theta$ is a parameter vector. As any joint can be decomposed in this manner according to the product rule, this factorization provides the foundation for many models including ours. The primary challenge in auto regressive models is defining a sufficiently expressive family for the conditionals where parameter estimation is efficient. Deep autoregressive models parameter ize the conditionals with a neural network that is provided the context $P a(\mathbf{x}_{\pi(i)})$ .
其中 $\pi:[D]\to[D]$ 是一个定义维度顺序的排列,$P a(\mathbf{x}{\pi(i)})=\mathbf{x}{\pi(1)},\ldots,\mathbf{x}{\pi(i-1)}$ 定义了图模型中 $x_{\pi(i)}$ 的父节点,$\theta$ 是参数向量。由于任何联合分布都可以根据乘积规则以这种方式分解,这种分解为包括我们模型在内的许多模型奠定了基础。自回归模型的主要挑战是为条件分布定义一个表达能力足够强且参数估计高效的族。深度自回归模型通过神经网络对条件分布进行参数化,该网络接收上下文 $P a(\mathbf{x}_{\pi(i)})$。
Decomposition (1) converts the joint modeling problem into a sequence modeling problem. Forward (ancestral) sampling draws root variable $x_{\pi(1)}$ first, then samples the remaining dimensions in order $x_{\pi(2)},\ldots,x_{\pi(D)}$ from their respective conditionals. Given a particular autoregressive decomposition of the joint, forward sampling supports a single data generation order. The joint model density for an observed variable can be computed exactly by evaluating each conditional, allowing density estimation and maximum likelihood parameter estimation,
分解 (1) 将联合建模问题转化为序列建模问题。前向 (祖先) 采样首先抽取根变量 $x_{\pi(1)}$ ,然后按顺序 $x_{\pi(2)},\ldots,x_{\pi(D)}$ 从各自的条件分布中采样剩余维度。给定联合分布的特定自回归分解形式时,前向采样仅支持单一数据生成顺序。通过评估每个条件分布,可精确计算观测变量的联合模型密度,从而实现密度估计和最大似然参数估计。

With some choices of network architecture, the conditionals can be computed in parallel by masking weights (Germain et al., 2015; van den Oord et al., 2016b). In the PixelCNN model family, masked convolutions are causal: the features output by a masked convolution can only depend on features earlier in the order.
在某些网络架构的选择下,可以通过掩码权重并行计算条件概率 (Germain et al., 2015; van den Oord et al., 2016b)。在PixelCNN模型系列中,掩码卷积具有因果性:掩码卷积输出的特征只能依赖于顺序中较早的特征。
While the choice of order is arbitrary, temporal and sequential data modalities have a natural ordering from the first dimension in the sequence to the last. For spatial data such as images, a natural ordering is not clear. For computational reasons, a raster scan order is generally used where the top left pixel is modeled unconditionally and generation proceeds in row-major fashion across each row from left to right, depicted in Figure 1, second column.
虽然顺序的选择是任意的,但时间和序列数据模态具有从序列的第一个维度到最后一个维度的自然排序。对于图像等空间数据,自然排序并不明确。出于计算原因,通常采用光栅扫描顺序,即左上角像素无条件建模,生成过程按行主序从左到右逐行进行,如图1第二列所示。
3 IMAGE COMPLETION WITH MAXIMUM RECEPTIVE FIELD
3 最大感受野的图像补全
For estimating the distribution of 2D images, a raster scan ordering is perhaps as good of an order as any other choice. That said, the raster scan order has necessitated architectural innovations to allow the neural network to access information far back in the sequence such as twodimensional PixelRNNs (van den Oord et al., 2016b), two- stream shift-based convolutional architectures (van den Oord et al., 2016a), and self-attention combined with convolution (Chen et al., 2018). These structures significantly improve test-set likelihoods and sample quality, but marry network architectures to the raster scan order.
在估计二维图像的分布时,栅格扫描顺序可能与其他选择一样合适。然而,栅格扫描顺序需要架构创新,以使神经网络能够访问序列中较远的信息,例如二维PixelRNN (van den Oord et al., 2016b)、基于双流位移的卷积架构 (van den Oord et al., 2016a),以及卷积与自注意力结合的方法 (Chen et al., 2018)。这些结构显著提高了测试集似然和样本质量,但也将网络架构与栅格扫描顺序紧密绑定。
Fixing a particular order is limiting for missing data completion tasks. Letting $\pi(i)=i$ denote the raster scan order, PixelRNN and PixelCNN architectures can complete only the bottom part of the image via forward sampling: given observations $x_{1},\ldots,x_{d}$ , raster scan auto regressive models sequentially sample,
固定特定顺序对缺失数据补全任务具有限制性。令 $\pi(i)=i$ 表示光栅扫描顺序时,PixelRNN和PixelCNN架构仅能通过前向采样完成图像底部区域:给定观测值 $x_{1},\ldots,x_{d}$ 后,光栅扫描自回归模型会依次采样

If all dimensions other than $x_{i}$ are observed, ideally we would sample $\hat{x}_{i}$ using maximum conditioning context,
如果除 $x_{i}$ 外的所有维度都被观测到,理想情况下我们会使用最大条件上下文对 $\hat{x}_{i}$ 进行采样。
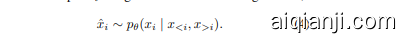
Unfortunately, the raster scan model only predicts distributions of the form $p_{\theta}(x_{i}\mid x_{<i})$ , and ignores observations $x_{>i}$ during completion. In the worst case, a model with a raster scan generation order cannot observe any of the context for an inpainting task where the top half of the image is unknown (Figure 1, $\mathrm{PixelCNN{++}}$ ). This leads to image completions that do not respect global structure. Small numbers of dimensions could be sampled by computing the posterior, e.g. for $i=1$ ,
遗憾的是,光栅扫描模型仅能预测形式为 $p_{\theta}(x_{i}\mid x_{<i})$ 的分布,且在补全过程中会忽略观测值 $x_{>i}$。最坏情况下,对于图像上半部分未知的修复任务(图1:$\mathrm{PixelCNN{++}}$),采用光栅扫描生成顺序的模型将无法观察到任何上下文信息。这会导致图像补全结果与全局结构不符。虽然可以通过计算后验分布来采样少量维度(例如 $i=1$ 时),

but this is expensive as each summand requires neural network evaluation, and becomes intractable when several dimensions are unknown. Instead of approximating the posterior, we estimate parameters $\theta$ that achieve high likelihood with multiple auto regressive decomposition s,
但这种方法成本高昂,因为每个求和项都需要进行神经网络评估,且在多个维度未知时会变得难以处理。我们不再近似后验分布,而是通过多重自回归分解来估计能实现高似然度的参数$\theta$。

with $p_{\pi}$ denoting a uniform distribution over several orderings. The joint distribution under $\pi$ factorizes according to (1). The resulting conditionals are all parameterized by the same neural network. By choosing order prior $p_{\pi}$ that supports a $\pi$ such that $\pi(D)=i$ , we can use the network with such an ordering to query (4) directly.
其中 $p_{\pi}$ 表示对几种排序的均匀分布。$\pi$ 下的联合分布根据 (1) 式进行分解。最终的条件分布均由同一个神经网络参数化。通过选择支持 $\pi(D)=i$ 的排序先验 $p_{\pi}$,我们可以直接使用具有此类排序的网络来查询 (4)。
During optimization with stochastic gradient descent, we make single-sample estimates of the inner expectation in (6) according to order-agnostic training (Uria et al., 2014; Germain et al., 2015), using a single order per batch.
在使用随机梯度下降进行优化时,我们根据与顺序无关的训练方法 (Uria et al., 2014; Germain et al., 2015),对(6)式中的内部期望进行单样本估计,每个批次仅使用单一顺序。
For a test-time task where ${x_{i}:i\in T_{\mathrm{obs}}}$ are observed, we select a $\pi$ that the model was trained with such that
对于一个测试时任务,其中观测到 ${x_{i}:i\in T_{\mathrm{obs}}}$,我们选择模型训练时使用的 $\pi$ 使得
$$
{\pi(1),\ldots,\pi(|T_{\mathrm{obs}}|)}=T_{\mathrm{obs}},
$$
$$
{\pi(1),\ldots,\pi(|T_{\mathrm{obs}}|)}=T_{\mathrm{obs}},
$$
i.e. the first $|T_{\mathrm{obs}}|$ dimensions in the generation order are the observed dimensions, then sample according to the rest of the order so that the model posterior over each unknown dimension is conditioned either on observed or previously sampled dimensions.
即在生成顺序中前 $|T_{\mathrm{obs}}|$ 个维度为观测维度,随后按照剩余顺序进行采样,使得模型对每个未知维度的后验分布均以已观测或先前采样的维度为条件。
4 LOCAL MASKING
4 局部掩码
In this section, we develop locally masked convolutions (LMCONV): a modification to the standard convolution operator that allows control over generation order and parallel computation of conditionals for evaluating likelihood. In the first convolutional layer of a neural network, $C_{\mathrm{out}}$ filters of size $k\times k$ are applied to the input image with spatial invariance: the same parameters are used at all locations in a sliding window. Each filter has $k^{2}*C_{\mathrm{in}}$ parameters. For images with disc ret i zed intensities, convolutional auto regressive networks transform a spatial $H\times W$ , multi-channel image into a tensor of log-probabilities that define the conditional distributions of (1). These log-probabilities take the form of an $H\times W$ image, with channel count equal to the number of color channels times the number of bins per color channel. The output log-probabilities at coordinate $i,j$ in the output define the distribution $p_{\theta}(x_{i,j}\mid P a(p(x_{i,j}))$ . Critically, this distribution must not depend on observations of successors in the Bayesian network, or the product of conditionals will not define a valid distribution due to cyclicity.
在本节中,我们提出了局部掩码卷积 (LMCONV):一种对标准卷积算子的改进,能够控制生成顺序并并行计算条件概率以评估似然。在神经网络的第一个卷积层中,会将 $C_{\mathrm{out}}$ 个尺寸为 $k\times k$ 的滤波器以空间不变性的方式应用于输入图像:在滑动窗口的所有位置使用相同的参数。每个滤波器具有 $k^{2}*C_{\mathrm{in}}$ 个参数。对于具有离散化强度的图像,卷积自回归网络将空间尺寸为 $H\times W$ 的多通道图像转换为对数概率张量,这些对数概率定义了(1)式的条件分布。这些对数概率的形式为 $H\times W$ 的图像,其通道数等于颜色通道数乘以每个颜色通道的分箱数。输出中坐标 $i,j$ 处的输出对数概率定义了分布 $p_{\theta}(x_{i,j}\mid P a(p(x_{i,j}))$ 。关键的是,该分布不能依赖于贝叶斯网络中后继节点的观测值,否则由于循环性,条件概率的乘积将无法定义有效分布。
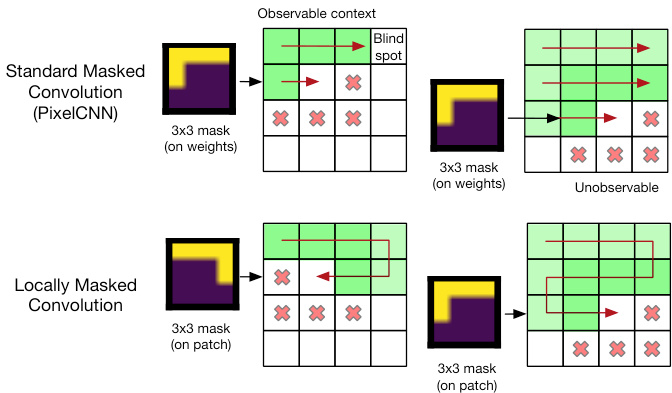
Figure 4: A comparison of standard weight masked convolutions and the proposed locally masked convolution.
图 4: 标准权重掩码卷积与提出的局部掩码卷积对比。
NADE (Larochelle and Murray, 2011) circumvents the problem by masking the input image, though requires independent forward passes to compute each factor of the auto regressive decomposition (1). Instead, the PixelCNN model family controls information flow through the network by setting certain weights of the convolution filters to zero, similar to how MADE (Germain et al., 2015) masks the weight matrices in fully-connected layers. We depict masked convolutions for the first convolutional layer in Figure 4. As a single mask is applied to the $C_{\mathrm{in}}\times k\times k$ parameter tensor defining each convolutional filter, the same masking pattern is applied at all locations in the image. Sharing the masking pattern constrains the possible orders, and leads to blind spots which the output distribution is unable to observe.
NADE (Larochelle and Murray, 2011) 通过掩码输入图像规避了该问题,但需要独立前向传递来计算自回归分解 (1) 的每个因子。相比之下,PixelCNN 模型家族通过将卷积滤波器的特定权重设为零来控制信息流,类似于 MADE (Germain et al., 2015) 在全连接层中掩码权重矩阵的方式。我们在图 4 中展示了第一卷积层的掩码卷积操作。由于每个卷积滤波器的 $C_{\mathrm{in}}\times k\times k$ 参数张量采用单一掩码模式,该掩码模式会作用于图像所有位置。共享掩码模式会限制可能的顺序关系,并导致输出分布无法观测到的盲区。
In practice, convolutions are implemented through general matrix multiplication (GEMM) due to widely available, heavily optimized and parallel i zed implementations of the operation on GPU and CPU. To use matrix multiplication, the input to a layer is rearranged in memory via the $\mathrm{im}2\mathrm{col}$ algorithm, which extracts $C_{\mathrm{in}}\times k\times k$ patches from the $C_{\mathrm{in}}\times H\times W$ input at each location that a convolutional filter will be applied. Assuming padding and a stride of 1 is used, the rearrangement yields matrix $X$ with $C_{\mathrm{in}}k^{2}$ rows and $HW$ columns. To perform convolution, the framework left-multiplies weight matrix $\mathcal{W}$ , storing $Y=\mathcal{W}X$ , adds a bias, and finally rearranges $Y$ into a spatial format via the col2im algorithm.
实践中,由于GPU和CPU上广泛提供且经过高度优化并行化的通用矩阵乘法(GEMM)实现,卷积运算通常通过GEMM来完成。为了使用矩阵乘法,层的输入会通过$\mathrm{im}2\mathrm{col}$算法在内存中重新排列,该算法从$C_{\mathrm{in}}\times H\times W$的输入中提取每个卷积滤波器将应用位置的$C_{\mathrm{in}}\times k\times k$补丁。假设使用填充且步长为1,重排后得到具有$C_{\mathrm{in}}k^{2}$行和$HW$列的矩阵$X$。执行卷积时,框架会左乘权重矩阵$\mathcal{W}$,存储$Y=\mathcal{W}X$,添加偏置,最后通过col2im算法将$Y$重新排列为空间格式。
We exploit this data rearrangement to arbitrarily mask the input to the convolutional filter at each location it is
我们利用这种数据重排方式,在卷积滤波器每个位置处对输入进行任意掩码处理
applied. The inputs to the convolution at each location, i.e. the input patches, form columns of $X$ . For a given generation order, we construct mask matrix $\mathcal{M}$ of the same dimensions as $X$ and set $X=\mathcal{M}\odot X$ prior to matrix multiplication. In particular, our locally masked convolution masks patches of the input to each layer, rather than masking weights and rather than masking the initial input to the network. LMCONV combines the flexibility of NADE and the parallel iz ability of MADE and PixelCNN. The LMCONV algorithm is summarized in Algorithm 1, and mask construction is detailed in Algorithm 2.
应用。在每个位置进行卷积的输入,即输入补丁,构成矩阵$X$的列。对于给定的生成顺序,我们构建与$X$维度相同的掩码矩阵$\mathcal{M}$,并在矩阵乘法前设置$X=\mathcal{M}\odot X$。具体而言,我们的局部掩码卷积是对每一层的输入补丁进行掩码,而不是对权重或网络的初始输入进行掩码。LMCONV结合了NADE的灵活性与MADE和PixelCNN的并行化能力。LMCONV算法总结在算法1中,掩码构造细节详见算法2。
We implement two versions of the layer with the PyTorch machine learning framework (Paszke et al., 2019). The first is an implementation that uses auto differentiation to compute gradients. As only the forward pass is defined by the user, the implementation is under 20 lines of Python.
我们基于PyTorch机器学习框架(Paszke等人,2019)实现了该层的两个版本。第一种是使用自动微分计算梯度的实现。由于用户仅需定义前向传播,该实现仅需不到20行Python语言代码。
However, reverse-mode auto differentiation incurs significant memory overheads during back propagation as the output of nearly every operation during the forward pass must be stored until gradient computation (Griewank and Walther, 2000; Jain et al., 2020). Data rearrangement with $\mathrm{im}2\mathrm{col}$ is memory intensive as features patches overlap and are duplicated. We implement a custom, memory efficient backward pass that only stores the input, the mask and the output of the layer during the forward pass and recomputes the $\mathrm{im}2\mathrm{col}$ operation during the backward pass. Re computing the im2col operation achieves $2.7\times$ memory savings at a $1.3\times$ slowdown.
然而,反向模式自动微分在反向传播过程中会产生显著的内存开销,因为前向传播阶段几乎所有操作的输出都必须存储到梯度计算时 (Griewank and Walther, 2000; Jain et al., 2020)。使用 $\mathrm{im}2\mathrm{col}$ 进行数据重排时,由于特征块重叠和重复,内存消耗巨大。我们实现了一种定制化的高效内存反向传播方案,在前向传播阶段仅存储该层的输入、掩码和输出,并在反向传播阶段重新计算 $\mathrm{im}2\mathrm{col}$ 操作。通过重新计算 im2col 操作,我们实现了 $2.7\times$ 的内存节省,代价是 $1.3\times$ 的速度下降。
Using locally masked convolutions, we can experiment with many different image generation orders. In this work, we consider three classes of orderings: raster scan, implemented in baseline PixelCNNs, an S-curve order that traverses rows in alternating directions, and a Hilbert space-filling curve order that generates nearby pixels in the image consecutively. Alternate orderings provide several benefits. Nearby pixels in an image are highly correlated. By generating these pixels close in a Hilbert curve order, we might expect information to propagate from the most important, nearby observations for each dimension and reduce the vanishing gradient problem.
通过使用局部掩码卷积,我们可以尝试多种不同的图像生成顺序。在本研究中,我们考虑了三种顺序类型:基线PixelCNN中实现的栅格扫描顺序、交替方向遍历行的S形曲线顺序,以及连续生成图像中相邻像素的希尔伯特空间填充曲线顺序。这些替代顺序具有多重优势:图像中的相邻像素具有高度相关性。通过采用希尔伯特曲线顺序近距离生成这些像素,我们可以期望信息从每个维度最重要、最邻近的观测点传播,从而缓解梯度消失问题。
If the image is considered a graph with nodes for each pixel and edges connecting adjacent pixels, a convolutional auto regressive model using an order defined by a Hamiltonian path over the image graph will also suffer no blind spot in a $D$ layer network. To see this, note that the features corresponding to dimension $x_{\pi(i)}$ in the Hamiltonian path order will always be able to observe the previous layer’s features corresponding to $x_{\pi(i-1)}$ . After at least $D$ layers of depth, the features for $x_{\pi(i)}$ will incorporate information from all $i-1$ previous dimensions. In practice, information propagates with fewer required layers in these architectures as multiple neighbors are observed in each layer. Finally, we select multiple orderings at inference and average the resulting joint distributions to compute better likelihood estimates.
如果将图像视为一个图,其中每个像素为节点,相邻像素间通过边连接,那么使用由图像图上的哈密尔顿路径定义的顺序的卷积自回归模型,在$D$层网络中也同样不会存在盲点。这是因为按照哈密尔顿路径顺序,维度$x_{\pi(i)}$对应的特征总能观察到上一层$x_{\pi(i-1)}$对应的特征。在至少$D$层深度后,$x_{\pi(i)}$的特征将整合来自前$i-1$个维度的所有信息。实际应用中,由于每层观察多个相邻节点,信息传播所需的层数更少。最后,在推理时我们选择多种顺序并对所得联合分布取平均,以计算更优的似然估计。
5 ARCHITECTURE
5 架构
We use a network architecture similar to $\mathrm{PixelCNN{++}}$ (Salimans et al., 2017), the best-in-class density estimator in the fully convolutional auto regressive PixelCNN model family. Convolution operations are masked according to Algorithm 1. While our locally masked convolutions can benefit from self-attention mechanisms used in later work, we choose a fully convolutional architecture for simplicity and to study the benefit of local masking in isolation of other architectural innovations. We make three modifications to the $\mathrm{PixelCNN{++}}$ architecture that simplify it and allow for arbitrary generation orders. Gated PixelCNN uses a two-stream architecture composed of two network stacks with $\textstyle\left\lfloor{\frac{k}{2}}\right\rfloor\times1$ and $\textstyle\left\lfloor{\frac{k}{2}}\right\rfloor\times k$ convolutions to enforce the raster scan order. In the horizontal stream, Gated PixelCNN applies non-square convolutions and feature map shifts or pads to extract information within the same row, to the left of the current dimension. In the vertical stream, Gated PixelCNN extracts information from above. Skip connections between streams allow information to propagate. $\mathrm{PixelCNN{++}}$ uses a similar architecture based on a U-Net (Ronne berger et al., 2015) with approximately 54M parameters. We replace the two streams with a simple, single stream with the same depth, using LMCONV to maintain the auto regressive property. Masks for these convolutions are computed and cached at the beginning of training. Due to the regularizing effect of order-agnostic training, we do not use dropout.
我们采用与$\mathrm{PixelCNN{++}}$ (Salimans等人,2017)相似的网络架构,这是全卷积自回归PixelCNN模型家族中最先进的密度估计器。卷积操作根据算法1进行掩码处理。虽然我们的局部掩码卷积可以从后续工作中使用的自注意力机制中受益,但为了简化研究并单独考察局部掩码的效益,我们选择了全卷积架构。我们对$\mathrm{PixelCNN{++}}$架构进行了三处修改以简化结构并支持任意生成顺序。
门控PixelCNN采用双流架构,由两个网络堆栈组成,分别使用$\textstyle\left\lfloor{\frac{k}{2}}\right\rfloor\times1$和$\textstyle\left\lfloor{\frac{k}{2}}\right\rfloor\times k$卷积来强制光栅扫描顺序。在水平流中,门控PixelCNN通过非方形卷积和特征图移位/填充来提取同一行当前维度左侧的信息;在垂直流中则提取上方信息。流间的跳跃连接允许信息传播。$\mathrm{PixelCNN{++}}$采用基于U-Net (Ronneberger等人,2015)的类似架构,包含约5400万参数。我们将其替换为相同深度的单流结构,使用LMCONV保持自回归特性。这些卷积的掩码在训练开始时计算并缓存。由于顺序无关训练的正则化效果,我们未使用dropout。
Table 1: Average negative log likelihood of binarized and grayscale MNIST digits under our model. Lower is better.
| BINARIZEDMNIST,28x28 | NLL (nats) |
| DARN (Intractable) (Gregor et al., 2014) NADE (Uria et al.,2014) EoNADE 2hl (128orders)(Uriaet al.,2014) EoNADE-5 2hl (128 orders) (Raiko et al.,2014) | 84.13 88.33 85.10 84.68 86.64 |
| Ours,S-curve(1 order) Ours,S-curve(8orders) GRAYSCALEMNIST,28x28 | 78.47 77.58 |
| Spatial PixelCNN (Akoury and Nguyen, 2017) PixelCNN++(1 stream) Ours,S-curve(1 order) Ours,S-curve (8orders) | NLL (bpd) 0.88 0.77 0.68 |
表 1: 二值化和灰度 MNIST 数字在我们模型下的平均负对数似然。数值越低越好。
| BINARIZEDMNIST,28x28 | NLL (nats) |
|---|---|
| DARN (Intractable) (Gregor et al., 2014) NADE (Uria et al.,2014) EoNADE 2hl (128orders)(Uriaet al.,2014) EoNADE-5 2hl (128 orders) (Raiko et al.,2014) | 84.13 88.33 85.10 84.68 86.64 |
| Ours,S-curve(1 order) Ours,S-curve(8orders) GRAYSCALEMNIST,28x28 | 78.47 77.58 |
| Spatial PixelCNN (Akoury and Nguyen, 2017) PixelCNN++(1 stream) Ours,S-curve(1 order) Ours,S-curve (8orders) | NLL (bpd) 0.88 0.77 0.68 |
Second, we use dilated convolutions (Yu and Koltun, 2015) at regular intervals in the model rather than downsampling the feature map. Down sampling precludes many orders, as the operation aggregates information from contiguous squares of pixels together without a mask. Dilated convolutions expand the receptive field without limiting the order, as local masks can be customized to hide or reveal specific features accessed by the filter.
其次,我们在模型中定期使用空洞卷积 (dilated convolutions) (Yu and Koltun, 2015) ,而不是对特征图进行下采样。下采样会排除许多阶数,因为该操作在没有掩码的情况下将相邻像素块的信息聚合在一起。空洞卷积在不限制阶数的情况下扩展了感受野,因为可以自定义局部掩码来隐藏或显示滤波器访问的特定特征。
Finally, we normalize the feature map across the channel dimension (Li et al., 2019). Normalization allows masks to have varying numbers of ones at each spatial location by rescaling features to the same scale.
最后,我们在通道维度上对特征图进行归一化处理 (Li et al., 2019)。归一化通过将特征重新缩放到相同尺度,使得每个空间位置上的掩码可以拥有不同数量的激活值。
As in $\mathrm{PixelCNN{++}}$ , our model represents each conditional with a mixture of 10 disc ret i zed logistic distributions that imposes a distribution over binned pixel intensities. For the binarized MNIST dataset (Salak hut dino v and Murray, 2008), we instead use a softmax over two logits. We train with 8 variants of an S-curve (zig-zag) order that traverses each row of the image in alternating directions so that consecutively generated pixels are adjacent, and so that locally masked CNNs with sufficient depth can achieve the maximum allowed receptive field.
与 $\mathrm{PixelCNN{++}}$ 类似,我们的模型用10个离散化逻辑分布的混合表示每个条件,对分箱像素强度施加分布。对于二值化MNIST数据集 (Salak hut dino v and Murray, 2008),我们改用两个logits的softmax。训练时采用8种S形(锯齿形)扫描顺序变体,通过交替方向遍历图像的每一行,使得连续生成的像素相邻,且具有足够深度的局部掩码CNN能达到最大允许感受野。
Table 2: Average negative log likelihood of CIFAR10 images under our model. Lower is better.
| CIFAR10,32x32 | NLL (bpd) |
| UniformDistribution | 8.00 |
| Multivariate Gaussian(vanden Oord et al.,2016b) | 4.70 |
| Attention-based Image Transformer (Parmar et al.,2018) | 2.90 |
| PixelSNAIL(Chen et al.,2018) | 2.85 |
| Sparse Transformer (Child et al.,2019) | 2.80 |
| Convolutional | |
| PixelCNN (1 stream)(van den Oord et al.,2016b) | 3.14 |
| Gated PixelCNN (2 stream)(van den Oord et al.,2016a) | 3.03 |
| PixelCNN++(1 stream) | |
| PixelCNN++(2 stream)(Salimans et al.,2017) | 2.99 |
| 2.92 | |
| Ours,S-curve(1 stream,1 order) Ours,S-curve(1 stream,8 orders) | 2.91 |
表 2: 我们的模型在CIFAR10图像上的平均负对数似然。数值越低越好。
| CIFAR10,32x32 | NLL (bpd) |
|---|---|
| UniformDistribution | 8.00 |
| Multivariate Gaussian (van den Oord et al., 2016b) | 4.70 |
| Attention-based Image Transformer (Parmar et al., 2018) | 2.90 |
| PixelSNAIL (Chen et al., 2018) | 2.85 |
| Sparse Transformer (Child et al., 2019) | 2.80 |
| Convolutional | |
| PixelCNN (1 stream) (van den Oord et al., 2016b) | 3.14 |
| Gated PixelCNN (2 stream) (van den Oord et al., 2016a) | 3.03 |
| PixelCNN++ (1 stream) | |
| PixelCNN++ (2 stream) (Salimans et al., 2017) | 2.99 |
| 2.92 | |
| Ours, S-curve (1 stream, 1 order) Ours, S-curve (1 stream, 8 orders) | 2.91 |
Across all quantitative experiments, we use a model with approximately 46M parameters, trained with the Adam optimizer with a learning rate of $210^{-4}$ decayed by a factor of $1-510^{-6}$ per iteration with clipped gradients. For CelebA-HQ qualitative results, we increase filter count and train a model with 184M parameters. More details are provided in the appendix.
在所有定量实验中,我们使用了一个约4600万参数的模型,采用Adam优化器进行训练,初始学习率为$210^{-4}$,每迭代一次衰减$1-510^{-6}$因子,并采用梯度裁剪。针对CelebA-HQ的定性结果,我们增加了滤波器数量并训练了一个1.84亿参数的模型。更多细节见附录。
6 EXPERIMENTS
6 实验
To evaluate the benefits of our approach, we study three scientific questions: (1) do locally masked auto regressive ensembles estimate more accurate likelihoods on image datasets than single-order models?, (2) can the model generalize to novel orders? and (3) how important is order selection for image completion?
为了评估我们方法的优势,我们研究了三个科学问题:(1) 局部掩码自回归集成模型在图像数据集上的似然估计是否比单序模型更准确?(2) 该模型能否泛化到新序列?(3) 序列选择对图像补全有多重要?
We estimate the distribution of three image datasets: $28\times28$ grayscale and binary (Salak hut dino v and Murray, 2008) MNIST digits, $32\times32$ 8-bit color CIFAR10 natural images, and high-resolution CelebA-HQ 5-bit color face photographs (Karras et al., 2018). Unlike classification, density estimation remains challenging on these datasets. We train the CelebA-HQ models at $256\times256$ resolution to compare with prior density estimation work, and at a bilinearly down sampled $64\times64$ resolution.
我们评估了三个图像数据集的分布情况:$28\times28$ 灰度与二值化(Salak hut dino v and Murray, 2008)的MNIST手写数字、$32\times32$ 8位色CIFAR10自然图像,以及高分辨率5位色CelebA-HQ人脸照片(Karras et al., 2018)。与分类任务不同,这些数据集的密度估计仍具挑战性。为与先前密度估计研究对比,我们在$256\times256$分辨率下训练CelebA-HQ模型,同时采用双线性降采样至$64\times64$分辨率进行训练。
Our locally masked model achieves better likelihoods than PixelCNN $++$ by using multiple generation orders. We then show that the model can generalize to generation orders that it has not been trained with. Finally, for image completion, we achieve the best results over strong baselines by using orders that expose all observed pixels.
我们采用多生成顺序的局部掩码模型在似然度上优于PixelCNN++。实验表明,该模型能泛化至未训练过的生成顺序。最终在图像补全任务中,通过采用完全暴露观测像素的生成顺序,我们在强基线模型上取得了最佳效果。
Table 3: Average conditional negative log likelihood for Top, Left and Bottom half image completion.
| BINARIZEDMNIST28x28(nats) | T | L | B |
| Ours (adversarialorder) | 41.76 | 39.83 | 43.35 |
| Ours(1max contextorder) | 34.99 | 32.47 | 36.57 |
| Ours (2max context orders) | 34.82 | 32.25 | 36.36 |
| CIFAR1032x32(bpd) | T | L | B |
| PixelCNN++,1stream | 3.07 | 3.10 | 3.05 |
| PixelCNN++,2stream | 2.97 | 2.98 | 2.93 |
| Ours(1 stream,adversarial order) | 2.93 | 2.98 | 3.05 |
| Ours (1 stream,1 max context order) | 2.77 | 2.83 | 2.89 |
| Ours (1 stream,2max context orders) | 2.76 | 2.82 | 2.88 |
表 3: 顶部、左侧和底部半图像补全的平均条件负对数似然
| BINARIZEDMNIST28x28(nats) | T | L | B |
|---|---|---|---|
| Ours (adversarialorder) | 41.76 | 39.83 | 43.35 |
| Ours(1max contextorder) | 34.99 | 32.47 | 36.57 |
| Ours (2max context orders) | 34.82 | 32.25 | 36.36 |
| CIFAR1032x32(bpd) | T | L | B |
| PixelCNN++,1stream | 3.07 | 3.10 | 3.05 |
| PixelCNN++,2stream | 2.97 | 2.98 | 2.93 |
| Ours(1 stream,adversarial order) | 2.93 | 2.98 | 3.05 |
| Ours (1 stream,1 max context order) | 2.77 | 2.83 | 2.89 |
| Ours (1 stream,2max context orders) | 2.76 | 2.82 | 2.88 |
6.1 WHOLE-IMAGE DENSITY ESTIMATION
6.1 全图像密度估计
Tractable generative models are generally evaluated via the average negative log likelihood (NLL) of test data. For interpret ability, many papers normalize base 2 NLL by the number of dimensions. By normalizing, we can measure bits per dimension (bpd), or a lower-bound for the expected number of bits needed per pixel to losslessly compress images using a Huffman code with $p(\mathbf{x})$ estimated by our model. Better estimates of the distribution should result in higher compression rates. Tables 1 and 2 show likelihoods for our model and prior models.
可处理的生成模型通常通过测试数据的平均负对数似然 (NLL) 进行评估。为了便于解释,许多论文会按维度数对以 2 为底的 NLL 进行归一化。通过归一化,我们可以测量每维度比特数 (bpd),或使用霍夫曼编码无损压缩图像时每个像素所需比特数的期望下界,其中 $p(\mathbf{x})$ 由我们的模型估计。更好的分布估计应能带来更高的压缩率。表 1 和表 2 展示了我们的模型与先前模型的似然值。
On binarized MNIST (Table 1), our locally masked PixelCNN achieves significantly higher likelihoods (lower NLL) than baselines, including neural auto regressive models NADE, EoNADE, and MADE that average across large numbers of orderings. This is due to architectural advantages of our CNN and increased model capacity. Our model also outperforms the standard PixelCNN, which suffers from a blind spot problem due to sharing the same mask at all locations. Likelihood is f
