SMPConv: Self-moving Point Representations for Continuous Convolution

SMPConv：连续卷积的自移动点表征

Abstract

摘要

Continuous convolution has recently gained prominence due to its ability to handle irregularly sampled data and model long-term dependency. Also, the promising experimental results of using large convolutional kernels have catalyzed the development of continuous convolution since they can construct large kernels very efficiently. Leveraging neural networks, more specifically multilayer perceptrons $(M L P s)$ , is by far the most prevalent approach to implementing continuous convolution. However, there are a few drawbacks, such as high computational costs, complex hyper parameter tuning, and limited descriptive power of filters. This paper suggests an alternative approach to building a continuous convolution without neural networks, resulting in more computationally efficient and improved performance. We present self-moving point representations where weight parameters freely move, and interpolation schemes are used to implement continuous functions. When applied to construct convolutional kernels, the experimental results have shown improved performance with drop-in replacement in the existing frameworks. Due to its lightweight structure, we are first to demonstrate the effectiveness of continuous convolution in a large-scale setting, e.g., ImageNet, presenting the improvements over the prior arts. Our code is available on https://github.com/sangnekim/SMPConv

连续卷积近来因其处理不规则采样数据和建模长期依赖的能力而备受关注。此外，大卷积核在实验中展现的优异表现进一步推动了连续卷积的发展，因为它们能高效构建大核结构。目前最主流的实现方式是利用神经网络（更具体而言是多层感知机 (MLPs)），但这种方法存在计算成本高、超参数调优复杂以及滤波器描述能力有限等缺陷。本文提出了一种无需神经网络的连续卷积构建方案，在提升计算效率的同时改进了性能。我们引入了自移动点表征技术，通过自由移动的权重参数和插值方案实现连续函数。当应用于构建卷积核时，实验表明该方案能在现有框架中即插即用地提升性能。得益于轻量化结构，我们首次在大规模场景（如ImageNet）中验证了连续卷积的有效性，其表现超越了现有技术。代码已开源：https://github.com/sangnekim/SMPConv

1. Introduction

1. 引言

There has been a recent surge of interest in representing the convolutional kernel as a function over a continuous input domain. It can easily handle irregularly sampled data both in time [1, 64] and space [67, 71], overcoming the drawbacks of the discrete convolution operating only on disc ret i zed sampled data with pre-defined resolutions and grids. With the progress in modeling and training continuous kernels, it has enjoyed great success in many practical scenarios, such as 3D point cloud classification and segmentation [40,45,57,63,70], image super resolution [62], object tracking [11], to name a few. Furthermore, the recent trends of using large convolutional kernels with strong empirical results urge us to develop a more efficient way to implement it [14,35], and the continuous convolution will be a promising candidate because of its capability to readily construct arbitrarily large receptive fields [48, 49].

近年来，将卷积核表示为连续输入域上的函数引起了广泛关注。这种方法能轻松处理时间和空间上的不规则采样数据 [1, 64][67, 71]，克服了离散卷积仅能在预定义分辨率和网格的离散采样数据上运算的缺陷。随着连续核建模与训练技术的进步，该方法已在诸多实际场景中取得显著成功，例如3D点云分类与分割 [40,45,57,63,70]、图像超分辨率 [62]、目标跟踪 [11] 等。此外，当前使用大卷积核并取得强劲实证效果的趋势 [14,35]，促使我们需要开发更高效的实现方式，而连续卷积因其能轻松构建任意大感受野的特性 [48, 49]，将成为极具潜力的候选方案。

One of the dominant approaches to modeling the continuous kernel is to use a particular type of neural network architecture, taking as inputs low-dimensional input coordinates and generating the kernel values [48, 49], known as neural fields [42, 53] or simply MLPs. Using neural fields to represent the kernels, we can query kernel values at arbitrary resolutions in parallel and construct the large kernels with a fixed parameter budget, as opposed to the conventional discrete convolutions requiring more parameters to enlarge receptive fields. Thanks to recent advances to overcome the spectral bias on training neural fields [53], they can also represent functions with high-frequency components, which enables learned kernels to capture fine details of input data.

对连续核进行建模的主要方法之一是采用一种特定类型的神经网络架构，它以低维输入坐标作为输入并生成核值 [48, 49]，这种方法被称为神经场 (neural fields) [42, 53] 或简称为 MLP。通过使用神经场来表示核，我们可以并行查询任意分辨率下的核值，并在固定参数预算下构建大核，这与传统离散卷积需要更多参数来扩大感受野形成对比。得益于近期克服神经场训练中频谱偏差的研究进展 [53]，它们还能表示具有高频分量的函数，这使得学习到的核能够捕捉输入数据的精细细节。

While promising in various tasks and applications, this approach has a few downsides. First, it incurs considerable computational burdens to already computation-heavy processes of training deep neural networks. Each training iteration involves multiple forward and backward passes of MLPs to generate kernels and update the parameters of MLPs. This additional complexity prevents it from being applied to large-scale problems, such as ImageNet-scale, since it needs deeper and wider MLP architectures to construct more complex kernels with more input and output channels. Although MLPs can generate larger sizes and numbers of kernels without adding more parameters, it has been known that the size of MLPs mainly determines the complexity of the functions they represent and, eventually, the performance of the CNNs.

尽管在各种任务和应用中前景广阔，但这种方法存在一些缺点。首先，它给本就计算密集的深度神经网络训练过程带来了相当大的计算负担。每次训练迭代都涉及多层感知机 (MLP) 的多次前向和反向传播以生成卷积核并更新 MLP 参数。这种额外的复杂性使其难以应用于大规模问题（例如 ImageNet 级别），因为需要更深更宽的 MLP 架构来构建具有更多输入输出通道的复杂卷积核。虽然 MLP 无需增加参数就能生成更大尺寸和数量的卷积核，但众所周知，MLP 的规模主要决定了其所表征函数的复杂度，并最终影响 CNN 的性能。

Furthermore, the kernels generated by an MLP depend heavily on the architectural priors. As a universal function approx im at or, a neural network with sufficient depth and width can express any continuous functions [26]. However, we have empirically observed strong evidence that the architecture of neural networks has played a significant role in many practical settings, suggesting that various architectural changes to the kernel-generating MLPs would significantly affect the performance of CNNs. Considering a large number of hyper parameters in training neural networks, adding more knobs to tune, e.g., activation functions, width, depth, and many architectural variations of MLPs., would not be a pragmatic solution for both machine learning researchers and practitioners.

此外，由多层感知机 (MLP) 生成的核函数高度依赖于架构先验。作为通用函数逼近器，具备足够深度和宽度的神经网络能够表达任意连续函数 [26]。然而，我们通过实证观察到大量证据表明，神经网络架构在许多实际场景中起着关键作用，这意味着对核生成 MLP 进行各种架构调整会显著影响 CNN 的性能。考虑到训练神经网络涉及大量超参数，若额外增加可调节选项（如激活函数、宽度、深度以及 MLP 的多种架构变体），对机器学习研究者和实践者而言都非务实之选。

In this paper, we aim to build continuous convolution kernels with negligible computational cost and minimal archit ect ural priors. We propose to use moving point representations and implement infinite resolution by interpolating nearby moving points at arbitrary query locations. The moving points are the actual kernel parameters, and we connect the neighboring points to build continuous kernels. Recent techniques in neural fields literature inspire it, where they used grid or irregularly distributed points to represent features or quantities in questions (density or colors) for novel view synthesis [6, 54, 69, 72, 75]. The suggested approach only introduces minor computational costs (interpolation costs) and does not consist of neural networks (only point representations and interpolation kernels). Moreover, the spectral bias presented in training MLPs [47] does not exist in the suggested representation. Each point representation covers the local area of the input domain and is updated independently of each other, contrasted with MLPs, where updating each parameter would affect the entire input domain. Therefore, highly different values of nearby points can easily express high-frequency components of the function.

本文旨在构建计算成本可忽略且架构先验极少的连续卷积核。我们提出采用移动点表示法，通过在任意查询位置对邻近移动点进行插值来实现无限分辨率。移动点即为实际核参数，通过连接相邻点构建连续核函数。该方法受神经场领域近期技术启发[6, 54, 69, 72, 75]，这些研究使用网格或不规则分布点来表示新视角合成中的特征或目标量（如密度或颜色）。所提方案仅引入微小计算成本（插值开销），且不包含神经网络（仅有点表示和插值核）。此外，多层感知器(MLP)训练中存在的频谱偏差[47]在该表示中并不存在。每个点表示覆盖输入域的局部区域，且更新过程相互独立——这与MLP形成鲜明对比，后者参数更新会影响整个输入域。因此，邻近点的高度差异化取值可轻松表达函数的高频分量。

The proposed method can also be more parameter efficient than the discrete convolution to construct the large kernels. Depending on the complexity of the kernels to be learned, a few numbers of points may be sufficient to cover a large receptive field (e.g., a unimodal function can be approximated by a single point). Many works have extensively exploited non-full ranks of the learned kernels to implement efficient convolutions or compress the models [35]. Our approach can likewise benefit from the pres- ence of learned kernels with low-frequency components.

所提方法在构建大卷积核时也能比离散卷积更节省参数量。根据待学习卷积核的复杂度，少量采样点可能就足以覆盖大感受野（例如，单峰函数可用单个点近似）。已有许多工作广泛利用学习卷积核的非满秩特性来实现高效卷积或模型压缩 [35]。我们的方法同样能受益于学习到的低频成分卷积核。

We conduct comprehensive experimental results to show the effectiveness of the proposed method. First, we demonstrate that moving point representations can approximate continuous functions very well in 1D and 2D function fitting experiments. Then, we test its ability to handle longterm dependencies on various sequential datasets. Finally, we also evaluate our model on 2D image data. Especially, we perform large-scale experiments on the ImageNet classification dataset (to our knowledge, it is the first attempt to use continuous convolution for such a large-scale problem). Our proposed method can be used as a drop-in replacement of convolution layers for all the above tasks without bells and whistles. The experimental results show that it consistently improves the performance of the prior arts.

我们通过全面的实验结果验证了所提方法的有效性。首先，在一维和二维函数拟合实验中证明移动点表示能很好地逼近连续函数。其次，在多个序列数据集上测试了其处理长期依赖关系的能力。最后，还在二维图像数据上评估了模型性能，特别是在ImageNet分类数据集上进行了大规模实验（据我们所知，这是首次将连续卷积应用于如此大规模的问题）。该方法无需任何修饰即可作为卷积层的即插即用替代方案，实验结果表明其性能始终优于现有技术。

2. Related works

2. 相关工作

Neural fields and continuous convolution. Neural fields have recently emerged as an alternative neural network representation [53]. It is a field parameterized by a neural network, such as simple MLP, taking as lowdimensional coordinates input and generating quantity in questions. It has shown great success in various visual computing domains, such as novel view synthesis [42], 3D shape representation [41, 44], and data compression [18], to name a few. Since it is a function over a continuous input domain, it can produce outputs at arbitrary resolutions. Recent studies have exploited its continuous nature to model continuous kernels for CNNs [48, 49, 63]. [63] used an MLP architecture to implement the continuous kernel to handle irregularly sampled data, such as 3D point clouds. While successful, the descriptive power of the learned kernel is limited due to its bias toward learning low-frequency components. With the recent advances in overcoming the spectral bias [53], [49] has explored various activation functions to improve the performance of CNNs. To further im- prove, [48] proposed to learn the receptive field sizes and showed impressive performance on multiple tasks.

神经场与连续卷积。神经场近年来作为一种替代性神经网络表征崭露头角 [53]。它是由神经网络（如简单MLP）参数化的场，接收低维坐标输入并生成目标量值。该技术在多个视觉计算领域展现出卓越成效，包括新视角合成 [42]、3D形状表征 [41,44] 以及数据压缩 [18] 等。由于其在连续输入域上定义，可生成任意分辨率的输出。最新研究利用其连续性特性为CNN建模连续卷积核 [48,49,63]。[63] 采用MLP架构实现连续核来处理不规则采样数据（如3D点云），但所学卷积核因偏向低频成分而导致表征能力受限。随着克服频谱偏差 [53] 的技术进步，[49] 探索了多种激活函数来提升CNN性能。[48] 进一步提出学习感受野大小的方法，在多项任务中展现出优异表现。

We also propose a method that can likewise be classified as a neural field. However, we implement a field without neural networks, using self-moving point representations and interpolation schemes. It significantly reduces the computational costs to compute the kernels during training compared to the conventional MLP-based methods. Furthermore, it removes the burden of numerous hyperparameter searches for a newly introduced neural network in the already complicated training procedure.

我们还提出了一种同样可归类为神经场 (neural field) 的方法。但不同于传统基于MLP的方法，我们采用自移动点表示和插值方案实现了无需神经网络的场表示。相比传统方法，该方法显著降低了训练期间计算核函数的计算成本，同时避免了在已复杂的训练流程中为新引入神经网络进行大量超参数搜索的负担。

Grid and point representations. Although MLP-based neural fields have succeeded in many tasks, they require substantial computational costs for training and inference, and the spectral bias presented in MLPs often degrades the performance. In order to reduce the computations and avoid the issues of using MLPs, classical grid-based representations have been adopted in the neural fields. Plenoxels [72] stores the coefficients of spherical harmonic in the 3D voxel structure and implements the infinite resolution via the inter pol ation methods, reducing the training time from days to minutes. Instant-NGP [43] further optimized the speed using a hash-based indexing algorithm. The combination of grid representations and MLPs has been extensively explored to find better solutions [6, 54].

网格与点表示法。尽管基于MLP的神经场已在众多任务中取得成功，但其训练和推理过程需要高昂的计算成本，且MLP固有的频谱偏差常导致性能下降。为降低计算量并规避MLP的缺陷，神经场领域重新采用了传统的基于网格的表示方法。Plenoxels [72] 将球谐系数存储在三维体素结构中，并通过插值方法实现无限分辨率，将训练时间从数天缩短至分钟级。Instant-NGP [43] 进一步采用基于哈希的索引算法优化了速度。学界已广泛探索网格表示与MLP的混合架构以寻求更优方案 [6, 54]。

Point representations have been recently suggested in neural fields to improve the shortcomings in grid-based representations, thanks to their flexibility and express i bility [69, 75]. They can generate outputs over a continuous input domain by interpolating neighboring points given a query point. It can be more accurate and parameter efficient than the grid-based ones since it can adaptively locate points, considering the complexity of functions, e.g., fewer points in low-frequency areas. Although our work is largely inspired by these works, 1. we repurpose the point representations to build continuous convolutional kernels, 2. we do not use MLPs that would introduce additional modeling complexity, 3. our method does not require complex initializations (or algorithms) to relocate points, such as depthbased initialization [69] and mask-based initialization [75].

点表征 (point representations) 最近在神经场 (neural fields) 中被提出，以改善基于网格表征的缺陷，这得益于其灵活性和表达能力 [69, 75]。它们可以通过在给定查询点时插值邻近点，在连续输入域上生成输出。由于它能根据函数的复杂性（例如在低频区域使用较少的点）自适应地定位点，因此比基于网格的表征更准确且参数效率更高。尽管我们的工作很大程度上受到这些研究的启发，但 1. 我们重新利用点表征来构建连续卷积核，2. 我们不使用会增加额外建模复杂度的多层感知机 (MLP)，3. 我们的方法不需要复杂的初始化（或算法）来重新定位点，例如基于深度的初始化 [69] 和基于掩码的初始化 [75]。

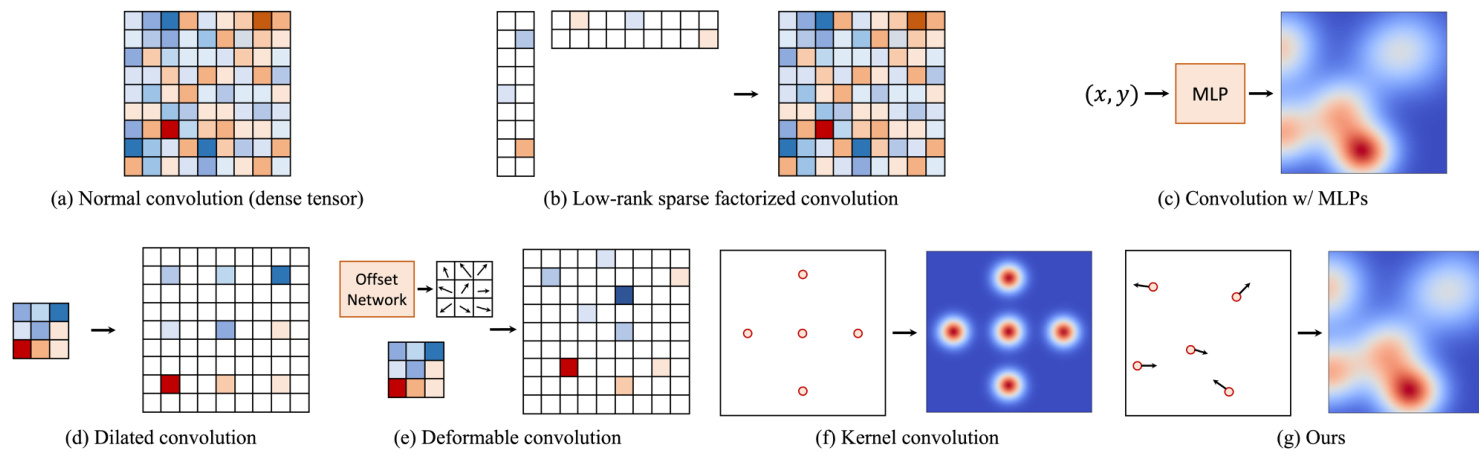
Figure 1. A various methods for large kernel construction.

图 1: 大卷积核构建的多种方法

Large kernel convolution. Since the great success of VGG-style CNNs [25, 27, 52, 56] in ImageNet [13], we repeatedly apply small kernels (e.g., $3\times3$ kernel) with deep layers to get a large receptive field and deal with long-term dependencies. With the massive success of transformers in the vision domain [16,17,37,60], which have a large receptive field, recent studies have started to revisit the descriptive power of large kernels [14, 35, 38, 58]. RepLKNet [14] has shown we can increase the kernel size up to $31\times31$ with the help of the re parameter iz ation trick. More recently, SLaK [35] managed to scale the kernel size to $51\times51$ and $61\times61$ , showing improved performance with dynamic sparsity and low-rank factorization (Fig. 1-(b)). While promising, the number of parameters increases according to the kernel size, which is a major bottleneck in representing large kernels.

大核卷积。自VGG风格的CNN [25, 27, 52, 56]在ImageNet [13]上取得巨大成功以来，我们通过重复应用小核（例如 $3\times3$ 核）配合深层网络来获得大感受野并处理长程依赖关系。随着Transformer [16,17,37,60]在视觉领域因其大感受野特性获得巨大成功，近期研究开始重新审视大核的描述能力 [14, 35, 38, 58]。RepLKNet [14]证明借助重参数化技巧可将核尺寸增大至 $31\times31$。最新研究SLaK [35]更将核尺寸扩展至 $51\times51$ 和 $61\times61$，通过动态稀疏性与低秩分解（图1-(b)）展示了性能提升。尽管前景可观，参数量会随核尺寸增大而增加，这成为表征大核的主要瓶颈。

The continuous kernel can construct large kernels with a fixed parameter budget (Fig. 1-(c)). CKConv [49] and Flex- Conv [48] have exploited this property and demonstrated that their method can model long-term dependencies by constructing large kernels on various datasets. However, they introduce a considerable amount of computations to the training process, and they have yet to perform largescale experiments, e.g., ImageNet. To the best of our knowledge, our approach is the first to conduct such a large-scale experiment using continuous convolution.

连续卷积核能够在固定参数预算下构建大尺寸核 (图 1-(c))。CKConv [49] 和 Flex-Conv [48] 利用这一特性，通过在不同数据集上构建大尺寸核证明了其方法对长程依赖关系的建模能力。然而，这些方法会显著增加训练过程的计算量，且尚未进行大规模实验 (例如 ImageNet)。据我们所知，本研究是首个使用连续卷积进行如此大规模实验的工作。

On the other hand, dilated convolutions [7, 8] can also be used to enlarge receptive fields with a small number of parameters, and they also do not introduce additional computations during training (Fig. 1-(d)). Deformable convolutions [10] look similar to ours in terms of moving points arbitrarily (Fig. 1-(e)). However, they learn how to deform the kernels (or predict the offset) during inference. On the other hand, we adjust the locations of the point representations during training to find the optimal large kernels. A concurrent work suggests learning the offsets during training [24]. In contrast to ours, it is a discrete formulation, thus losing the benefits of continuous convolution. Furthermore, we adjust the receptive fields of each point representation separately, yielding more expressive representations.

另一方面，空洞卷积 (dilated convolution) [7, 8] 也能用较少参数扩大感受野，且不会在训练时引入额外计算 (图 1-(d))。可变形卷积 (deformable convolution) [10] 在任意移动点位的特性上与我们的方法类似 (图 1-(e))，但其在推理时学习如何变形卷积核 (或预测偏移量)。而我们的方法通过在训练时调整点位表征的位置来寻找最优大卷积核。一项同期研究提出在训练时学习偏移量 [24]，但与我们的连续卷积形式不同，其采用离散表述因而丧失了连续卷积的优势。此外，我们单独调整每个点位表征的感受野，从而获得更具表现力的表征。

Continuous convolution for point clouds. There have been many continuous convolution approaches to handle 3D point cloud data, which is an important example of irregularly sampled data. PointNet [45] and PointNe $^{++}$ [46] are pioneer works that use average pooling and $1\times1$ convolution to aggregate features. [34, 36, 63, 66] leveraged MLPs to implement continuous convolution. KPConv [57] is also considered a continuous convolution and shares some similarities with ours (Fig. 1-f). They also used point representation and interpolation kernels for handling point clouds. However, their points are fixed over the training, unlike ours. They also proposed a deformable version, which requires additional neural networks to predict the offset of the kernel points.

点云的连续卷积。已有多种连续卷积方法用于处理3D点云数据，这是不规则采样数据的重要实例。PointNet [45] 和 PointNe$^{++}$ [46] 是开创性工作，使用平均池化和$1\times1$卷积来聚合特征。[34, 36, 63, 66] 利用多层感知机 (MLP) 实现连续卷积。KPConv [57] 也被视为连续卷积，与我们的方法存在相似之处 (图 1-f)。该方法同样采用点表示和插值核来处理点云，但其核点位置在训练过程中固定，而我们的方法则不同。他们还提出了可变形版本，需要通过额外神经网络预测核点偏移量。

3. SMPConv

3. SMPConv

3.1. Self-moving point representation

3.1. 自移动点表示

This section describes the proposed self-moving point representation to represent a continuous function. Let $d$ be the size of the input coordinates dimension, e.g., 1 in timeseries data and 2 in the spatial domain. SMP : Rd → RNc is a vector-valued function, mapping from the input coordinates to the output kernel vectors, where $N_{c}$ is a channel size. Given a query point $x\in\mathbb{R}^{d}$ , we define a continuous

本节介绍所提出的自移动点表示法，用于表示连续函数。设 $d$ 为输入坐标维度的大小，例如时间序列数据中为1，空间域中为2。SMP: Rd → RNc 是一个向量值函数，将输入坐标映射到输出核向量，其中 $N_{c}$ 是通道大小。给定一个查询点 $x\in\mathbb{R}^{d}$，我们定义一个连续的

kernel function as follows.

核函数如下。

$$
\mathrm{SMP}(x;\phi)=\frac{1}{|\mathcal{N}(x)|}\sum_{i\in\mathcal{N}(x)}g(x,p_{i},r_{i})w_{i},
$$

$$
\mathrm{SMP}(x;\phi)=\frac{1}{|\mathcal{N}(x)|}\sum_{i\in\mathcal{N}(x)}g(x,p_{i},r_{i})w_{i},
$$

where $\boldsymbol{\phi}={{p_{i}}_{i=1}^{N_{p}},{w_{i}}_{i=1}^{N_{p}},{r_{i}}_{i=1}^{N_{p}}}$ is a set of learn- able parameters, and $N_{p}$ is the number of points that are used to represent the function. $p_{i}\in\mathbb{R}^{d}$ is the coordinates of self-moving point representation $w_{i}\in\mathbb{R}^{N_{c}}$ , and each point representation also has a learnable radius, $r_{i}\in\mathbb{R}^{+}$ is a positive real number, which we implement it by clipping for numerical stability. We define a distance function $\dot{\boldsymbol g}:\dot{\mathbb R}^{d}\times\mathbb R^{d}\times\mathbb R^{+}\to\mathbb R$ as follows,

其中 $\boldsymbol{\phi}={{p_{i}}_{i=1}^{N_{p}},{w_{i}}_{i=1}^{N_{p}},{r_{i}}_{i=1}^{N_{p}}}$ 是一组可学习参数，$N_{p}$ 是用于表示函数的点数。$p_{i}\in\mathbb{R}^{d}$ 是自移动点表示的坐标，$w_{i}\in\mathbb{R}^{N_{c}}$，每个点表示还有一个可学习的半径，$r_{i}\in\mathbb{R}^{+}$ 是一个正实数，出于数值稳定性考虑我们通过裁剪实现。我们定义一个距离函数 $\dot{\boldsymbol g}:\dot{\mathbb R}^{d}\times\mathbb R^{d}\times\mathbb R^{+}\to\mathbb R$ 如下：

$$
g(x,p_{i},r_{i})=1-\frac{|x-p_{i}|{1}}{r{i}},
$$

$$
g(x,p_{i},r_{i})=1-\frac{|x-p_{i}|{1}}{r{i}},
$$

where $|\cdot|{1}$ is a L1 distance. $\mathcal{N}(x)$ is a set of indices of neighboring points of a query coordinate $x$ , defined as ${\mathcal{N}}(x)={i|g(x,p{i},r_{i})>0,\forall i}$ . Thus, points beyond a certain distance (depending on the radius) will not affect the query point. Hence, SMP generates output vectors by a weighted average of the nearby point representations. Note that all three parameters ${p_{i}},{w_{i}},{r_{i}}$ are jointly trained with the CNN model parameters, and the gradients w.r.t those parameters can be easily computed using an automatic differentiation library. As the name SMP suggests, the coordinates ${p_{i}}$ are updated during training, resulting in moving points representation.

其中 $|\cdot|{1}$ 是 L1 距离。$\mathcal{N}(x)$ 是查询坐标 $x$ 的邻近点索引集合，定义为 ${\mathcal{N}}(x)={i|g(x,p{i},r_{i})>0,\forall i}$。因此，超出特定距离（取决于半径）的点不会影响查询点。于是，SMP 通过邻近点表示的加权平均生成输出向量。注意，所有三个参数 ${p_{i}},{w_{i}},{r_{i}}$ 都与 CNN 模型参数联合训练，且这些参数的梯度可通过自动微分库轻松计算。正如 SMP 名称所示，坐标 ${p_{i}}$ 在训练过程中会更新，从而形成移动点表示。

Compared to a fixed-point representation, where ${p_{i}}$ are not trainable, ours can approximate complex functions more precisely. Since each point can move freely, more points can be gathered in high-frequency areas. On the other hand, few points can easily represent low-frequency components, resulting in more parameter-efficient representation. For example, a single point may be sufficient to approximate unimodal functions.

与定点表示法（其中${p_{i}}$不可训练）相比，我们的方法能更精确地逼近复杂函数。由于每个点可自由移动，更多点能聚集在高频区域。另一方面，少量点即可轻松表示低频分量，从而实现更高参数效率的表示。例如，单个点可能足以逼近单峰函数。

3.2. SMPConv

3.2. SMPConv

We leverage the suggested representation to implement a continuous convolution operator. In one dimensional case, $d=1$ , a continuous convolution can be formulated as,

我们利用所提出的表示方法实现了一个连续卷积算子。在一维情况下（$d=1$），连续卷积可以表示为：

$$
\big(f\ast\mathrm{SMP}\big)(x)=\sum_{c=1}^{N_{c}}\int_{\mathbb{R}}f_{c}(\tau)\mathrm{SMP}_{c}(x-\tau)d\tau,
$$

$$
\big(f\ast\mathrm{SMP}\big)(x)=\sum_{c=1}^{N_{c}}\int_{\mathbb{R}}f_{c}(\tau)\mathrm{SMP}_{c}(x-\tau)d\tau,
$$

where $f:\mathbb{R}\to\mathbb{R}^{N_{c}}$ is a input function and the $f_{c}$ and $\operatorname{SMP}{c}$ denote the $c$ -th element of the inputs. The convolution operator generates a function, computing the filter responses by summing over entire $N_{c}$ channels. One SMP representation corresponds a convolution operator, and multiple SMPs are used to implement one convolutional layer to generate multiple output channels. In contrast to the previous MLPbased continuous convolution, which uses one neural network for one convolutional layer, our approach has separate parameters for each convolution filter in a layer. It gives more freedom to each filter and results in more descriptive power of the learned filter.

其中 $f:\mathbb{R}\to\mathbb{R}^{N_{c}}$ 是输入函数，$f_{c}$ 和 $\operatorname{SMP}{c}$ 表示输入的第 $c$ 个元素。卷积算子生成一个函数，通过对所有 $N_{c}$ 个通道求和来计算滤波器响应。一个SMP表示对应一个卷积算子，多个SMP用于实现一个卷积层以生成多个输出通道。与之前基于MLP的连续卷积（每个卷积层使用一个神经网络）相比，我们的方法为层中的每个卷积滤波器设置了独立参数。这为每个滤波器提供了更大自由度，从而增强了所学滤波器的描述能力。

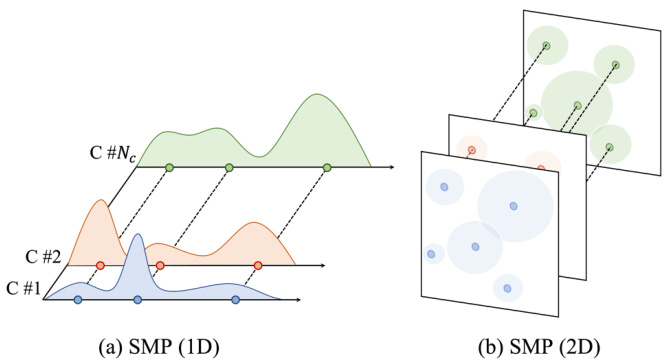
Figure 2. Self-moving point representation. (a) SMP as a function of the one-dimensional input domain, and (b) SMP as a function of the two-dimensional input domain. ‘C #1’ means the first channel. Each channel shares the location of the points, whereas each channel has its own weight parameters.

图 2: 自移动点表示。(a) 一维输入域下的 SMP 函数，(b) 二维输入域下的 SMP 函数。"C #1"表示第一通道。各通道共享点位置，但每个通道拥有独立的权重参数。

As depicted in Fig. 2, the kernels of each filter share the position parameters. That is, each filter of one layer has its own position parameters. Although we could use different SMP for different channels. However, it will considerably increase the number of learnable parameters $\it{{p_{i}}}$ per channel), and we believe that locating points at the same location for a convolutional filter can be a reasonable prior, where a convolutional filter can focus on specific areas in the input domain.

如图 2 所示，每个滤波器的核共享位置参数。也就是说，每一层的每个滤波器都有自己独立的位置参数。尽管我们可以为不同通道使用不同的 SMP (Spatial Modulation Parameters)，但这会显著增加每个通道的可学习参数量 $\it{{p_{i}}}$。我们认为，让卷积滤波器的定位点保持相同位置是一种合理的先验设定，这样卷积滤波器可以专注于输入域中的特定区域。

We leverage our continuous formulation to construct large kernels, motivated by the recent success of using them in many tasks. We can create arbitrary size large kernels by querying multiple disc ret i zed coordinates to SMP.

我们借鉴近期多项任务中使用大核的成功经验，基于连续公式化方法构建大核。通过向SMP查询多个离散化坐标点，可实现任意尺寸的大核构建。

3.3. Training

3.3. 训练

Training a large kernel has been challenging and computationally heavy, and naive training practice has yet to show promising results. Recently, [14, 15] proposed a reparameterization trick to combine different-size kernels as a separate branch, resulting in improved performance and more stable training. We also applied the same trick to train CNNs with SMPConv.

训练大卷积核一直具有挑战性且计算成本高昂，而简单的训练方法尚未展现出理想效果。近期，[14, 15]提出了一种重参数化技巧，通过将不同尺寸的卷积核组合为独立分支，从而提升性能并增强训练稳定性。我们同样采用该技巧来训练带有SMPConv的CNN。

We empirically figured out that performance degradation occurs when the coordinates ${p_{i}}$ are forced to fit inside the kernel by clipping. Thus, we let the coordinates be freely updated during training.

我们通过实验发现，当通过裁剪强制将坐标 ${p_{i}}$ 限制在内核范围内时，会出现性能下降。因此，我们在训练过程中让坐标自由更新。

We also found that the initialization of the parameters $\phi$ matters. For point locations, ${p_{i}}$ , we randomly sample from a gaussian distribution with small $\sigma$ . It initially locates the points in the center and gradually spreads out over the training process. We empirically found that this strategy yields more stable training, especially at the beginning of the training. We also initialized with small values for ${r_{i}}$ , which each weight parameter firstly has a narrow sight. Over the course of training, ${r_{i}}$ also gradually increases if necessary.

我们还发现参数 $\phi$ 的初始化很关键。对于点位置 ${p_{i}}$，我们从一个 $\sigma$ 较小的高斯分布中随机采样。这样初始时点会集中在中心区域，并在训练过程中逐渐扩散。实证表明该策略能带来更稳定的训练效果，尤其在训练初期。对于 ${r_{i}}$ 我们也采用较小初始值，使每个权重参数初始视野较窄。在训练过程中，${r_{i}}$ 会根据需要逐步增大。

Table 1. Training time (sec/epoch) and throughput (examples/sec) comparison with CIFAR10 on a single RTX3090 GPU. Both are tested with a batch size of 64 and input resolution of $32\times32$ . The $k$ is kernel size. The time is the average training time of the first 10 epochs.

Method	k	Params.	Time↓	Throughput↑
Deformable [10]	3	0.29M	61.2	4390.7
	5	1.37M	157.3	1618.9
	7	4.39M	293.1	882.3
FlexConv [48]	33	0.67M	92.9	1923.4
SMPConv	33	0.49M	40.1	4258.4

表 1: 在单块 RTX3090 GPU 上使用 CIFAR10 数据集的训练时间 (秒/周期) 和吞吐量 (样本数/秒) 对比。测试时批量大小为 64，输入分辨率为 $32\times32$。$k$ 表示卷积核尺寸，时间为前 10 个周期的平均训练时间。

方法	k	参数量	时间↓	吞吐量↑
Deformable [10]	3	0.29M	61.2	4390.7
	5	1.37M	157.3	1618.9
	7	4.39M	293.1	882.3
FlexConv [48]	33	0.67M	92.9	1923.4
SMPConv	33	0.49M	40.1	4258.4

3.4. Efficiency

3.4. 效率

Assuming the size of a convolution filter is $C\times N\times N$ , where $C$ is the number of kernels and $N$ is the height and width of filter, $C N^{2}$ parameters are required in dense convolution (Fig. 1-(a)). Therefore, the number of parameters is proportional to kernel resolution $N\times N$ . On the other hand, SMP needs $(1+d+C)N_{p}$ parameters, where $d$ is the size of the input coordinates dimension, and $N_{p}$ is the number of weight points. We used $N_{p}\ll N^{2}$ , so SMP is more efficient than dense convolution in terms of the number of parameters. Furthermore, as the number of parameters does not depend on kernel resolution, SMP can represent kernels of any size, such as large or continuous kernels with fixed budget parameters.

假设卷积滤波器的大小为 $C\times N\times N$ ，其中 $C$ 是卷积核数量， $N$ 是滤波器的高度和宽度，密集卷积 (图 1-(a)) 需要 $C N^{2}$ 个参数。因此，参数数量与卷积核分辨率 $N\times N$ 成正比。另一方面，SMP (Sparse Matrix Processing) 需要 $(1+d+C)N_{p}$ 个参数，其中 $d$ 是输入坐标维度的大小， $N_{p}$ 是权重点数量。我们设定 $N_{p}\ll N^{2}$ ，因此在参数数量方面 SMP 比密集卷积更高效。此外，由于参数数量不依赖于卷积核分辨率，SMP 可以用固定预算参数表示任意大小的卷积核，例如大型或连续卷积核。

Due to the point representations and interpolation schemes without supplementary neural networks, SMPConv has an advantage of computational complexity. On the other hand, the existing large kernel convolutions are computationally heavy. Deformable convolution (Fig. 1- (e)), for example, requires offset prediction networks and convolution with interpolated inputs during both training and inference, resulting in additional computation and parameter costs. Additionally, it relies on dense convolution, making it impractical to increase kernel size signifi- cantly. Similarly, MLP-based methods(Fig. 1-(c)) like FlexConv [48] leverage kernel generation neural network, and it also increases computational burdens. The results presented in Tab. 1 demonstrate that SMPConv outperforms the existing large kernel convolutions in terms of speed.

由于采用点表示法和无需辅助神经网络的插值方案，SMPConv在计算复杂度方面具有优势。相比之下，现有的大核卷积计算量较大。以可变形卷积（图1-(e)）为例，它需要在训练和推理过程中进行偏移量预测网络和插值输入的卷积操作，导致额外的计算和参数开销。此外，它依赖于密集卷积，因此难以显著增大核尺寸。类似地，基于MLP的方法（图1-(c)）如FlexConv [48]利用核生成神经网络，同样增加了计算负担。表1所示结果表明，SMPConv在速度方面优于现有的大核卷积方法。

4. Experiments

4. 实验

4.1. Continuous function approximation

4.1. 连续函数逼近

Firstly, we conducted a fitting experiment to validate that our self-moving point representation can work as an approximator for a continuous function. To do so, we used two sinusoidal-based functions as the ground truth. Given a function, SMP is optimized to represent the sampled function on a $51\times51$ grid. In this experiment, we designed SMP with 204 points. The fitting result has been shown in Fig. 3. It demonstrates that our proposed method reasonably well approximates a given continuous function with fewer points. Additionally, we compared with the fixed point representation and observed that optimizing the position of points together helps to better approximate the func- tion as the number of points is equal.

首先，我们进行了拟合实验以验证自移动点表示法可作为连续函数的近似器。为此，我们采用两个基于正弦的函数作为基准真值。给定函数后，SMP（自移动点）经过优化，用于表示在$51\times51$网格上的采样函数。本实验中，我们设计了包含204个点的SMP。拟合结果如图3所示，表明所提方法能以较少的点合理近似给定连续函数。此外，通过与固定点表示法的对比发现，在点数相同的情况下，同步优化点的位置有助于更好地逼近函数。

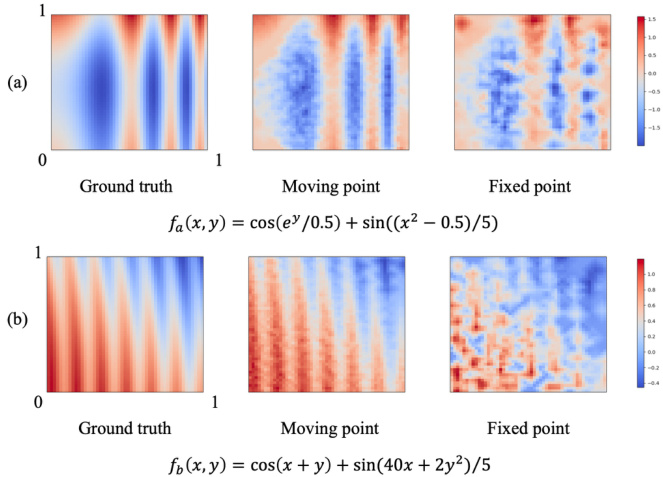
Figure 3. Comparison between the moving point and the fixed point representations through the fitting. Our proposed moving point representations can approximate given continuous functions with higher accuracy.

图 3: 移动点与固定点表示法在拟合过程中的对比。我们提出的移动点表示法能以更高精度逼近给定连续函数。

4.2. Sequential data classification

4.2. 序列数据分类

To demonstrate that SMPConv can handle long-term dependencies well, we evaluated our method on various sequential data tasks, such as sequential image and time-series classification. To do so, we followed FlexTCN [48] to construct a SMPConv architecture for causal 1D CNN whose kernel size is same as the input sequence length. We substituted their parameterized kernels with ours without additional modifications. To maintain a similar number of network parameters, SMPConv contains 30 weight points in each SMP. To alleviate the computation burdens caused by the convolution with large kernels, we have considered exploiting the computations through a fast Fourier transform. More network and experimental details are in Appendix A.1.

为验证SMPConv能有效处理长程依赖关系，我们在序列图像分类和时间序列分类等任务上评估了该方法。参照FlexTCN [48]的架构设计，我们构建了因果一维卷积网络（causal 1D CNN）的SMPConv实现，其卷积核尺寸与输入序列长度相同。在保持网络参数量相近的前提下（每个SMP包含30个权重点），我们直接替换了原方案的参数化卷积核。针对大尺寸卷积核带来的计算负担，我们探索了基于快速傅里叶变换的加速方案。完整网络结构与实验细节见附录A.1。

Sequential image. We tested our SMPConv on the 1D version of images from the datasets, sequential MNIST (sMNIST), permuted MNIST(pMNIST) [32], and sequential CIFAR10 (sCIFAR10) [4]. These datasets have long input sequence lengths, for example, 784 for sMNIST and pMNIST, and 1024 for sCIFAR10. Note that it is hard to model these datasets without proper kernel representations.

序列图像。我们在数据集的一维版本上测试了SMPConv，包括顺序MNIST (sMNIST)、置换MNIST (pMNIST) [32] 和顺序CIFAR10 (sCIFAR10) [4]。这些数据集具有较长的输入序列长度，例如sMNIST和pMNIST为784，sCIFAR10为1024。需要注意的是，如果没有合适的核表示，对这些数据集进行建模将非常困难。

Table 2. Sequential image classification results.

表 2: 序列图像分类结果

模型	参数量	sMNIST	pMNIST	sCIFAR10
DilRNN [4]	44k	98.0 87.2	96.1
LSTM [2]	70k		85.7
GRU [2]	70k	96.2	87.3
TCN [2]	70k	99.0	97.2
r-LSTM [61]	500k	98.4	95.2	72.2
IndRNN [33]	83k	99.0	96.0
TrellisNet [3]	8M	99.20 99.28	98.13	73.42
URLSTM [21]	-		96.96	71.00
HiPPO [19]	0.5M		98.30
coRNN [51]	134k	99.4	97.3
CKCNN [49]	98k	99.31	98.00	62.25
LSSL [22]		99.53	98.76	84.65
S4 [20]		99.63	98.70	91.13
FlexTCN [48] Ours	375k 373k	99.62 99.75	98.63	80.82 84.86

As shown in Tab. 2, the proposed model has achieved stateof-the-art results on both sMNIST and pMNIST. For sCIFAR10 dataset, our model has outperformed all the comparative models except S4 [20]. Compared with the FlexTCN, which has a similar network base, our model improved the accuracy by $4%$ . These results show that our proposed model is suitable and effective for sequential images.

如表 2 所示，所提出的模型在 sMNIST 和 pMNIST 上均取得了最先进的结果。对于 sCIFAR10 数据集，我们的模型表现优于除 S4 [20] 之外的所有对比模型。与网络结构相似的 FlexTCN 相比，我们的模型将准确率提高了 $4%$。这些结果表明，我们提出的模型适用于序列图像且效果显著。

Time-series. We evaluated our model on time-series sequence datasets, character trajectories (CT) [1], and speech commands (SC) [64]. The results have been displayed in Tab. 3. In the relatively shorter MFCC features data, SMPConv achieved test accuracy similar to FlexTCN. To validate that our proposed model can model extremely long sequences, we conducted experiments on the SC-raw dataset, which has a sequence length of 16000. Similar to the sequence image classification result, our model outperformed FlexTCN with a large margin of $+3%$ .

时间序列。我们在时间序列数据集、字符轨