Abstract
摘要
In this paper we revisit the efficacy of knowledge distillation as a function matching and metric learning problem. In doing so we verify three important design decisions, namely the normalisation, soft maximum function, and projection layers as key ingredients. We theoretically show that the projector implicitly encodes information on past examples, enabling relational gradients for the student. We then show that the normalisation of representations is tightly coupled with the training dynamics of this projector, which can have a large impact on the students performance. Finally, we show that a simple soft maximum function can be used to address any significant capacity gap problems. Experimental results on various benchmark datasets demonstrate that using these insights can lead to superior or comparable performance to state-ofthe-art knowledge distillation techniques, despite being much more computationally efficient. In particular, we obtain these results across image classification (CIFAR100 and ImageNet), object detection (COCO2017), and on more difficult distillation objectives, such as training data efficient transformers, whereby we attain a $77.2%$ top-1 accuracy with DeiT-Ti on ImageNet. Code and models are publicly available.
本文重新审视了知识蒸馏作为函数匹配和度量学习问题的有效性。通过研究验证了三个关键设计决策:归一化处理、软最大值函数和投影层的重要作用。我们从理论上证明投影器隐式编码了历史样本信息,从而为学生模型提供了关系梯度。研究表明表征归一化与投影器的训练动态紧密耦合,这对学生模型性能具有重大影响。最后提出采用简单软最大值函数即可解决显著容量差距问题。在多个基准数据集(CIFAR100、ImageNet的图像分类任务,COCO2017的目标检测任务)上的实验表明,基于这些见解的方法能取得优于或媲美最先进知识蒸馏技术的性能,同时计算效率显著提升。特别是在训练数据高效的Transformer模型等更具挑战性的蒸馏目标上,我们使用DeiT-Ti在ImageNet上达到了77.2%的top-1准确率。代码和模型均已开源。
Introduction
引言
Deep neural networks have achieved remarkable success in various applications, ranging from computer vision (Krizhevsky, Sutskever, and Hinton 2012) to natural language processing (Vaswani et al. 2017). However, the high computational cost and memory requirements of deep models have limited their deployment in resource-constrained environments. Knowledge distillation is a popular technique to address this problem through transferring the knowledge of a large teacher model to that of a smaller student model. This technique involves training the student to imitate the output of the teacher, either by directly minimizing the difference between intermediate features or by minimizing the Kullback-Leibler (KL) divergence between their soft predictions. Although knowledge distillation has shown to be very effective, there are still some limitations related to the computational and memory overheads in constructing and evaluating the losses, as well as an insufficient theoretical explanation for the underlying core principles.
深度神经网络在从计算机视觉 (Krizhevsky, Sutskever, and Hinton 2012) 到自然语言处理 (Vaswani et al. 2017) 的各种应用中取得了显著成功。然而,深度模型的高计算成本和内存需求限制了其在资源受限环境中的部署。知识蒸馏 (knowledge distillation) 是一种通过将大型教师模型的知识迁移到较小学生模型中来解决这一问题的流行技术。该技术通过直接最小化中间特征的差异或最小化其软预测之间的Kullback-Leibler (KL) 散度来训练学生模仿教师的输出。尽管知识蒸馏已被证明非常有效,但在构建和评估损失时的计算和内存开销方面仍存在一些限制,以及对潜在核心原理的理论解释不足。

Figure 1: Proposed feature distillation pipeline using three distinct components: linear projection (a), batch norm (b), and a LogSum distance (c). We provide an interpret able explanation for each each of these three components, which results in a very cheap and effective recipe for distillation.
图 1: 提出的特征蒸馏流程包含三个独立组件:线性投影 (a)、批归一化 (b) 和 LogSum 距离度量 (c)。我们为这三个组件分别提供了可解释性说明,最终形成了一种高效低成本的特征蒸馏方案。
To overcome these limitations, we revisit knowledge distillation from both a function matching and metric learning perspective. We perform an extensive ablation of three important components of knowledge distillation, namely the distance metric, normalisation, and projector network. Alongside this ablation we provide a theoretical perspective and unification of these design principles through exploring the underlying training dynamics. Finally, we extend these principles to a few large scale vision tasks, whereby we achieve comparable or improved performance over state-of-the-art. The most significant result of which pertains to the dataefficient training of transformers, whereby a performance gain of $2.2%$ is achieved over the best-performing distillation methods that are designed explicitly for this task. Our main contributions can be summarised as follows.
为克服这些局限性,我们从函数匹配和度量学习的角度重新审视知识蒸馏。我们对知识蒸馏的三个关键组件(距离度量、归一化和投影网络)进行了全面消融实验。结合消融分析,我们通过探究底层训练动态为这些设计原则提供了理论视角与统一框架。最终,我们将这些原则扩展到若干大规模视觉任务中,实现了与最先进方法相当或更优的性能。其中最具突破性的成果体现在Transformer的数据高效训练方面——相比专为该任务设计的最佳蒸馏方法,我们取得了2.2%的性能提升。主要贡献可归纳如下:
• We explore three distinct design principles from knowledge distillation, namely the projection, normalisation, and distance function. In doing so we demonstrate their and coupling with each other, both through analytical means and by observing the training dynamics. • We show that a projection layer implicitly encodes relational information from previous samples. Using this knowledge we can remove the need to explicitly construct correlation matrices or memory banks that will inevitably incur a significant memory overhead.
• 我们探索了知识蒸馏 (knowledge distillation) 中的三种设计原则:投影 (projection)、归一化 (normalisation) 和距离函数 (distance function),并通过理论分析和训练动态观察,揭示了它们之间的耦合关系。
• 我们发现投影层隐式编码了先前样本的关系信息,利用这一特性可消除显式构建相关矩阵或内存库的需求,从而避免显著的内存开销。
• We propose a simple recipe for knowledge distillation using a linear projection, batch normalisation, and a LogSum function. These three design choices can attain competitive or improved performance to state-of-the-art for image classification, object detection, and the data efficient training of transformers.
• 我们提出了一种简单的知识蒸馏方法,采用线性投影、批量归一化和LogSum函数。这三种设计选择在图像分类、目标检测和Transformer数据高效训练方面能达到与最先进技术相当或更优的性能。
Related Work
相关工作
Knowledge Distillation Knowledge distillation is the process of transferring the knowledge from a large, complex model to a smaller, simpler model. Its usage was originally proposed in the context of image classification (Hinton, Vinyals, and Dean 2015) whereby the soft teacher predictions would encode relational information between classes. Spherical KD (Guo et al. 2020) extended this idea by rescaling the logits, prime aware adaptive distillation (Zhang et al. 2020) introduced an adaptive weighting strategy, while DKD (Zhao, Song, and Qiu 2022) proposed to decouple the original formulation into target class and non-target class probabilities.
知识蒸馏
知识蒸馏是将知识从庞大复杂的模型迁移到更小、更简单模型的过程。该方法最初由Hinton、Vinyals和Dean (2015) 在图像分类领域提出,通过教师模型的软预测编码类别间关联信息。球形知识蒸馏 (Spherical KD) (Guo等 2020) 通过对数概率重缩放扩展了这一思想,主感知自适应蒸馏 (Zhang等 2020) 引入了自适应加权策略,而DKD (Zhao、Song和Qiu 2022) 则提出将原始公式解耦为目标类与非目标类概率。
Hinted losses (Romero et al. 2015) were a natural extension of the logit-based approach whereby the intermediate feature maps are used as hints for the student. Attention transfer (Zagoruyko and Komodakis 2019) then pro- posed to re-weight this loss using spatial attention maps. ReviewKD (Chen et al. 2021a) addressed the problem relating to the arbitrary selection of layers by aggregating information across all the layers using trainable attention blocks. Neuron selectivity transfer (Huang and Wang 2017), similarity-preserving KD (Tung and Mori 2019), and relational KD (Park et al. 2019) construct relational batch and feature matrices that can be used as inputs for the distillation losses. Similarly FSP matrices $(Yim 2017 ) $ were proposed to extract the relational information through a residual block. In contrast to this theme, we show that a simple projection layer can implicitly capture most relational information, thus removing the need to construct any expensive relational structures.
提示损失 (Hinted losses) [Romero et al. 2015] 是 logit 方法的自然延伸,通过将中间特征图作为学生的提示信息。注意力迁移 (Attention transfer) [Zagoruyko and Komodakis 2019] 随后提出使用空间注意力图对该损失进行重新加权。ReviewKD [Chen et al. 2021a] 通过使用可训练注意力块聚合所有层的信息,解决了层选择任意性的问题。神经元选择性迁移 (Neuron selectivity transfer) [Huang and Wang 2017]、相似性保持知识蒸馏 (similarity-preserving KD) [Tung and Mori 2019] 和关系知识蒸馏 (relational KD) [Park et al. 2019] 构建了可作为蒸馏损失输入的关系批次和特征矩阵。类似地,FSP 矩阵 $({Yim}2017 )$ 被提出用于通过残差块提取关系信息。与此相反,我们证明简单的投影层可以隐式捕获大部分关系信息,从而无需构建任何昂贵的关系结构。
Representation distillation was originally proposed alongside a contrastive based loss (Tian, Krishnan, and Isola 2019) and has since been extended using a Wasser stein distance (Chen et al. 2020a), information theory (Miles, Rodriguez, and Miko la jc zyk 2022), graph theory (Ma, Chen, and Akata 2022), and complementary gradient information (Zhu et al. 2021a). Distillation also been empirically shown to benefit from longer training schedules and more data-augmentation (Beyer et al. 2022), which is similarly observed with HSAKD (Yang et al. 2021) and SSKD (Xu et al. 2020). Distillation between CNNs and transformers has also been a very practically motivated task for data-efficient training (Touvron et al. 2021) and has shown to benefit from an ensemble of teacher architectures (Ren et al. 2022). However, we show that just a simple extension of some fundamental distillation design principles is much more effective.
表示蒸馏最初是与基于对比的损失函数 (Tian, Krishnan, and Isola 2019) 一同提出的,随后被拓展应用到 Wasserstein 距离 (Chen et al. 2020a)、信息论 (Miles, Rodriguez, and Miko la jc zyk 2022)、图论 (Ma, Chen, and Akata 2022) 以及互补梯度信息 (Zhu et al. 2021a) 等领域。实证研究表明,蒸馏还能从更长的训练周期和更多的数据增强中获益 (Beyer et al. 2022),这一现象在 HSAKD (Yang et al. 2021) 和 SSKD (Xu et al. 2020) 中也得到了类似观察。CNN 与 Transformer 之间的蒸馏同样是出于数据高效训练的实际需求 (Touvron et al. 2021),并且已证实能通过教师架构集成获得提升 (Ren et al. 2022)。然而,我们的研究表明,仅需对一些基础蒸馏设计原则进行简单扩展,就能实现显著更好的效果。
Self-distillation is another branch of knowledge distillation that instead proposes to instead distill knowledge within the network itself (Zhang et al. 2019). This paradigm removes the need to have any pre-trained teacher readily available and has since been applied in the context of deep metric learning (Roth et al. 2021), graph neural networks (Chen et al. 2021b), and image classification (Miles and Miko la jc zyk 2020). Its success of which has since driven many theoretical advancements (Mobahi, Farajtabar, and Bartlett 2020; AllenZhu and Li 2023; Zhang and Sabuncu 2020) and is still an active area of research.
自蒸馏 (self-distillation) 是知识蒸馏的另一个分支,其核心思想是在网络内部进行知识提炼 (Zhang et al. 2019)。这种方法无需依赖任何预训练的教师模型,已被成功应用于深度度量学习 (Roth et al. 2021)、图神经网络 (Chen et al. 2021b) 和图像分类 (Miles and Miko la jc zyk 2020) 等领域。其显著成效推动了多项理论突破 (Mobahi, Farajtabar, and Bartlett 2020; AllenZhu and Li 2023; Zhang and Sabuncu 2020),目前仍是活跃的研究方向。
Self-Supervised Learning Self-supervised learning (SSL) is an increasingly popular field of machine learning whereby a model is trained to learn a useful representation of unlabelled data. Its popularity has been driven by the increasing cost of manual labelling and has since been crucial for training large transformer models. Various pretext tasks have been proposed to learn these representations, such as image inpainting (He et al. 2022), color iz ation (Zhang, Isola, and Efros 2016), or prediction of the rotation (Gidaris, Singh, and Komodakis 2018) or position of patches (Doersch, Gupta, and Efros 2015; Carlucci et al. 2019). SimCLR (Chen et al. 2020b) approached self-supervision using a contrastive loss with multi-view augmentation to define the positive and negative pairs. They found a large memory bank of negative representations was necessary to achieve good performance, but would incur a significant memory overhead. MoCo (He et al. 2020) extending this work with a momentum encoder, which was subsequently extended by MoCov2 (Chen et al. 2020c) and MoCov3 (Chen, Xie, and He 2021).
自监督学习
自监督学习 (SSL) 是机器学习中日益流行的领域,其通过训练模型从未标注数据中学习有用的表征。该方法的兴起源于人工标注成本的增长,并已成为训练大型Transformer模型的关键技术。研究者提出了多种代理任务来学习这些表征,例如图像修复 (He et al. 2022)、着色 (Zhang, Isola, and Efros 2016)、旋转预测 (Gidaris, Singh, and Komodakis 2018) 或图像块位置预测 (Doersch, Gupta, and Efros 2015; Carlucci et al. 2019)。SimCLR (Chen et al. 2020b) 采用对比损失与多视图增强来定义正负样本对进行自监督学习,发现需要构建大型负样本记忆库才能获得良好性能,但这会导致显著的内存开销。MoCo (He et al. 2020) 通过动量编码器扩展了这项工作,后续又由MoCov2 (Chen et al. 2020c) 和MoCov3 (Chen, Xie, and He 2021) 进一步改进。
Feature de correlation is another approach to SSL that avoids the need for negative pairs to address representation collapse. Both Barlow twins (Zbontar et al. 2021) and VICReg (Bardes, Ponce, and LeCun 2022a) achieve this by maximising the variance within a batch, while preserving invariance to augmentations. Both contrastive learning and feature de correlation have since been extended to dense prediction tasks (Bardes, Ponce, and LeCun 2022b) and unified with knowledge distillation (Miles et al. 2023).
特征去相关 (feature de correlation) 是另一种自监督学习 (SSL) 方法,它无需负样本对即可解决表征坍塌问题。Barlow Twins (Zbontar et al. 2021) 和 VICReg (Bardes, Ponce, and LeCun 2022a) 都通过最大化批次内方差同时保持对数据增强的不变性来实现这一目标。对比学习和特征去相关方法随后被扩展到密集预测任务 (Bardes, Ponce, and LeCun 2022b) 并与知识蒸馏 (Miles et al. 2023) 进行了统一。
Understanding the Role of the Projector
理解投影仪的作用
Knowledge distillation (KD) is a technique used to transfer knowledge from a large, powerful model (teacher) to a smaller, less powerful one (student). In the classification setting, it can be done using the soft teacher predictions as pseudo-labels for the student. Unfortunately, this approach does not trivially generalise to non-classification tasks (Liu et al. 2019) and the classifier may collapse a lot of information (Tishby 2015) that can be useful for distillation. Another approach is to use feature maps from the earlier layers for distillation (Romero et al. 2015; Zagoruyko and Komodakis 2019), however, its usage presents two primary challenges: the difficulty in ensuring consistency across different architectures (Chen et al. 2021a) and the potential degradation in the student’s downstream performance for cases where the inductive biases of the two networks differ (Tian, Krishnan, and Isola 2019) A compromise, which strikes a balance between the two approaches discussed above, is to distill the representation directly before the output space. Representation distillation has been successfully adopted in past works (Tian, Krishnan, and Isola 2019; Zhu et al. 2021a; Miles, Rodriguez, and Miko la jc zyk 2022) and is the focus of this paper. The exact training framework used is described in figure 1. The projection layer shown was originally used to simply match the student and teacher dimensions (Romero et al. 2015), however, we will show that its role is much more important and it can lead to significant performance improvements even when the two feature dimensions already match. The two representations are typically both followed by some normalisation scheme as a way of appropriately scaling the gradients. However, we find this normalisation has a more interesting property in its relation to what information is encoded in the learned projector weights.
知识蒸馏 (Knowledge Distillation, KD) 是一种将知识从强大模型(教师模型)迁移到较小模型(学生模型)的技术。在分类任务中,可以通过使用教师模型的软预测作为学生模型的伪标签来实现。然而,这种方法难以直接推广到非分类任务 (Liu et al. 2019),且分类器可能压缩大量对蒸馏有用的信息 (Tishby 2015)。另一种方法是利用早期层的特征图进行蒸馏 (Romero et al. 2015; Zagoruyko and Komodakis 2019),但这种方法存在两个主要挑战:难以确保不同架构间的一致性 (Chen et al. 2021a),以及当两个网络的归纳偏置不同时可能导致学生模型下游性能下降 (Tian, Krishnan, and Isola 2019)。
作为上述两种方法的折中方案,直接在输出空间前对表征进行蒸馏能够取得平衡。表征蒸馏已在先前工作中被成功应用 (Tian, Krishnan, and Isola 2019; Zhu et al. 2021a; Miles, Rodriguez, and Miko la jc zyk 2022),也是本文的研究重点。具体训练框架如图 1 所示。其中显示的投影层最初仅用于匹配学生模型和教师模型的维度 (Romero et al. 2015),但我们将证明其作用更为关键——即使特征维度已匹配,该层仍能带来显著的性能提升。两种表征通常都会经过某种归一化方案以调整梯度规模。然而我们发现,这种归一化与学习到的投影权重所编码信息之间的关系具有更深刻的特性。
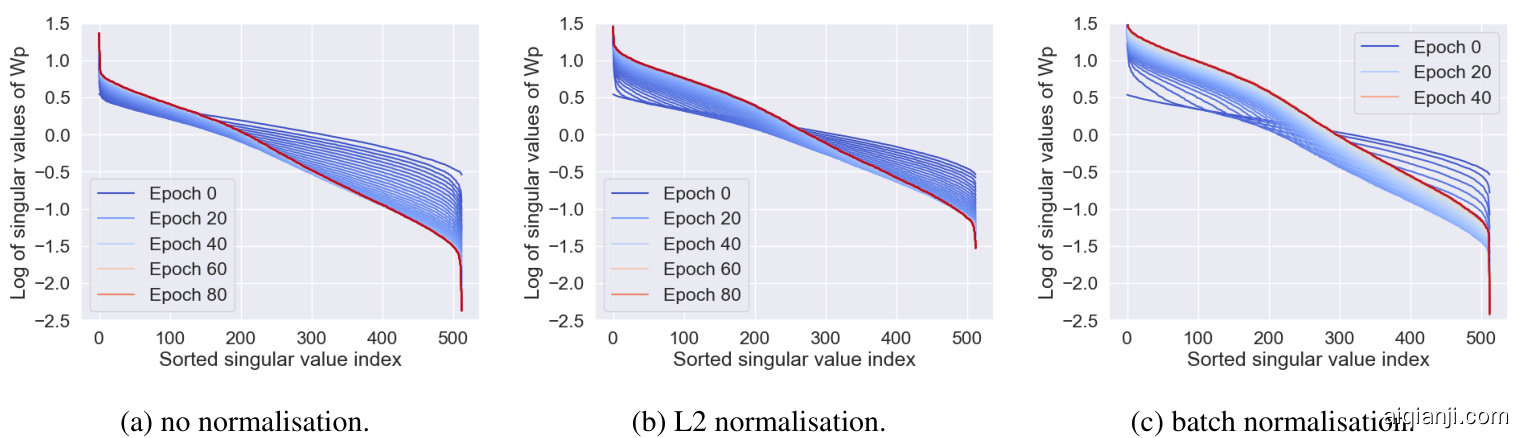
Figure 2: Evolution of singular values of the projection weights $\mathbf{W}_{p}$ under three different representation normalisation schemes. The student is a Resnet-18, while the teacher is a ResNet-50. The three curves shows the evolution of singular values for the projector weights when the representations undergo no normalisation, L2 normalisation, and batch norm respectively.
图 2: 三种不同表示归一化方案下投影权重 $\mathbf{W}_{p}$ 的奇异值演化。学生网络为ResNet-18,教师网络为ResNet-50。三条曲线分别展示了表示未经归一化、L2归一化和批归一化时投影器权重的奇异值变化情况。
In this work we provide a theoretical perspective to motivate some simple and effective design choices for knowledge distillation. In contrast to the recent works (Tung and Mori 2019; Miles, Rodriguez, and Miko la jc zyk 2022), we show that an explicit construction of complex relational structures, such as feature kernels (He and Ozay 2022) is not necessary. In fact, most of this structure can be learned implicitly through the tightly coupled interaction of a learnable projection layer and an appropriate normalisation scheme. In the following sections we investigate the training dynamics of the projection layer with the choice of normalisation scheme. We explore the impact and trade-offs that arise from the architecture design of the projector. Finally, we propose a simple modification to the distance metric to address issues arising from a large capacity gap between the student and teacher models. Although we do not aim to necessarily propose a new method for distillation, we uncover a cheap and simple recipe that can transfer to various distillation settings and tasks. Furthermore, we provide a new theoretical perspective on the underlying principles of distillation that can translate to large scale vision tasks.
在本工作中,我们从理论视角出发,为知识蒸馏(knowledge distillation)提出了一些简单有效的设计选择。与近期研究 (Tung and Mori 2019; Miles, Rodriguez, and Miko la jc zyk 2022) 不同,我们证明无需显式构建复杂的关系结构(例如特征核 (He and Ozay 2022))。事实上,这些结构的大部分可以通过可学习投影层与适当归一化方案的紧密耦合交互实现隐式学习。在后续章节中,我们将研究投影层在不同归一化方案下的训练动态,探讨投影器架构设计带来的影响与权衡。最后,我们提出对距离度量的简单改进,以解决学生模型与教师模型间巨大容量差距导致的问题。虽然本研究并非旨在提出新的蒸馏方法,但我们发现了一种可迁移至多种蒸馏场景与任务的低成本简易方案。此外,我们从理论层面重新阐释了蒸馏的基本原理,这些原理可扩展至大规模视觉任务。
The projection weights encode relational information from previous samples. The projection layer plays a crucial role in KD as it provides an implicit encoding of previous samples and its weights can capture the relational information needed to transfer information regarding the correlation between features. We observe that even a single linear projector layer can provide significant improvements in accuracy (see Supplementary). This improvement suggests that the projections role in distillation can be described more concisely as being an encoder of essential information needed for the distillation loss itself. Most recent works propose a manual construction of some relational information to be used as part of a loss (Park et al. 2019; Tung and Mori 2019), however, we posit that an implicit and learnable approach is much more effective. To explore this phenomenon in more detail, we consider the update equations for the projector weights and its training dynamics. Without loss in generality, consider a simple L2 loss and a linear bias-free projection layer.
投影权重编码了来自先前样本的关系信息。投影层在知识蒸馏(KD)中起着关键作用,它提供了对先前样本的隐式编码,其权重能够捕获传递特征间相关性信息所需的关系信息。我们观察到,即便是单个线性投影层也能显著提升准确率(参见补充材料)。这一改进表明,投影在蒸馏中的作用可以更简洁地描述为对蒸馏损失本身所需关键信息的编码器。最近的研究大多采用人工构建某些关系信息作为损失函数的一部分(Park等人2019;Tung和Mori 2019),但我们认为隐式可学习的方法更为有效。为深入探究这一现象,我们考察了投影权重的更新方程及其训练动态。不失一般性,考虑简单的L2损失和无偏置线性投影层。
$$
D(\mathbf{Z}{s},\mathbf{Z}{t};\mathbf{W}{p})=\frac{1}{2}\left\lVert\mathbf{Z}{s}\mathbf{W}{p}-\mathbf{Z}{t}\right\rVert_{2}^{2}
$$
Where $\mathbf{Z}{s}$ and $\mathbf{Z}{t}$ are the student and teacher representations respectively, while $\mathbf{W}_{p}$ is the matrix representing the linear projection. Using the trace property of the Frobenius norm, we can then express this loss as follows:
其中 $\mathbf{Z}{s}$ 和 $\mathbf{Z}{t}$ 分别是学生和教师的表示,而 $\mathbf{W}_{p}$ 是表示线性投影的矩阵。利用Frobenius范数的迹性质,我们可以将此损失表达如下:
$$
\begin{array}{r l r}&{}&{D(\mathbf{Z}_{s},\mathbf{Z}{t};\mathbf{W}{p})=\displaystyle\frac{1}{2}t r\left(\left(\mathbf{Z}{s}\mathbf{W}{p}-\mathbf{Z}{t}\right)^{T}\left(\mathbf{Z}{s}\mathbf{W}{p}-\mathbf{Z}{t}\right)\right)}\ &{}&{(2,}\ &{=\displaystyle\frac{1}{2}t r(\mathbf{W}{p}^{T}\mathbf{Z}{s}^{T}\mathbf{Z}{s}\mathbf{W}{p}-\mathbf{Z}{t}^{T}\mathbf{Z}{s}\mathbf{W}{p}}&{(3)}\ &{}&{-\mathbf{W}{p}^{T}\mathbf{Z}{s}^{t}\mathbf{Z}{t}+\mathbf{Z}{t}^{T}\mathbf{Z}_{t})}&{(4),}\end{array}
$$
Taking the derivative with respect to $\mathbf{W}{p}$ , we can derive the update rule $\dot{\mathbf{W}}_{p}$
对 $\mathbf{W}{p}$ 求导,可以推导出更新规则 $\dot{\mathbf{W}}_{p}$
$$
\dot{\mathbf{W}}{p}=-\frac{\partial D(\mathbf{W}{p})}{\partial\mathbf{W}{p}}=-\mathbf{Z}{s}^{T}\mathbf{Z}{s}\mathbf{W}{p}+\mathbf{Z}{s}^{T}\mathbf{Z}_{t}
$$
which can be further simplified
可进一步简化为
$$
\boxed{\dot{\mathbf{W}}{p}=\mathbf{C}{s t}-\mathbf{C}{s}\mathbf{W}_{p}}
$$
where $\mathbf{C}{s}=\mathbf{Z}{s}^{T}\mathbf{Z}{s}\in\mathbb{R}^{d_{s}\times d_{s}}$ and $\mathbf{C}{s t}=\mathbf{Z}{s}^{T}\mathbf{Z}{t}\in\mathbb{R}^{d_{s}\times d_{t}}$ denote self and cross correlation matrices respectively. Due to the capacity gap between the student network and the teacher network, there is no perfect linear projection between these two representation spaces. Instead, the projector will converge on an approximate projection that we later show is governed by the normalisation being employed.
其中 $\mathbf{C}{s}=\mathbf{Z}{s}^{T}\mathbf{Z}{s}\in\mathbb{R}^{d_{s}\times d_{s}}$ 和 $\mathbf{C}{s t}=\mathbf{Z}{s}^{T}\mathbf{Z}{t}\in\mathbb{R}^{d_{s}\times d_{t}}$ 分别表示自相关矩阵和互相关矩阵。由于学生网络与教师网络之间存在能力差距,这两个表征空间不存在完美的线性投影关系。投影器最终会收敛于一个近似投影,后文将证明该近似程度取决于所使用的归一化方法。
Whitened features: consider using self-supervised learning in conjunction with distillation whereby the student features are whitened to have perfect de correlation (Ermolov et al. 2020), or alternatively, they are batch normalised and sufficiently regular is ed with a feature de correlation term (Bardes, Ponce, and LeCun 2022a). In this setting, the fixed point solution for the weights will be symmetric and will capture the cross relationship between student and teacher features.
白化特征:考虑将自监督学习与蒸馏结合使用,使学生特征经过白化处理以实现完美的去相关 (Ermolov et al. 2020),或者对它们进行批量归一化并通过特征去相关项进行充分正则化 (Bardes, Ponce, and LeCun 2022a)。在此设置中,权重的固定点解将是对称的,并能捕捉学生和教师特征之间的交叉关系。
$$
\begin{array}{r}{\mathbf{C}{s t}-\mathbf{C}{s}\mathbf{W}{p}=0\mathrm{where}\mathbf{C}{s}=\mathbf{I}}\ {\rightarrow\mathbf{W}{p}=\mathbf{C}_{s t}\mathrm{\qquad~}}\end{array}
$$
Other normalisation schemes, such as those that jointly normalise the projected features and the teacher features, will have a much more involved analysis but will unlikely provide any additional insights on the dynamics of training itself. Thus, we propose to empirically explore the training trajectories of the projector weights singular values. This exploration will help quantify how the projector is mapping the student features to the teachers space. We cover this in the next section along with some additional insights into what is being learned and distilled.
其他归一化方案(例如同时对投影特征和教师特征进行归一化的方案)将涉及更复杂的分析,但不太可能为训练动态本身提供更多洞见。因此,我们建议通过实验探索投影器权重奇异值的训练轨迹。这种探索有助于量化投影器如何将学生特征映射到教师空间。我们将在下一节讨论这一点,并对所学和蒸馏的内容提供一些额外见解。
The choice of normalisation directly affects the training dynamics of $\mathbf{W}{p}$ . Equation 6 shows that the projector weights can encode relational information between the student and teacher’s features. This suggests redundancy in explicitly constructing and updating a large memory bank of previous representations (Tian, Krishnan, and Isola 2019). By considering a weight decay $\eta$ and a learning rate $\alpha_{p}$ , the update equation can be given as follows:
归一化方式的选择直接影响 $\mathbf{W}{p}$ 的训练动态。公式6表明,投影器权重能够编码学生与教师特征间的关联信息,这意味着显式构建和更新大型历史表征存储库存在冗余 (Tian, Krishnan and Isola 2019)。引入权重衰减 $\eta$ 和学习率 $\alpha_{p}$ 后,更新方程可表示为:
$$
\begin{array}{c}{\mathbf{W}{p}\rightarrow\mathbf{W}{p}+\alpha_{p}\dot{\mathbf{W}}{p}-\eta\mathbf{W}{p}}\ {=(1-\eta)\mathbf{W}{p}+\alpha_{p}\dot{\mathbf{W}}_{p}}\end{array}
$$
By setting $\eta=\alpha_{p}$ we can see that the projection layer will reduce to a moving average of relational features, which is very similar to the momentum encoder used by CRD (Tian, Krishnan, and Isola 2019). Other works suggest to extract relational information on-the-fly by constructing correlation or Gram matrices (Miles, Rodriguez, and Miko la jc zyk 2022; Peng et al. 2019). We show that this is also not necessary and more complex information can be captured through a simple linear projector. We also demonstrate that, in general, the use of a projector will scale much more favourably for larger batch sizes and feature dimensions. We also note that the handcrafted design of kernel functions (Joshi et al. 2021; He and Ozay 2022) may not generalise to real large scale datasets without significant hyper parameter tuning.
通过设定 $\eta=\alpha_{p}$ 可以看出,投影层将简化为关系特征的移动平均值,这与CRD (Tian, Krishnan和Isola 2019) 使用的动量编码器非常相似。其他研究建议通过构建相关性或Gram矩阵实时提取关系信息 (Miles, Rodriguez和Miko la jc zyk 2022; Peng等2019)。我们证明这也并非必要,更复杂的信息可以通过简单的线性投影器捕获。我们还表明,通常情况下,投影器的使用在更大批次规模和特征维度下具有更优的扩展性。同时我们注意到,手工设计的内核函数 (Joshi等2021; He和Ozay 2022) 若未经大量超参数调优,可能难以泛化到真实的大规模数据集。
From the results in table 1, we observe that when fixing all other settings, the choice of normalisation can significantly affect the student’s performance. To explore this in more detail, we consider the training trajectories of $\mathbf{W}_{p}$ under different normalisation schemes. We find that the choice of normalisation not only controls the training dynamics, but also the fixed point solution (see equation 6). We argue that the efficacy of distillation is dependent on how much relational information can be encoded in the learned weights and how much information is lost through the projection. To jointly evaluate these two properties we show the evolution of singular values of the projector weights during training. The results can be seen in figure 2 and show that the better performing normalisation methods (table 1) are shrinking far fewer singular values towards zero. This shrinkage can be described as collapsing the input along some dimension, which will induce some information loss and it is this information loss that degenerates the efficacy of the distillation process.
从表1的结果中我们观察到,当固定其他所有设置时,归一化方式的选择会显著影响学生模型的性能。为了更详细地探究这一点,我们分析了不同归一化方案下投影权重$\mathbf{W}_{p}$的训练轨迹。研究发现,归一化选择不仅控制着训练动态,还会影响定点解的性质(参见公式6)。我们认为蒸馏效果取决于学习权重能编码多少关系信息,以及投影过程中损失了多少信息。为了综合评估这两个特性,我们展示了训练过程中投影权重奇异值的演变情况。结果如图2所示,性能更优的归一化方法(表1)会使更少的奇异值收缩至零。这种收缩可视为沿某些维度坍缩输入信息,从而导致信息损失,而正是这种信息损失降低了蒸馏过程的有效性。
Table 1: Normalisation ablation for distillation across a range of architecture pairs on ImageNet-1K $20%$ subset.
| Teacher Student | RegNet MBv2 | ViT MBv3 | ConvNeXt EffNet-bo |
| Nodistillation | 50.89 | 54.13 | 64.48 |
| L2Norm | 52.91 | 54.65 | 64.23 |
| Group Norm | 55.63 | 59.08 | 65.52 |
| BatchNorm | 56.09 | 59.28 | 67.95 |
表 1: ImageNet-1K 20% 子集上不同架构对间蒸馏的归一化消融实验
| Teacher Student | RegNet MBv2 | ViT MBv3 | ConvNeXt EffNet-bo |
|---|---|---|---|
| No distillation | 50.89 | 54.13 | 64.48 |
| L2Norm | 52.91 | 54.65 | 64.23 |
| Group Norm | 55.63 | 59.08 | 65.52 |
| BatchNorm | 56.09 | 59.28 | 67.95 |
Larger projector networks learn to de correlate the input-output features. One natural extension of the previous observations is to use a larger projector network to encode more information relevant for the distillation loss. Unfortunately, we observe that a trivial expansion of the projection architecture does not necessarily improve the students performance. To explain this observation we evaluate a measure of de correlation between the input and output features of these projector networks. The results can be seen in figure 3 and we can see that the larger projectors learn to de correlate more and more features from the input. This de correlation can lead to the projector learning features that are not shared with the student backbone, which will subsequently diminish the effectiveness of distillation. These observations suggest that there is an inherent trade-off between the projector capacity and the efficacy of distillation. We note that the handcrafted design of the projector architecture is a motivated direction for further research (Chen et al. 2022b; Navaneet et al. 2021). However, in favour of simplicity, we choose to use a linear projector for all of our large scale evaluations.
较大的投影网络学会对输入-输出特征进行解相关。基于前述观察结果的自然延伸是使用更大的投影网络来编码与蒸馏损失相关的更多信息。但实验发现,简单扩大投影架构并不总能提升学生模型的性能。为解释该现象,我们评估了这些投影网络输入与输出特征间的解相关性。如图3所示,规模更大的投影网络会解耦越来越多的输入特征。这种解相关可能导致投影网络学习到与学生模型主干不共享的特征,从而削弱蒸馏效果。这些发现表明,投影网络容量与蒸馏效能之间存在固有权衡。我们注意到,投影网络架构的手工设计是值得深入研究的课题 (Chen et al. 2022b; Navaneet et al. 2021)。但出于简化考虑,在全部大规模评估中我们均采用线性投影器。
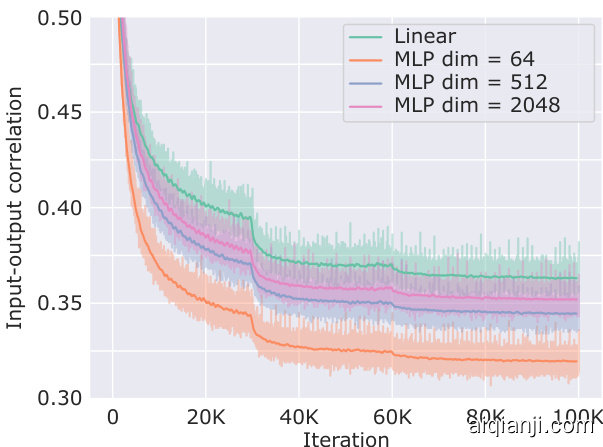
Figure 3: Correlation between input-output features using different projector architectures. All projectors considered will gradually de correlate the input-output features.
图 3: 不同投影器架构下的输入-输出特征相关性。所有被考察的投影器都会逐渐降低输入-输出特征间的相关性。
Table 2: LogSum ablation across various architecture pairs. Left: $20%$ subset. Right: Full ImageNet. The soft maximum function provides consistent improvement across both the $\mathrm{CNN{\rightarrow}C N N}$ and $\scriptstyle{\mathrm{ViT}}\to C{\mathrm{NN}}$ distillation settings.
| Teacher Student | ViT MBv3 | ConvNeXt EffNet-b0 | ResNet50 ResNet18 |
| wo/LogSum | 59.28 | 67.95 | 70.03 |
| w/ LogSum | 59.80 | 68.51 | 71.29 |
表 2: 不同架构组合间的LogSum消融实验。左: 20%数据子集。右: 完整ImageNet数据集。软最大值函数在CNN→CNN和ViT→CNN两种蒸馏设置中均带来稳定提升。
| 教师模型-学生模型 | ViT-MBv3 | ConvNeXt-EffNet-b0 | ResNet50-ResNet18 |
|---|---|---|---|
| 无LogSum | 59.28 | 67.95 | 70.03 |
| 有LogSum | 59.80 | 68.51 | 71.29 |
The soft maximum function can address distilling across a large capacity gap. When the capacity gap between the student and the teacher is large, representation distillation can become challenging. More specifically, the student network may have insufficient capacity to perfectly align these two spaces and in attempting to do so may degrade its downstream performance. To addresses this issue we explore the use of a soft maximum function which will soften the contribution of relatively close matches in a batch. In this way the loss can be adjusted to compensate for poorly aligned features which may arise when the capacity gap is large. The family of functions which share these properties can be more broadly defined through a property of their gradients. In favour of simplicity, we use the simple LogSum function throughout our experiments.
软最大值函数可以解决大容量差距下的蒸馏问题。当学生模型与教师模型之间的容量差距较大时,表征蒸馏会变得更具挑战性。具体而言,学生网络可能没有足够的能力完美对齐这两个空间,在尝试这样做的过程中可能会降低其下游性能。为解决这一问题,我们探索使用软最大值函数来软化批次中相对接近的匹配项的贡献。通过这种方式,可以调整损失以补偿容量差距较大时可能出现的特征对齐不良问题。具有这些特性的函数族可以通过其梯度属性更广泛地定义。为了简单起见,我们在所有实验中都使用了简单的LogSum函数。
$$
D(\mathbf{Z}{s},\mathbf{Z}{t};\mathbf{W}{p})=l o g\sum_{i}\lvert\mathbf{Z}{s}\mathbf{W}{p}-\mathbf{Z}{t}\rvert_{i}^{\alpha}
$$
where $\alpha$ is a smoothing factor. We also note that other functions, such as the $L o g S u m E x p$ , with a temperature parameter $\tau$ , have been used in SimCLR and CRD to a similar effect. Table 1 shows the importance of feature normalisation across a variety of student-teacher architecture pairs. Batch normalisation provides the most consistent improvement that even extends to the Transformer $\to\mathrm{CNN}$ setting. In table 2 we highlight the importance of the LogSum function, which is most effective in the large capacity gap settings, as evident from the $1%$ improvement for ${\tt R}50\rightarrow{\tt R}18$ . Table 3 provides an ablation of the importance of the $\alpha$ parameter, whereby we observe that the performance is relatively robust to a wide range of values, but consistently optimal in the range 4-5.
其中 $\alpha$ 是平滑因子。我们注意到其他函数(如带温度参数 $\tau$ 的 $LogSumExp$)在SimCLR和CRD中也产生了类似效果。表1展示了不同师生架构组合中特征归一化的重要性。批归一化带来了最稳定的改进,甚至适用于Transformer $\to\mathrm{CNN}$ 场景。表2强调了LogSum函数的重要性,该函数在大容量差距设置中效果最显著,这在 ${\tt R}50\rightarrow{\tt R}18$ 的 $1%$ 性能提升中得到印证。表3对 $\alpha$ 参数的重要性进行了消融实验,结果表明性能在较大取值范围内相对稳定,但在4-5区间始终保持最优。
Table 3: Ablating the importance of $\alpha$ . Distillation is generally robust for various values of $\alpha$ , but consistently optimal in range 4-5 across various architecture pairs.
| Teacher Student | ResNet50 ResNet18 | ConvNeXt EffNet-b0 |
| 1.0 | 61.74 | 65.52 |
| 2.0 | 62.23 | 66.61 |
| 3.0 | 63.10 | 67.72 |
| 4.0 | 63.32 | 68.51 |
| 5.0 | 63.40 | 67.69 |
表 3: 消融实验验证 $\alpha$ 的重要性。蒸馏方法在不同 $\alpha$ 值下普遍表现稳健,但在 4-5 的范围内对各种架构组合始终最优。
| Teacher Student | ResNet50 ResNet18 | ConvNeXt EffNet-b0 |
|---|---|---|
| 1.0 | 61.74 | 65.52 |
| 2.0 | 62.23 | 66.61 |
| 3.0 | 63.10 | 67.72 |
| 4.0 | 63.32 | 68.51 |
| 5.0 | 63.40 | 67.69 |
Benchmark Evaluation
基准评估
Implementation details. We follow the same training schedule as CRD (Tian, Krishnan, and Isola 2019) for both the CIFAR100 and ImageNet experiments. For the object detection, we use the same training schedule as ReviewKD (Chen et al. 2021a), while for the data efficient training we use the same as Co-Advice (Ren et al. 2022). All experiments were performed on a single NVIDIA RTX A5000. When using batch normalisation for the representations, we removed the affine parameters and set $\epsilon=0.0001$ . For all experiments we jointly train the student using a task loss $\mathcal{L}_{t a s k}$ and the feature distillation loss given in equation 11.
实现细节。对于CIFAR100和ImageNet实验,我们采用与CRD (Tian, Krishnan和Isola 2019)相同的训练计划。在目标检测任务中,我们使用与ReviewKD (Chen等 2021a)相同的训练方案,而在数据高效训练方面则沿用Co-Advice (Ren等 2022)的配置。所有实验均在单张NVIDIA RTX A5000显卡上完成。当对表征使用批量归一化时,我们移除了仿射参数并设置$\epsilon=0.0001$。所有实验都通过联合优化任务损失$\mathcal{L}_{task}$和公式11给出的特征蒸馏损失来训练学生模型。
$$
\mathcal{L}=\mathcal{L}{t a s k}+D(\mathbf{Z}{s},\mathbf{Z}{t};\mathbf{W}_{p})
$$
Data Efficient Training for Transformers
Transformer的高效数据训练
Transformers h
