GAN-BERT: Generative Adversarial Learning for Robust Text Classification with a Bunch of Labeled Examples
GAN-BERT:基于生成对抗学习的鲁棒文本分类方法(仅需少量标注样本)
Abstract
摘要
Recent Transformer-based architectures, e.g., BERT, provide impressive results in many Natural Language Processing tasks. However, most of the adopted benchmarks are made of (sometimes hundreds of) thousands of examples. In many real scenarios, obtaining highquality annotated data is expensive and timeconsuming; in contrast, unlabeled examples characterizing the target task can be, in general, easily collected. One promising method to enable semi-supervised learning has been proposed in image processing, based on SemiSupervised Generative Adversarial Networks. In this paper, we propose GAN-BERT that extends the fine-tuning of BERT-like architectures with unlabeled data in a generative adversarial setting. Experimental results show that the requirement for annotated examples can be drastically reduced (up to only 50-100 annotated examples), still obtaining good performances in several sentence classification tasks.
基于Transformer的最新架构(如BERT)在众多自然语言处理任务中展现出卓越性能。然而现有基准测试大多依赖(有时多达数十万)标注样本。实际场景中,获取高质量标注数据往往成本高昂且耗时,而目标任务的未标注数据通常易于收集。半监督生成对抗网络已在图像处理领域展现出解决这一问题的潜力。本文提出GAN-BERT,通过在生成对抗框架中结合未标注数据来扩展类BERT架构的微调方法。实验表明,该方法在多个句子分类任务中仅需极少量标注样本(50-100个)即可保持优异性能。
1 Introduction
1 引言
In recent years, Deep Learning methods have become very popular in Natural Language Processing (NLP), e.g., they reach high performances by relying on very simple input representations (for example, in (Kim, 2014; Goldberg, 2016; Kim et al., 2016)). In particular, Transformer-based architectures, e.g., BERT (Devlin et al., 2019), provide representations of their inputs as a result of a pre-training stage. These are, in fact, trained over large scale corpora and then effectively finetuned over a targeted task achieving state-of-the-art results in different and heterogeneous NLP tasks. These achievements are obtained when thousands of annotated examples exist for the final tasks. As experimented in this work, the quality of BERT fine-tuned over less than 200 annotated instances shows significant drops, especially in classification tasks involving many categories. Unfortunately, obtaining annotated data is a time-consuming and costly process. A viable solution is adopting semisupervised methods, such as in (Weston et al., 2008; Chapelle et al., 2010; Yang et al., 2016; Kipf and Welling, 2016) to improve the generalization capability when few annotated data is available, while the acquisition of unlabeled sources is possible.
近年来,深度学习(Deep Learning)方法在自然语言处理(NLP)领域变得非常流行,例如,它们通过依赖非常简单的输入表示就能达到高性能(如(Kim, 2014; Goldberg, 2016; Kim et al., 2016))。特别是基于Transformer的架构,如BERT(Devlin et al., 2019),通过预训练阶段生成输入表示。这些模型实际上是在大规模语料库上进行训练,然后针对特定任务进行有效微调,在各种异构NLP任务中取得最先进的结果。这些成就是在最终任务存在数千个标注样本的情况下获得的。正如本实验所示,在少于200个标注实例上微调的BERT质量会出现显著下降,尤其是在涉及多类别的分类任务中。遗憾的是,获取标注数据是一个耗时且昂贵的过程。一个可行的解决方案是采用半监督方法(如(Weston et al., 2008; Chapelle et al., 2010; Yang et al., 2016; Kipf and Welling, 2016)),在标注数据较少但可以获取未标注数据源的情况下提高泛化能力。
One effective semi-supervised method is implemented within Semi-Supervised Generative Adversarial Networks (SS-GANs). Usually, in GANs (Goodfellow et al., 2014) a “generator” is trained to produce samples resembling some data distribution. This training process “adversarial ly” depends on a “disc rim in at or”, which is instead trained to distinguish samples of the generator from the real instances. SS-GANs (Salimans et al., 2016) are an extension to GANs where the disc rim in at or also assigns a category to each example while discriminating whether it was automatically generated or not.
一种有效的半监督方法是在半监督生成对抗网络 (SS-GANs) 中实现的。通常,在 GANs (Goodfellow et al., 2014) 中,"生成器"被训练用于生成与某些数据分布相似的样本。这一训练过程"对抗性"依赖于一个"判别器",后者则被训练用于区分生成器的样本与真实实例。SS-GANs (Salimans et al., 2016) 是 GANs 的扩展,其中判别器在判断样本是否为自动生成的同时,还会为每个样本分配一个类别。
In SS-GANs, the labeled material is thus used to train the disc rim in at or, while the unlabeled examples (as well as the ones automatically generated) improve its inner representations. In image processing, SS-GANs have been shown to be effective: exposed to few dozens of labeled examples (but thousands of unlabeled ones), they obtain performances competitive with fully supervised settings.
在SS-GAN中,标注数据用于训练判别器 (discriminator),而未标注样本(以及自动生成的样本)则用于提升其内部表征。在图像处理领域,SS-GAN已被证明具有显著效果:仅需接触数十个标注样本(但配合数千个未标注样本),其性能便可媲美全监督场景下的模型表现。
In this paper, we extend the BERT training with unlabeled data in a generative adversarial setting. In particular, we enrich the BERT fine-tuning process with an SS-GAN perspective, in the so-called GAN-BERT1 model. That is, a generator produces “fake” examples resembling the data distribution, while BERT is used as a disc rim in at or. In this way, we exploit both the capability of BERT to produce high-quality representations of input texts and to adopt unlabeled material to help the network in generalizing its representations for the final tasks. At the best of our knowledge, using SS-GANs in NLP has been investigated only by (Croce et al., 2019) with the so-called Kernel-based GAN. In that work, authors extend a Kernel-based Deep Architecture (KDA, (Croce et al., 2017)) with an SS-GAN perspective. Sentences are projected into low-dimensional embeddings, which approximate the implicit space generated by using a Semantic Tree Kernel function. However, it only marginally investigated how the GAN perspective could extend deep architecture for NLP tasks. In particular, a KGAN operates in a pre-computed embedding space by approximating a kernel function (Annesi et al., 2014). While the SS-GAN improves the quality of the Multi-layered Perceptron used in the KDA, it does not affect the input representation space, which is statically derived by the kernel space approximation. In the present work, all the parameters of the network are instead considered during the training process, in line with the SSGAN approaches.
本文提出了一种在生成对抗环境下利用无标注数据扩展BERT训练的方法。具体而言,我们在BERT微调过程中引入SS-GAN框架,构建了名为GAN-BERT1的模型。该模型通过生成器合成符合数据分布的"伪"样本,同时将BERT作为判别器使用。这种方法既发挥了BERT生成高质量文本表征的能力,又能利用无标注数据帮助网络泛化最终任务的表征能力。据我们所知,NLP领域仅有(Croce et al., 2019)通过基于核的GAN(Kernel-based GAN)探索过SS-GAN的应用。该研究在基于核的深度架构(KDA,(Croce et al., 2017))中引入SS-GAN视角,将句子投影到低维嵌入空间来近似语义树核函数生成的隐空间。但其对GAN如何扩展NLP深度架构的探索较为有限:KGAN通过近似核函数在预计算的嵌入空间中操作(Annesi et al., 2014),虽然SS-GAN提升了KDA中多层感知机的性能,但并未改变由核空间近似静态生成的输入表征空间。本研究则遵循SSGAN范式,在训练过程中优化网络全部参数。
We empirically demonstrate that the SS-GAN schema applied over BERT, i.e., GAN-BERT, reduces the requirement for annotated examples: even with less than 200 annotated examples it is possible to obtain results comparable with a fully supervised setting. In any case, the adopted semisupervised schema always improves the result obtained by BERT.
我们通过实验证明,基于BERT应用SS-GAN框架(即GAN-BERT)能降低对标注数据的需求:即使使用少于200个标注样本,仍可获得与全监督设置相当的结果。无论何种情况,采用的半监督框架始终能提升BERT的表现。
In the rest of this paper, section 2 provides an introduction to SS-GANs. In sections 3 and 4, GAN-BERT and the experimental evaluations are presented. In section 5 conclusions are derived.
在本文的其余部分中,第2节介绍了SS-GANs。第3节和第4节分别介绍了GAN-BERT和实验评估。第5节得出了结论。
2 Semi-supervised GANs
2 半监督生成对抗网络 (Semi-supervised GANs)
SS-GANs (Salimans et al., 2016) enable semi- supervised learning in a GAN framework. A discriminator is trained over a $(k+1)$ -class objective: “true” examples are classified in one of the target $(1,...,k)$ classes, while the generated samples are classified into the $k+1$ class.
SS-GANs (Salimans et al., 2016) 实现了GAN框架中的半监督学习。判别器通过一个 $(k+1)$ 类目标进行训练:真实样本被分类到目标 $(1,...,k)$ 类别之一,而生成的样本则被归类到第 $k+1$ 类。
More formally, let $\mathcal{D}$ and $\mathcal{G}$ denote the discriminator and generator, and $p_{d}$ and $p\boldsymbol{\mathscr{G}}$ denote the real data distribution and the generated examples, respectively. In order to train a semi-supervised $k$ -class classifier, the objective of $\mathcal{D}$ is extended as follows. Let us define $p_{m}(\hat{y}=y|x,y=k+1)$ the probability provided by the model $m$ that a generic example $x$ is associated with the fake class and $p_{m}(\hat{y}=y|x,y\in(1,...,k))$ that $x$ is considered real, thus belonging to one of the target classes. The loss function of $\mathcal{D}$ is defined as: LD = LDsup. + LDunsup. where:
更正式地说,令 $\mathcal{D}$ 和 $\mathcal{G}$ 分别表示判别器 (discriminator) 和生成器 (generator),$p_{d}$ 和 $p\boldsymbol{\mathscr{G}}$ 分别表示真实数据分布和生成样本分布。为了训练一个半监督的 $k$ 类分类器,$\mathcal{D}$ 的目标被扩展如下:定义 $p_{m}(\hat{y}=y|x,y=k+1)$ 为模型 $m$ 将样本 $x$ 判定为伪造类别的概率,$p_{m}(\hat{y}=y|x,y\in(1,...,k))$ 为 $x$ 被判定为真实样本(即属于某个目标类别)的概率。判别器 $\mathcal{D}$ 的损失函数定义为:LD = LDsup. + LDunsup. 其中:
$$
\begin{array}{c}{L_{\mathcal{D}_ {\mathrm{sup.}}=-\mathbb{E}_ {x,y\sim p_{d}}}\mathrm{log}\left[p_{\mathrm{m}}(\hat{y}=y|x,y\in(1,...,k))\right]}\ {L_{\mathcal{D}_{\mathrm{unsup.}}=-\mathbb{E}_{x\sim p_{d}}}\mathrm{log}\left[1-p_{\mathrm{m}}\left(\hat{y}=y|x,y=k+1\right)\right]}\ {-\mathbb{E}_ {x\sim\mathcal{G}}\mathrm{log}\left[p_{\mathrm{m}}(\hat{y}=y|x,y=k+1)\right]}\end{array}
$$
$$
\begin{array}{c}{L_{\mathcal{D}_ {\mathrm{sup.}}=-\mathbb{E}_ {x,y\sim p_{d}}}\mathrm{log}\left[p_{\mathrm{m}}(\hat{y}=y|x,y\in(1,...,k))\right]}\ {L_{\mathcal{D}_ {\mathrm{unsup.}}=-\mathbb{E}_ {x\sim p_{d}}}\mathrm{log}\left[1-p_{\mathrm{m}}\left(\hat{y}=y|x,y=k+1\right)\right]}\ {-\mathbb{E}_ {x\sim\mathcal{G}}\mathrm{log}\left[p_{\mathrm{m}}(\hat{y}=y|x,y=k+1)\right]}\end{array}
$$
$L_{\mathcal{D}_ {\mathrm{sup.}}}$ measures the error in assigning the wrong class to a real example among the original $k$ categories. $L_{D_{\mathrm{unsup}}}$ . measures the error in incorrectly recognizing a real (unlabeled) example as fake and not recognizing a fake example.
$L_{\mathcal{D}_ {\mathrm{sup.}}}$ 衡量在原始 $k$ 个类别中为真实样本分配错误类别的误差。$L_{D_{\mathrm{unsup}}}$ 衡量将真实(未标注)样本误判为伪造样本,以及未能识别伪造样本的误差。
At the same time, $\mathcal{G}$ is expected to generate examples that are similar to the ones sampled from the real distribution $p_{d}$ . As suggested in (Salimans et al., 2016), $\mathcal{G}$ should generate data approximating the statistics of real data as much as possible. In other words, the average example generated in a batch by $\mathcal{G}$ should be similar to the real prototypical one. Formally, let’s $f(x)$ denote the activation on an intermediate layer of $\mathcal{D}$ . The feature matching loss of $\mathcal{G}$ is then defined as:
同时,$\mathcal{G}$ 需要生成与从真实分布 $p_{d}$ 中采样的样本相似的示例。如 (Salimans et al., 2016) 所述,$\mathcal{G}$ 应尽可能生成接近真实数据统计特性的数据。换言之,$\mathcal{G}$ 在批次中生成的平均样本应与真实原型样本相似。形式上,设 $f(x)$ 表示 $\mathcal{D}$ 中间层的激活值,则 $\mathcal{G}$ 的特征匹配损失定义为:
$$
L_{G_{\mathrm{featurematching}}=\left|\left|\mathbb{E}_ {x}\sim p_{d}f(x)-\mathbb{E}_ {x}\sim\varsigma f(x)\right|\right|_{2}^{2}}
$$
$$
L_{G_{\mathrm{featurematching}}=\left|\left|\mathbb{E}_ {x}\sim p_{d}f(x)-\mathbb{E}_ {x}\sim\varsigma f(x)\right|\right|_{2}^{2}}
$$
that is, the generator should produce examples whose intermediate representations provided in input to $\mathcal{D}$ are very similar to the real ones. The $\mathcal{G}$ loss also considers the error induced by fake examples correctly identified by $\mathcal{D}$ , i.e.,
即生成器应产生这样的示例:其提供给判别器 $\mathcal{D}$ 的中间表示与真实样本高度相似。生成器 $\mathcal{G}$ 的损失还包含被 $\mathcal{D}$ 正确识别的伪造样本所导致的误差,也就是说,
$$
L_{{\mathcal{G}}_ {u n s u p.}}{=}{-}\mathbb{E}_ {x\sim{\mathcal{G}}}\log[1-p_{m}({\hat{y}}=y|x,y=k+1)]
$$
$$
L_{{\mathcal{G}}_ {u n s u p.}}{=}{-}\mathbb{E}_ {x\sim{\mathcal{G}}}\log[1-p_{m}({\hat{y}}=y|x,y=k+1)]
$$
The G loss is LG = LGfeature matching $L_{\mathcal{G}}=L_{\mathcal{G}_ {\mathrm{featurematching}}}+L_{\mathcal{G}_{u n s u p.}}$ .
G损失为LG = LG特征匹配 $L_{\mathcal{G}}=L_{\mathcal{G}_ {\mathrm{featurematching}}}+L_{\mathcal{G}_{u n s u p.}}$ 。
While SS-GANs are usually used with image inputs, we will show that they can be adopted in combination with BERT (Devlin et al., 2019) over inputs encoding linguistic information.
虽然SS-GAN通常用于图像输入,但我们将展示它们可以与BERT (Devlin et al., 2019)结合使用,处理编码语言信息的输入。
3 GAN-BERT: Semi-supervised BERT with Adversarial Learning
3 GAN-BERT: 基于对抗学习的半监督BERT
Bidirectional Encoder Representations from Transformers (BERT) (Devlin et al., 2019) belongs to the family of the so-called transfer learning methods, where a model is first pre-trained on general tasks and then fine-tuned on the final target tasks. In Computer Vision, transfer learning has been shown beneficial in many different tasks, i.e., pre-training a neural network model on a known task, followed by a fine-tuning stage on a (different) target task (see, for example, (Girshick et al., 2013)). BERT is a very deep model that is pre-trained over large corpora of raw texts and then is fine-tuned on target annotated data. The building block of BERT is the Transformer (Vaswani et al., 2017), an attentionbased mechanism that learns contextual relations between words (or sub-words, i.e., word pieces, (Schuster and Nakajima, 2012)) in a text.
基于Transformer的双向编码器表征 (BERT) (Devlin et al., 2019) 属于迁移学习方法家族,这类方法首先在通用任务上对模型进行预训练,然后在最终目标任务上进行微调。在计算机视觉领域,迁移学习已被证明对许多不同任务有益,即在已知任务上预训练神经网络模型,然后在(不同的)目标任务上进行微调阶段 (例如参见 (Girshick et al., 2013))。BERT是一个非常深的模型,它在大型原始文本语料库上进行预训练,然后在目标标注数据上进行微调。BERT的基本构建模块是Transformer (Vaswani et al., 2017),这是一种基于注意力的机制,用于学习文本中单词(或子词,即word pieces, (Schuster and Nakajima, 2012))之间的上下文关系。
BERT provides contextual i zed embeddings of the words composing a sentence as well as a sentence embedding capturing sentence-level semantics: the pre-training of BERT is designed to capture such information by relying on very large corpora. After the pre-training, BERT allows encoding (i) the words of a sentence, (ii) the entire sentence, and (iii) sentence pairs in dedicated embeddings. These can be used in input to further layers to solve sentence classification, sequence labeling or relational learning tasks: this is achieved by adding task-specific layers and by fine-tuning the entire architecture on annotated data.
BERT能够为句子中的单词提供上下文嵌入,同时也能捕捉句子层面的语义信息:其预训练过程依赖大规模语料库来捕获此类信息。预训练完成后,BERT可以对(i)句子中的单词、(ii)整句以及(iii)句子对进行专用嵌入编码。这些嵌入可作为后续层的输入,用于解决句子分类、序列标注或关系学习等任务:具体实现方式是通过添加任务特定层,并在标注数据上对整个架构进行微调。
In this work, we extend BERT by using SSGANs for the fine-tuning stage. We take an already pre-trained BERT model and adapt the fine-tuning by adding two components: i) task-specific layers, as in the usual BERT fine-tuning; ii) SS-GAN layers to enable semi-supervised learning. Without loss of generality, let us assume we are facing a sentence classification task over $k$ categories. Given an input sentence $s=(t_{1},...,t_{n})$ BERT produces in output $n+2$ vector representations in $R^{d}$ , i.e., $(h_{C L S},h_{t_{1}},...,h_{t_{n}},h_{S E P})$ . As suggested in (Devlin et al., 2019), we adopt the $h_{C L S}$ representation as a sentence embedding for the target tasks.
在本工作中,我们通过使用SSGANs对BERT进行微调阶段的扩展。我们采用一个已预训练的BERT模型,并通过添加两个组件来调整微调过程:i) 任务特定层,与常规BERT微调相同;ii) SS-GAN层以实现半监督学习。不失一般性,假设我们面临一个包含$k$个类别的句子分类任务。给定输入句子$s=(t_{1},...,t_{n})$,BERT会输出$n+2$个在$R^{d}$中的向量表示,即$(h_{C L S},h_{t_{1}},...,h_{t_{n}},h_{S E P})$。如(Devlin et al., 2019)所建议,我们采用$h_{C L S}$表示作为目标任务的句子嵌入。
As shown in figure 1, we add on top of BERT the SS-GAN architecture by introducing i) a discriminator $\mathcal{D}$ for classifying examples, and ii) a generator $\mathcal{G}$ acting adversarial ly. In particular, $\mathcal{G}$ is a Multi Layer Perceptron (MLP) that takes in input a 100-dimensional noise vector drawn from $N(\mu,\sigma^{2})$ and produces in output a vector $h_{f a k e}\in R^{d}$ . The disc rim in at or is another MLP that receives in input a vector $h_{ * }\in R^{d}$ ; $h_{*}$ can be either $\boldsymbol{h}_ {f a k e}$ produced by the generator or $h_{C L S}$ for unlabeled or labeled examples from the real distribution. The last layer of $\mathcal{D}$ is a softmax-activated layer, whose output is a $k+1$ vector of logits, as discussed in section 2.
如图 1 所示,我们在 BERT 基础上引入 SS-GAN 架构:i) 添加用于样本分类的判别器 $\mathcal{D}$,ii) 加入对抗操作的生成器 $\mathcal{G}$。具体而言,$\mathcal{G}$ 是一个多层感知机 (MLP),其输入为从 $N(\mu,\sigma^{2})$ 采样的 100 维噪声向量,输出为向量 $h_{f a k e}\in R^{d}$。判别器是另一个 MLP,其输入向量 $h_{*}\in R^{d}$ 可以是生成器产生的 $\boldsymbol{h}_ {f a k e}$,也可以是来自真实分布的未标注/已标注样本的 $h_{C L S}$。如第 2 节所述,$\mathcal{D}$ 的最后一层是 softmax 激活层,输出为 $k+1$ 维 logits 向量。
During the forward step, when real instances are sampled (i.e., $h_{ * }=h_{C L S},$ ), $\mathcal{D}$ should classify them in one of the $k$ categories; when $\begin{array}{r}{h_{*}=h_{f a k e}}\end{array}$ , it should classify each example in the $k+1$ category. As discussed in section 2, the training process tries to optimize two competing losses, i.e., $L_{D}$ and $L_{G}$ .
在前向步骤中,当采样到真实实例时(即 $h_{ * }=h_{C L S},$ ),$\mathcal{D}$ 应将其分类到 $k$ 个类别之一;当 $\begin{array}{r}{h_{*}=h_{f a k e}}\end{array}$ 时,则应将其分类到第 $k+1$ 个类别。如第2节所述,训练过程需要优化两个相互竞争的损失函数,即 $L_{D}$ 和 $L_{G}$。
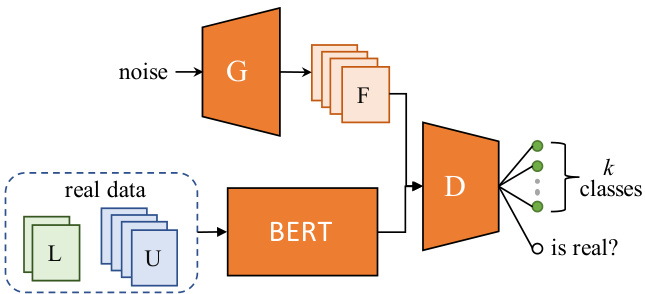
Figure 1: GAN-BERT architecture: $\mathcal{G}$ generates a set of fake examples F given a random distribution. These, along with unlabeled U and labeled $\mathrm{L}$ vector representations computed by BERT are used as input for the disc rim in at or $\mathcal{D}$ .
图 1: GAN-BERT架构:给定随机分布,$\mathcal{G}$生成一组伪样本F。这些伪样本与未标记数据U和已标记数据$\mathrm{L}$的BERT向量表示共同作为判别器$\mathcal{D}$的输入。
During back-propagation, the unlabeled examples contribute only to $L_{D_{u n s u p.}}$ , i.e., they are considered in the loss computation only if they are erroneously classified into the $k+1$ category. In all other cases, their contribution to the loss is masked out. The labeled examples thus contribute to the supervised loss $L_{D_{s u p.}}$ . Finally, the examples generated by $\mathcal{G}$ contribute to both $L_{D}$ and $L_{G}$ , i.e., $\mathcal{D}$ is penalized when not finding examples generated by $\mathcal{G}$ and vice-versa. When updating $\mathcal{D}$ , we also change the BERT weights in order to fine-tune its inner representations, so considering both the labeled and the unlabeled data2.
在反向传播过程中,未标注样本仅对 $L_{D_{u n s u p.}}$ 产生贡献,即只有当它们被错误分类至 $k+1$ 类别时才会参与损失计算。其余情况下,这些样本对损失的贡献会被屏蔽。标注样本则作用于监督损失 $L_{D_{s u p.}}$。最终,由 $\mathcal{G}$ 生成的样本会同时影响 $L_{D}$ 和 $L_{G}$,即当 $\mathcal{D}$ 未能识别 $\mathcal{G}$ 生成的样本时会受到惩罚,反之亦然。更新 $\mathcal{D}$ 时,我们也会调整 BERT 权重以微调其内部表征,从而同时利用标注和未标注数据[2]。
After training, $\mathcal{G}$ is discarded while retaining the rest of the original BERT model for inference. This means that there is no additional cost at inference time with respect to the standard BERT model. In the following, we will refer to this architecture as GAN-BERT.
训练完成后,$\mathcal{G}$ 被丢弃,同时保留原始 BERT 模型的其余部分用于推理。这意味着在推理时相对于标准 BERT 模型不会产生额外成本。在下文中,我们将此架构称为 GAN-BERT。
4 Experimental Results
4 实验结果
In this section, we assess the impact of GAN-BERT over sentence classification tasks characterized by different training conditions, i.e., number of examples and number of categories. We report measures of our approach to support the development of deep learning models when exposed to few labeled examples over the following tasks: Topic Classification over the 20 News Group (20N) dataset (Lang, 1995), Question Classification (QC) on the UIUC dataset (Li and Roth, 2006), Sentiment Analysis over the $S S\mathbb{T}-5$ dataset (Socher et al., 2013). We will also report the performances over a sentence pair task, i.e., over the MNLI dataset (Williams et al., 2018). For each task, we report the performances with the metric commonly used for that specific dataset, i.e., accuracy for $S S\mathbb{T}-5$ and QC, while F1 is used for 20N and MNLI datasets. As a comparison, we report the performances of the BERT-base model fine-tuned as described in (Devlin et al., 2019) on the available training material. We used BERT-base as the starting point also for the training of our approach. GAN-BERT is implemented in Tensorflow by extending the original BERT implementation 3.
在本节中,我们评估了GAN-BERT在不同训练条件(即样本数量和类别数量)下的句子分类任务中的表现。我们通过以下任务报告了该方法在少标签样本场景下对深度学习模型开发的支持效果:基于20 News Group (20N)数据集的主题分类(Lang, 1995)、UIUC数据集的问题分类(QC)(Li and Roth, 2006)、$S S\mathbb{T}-5$数据集的情感分析(Socher et al., 2013)。同时我们还报告了在句子对任务(即MNLI数据集(Williams et al., 2018))上的性能表现。针对每个任务,我们采用该数据集常用评估指标:$S S\mathbb{T}-5$和QC使用准确率,20N和MNLI使用F1值。作为对比,我们展示了BERT-base模型(Devlin et al., 2019)在相同训练数据上的微调结果。我们的方法同样以BERT-base为初始模型进行训练,GAN-BERT通过扩展原始BERT实现3在Tensorflow中完成部署。
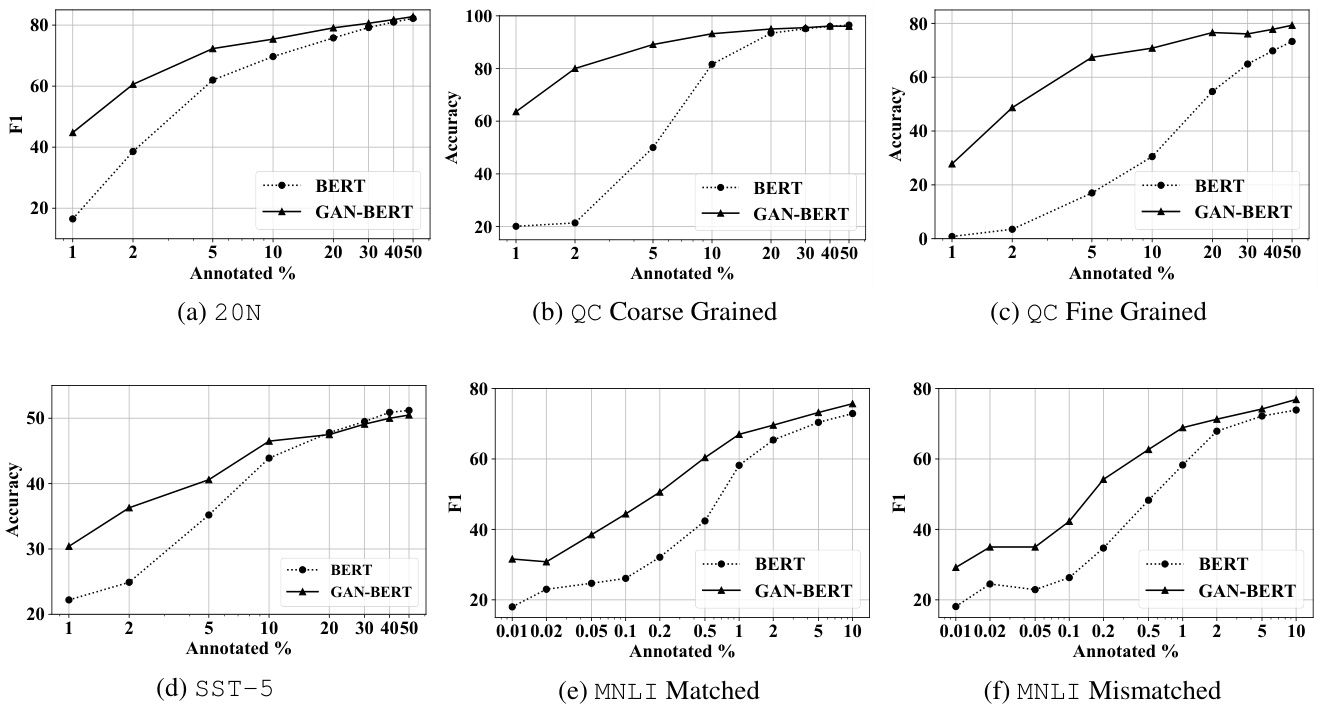
Figure 2: Learning curves for the six tasks. We run all the models for 3 epochs except for $_ {20\mathrm{N}}$ (15 epochs). The sequence length we used is: 64 for QC coarse, QC fine, and $S S\mathbb{T}-5$ ; 128 for both MNLI settings; 256 for $_{20\mathrm{N}}$ . Learning rate was set for all to 2e-5, except for $20\mathrm{N}$ (5e-6).
图 2: 六个任务的学习曲线。除 $_ {20\mathrm{N}}$ (15个周期) 外,所有模型均运行3个周期。使用的序列长度为:QC coarse、QC fine和 $S S\mathbb{T}-5$ 为64;两种MNLI设置为128;$_{20\mathrm{N}}$ 为256。除 $20\mathrm{N}$ (5e-6) 外,所有任务的学习率均设为2e-5。
In more detail, $\mathcal{G}$ i
