Investigating the Effects of Sparse Attention on Cross-Encoders
探究稀疏注意力对交叉编码器的影响
Ferdinand Schlatt, Maik Frobe, and Matthias Hagen
Ferdinand Schlatt, Maik Frobe, Matthias Hagen
Friedrich-Schiller-Universit t Jena
弗里德里希·席勒大学耶拿
Abstract Cross-encoders are effective passage and document re-rankers but less efficient than other neural or classic retrieval models. A few previous studies have applied windowed self-attention to make crossencoders more efficient. However, these studies did not investigate the potential and limits of different attention patterns or window sizes. We close this gap and systematically analyze how token interactions can be reduced without harming the re-ranking effectiveness. Experimenting with asymmetric attention and different window sizes, we find that the query tokens do not need to attend to the passage or document tokens for effective re-ranking and that very small window sizes suffice. In our experiments, even windows of 4 tokens still yield effectiveness on par with previous cross-encoders while reducing the memory requirements by at least $22%\mathrm{/}59%$ and being $1%%43%$ faster at inference time for passages / documents. Our code is publicly available.1
摘要
交叉编码器(Cross-encoder)是高效的段落和文档重排序器,但效率低于其他神经或经典检索模型。先前少数研究尝试通过窗口自注意力机制提升交叉编码器效率,但未深入探究不同注意力模式与窗口尺寸的潜力边界。本研究填补这一空白,系统分析如何在保持重排序效果的前提下减少token交互。通过非对称注意力与多窗口尺寸实验,我们发现:查询token无需关注文档token即可实现有效重排序,且极小窗口尺寸已足够。实验表明,仅4个token的窗口仍能保持与传统交叉编码器相当的效果,同时内存需求降低22%~59%,段落/文档推理速度提升1%~43%。代码已开源。
Keywords: Cross-encoder $\cdot$ Re-ranking $\cdot$ Windowed attention $\cdot$ Cross-attention
关键词:交叉编码器 (Cross-encoder) $\cdot$ 重排序 (Re-ranking) $\cdot$ 窗口注意力 (Windowed attention) $\cdot$ 交叉注意力 (Cross-attention)
1 Introduction
1 引言
Pre-trained transformer-based language models (PLMs) are important components of modern retrieval and re-ranking pipelines as they help to mitigate the vocabulary mismatch problem of lexical systems [61, 84]. Especially cross-encoders are effective [52, 55, 57, 81] but less efficient than bi-encoders or other classic machine learning-based approaches with respect to inference run time, memory footprint, and energy consumption [68]. The run time issue is particularly problematic for practical applications as searchers often expect results after a few hundred milliseconds [2]. To increase the efficiency but maintain the effectiveness of cross-encoders, previous studies have, for instance, investigated reducing the number of token interactions by applying sparse attention patterns [44, 70].
基于Transformer的预训练语言模型(PLM)是现代检索与重排序流程的关键组成部分,它们能有效缓解词法系统的词汇不匹配问题[61, 84]。特别是交叉编码器(cross-encoder)展现出卓越效果[52, 55, 57, 81],但在推理耗时、内存占用和能耗方面,其效率低于双编码器(bi-encoder)或其他经典机器学习方法[68]。对于实际应用场景,运行时间问题尤为突出,因为用户通常期望在几百毫秒内获得结果[2]。为提升交叉编码器效率同时保持其效果,先前研究探索了多种方案,例如通过应用稀疏注意力模式来减少token交互次数[44, 70]。
Sparse attention PLMs restrict the attention of most tokens to local windows, thereby reducing token interactions and improving efficiency [72]. Which tokens have local attention is a task-specific decision. For instance, cross-encoders using the Longformer model [3] apply normal global attention to query tokens but local attention to document tokens. The underlying idea is that a document token does not require the context of the entire document to determine whether it is relevant to a query—within a document, most token interactions are unnecessary, and a smaller context window suffices (cf. Figure 1 (b) for a visualization).
稀疏注意力预训练语言模型(PLM)通过将大多数token的注意力限制在局部窗口内,从而减少token交互并提升效率[72]。哪些token采用局部注意力是任务相关的决策。例如,使用Longformer模型[3]的交叉编码器对查询token采用常规全局注意力,而对文档token采用局部注意力。其核心思想是:文档token不需要整个文档的上下文来判断其与查询的相关性——在文档内部,大多数token交互是不必要的,较小的上下文窗口就已足够(可视化效果参见图1(b))。
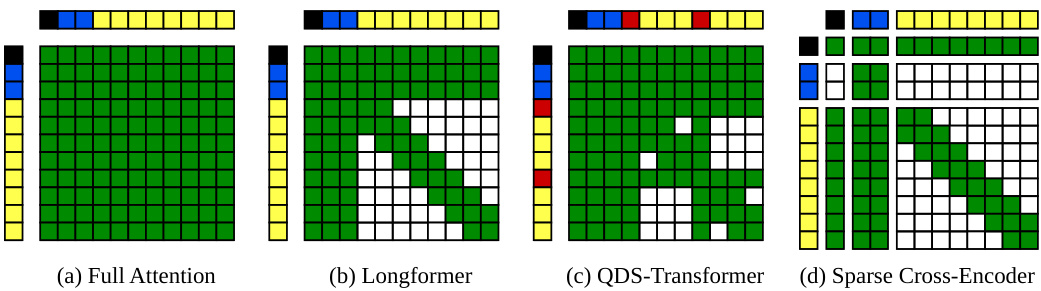
Figure 1: Previous cross-encoder attention patterns (a, b, and c) and our newly proposed sparse cross-encoder (d). The marginal boxes denote input tokens (black: [CLS], blue: query, yellow: passage / document, red: start of sentence). The inner green boxes indicate token attention. Our new pattern considers the sub-sequences separately (indicated by the added spacing) and is asymmetric.
图 1: 传统交叉编码器注意力模式 (a、b、c) 与我们新提出的稀疏交叉编码器 (d)。外框表示输入token (黑色: [CLS], 蓝色: 查询语句, 黄色: 段落/文档, 红色: 句子起始符)。内部绿色框表示token注意力机制。我们的新范式采用非对称设计,并对子序列进行分离处理 (通过间距示意)。
Previously, sparse attention has been applied to cross-encoders to be able to re-rank long documents without cropping or splitting them [44, 70]. However, the impact of sparsity on effectiveness has not been investigated in detail. To close this gap, we explore the limits of sparse cross-encoders and try to clarify which token interactions are (un)necessary. As mechanisms to reduce token interactions, we investigate local attention window sizes and disabling attention between sub-sequences (e.g., between the query and the passage or document). Our analyses are based on the following two assumptions.
此前,稀疏注意力 (sparse attention) 已被应用于交叉编码器 (cross-encoders) ,使其能够在不截断或分割的情况下对长文档进行重排序 [44, 70] 。然而,稀疏性对效果的影响尚未得到详细研究。为填补这一空白,我们探索了稀疏交叉编码器的极限,并试图厘清哪些 token 交互是(非)必要的。作为减少 token 交互的机制,我们研究了局部注意力窗口大小以及禁用子序列间(例如查询与段落或文档之间)的注意力。我们的分析基于以下两个假设。
(1) Cross-encoders create contextual i zed embeddings that encode query and passage or document semantics. We hypothesize that the contextual i zed embeddings of passage or document tokens do not actually need to encode fine-grained semantics. Rather, an overall “gist” in the form of small local context windows is sufficient to estimate relevance well.
(1) 交叉编码器 (Cross-encoders) 会生成上下文嵌入,用于编码查询与段落或文档的语义。我们假设段落或文档 token 的上下文嵌入实际上无需编码细粒度语义,仅需通过小型局部上下文窗口形成的整体"主旨"即可有效估算相关性。
(2) Cross-encoders allow queries and documents to exchange information via symmetric attention. We hypothesize that full symmetry is unnecessary as we view the query–document relevance relationship as asymmetric: for ranking, it should suffice to determine whether a result is relevant to a query, not vice versa. To further reduce token interactions, we propose a novel configurable asymmetric cross-attention pattern with varying amounts of interaction between [CLS], query, and passage or document tokens (cf. Figure $1(\mathrm{d})$ ).
(2) 交叉编码器 (cross-encoders) 允许查询和文档通过对称注意力机制交换信息。我们认为完全对称是不必要的,因为查询-文档的相关性关系本质上是非对称的:对于排序任务,只需判断结果是否与查询相关,反之则无必要。为了进一步减少 token 交互,我们提出了一种新颖的可配置非对称交叉注意力模式,其中 [CLS]、查询、段落或文档 token 之间的交互程度各不相同 (参见图 $1(\mathrm{d})$ )。
In experiments on re-ranking tasks from the TREC Deep Learning tracks [26– 29] and the TIREx benchmark [36], our new model’s effectiveness is consistently on par with previous (sparse) cross-encoder models, even with a local window size of only four tokens and asymmetric attention. Further efficiency analyses for sequences with 174 / 4096 tokens show that our spars if i cation techniques reduce the memory requirements by at least 22% / 59% and yield inference times that are at least 1% / 43% faster.
在TREC深度学习赛道[26–29]和TIREx基准测试[36]的重新排序任务实验中,即使仅使用四个token的局部窗口和不对称注意力机制,我们新模型的效果始终与之前的(稀疏)交叉编码器模型相当。针对174/4096个token序列的进一步效率分析表明,我们的稀疏化技术将内存需求降低了至少22%/59%,并使推理速度提升了至少1%/43%。
2 Related Work
2 相关工作
One strategy for using PLMs in ranking is to separate the encoding of queries and documents (or passages) [45, 46, 61, 67]. Such bi-encoder models are efficient retrievers as the document encodings can be indexed, so only the query needs to be encoded at retrieval time. However, the good efficiency of bi-encoders comes at reduced effectiveness compared to cross-encoders [40], especially in out-of-domain scenarios [66]. Consequently, bi-encoders are often used for firststage retrieval, while the more effective but less efficient cross-encoders serve as second-stage re-rankers [52, 55, 57, 81]. We focus on improving the efficiency of cross-encoders while maintaining their effectiveness.
在排序任务中使用预训练语言模型 (PLM) 的一种策略是将查询和文档 (或段落) 的编码分开处理 [45, 46, 61, 67]。这种双编码器模型 (bi-encoder) 作为检索器非常高效,因为文档编码可以被索引化,检索时只需对查询进行编码。然而,与交叉编码器 (cross-encoder) 相比 [40],双编码器的高效性是以降低效果为代价的,尤其是在域外场景中 [66]。因此,双编码器通常用于第一阶段的检索,而效果更好但效率较低的交叉编码器则作为第二阶段的重新排序器 [52, 55, 57, 81]。我们专注于在保持交叉编码器效果的同时提高其效率。
One strategy to make cross-encoders more efficient is to reduce the model size via knowledge distillation [41, 42, 50]. During knowledge distillation, a smaller and more efficient model aims to mimic a larger “teacher” model. The distilled models can often match the effectiveness of the teacher model at only a fraction of the computational costs [79], indicating that PLMs can be “over parameterized” for re-ranking [40]. We follow a similar idea and try to reduce token interactions in cross-encoders using sparse attention techniques to substantially lower computational costs at comparable effectiveness.
提升交叉编码器效率的一种策略是通过知识蒸馏 (knowledge distillation) [41, 42, 50] 缩小模型规模。在知识蒸馏过程中,更小更高效的模型会尝试模仿较大的"教师"模型。蒸馏后的模型通常能以教师模型几分之一的计算成本达到相近的效果 [79],这表明预训练语言模型 (PLM) 在重排序任务中可能存在"参数过量"问题 [40]。我们采用类似思路,尝试通过稀疏注意力技术减少交叉编码器的token交互,从而在保持效果相当的前提下显著降低计算成本。
Previously, sparse attention PLMs aimed to increase the process able input length [72]. Instead of full attention across the entire input, a sparse PLM restricts attention to neighboring tokens. For instance, the Sparse Transformer [12] uses a block-sparse kernel, splitting the input into small blocks where tokens only attend to tokens in their block. Additional strided attention allows for attention between blocks. The Longformer [3], BigBird [83], and ETC [1] use a different approach. Tokens can attend to a fixed window of neighboring tokens, with additional global attention tokens that can attend to the entire sequence.
此前,稀疏注意力预训练语言模型 (PLM) 旨在提升可处理输入长度 [72]。与对整个输入进行全局注意力不同,稀疏 PLM 将注意力限制在相邻 token 上。例如,Sparse Transformer [12] 采用块稀疏核 (block-sparse kernel),将输入分割为小块,使 token 仅关注其所在块内的 token。通过额外的跨步注意力 (strided attention) 实现块间注意力交互。Longformer [3]、BigBird [83] 和 ETC [1] 则采用不同策略:token 可关注固定窗口内的邻近 token,同时设置能关注整个序列的全局注意力 token。
For efficient windowed self-attention, the Longformer, BigBird, and ETC use block-sparse matrices. However, block-sparse techniques often make concessions on the flexibility of window sizes or incur additional overhead that does not affect the resulting predictions. We compare several previously proposed windowed selfattention implementations and find them inefficient in terms of time or space compared to the reduction in operations. Therefore, we implement a custom CUDA kernel and compare it to other implementations (cf. Section 4.2).
为实现高效的窗口化自注意力机制,Longformer、BigBird和ETC采用了块稀疏矩阵技术。然而,块稀疏方法通常需要牺牲窗口尺寸的灵活性,或引入不影响最终预测结果的额外开销。我们对比了先前提出的多种窗口化自注意力实现方案,发现其在时间或空间效率上相比计算量减少的收益并不理想。为此,我们实现了定制化的CUDA内核,并与其他实现方案进行对比(参见第4.2节)。
Sparse attention PLMs have also been applied to document re-ranking. For example, the Longformer without global attention was used as a cross-encoder to re-rank long documents [70]. However, effectiveness was not convincing as later-appearing document tokens were unable to attend to query tokens. The QDS-Transformer [44] fixed this problem by correctly applying global attention to query tokens and achieved better retrieval effectiveness than previous crossencoder strategies that split documents [30, 82]. While the QDS-Transformer was evaluated with different window sizes, the effectiveness results were inconclusive. A model fine-tuned on a window size of 64 tokens was tested with smaller (down to 16 tokens) and larger window sizes (up to 512)—always yielding worse effectiveness. We hypothesize that models specifically fine-tuned for smaller window sizes will be as effective as models fine-tuned for larger window sizes.
稀疏注意力预训练语言模型 (PLM) 也被应用于文档重排序。例如,不带全局注意力的 Longformer 被用作交叉编码器对长文档进行重排序 [70]。但由于文档后部 token 无法关注查询 token,其效果并不理想。QDS-Transformer [44] 通过正确地对查询 token 应用全局注意力解决了这个问题,其检索效果优于之前采用文档分割策略的交叉编码器方法 [30, 82]。虽然 QDS-Transformer 在不同窗口尺寸下进行了评估,但效果结果并不明确。使用 64 token 窗口微调的模型在更小(低至 16 token)和更大(高达 512)窗口测试时,效果始终更差。我们推测:专门针对较小窗口微调的模型,其效果将与针对较大窗口微调的模型相当。
Besides analyzing models fine-tuned for different window sizes, we hypothesize that token interactions between some input sub-sequences are unnecessary. For example, bi-encoder models show that independent contextual iz ation of query and document tokens can be effective [45, 46, 61, 67]. However, the symmetric attention mechanisms of previous sparse PLM architectures do not accommodate asymmetric attention patterns. We develop a new cross-encoder variant that combines windowed self-attention from sparse PLMs with asymmetric cross-attention. Cross-attention allows a sequence to attend to an arbitrary other sequence and is commonly used in transformer architectures for machine translation [73], computer vision [35, 59, 71], and in multi-modal settings [43].
除了分析针对不同窗口大小进行微调的模型外,我们假设某些输入子序列之间的token交互是不必要的。例如,双编码器模型表明,查询和文档token的独立上下文化可能有效 [45, 46, 61, 67]。然而,先前稀疏PLM架构的对称注意力机制无法适应非对称注意力模式。我们开发了一种新的交叉编码器变体,将稀疏PLM的窗口自注意力与非对称交叉注意力相结合。交叉注意力允许一个序列关注任意其他序列,并常用于机器翻译 [73]、计算机视觉 [35, 59, 71] 以及多模态场景 [43] 的Transformer架构中。
3 Sparse Asymmetric Attention Using Cross-Encoders
3 基于交叉编码器的稀疏非对称注意力机制
We propose a novel sparse asymmetric attention pattern for re-ranking documents (and passages) with cross-encoders. Besides combining existing windowed self-attention and cross-attention ideas, our pattern also flexibly allows for asymmetric query–document interactions (e.g., allowing a document to attend to the query but not vice versa). To this end, we partition the input sequence into the [CLS] token, query tokens, and document tokens, with customizable attention between these groups and local attention windows around document tokens.
我们提出了一种新颖的稀疏非对称注意力模式,用于通过交叉编码器对文档(及段落)进行重排序。该模式不仅融合了现有的窗口化自注意力和交叉注意力思想,还能灵活支持非对称的查询-文档交互(例如允许文档关注查询,但反之则不行)。为此,我们将输入序列划分为[CLS]标记、查询标记和文档标记,并支持这些分组之间的可定制注意力机制,同时在文档标记周围设置局部注意力窗口。
Figure 1 depicts our and previous cross-encoder attention patterns. In full attention, each token can attend to every other token. Instead, Longformerbased cross-encoders apply windowed self-attention to document tokens to which the QDS-Transformer adds global attention tokens per sentence. Our pattern is similar to the Longformer but deactivates attention from query tokens to [CLS] and document tokens. But, [CLS] and document tokens still have access to query tokens. Our hypothesis is that cross-encoders do not need symmetric query–document attention for re-ranking as a one-sided relationship suffices.
图 1: 展示了我们与先前交叉编码器 (cross-encoder) 的注意力模式。在全注意力 (full attention) 中,每个 Token 可关注其他所有 Token。而基于 Longformer 的交叉编码器对文档 Token 采用窗口化自注意力 (windowed self-attention),QDS-Transformer 在此基础上为每个句子添加全局注意力 Token。我们的模式与 Longformer 类似,但禁用了从查询 Token 到 [CLS] 和文档 Token 的注意力。不过,[CLS] 和文档 Token 仍可访问查询 Token。我们的假设是:重排序任务中交叉编码器不需要对称的查询-文档注意力机制,单向关系已足够。
3.1 Preliminaries
3.1 预备知识
The transformer encoder internally uses a dot-product attention mechanism [73]. For a single transformer layer, three separate linear transformations map the embedding matrix $O^{\prime}$ of the previous layer to three vector-lookup matrices $Q$ , $K$ , and $V$ . An $s\times s$ attention probability matrix that contains the probabilities of a token attending to another is obtained by softmaxing the $\sqrt{h}$ - normalized product $Q K^{T}$ . The attention probabilities are then used as weights for the vector-lookup matrix $V$ to obtain the layer’s output embedding matrix:
Transformer编码器内部采用了点积注意力机制[73]。对于单个Transformer层,通过三个独立的线性变换将前一层的嵌入矩阵$O^{\prime}$映射为三个向量查找矩阵$Q$、$K$和$V$。通过将$\sqrt{h}$归一化后的乘积$Q K^{T}$进行softmax运算,可得到一个$s\times s$的注意力概率矩阵,该矩阵包含了一个token关注另一个token的概率。随后,这些注意力概率被用作向量查找矩阵$V$的权重,以获取该层的输出嵌入矩阵:
$$
{\cal O}=\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q K^{T}}{\sqrt{h}}\right)V.
$$
$$
{\cal O}=\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q K^{T}}{\sqrt{h}}\right)V.
$$
3.2 Windowed Self-Attention
3.2 窗口自注意力 (Windowed Self-Attention)
Windowed self-attention was proposed for more efficient sparse PLM architectures [1, 3, 83]. The idea is that a token does not attend to the entire input sequence of length $s$ , but only to a local window of $w$ tokens, with $w\ll s$ (e.g., $w=4$ means that a token attends to $2\cdot4+1$ tokens: to the 4 tokens before itself, to itself, and to the 4 tokens after itself). For a window size $w$ , windowed self-attention changes the dot-products of the transformer attention mechanism to windowed variants $\boxdot$ and $\odot_{w}$ :
窗口自注意力 (windowed self-attention) 被提出用于更高效的稀疏PLM架构 [1, 3, 83]。其核心思想是:一个token不需要关注长度为$s$的整个输入序列,而只需关注包含$w$个token的局部窗口 (其中$w\ll s$,例如$w=4$表示一个token会关注$2\cdot4+1$个token:自身之前的4个token、自身以及自身之后的4个token)。对于窗口大小$w$,窗口自注意力将transformer注意力机制的点积运算替换为窗口化变体$\boxdot$和$\odot_{w}$:
$$
\begin{array}{l}{{\displaystyle{\cal O}=\mathrm{Attention}_ {w}(Q,K,V)=\mathrm{softmax}\left(\frac{Q\boxdot{\Xi}_ {w}K^{T}}{\sqrt{h}}\right)\odot_{w}V,\mathrm{with}~}}\ {{\displaystyle Q_{(s\times h)}\boxdot{\Xi}_ {w}K_{(h\times s)}^{T}\to A_{(s\times2w+1)},\quad\mathrm{where}a_{i,j}=\sum_{l=1}^{h}q_{i,l}\cdot k_{l,i+j-w-1},}}\ {{\displaystyle\qquad\quad}}\ {{P_{(s\times2w+1)}\odot_{w}V_{(s\times h)}\to{\cal O}_ {(s\times h)},\qquad\mathrm{where}o_{i,l}=\sum_{j=1}^{2w+1}p_{i,j}\cdot v_{i+j-w-1,l}.}}\end{array}
$$
$$
\begin{array}{l}{{\displaystyle{\cal O}=\mathrm{Attention}_ {w}(Q,K,V)=\mathrm{softmax}\left(\frac{Q\boxdot{\Xi}_ {w}K^{T}}{\sqrt{h}}\right)\odot_{w}V,\mathrm{with}~}}\ {{\displaystyle Q_{(s\times h)}\boxdot{\Xi}_ {w}K_{(h\times s)}^{T}\to A_{(s\times2w+1)},\quad\mathrm{where}a_{i,j}=\sum_{l=1}^{h}q_{i,l}\cdot k_{l,i+j-w-1},}}\ {{\displaystyle\qquad\quad}}\ {{P_{(s\times2w+1)}\odot_{w}V_{(s\times h)}\to{\cal O}_ {(s\times h)},\qquad\mathrm{where}o_{i,l}=\sum_{j=1}^{2w+1}p_{i,j}\cdot v_{i+j-w-1,l}.}}\end{array}
$$
Thus, $\left\vert\cdot\right\vert_{w}$ outputs a band matrix subset of the standard matrix–matrix multiplication, stored in a space-efficient form (non-band entries omitted), and $\odot_{w}$ multiplies a space-efficiently stored band matrix and a standard matrix. To ensure correctness, we zero-pad windows exceeding the sequence bounds: when either $i+j-w\le0$ or $i+j-w>s$ , we set $k_{l,i+j-w-1}=v_{i+j-w-1,l}=0$ .
因此,$\left\vert\cdot\right\vert_{w}$ 输出标准矩阵乘法的带状矩阵子集,并以节省空间的形式存储(非带状条目被省略),而 $\odot_{w}$ 则将节省空间存储的带状矩阵与标准矩阵相乘。为确保正确性,我们对超出序列边界的窗口进行零填充:当 $i+j-w\le0$ 或 $i+j-w>s$ 时,设 $k_{l,i+j-w-1}=v_{i+j-w-1,l}=0$。
For a visual impression of windowed attention, consider the lower right document-to-document attention matrix in Figure $1(\mathrm{d})$ . Only the diagonal band is computed: in Figure $1(\mathrm{d})$ for $w=1$ .
为了直观感受窗口注意力机制,请观察图 1(d) 右下角的文档间注意力矩阵。仅计算对角带状区域:在图 1(d) 中对应 $w=1$ 的情况。
Compared to full self-attention, in theory, windowed self-attention reduces the space complexity from $\mathcal{O}(s^{2})$ to $\mathcal{O}(s\cdot(2w+1))$ and the (naive) computa tional complexity from $\mathcal{O}(s^{2}\cdot h)$ to $\mathcal{O}(s\cdot(2w+1)\cdot h)$ . However, fully achieving these improvements is difficult in practice. Previous windowed self-attention imple ment at ions avoided writing hardware-specific kernels and made concessions regarding flexibility, time efficiency, or space efficiency [3, 83]. Therefore, we implement our own CUDA kernel for windowed self-attention; Section 4.2 compares our implementation’s efficiency to previous implementations.
与全自注意力机制相比,理论上窗口自注意力将空间复杂度从 $\mathcal{O}(s^{2})$ 降至 $\mathcal{O}(s\cdot(2w+1))$ ,并将(朴素)计算复杂度从 $\mathcal{O}(s^{2}\cdot h)$ 降至 $\mathcal{O}(s\cdot(2w+1)\cdot h)$ 。然而实践中完全实现这些改进存在困难。先前的窗口自注意力实现方案为避免编写硬件专用内核,在灵活性、时间效率或空间效率上做出了妥协 [3, 83]。因此我们实现了自研的窗口自注意力CUDA内核,第4.2节将我们的实现效率与先前方案进行对比。
3.3 Cross-Attention
3.3 交叉注意力 (Cross-Attention)
Cross-attention is a type of attention where a token sequence does not attend to itself, as in self-attention, but to a different sequence. We use cross-attention to configure attention between different token types. Instead of representing a crossencoder’s input as a single sequence, we split it into three disjoint sub sequences: the [CLS] token, the query tokens, and the document tokens (Figure 1 (d) visually represents this for our proposed pattern by splitting the marginal vectors; the [SEP] tokens are part of “their” respective sub sequence). Each sub sequence can then have its own individual attention function Attention $(Q,K,V)$ .
交叉注意力 (cross-attention) 是一种注意力机制,其中 token 序列不像自注意力那样关注自身,而是关注另一个不同的序列。我们使用交叉注意力来配置不同 token 类型之间的注意力关系。与将交叉编码器输入表示为单一序列不同,我们将其拆分为三个互不相交的子序列:[CLS] token、查询 token 和文档 token (图 1(d) 通过分割边缘向量直观展示了我们提出的模式;[SEP] token 属于它们各自对应的子序列)。每个子序列都可以拥有独立的注意力函数 Attention $(Q,K,V)$。
We split the vector-lookup matrices column-wise into [CLS], query, and document token-specific sub matrices $Q_{c}$ , $Q_{q}$ , $Q_{d}$ , etc. These matrices are precomputed and shared between the different attention functions for efficiency. Restricting attention between sub sequences then means to call the attention function for a sub sequence’s $Q$ -matrix and the respective $K$ - and $V$ -matrices of the attended-to sub sequences. For example, to let a document attend to itself and the query, the function call is $\mathrm{Attention}(Q_{d},[K_{q},K_{d}],[V_{q},V_{d}])$ , where $[\cdot,\cdot]$ denotes matrix concatenation by columns (i.e., $[M,M^{\prime}]$ yields a matrix whose “left” columns come from $M$ and the “right” columns from $M^{\prime}$ ).
我们将向量查找矩阵按列分割为[CLS]、查询和文档token特定的子矩阵$Q_{c}$、$Q_{q}$、$Q_{d}$等。为提高效率,这些矩阵会预先计算并在不同注意力函数间共享。限制子序列间的注意力意味着调用某个子序列的$Q$矩阵与被关注子序列对应的$K$和$V$矩阵的注意力函数。例如,若要让文档关注自身及查询,函数调用为$\mathrm{Attention}(Q_{d},[K_{q},K_{d}],[V_{q},V_{d}])$,其中$[\cdot,\cdot]$表示按列拼接矩阵(即$[M,M^{\prime}]$生成的矩阵其"左侧"列来自$M$,"右侧"列来自$M^{\prime}$)。
3.4 Locally Windowed Cross-Attention
3.4 局部窗口化交叉注意力 (Locally Windowed Cross-Attention)
The above-described cross-attention mechanism using concatenation is not directly applicable in our case, as we want to apply windowed self-attention to document tokens and asymmetric attention to query tokens. Instead of concatenating the matrices $K$ and $V$ , our mechanism uses tuples $\mathcal{N}$ and $\nu$ of matrices and a tuple $\mathcal{W}$ of window sizes to assign different attention window sizes $w\in\mathcal{W}$ to each attended-to sub sequence. As a result, we can combine windowed selfattention with asymmetric attention based on token types. Formally, given $j$ - tuples $\mathcal{N}$ and $\nu$ of matrices $K_{i}$ and $V_{i}$ and a $j$ -tuple $\mathcal{W}$ of window sizes $w_{i}$ , our generalized windowed cross-attention mechanism works as follows:
上述使用拼接操作的交叉注意力机制并不直接适用于我们的场景,因为我们需要对文档token应用窗口化自注意力,而对查询token实施非对称注意力。我们的机制不拼接矩阵$K$和$V$,而是采用矩阵元组$\mathcal{N}$和$\nu$以及窗口尺寸元组$\mathcal{W}$,为每个被关注的子序列分配不同的注意力窗口大小$w\in\mathcal{W}$。这使得我们能基于token类型,将窗口化自注意力与非对称注意力相结合。具体而言,给定$j$维矩阵元组$\mathcal{N}$和$\nu$(包含$K_{i}$和$V_{i}$)以及$j$维窗口尺寸元组$\mathcal{W}$(包含$w_{i}$),广义窗口化交叉注意力机制运作流程如下:
$$
\begin{array}{l}{{\displaystyle\mathrm{Attention}_ {\mathcal{W}}(Q,K,\mathcal{V}) = \sum_{i=1}^{j}P_{i}\odot_{w_{i}}V_{i}\mathrm{, where}}}\ {{\displaystyle[P_{1},\ldots,P_{j}]=\mathrm{softmax}\left(\frac{\left[A_{1},\ldots,A_{j}\right]}{\sqrt{h}}\right) \mathrm{and} A_{i}=Q\boxtimes_{w_{i}}K_{i}.}}\end{array}
$$
$$
\begin{array}{l}{{\displaystyle\mathrm{Attention}_ {\mathcal{W}}(Q,K,\mathcal{V}) = \sum_{i=1}^{j}P_{i}\odot_{w_{i}}V_{i}\mathrm{, where}}}\ {{\displaystyle[P_{1},\ldots,P_{j}]=\mathrm{softmax}\left(\frac{\left[A_{1},\ldots,A_{j}\right]}{\sqrt{h}}\right) \mathrm{and} A_{i}=Q\boxtimes_{w_{i}}K_{i}.}}\end{array}
$$
Our proposed attention pattern (visualization in Figure $1(\mathrm{d})$ ) is then formally defined as follows. The [CLS] token has full attention over all subsequences (Equation 1; for notation convenience, we use $w=\infty$ to refer to full self-attention), the query tokens can only attend to query tokens (Equation 2), and the document tokens can attend to all sub sequences but use windowed selfattention on their own sub sequence (Equation 3):
我们提出的注意力模式(可视化见图1(d))正式定义如下。[CLS] token对所有子序列具有完整注意力(公式1;为便于表示,我们使用$w=\infty$表示完整的自注意力),查询token只能关注查询token(公式2),而文档token可以关注所有子序列,但在其自身子序列上使用窗口化自注意力(公式3):
$$
\begin{array}{r l}&{O_{c}=\mathrm{Attention}_ {(\infty,\infty,\infty)}(Q_{c},(K_{c},K_{q},K_{d}),(V_{c},V_{q},V_{d})),}\ &{O_{q}=\mathrm{Attention}_ {(\infty)}(Q_{q},(K_{q}),(V_{q})),}\ &{O_{d}=\mathrm{Attention}_ {(\infty,\infty,w)}(Q_{d},(K_{c},K_{q},K_{d}),(V_{c},V_{q},V_{d})).}\end{array}
$$
$$
\begin{array}{r l}&{O_{c}=\mathrm{Attention}_ {(\infty,\infty,\infty)}(Q_{c},(K_{c},K_{q},K_{d}),(V_{c},V_{q},V_{d})),}\ &{O_{q}=\mathrm{Attention}_ {(\infty)}(Q_{q},(K_{q}),(V_{q})),}\ &{O_{d}=\mathrm{Attention}_ {(\infty,\infty,w)}(Q_{d},(K_{c},K_{q},K_{d}),(V_{c},V_{q},V_{d})).}\end{array}
$$
3.5 Experimental Setup
3.5 实验设置
We fine-tune various models using the Longformer and our proposed attention pattern with window sizes $w\in{\infty,64,16,4,1,0}$ ( $\infty$ : full self-attention). We start from an already fine-tuned and distilled cross-encoder mode $^2$ which also serves as our baseline [62]. We additionally fine-tune a QDS-Transformer model with its default $w=64$ window for comparison. All models are fine-tuned for 100,000 steps with 1,000 linear warm-up steps and a batch size of 32 (16 document pairs) with margin MSE loss using MS MARCO-based knowledge distillation triples [40]. For documents, we extend the models fine-tuned on passages using positional interpolation [10] and further fine-tune them on document pairs from MS MARCO Document [54] for 20,000 steps using RankNet loss [8]. Negative documents are sampled from the top 200 documents retrieved by BM25 [65]. We use a learning rate of $7\cdot10^{-6}$ , an AdamW optimizer [51], and a weight decay of 0.01. We truncate passages and documents to a maximum sequence length of 512 and 4096 tokens, respectively. All models were implemented in PyTorch [58] and Py Torch Lightning [34] and fine-tuned on a single NVIDIA A100 40GB GPU.
我们使用Longformer和提出的注意力模式(窗口大小$w\in{\infty,64,16,4,1,0}$)($\infty$表示完全自注意力)对各种模型进行微调。我们从已微调并蒸馏的交叉编码器模型$^2$开始,该模型也作为我们的基线[62]。此外,我们还微调了一个QDS-Transformer模型(默认窗口$w=64$)以进行比较。所有模型均使用基于MS MARCO的知识蒸馏三元组[40],通过margin MSE损失进行100,000步微调,包含1,000步线性预热,批量大小为32(16个文档对)。对于文档,我们通过位置插值[10]扩展了在段落上微调的模型,并进一步使用RankNet损失[8]在MS MARCO Document[54]的文档对上进行了20,000步微调。负样本文档从BM25[65]检索的前200篇文档中采样。我们使用学习率$7\cdot10^{-6}$、AdamW优化器[51]和0.01的权重衰减。段落和文档的最大序列长度分别截断为512和4096个token。所有模型均在PyTorch[58]和PyTorch Lightning[34]中实现,并在单个NVIDIA A100 40GB GPU上完成微调。
We evaluate the models on the TREC 2019–2022 Deep Learning (DL) passage and document retrieval tasks [26–29] and the TIREx benchmark [36]. For each TREC DL task, we re-rank the top 100 passages / documents retrieved by BM25 using pyserini [49]. For TIREx, we use the official first-stage retrieval files retrieved by BM25 and ChatNoir [4, 60] and also re-rank the top 100 documents. We measure nDCG $@10$ and access all corpora and tasks via ir datasets [53], using the default text field for passages and documents.
我们在TREC 2019-2022深度学习(DL)段落和文档检索任务[26-29]以及TIREx基准测试[36]上评估模型性能。针对每个TREC DL任务,我们使用pyserini[49]对BM25检索出的前100个段落/文档进行重排序。对于TIREx基准,我们采用官方提供的BM25和ChatNoir[4,60]第一阶段检索结果,同样对前100篇文档进行重排序。我们通过ir datasets[53]访问所有语料库和任务,使用默认文本字段处理段落和文档,并以nDCG $@10$ 作为评估指标。
To evaluate time and space efficiency, we generate random data with a query length of 10 tokens and passage / document lengths from 54 to 4086 tokens. For the QDS-Transformer, we set global sentence attention at every 30th token, corresponding to the average sentence length in MS MARCO documents. We use the largest possible batch size per model, but up to a maximum of 100.
为评估时间和空间效率,我们生成了查询长度为10个token、段落/文档长度从54到4086个token的随机数据。对于QDS-Transformer,我们在每30个token处设置全局句子注意力,这与MS MARCO文档的平均句子长度相对应。我们为每个模型使用尽可能大的批次大小,但最多不超过100。
4 Empirical Evaluation
4 实证评估
We compare our sparse cross-encoder’s re-ranking effectiveness and efficiency to full attention and previous sparse cross-encoder implementations. We also examine the impact of different small window sizes and of our attention deactivation pattern—analyses that provide further insights into how cross-encoders work.
我们比较了稀疏交叉编码器 (sparse cross-encoder) 在重排序效果和效率方面与全注意力机制及先前稀疏交叉编码器实现的差异。同时研究了不同小窗口尺寸和注意力停用模式的影响,这些分析为理解交叉编码器工作机制提供了更深层次的见解。
4.1 Effectiveness Results
4.1 有效性结果
In-domain Effectiveness Table 1 reports the nDCG@10 of various models with different attention patterns and window sizes on the TREC Deep Learning passage and document re-ranking tasks. We group Full Attention and Longformer models into the same category because they have the same pattern but different window sizes in our framework. We fine-tune separate models for passage and document re-ranking (cf. Section 3.5) except models with $w=\infty$ . Their lack of efficiency prevents training on long sequences, and we only fine-tune them on passages but include their MaxP scores [30] for documents (in gray).
领域内有效性
表1报告了在TREC深度学习段落和文档重排序任务中,不同注意力模式和窗口大小的各模型nDCG@10指标。我们将Full Attention和Longformer模型归为同一类别,因为它们在我们的框架中具有相同模式但窗口大小不同。除窗口大小$w=\infty$的模型外,我们分别针对段落和文档重排序任务微调了独立模型(参见第3.5节)。由于效率不足,这些模型无法在长序列上训练,因此我们仅对段落进行微调,但包含其文档MaxP分数30。
Table 1: Re-ranking effectiveness as nDCG@10 on TREC Deep Learning [26– 29]. The highest score per task is given in bold. Scores obtained using a MaxP strategy are grayed out. † denotes significant equivalence within $\pm0.02$ (paired TOST [69], $p<0.003$ ), compared to Full Attention $w=\infty$ for passage tasks and Longformer $w=64$ for document tasks.
| Task w= | Full Att./ Longformer | Sparse | Cross-Encoder | QDS 64 | |||||||||||
| 8 | 64 | 16 | 4 1 | 0 | 8 | 64 | 16 | 4 | 1 | 0 | |||||
| a ass P | 2019 | .724 | .719t .725t | .719 | .714 | .694 | .722 | .717 | .724 | .728 | .715 | .696 | .720t | ||
| 2020 | .674 | .681.680 | .684 | .676 | .632 | .666 | .672 | .661 | .665 | .649 | .605 | .682 | |||
| 2021 2022 | .656 .496 | .653.650 .494.487 | .645 .486 | .629 .481 | .602 | .656 | .650 .492t | .639 | .647 | .625 | .593 | .656 | |||
| Avg. | .619 | .619t .616t .615t | .607 | .441 .572 | .490 .615t | .615t | .479 .607 | .484 | .471 | .427 | .495t | ||||
| ent um C O | 2019 | .658 | .683 | .678 | .667 | .638 | .672 | .612t | .596 | .560 | .620 | ||||
| .622 | .640 | .639 | .661 | .689 .655 | .663 | .636 | .638 | .685 .650 | .669 .642 | .692 | .646 | .697 | |||
| 2020 | .678 | .671 | .681 | .683 | .683 | .644 .629 | .677 | .681 | .681 | .670 | .657 .679 | .638 .644 | .639 | ||
| 2021 | .424 | .425 | .431 | .425 | .409 | .389 | .421 | .446 | .443 | .417 | .424 | .405 | .676 | ||
| 2022 | .428 | ||||||||||||||
| Avg. | .575 | .582 .586t.587 | .584t | .556 | .573 | .590 | .594 | .577 | .589 | .561 | .587t | ||||
表 1: TREC深度学习[26–29]数据集上nDCG@10的重新排序效果。每项任务的最高分以粗体显示。使用MaxP策略获得的分数以灰色显示。†表示在段落任务中与Full Attention $w=\infty$、文档任务中与Longformer $w=64$相比具有显著等效性( $\pm0.02$ ) (配对TOST[69], $p<0.003$ )。
| Task w= | Full Att./ Longformer | Sparse | Cross-Encoder | QDS 64 |
|---|---|---|---|---|
| 8 | 64 | 16 | 4 1 | |
| a ass P | 2019 | .724 | .719t .725t | |
| 2020 | .674 | .681.680 | ||
| 2021 2022 | .656 .496 | .653.650 .494.487 | ||
| Avg. | .619 | .619t .616t .615t | ||
| ent um C O | 2019 | .658 | .683 | .678 |
| .622 | .640 | .639 | ||
| 2020 | .678 | .671 | .681 | |
| 2021 | .424 | .425 | .431 | |
| 2022 | ||||
| Avg. | .575 | .582 .586t.587 |
Since we hypothesize that sparse attention will not substantially affect the re-ranking effectiveness, we test for significant equivalence instead of differences. Therefore, we cannot use the typical t-test, but instead use a paired TOST procedure (two one-sided t-tests [69]; $p<0.003$ , multiple test correction [47]) to determine if the difference between two models is within $\pm0.02$ . We deem $\pm0.02$ a reasonable threshold for equivalence since it is approximately the difference between the top two models in the different TREC Deep Learning tasks.
由于我们假设稀疏注意力不会显著影响重排序效果,因此我们测试的是显著性等价而非差异。为此,我们无法使用常规t检验,而是采用配对TOST程序(双单侧t检验[69];$p<0.003$,多重检验校正[47])来判断两个模型间的差异是否在$\pm0.02$范围内。我们将$\pm0.02$视为合理的等价阈值,因为该数值约等于不同TREC深度学习任务中前两名模型间的差异。
We consider two different reference models for the passage and document re-ranking tasks. The Full Attention cross-encoder has complete information access in the passage re-ranking setting and serves as the reference model for the passage tasks. Since the models without windowed attention ( $w=\infty$ ) only process a limited number of tokens in the document re-ranking setting, we use the standard Longformer ( $w=64$ ) as the reference model for document tasks.
我们为段落和文档重排序任务考虑两种不同的参考模型。在段落重排序场景中,全注意力交叉编码器 (Full Attention cross-encoder) 拥有完整的信息访问权限,因此作为段落任务的参考模型。由于无窗口注意力 ( $w=\infty$ ) 模型在文档重排序场景中仅处理有限数量的 token,我们采用标准 Longformer ( $w=64$ ) 作为文档任务的参考模型。
We first examine the effectiveness of the QDS-Transformer. In contrast to the original work [44], it does not improve re-ranking effectiveness despite having more token interactions. The reference models are statistically equivalent to the QDS-Transf
