Transformer Feed-Forward Layers Are Key-Value Memories

Transformer的前馈层是键值记忆体

Mor Geva1,2 Roei Schuster1,3 Jonathan Berant1,2 Omer Levy1 1Blavatnik School of Computer Science, Tel-Aviv University 2Allen Institute for Artificial Intelligence 3Cornell Tech

Mor Geva1,2 Roei Schuster1,3 Jonathan Berant1,2 Omer Levy1 1Blavatnik计算机学院 特拉维夫大学 2艾伦人工智能研究所 3康奈尔理工大学

{morgeva@mail,joberant@cs,levyomer@cs}.tau.ac.il, rs864@cornell.edu

{morgeva@mail,joberant@cs,levyomer@cs}.tau.ac.il, rs864@cornell.edu

Abstract

摘要

Feed-forward layers constitute two-thirds of a transformer model’s parameters, yet their role in the network remains under-explored. We show that feed-forward layers in transformerbased language models operate as key-value memories, where each key correlates with textual patterns in the training examples, and each value induces a distribution over the output vocabulary. Our experiments show that the learned patterns are human-interpret able, and that lower layers tend to capture shallow patterns, while upper layers learn more semantic ones. The values complement the keys’ input patterns by inducing output distributions that concentrate probability mass on tokens likely to appear immediately after each pattern, particularly in the upper layers. Finally, we demonstrate that the output of a feed-forward layer is a composition of its memories, which is subsequently refined throughout the model’s layers via residual connections to produce the final output distribution.

前馈层占据Transformer模型三分之二的参数量，但其在网络中的作用仍未得到充分研究。我们发现基于Transformer的大语言模型中，前馈层扮演着键值记忆体的角色——每个键(key)与训练样本中的文本模式相关联，而每个值(value)则诱导输出词表上的概率分布。实验表明：这些学习到的模式具有人类可解释性，其中底层倾向于捕捉浅层模式，而高层则学习更具语义性的模式；值通过将概率质量集中在各模式后续可能出现的token上（尤其在高层级）来补充键的输入模式。最后我们证明，前馈层的输出是其记忆体的组合产物，这些产物会通过残差连接在模型各层中逐步精炼，最终形成输出分布。

1 Introduction

1 引言

Transformer-based language models (Vaswani et al., 2017) are at the core of state-of-the-art natural language processing (Devlin et al., 2019; Brown et al., 2020), largely due to the success of selfattention. While much literature has been devoted to analyzing the function of self-attention layers (Voita et al., 2019; Clark et al., 2019; Vig and Be- linkov, 2019), they account for only a third of a typical transformer’s parameters $\mathrm{4}d^{2}$ per layer, where $d$ is the model’s hidden dimension). Most of the parameter budget is spent on position-wise feedforward layers ( $\mathrm{\Delta}8d^{2}$ per layer), yet their role remains under-explored. What, if so, is the function of feed-forward layers in a transformer language model?

基于Transformer的语言模型 (Vaswani等人，2017) 是当前最先进自然语言处理技术的核心 (Devlin等人，2019；Brown等人，2020)，这主要归功于自注意力(self-attention)机制的成功。尽管已有大量文献致力于分析自注意力层的功能 (Voita等人，2019；Clark等人，2019；Vig和Belinkov，2019)，但它们仅占典型Transformer参数量的三分之一 (每层$\mathrm{4}d^{2}$，其中$d$为模型隐藏维度)。大部分参数预算被用于逐位置前馈层 (每层$\mathrm{\Delta}8d^{2}$)，但其作用仍未得到充分探索。那么，Transformer语言模型中的前馈层究竟发挥着什么功能？

We show that feed-forward layers emulate neural memories (Sukhbaatar et al., 2015), where the first parameter matrix in the layer corresponds to keys, and the second parameter matrix to values. Figure 1 shows how the keys (first parameter matrix) inter- act with the input to produce coefficients, which are then used to compute a weighted sum of the values (second parameter matrix) as the output. While the theoretical similarity between feed-forward layers and key-value memories has previously been suggested by Sukhbaatar et al. (2019), we take this observation one step further, and analyze the “memories” that the feed-forward layers store.

我们证明前馈层模拟了神经记忆 (Sukhbaatar et al., 2015)，其中层中的第一个参数矩阵对应键，第二个参数矩阵对应值。图 1: 展示了键 (第一个参数矩阵) 如何与输入交互产生系数，随后这些系数被用于计算值 (第二个参数矩阵) 的加权和作为输出。虽然 Sukhbaatar 等人 (2019) 之前曾提出前馈层与键值记忆在理论上的相似性，但我们将这一观察进一步推进，分析了前馈层存储的"记忆"。

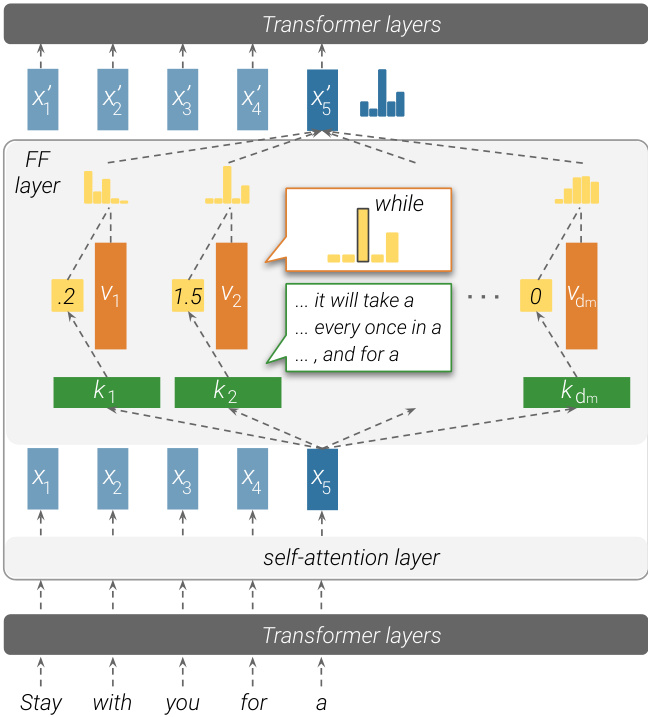
Figure 1: An illustration of how a feed-forward layer emulates a key-value memory. Input vectors (here, ${\bf x}_ {5}$ ) are multiplied by keys to produce memory coefficients (e.g., the memory coefficient for $\mathbf{v}_{1}$ is 0.2), which then weigh distributions over the output vocabulary, stored in the values. The feed-forward layer’s output is thus the weighted sum of its values.

图 1: 前馈层模拟键值存储机制的示意图。输入向量(此处为 ${\bf x}_ {5}$ )与键相乘生成存储系数(例如 $\mathbf{v}_{1}$ 的存储系数为0.2)，随后这些系数对存储在值中的输出词表分布进行加权。前馈层的输出即为各值的加权求和结果。

We find that each key correlates with a specific set of human-interpret able input patterns, such as $n$ -grams or semantic topics. For example, $k_{2}$ in Figure 1 is triggered by inputs that describe a period of time and end with $\mathbf{\omega}^{\leftarrow}a^{\rightarrow}$ . Simultaneously, we observe that each value can induce a distribution over the output vocabulary, and that this distribution correlates with the next-token distribution of the corresponding keys in the upper layers of the model. In the above example, the corresponding value $v_{2}$ represents a distribution that puts most of its probability mass on the word “while”.

我们发现每个键都与一组人类可解释的特定输入模式相关，例如 $n$ -gram 或语义主题。例如，图 1 中的 $k_{2}$ 由描述时间段的输入触发，并以 $\mathbf{\omega}^{\leftarrow}a^{\rightarrow}$ 结尾。同时，我们观察到每个值都能在输出词汇表上诱导出一个分布，且该分布与模型上层中对应键的下一个 token 分布相关。在上述例子中，对应值 $v_{2}$ 表示的分布将大部分概率质量集中在单词 "while" 上。

Lastly, we analyze how the language model, as a whole, composes its final prediction from individual memories. We observe that each layer combines hundreds of active memories, creating a distribution that is qualitatively different from each of its component memories’ values. Meanwhile, the residual connection between layers acts as a refinement mechanism, gently tuning the prediction at each layer while retaining most of the residual’s information.

最后，我们分析了语言模型作为一个整体是如何从各个记忆片段组合出最终预测的。我们观察到每一层都会整合数百个活跃记忆片段，形成的分布与各组成部分的记忆值在性质上截然不同。同时，层间的残差连接(residual connection)起到了精调机制的作用，在保留大部分残差信息的同时，逐层微调预测结果。

In conclusion, our work sheds light on the function of feed-forward layers in transformer-based language models. We show that feed-forward layers act as pattern detectors over the input across all layers, and that the final output distribution is gradually constructed in a bottom-up fashion.1

总之，我们的工作揭示了基于Transformer的语言模型中前馈层的作用。研究表明，前馈层在所有层级上充当输入模式检测器，且最终输出分布是以自底向上的方式逐步构建的。[20]

2 Feed-Forward Layers as Un normalized Key-Value Memories

2 前馈层作为未归一化的键值记忆

Feed-forward layers A transformer language model (Vaswani et al., 2017) is made of intertwined self-attention and feed-forward layers. Each feedforward layer is a position-wise function, processing each input vector independently. Let $\mathbf{x}\in\mathbb{R}^{d}$ be a vector corresponding to some input text prefix. We can express the feed-forward layer $\mathrm{FF}(\cdot)$ as follows (bias terms are omitted):

前馈层
Transformer语言模型 (Vaswani et al., 2017) 由交错的自注意力层和前馈层构成。每个前馈层都是位置级函数，独立处理每个输入向量。设 $\mathbf{x}\in\mathbb{R}^{d}$ 为对应某个输入文本前缀的向量，前馈层 $\mathrm{FF}(\cdot)$ 可表示为（省略偏置项）：

$$
\mathrm{FF}({\bf x})=f({\bf x}\cdot K^{\top})\cdot V
$$

$$
\mathrm{FF}({\bf x})=f({\bf x}\cdot K^{\top})\cdot V
$$

Here, $K,V\in\mathbb{R}^{d_{m}\times d}$ are parameter matrices, and $f$ is a non-linearity such as ReLU.

这里，$K,V\in\mathbb{R}^{d_{m}\times d}$ 是参数矩阵，$f$ 是一个非线性函数，例如 ReLU。

Neural memory A neural memory (Sukhbaatar et al., 2015) consists of $d_{m}$ key-value pairs, which we call memories.2 Each key is represented by a $d$ -dimensional vector $\mathbf{k}_ {i}\in\mathbb{R}^{d}$ , and together form the parameter matrix $K\in\mathbb{R}^{d_{m}\times d}$ ; likewise, we define the value parameters as $V\in\mathbb{R}^{d_{m}\times d}$ . Given an input vector $\mathbf{x}\in\mathbb{R}^{d}$ , we compute a distribution over the keys, and use it to compute the expected value:

神经记忆 (Neural memory)
神经记忆 (Sukhbaatar et al., 2015) 由 $d_{m}$ 个键值对组成，我们称之为记忆。每个键由一个 $d$ 维向量 $\mathbf{k}_ {i}\in\mathbb{R}^{d}$ 表示，并共同构成参数矩阵 $K\in\mathbb{R}^{d_{m}\times d}$；类似地，我们将值参数定义为 $V\in\mathbb{R}^{d_{m}\times d}$。给定输入向量 $\mathbf{x}\in\mathbb{R}^{d}$，我们计算键上的分布，并利用它计算期望值：

$$
\begin{array}{l}{{\displaystyle p(k_{i}\mid x)\propto\exp(\mathbf{x}\cdot\mathbf{k}_ {i})}~}\ {{\displaystyle\mathbf{MN}(\mathbf{x})=\sum_{i=1}^{d_{m}}p(k_{i}\mid x)\mathbf{v}_{i}}}\end{array}
$$

$$
\begin{array}{l}{{\displaystyle p(k_{i}\mid x)\propto\exp(\mathbf{x}\cdot\mathbf{k}_ {i})}~}\ {{\displaystyle\mathbf{MN}(\mathbf{x})=\sum_{i=1}^{d_{m}}p(k_{i}\mid x)\mathbf{v}_{i}}}\end{array}
$$

With matrix notation, we arrive at a more compact formulation:

通过矩阵表示法，我们得到了更简洁的公式：

$$
\mathbf{MN}(\mathbf{x})=\mathrm{softmax}(\mathbf{x}\cdot\boldsymbol{K}^{\top})\cdot\boldsymbol{V}
$$

$$
\mathbf{MN}(\mathbf{x})=\mathrm{softmax}(\mathbf{x}\cdot\boldsymbol{K}^{\top})\cdot\boldsymbol{V}
$$

Feed-forward layers emulate neural memory Comparing equations 1 and 2 shows that feedforward layers are almost identical to key-value neural memories; the only difference is that neural memory uses softmax as the non-linearity $f(\cdot)$ , while the canonical transformer does not use a normalizing function in the feed-forward layer. The hidden dimension $d_{m}$ is essentially the number of memories in the layer, and the activation $\mathbf{m}=f(\mathbf{x}\cdot K^{\top})$ , commonly referred to as the hidden layer, is a vector containing an un normalized non-negative coefficient for each memory. We refer to each $\mathbf{m}_{i}$ as the memory coefficient of the ith memory cell.

前馈层模拟神经记忆
对比公式1和公式2可以看出，前馈层与键值神经记忆几乎完全相同；唯一的区别在于神经记忆使用softmax作为非线性函数 $f(\cdot)$ ，而标准Transformer在前馈层中不使用归一化函数。隐藏维度 $d_{m}$ 本质上表示该层的记忆数量，激活值 $\mathbf{m}=f(\mathbf{x}\cdot K^{\top})$ （通常称为隐藏层）是一个包含每个记忆未归一化非负系数的向量。我们将每个 $\mathbf{m}_{i}$ 称为第i个记忆单元的记忆系数。

Sukhbaatar et al. (2019) make an analogous observation, and incorporate the parameters of the feed-forward layers as persistent memory cells in the self-attention layers. While this re parameter iz ation works in practice, the experiment does not tell us much about the role of feed-forward layers in the canonical transformer. If transformer feed-forward layers are indeed key-value memories, then what memories do they store?

Sukhbaatar等人(2019)提出了类似观察，并将前馈层参数作为持久记忆单元整合到自注意力层中。虽然这种参数重设在实践中有效，但该实验并未揭示前馈层在标准Transformer中的作用。若Transformer前馈层确实是键值记忆体，那么它们存储了哪些记忆？

We conjecture that each key vector $\mathbf{k}_ {i}$ captures a particular pattern (or set of patterns) in the input sequence (Section 3), and that its corresponding value vector $\mathbf{v}_{i}$ represents the distribution of tokens that follows said pattern (Section 4).

我们推测每个键向量 $\mathbf{k}_ {i}$ 捕捉了输入序列中的特定模式（或模式集合）（第3节），而其对应的值向量 $\mathbf{v}_{i}$ 则表示跟随该模式的token分布（第4节）。

3 Keys Capture Input Patterns

3 Keys Capture Input Patterns

We posit that the key vectors $K$ in feed-forward layers act as pattern detectors over the input sequence, where each individual key vector $\mathbf{k}_ {i}$ corresponds to a specific pattern over the input prefix $x_{1},\ldots,x_{j}$ . To test our claim, we analyze the keys of a trained language model’s feed-forward layers. We first retrieve the training examples (prefixes of a sentence) most associated with a given key, that is, the input texts where the memory coefficient is highest. We then ask humans to identify patterns within the retrieved examples. For almost every key $\mathbf{k}_{i}$ in our sample, a small set of well-defined patterns, recognizable by humans, covers most of the examples associated with the key.

我们假设前馈层中的关键向量 $K$ 充当输入序列的模式检测器，其中每个单独的关键向量 $\mathbf{k}_ {i}$ 对应于输入前缀 $x_{1},\ldots,x_{j}$ 上的特定模式。为了验证这一观点，我们分析了一个训练好的语言模型前馈层的键向量。首先，我们检索与给定键最相关的训练样本（句子的前缀），即在记忆系数最高的输入文本。然后，我们请人类识别检索样本中的模式。对于样本中几乎每个键 $\mathbf{k}_{i}$，一小组人类可识别的明确定义模式覆盖了与该键相关的大多数样本。

Table 1: Examples of human-identified patterns that trigger different memory keys.

Key	Pattern	Exampletriggerprefixes
k449	Endswith“substitutes (shallow)	Atthemeeting,Eltonsaidthat“forartisticreasonstherecouldbenosubstitutes InGermanservice,theywereusedassubstitutes Twoweekslater,hecameoffthesubstitutes
	Military, ends with "base"/"bases’ (shallow+semantic)	On1ApriltheSRSGauthorisedtheSADFtoleavetheirbases AircraftfromallfourcarriersattackedtheAustralianbase BombersfyingmissionstoRabaulandotherJapanesebases
	a“part of" relation (semantic)	InJune2012shewasnamedasoneoftheteamthatcompeted HewasalsoapartoftheIndiandelegation ToyStoryisalsoamongthetoptenintheBFIlistofthe5ofilmsyoushould
	Endswitha time range (semantic)	Worldwide,mosttornadoesoccurinthelateafternoon,between3pmand7 Weekendtollsareineffectfrom7:0opmFridayuntil Thebuildingisopentothepublicsevendaysaweek,from11:o0amto
	TV shows (semantic)	Timeshiftingviewingadded57percenttotheepisode's Thefirstseasonsetthattheepisodewasincludedinwasaspartofthe FromtheoriginalNBCdaytimeversion,archived

表 1: 触发不同记忆键的人类识别模式示例

Key	Pattern	Exampletriggerprefixes
k449	以"substitutes"结尾 (浅层)	Atthemeeting,Eltonsaidthat“forartisticreasonstherecouldbenosubstitutes InGermanservice,theywereusedassubstitutes Twoweekslater,hecameoffthesubstitutes
	军事相关，以"base"/"bases"结尾 (浅层+语义)	On1ApriltheSRSGauthorisedtheSADFtoleavetheirbases AircraftfromallfourcarriersattackedtheAustralianbase BombersfyingmissionstoRabaulandotherJapanesebases
	"part of"关系 (语义)	InJune2012shewasnamedasoneoftheteamthatcompeted HewasalsoapartoftheIndiandelegation ToyStoryisalsoamongthetoptenintheBFIlistofthe5ofilmsyoushould
	以时间范围结尾 (语义)	Worldwide,mosttornadoesoccurinthelateafternoon,between3pmand7 Weekendtollsareineffectfrom7:0opmFridayuntil Thebuildingisopentothepublicsevendaysaweek,from11:o0amto
	电视节目 (语义)	Timeshiftingviewingadded57percenttotheepisode's Thefirstseasonsetthattheepisodewasincludedinwasaspartofthe FromtheoriginalNBCdaytimeversion,archived

3.1 Experiment

3.1 实验

We conduct our experiment over the language model of Baevski and Auli (2019), a 16-layer transformer language model trained on WikiText103 (Merity et al., 2017). This model defines $d=1024$ and $d_{m}=4096$ , and has a total of $d_{m}\cdot16=65,53$ 6 potential keys to analyze. We randomly sample 10 keys per layer (160 in total).

我们在Baevski和Auli (2019)提出的16层Transformer语言模型上进行实验，该模型基于WikiText103 (Merity et al., 2017)训练。该模型定义$d=1024$和$d_{m}=4096$，共有$d_{m}\cdot16=65,536$个待分析潜在键。我们每层随机采样10个键（共160个）。

Retrieving trigger examples We assume that patterns stored in memory cells originate from examples the model was trained on. Therefore, given a key $\mathbf{k}_ {i}^{\ell}$ that corresponds to the $i$ -th hidden dimension of the $\ell$ -th feed-forward layer, we compute the memory coefficient $\mathrm{ReLU}(\mathbf{x}_ {j}^{\ell}\cdot\mathbf{k}_ {i}^{\ell})$ for every prefix $x_{1},\ldots,x_{j}$ of every sentence from the WikiText103’s training set.3 For example, for the hypothetical sentence “I love dogs”, we will compute three coefficients, for the prefixes ${}^{\leftarrow}I^{\prime\prime}$ , “I love”, and $^{\leftarrow}I$ love dogs”. Then, we retrieve the top-t trigger examples, that is, the $t$ prefixes whose representation at layer $\ell$ yielded the highest inner product with $\mathbf{k}_{i}^{\ell}$ .

检索触发示例
我们假设存储在记忆单元中的模式源自模型训练时的示例。因此，给定一个对应于第 $\ell$ 个前馈层第 $i$ 个隐藏维度的键 $\mathbf{k}_ {i}^{\ell}$，我们为WikiText103训练集中每个句子的每个前缀 $x_{1},\ldots,x_{j}$ 计算记忆系数 $\mathrm{ReLU}(\mathbf{x}_ {j}^{\ell}\cdot\mathbf{k}_ {i}^{\ell})$。例如，对于假设句子“I love dogs”，我们将计算三个系数，分别对应前缀 ${}^{\leftarrow}I^{\prime\prime}$、“I love”和 $^{\leftarrow}I$ love dogs”。然后，我们检索前 $t$ 个触发示例，即在第 $\ell$ 层表示与 $\mathbf{k}_{i}^{\ell}$ 内积最高的 $t$ 个前缀。

Pattern analysis We let human experts (NLP graduate students) annotate the top-25 prefixes retrieved for each key, and asked them to (a) identify repetitive patterns that occur in at least 3 prefixes (which would strongly indicate a connection to the key, as this would unlikely happen if sentences were drawn at random) (b) describe each recognized pattern, and (c) classify each recognized pattern as “shallow” (e.g. recurring n-grams) or “semantic” (recurring topic). Each key and its corresponding top-25 prefixes were annotated by one expert. To assure that every pattern is grounded in at least 3 prefixes, we instruct the experts to specify, for each of the top-25 prefixes, which pattern(s) it contains. A prefix may be associated with multiple (shallow or semantic) patterns.

模式分析
我们让人类专家（自然语言处理研究生）对每个关键词检索到的前25个前缀进行标注，并要求他们：(a) 识别至少出现在3个前缀中的重复模式（这强烈表明与关键词的关联性，因为随机抽取的句子不太可能出现这种情况），(b) 描述每个识别的模式，以及 (c) 将每个识别的模式分类为“浅层”（例如重复出现的n元语法）或“语义”（重复出现的主题）。每个关键词及其对应的前25个前缀由一位专家标注。为确保每个模式至少基于3个前缀，我们要求专家为每个前25个前缀指定其包含的模式。一个前缀可能与多个（浅层或语义）模式相关联。

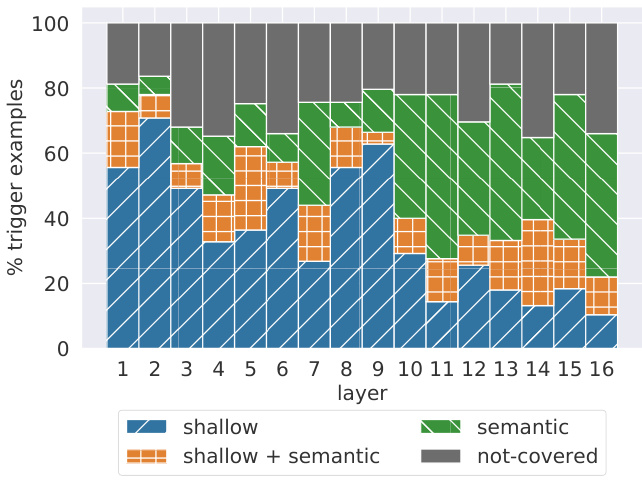
Figure 2: Breakdown of the labels experts assigned to trigger examples in each layer. Some examples were not associated with any pattern (“not-covered”).

图 2: 专家对各层级触发示例标注的分类情况。部分示例未关联任何模式（"not-covered"）。

Table 1 shows example patterns. A fullyannotated example of the top-25 prefixes from a single memory key is shown in Appendix A.

表 1: 示例模式。附录A展示了一个完整标注的示例，包含单个记忆键的前25个前缀。

3.2 Results

3.2 结果

Memories are associated with humanrecognizable patterns Experts were able to identify at least one pattern for every key, with an average of 3.6 identified patterns per key. Furthermore, the vast majority of retrieved prefixes $(65%-80%)$ ) were associated with at least one identified pattern (Figure 2). Thus, the top examples triggering each key share clear patterns that humans can recognize.

记忆与人类可识别的模式相关联
专家们能够为每个关键点识别出至少一个模式，平均每个关键点识别出3.6个模式。此外，绝大多数检索到的前缀$(65%-80%)$与至少一个已识别模式相关联 (图 2)。因此，触发每个关键点的顶部示例具有人类可识别的清晰模式。

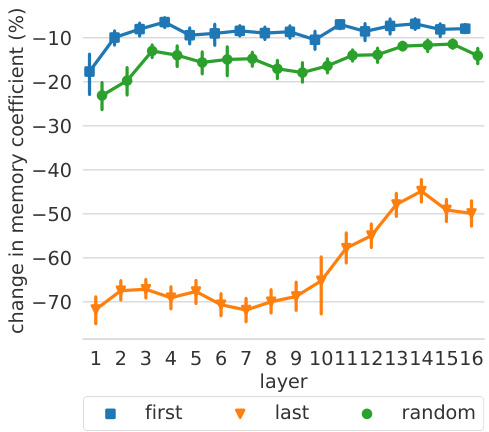
Figure 3: Relative change in memory coefficient caused by removing the first, the last, or a random token from the input.

图 3: 从输入中移除第一个、最后一个或随机token所引起的记忆系数相对变化。

Shallow layers detect shallow patterns Comparing the amount of prefixes associated with shallow patterns and semantic patterns (Figure 2), the lower layers (layers 1-9) are dominated by shallow patterns, often with prefixes that share the last word (e.g. $\mathbf{k}_ {449}^{1}$ in Table 1). In contrast, the upper layers (layers 10-16) are characterized by more semantic without clear surface-form similarities (e.g. $\mathbf{k}_{1935}^{16}$ in Table 1). This observation corroborates recent findings that lower (upper) layers in deep contextualized models encode shallow (semantic) features of the inputs (Peters et al., 2018; Jawahar et al., 2019; Liu et al., 2019).

浅层检测浅层模式
通过比较与浅层模式和语义模式相关的前缀数量（图 2），下层（第1-9层）主要由浅层模式主导，其前缀通常共享最后一个单词（例如表 1中的 $\mathbf{k}_ {449}^{1}$）。相比之下，上层（第10-16层）则更多表现为语义特征，且无明显表面形式相似性（例如表 1中的 $\mathbf{k}_{1935}^{16}$）。这一观察结果印证了近期研究结论：深度上下文模型中的下层（上层）编码输入的浅层（语义）特征 (Peters et al., 2018; Jawahar et al., 2019; Liu et al., 2019)。

To further test this hypothesis, we sample 1600 random keys (100 keys per layer) and apply local modifications to the top-50 trigger examples of every key. Specifically, we remove either the first, last, or a random token from the input, and measure how this mutation affects the memory coefficient. Figure 3 shows that the model considers the end of an example as more salient than the beginning for predicting the next token. In upper layers, removing the last token has less impact, supporting our conclusion that upper-layer keys are less correlated with shallow patterns.

为了进一步验证这一假设，我们从每层随机抽取100个密钥（共计1600个密钥），并对每个密钥的前50个触发样本进行局部修改。具体而言，我们从输入中删除首个、末尾或随机一个token，并测量这种变异对记忆系数的影响。图3显示，模型在预测下一个token时，对样本结尾的关注度显著高于开头部分。在高层网络中，删除末尾token产生的影响更小，这支持了我们的结论：高层密钥与浅层模式的相关性较低。

4 Values Represent Distributions

4 值代表分布

After establishing that keys capture patterns in training examples, we turn to analyze the information stored in their corresponding values. We show that each value $\mathbf{v}_ {i}^{\ell}$ can be viewed as a distribution over the output vocabulary, and demonstrate that this distribution complements the patterns in the corresponding key $\mathbf{k}_{i}^{\ell}$ in the model’s upper layers (see Figure 1).

在确认键(key)能够捕捉训练样本中的模式后，我们转而分析其对应值(value)中存储的信息。研究表明，每个值$\mathbf{v}_ {i}^{\ell}$可视为输出词汇表上的概率分布，且该分布能够补充模型高层中对应键$\mathbf{k}_{i}^{\ell}$的模式 (见图1)。

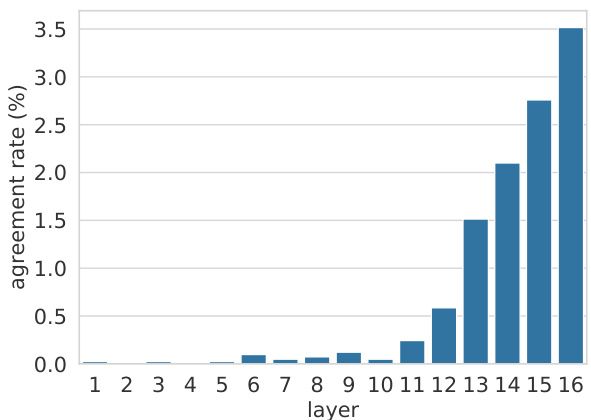
Figure 4: Agreement rate between the top-ranked token based on the value vector $\mathbf{v}_ {i}^{\ell}$ , and the next token of the top-ranked trigger example associated with the key vector $\mathbf{k}_{i}^{\ell}$ .

图 4: 基于值向量 $\mathbf{v}_ {i}^{\ell}$ 的最高排名token与关键向量 $\mathbf{k}_{i}^{\ell}$ 相关联的最高排名触发示例的下一个token之间的一致率。

Casting values as distributions over the vocabulary. We begin by converting each value vector $\mathbf{v}_{i}^{\ell}$ into a probability distribution over the vocabulary by multiplying it by the output embedding matrix $E$ and applying a softmax:4

将数值转换为词汇表上的分布。我们首先通过将每个值向量 $\mathbf{v}_{i}^{\ell}$ 与输出嵌入矩阵 $E$ 相乘并应用 softmax 函数，将其转换为词汇表上的概率分布:4

$$
\mathbf{p}_ {i}^{\ell}=\mathrm{softmax}(\mathbf{v}_{i}^{\ell}\cdot E).
$$

$$
\mathbf{p}_ {i}^{\ell}=\mathrm{softmax}(\mathbf{v}_{i}^{\ell}\cdot E).
$$

The probability distribution $\mathbf{p}_ {i}^{\ell}$ is un calibrated, since the value vector $\mathbf{v}_ {i}^{\ell}$ is typically multiplied by the input-dependent memory coefficient $\mathbf{m}_ {i}^{\ell}$ , changing the skewness of the output distribution. That said, the ranking induced by $\mathbf{p}_{i}^{\ell}$ is invariant to the coefficient, and can still be examined. This conversion assumes (naïvely) that all model’s layers operate in the same embedding space.

概率分布 $\mathbf{p}_ {i}^{\ell}$ 未经校准，因为值向量 $\mathbf{v}_ {i}^{\ell}$ 通常会乘以与输入相关的记忆系数 $\mathbf{m}_ {i}^{\ell}$，从而改变输出分布的偏度。尽管如此，由 $\mathbf{p}_{i}^{\ell}$ 诱导的排序对该系数保持不变，仍可被检验。这一转换（简单）假设所有模型层在相同的嵌入空间中操作。

Value predictions follow key patterns in upper layers. For every layer $\ell$ and memory dimension $i$ , we compare the top-ranked token according to $\mathbf{v}_ {i}^{\ell}$ , $(\mathrm{argmax}(\mathbf{p}_ {i}^{\ell}))$ to the next token $w_{i}^{\ell}$ in the top1 trigger example according to $\mathbf{k}_ {i}^{\ell}$ (the example whose memory coefficient for $\mathbf{k}_ {i}^{\ell}$ is the highest). Figure 4 shows the agreement rate, i.e. the fraction of memory cells (dimensions) where the value’s top prediction matches the key’s top trigger example (argmax $(\mathbf{p}_ {i}^{\ell})=w_{i}^{\ell})$ . It can be seen that the agreement rate is close to zero in the lower layers (1-10), but starting from layer 11, the agreement rate quickly rises until $3.5%$ , showing higher agreement between keys and values on the identity of the top-ranked token. Importantly, this value is orders of magnitude higher than a random token prediction from the vocabulary, which would produce a far lower agreement rate $(0.0004%)$ , showing that upper-layer memories manifest non-trivial predictive power.

值预测遵循上层的关键模式。对于每一层 $\ell$ 和记忆维度 $i$，我们根据 $\mathbf{v}_ {i}^{\ell}$ 比较排名最高的 token $(\mathrm{argmax}(\mathbf{p}_ {i}^{\ell}))$ 与 $\mathbf{k}_ {i}^{\ell}$ 的 top1 触发示例中的下一个 token $w_{i}^{\ell}$（即 $\mathbf{k}_ {i}^{\ell}$ 记忆系数最高的示例）。图 4 显示了一致率，即值的 top 预测与键的 top 触发示例匹配的记忆单元（维度）比例（argmax $(\mathbf{p}_ {i}^{\ell})=w_{i}^{\ell})$）。可以看出，较低层（1-10）的一致率接近于零，但从第 11 层开始，一致率迅速上升至 $3.5%$，表明键和值在 top-ranked token 的识别上具有更高的一致性。重要的是，该值比从词汇表中随机预测 token 的一致率高出多个数量级（随机预测的一致率为 $(0.0004%)$），这表明上层记忆具有显著的预测能力。

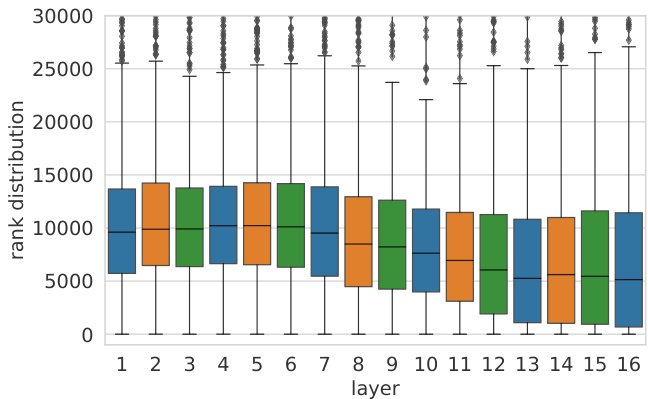
Figure 5: Distribution of the rank of the next-token in the top-1 trigger example of $\mathbf{k}_ {i}^{\ell}~(w_{i}^{\ell})$ , according to the ranking induced by the value vector $\mathbf{v}_{i}^{\ell}$ . We cut the tail of the distribution, which stretches up to the vocabulary size ( ${\sim}270\mathrm{K}$ tokens).

图 5: 根据值向量 $\mathbf{v}_ {i}^{\ell}$ 排序得出的 $\mathbf{k}_ {i}^{\ell}~(w_{i}^{\ell})$ 在top-1触发样本中下一token的排名分布。我们截断了分布的尾部 (该部分延伸至词汇表大小 ${\sim}270\mathrm{K}$ tokens)。

Next, we take the next token of $\mathbf{k}_ {i}^{\ell}$ ’s top-1 trigger example $(w_{i}^{\ell})$ , and find where it ranks in the value vector’s distribution $\mathbf{p}_ {i}^{\ell}$ . Figure 5 shows that the rank of the next token of a trigger example increases through the layers, meaning that $w_{i}^{\ell}$ tends to get higher probability in the upper layers.

接下来，我们取出 $\mathbf{k}_ {i}^{\ell}$ 的 top-1 触发样本 $(w_{i}^{\ell})$ 的下一个 token，并查找它在值向量分布 $\mathbf{p}_ {i}^{\ell}$ 中的排名。图 5 显示，触发样本的下一个 token 的排名随着层数的增加而上升，这意味着 $w_{i}^{\ell}$ 在更高层中倾向于获得更高的概率。

Detecting predictive values. To examine if we can automatically detect values with high agreement rate, we analyze the probability of the values’ top prediction, i.e., $(\operatorname*{max}(\mathbf{p}_ {i}^{\ell}))$ . Figure 6 shows that although these distributions are not calibrated, distributions with higher maximum probabilities are more likely to agree with their key’s top trigger example. We then take the 100 values with highest probability across all layers and dimensions (97 out of the 100 are in the upper layers, 11-16), and for each value $\mathbf{v}_ {i}^{\ell}$ , analyze the top-50 trigger examples of $\mathbf{k}_{i}^{\ell}$ . We find that in almost half of the values (46 out of 100), there is at least one trigger example that agrees with the value’s top prediction. Examples are provided in Table 2.

检测预测值。为了检验是否能自动检测出高一致率的值，我们分析了这些值最高预测的概率，即 $(\operatorname*{max}(\mathbf{p}_ {i}^{\ell}))$。图6显示，尽管这些分布未经过校准，但具有较高最大概率的分布更可能与其键的顶部触发示例一致。随后，我们选取所有层和维度中概率最高的100个值（其中97个位于上层11-16），并对每个值 $\mathbf{v}_ {i}^{\ell}$ 分析其对应键 $\mathbf{k}_{i}^{\ell}$ 的前50个触发示例。研究发现，近半数（100个中的46个）的值至少有一个触发示例与其最高预测结果一致。具体示例如表2所示。

Discussion. When viewed as distributions over the output vocabulary, values in the upper layers tend to assign higher probability to the nexttoken of examples triggering the corresponding keys. This suggests that memory cells often store information on how to directly predict the output (the distribution of the next word) from the input (patterns in the prefix). Conversely, the lower layers do not exhibit such clear correlation between the keys’ patterns and the corresponding values’ distributions. A possible explanation is that the lower layers do not operate in the same embedding space, and therefore, projecting values onto the vocabulary using the output embeddings does not produce distributions that follow the trigger examples. However, our results imply that some intermediate layers do operate in the same or similar space to upper layers (exhibiting some agreement), which in itself is non-trivial. We leave further exploration of this phenomenon to future work.

讨论。当将上层中的值视为输出词汇表上的分布时，它们往往会给触发对应键的示例的下一个token分配更高的概率。这表明记忆单元通常存储了如何直接从输入（前缀中的模式）预测输出（下一个词的分布）的信息。相反，下层并未表现出键的模式与对应值的分布之间存在如此明显的关联。一个可能的解释是，下层并不在相同的嵌入空间中运作，因此使用输出嵌入将值投影到词汇表上时，生成的分布不会遵循触发示例的模式。然而，我们的结果表明，某些中间层确实在与上层相同或相似的空间中运作（表现出一定的一致性），这本身就是一个重要的发现。我们将对此现象的进一步探索留待未来工作。

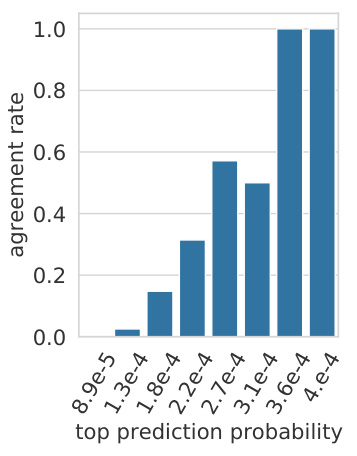
Figure 6: Agreement rate (between the top-ranked token based on the value vector $\mathbf{v}_ {i}^{\ell}$ and the next token of the top-ranked trigger example associated with the key vector $\mathbf{k}_{i}^{\ell}.$ ) as a function of the maximal probability assigned by the value vector.

图 6: 基于值向量 $\mathbf{v}_ {i}^{\ell}$ 的最高排名token与关键向量 $\mathbf{k}_{i}^{\ell}$ 关联的最高排名触发示例的下一个token之间的一致率，作为值向量分配的最大概率的函数。

5 Aggregating Memories

5 记忆聚合

So far, our discussion has been about the function of a single memory cell in feed-forward layers. How does the information from multiple cells in multiple layers aggregate to form a model-wide prediction? We show that every feed-forward layer combines multiple memories to produce a distribution that is qualitatively different from each of its component memories’ value distributions (Section 5.1). These layer-wise distributions are then combined via residual connections in a refinement process, where each feed-forward layer updates the residual’s distribution to finally form the model’s output (Section 5.2).

到目前为止，我们的讨论一直集中在单个记忆单元在前馈层中的功能。来自多层多个单元的信息如何聚合形成模型整体的预测？我们发现，每个前馈层都会组合多个记忆，产生一个在性质上不同于其各组成记忆值分布的分布（见5.1节）。这些逐层分布随后通过残差连接在精炼过程中进行组合，其中每个前馈层都会更新残差的分布，最终形成模型的输出（见5.2节）。

Table 2: Example values, their top prediction, the fraction of their key’s top-50 trigger examples that agree with their prediction, and a matching trigger example (with the target token marked in blue).

Value	Prediction	Precision@50	Triggerexample
V222 15	each	68%	Butwhenbeesandwaspsresembleeach
16 V752	played	16%	HerfirstrolewasinVijayLalwani'spsychologicalthrillerKarthikCalling Karthik,wherePadukonewascastasthesupportivegirlfriendofadepressed man(played
V2601 13	extratropical	4%	Mostofthewinterprecipitationistheresultofsynopticscale,lowpressure weathersystems(largescalestormssuchasextratropical
15 V881	part	92%	Cometservedonlybriefywiththefleet,owinginlargepart
16 V2070	line	84%	SailingfromLorientinOctober1805withoneshipoftheline
V3186 12	jail	4%	OnMay11,2011,fourdays afterscoring6touchdownsfortheSlaughter,Grady wassentencedtotwentydaysinjail

表 2: 示例数值、其最高预测结果、其关键触发示例中与预测一致的前50名比例，以及匹配的触发示例（目标token用蓝色标出）。

数值	预测结果	前50名准确率	触发示例
V222 15	each	68%	Butwhenbeesandwaspsresembleeach
16 V752	played	16%	HerfirstrolewasinVijayLalwani'spsychologicalthrillerKarthikCalling Karthik,wherePadukonewascastasthesupportivegirlfriendofadepressed man(played
V2601 13	extratropical	4%	Mostofthewinterprecipitationistheresultofsynopticscale,lowpressure weathersystems(largescalestormssuchasextratropical
15 V881	part	92%	Cometservedonlybriefywiththefleet,owinginlargepart
16 V2070	line	84%	SailingfromLorientinOctober1805withoneshipoftheline
V3186 12	jail	4%	OnMay11,2011,fourdays afterscoring6touchdownsfortheSlaughter,Grady wassentencedtotwentydaysinjail

5.1 Intra-Layer Memory Composition

5.1 层内内存构成

The feed-forward layer’s output can be defined as the sum of value vectors weighted by their memory coefficients, plus a bias term:

前馈层的输出可以定义为值向量按其记忆系数加权之和，加上偏置项：

$$
\mathbf{y}^{\ell}=\sum_{i}\mathrm{ReLU}(\mathbf{x}^{\ell}\cdot\mathbf{k}_ {i}^{\ell})\cdot\mathbf{v}_{i}^{\ell}+\mathbf{b}^{\ell}.
$$

$$
\mathbf{y}^{\ell}=\sum_{i}\mathrm{ReLU}(\mathbf{x}^{\ell}\cdot\mathbf{k}_ {i}^{\ell})\cdot\mathbf{v}_{i}^{\ell}+\mathbf{b}^{\ell}.
$$

If each value vector $\mathbf{v}_{i}^{\ell}$ contains information about the target token’s distribution, how is this information aggregated into a single output distribution? To find out, we analyze the behavior of 4,000 randomly-sampled prefixes from the validation set. Here, the validation set is used (rather than the training set used to find trigger examples) since we are trying to characterize the model’s behavior at inference time, not find the examples it “memorizes” during training.

如果每个值向量 $\mathbf{v}_{i}^{\ell}$ 都包含目标token分布的信息，这些信息如何聚合为单一输出分布？为探究这一点，我们分析了从验证集中随机采样的4,000个前缀的行为。此处使用验证集（而非用于寻找触发样本的训练集）是因为我们试图表征模型在推理时的行为，而非寻找其在训练期间"记忆"的样本。

We first measure the fraction of “active” memories (cells with a non-zero coefficient). Figure 7 shows that a typical example triggers hundreds of memories per layer $10%-50%$ of 4096 dimen- sions), but the majority of cells remain inactive. Interestingly, the number of active memories drops towards layer 10, which is the same layer in which semantic patterns become more prevalent than shallow patterns, according to expert annotations (see Section 3, Figure 2).

我们首先测量了"活跃"记忆(具有非零系数的单元)的比例。图7显示，一个典型示例每层会触发数百个记忆(占4096维度的10%-50%)，但大多数单元仍处于非活跃状态。有趣的是，活跃记忆数量在第10层附近开始下降，而根据专家标注(见第3节图2)，该层正是语义模式开始比浅层模式更普遍的层级。

While there are cases where a single memory cell dominates the output of a layer, the majority of outputs are clearly compositional. We count the number of instances where the feed-forward layer’s top prediction is different from all of the memories’ top predictions. Formally, we denote:

虽然存在单个记忆单元主导层输出的情况，但大多数输出明显具有组合性。我们统计了前馈层最高预测与所有记忆单元最高预测不同的实例数量。具体表示为：

$$
\mathrm{top}({\bf h})=\mathrm{argmax}({\bf h}\cdot E)
$$

$$
\mathrm{top}({\bf h})=\mathrm{argmax}({\bf h}\cdot E)
$$

as a generic shorthand for the top prediction from the vocabulary distribution induced by the vector

作为由向量诱导出的词汇分布中最高预测的通用简称

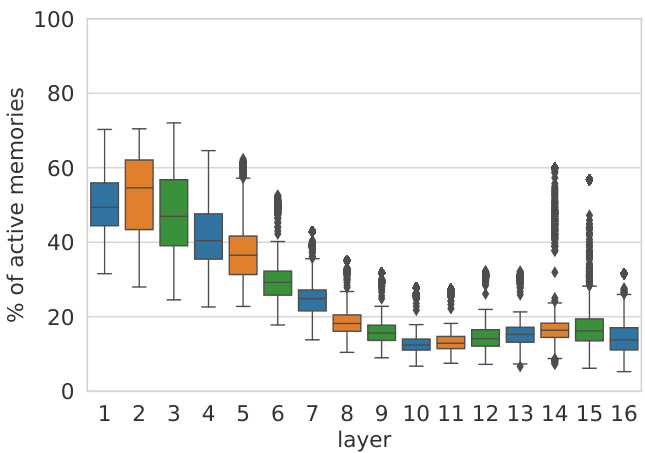
Figure 7: The fraction of active memories (i.e., with positive memory coefficient) out of 4096 memories in every layer, for a random sample of 4,000 examples.

图 7: 随机抽取的4,000个样本中，每一层4096个记忆里活跃记忆(即记忆系数为正)所占的比例。

h, and compute the number of examples where the following condition holds:

h，并计算满足以下条件的示例数量：

$$
\forall i:\mathrm{top}(\mathbf{v}_{i}^{\ell})\neq\mathrm{top}(\mathbf{y}^{\ell})
$$

$$
\forall i:\mathrm{top}(\mathbf{v}_{i}^{\ell})\neq\mathrm{top}(\mathbf{y}^{\ell})
$$

Figure 8 shows that, for any layer in the network, the layer’s final prediction is different than every one of the memories’ predictions in at least ${\sim}68%$ of the examples. Even in the upper layers, where the memories’ values are more correlated with the output space (Section 4), the layer-level prediction is typically not the result of a single dominant memory cell, but a composition of multiple memories.

图 8 表明，对于网络中的任何一层，该层的最终预测在至少 ${\sim}68%$ 的样本中都与每个记忆单元的预测不同。即使在高层（记忆值与输出空间相关性更强的部分，如第 4 节所述），层级的预测通常也不是由单个主导记忆单元决定的，而是多个记忆单元组合的结果。

We further analyze cases where at least one memory cell agrees with the layer’s prediction, and find that (a) in $60%$ of the examples the target token is a common stop word in the vocabulary (e.g. “the” or “of”), and (b) in $43%$ of the cases the input prefix has less than 5 tokens. This suggests that very common patterns in the training data might be “cached” in individual memory cells, and do not require compositional it y.

我们进一步分析了至少有一个记忆单元与层级预测一致的案例，发现：(a) 在 $60%$ 的样本中目标token是词汇表中的常见停用词（如"the"或"of"），(b) 在 $43%$ 的案例中输入前缀少于5个token。这表明训练数据中的高频模式可能被"缓存"在单个记忆单元中，无需组合处理。

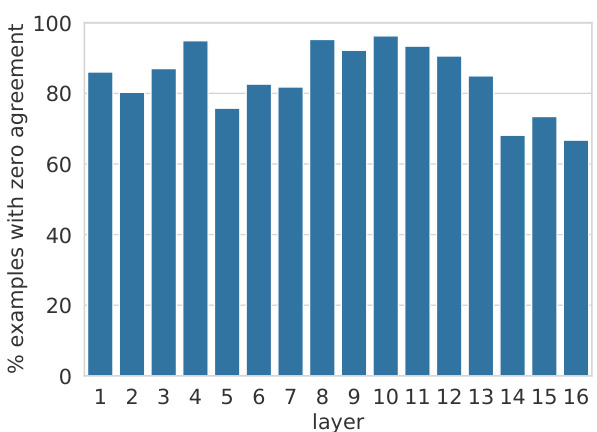
Figure 8: The fraction of examples in a random sample of 4,000 examples where the layer’s prediction is different from the prediction of all of its memories.

图 8: 在随机抽样的 4000 个样本中，该层的预测结果与其所有记忆的预测结果不同的样本比例。

5.2 Inter-Layer Prediction Refinement

5.2 层间预测优化

While a single feed-forward layer composes its memories in parallel, a multi-layer model uses the residual connection $\mathbf{r}$ to sequentially compose predictions to produce the model’s final output:5

虽然单层前馈网络并行组合记忆，但多层模型通过残差连接 $\mathbf{r}$ 逐步组合预测以生成最终输出：5

$$
\begin{array}{r l}&{\mathbf{x}^{\ell}=\mathrm{LayerNorm}(\mathbf{r}^{\ell})}\ &{\mathbf{y}^{\ell}=\mathrm{FF}(\mathbf{x}^{\ell})}\ &{\mathbf{o}^{\ell}=\mathbf{y}^{\ell}+\mathbf{r}^{\ell}}\end{array}
$$

$$
\begin{array}{r l}&{\mathbf{x}^{\ell}=\mathrm{LayerNorm}(\mathbf{r}^{\ell})}\ &{\mathbf{y}^{\ell}=\mathrm{FF}(\mathbf{x}^{\ell})}\ &{\mathbf{o}^{\ell}=\mathbf{y}^{\ell}+\mathbf{r}^{\ell}}\end{array}
$$

We hypothesize that the model uses the sequential composition apparatus as a means to refine its prediction from layer to layer, often deciding what the prediction will be at one of the lower layers.

我们假设该模型使用序列组合机制作为逐层优化预测的手段，通常会在较低层之一就决定预测结果。

To test our hypothesis, we first measure how often the probability distribution induced by the residual vector $\mathbf{r}^{\ell}$ matches the model’s final output $\mathbf{o}^{L}$ ( $L$ being the total number of layers):

为了验证我们的假设，我们首先测量由残差向量 $\mathbf{r}^{\ell}$ 诱导的概率分布与模型最终输出 $\mathbf{o}^{L}$ ( $L$ 为总层数) 匹配的频率：

$$
\mathrm{top}(\mathbf{r}^{\ell})=\mathrm{top}(\mathbf{o}^{L})
$$

$$
\mathrm{top}(\mathbf{r}^{\ell})=\mathrm{top}(\mathbf{o}^{L})
$$

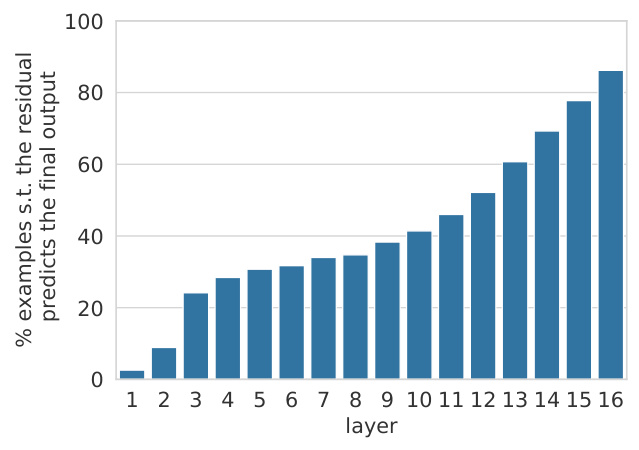
Figure 9 shows that roughly a third of the model’s predictions are determined in the bottom few layers. This number grows rapidly from layer 10 onwards, implying that the majority of “hard” decisions occur before the final layer.

图 9: 显示约三分之一的模型预测由底部少数几层决定。从第10层开始，这一数字迅速增长，意味着大多数"困难"决策发生在最终层之前。

We also measure the probability mass $p$ that each layer’s residual vector $\mathbf{r}^{\ell}$ assigns to the model’s

我们还测量了每层残差向量 $\mathbf{r}^{\ell}$ 分配给模型的概率质量 $p$。

Figure