Planning to Explore via Self-Supervised World Models
通过自监督世界模型进行探索规划
Ramanan Sekar 1 * Oleh Rybkin 1 * Kostas Daniilidis 1 Pieter Abbeel 2 Danijar Hafner 3 4 Deepak Pathak 5 6
Ramanan Sekar 1* Oleh Rybkin 1* Kostas Daniilidis 1 Pieter Abbeel 2 Danijar Hafner 3 4 Deepak Pathak 5 6
Abstract
摘要
Reinforcement learning allows solving complex tasks, however, the learning tends to be taskspecific and the sample efficiency remains a challenge. We present Plan 2 Explore, a selfsupervised reinforcement learning agent that tackles both these challenges through a new approach to self-supervised exploration and fast adaptation to new tasks, which need not be known during exploration. During exploration, unlike prior methods which retrospectively compute the novelty of observations after the agent has already reached them, our agent acts efficiently by leveraging planning to seek out expected future novelty. After exploration, the agent quickly adapts to multiple downstream tasks in a zero or a few-shot manner. We evaluate on challenging control tasks from high-dimensional image inputs. Without any training supervision or taskspecific interaction, Plan 2 Explore outperforms prior self-supervised exploration methods, and in fact, almost matches the performances oracle which has access to rewards. Videos and code: https://ramanans1.github.io/ plan 2 explore/
强化学习能够解决复杂任务,但学习过程往往针对特定任务且样本效率仍是挑战。我们提出Plan 2 Explore,这是一种自监督强化学习智能体,通过新颖的自监督探索方法和快速适应新任务的能力(探索期间无需知晓任务)来应对这些挑战。在探索阶段,与现有方法仅在智能体到达观测点后回溯计算新颖性不同,我们的智能体通过规划主动寻求预期未来新颖性来高效行动。探索结束后,该智能体能以零样本或少样本方式快速适应多个下游任务。我们在高维图像输入的复杂控制任务上进行了评估。在没有任何训练监督或任务特定交互的情况下,Plan 2 Explore超越了现有自监督探索方法,其性能甚至接近可获取奖励信息的预言机系统。视频与代码:https://ramanans1.github.io/plan2explore/
Figure 1. The agent first leverages planning to explore in a selfsupervised manner, without task-specific rewards, to efficiently learn a global world model. After the exploration phase, it receives reward functions at test time to adapt to multiple downstream tasks, such as standing, walking, running, and flipping using either zero or few tasks-specific interactions.
图 1: 该智能体首先利用规划以自监督方式进行探索 (无需任务特定奖励) ,高效学习全局世界模型。探索阶段结束后,它会在测试时接收奖励函数,从而适应多种下游任务,例如通过零样本或少样本任务特定交互实现站立、行走、奔跑和翻转等动作。
Task-agnostic RL Because data collection is often expensive, it would be ideal to not keep collecting data for each new task. Hence, we explore the environment once without reward to collect a diverse dataset for later solving any downstream task, as shown in Figure 1. After the task-agnostic exploration phase, the agent is provided with downstream reward functions and needs to solve the tasks with limited or no further environment interaction. Such a self-supervised approach would allow solving various tasks without having to repeat the expensive data collection for each new task.
任务无关的强化学习
由于数据收集通常成本高昂,理想情况是不必为每个新任务持续收集数据。因此,我们会在无奖励的情况下对环境进行一次探索,收集多样化的数据集以供后续解决任何下游任务,如图 1 所示。在任务无关的探索阶段结束后,智能体会获得下游奖励函数,并需要在有限或无需进一步环境交互的情况下解决任务。这种自监督方法可以解决各种任务,而无需为每个新任务重复昂贵的数据收集过程。
1. Introduction
1. 引言
The dominant approach in sensor i motor control is to train the agent on one or more pre-specified tasks either via rewards in reinforcement learning, or via demonstrations in imitation learning. However, learning each task from scratch is often inefficient, requiring a large amount of task-specific environment interaction for solving each task. How can an agent quickly generalize to unseen tasks it has never experienced before in a zero or few-shot manner?
传感器和运动控制领域的主流方法是通过强化学习中的奖励机制或模仿学习中的示范来训练智能体完成一个或多个预设任务。然而,从零开始学习每个任务通常效率低下,需要大量针对特定任务的环境交互才能解决。如何让智能体以零样本或少样本方式快速泛化到从未经历过的未知任务?
Intrinsic motivation To explore complex environments in the absence of rewards, the agent needs to follow a form of intrinsic motivation that is computed from inputs that could be high-dimensional images. For example, an agent could seek inputs that it cannot yet predict accurately (Schmidhuber, 1991b; Oudeyer et al., 2007; Pathak et al., 2017), maximally influence its inputs (Klyubin et al., 2005; Eysenbach et al., 2018), or visit rare states (Poupart et al., 2006; Lehman & Stanley, 2011; Bellemare et al., 2016; Burda et al., 2018). However, most prior methods learn a modelfree exploration policy to act in the environment which needs large amounts of samples for finetuning or adaptation when presented with rewards for downstream tasks.
内在动机
在缺乏奖励的情况下探索复杂环境时,智能体需要遵循一种从可能为高维图像的输入中计算得出的内在动机形式。例如,智能体可能会寻求那些它尚无法准确预测的输入 (Schmidhuber, 1991b; Oudeyer et al., 2007; Pathak et al., 2017),最大化影响其输入 (Klyubin et al., 2005; Eysenbach et al., 2018),或访问罕见状态 (Poupart et al., 2006; Lehman & Stanley, 2011; Bellemare et al., 2016; Burda et al., 2018)。然而,大多数现有方法学习的是无模型探索策略,用于在环境中行动,这在下游任务出现奖励时需要大量样本进行微调或适应。
Retrospective novelty Model-free exploration methods not only require large amounts of experience to adapt to downstream tasks, they can also be inefficient during exploration. These agents usually first act in the environment, collect trajectories and then calculate an intrinsic reward as the agent’s current estimate of novelty. This approach misses out on efficiency by operating retrospectively, that is, the novelty of inputs is computed after the agent has already reached them. For instance, in curiosity (Pathak et al., 2017), novelty is measured by computing error between the prediction of the next state and the ground truth only after the agent has visited the next state. Hence, it seeks out previously novel inputs that have already been visited and would not be novel anymore. Instead, one should directly seek out future inputs that are expected to be novel.
回顾式新颖性
无模型探索方法不仅需要大量经验来适应下游任务,在探索过程中也可能效率低下。这些智能体通常先在环境中行动,收集轨迹,然后计算内在奖励作为当前对新颖性的估计。这种回顾式操作方式会错失效率,即在智能体已经到达输入后才计算其新颖性。例如,在好奇心驱动方法 (Pathak et al., 2017) 中,只有在智能体访问下一个状态后,才通过计算下一状态预测值与真实值的误差来衡量新颖性。因此,它会寻找那些已被访问过、不再具备新颖性的先前输入。相反,我们应该直接寻找预期具有新颖性的未来输入。
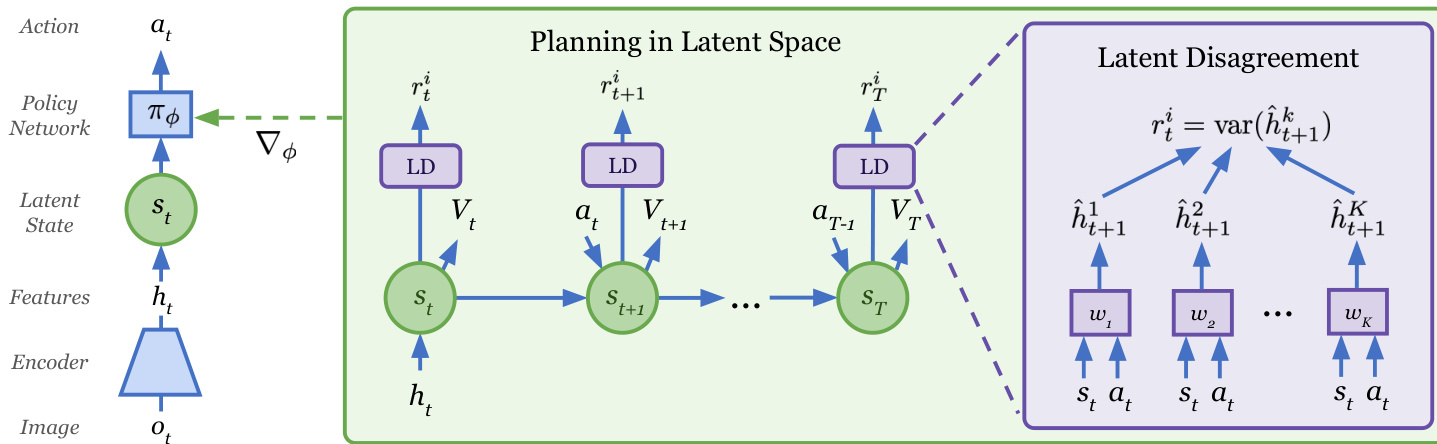
Figure 2. Overview of Plan 2 Explore. Each observation $o_{t}$ at time $t$ is first encoded into features $h_{t}$ which are then used to infer a recurrent latent state $s_{t}$ . At each training step, the agent leverages planning to explore by imagining the consequences of the actions of policy $\pi_{\phi}$ using the current world model. The planning objective is to maximize expected novelty $r_{t}^{i}$ over all future time steps, computed as the disagreement in the predicted next image embedding $h_{t+1}$ from an ensemble of learned transition dynamics $w_{k}$ . This planning objective is back propagated all the way through the imagined rollout states to improve the exploration policy $\pi_{\phi}$ . The learned model is used for planning to explore in latent space, and the data collected during exploration is in turn used to improve the model. This world model is then later used to plan for novel tasks at test time by replacing novelty reward with task reward.
图 2: Plan 2 Explore 框架概览。每个时刻 $t$ 的观测值 $o_{t}$ 首先被编码为特征 $h_{t}$,随后用于推断循环潜在状态 $s_{t}$。在每次训练步骤中,智能体利用当前世界模型,通过想象策略 $\pi_{\phi}$ 动作的后果来进行规划探索。规划目标是最大化所有未来时间步的预期新颖性 $r_{t}^{i}$,该值通过一组学习到的转移动态 $w_{k}$ 对下一图像嵌入 $h_{t+1}$ 的预测差异计算得出。该规划目标通过反向传播贯穿整个想象推演状态,以改进探索策略 $\pi_{\phi}$。学习到的模型用于潜在空间中的探索规划,而探索期间收集的数据又用于改进模型。在测试阶段,该世界模型可通过将新颖性奖励替换为任务奖励,用于新任务的规划。
Planning to explore We address both of these challenges – quick adaptation and expected future novelty – within a common framework while learning directly from highdimensional image inputs. Instead of maximizing intrinsic rewards in retrospect, we learn a world model to plan ahead and seek out the expected novelty of future situations. This lets us learn the exploration policy purely from imagined model states, without causing additional environment interaction (Sun et al., 2011; Shyam et al., 2019). The exploration policy is optimized purely from trajectories imagined under the model to maximize the intrinsic rewards computed by the model itself. After the exploration phase, the learned world model is used to train downstream task policies in imagination via offline reinforcement learning, without any further environment interaction.
规划探索
我们在一个共同框架内解决了这两个挑战——快速适应和预期的未来新奇性——同时直接从高维图像输入中学习。不同于事后最大化内在奖励,我们通过学习一个世界模型来提前规划并寻找未来情境的预期新奇性。这使得我们能够纯粹从想象出的模型状态中学习探索策略,无需额外的环境交互 (Sun et al., 2011; Shyam et al., 2019)。探索策略完全基于模型想象的轨迹进行优化,以最大化模型自身计算的内在奖励。在探索阶段结束后,学习到的世界模型通过离线强化学习在想象中训练下游任务策略,无需任何进一步的环境交互。
Challenges The key challenges for planning to explore are to train an accurate world model from high-dimensional inputs and to define an effective exploration objective. We focus on world models that predict ahead in a compact latent space and have recently been shown to solve challenging control tasks from images (Hafner et al., 2019; Zhang et al., 2019). Predicting future compact representations facilitates accurate long-term predictions and lets us efficiently predict thousands of future sequences in parallel for policy learning.
挑战
规划探索的关键挑战在于从高维输入中训练出准确的世界模型,并定义有效的探索目标。我们专注于在紧凑的潜在空间中进行预测的世界模型,这类模型近期已被证明能解决基于图像的复杂控制任务 (Hafner et al., 2019; Zhang et al., 2019)。预测未来的紧凑表征有助于实现精准的长期预测,并让我们能够高效地并行预测数千条未来序列以进行策略学习。
An ideal exploration objective should seek out inputs that the agent can learn the most from (epistemic uncertainty) while being robust to stochastic parts of the environment that cannot be learned accurately (aleatoric uncertainty). This is formalized in the expected information gain (Lindley, 1956), which we approximate as the disagreement in predictions of an ensemble of one-step models. These one-step models are trained alongside the world model and mimic its transition function. The disagreement is positive for novel states, but given enough samples, it eventually reduces to zero even for stochastic environments because all one-step predictions converge to the mean of the next input (Pathak et al., 2019).
理想的探索目标应寻找智能体最能从中学习的输入(认知不确定性),同时对环境中无法准确学习的随机部分(偶然不确定性)保持稳健。这一目标通过预期信息增益(Lindley, 1956)得以形式化,我们将其近似为一组单步模型预测间的分歧度。这些单步模型与世界模型同步训练,模拟其转移函数。对于新异状态,分歧度为正;但在获得足够样本后,即使对于随机环境,分歧度最终也会降为零,因为所有单步预测都会收敛至下一输入的均值(Pathak et al., 2019)。
Contributions We introduce Plan 2 Explore, a selfsupervised reinforcement learning agent that leverages planning to efficiently explore visual environments without rewards. Across 20 challenging control tasks without access to proprio ce pti ve states or rewards, Plan 2 Explore achieves state-of-the-art zero-shot and adaptation performance. Moreover, we empirically study the questions:
贡献
我们提出了Plan 2 Explore,这是一种自监督强化学习智能体,利用规划高效探索无奖励的视觉环境。在20个无法获取本体感知状态或奖励的挑战性控制任务中,Plan 2 Explore实现了最先进的零样本和适应性能。此外,我们通过实证研究了以下问题:
• How does planning to explore via latent disagreement compare to a supervised oracle and other model-free and model-based intrinsic reward objectives? • How much task-specific experience is enough to finetune a self-supervised model to reach the performance of a task-specific agent? • To what degree does a self-supervised model generalize to unseen tasks compared to a task-specific model trained on a different task in the same environment? • What is the advantage of maximizing expected future novelty in comparison to retrospective novelty?
• 通过潜在分歧进行探索的规划与监督式先知方法及其他无模型和基于模型的内在奖励目标相比如何?
• 需要多少任务特定经验才能微调自监督模型,使其达到任务特定智能体的性能?
• 与在同一环境中针对不同任务训练的任务特定模型相比,自监督模型对未见任务的泛化能力如何?
• 最大化预期未来新颖性与回顾性新颖性相比有何优势?
2. Control with Latent Dynamics Models
2. 基于潜在动力学模型的控制
World models summarize past experience into a representation of the environment that enables predicting imagined future sequences (Sutton, 1991; Watter et al., 2015; Ha & Schmid huber, 2018). When sensory inputs are highdimensional observations, predicting compact latent states $s_{t}$ lets us predict many future sequences in parallel due to memory efficiency.1 Specifically, we use the latent dynamics model of PlaNet (Hafner et al., 2019), that consists of the following key components that are illustrated in Figure 2,
世界模型将过去的经验总结为环境的表征,从而能够预测想象的未来序列 (Sutton, 1991; Watter et al., 2015; Ha & Schmidhuber, 2018)。当感官输入是高维观测时,预测紧凑的潜在状态 $s_{t}$ 可以让我们由于内存效率而并行预测许多未来序列。具体来说,我们使用 PlaNet (Hafner et al., 2019) 的潜在动力学模型,该模型由图 2 所示的以下关键组件组成,
$$
\begin{array}{l l}{{\mathrm{Imageencoder:}}}&{{h_{t}=e_{\theta}(o_{t})}}\ {{\mathrm{Posteriordynamics:}}}&{{q_{\theta}(s_{t}\mid s_{t-1},a_{t-1},h_{t})}}\ {{\mathrm{Priordynamics:}}}&{{p_{\theta}(s_{t}\mid s_{t-1},a_{t-1})}}\ {{\mathrm{Rewardpredictor:}}}&{{p_{\theta}(r_{t}\mid s_{t})}}\ {{\mathrm{Image~decoder:}}}&{{p_{\theta}(o_{t}\mid s_{t}).}}\end{array}
$$
$$
\begin{array}{l l}{{\mathrm{图像编码器:}}}&{{h_{t}=e_{\theta}(o_{t})}}\ {{\mathrm{后验动态模型:}}}&{{q_{\theta}(s_{t}\mid s_{t-1},a_{t-1},h_{t})}}\ {{\mathrm{先验动态模型:}}}&{{p_{\theta}(s_{t}\mid s_{t-1},a_{t-1})}}\ {{\mathrm{奖励预测器:}}}&{{p_{\theta}(r_{t}\mid s_{t})}}\ {{\mathrm{图像解码器:}}}&{{p_{\theta}(o_{t}\mid s_{t}).}}\end{array}
$$
The image encoder is implemented as a CNN, and the posterior and prior dynamics share an RSSM (Hafner et al., 2019). The temporal prior predicts forward without ac- cess to the corresponding image. The reward predictor and image decoder provide a rich learning signal to the dynamics. The distributions are parameterized as diagonal Gaussians. All model components are trained jointly similar to a variation al auto encoder (VAE) (Kingma & Welling, 2013; Rezende et al., 2014) by maximizing the evidence lower bound (ELBO).
图像编码器采用CNN实现,后验动态与先验动态共享一个RSSM (Hafner et al., 2019)。时序先验在不访问对应图像的情况下进行前向预测。奖励预测器和图像解码器为动态系统提供了丰富的学习信号。所有分布均参数化为对角高斯分布。模型各组件通过最大化证据下界(ELBO)联合训练,训练方式类似于变分自编码器(VAE) (Kingma & Welling, 2013; Rezende et al., 2014)。
Given this learned world model, we need to derive behaviors from it. Instead of online planning, we use Dreamer (Hafner et al., 2020) to efficiently learn a parametric policy inside the world model that considers long-term rewards. Specifically, we learn two neural networks that operate on latent states of the model. The state-value estimates the sum of future rewards and the actor tries to maximize these predicted values,
基于这个学习到的世界模型,我们需要从中推导出行为。我们采用Dreamer (Hafner et al., 2020) 方法,在世界模型中高效学习一个考虑长期奖励的参数化策略,而非在线规划。具体而言,我们训练两个在模型潜在状态上运作的神经网络:状态价值网络用于预估未来奖励总和,行动者网络则试图最大化这些预测值。
$$
{\mathrm{Actor}}\colon\pi(a_{t}\mid s_{t})\qquad{\mathrm{Value}}\colon\quad V(s_{t}).
$$
$$
{\mathrm{Actor}}\colon\pi(a_{t}\mid s_{t})\qquad{\mathrm{Value}}\colon\quad V(s_{t}).
$$
The learned world model is used to predict the sequences of future latent states under the current actor starting from the latent states obtained by encoding images from the replay buffer. The value function is computed at each latent state and the actor policy is trained to maximize the predicted values by propagating their gradients through the neural network dynamics model as shown in Figure 2.
学习到的世界模型用于从回放缓冲区编码图像获得的潜在状态出发,在当前行动者策略下预测未来潜在状态序列。如图2所示,价值函数在每个潜在状态处计算,并通过神经网络动力学模型传播梯度来训练行动者策略以最大化预测价值。
3. Planning to Explore
3. 探索规划
We consider a learning setup with two phases, as illustrated in Figure 1. During self-supervised exploration, the agent gathers information about the environment and summarizes
我们考虑一个包含两个阶段的学习设置,如图 1 所示。在自监督探索阶段,AI智能体 (AI Agent) 收集环境信息并进行总结
Algorithm 2 Zero and Few-Shot Task Adaptation
算法 2: 零样本与少样本任务适配
this past experience in the form of a parametric world model. After exploration, the agent is given a downstream task in the form of a reward function that it should adapt to with no or limited additional environment interaction.
这段过往经验以参数化世界模型的形式存在。探索完成后,智能体会获得一个以下游任务形式呈现的奖励函数,它需要在零或有限的环境交互下适应该任务。
During exploration, the agent begins by learning a global world model using data collected so far, and then this model is in turn used to direct agent’s exploration to collect more data, as described in Algorithm 1. This is achieved by training an exploration policy inside of the world model to seek out novel states. Novelty is estimated by ensemble disagreement in latent predictions made by 1-step transition models trained alongside the global recurrent world model. More details to follow in Section 3.1.
在探索过程中,智能体首先利用当前收集的数据学习全局世界模型(world model),随后该模型被用于引导智能体探索以收集更多数据,如算法1所述。这一机制通过在世界模型中训练探索策略来实现,该策略旨在寻找新颖状态。新颖性通过以下方式评估:与全局循环世界模型同步训练的1步转移模型在潜在预测中产生的集成分歧。更多细节详见第3.1节。
During adaptation, we can efficiently optimize a task policy by imagination inside of the world model, as shown in Algorithm 2. Since our self-supervised model is trained without being biased toward a specific task, a single trained model can be used to solve multiple downstream tasks.
在适应阶段,我们可以通过在世界模型内部进行想象来高效优化任务策略,如算法2所示。由于我们的自监督模型训练时未偏向特定任务,单个训练好的模型可用于解决多个下游任务。
3.1. Latent Disagreement
3.1. 潜在分歧
To efficiently learn a world model of an unknown environment, a successful strategy should explore the environment such as to collect new experience that improves the model the most. For this, we quantify the model’s uncertainty about its predictions for different latent states. An exploration policy then seeks out states with high uncertainty. The model is then trained on the newly acquired trajectories and reduces its uncertainty in these and the process is repeated.
为了高效学习未知环境的世界模型,成功的策略应通过探索环境来收集最能改进模型的新经验。为此,我们量化模型对不同潜在状态预测的不确定性。随后,探索策略会主动寻找具有高不确定性的状态。模型在新获取的轨迹上进行训练,降低这些状态的不确定性,并重复该过程。
Quantifying uncertainty is a long-standing open challenge in deep learning (MacKay, 1992; Gal, 2016). In this paper, we use ensemble disagreement as an empirically successful method for quantifying uncertainty (Lakshmi narayan an et al., 2017; Osband et al., 2018). As shown in Figure 2, we train a bootstrap ensemble (Breiman, 1996) to predict, from each model state, the next encoder features. The variance of the ensemble serves as an estimate of uncertainty.
量化不确定性是深度学习领域长期存在的开放挑战 (MacKay, 1992; Gal, 2016)。本文采用集成分歧 (ensemble disagreement) 作为量化不确定性的实证有效方法 (Lakshminarayanan et al., 2017; Osband et al., 2018)。如图 2 所示,我们训练了一个自助法集成 (bootstrap ensemble) (Breiman, 1996),从每个模型状态预测下一个编码器特征。集成结果的方差被用作不确定性的估计值。
Intuitively, because the ensemble models have different initi aliz ation and observe data in a different order, their predictions differ for unseen inputs. Once the data is added to the training set, however, the models will converge towards more similar predictions, and the disagreement decreases. Eventually, once the whole environment is explored, the models should converge to identical predictions.
直观上看,由于集成模型具有不同的初始化参数且数据观测顺序不同,它们对未见输入的预测会存在差异。然而,一旦数据被加入训练集,这些模型会逐渐收敛至更相似的预测结果,分歧随之降低。最终当整个环境被充分探索后,各模型应会收敛至完全一致的预测。
Formally, we define a bootstrap ensemble of one-step predictive models with parameters ${w_{k}|k\in[1;K]}$ . Each of these models takes a model state $s_{t}$ and action $a_{t}$ as input and predicts the next image embedding $h_{t+1}$ . The models are trained with the mean squared error, which is equivalent to Gaussian log-likelihood,
形式上,我们定义了一个一步预测模型的引导集成 (bootstrap ensemble),其参数为 ${w_{k}|k\in[1;K]}$。每个模型以模型状态 $s_{t}$ 和动作 $a_{t}$ 作为输入,并预测下一个图像嵌入 $h_{t+1}$。这些模型通过均方误差(等同于高斯对数似然)进行训练。
$$
\begin{array}{r l}&{\mathrm{Ensemble~predictors:}\quad q(h_{t+1}\mid w_{k},s_{t},a_{t})}\ &{q(h_{t+1}\mid w_{k},s_{t},a_{t})\triangleq\mathcal{N}(\mu(w_{k},s_{t},a_{t}),1).}\end{array}
$$
$$
\begin{array}{r l}&{\mathrm{集成预测器:}\quad q(h_{t+1}\mid w_{k},s_{t},a_{t})}\ &{q(h_{t+1}\mid w_{k},s_{t},a_{t})\triangleq\mathcal{N}(\mu(w_{k},s_{t},a_{t}),1).}\end{array}
$$
We quantify model uncertainty as the variance over predicted means of the different ensemble members and use this disagreement as the intrinsic reward $\operatorname{ir}_ {t}\triangleq\operatorname{D}(s_{t},a_{t})$ to train the exploration policy,
我们通过不同集成成员预测均值的方差来量化模型不确定性,并将这种分歧作为内在奖励 $\operatorname{ir}_ {t}\triangleq\operatorname{D}(s_{t},a_{t})$ 用于训练探索策略。
$$
\begin{array}{r l}&{\mathrm{D}\big(s_{t},a_{t}\big)\triangleq\operatorname{Var}\big({\mu(w_{k},s_{t},a_{t})\big\vert k\in[1;K]}\big)}\ &{\qquad=\displaystyle\frac{1}{K-1}\sum_{k}\big(\mu(w_{k},s_{t},a_{t})-\mu^{\prime}\big)^{2},}\ &{\mu^{\prime}\triangleq\displaystyle\frac{1}{K}\sum_{k}\mu\big(w_{k},s_{t},a_{t}\big).}\end{array}
$$
$$
\begin{array}{r l}&{\mathrm{D}\big(s_{t},a_{t}\big)\triangleq\operatorname{Var}\big({\mu(w_{k},s_{t},a_{t})\big\vert k\in[1;K]}\big)}\ &{\qquad=\displaystyle\frac{1}{K-1}\sum_{k}\big(\mu(w_{k},s_{t},a_{t})-\mu^{\prime}\big)^{2},}\ &{\mu^{\prime}\triangleq\displaystyle\frac{1}{K}\sum_{k}\mu\big(w_{k},s_{t},a_{t}\big).}\end{array}
$$
The intrinsic reward is non-stationary because the world model and the ensemble predictors change throughout exploration. Indeed, once certain states are visited by the agent and the model gets trained on them, these states will become less interesting for the agent and the intrinsic reward for visiting them will decrease.
内在奖励是非平稳的,因为世界模型和集成预测器会在探索过程中不断变化。实际上,一旦智能体访问了某些状态并且模型在这些状态上进行了训练,这些状态对智能体来说就会变得不那么有趣,访问它们的内在奖励也会降低。
We learn the exploration policy using Dreamer (Section 2). Since the intrinsic reward is computed in the compact representation space of the latent dynamics model, we can optimize the learned actor and value from imagined latent trajectories without generating images. This lets us efficiently optimize the intrinsic reward without additional environment interaction. Furthermore, the ensemble of lightweight 1-step models adds little computational overhead as they are trained together efficiently in parallel across all time steps.
我们使用Dreamer(第2节)来学习探索策略。由于内在奖励是在潜在动态模型的紧凑表示空间中计算的,我们可以通过想象的潜在轨迹来优化学习到的行动者和价值函数,而无需生成图像。这使得我们能够高效地优化内在奖励,无需额外的环境交互。此外,轻量级1步模型集合几乎不会增加计算开销,因为它们可以在所有时间步上高效并行训练。
3.2. Expected Information Gain
3.2. 预期信息增益
Latent disagreement has an information-theoretic interpretation. This subsection derives our method from the amount of information gained by interacting with the environment, which has its roots in optimal Bayesian experiment design (Lindley, 1956; MacKay, 1992).
潜在分歧具有信息论解释。本小节从与环境交互中获得的信息量推导出我们的方法,其根源可追溯到最优贝叶斯实验设计 (Lindley, 1956; MacKay, 1992)。
Because the true dynamics are unknown, the agent treats the optimal dynamics parameters as a random variable $w$ To explore the environment as efficiently as possible, the agent should seek out future states that are informative of our belief over the parameters.
因为真实动态未知,智能体将最优动态参数视为随机变量 $w$。为了尽可能高效地探索环境,智能体应寻找能提供参数置信度信息量的未来状态。
Mutual information formalizes the amount of bits that a future trajectory provides about the optimal model parameters on average. We aim to find a policy that shapes the distribution over future states to maximize the mutual information between the image embeddings $h_{1:T}$ and parameters $w$ ,
互信息量化了未来轨迹平均提供的关于最优模型参数的比特数。我们的目标是找到一个策略,通过塑造未来状态的分布来最大化图像嵌入 $h_{1:T}$ 与参数 $w$ 之间的互信息。
$$
\operatorname{I}(h_{t+1};w\mid s_{t},a_{t})
$$
$$
\operatorname{I}(h_{t+1};w\mid s_{t},a_{t})
$$
We operate on latent image embeddings to save computation. To select the most promising data during exploration, the agent maximizes the expected information gain,
我们通过对潜在图像嵌入(latent image embeddings)进行操作以节省计算量。在探索阶段选择最有潜力的数据时,智能体会最大化预期信息增益,

This expected information gain can be rewritten as conditional entropy of trajectories subtracted from marginal entropy of trajectories, which correspond to, respectively, the aleatoric and the total uncertainty of the model,
该预期信息增益可重写为轨迹的条件熵减去轨迹的边际熵,分别对应模型的偶然不确定性和总不确定性。
$$
\begin{array}{r l}&{\operatorname{I}(h_{t+1};w\mid s_{t},a_{t})}\ &{\quad=\operatorname{H}(h_{t+1}\mid s_{t},a_{t})-\operatorname{H}(h_{t+1}\mid w,s_{t},a_{t}).}\end{array}
$$
$$
\begin{array}{r l}&{\operatorname{I}(h_{t+1};w\mid s_{t},a_{t})}\ &{\quad=\operatorname{H}(h_{t+1}\mid s_{t},a_{t})-\operatorname{H}(h_{t+1}\mid w,s_{t},a_{t}).}\end{array}
$$
We see that the information gain corresponds to the epistemic uncertainty, i.e. the reducible uncertainty of the model that is left after subtracting the expected amount of data noise from the total uncertainty.
我们注意到信息增益对应于认知不确定性 (epistemic uncertainty),即在总不确定性中减去预期数据噪声后剩余的模型可减少不确定性。
Trained via squared error, our ensemble members are conditional Gaussians with means produced by neural networks and fixed variances. The ensemble can be seen as a mixture distribution of parameter point masses,
通过平方误差训练,我们的集成成员是条件高斯分布,其均值由神经网络生成且方差固定。该集成可视为参数点质量的混合分布,
$$
\begin{array}{c}{\displaystyle p(w)\triangleq\frac{1}{K}\sum_{k}\delta(w-w_{k})}\ {\displaystyle p(h_{t+1}\mid w_{k},s_{t},a_{t})\triangleq\mathcal{N}(h_{t+1}\mid\mu(w_{k},s_{t},a_{t}),\sigma^{2}).}\end{array}
$$
$$
\begin{array}{c}{\displaystyle p(w)\triangleq\frac{1}{K}\sum_{k}\delta(w-w_{k})}\ {\displaystyle p(h_{t+1}\mid w_{k},s_{t},a_{t})\triangleq\mathcal{N}(h_{t+1}\mid\mu(w_{k},s_{t},a_{t}),\sigma^{2}).}\end{array}
$$
Because the variance is fixed, the conditional entropy does not depend on the state or action in our case $D$ is the
因为方差是固定的,所以在我们的情况下条件熵不依赖于状态或动作 $D$ 是
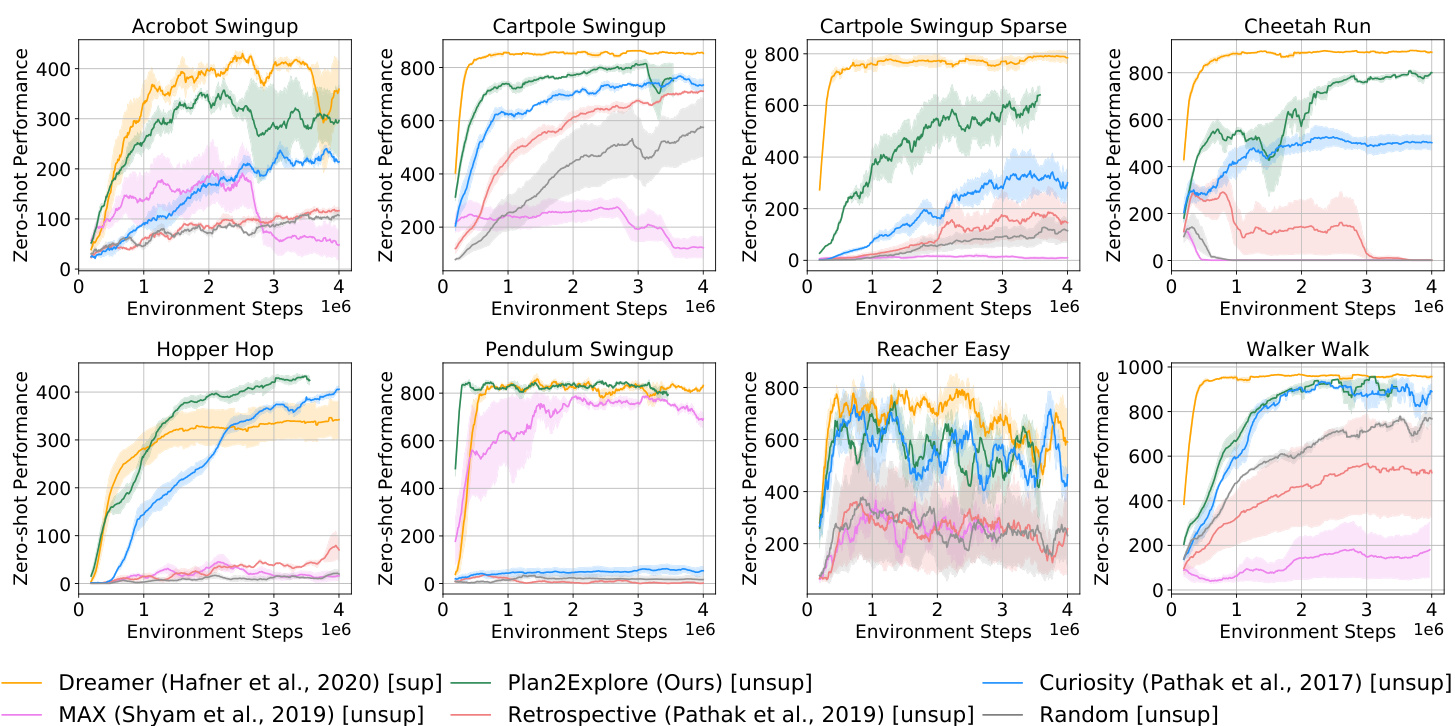
Figure 3. Zero-shot RL performance from raw pixels. After training the agent without rewards, we provide it with a task by specifying the reward function at test time. Throughout the exploration, we take snapshots of the agent to train a task policy on the final task and plot its zero-shot performance. We see that Plan 2 Explore achieves state-of-the-art zero-shot task performance on a range of tasks, and even demonstrates competitive performance to Dreamer (Hafner et al., 2020), a state-of-the-art supervised RL agent. This indicates that Plan 2 Explore is able to explore and learn a global model of the environment that is useful for adapting to new tasks, demonstrating the potential of self-supervised RL. Results on all 20 tasks are in the appendix Figure 6 and videos on the project website.
图 3: 基于原始像素的零样本强化学习性能。在无奖励训练智能体后,我们通过在测试时指定奖励函数来提供任务。在整个探索过程中,我们对智能体进行快照以训练最终任务策略,并绘制其零样本性能。Plan 2 Explore 在一系列任务中实现了最先进的零样本任务性能,甚至与监督强化学习智能体 Dreamer (Hafner et al., 2020) 展现出竞争力。这表明 Plan 2 Explore 能够探索并学习对环境有用的全局模型,从而适应新任务,展现了自监督强化学习的潜力。完整20项任务结果见附录图6,项目网站提供视频演示。
dimensionality of the predicted embedding),
预测嵌入的维度
$$
\begin{array}{r}{\mathrm{H}\big(h_{t+1}\mid w,s_{t},a_{t}\big)=\displaystyle\frac{1}{K}\sum_{k}\mathrm{H}\big(h_{t+1}\mid w_{k},s_{t},a_{t}\big)}\ {=\displaystyle\frac{D}{K}\sum_{k}\ln\sigma_{k}\big(s_{t},a_{t}\big)+\mathrm{const.}}\end{array}
$$
$$
\begin{array}{r}{\mathrm{H}\big(h_{t+1}\mid w,s_{t},a_{t}\big)=\displaystyle\frac{1}{K}\sum_{k}\mathrm{H}\big(h_{t+1}\mid w_{k},s_{t},a_{t}\big)}\ {=\displaystyle\frac{D}{K}\sum_{k}\ln\sigma_{k}\big(s_{t},a_{t}\big)+\mathrm{const.}}\end{array}
$$
We note that this fixed variance approach is applicable even in environments with heteros ced a stic variance, where it will measure the information gain about the mean prediction.
我们注意到,这种固定方差方法即使在具有异方差性的环境中也适用,此时它将衡量关于均值预测的信息增益。
Maximizing information gain then means to simply maximize the marginal entropy of the ensemble prediction. For this, we make the following observation: the marginal entropy is maximized when the ensemble means are far apart (disagreement) so the modes overlap the least, maximally spreading out probability mass. As the marginal entropy has no closed-form expression suitable for optimization, we instead use the empirical variance over ensemble means to measure how far apart they are,
最大化信息增益即意味着最大化集成预测的边际熵。为此,我们观察到:当集成均值相距较远(存在分歧)时,模态重叠最少,概率质量分布最分散,此时边际熵达到最大。由于边际熵缺乏适合优化的闭式表达式,我们改用集成均值的经验方差来衡量其分散程度,
$$
\begin{array}{c}{\displaystyle\mathrm{D}\big(\boldsymbol{s}_ {t},\boldsymbol{a}_ {t}\big)\triangleq\frac{1}{K-1}\sum_{k}\big(\mu\big(\boldsymbol{w}_ {k},\boldsymbol{s}_ {t},\boldsymbol{a}_ {t}\big)-\mu^{\prime}\big)^{2},}\ {\displaystyle\mu^{\prime}\triangleq\frac{1}{K}\sum_{k}\mu\big(\boldsymbol{w}_ {k},\boldsymbol{s}_ {t},\boldsymbol{a}_{t}\big).}\end{array}
$$
$$
\begin{array}{c}{\displaystyle\mathrm{D}\big(\boldsymbol{s}_ {t},\boldsymbol{a}_ {t}\big)\triangleq\frac{1}{K-1}\sum_{k}\big(\mu\big(\boldsymbol{w}_ {k},\boldsymbol{s}_ {t},\boldsymbol{a}_ {t}\big)-\mu^{\prime}\big)^{2},}\ {\displaystyle\mu^{\prime}\triangleq\frac{1}{K}\sum_{k}\mu\big(\boldsymbol{w}_ {k},\boldsymbol{s}_ {t},\boldsymbol{a}_{t}\big).}\end{array}
$$
To summarize, our exploration objective defined in Section 3.1, which maximizes the variance of ensemble means,
总结我们在3.1节中定义的探索目标,即最大化集成均值的方差,
approximates the information gain and thus should find trajectories that will efficiently reduce the model uncertainty.
近似信息增益,因此应能找到有效降低模型不确定性的轨迹。
4. Experimental Setup
4. 实验设置
Environment Details We use the DM Control Suite (Tassa et al., 2018), a standard benchmark for continuous control. All experiments use visual observations only, of size $64\times64\times3$ pixels. The episode length is 1000 steps and we apply an action repeat of $R=2$ for all the tasks. We run every experiment with three different random seeds with standard deviation shown in the shaded region. Further details are in the appendix.
环境细节
我们使用DM Control Suite (Tassa et al., 2018) 作为连续控制的标准基准。所有实验仅使用尺寸为 $64\times64\times3$ 像素的视觉观测。每轮实验长度为1000步,所有任务均采用 $R=2$ 的动作重复策略。每个实验使用三个不同的随机种子运行,阴影区域显示标准差。更多细节见附录。
Implementation We use (Hafner et al., 2020) with the original hyper parameters unless specified otherwise to op- timize both exploration and task policies of Plan 2 Explore. We found that additional capacity provided by increasing the hidden size of the GRU in the latent dynamics model to 400 and the deterministic and stochastic components of the latent space to 60 helped performance. For a fair comparison, we maintain this model size for Dreamer and other baselines. For latent disagreement, we use an ensemble of 5 one-step prediction models implemented as 2 hidden-layer MLP. Full details are in the appendix.
实现
我们采用 (Hafner et al., 2020) 的原始超参数(除非另有说明)来优化 Plan 2 Explore 的探索策略和任务策略。我们发现,将潜在动态模型中 GRU 的隐藏层大小增至 400,并将潜在空间的确定性和随机性组件设为 60,所提供的额外容量有助于提升性能。为确保公平比较,我们在 Dreamer 及其他基线模型中保持相同的模型规模。对于潜在分歧,我们使用由 5 个单步预测模型组成的集成,这些模型实现为 2 隐藏层的 MLP。完整细节见附录。
Baselines We compare our agent to a state-of-the-art taskoriented agent that receives rewards throughout training,
基线方法 我们将我们的智能体与一个在训练过程中接收奖励的最新任务导向智能体进行比较,
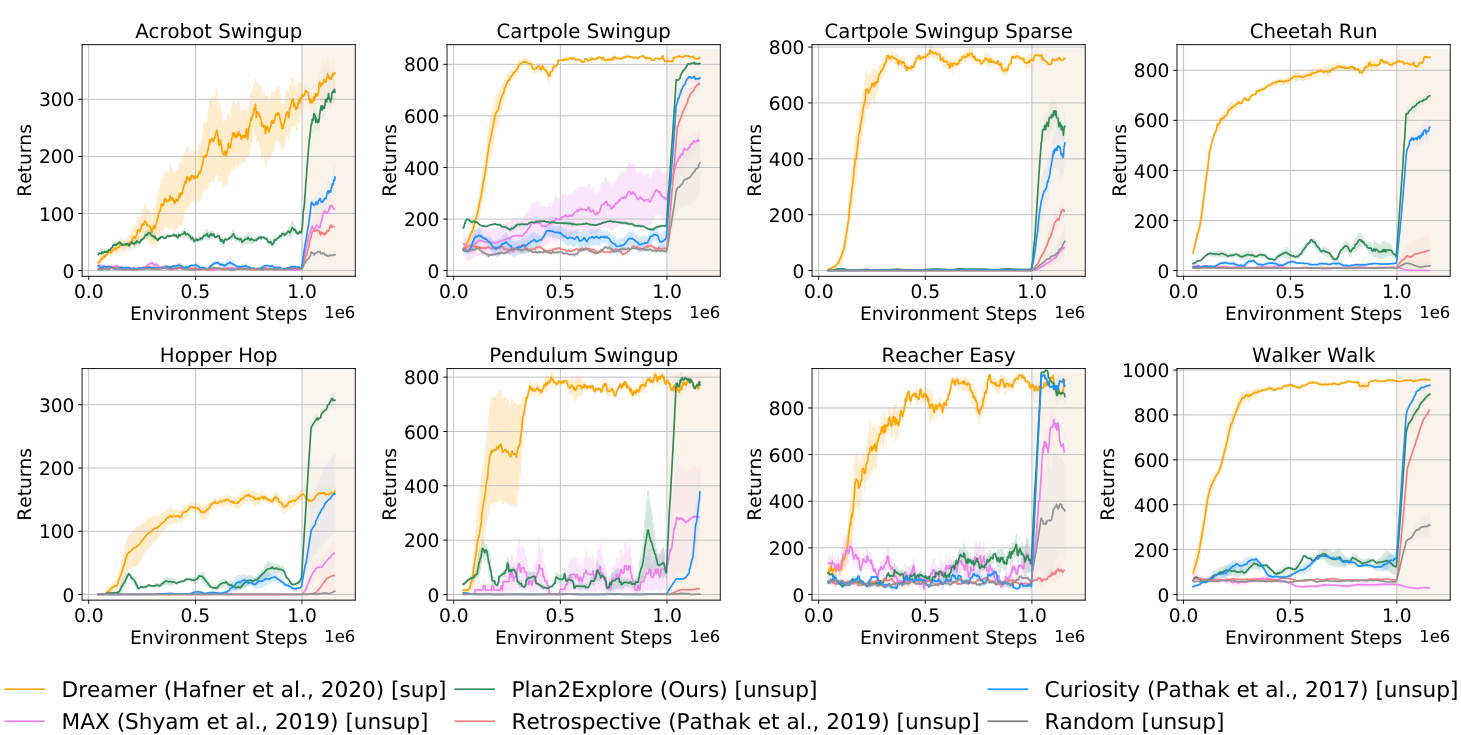
Figure 4. Performance on few-shot adaptation from raw pixels without state-space input. After the exploration phase of 1M steps (white background), during which the agent does not observe the reward and thus does not solve the task, we let the agent collect a small amount of data from the environment (shaded background). We see that Plan 2 Explore is able to explore the environment efficiently in only 1000 episodes, and then adapt its behavior immediately after observing the reward. Plan 2 Explore adapts rapidly, producing effective behavior competitive to state-of-the-art supervised reinforcement learning in just a few collected episodes.
图 4: 无状态空间输入的原始像素少样本适应性能。在100万步探索阶段(白色背景)后,智能体未观测到奖励因而未完成任务,随后让其从环境中收集少量数据(阴影背景)。可见Plan 2 Explore仅用1000回合就能高效探索环境,并在观测到奖励后立即调整行为。该方法快速适应,仅收集少量回合就能产生与最先进的监督强化学习相媲美的有效行为。
Dreamer (Hafner et al., 2020). We also compare to state-ofthe-art unsupervised agents: Curiosity (Pathak et al., 2017) and Model-based Active Exploration (Shyam et al., 2019, MAX). Because Curiosity is inefficient during fine-tuning and would not be able to solve a task in a zero-shot way, we adapt it into the model-based setting. We further adapt MAX to work with image observations as (Shyam et al., 2019) only addresses learning from low-dimensional states. We use (Hafner et al., 2020) as the base agent for all methods to provide a fair comparison. We additionally compare to a random data collection policy that uniformly samples from the action space of the environment. All methods share the same model hyper parameters to provide a fair comparison.
Dreamer (Hafner等人,2020)。我们还与最先进的无监督智能体进行了比较:Curiosity (Pathak等人,2017) 和基于模型的主动探索 (Shyam等人,2019,MAX)。由于Curiosity在微调阶段效率低下且无法以零样本方式解决任务,我们将其调整为基于模型的设置。我们进一步调整MAX以处理图像观测,因为 (Shyam等人,2019) 仅涉及从低维状态学习。我们使用 (Hafner等人,2020) 作为所有方法的基准智能体以确保公平比较。此外,我们还比较了从环境动作空间均匀采样的随机数据收集策略。所有方法共享相同的模型超参数以保证公平性。
5. Results and Analysis
5. 结果与分析
Our experiments focus on evaluating whether our proposed Plan 2 Explore agent efficiently explores and builds a model of the world that allows quick adaptation to solve tasks in zero or few-shot manner. The rest of the subsections are organized in terms of the key scientific questions we would like to investigate as discussed in the introduction.
我们的实验重点评估所提出的Plan 2 Explore智能体是否能高效探索并构建世界模型,从而实现零样本或少样本方式快速适应任务解决。其余小节围绕引言中讨论的关键科学问题展开组织。
5.1. Does the model transfer to solve tasks zero-shot?
5.1 模型能否零样本迁移解决任务?
To test whether Plan 2 Explore has learned a global model of the environment that can be used to solve new tasks, we evaluate the zero-shot performance of our agent. Our agent learns a model without using any task-specific information. After that, a separate downstream agent is trained in imagination, which optimizes the task reward using only the self-supervised world model and no new interaction with the world. To specify the task, we provide the agent with the reward function that is used to label its replay buffer with rewards and train a reward predictor. This process is described in the Algorithm 2, with step 10 omitted.
为了测试Plan 2 Explore是否学会了可用于解决新任务的环境全局模型,我们评估了智能体的零样本性能。我们的智能体在训练过程中不使用任何任务特定信息。随后,一个独立的下游智能体在想象中进行训练,仅使用自监督世界模型优化任务奖励,无需与环境进行新的交互。为了指定任务,我们向智能体提供奖励函数,该函数用于在回放缓冲区中标注奖励并训练奖励预测器。该过程在算法2中描述(省略了步骤10)。
In Figure 3, we compare the zero-shot performance of our downstream agent with different amounts of exploration data. This is done by training the downstream agent in imagination at each training checkpoint. The same architecture and hyper-parameters are used for all the methods for a fair comparison. We see that Plan 2 Explore overall performs better than prior state-of-the-art exploration strategies from high dimensional pixel input, sometimes being the only successful unsupervised method. Moreover, the zero-shot performance of Plan 2 Explore is competitive to Dreamer, even outperforming it in the hopper hop task.
在图 3 中,我们比较了下游智能体在不同探索数据量下的零样本性能。这是通过在每次训练检查点时在想象中训练下游智能体来实现的。所有方法均采用相同的架构和超参数以确保公平比较。我们发现 Plan 2 Explore 总体表现优于先前基于高维像素输入的最先进探索策略,有时甚至是唯一成功的无监督方法。此外,Plan 2 Explore 的零样本性能与 Dreamer 相当,在 hopper hop 任务中甚至优于后者。
Plan 2 Explore was able to successfully learn a good model of the environment and efficiently derive task-oriented behaviors from this model. We emphasize that Plan 2 Explore explores without task rewards, and Dreamer is the oracle as it is given task rewards during exploration. Yet, Plan 2 Explore almost matches the performance of this oracle.
Plan 2 Explore 成功学习了环境的优质模型,并能高效从中推导出任务导向行为。需强调的是,Plan 2 Explore 在探索过程中不依赖任务奖励,而作为参照基准的 Dreamer 在探索阶段可获得任务奖励。尽管如此,Plan 2 Explore 的性能仍几乎与这一基准持平。
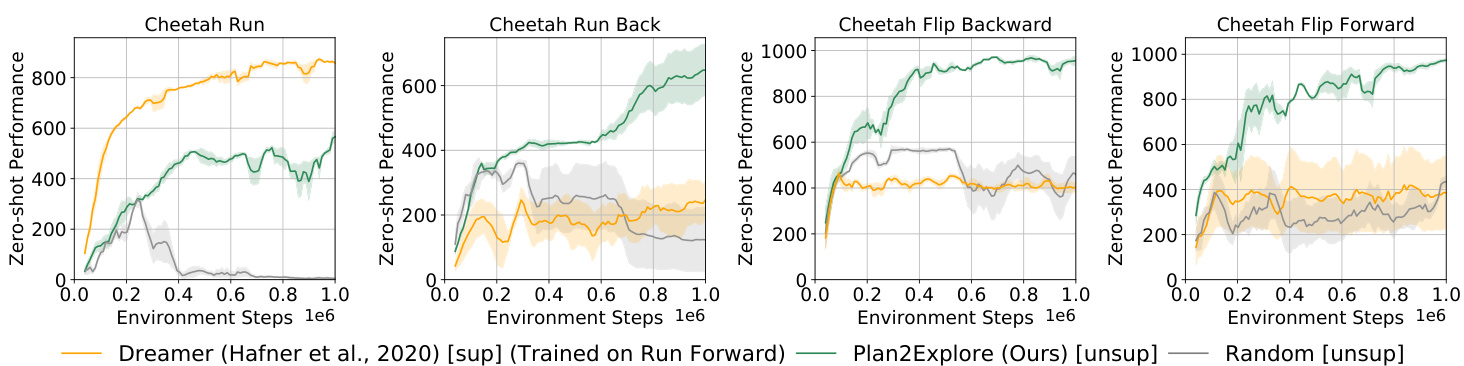
Figure 5. Do task-specific models generalize? We test Plan 2 Explore on zero-shot performance on four different tasks in the cheetah environment from raw pixels without state-space input. Throughout the exploration, we take snapshots of policy to plot its zero-shot performance. In addition to random exploration, we compare to an oracle agent, Dreamer, that uses the data collected when trained on the run forward task with rewards. Although Dreamer trained on ’run forward’ is able to solve the task it is trained on, it struggles on the other tasks, indicating that it has not learned a global world model.
图 5: 任务专用模型是否具备泛化能力?我们在猎豹环境中仅使用原始像素输入(无状态空间输入),测试了Plan 2 Explore在四项任务上的零样本性能。在探索过程中,我们记录策略快照以绘制其零样本表现曲线。除随机探索外,我们还对比了使用带奖励的"向前奔跑"任务训练数据的神谕智能体Dreamer。尽管Dreamer能解决其训练任务"向前奔跑",但在其他任务上表现欠佳,表明其未能学习到全局世界模型。
5.2. How much task-specific interaction is needed for finetuning to reach the supervised oracle?
5.2. 微调需要多少任务特定的交互才能达到监督式神谕 (supervised oracle) 水平?
While zero-shot learning might suffice for some tasks, in general, we will want to adapt our model of the world to task-specific information. In this section, we test whether few-shot adaptation of the model to a particular task is competitive to training a fully supervised task-specific model. To adapt our model, we only add 100−150 supervised episodes which falls under ‘few-shot’ adaptation. Furthermore, in this setup, to evaluate the data efficiency of Plan 2 Explore we set the number of exploratory episodes to only 1000.
虽然零样本学习可能足以应对某些任务,但通常我们会希望将世界模型适配到特定任务的信息上。本节测试模型针对特定任务的少样本适配是否与训练完全监督的任务专用模型具有竞争力。为适配模型,我们仅添加100-150个监督片段,这属于"少样本"适配范畴。此外,在此设置中,为评估Plan 2 Explore的数据效率,我们将探索片段数量设定为仅1000个。
In the exploration phase of Figure 4, i.e., left of the vertical line, our agent does not aim to solve the task, as it is still unknown, however, we expect that during some period of exploration it will coincidentally achieve higher rewards as it explores the parts of the state space relevant for the task. The performance of unsupervised methods is coincidental until 1000 episodes and then it switches to task-oriented behavior for the remaining 150 episodes, while for supervised, it is task-oriented throughout. That’s why we see a big jump for unsupervised methods where the shaded region begins.
在图4的探索阶段(即垂直线左侧),我们的AI智能体并不以解决任务为目标,因为任务本身尚属未知。然而我们预期,在探索过程中它会偶然获得较高奖励,这是由于探索到了与任务相关的状态空间区域。无监督方法的性能在1000回合前具有偶然性,之后150回合才转为任务导向行为;而有监督方法始终是任务导向的。这就是为什么无监督方法在阴影区域起始处会出现大幅跃升。
In the few-shot learning setting, Plan 2 Explore eventually performs competitively to Dreamer on all tasks, significantly outperforming it on the hopper task. Plan 2 Explore is also able to adapt quickly or similar to other unsupervised agents on all tasks. These results show that a self-supervised agent, when presented with a task specification, should be able to rapidly adapt its model to the task information, matching or outperforming the fully supervised agent trained only for that task. Moreover, Plan 2 Explore is able to learn this general model with a small number of samples, matching Dreamer, which is fully task-specific, in data efficiency. This shows the potential of an unsupervised pre-training in reinforcement learning. Please re
