A Universal Framework for Accurate and Efficient Geometric Deep Learning of Molecular Systems
分子系统精确高效几何深度学习的通用框架
ABSTRACT
摘要
Molecular sciences address a wide range of problems involving molecules of different types and sizes and their complexes. Recently, geometric deep learning, especially Graph Neural Networks (GNNs), has shown promising performance in molecular science applications. However, most existing works often impose targeted inductive biases to a specific molecular system, and are inefficient when applied to macromolecules or large-scale tasks, thereby limiting their applications to many real-world problems. To address these challenges, we present PAMNet, a universal framework for accurately and efficiently learning the representations of three-dimensional (3D) molecules of varying sizes and types in any molecular system. Inspired by molecular mechanics, PAMNet induces a physics-informed bias to explicitly model local and non-local interactions and their combined effects. As a result, PAMNet can reduce expensive operations, making it time and memory efficient. In extensive benchmark studies, PAMNet outperforms state-of-the-art baselines regarding both accuracy and efficiency in three diverse learning tasks: small molecule properties, RNA 3D structures, and protein-ligand binding affinities. Our results highlight the potential for PAMNet in a broad range of molecular science applications.
分子科学研究涉及各种类型和尺寸的分子及其复合物的广泛问题。近年来,几何深度学习(尤其是图神经网络 (GNNs))在分子科学应用中展现出优异性能。然而,现有研究大多针对特定分子系统引入定向归纳偏置,在处理大分子或大规模任务时效率低下,限制了其在现实问题中的应用。为解决这些挑战,我们提出了PAMNet——一个通用框架,能够准确高效地学习任何分子系统中不同尺寸和类型的三维 (3D) 分子表征。受分子力学启发,PAMNet通过物理信息偏置显式建模局部与非局部相互作用及其协同效应,从而减少昂贵计算操作,实现时间和内存高效性。在涵盖小分子性质、RNA三维结构和蛋白质-配体结合亲和力的三大学习任务基准测试中,PAMNet在准确性与效率方面均超越现有最优基线。这些结果表明PAMNet在分子科学领域具有广泛的应用潜力。
Introduction
引言
The wide variety of molecular types and sizes poses numerous challenges in the computational modeling of molecular systems for drug discovery, structural biology, quantum chemistry, and others1. To address these challenges, recent advances in geometric deep learning (GDL) approaches have become increasingly important2,3. Especially, Graph Neural Networks (GNNs) have demonstrated superior performance among various GDL approaches 4–6. GNNs treat each molecule as a graph and perform message passing scheme on it7. By representing atoms or groups of atoms like functional groups as nodes, and chemical bonds or any pairwise interactions as edges, molecular graphs can naturally encode the structural information in molecules. In addition to this, GNNs can incorporate symmetry and achieve invariance or e qui variance to transformations such as rotations, translations, and reflections 8, which further contributes to their effectiveness in molecular science applications. To enhance their ability to capture molecular structures and increase the expressive power of their models, previous GNNs have utilized auxiliary information such as chemical properties 9–12, atomic pairwise distances in Euclidean space7,13,14, angular information 15–18, etc.
分子类型和尺寸的多样性给药物发现、结构生物学、量子化学等领域的分子系统计算建模带来了诸多挑战[1]。为解决这些挑战,几何深度学习 (geometric deep learning, GDL) 方法的最新进展显得愈发重要[2,3]。其中,图神经网络 (Graph Neural Networks, GNNs) 在各种GDL方法中展现出卓越性能[4-6]。GNNs将每个分子视为图结构,并在此基础上执行消息传递机制[7]。通过将原子或官能团等原子团表示为节点,化学键或任何成对相互作用表示为边,分子图能自然地编码分子结构信息。此外,GNNs还能整合对称性,实现对旋转、平移和反射等变换的不变性或等变性[8],这进一步提升了其在分子科学应用中的有效性。为增强分子结构捕捉能力并提高模型表达能力,现有GNNs已利用化学性质[9-12]、欧氏空间中的原子间距离[7,13,14]、角度信息[15-18]等辅助信息。
In spite of the success of GNNs, their application in molecular sciences is still in its early stages. One reason for this is that current GNNs often use targeted inductive bias for modeling a specific type of molecular system, and cannot be directly transferred to other contexts although all molecule structures and their interactions follow the same law of physics. For example, GNNs designed for modeling proteins may include operations that are specific to the structural characteristics of amino acids19,20, which are not relevant for other types of molecules. Additionally, GNNs that incorporate comprehensive geometric information can be computationally expensive, making them difficult to scale to tasks involving a large number of molecules (e.g., high-throughput compound screening) or macromolecules (e.g., proteins and RNAs). For instance, incorporating angular information can significantly improve the performance of $\mathrm{GNNs^{15-18}}$ , but also increases the complexity of the model, requiring at least $O(N k^{2})$ messages to be computed where $N$ and $k$ denote the number of nodes and the average degree in a graph.
尽管图神经网络 (GNN) 取得了成功,但它们在分子科学中的应用仍处于早期阶段。其中一个原因是当前的 GNN 通常针对特定类型的分子系统使用定向归纳偏置建模,无法直接迁移到其他场景——尽管所有分子结构及其相互作用都遵循相同的物理定律。例如,为蛋白质建模设计的 GNN 可能包含氨基酸结构特征特有的操作 [19,20],这些操作与其他类型分子无关。此外,整合全面几何信息的 GNN 计算成本高昂,难以扩展到涉及大量分子 (如高通量化合物筛选) 或大分子 (如蛋白质和 RNA) 的任务。例如,引入角度信息能显著提升 $\mathrm{GNN^{15-18}}$ 的性能,但也会增加模型复杂度,需要计算至少 $O(N k^{2})$ 条消息 (其中 $N$ 和 $k$ 分别表示图中的节点数和平均度数)。
To tackle the limitations mentioned above, we propose a universal GNN framework, Physics-Aware Multiplex Graph Neural Network (PAMNet), for the accurate and efficient representation learning of 3D molecules ranging from small molecules to macromolecules in any molecular system. PAMNet induces a physics-informed bias inspired by molecular mechanics 21, which separately models local and non-local interactions in molecules based on different geometric information. To achieve this, we represent each molecule as a two-layer multiplex graph, where one plex only contains local interactions, and the other plex contains additional non-local interactions. PAMNet takes the multiplex graphs as input and uses different operations to incorporate the geometric information for each type of interaction. This flexibility allows PAMNet to achieve efficiency by avoiding the use of computationally expensive operations on non-local interactions, which consist of the majority of interactions in a molecule. Additionally, a fusion module in PAMNet allows the contribution of each type of interaction to be learned and fused for the final feature or prediction. To preserve symmetry, PAMNet utilizes E(3)-invariant representations and operations when predicting scalar properties, and is extended to predict E(3)-e qui variant vectorial properties by considering the geometric vectors in molecular structures that arise from quantum mechanics.
为解决上述局限性,我们提出了一种通用图神经网络框架——物理感知多重图神经网络 (Physics-Aware Multiplex Graph Neural Network, PAMNet),用于准确高效地学习从有机小分子到任意分子系统中大分子的三维分子表征。PAMNet引入受分子力学[21]启发的物理先验偏置,基于不同几何信息分别建模分子中的局部与非局部相互作用。为此,我们将每个分子表示为双层多重图 (multiplex graph),其中一层仅包含局部相互作用,另一层则包含额外的非局部相互作用。PAMNet以多重图作为输入,针对不同类型的相互作用采用差异化操作整合几何信息。这种灵活性使PAMNet能通过避免对占分子相互作用主体的非局部作用进行昂贵计算来实现高效性。此外,PAMNet中的融合模块可学习各类相互作用的贡献度并融合为最终特征或预测结果。为保持对称性,PAMNet在预测标量性质时采用E(3)等变表征与运算,并通过考虑量子力学产生的分子结构几何向量,进一步扩展至预测E(3)等变矢量性质。
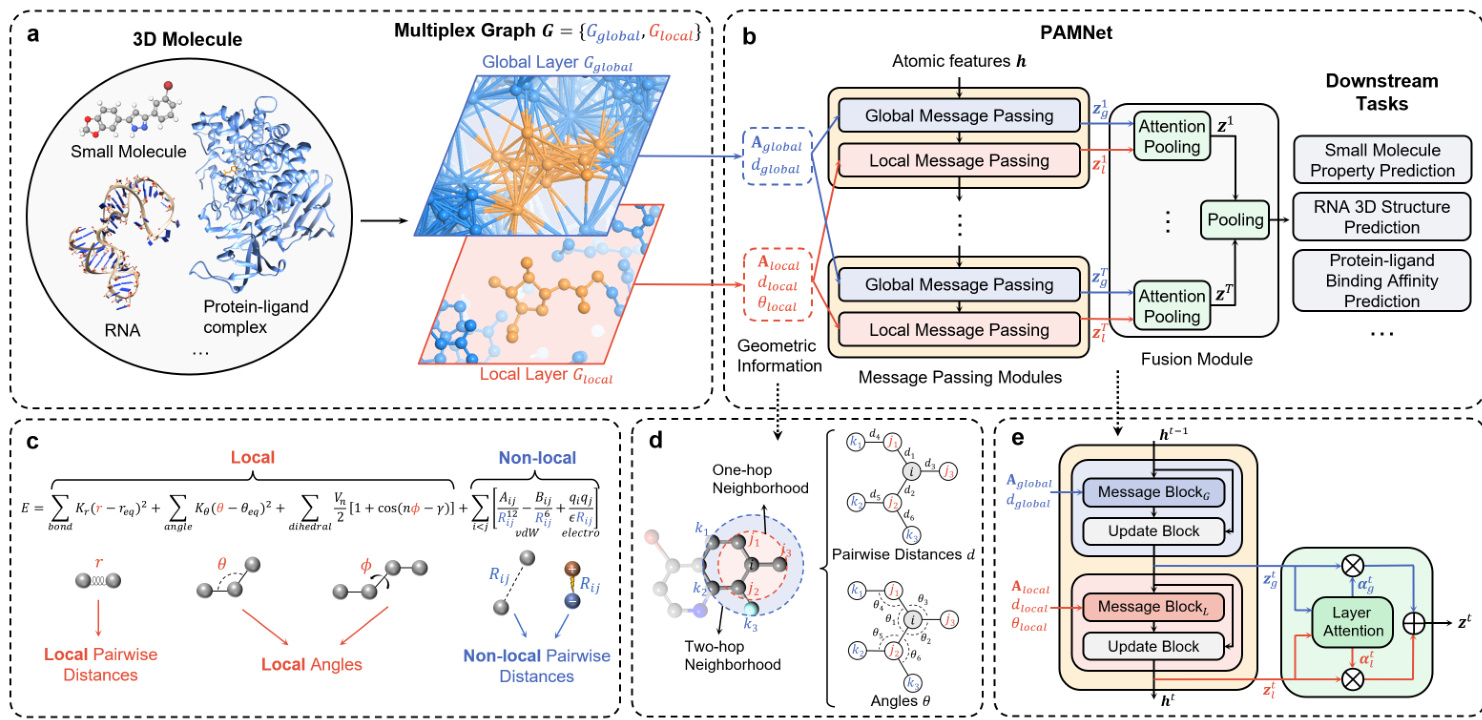
Figure 1. Overview of PAMNet. a, Based on the 3D structure of any molecule or molecular system, a two-layer multiplex graph $G={G_{g l o b a l},G_{l o c a l}}$ is constructed to separate the modeling of global and local interactions. b, PAMNet takes $G$ as input and learns node-level or graph-level representation for downstream tasks. PAMNet contains stacked message passing modules that update the node embeddings $\mathbf{z}$ in $G$ , and a fusion module that learns to combine the updated embeddings. In each message passing module, two message passing schemes are designed to encode the different geometric information in $G$ ’s two layers. In the fusion module, a two-step pooling process is proposed. c, Calculation of molecular energy $E$ in molecular mechanics. d, An example of the geometric information in $G$ . By considering the one-hop neighbors ${j}$ and two-hop neighbors ${k}$ of atom $i$ , we can define the pairwise distances $d$ and the related angles θ . e, Detailed architecture of the message passing module and the attention pooling in PAMNet.
图 1: PAMNet概述。a) 基于任意分子或分子系统的3D结构,构建双层复用图 $G={G_{g l o b a l},G_{l o c a l}}$ 以分离全局和局部相互作用的建模。b) PAMNet以 $G$ 作为输入,学习节点级或图级表征用于下游任务。PAMNet包含堆叠的消息传递模块(用于更新 $G$ 中的节点嵌入 $\mathbf{z}$ )和融合模块(学习组合更新后的嵌入)。每个消息传递模块中设计了两种消息传递方案,分别编码 $G$ 两层中的不同几何信息。融合模块提出了两步池化过程。c) 分子力学中分子能量 $E$ 的计算。d) $G$ 中几何信息的示例。通过考虑原子 $i$ 的一跳邻居 ${j}$ 和二跳邻居 ${k}$ ,可定义成对距离 $d$ 和相关角度θ。e) PAMNet中消息传递模块和注意力池化的详细架构。
To demonstrate the effectiveness of PAMNet, we conduct a comprehensive set of experiments on a variety of tasks involving different molecular systems, including small molecules, RNAs, and protein-ligand complexes. These tasks include predicting small molecule properties, RNA 3D structures, and protein-ligand binding affinities. We compare PAMNet to state-of-the-art baselines in each task and the results show that PAMNet outperforms the baselines in terms of both accuracy and efficiency across all three tasks. Given the diversity of the tasks and the types of molecules involved, the superior performance of PAMNet shows its versatility to be applied in various real-world scenarios.
为验证PAMNet的有效性,我们在涉及小分子、RNA和蛋白质-配体复合物等多种分子系统的任务上开展了一系列综合实验。这些任务包括预测小分子性质、RNA三维结构以及蛋白质-配体结合亲和力。我们将PAMNet与各任务中最先进的基线方法进行对比,结果表明PAMNet在所有三项任务的准确性和效率方面均优于基线方法。鉴于任务多样性和所涉分子类型的广泛性,PAMNet的卓越性能展现了其在多种现实场景中的应用潜力。
Overview of PAMNet
PAMNet 概述
Multiplex graph representation. Given any 3D molecule or molecular system, we define a multiplex graph representation as the input of our PAMNet model based on the original 3D structure (Fig. 1a). The construction of multiplex graphs is inspired by molecular mechanics 21, in which the molecular energy $E$ is separately modeled based on local and non-local interactions (Fig. 1c). In detail, the local terms $ E_{\mathrm{bond}}+E_{\mathrm{angle}}+E_{\mathrm{dihedral}}$ model local, covalent interactions including $E_{\mathrm{bond}}$ that depends on bond lengths, $E_{\mathrm{angle}}$ on bond angles, and $E_{\mathrm{dihedral}}$ on dihedral angles. The non-local terms $E_{\mathrm{vdW}}+E_{\mathrm{electro}}$ model non-local, non-covalent interactions including van der Waals and electrostatic interactions which depend on inter atomic distances. Motivated by this, we also decouple the modeling of these two types of interactions in PAMNet. For local interactions, we can define them either using chemical bonds or by finding the neighbors of each node within a relatively small cutoff distance, depending on the given task. For global interactions that contain both local and non-local ones, we define them by finding the neighbors of each node within a relatively large cutoff distance. For each type of interaction, we use a layer to represent all atoms as nodes and the interactions as edges. The resulting layers that share the same group of atoms form a two-layer multiplex graph $G={G_{g l o b a l},G_{l o c a l}}$ which represents the original 3D molecular structure (Fig. 1a).
多重图表示。给定任意3D分子或分子系统,我们基于原始3D结构定义了作为PAMNet模型输入的多重图表示 (图 1a)。多重图的构建灵感来源于分子力学[21],其中分子能量$E$根据局部与非局部相互作用分别建模 (图 1c)。具体而言,局部项$E_{\mathrm{bond}}+E_{\mathrm{angle}}+E_{\mathrm{dihedral}}$建模共价键局部相互作用,包括取决于键长的$E_{\mathrm{bond}}$、键角的$E_{\mathrm{angle}}$以及二面角的$E_{\mathrm{dihedral}}$;非局部项$E_{\mathrm{vdW}}+E_{\mathrm{electro}}$建模非共价键的长程相互作用,包括依赖于原子间距离的范德华力与静电作用。受此启发,我们在PAMNet中也解耦了这两类相互作用的建模:对于局部相互作用,可根据任务需求通过化学键或较小截断距离内的邻近节点定义;对于包含局部与非局部作用的全局相互作用,则通过较大截断距离内的邻近节点定义。每种相互作用类型均使用一个图层表示,其中原子作为节点、相互作用作为边。最终由共享原子群的两层图$G={G_{global},G_{local}}$构成的多重图,即可表征原始3D分子结构 (图 1a)。
Message passing modules. To update the node embeddings in the multiplex graph $G$ , we design two message passing modules that incorporate geometric information: Global Message Passing and Local Message Passing for updating the node embeddings in $G_{g l o b a l}$ and $G_{l o c a l}$ , respectively (Fig. 1b). These message passing modules are inspired by physical principles from molecular mechanics (Fig. 1c): When modeling the molecular energy $E$ , the terms for local interactions require geometric information including inter atomic distances (bond lengths) and angles (bond angles and dihedral angles), while the terms for non-local interactions only require inter atomic distances as geometric information. The message passing modules in PAMNet also use geometric information in this way when modeling these interactions (Fig. 1b and Fig. 1e). Specifically, we capture the pairwise distances and angles contained within up to two-hop neighborhoods (Fig. 1d). The Local Message Passing requires the related adjacency matrix $\mathbf{A}{l o c a l}$ , pairwise distances $d_{l o c a l}$ and angles $\theta_{l o c a l}$ , while the Global Message Passing only needs the related adjacency matrix $\mathbf{A}{g l o b a l}$ and pairwise distances $d_{g l o b a l}$ . Each message passing module then learns the node embeddings $\mathbf{z}{g}$ or $\mathbf{z}{l}$ in $G_{g l o b a l}$ and $G_{l o c a l}$ , respectively.
消息传递模块。为了更新多重图 $G$ 中的节点嵌入,我们设计了两个结合几何信息的消息传递模块:全局消息传递和局部消息传递,分别用于更新 $G_{global}$ 和 $G_{local}$ 中的节点嵌入 (图 1b)。这些消息传递模块的灵感来自分子力学的物理原理 (图 1c):在建模分子能量 $E$ 时,局部相互作用项需要包括原子间距离 (键长) 和角度 (键角和二面角) 在内的几何信息,而非局部相互作用项仅需原子间距离作为几何信息。PAMNet 中的消息传递模块在建模这些相互作用时也以类似方式使用几何信息 (图 1b 和图 1e)。具体而言,我们捕获了最多两跳邻域内的成对距离和角度 (图 1d)。局部消息传递需要相关的邻接矩阵 $\mathbf{A}{local}$、成对距离 $d_{local}$ 和角度 $\theta_{local}$,而全局消息传递仅需相关的邻接矩阵 $\mathbf{A}{global}$ 和成对距离 $d_{global}$。每个消息传递模块随后分别学习 $G_{global}$ 和 $G_{local}$ 中的节点嵌入 $\mathbf{z}{g}$ 或 $\mathbf{z}_{l}$。
For the operations in our message passing modules, they can preserve different symmetries: E(3)-invariance and E(3)- e qui variance, which contain essential inductive bias incorporated by GNNs when dealing with graphs with geometric information8. E(3)-invariance is preserved when predicting E(3)-invariant scalar quantities like energies, which remain unchanged when the original molecular structure undergoes any E(3) transformation including rotation, translation, and reflection. To preserve E(3)-invariance, the input node embeddings $\pmb{h}$ and geometric features are all E(3)-invariant. To update these features, PAMNet utilizes operations that can preserve the invariance. In contrast, E(3)-e qui variance is preserved when predicting E(3)-e qui variant vectorial quantities like dipole moment, which will change according to the same transformation applied to the original molecular structure through E(3) transformation. To preserve E(3)-e qui variance, an extra associated geometric vector $\vec{\nu}\in\mathbb{R}^{3}$ is defined for each node. These geometric vectors are updated by operations inspired by quantum mechanics 22, allowing for the learning of E(3)-e qui variant vectorial representations. More details about the explanations of E(3)-invariance, E(3)-e qui variance, and our operations can be found in Methods.
在我们的消息传递模块中,操作可以保持不同的对称性:E(3)不变性 (E(3)-invariance) 和 E(3)等变性 (E(3)-equivariance),这些对称性包含了图神经网络 (GNN) 在处理具有几何信息的图时引入的关键归纳偏置 [8]。当预测能量等 E(3)不变标量时,E(3)不变性得以保持,这些标量在原始分子结构经历任何 E(3)变换(包括旋转、平移和反射)时保持不变。为了保持 E(3)不变性,输入的节点嵌入 $\pmb{h}$ 和几何特征都是 E(3)不变的。PAMNet 使用能够保持这种不变性的操作来更新这些特征。相比之下,当预测偶极矩等 E(3)等变矢量时,E(3)等变性得以保持,这些矢量会根据通过 E(3)变换应用于原始分子结构的相同变换而改变。为了保持 E(3)等变性,每个节点额外定义了一个关联的几何向量 $\vec{\nu}\in\mathbb{R}^{3}$。这些几何向量通过受量子力学启发的操作 [22] 进行更新,从而学习 E(3)等变的矢量表示。关于 E(3)不变性、E(3)等变性及我们操作的更多细节,请参阅方法部分。
Fusion module. After updating the node embeddings $\mathbf{z}{g}$ or $\mathbf{z}{l}$ of the two layers in the multiplex graph $G$ , we design a fusion module with a two-step pooling process to combine $\mathbf{z}{g}$ and $\mathbf{z}{l}$ for downstream tasks (Figure 1b). In the first step, we design an attention pooling module based on attention mechanism 23 for each hidden layer $t$ in PAMNet. Since $G_{g l o b a l}$ and $G_{l o c a l}$ contains the same set of nodes ${N}$ , we apply the attention mechanism to each node $n\in{N}$ to learn the attention weights $(\alpha_{g}^{t}$ and $\alpha_{l}^{t}$ ) between the node embeddings of $n$ in $G_{g l o b a l}$ and $G_{l o c a l}$ , which are $\mathbf{z}{g}^{t}$ and $\mathbf{z}{l}^{t}$ . Then the attention weights are treated as the importance of $\pmb{z}{g}^{t}$ and $\mathbf{z}_{l}^{t}$ to compute the combined node embedding $\mathbf{z}^{t}$ in each hidden layer $t$ based on a weighted summation (Figure 1e). In the second step, the ${\bf z}^{t}$ of all hidden layers are summed together to compute the node embeddings of the original input. If a graph embedding is desired, we compute it using an average or a summation of the node embeddings.
融合模块。在更新多重图 $G$ 中两个层的节点嵌入 $\mathbf{z}{g}$ 或 $\mathbf{z}{l}$ 后,我们设计了一个包含两步池化过程的融合模块,将 $\mathbf{z}{g}$ 和 $\mathbf{z}{l}$ 结合用于下游任务 (图 1b)。第一步,我们为 PAMNet 中的每个隐藏层 $t$ 设计了一个基于注意力机制 [23] 的注意力池化模块。由于 $G_{global}$ 和 $G_{local}$ 包含相同的节点集 ${N}$,我们对每个节点 $n\in{N}$ 应用注意力机制,学习 $n$ 在 $G_{global}$ 和 $G_{local}$ 中的节点嵌入 $\mathbf{z}{g}^{t}$ 和 $\mathbf{z}{l}^{t}$ 之间的注意力权重 $(\alpha_{g}^{t}$ 和 $\alpha_{l}^{t})$。然后将注意力权重作为 $\pmb{z}{g}^{t}$ 和 $\mathbf{z}_{l}^{t}$ 的重要性,基于加权求和计算每个隐藏层 $t$ 中的组合节点嵌入 $\mathbf{z}^{t}$ (图 1e)。第二步,将所有隐藏层的 ${\bf z}^{t}$ 相加,计算原始输入的节点嵌入。如果需要图嵌入,我们使用节点嵌入的平均值或求和来计算。
Results and discussion
结果与讨论
In this section, we will demonstrate the performance of our proposed PAMNet regarding two aspects: accuracy and efficiency. Accuracy denotes how well the model performs measured by the metrics corresponding to a given task. Efficiency denotes the memory consumed and the inference time spent by the model.
在本节中,我们将从准确性和效率两个方面展示所提出的PAMNet性能。准确性指模型在给定任务对应指标下的表现优劣,效率则涉及模型消耗的内存及推理耗时。
Performance of PAMNet regarding accuracy
PAMNet在准确率方面的表现
Small molecule property prediction. To evaluate the accuracy of PAMNet in learning representations of small 3D molecules, we choose QM9, which is a widely used benchmark for the prediction of 12 molecular properties of around 130k small organic molecules with up to 9 non-hydrogen atoms24. Mean absolute error (MAE) and mean standardized MAE (std. MAE)15 are used for quantitative evaluation of the target properties. Besides evaluating the original PAMNet which captures geometric information within two-hop neighborhoods of each node, we also develop a "simple" PAMNet, called PAMNet-s, that utilizes only the geometric information within one-hop neighborhoods. The PAMNet models are compared with several state-of-the-art models including SchNet13, PhysNet14, $\mathbf{M}\mathbf{G}\mathbf{CN}^{25}$ , $\mathrm{PaiNN}^{26}$ , DimeNet $++^{16}$ , and Sphere Net 27. More details of the experiments can be found in Methods and Supplementary Information.
小分子性质预测。为了评估PAMNet在学习3D小分子表征方面的准确性,我们选择了QM9数据集,该数据集广泛用于预测约13万个最多含9个非氢原子的小有机分子的12种分子性质[24]。我们采用平均绝对误差(MAE)和标准化平均绝对误差(std. MAE)[15]对目标性质进行定量评估。除了评估原始PAMNet(捕获每个节点两跳邻域内的几何信息)外,我们还开发了仅利用一跳邻域几何信息的简化版PAMNet(称为PAMNet-s)。PAMNet模型与多个前沿模型进行了对比,包括SchNet[13]、PhysNet[14]、$\mathbf{M}\mathbf{G}\mathbf{CN}^{25}$、$\mathrm{PaiNN}^{26}$、DimeNet$++^{16}$以及SphereNet[27]。实验详情请参阅方法与补充信息部分。
We compare the performance of PAMNet with those of the baseline models mentioned above on QM9, as shown in Table 1. PAMNet achieves 4 best and 6 second-best results among all 12 properties, while PAMNet-s achieves 3 second-best results. When evaluating the overall performance using the std. MAE across all properties, PAMNet and PAMNet-s rank 1 and 2 among all models with $10%$ and $5%$ better std. MAE than the third-best model (SphereNet), respectively. From the results, we can observe that the models incorporating only atomic pairwise distance $d$ as geometric information like SchNet, PhysNet, and MGCN generally perform worse than those models incorporating more geometric information like PaiNN, DimeNet++, SphereNet, and our PAMNet. Besides, PAMNet-s which captures geometric information only within one-hop neighborhoods performs worse than PAMNet which considers two-hop neighborhoods. These show the importance of capturing rich geometric information when representing 3D small molecules. The superior performance of PAMNet models demonstrates the power of our separate modeling of different interactions in molecules and the effectiveness of the message passing modules designed.
我们在QM9数据集上将PAMNet与上述基线模型的性能进行比较,结果如表1所示。PAMNet在全部12个性质中取得4项最优和6项次优结果,而PAMNet-s获得3项次优成绩。当采用所有性质的标准MAE(std. MAE)评估整体性能时,PAMNet和PAMNet-s分别以比第三名模型(SphereNet)优$10%$和$5%$的标准MAE位列第一和第二。结果表明,仅采用原子对距离$d$作为几何信息的模型(如SchNet、PhysNet和MGCN)普遍逊于整合更多几何信息的模型(如PaiNN、DimeNet++、SphereNet及我们的PAMNet)。此外,仅捕捉单跳邻域几何信息的PAMNet-s性能低于考虑双跳邻域的PAMNet,这印证了在表示3D小分子时捕获丰富几何信息的重要性。PAMNet模型的卓越性能验证了我们分离建模分子内不同相互作用的有效性,以及所设计消息传递模块的优越性。
Table 1. Performance comparison on QM9. The best results are marked in bold and the second-best results with underline.
表 1: QM9 上的性能对比。最佳结果以粗体标出,次优结果以下划线标出。
| 属性 | 单位 | SchNet | PhysNet | MGCN | PaiNN | DimeNet++ | SphereNet | PAMNet-s | PAMNet |
|---|---|---|---|---|---|---|---|---|---|
| μ | mD | 21 | 52.9 | 56 | 12 | 29.7 | 24.5 | 11.3 | 10.8 |
| a | 0.124 | 0.0615 | 0.030 | 0.045 | 0.0435 | 0.0449 | 0.0466 | 0.0447 | |
| EHOMO | meV | 47 | 32.9 | 42.1 | 27.6 | 24.6 | 22.8 | 23.9 | 22.8 |
| ELUMO | meV | 39 | 24.7 | 57.4 | 20.4 | 19.5 | 18.9 | 20.0 | 19.2 |
| meV | 74 | 42.5 | 64.2 | 45.7 | 32.6 | 31.1 | 32.4 | 31.0 | |
| (R2) | a | 0.158 | 0.765 | 0.11 | 0.066 | 0.331 | 0.268 | 0.094 | 0.093 |
| ZPVE | meV | 1.616 | 1.39 | 1.12 | 1.28 | 1.21 | 1.12 | 1.24 | 1.17 |
| Uo | meV | 12 | 8.15 | 12.9 | 5.85 | 6.32 | 6.26 | 6.05 | 5.90 |
| n | meV | 12 | 8.34 | 14.4 | 5.83 | 6.28 | 6.36 | 6.08 | 5.92 |
| H | meV | 12 | 8.42 | 16.2 | 5.98 | 6.53 | 6.33 | 6.19 | 6.04 |
| G | meV | 13 | 9.40 | 14.6 | 7.35 | 7.56 | 7.78 | 7.34 | 7.14 |
| 43 | cal molK | 0.034 | 0.0280 | 0.038 | 0.024 | 0.0230 | 0.0215 | 0.0234 | 0.0231 |
| std. MAE | % | 1.78 | 1.37 | 1.89 | 1.01 | 0.98 | 0.91 | 0.87 | 0.83 |
When predicting dipole moment $\mu$ as a scalar value, which is originally an E(3)-e qui variant vectorial property $\vec{\mu}$ , PAMNet preserves the E(3)-e qui variance to directly predict $\vec{\mu}$ first and then takes the magnitude of $\vec{\mu}$ as the final prediction. As a result, PAMNet and PAMNet-s all get lower MAE ( $10.8~\mathrm{mD}$ and $11.3\mathrm{mD},$ ) than the previous best result $\mathrm{\Delta}12\mathrm{mD},$ ) achieved by PaiNN, which is a GNN with e qui variant operations for predicting vectorial properties. Note that the remaining baselines all directly predict dipole moment as a scalar property by preserving invariance. We also examine that by preserving invariance in PAMNet and directly predicting dipole moment as a scalar property, the MAE $(24.0\mathrm{mD})$ is much higher than the e qui variant version. These results demonstrate that preserving e qui variance is more helpful than preserving invariance for predicting dipole moments.
在预测偶极矩$\mu$这一标量值时(其本质是E(3)-等变的矢量属性$\vec{\mu}$),PAMNet通过保持E(3)-等变性直接预测$\vec{\mu}$,再取其模长作为最终预测值。因此PAMNet与PAMNet-s的MAE($10.8~\mathrm{mD}$和$11.3\mathrm{mD}$)均低于此前由PaiNN(一种用于预测矢量属性的等变图神经网络)取得的最佳结果($\mathrm{\Delta}12\mathrm{mD}$)。需注意其他基线方法均通过保持不变性直接将偶极矩作为标量属性预测。实验表明,若在PAMNet中保持不变性并直接预测标量偶极矩,其MAE($24.0\mathrm{mD}$)将显著高于等变版本。这些结果证明对于偶极矩预测,保持等变性比保持不变性更具优势。
RNA 3D structure prediction. Besides small molecules, we further apply PAMNet to predict RNA 3D structures for evaluating the accuracy of PAMNet in learning representations of 3D macromolecules. Following the previous works28–30, we refer the prediction to be the task of identifying accurate structural models of RNA from less accurate ones: Given a group of candidate 3D structural models generated based on an RNA sequence, a desired model that serves as a scoring function needs to distinguish accurate structural models among all candidates. We use the same datasets as those used $\mathrm{in}^{30}$ , which include a dataset for training and a benchmark for evaluation. The training dataset contains 18 relatively older and smaller RNA molecules experimentally determined 31. Each RNA is used to generate 1000 structural models via the Rosetta FARFAR2 sampling method29. The benchmark for evaluation contains relatively newer and larger RNAs, which are the first 21 RNAs in the RNA-Puzzles structure prediction challenge 32. Each RNA is used to generate at least 1500 structural models using FARFAR2, where $1%$ of the models are near-native (i.e., within a RMSD of the experimentally determined native structure). In practice, each scoring function predicts the root mean square deviation (RMSD) from the unknown true structure for each structural model. A lower RMSD would suggest a more accurate structural model predicted. We compare PAMNet with four state-of-the-art baselines: ARES30, Rosetta (2020 version)29, $\mathrm{RASP}^{33}$ , and 3 d RNA score 28. Among the baselines, only ARES is a deep learning-based method, and is a GNN using e qui variant operations. More details of the experiments are introduced in Methods and Supplementary Information.
RNA 3D结构预测。除小分子外,我们进一步将PAMNet应用于RNA三维结构预测,以评估其学习大分子三维表征的准确性。沿袭前人研究[28-30],我们将该预测任务定义为从低精度模型中识别准确RNA结构模型:给定基于RNA序列生成的一组候选三维结构模型,需要作为评分函数的理想模型从所有候选中区分出准确结构模型。我们采用与文献[30]相同的数据集,包含训练集和评估基准集。训练集包含18个通过实验确定的较早期小型RNA分子[31],每个RNA通过Rosetta FARFAR2采样方法[29]生成1000个结构模型。评估基准集包含较新的大型RNA分子,取自RNA-Puzzles结构预测挑战赛[32]前21个RNA,每个RNA使用FARFAR2生成至少1500个结构模型,其中1%为近天然构象(即与实验测定天然结构的RMSD差值在2Å以内)。实际操作中,每个评分函数预测各结构模型与未知真实结构的均方根偏差(RMSD),RMSD值越低表明预测的结构模型越精确。我们将PAMNet与四种前沿基线方法对比:ARES[30]、Rosetta(2020版)[29]、RASP[33]和3dRNAscore[28]。其中仅ARES是基于深度学习的方法,且为使用等变操作的图神经网络(GNN)。实验细节详见方法与补充信息部分。
On the RNA-Puzzles benchmark for evaluation, PAMNet significantly outperforms all other four scoring functions as shown in Figure 2. When comparing the best-scoring structural model of each RNA (Figure 2a), the probability of the model to be near-native $\mathrm{\Delta}<2\mathrm{\mathring{A}}$ RMSD from the native structure) is $90%$ when using PAMNet, compared with 62, 43, 33, and $5%$ for ARES, Rosetta, RASP, and 3dRNAscore, respectively. As for the 10 best-scoring structural models of each RNA (Figure 2b), the probability of the models to include at least one near-native model is $90%$ when using PAMNet, compared with 81, 48, 48, and $33%$ for ARES, Rosetta, RASP, and 3dRNAscore, respectively. When comparing the rank of the best-scoring near-native structural model of each RNA (Figure 2c), the geometric mean of the ranks across all RNAs is 1.7 for PAMNet, compared with 3.6, 73.0, 26.4, and 127.7 for ARES, Rosetta, RASP, and 3dRNAscore, respectively. The lower mean rank of PAMNet indicates that less effort is needed to go down the ranked list of PAMNet to include one near-native structural model. A more detailed analysis of the near-native ranking task can be found in Supplementary Figure S1.
在RNA-Puzzles评估基准上,PAMNet显著优于其他四种评分函数,如图2所示。当比较每个RNA的最佳评分结构模型时(图2a),使用PAMNet时模型接近天然结构(RMSD $\mathrm{\Delta}<2\mathrm{\mathring{A}}$)的概率为$90%$,而ARES、Rosetta、RASP和3dRNAscore分别为62%、43%、33%和$5%$。对于每个RNA的10个最佳评分结构模型(图2b),使用PAMNet时包含至少一个接近天然模型的概率为$90%$,而ARES、Rosetta、RASP和3dRNAscore分别为81%、48%、48%和$33%$。在比较每个RNA最佳评分的接近天然结构模型的排名时(图2c),PAMNet在所有RNA中的排名几何平均值为1.7,而ARES、Rosetta、RASP和3dRNAscore分别为3.6、73.0、26.4和127.7。PAMNet较低的排名均值表明,在PAMNet的排名列表中需要更少的努力即可包含一个接近天然的结构模型。关于接近天然排名任务的更详细分析可参见补充图S1。
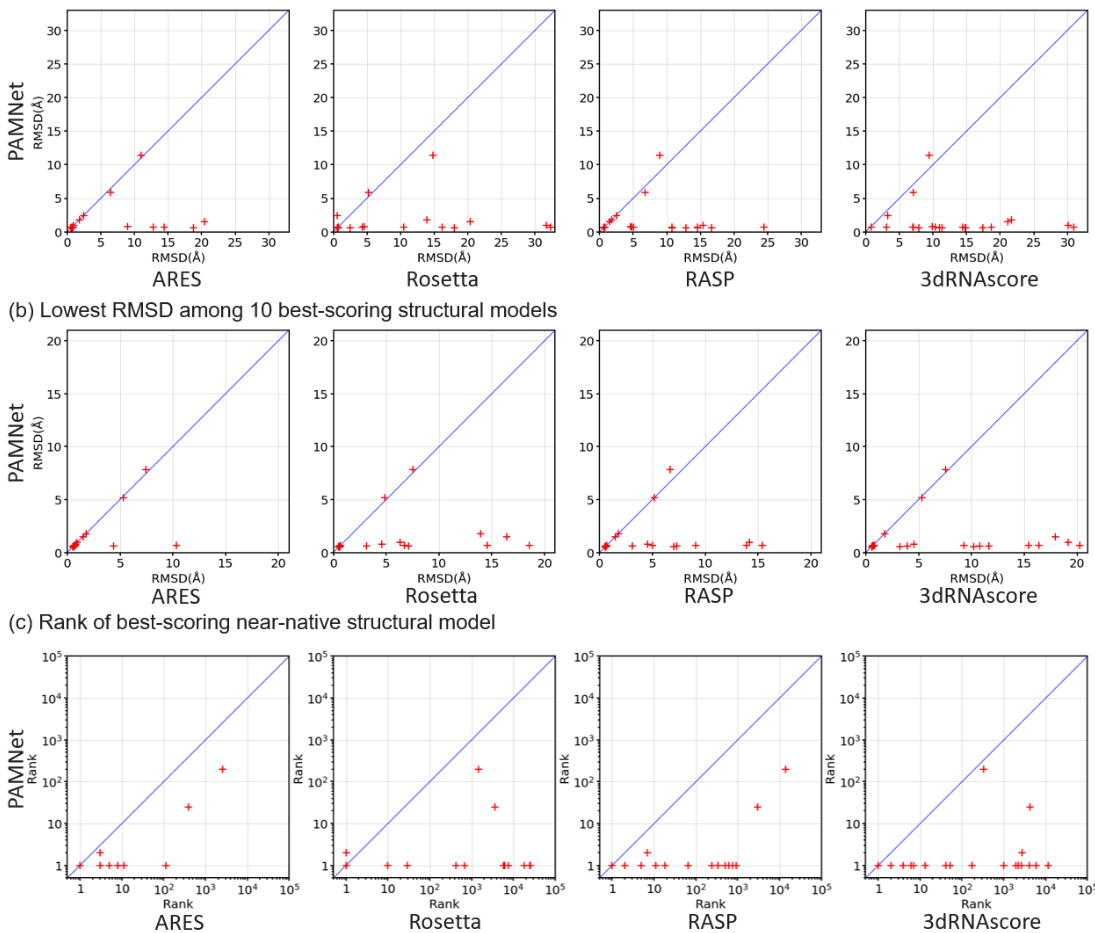
Figure 2. Performance comparison on RNA-Puzzles. Given a group of candidate structural models for each RNA, we rank the models using PAMNet and the other four leading scoring functions for comparison. Each cross in the figures corresponds to one RNA. (a) The best-scoring structural model of each RNA predicted by the scoring functions is compared. PAMNet in general identifies more accurate models (with lower RMSDs from the native structure) than those decided by the other scoring functions. (b) Comparison of the 10 best-scoring structural models. The identification s of PAMNet contain accurate models more frequently than those from other scoring functions. (c) The rank of the best-scoring near-native structural model for each RNA is used for comparison. PAMNet usually performs better than the other scoring functions by having a lower rank.
图 2: RNA-Puzzles性能对比。针对每组RNA候选结构模型,我们使用PAMNet和其他四种领先的评分函数进行模型排序。图中每个十字标记对应一个RNA。(a) 对比各评分函数预测的每个RNA最佳结构模型。PAMNet通常能识别出比其他评分函数更精确(与天然结构RMSD值更低)的模型。(b) 前10个最佳评分结构模型对比。PAMNet的识别结果比其他评分函数更频繁包含精确模型。(c) 对比每个RNA最佳近天然结构模型的排名。PAMNet通常通过获得更低排名而优于其他评分函数。
Protein-ligand binding affinity prediction. In this experiment, we evaluate the accuracy of PAMNet in representing the complexes that contain both small molecules and macromolecules. We use PDBbind, which is a well-known public database of experimentally measured binding affinities for protein-ligand complexes 34. The goal is to predict the binding affinity of each complex based on its 3D structure. We use the PDBbind v2016 dataset and preprocess each original complex to a structure that contains around 300 non hydrogen atoms on average with only the ligand and the protein residues within around it. To comprehensively evaluate the performance, we use Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Pearson’s correlation coefficient (R) and the standard deviation (SD) in regression following 18. PAMNet is compared with various comparative methods including machine learning-based methods (LR, SVR, and RF-Score35), CNN-based methods (Pafnucy36 and $\mathrm{{OnionNet}}^{37}$ ), and GNN-based methods (GraphDTA38, $\mathrm{SGCN}^{39}$ , GNN-DTI40, D-MPNN12, $\mathrm{MAT^{41}}$ , DimeNet15, $\mathrm{{CMPNN^{42}}}$ , and $\mathrm{SIGN^{18}}$ ). More details of the experiments are provided in Methods and Supplementary Information.
蛋白质-配体结合亲和力预测。在本实验中,我们评估了PAMNet在表征包含小分子和大分子的复合物时的准确性。我们使用PDBbind,这是一个著名的公共数据库,包含实验测量的蛋白质-配体复合物结合亲和力[34]。目标是根据每个复合物的3D结构预测其结合亲和力。我们使用PDBbind v2016数据集,并将每个原始复合物预处理为平均包含约300个非氢原子的结构,仅保留配体及其周围范围内的蛋白质残基。为了全面评估性能,我们采用均方根误差(RMSE)、平均绝对误差(MAE)、皮尔逊相关系数(R)和回归中的标准差(SD)作为指标[18]。PAMNet与多种对比方法进行比较,包括基于机器学习的方法(LR、SVR和RF-Score[35])、基于CNN的方法(Pafnucy[36]和$\mathrm{{OnionNet}}^{37}$)以及基于GNN的方法(GraphDTA[38]、$\mathrm{SGCN}^{39}$、GNN-DTI[40]、D-MPNN[12]、$\mathrm{MAT^{41}}$、DimeNet[15]、$\mathrm{{CMPNN^{42}}}$和$\mathrm{SIGN^{18}}$)。实验的更多细节见方法和补充信息。
We list the results of all models and compare their performance in Table 2 and Supplementary Table S1. PAMNet achieves the best performance regarding all 4 evaluation metrics in our experiment. When compared with the second-best model, SIGN, our PAMNet performs significantly better with p-value $<0.05$ . These results clearly demonstrate the accuracy of our model when learning representations of 3D macromolecule complexes.
我们在表2和补充表S1中列出了所有模型的结果并比较了它们的性能。PAMNet在我们的实验中实现了所有4个评估指标的最佳性能。与排名第二的模型SIGN相比,我们的PAMNet表现显著更优(p值$<0.05$)。这些结果清楚地证明了我们的模型在学习3D大分子复合物表征时的准确性。
In general, we find that the models with explicitly encoded 3D geometric information like DimeNet, SIGN, and our PAMNet outperform the other models without the information directly encoded. An exception is that DimeNet cannot beat CMPNN. This might be because DimeNet is domain-specific and is originally designed for small molecules rather than macromolecule
总体而言,我们发现显式编码3D几何信息的模型(如DimeNet、SIGN和我们的PAMNet)性能优于未直接编码该信息的其他模型。例外情况是DimeNet未能超越CMPNN,这可能是因为DimeNet具有领域特异性,其最初设计针对小分子而非大分子。
Table 2. Performance comparison on PDBbind. We report the averaged results together with standard deviations. For the evaluation metrics, $\downarrow$ denotes the lower the better, while $\uparrow$ denotes the higher the better. The best results are marked in bold and the second-best results with underline.
表 2: PDBbind 上的性能对比。我们报告了平均值和标准差。对于评估指标,$\downarrow$ 表示越低越好,而 $\uparrow$ 表示越高越好。最佳结果以粗体标出,次佳结果以下划线标出。
| 模型类型 | 模型 | RMSE↓ | MAE← | SD← | R↑ |
|---|---|---|---|---|---|
| 基于机器学习 | LR | 1.675 (0.000) | 1.358 (0.000) | 1.612 (0.000) | 0.671 (0.000) |
| SVR | 1.555 (0.000) | 1.264 (0.000) | 1.493 (0.000) | 0.727 (0.000) | |
| RF-Score | 1.446 (0.008) | 1.161 (0.007) | 1.335 (0.010) | 0.789 (0.003) | |
| 基于 CNN | Pafnucy | 1.585 (0.013) | 1.284 (0.021) | 1.563 (0.022) | 0.695 (0.011) |
| OnionNet | 1.407 (0.034) | 1.078 (0.028) | 1.391 (0.038) | 0.768 (0.014) | |
| 基于 GNN | GraphDTA | 1.562 (0.022) | 1.191 (0.016) | 1.558 (0.018) | 0.697 (0.008) |
| SGCN | 1.583 (0.033) | 1.250 (0.036) | 1.582 (0.320) | 0.686 (0.015) | |
| GNN-DTI | 1.492 (0.025) | 1.192 (0.032) | 1.471 (0.051) | 0.736 (0.021) | |
| D-MPNN | 1.493 (0.016) | 1.188 (0.009) | 1.489 (0.014) | 0.729 (0.006) | |
| MAT | 1.457 (0.037) | 1.154 (0.037) | 1.445 (0.033) | 0.747 (0.013) | |
| DimeNet | 1.453 (0.027) | 1.138 (0.026) | 1.434 (0.023) | 0.752 (0.010) | |
| CMPNN | 1.408 (0.028) | 1.117 (0.031) | 1.399 (0.025) | 0.765 (0.009) | |
| SIGN | 1.316 (0.031) | 1.027 (0.025) | 1.312 (0.035) | 0.797 (0.012) | |
| 我们的方法 | PAMNet | 1.263 (0.017) | 0.987 (0.013) | 1.261 (0.015) | 0.815 (0.005) |
| 数据集 | 模型 | 内存 (GB) | 推理时间 (s) |
|---|---|---|---|
| QM9 | DimeNet++ | 21.1 | 11.3 |
| QM9 | SphereNet | 22.7 | 11.1 |
| QM9 | PAMNet-s | 6.0 | 7.3 |
| QM9 | PAMNet | 6.2 | 11.0 |
| QM9 | ARES | 13.5 | 2.1 |
| RNA-Puzzles | PAMNet | 7.8 | 0.6 |
| RNA-Puzzles | |||
| PDBbind | SIGN | 19.7 | 12.0 |
| PDBbind | PAMNet | 13.1 | 1.8 |
Table 3. Results of efficiency evaluation. We compare PAMNet with the best-performed baselines in each of the three tasks regarding memory consumption and inference time. The most efficient results are marked in bold.
表 3: 效率评估结果。我们将 PAMNet 与三项任务中每项任务表现最佳的基线在内存消耗和推理时间方面进行比较。最高效的结果以粗体标出。
complexes. In contrast, our proposed PAMNet is more flexible to learn representations for various types of molecular systems. The superior performance of PAMNet for predicting binding affinity relies on the separate modeling of local and non-local interactions. For protein-ligand complexes, the local interactions mainly capture the interactions inside the protein and the ligand, while the non-local interactions can capture the interactions between protein and ligand. Thus PAMNet is able to effectively handle diverse interactions and achieve accurate results.
相比之下,我们提出的PAMNet能更灵活地学习各类分子系统的表征。PAMNet在预测结合亲和力方面的卓越性能依赖于其对局部与非局部相互作用的分别建模。对于蛋白质-配体复合物,局部相互作用主要捕获蛋白质和配体内部的相互作用,而非局部相互作用则能捕获蛋白质与配体间的相互作用。因此,PAMNet能有效处理多样化的相互作用并获得精确结果。
Performance of PAMNet regarding efficiency
PAMNet 的效率表现
To evaluate the efficiency of PAMNet, we compare it to the best-performed baselines in each task regarding memory consumption and inference time and summarize the results in Table 3. Theoretically, DimeNet++, SphereNet, and SIGN all require $O(N k^{2})$ messages in message passing, while our PAMNet requires ${\cal O}(N(k_{g}+{k_{l}}^{2}))$ ) messages instead, where $N$ is the number of nodes, $k$ is the average degree in a graph, $k_{g}$ and $k_{l}$ denotes the average degree in $G_{g}$ and $G_{l}$ in the corresponding multiplex graph $G$ . When $k_{g}\sim k$ and $k_{l}\ll k_{g}$ , PAMNet is much more efficient regarding the number of messages involved. A more detailed analysis of computational complexity is included in Methods. Based on the results in Table 3 empirically, we find PAMNet models all require less memory consumption and inference time than the best-performed baselines in all three tasks, which matches our theoretical analysis. We also compare the memory consumption when using a different largest cutoff distance $d$ of the related models in Figure 3. From the results, we observe that the memory consumed by DimeNet and SIGN increases much faster than PAMNet when $d$ increases. When fixing as an example, PAMNet requires $80%$ and $71%$ less memory than DimeNet and SIGN, respectively. Thus PAMNet is much more memory-efficient and is able to capture longer-range interactions than these baselines with restricted resources. The efficiency of PAMNet models comes from the separate modeling of local and non-local interactions in 3D molecular structures. By doing so, when modeling the non-local interactions, which make up the majority of all interactions, we utilize a relatively efficient message passing scheme that only encodes pairwise distances $d$ as the geometric information. Thus when compared with the models that require more comprehensive geometric information when modeling all interactions, PAMNet significantly reduces the computationally expensive operations. More information about the details of experimental settings is included in Methods.
为了评估PAMNet的效率,我们将其与各任务中表现最佳的基线方法在内存消耗和推理时间方面进行比较,并将结果总结在表3中。理论上,DimeNet++、SphereNet和SIGN在消息传递中都需要$O(N k^{2})$条消息,而我们的PAMNet仅需${\cal O}(N(k_{g}+{k_{l}}^{2}))$条消息。其中$N$表示节点数量,$k$为图的平均度数,$k_{g}$和$k_{l}$分别代表多重图$G$中$G_{g}$和$G_{l}$的平均度数。当$k_{g}\sim k$且$k_{l}\ll k_{g}$时,PAMNet在消息数量方面效率显著更高。关于计算复杂度的详细分析见方法部分。
根据表3的实验结果,我们发现PAMNet模型在所有三项任务中的内存消耗和推理时间均低于表现最佳的基线方法,这与理论分析一致。图3展示了不同最大截断距离$d$下相关模型的内存消耗对比。结果显示,当$d$增大时,DimeNet和SIGN的内存消耗增速远高于PAMNet。以固定为例,PAMNet的内存需求分别比DimeNet和SIGN减少80%和71%。因此PAMNet不仅内存效率更高,还能在有限资源下捕捉更长程的相互作用。
PAMNet的高效性源于其对3D分子结构中局部与非局部相互作用的分别建模。通过这种方式,在建模占主导地位的非局部相互作用时,我们采用了仅需编码成对距离$d$作为几何信息的高效消息传递方案。相比那些建模所有相互作用时需要更全面几何信息的模型,PAMNet显著减少了计算开销较大的操作。实验设置的详细信息见方法部分。
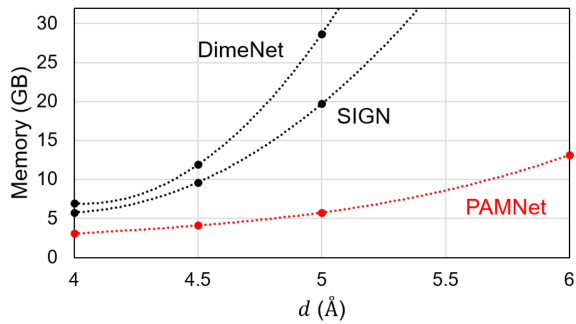
Figure 4. Ablation study of PAMNet. We compare the variants with the original PAMNet and report the differences.
图 4: PAMNet消融实验。我们将变体与原始PAMNet进行比较并报告差异。
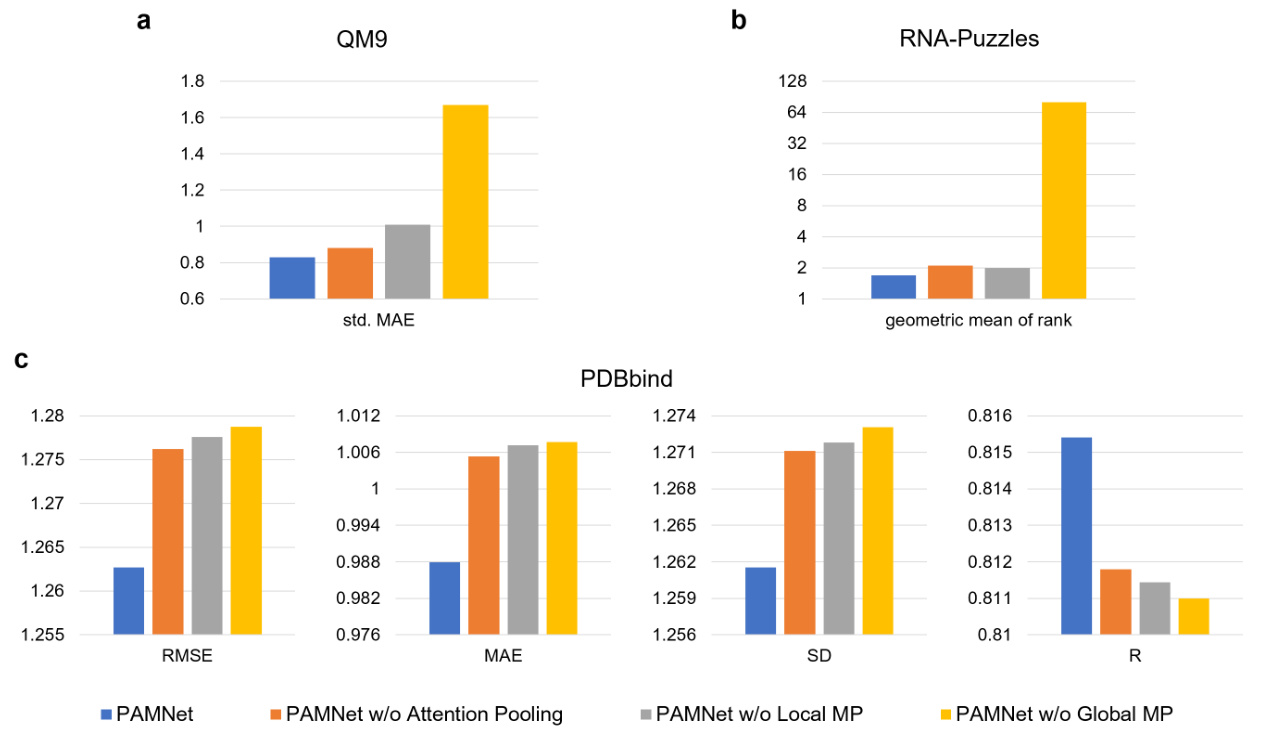
Figure 3. Memory consumption vs. the largest cutoff distance $d$ on PDBbind. We compare PAMNet with the GNN baselines that also explicitly incorporate the 3D molecular geometric information like pairwise distances and angles.
图 3: PDBbind 数据集上内存消耗与最大截断距离 $d$ 的关系。我们将 PAMNet 与同样显式结合 3D 分子几何信息 (如原子对距离和角度) 的 GNN 基线模型进行对比。
All components in PAMNet contribute to the performance
PAMNet中的所有组件都对性能有所贡献
To figure out whether all of the components in PAMNet, including the fusion module and the message passing modules, contribute to the performance of PAMNet, we conduct an ablation study by designing PAMNet variants. Without the attention pooling, we use the averaged results from the message passing modules in each hidden layer to build a variant. We also remove either the Local Message Passing or the Global Message Passing for investigation. The performances of all PAMNet variants are evaluated on the three benchmarks. Specifically, the std. MAE across all properties on QM9, the geometric mean of the ranks across all RNAs on RNA-Puzzles, and the four metrics used in the experiment on PDBbind are computed for comparison. The results in Figure 4 show that all variants decrease the performance of PAMNet in the evaluations, which clearly validates the contributions of all those components. Detailed results of the properties on QM9 can be found in Supplementary Table S2.
为了验证PAMNet中所有组件(包括融合模块和消息传递模块)是否都对性能有贡献,我们通过设计PAMNet变体进行了消融实验。去除注意力池化模块后,我们使用各隐藏层消息传递模块的平均结果构建了一个变体。此外,我们还分别移除了局部消息传递(Local Message Passing)和全局消息传递(Global Message Passing)进行测试。所有PAMNet变体的性能均在三个基准数据集上评估:计算QM9所有属性的标准差MAE、RNA-Puzzles中所有RNA的几何平均排名、以及PDBbind实验中使用的四项指标进行对比。图4结果显示,所有变体都会导致PAMNet性能下降,这明确验证了各组件的贡献。QM9各属性的详细结果可参见补充材料表S2。
Analysis of the contribution of local and global interactions
局部与全局交互作用贡献分析
A salient property of PAMNet is the incorporation of the attention mechanism in the fusion module, which takes the importance of node embeddings in $G_{l o c a l}$ and $G_{g l o b a l}$ of $G$ into consideration in learning combined node embeddings. Recall that for each node $n$ in the set of nodes ${N}$ in $G$ , the attention pooling in the fusion module learns the attention weights $\alpha_{l}$ and $\alpha_{g}$ between $n$ ’s node embedding $\mathbf{z}{l}$ in $G_{l o c a l}$ and $n$ ’s node embedding $\mathbf{z}{g}$ in $G_{g l o b a l}$ . $\alpha_{l}$ and $\alpha_{g}$ serve as the importance of $\mathbf{z}{l}$ and $\mathbf{z}{g}$ when computing the combined node embedding $\mathbf{z}$ . To better understand the contribution of $\mathbf{z}{l}$ and $\mathbf{z}{g}$ , we conduct a detailed analysis of the learned attention weights $\alpha_{l}$ and $\alpha_{g}$ in the three tasks we experimented with. Since the node embeddings are directly related to the involved interactions, such analysis can also reveal the contribution of local and global interactions on the predictions in different tasks. In each task, we take an average of all $\alpha_{l}$ or $\alpha_{g}$ to be the overall importance of the corresponding group of interactions. Then we compare the computed average attention weights $\overline{{\alpha_{l}}}$ and $\overline{{\alpha_{g}}}$ and list the results in Table 4. A higher attention weight in each task indicates a stronger contribution of the corresponding interactions on solving the task.
PAMNet的一个显著特性是在融合模块中引入了注意力机制,该机制在学习组合节点嵌入时考虑了节点在$G$的$G_{local}$和$G_{global}$中的重要性。对于$G$中节点集${N}$中的每个节点$n$,融合模块中的注意力池化会学习$n$在$G_{local}$中的节点嵌入$\mathbf{z}{l}$与$G_{global}$中的节点嵌入$\mathbf{z}{g}$之间的注意力权重$\alpha_{l}$和$\alpha_{g}$。$\alpha_{l}$和$\alpha_{g}$在计算组合节点嵌入$\mathbf{z}$时分别表示$\mathbf{z}{l}$和$\mathbf{z}{g}$的重要性。为了更好地理解$\mathbf{z}{l}$和$\mathbf{z}{g}$的贡献,我们对实验中的三个任务所学习到的注意力权重$\alpha_{l}$和$\alpha_{g}$进行了详细分析。由于节点嵌入与涉及的交互直接相关,这种分析还可以揭示局部和全局交互在不同任务预测中的贡献。在每个任务中,我们将所有$\alpha_{l}$或$\alpha_{g}$的平均值作为相应交互组的整体重要性,然后比较计算得到的平均注意力权重$\overline{{\alpha_{l}}}$和$\overline{{\alpha_{g}}}$,并将结果列在表4中。每个任务中较高的注意力权重表明相应交互在解决该任务时的贡献更强。
Table 4. Comparison of the average attention weights $\overline{{\alpha_{l}}}$ and $\overline{{\alpha_{g}}}$ for local and global interactions in attention pooling. The higher attention weight for each target is marked in bold.
表 4: 注意力池化中局部交互 $\overline{{\alpha_{l}}}$ 和全局交互 $\overline{{\alpha_{g}}}$ 的平均注意力权重对比。每个目标的较高注意力权重以粗体标出。
| 注意力权重 | QM9 | RNA-Puzzles | PDBbind | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ | α | EHOMO | ELUMO | (R²) | ZPVE | Uo | U | H | G | Cv | ||
| α1 | 0.64 | 0.53 | 0.50 | 0.50 | 0.29 | 0.54 | 0.60 | 0.60 | 0.60 | 0.57 | 0.58 | 0.22 |
| Og | 0.36 | 0.47 | 0.50 | 0.50 | 0.71 | 0.46 | 0.40 | 0.40 | 0.40 | 0.43 | 0.42 | 0.78 |
For the targets being predicted in QM9, we find that all of them have $\overline{{\alpha_{l}}}\geq\overline{{\alpha_{g}}}$ except the electronic spatial extent $\left\langle R^{2}\right\rangle$ , indicating a stronger contribution of the local interactions, which are defined by chemical bonds in this task. This may be because QM9 contains small molecules with only up to 9 non-hydrogen atoms, local interactions can capture a considerable portion of all atomic interactions. However, when predicting electronic spatial extent $\left\langle R^{2}\right\rangle$ , we notice that $\overline{{\alpha_{l}}}<\overline{{\alpha_{g}}}$ , which suggests that $\left\langle R^{2}\right\rangle$ is mainly affected by the global interactions that are the pairwise interactions within in this case. This is not surprising since $\left\langle R^{2}\right\rangle$ is the electric field area affected by the ions in the molecule, and is directly related to the diameter or radius of the molecule. Besides, previous study43 has demonstrated that graph properties like diameter and radius cannot be computed by message passing-based GNNs that rely entirely on local information, and additional global information is needed. Thus it is expected that global interactions have a stronger contribution than local interactions on predicting electronic spatial extent.
在QM9中被预测的目标中,我们发现除电子空间范围$\left\langle R^{2}\right\rangle$外,所有目标都满足$\overline{{\alpha_{l}}}\geq\overline{{\alpha_{g}}}$,表明局部相互作用(本任务中由化学键定义)贡献更强。这可能是因为QM9仅包含不超过9个非氢原子的小分子,局部相互作用能捕捉到相当比例的原子间作用。然而在预测电子空间范围$\left\langle R^{2}\right\rangle$时,我们注意到$\overline{{\alpha_{l}}}<\overline{{\alpha_{g}}}$,说明$\left\langle R^{2}\right\rangle$主要受全局相互作用(本案例中定义为内的成对相互作用)影响。这并不意外,因为$\left\langle R^{2}\right\rangle$表示分子中离子影响的电场区域,与分子直径或半径直接相关。此外,先前研究[43]表明,直径和半径等图属性无法通过完全依赖局部信息的基于消息传递的GNN计
