0.8% Nyquist computational ghost imaging via non-experimental deep learning

通过非实验性深度学习实现0.8%奈奎斯特计算重影成像

We present a framework for computational ghost imaging based on deep learning and customized pink noise speckle patterns. The deep neural network in this work, which can learn the sensing model and enhance image reconstruction quality, is trained merely by simulation. To demonstrate the subNyquist level in our work, the conventional computational ghost imaging results, reconstructed imaging results using white noise and pink noise via deep learning are compared under multiple sampling rates at different noise conditions. We show that the proposed scheme can provide highquality images with a sampling rate of $0.8%$ even when the object is outside the training dataset, and it is robust to noisy environments. This method is excellent for various applications, particularly those that require a low sampling rate, fast reconstruction efficiency, or experience strong noise interference.

我们提出了一种基于深度学习与定制粉红噪声散斑图案的计算重影成像框架。本工作中的深度神经网络仅通过模拟训练即可学习传感模型并提升图像重建质量。为验证方案的亚奈奎斯特采样特性，我们在不同噪声条件下对比了传统计算重影成像、基于深度学习的白噪声与粉红噪声重建结果。实验表明：即使目标物体不在训练集中，该方案仍能在0.8%采样率下获得高质量图像，且对噪声环境具有强鲁棒性。该方法特别适用于需要低采样率、快速重建或强噪声干扰的各类应用场景。

I. INTRODUCTION

I. 引言

Ghost imaging (GI) [1–4] is an innovative method for measuring the spatial correlations between light beams. With GI, the signal light field interacts with the object and is collected by a single-pixel detector, and the reference light field, which does not interact with the object, falls onto the imaging detector. Therefore, the image information is not present in either beam alone but only revealed in their correlations. Computational ghost imaging (CGI) [5, 6] was proposed to further ameliorate and simplify this framework. In CGI, The reference arm that records the speckles is replaced by loading pre-generated patterns directly onto the spatial light modulator or the digital micro mirror device (DMD). The unconventional image is then revealed by correlating the sequentially recorded intensities at the single-pixel detector with the corresponding patterns. CGI finds a lot of applications such as wide spectrum imaging [7–9], remote sensing [10], and quantum-secured imaging [11].

重影成像 (Ghost Imaging, GI) [1-4] 是一种测量光束间空间相关性的创新方法。在GI中，信号光场与物体相互作用后被单像素探测器收集，而未经物体调制的参考光场则投射至成像探测器。因此，图像信息并不单独存在于任一光束中，仅在其关联性中显现。计算重影成像 (Computational Ghost Imaging, CGI) [5,6] 的提出进一步优化并简化了这一框架。CGI通过将预生成图案直接加载至空间光调制器或数字微镜器件 (DMD) 上，取代了记录散斑的参考光路。随后通过将单像素探测器记录的时序强度信号与对应图案进行关联，即可重构非常规图像。CGI在宽光谱成像 [7-9]、遥感 [10] 和量子安全成像 [11] 等领域具有广泛应用。

However, CGI generally requires a large number of samplings to reconstruct a high-quality image, or the signal would have been submerged under correlation fluctuations and environmental noise. To suppress the environmental noise and correlation fluctuations, the required minimum number of sampling is proportional to the total pixel number of the pattern applied on DMD, i.e., the Nyquist sampling limit [12, 13]. The image could have a meager quality with a limited sampling number. This demanding requirement hindered CGI from fully replacing conventional photography. A large number of schemes have been proposed to improve CGI’s speed and decrease the sampling rate (sub-Nyquist). For instance, compressive sensing imaging can reconstruct images with a relatively low sampling rate by exploiting the sparsity of the objects [14–17]. It nevertheless largely depends on the sparsity of objects and is sensitive to noise [18]. Ortho normalized noise patterns can be used to suppress the noise and improve the image’s quality under a limited sampling number [19, 20]. In particular, the ortho normalized colored noise patterns can break the Nyquist limit down to $\sim5%$ [20]. Fourier and sequence-ordered Walsh-Hadamard patterns, which are orthogonal to each other in time or spatial domain, were also applied to the sub-Nyquist imaging [21–23]. The Russian doll [24] and cake-cutting [25] ordering of Walsh-Hadamard patterns can minimize the sampling ratio to 5%-10% Nyquist limit.

然而，计算重影成像 (CGI) 通常需要大量采样才能重建高质量图像，否则信号会被相关波动和环境噪声淹没。为了抑制环境噪声和相关波动，所需的最小采样数与数字微镜器件 (DMD) 上加载图案的总像素数成正比，即奈奎斯特采样极限 [12, 13]。在采样数有限的情况下，图像质量可能极差。这一严苛要求阻碍了CGI完全取代传统摄影。目前已有大量方案被提出以提高CGI速度并降低采样率（亚奈奎斯特）。例如，压缩感知成像通过利用物体的稀疏性，能以相对较低的采样率重建图像 [14-17]，但其效果很大程度上依赖于物体的稀疏性且对噪声敏感 [18]。正交归一化噪声图案可用于抑制噪声，并在有限采样数下提高图像质量 [19, 20]。特别是正交归一化彩色噪声图案能将奈奎斯特极限降低至 $\sim5%$ [20]。傅里叶变换和序列化沃尔什-哈达玛图案因其在时域或空域的正交性，也被应用于亚奈奎斯特成像 [21-23]。沃尔什-哈达玛图案的俄罗斯套娃 [24] 和蛋糕切割 [25] 排序法可将采样率最小化至奈奎斯特极限的5%-10%。

Recently, the deep learning (DL) technique is employed to identify images [26, 27] and improve the quality of images with the deep neural network (DNN) [28–36]. Specifically, computational ghost imaging via deep learning (CGIDL) has shown a minimum ratio of Nyquist limit down to $\sim5%$ [29, 33]. However, such work’s DNNs are trained by experimental CGI results. Only when the training environment is highly identical to the environment used for image reconstruction can the DNN be effective. This limits its universal applications and restricts it to achieve quick reconstructions. Usually at least thousands of inputs have to be generated for the training, which would be very time-consuming if conducting experimental training each time. Some studies have been performed to test the effectiveness of non-experimental CGI training DNN, the minimum ratios of the Nyquist limit were up to a few percent [30, 31, 35]. However, the sampling ratio is much higher for objects outside of training dataset than those in the training dataset [33]. Therefore, despite the proliferation of numerous algorithms, retrieving high-quality images outside of the training group with a meager Nyquist limit ratio by non-experimental training remains a challenge for the CGIDL system.

近年来，深度学习(DL)技术被用于图像识别[26, 27]，并通过深度神经网络(DNN)提升图像质量[28–36]。其中，基于深度学习的计算重影成像(CGIDL)已实现最低至$\sim5%$奈奎斯特极限采样率[29, 33]。但这类研究的DNN均需通过实验CGI数据进行训练，只有当训练环境与图像重建环境高度一致时，DNN才能有效工作。这限制了其普适性应用，难以实现快速重建。通常需要生成至少数千组训练输入，若每次均进行实验训练将极其耗时。已有研究尝试测试非实验CGI训练DNN的效果，其奈奎斯特极限最低采样率可达百分之几[30, 31, 35]，但对于训练集外的物体，其采样率远高于训练集内物体[33]。因此，尽管算法层出不穷，如何通过非实验训练在极低奈奎斯特极限采样率下，对训练集外物体实现高质量图像重建，仍是CGIDL系统面临的挑战。

This letter aims to minimize the necessary sampling number further and improve the imaging quality with the combination of DL and colored noise CGI. Recently, it has been shown that the synthesized colored noise patterns possess unique non-zero correlations between neighborhood pixels via amplitude modulation in the spatial frequency domain [37, 38]. In particular, The pink noise CGI owns positive cross-correlations in the second-order correlation [37]. It gives a good image quality under a boisterous environment or pattern distortion when the traditional CGI method fails. Combining DL with pink noise CGI shows that the imaging can be retrieved under an extremely low sampling rate $'\sim0.8%}$ ). We also show that we can get training patterns from the simulation without introducing the environmental noises, i.e., there is no need to get DNN training with a large number of experimental training inputs. The object used in the experiment can be independent of the training dataset, which can largely benefit CGIDL in the real application.

本信旨在进一步减少必要采样数量，并通过结合深度学习(DL)与彩色噪声关联成像(CGI)提升成像质量。近期研究表明，通过空间频域的幅度调制，合成彩色噪声模式在相邻像素间具有独特的非零相关性[37,38]。特别是粉红噪声CGI在二阶关联中呈现正相关特性[37]，当传统CGI方法失效时，它能在嘈杂环境或模式畸变下保持良好成像质量。实验表明：结合深度学习与粉红噪声CGI可在极低采样率( $'\sim0.8%}$ ).下重建图像。我们还证明可以从仿真中获取训练模式而无需引入环境噪声，即无需通过大量实验训练输入来训练深度神经网络(DNN)。实验中使用的物体可独立于训练数据集，这将极大促进CGIDL的实际应用。

II. DEEP LEARNING

II. 深度学习

FIG. 1: Architecture of DNN. It consists of four convolution layers, one image input layer, one fully connected layer (yellow), the rectified linear unit, and the batch normalization layers (red). In the upper line are CGI results (training inputs) and handwriting ground truths (training labels); In the bottom line are CGI results from the experiment (test inputs) and CGIDL results (test outputs) with block style.

图 1: DNN架构图。该网络包含四个卷积层、一个图像输入层、一个全连接层(黄色标注)、修正线性单元以及批归一化层(红色标注)。上方为CGI生成结果(训练输入)和手写真实样本(训练标签)；下方为实验获得的CGI结果(测试输入)与采用块状风格的CGIDL输出结果(测试输出)。

Our DNN model, as shown in Fig. 1, uses four convolution layers, one image input layer, and one fully connected layer. Small $3\times3$ receptive fields are applied throughout the whole convolution layers for better performance [39]. Batch normalization layers (BNL), rectified Linear Unit (ReLU) layers and zero padding are added between each convolution layer. The BNL is functioned to avoid internal covariate shift during the training process and speed up the training of DNN [40]. The ReLU layer applies a threshold operation to each element of the inputs [41]. The zero padding part was designed to maintain the characteristic of input images’ boundaries. To customize the size of training pictures, both the input and output layers are set to be $54\times98$ . The solver for training is employed by the Stochastic Gradient Descent with Momentum Optimizer (SGDMO) to reduce the oscillation via using momentum. The parameter vector can be updated via equation Eq. (1), which demonstrates the updating process during the iteration.

我们的DNN模型如图1所示，使用了四个卷积层、一个图像输入层和一个全连接层。所有卷积层均采用小尺寸$3\times3$感受野以获得更优性能[39]。每个卷积层之间添加了批归一化层(BNL)、修正线性单元(ReLU)层和零填充层。BNL用于避免训练过程中的内部协变量偏移并加速DNN训练[40]。ReLU层对输入数据的每个元素执行阈值运算[41]。零填充设计用于保持输入图像边界的特征。为适配训练图片尺寸，输入层和输出层均设置为$54\times98$。训练求解器采用带动量的随机梯度下降优化器(SGDMO)，通过动量机制减少振荡。参数向量可通过公式Eq.(1)进行更新，该公式展示了迭代过程中的更新机制。

$$
\theta_{\ell+1}=\theta_{\ell}-\alpha\nabla E\left(\theta_{\ell}\right)+\gamma\left(\theta_{\ell}-\theta_{\ell-1}\right),
$$

where $\ell$ is the iteration number, $\alpha$ is the learning rate, $\theta$ is the parameter vector, and $E(\theta)$ is the loss function, mean square error (MSE). The MSE is defined as

其中 $\ell$ 为迭代次数，$\alpha$ 为学习率，$\theta$ 为参数向量，$E(\theta)$ 为损失函数，即均方误差 (MSE)。MSE定义为

$$
\mathrm{MSE}=\frac{1}{N_{\mathrm{pixel}}}\sum_{i=1}^{N_{\mathrm{pixel}}}[\frac{G_{i}-X_{i}}{\langle G_{(o)}\rangle}]^{2}.
$$

Here, $G$ represents the pixel value of the resulted imaging. $G_{(o)}$ represents pixels that the light ought to be transmitted, i.e., the object area, while $G_{(b)}$ represents pixels that the light ought to be blocked, i.e., the background area. $X$ is the ground truth calculated by

这里，$G$ 表示成像结果的像素值。$G_{(o)}$ 表示光线应当透过的像素（即物体区域），而 $G_{(b)}$ 表示光线应当被阻挡的像素（即背景区域）。$X$ 是通过计算得到的地面实况值。

The third part on the right hand side of the equation is the feature of SGDMO, analog to the momentum where $\gamma$ determines the contribution of the previous gradient step to the current iteration [42]. Two strategies are applied to avoid over-fitting of training images. At the end of DNN, a dropout layer is applied with probability of dropping out input elements being 0.2, which is aimed to reduce the connection between convolution layers and the fully connected layer [43]. Meanwhile, we adopted a step decay schedule for the learning rate. The learning rate dropped from $10^{-3}$ to $10^{-4}$ after 75 epochs, which constrain the fitting parameters within a reasonable region. Lower the learning rate could avoid over fitting significantly with constant maximum epochs.

方程右侧的第三部分是SGDMO的特征，类似于动量机制，其中$\gamma$决定了前一步梯度对当前迭代的贡献[42]。为避免训练图像过拟合，我们采用了两种策略。在DNN末端设置了丢弃概率为0.2的dropout层，旨在减弱卷积层与全连接层之间的关联性[43]。同时采用阶梯式学习率衰减策略：经过75个epoch后，学习率从$10^{-3}$降至$10^{-4}$，从而将拟合参数约束在合理范围内。在固定最大epoch数条件下，降低学习率能显著缓解过拟合现象。

B. Network training

B. 网络训练

The proposed CGIDL scheme requires a training process based on pre-prepared dataset. After training in simulation, it owns ability to reconstruct the images. We use a set of 10000 digits from the MNIST handwritten digit database [44] as training images. All images are resized and normalized to $54\times98$ to test the smaller sampling ratio. These training images are reconstructed by the CGI algorithm. The training images and reconstruction training images then feed the DNN model as inputs and outputs, respectively, as shown in Fig. 2(a). The white noise and pink noise speckle patterns are used separately for the training process, using exactly the same protocol. The maximum epochs are set as 100, and the training iteration is 31200. The program is implemented via MATLAB R2019a Update 5 (9.6.0.1174912, 64-bit), and the DNN is implemented through DL Toolbox. The GPU-chip NVIDIA GTX1050 is used to accelerate the speed of the computation.

提出的CGIDL方案需要一个基于预先准备的数据集的训练过程。经过仿真训练后，它具备了图像重建的能力。我们使用来自MNIST手写数字数据库[44]的10000个数字作为训练图像。所有图像都被调整大小并归一化为$54\times98$，以测试较小的采样率。这些训练图像通过CGI算法进行重建。训练图像和重建训练图像分别作为输入和输出馈入DNN模型，如图2(a)所示。在训练过程中分别使用白噪声和粉红噪声散斑图案，采用完全相同的协议。最大训练周期设置为100，训练迭代次数为31200。程序通过MATLAB R2019a Update 5 (9.6.0.1174912, 64位)实现，DNN通过DL Toolbox实现。使用GPU芯片NVIDIA GTX1050加速计算速度。

The trained DNN is then tested by simulation and used for retrieving CGI results in the experiments. In the testing part, the CGI algorithm generates reconstructed images from testing images with both the MNIST handwritten digits and block style digits, where the later set is different from images in the training group. As shown in Fig. 2(b), the trained DNN, fed with reconstruction testing images, generates CGIDL results. Comparing the difference between CGIDL and testing images, we could measure the quality of the trained DNN. Well-performed DNN can be used for retrieving CGI in the experiment.

训练完成的深度神经网络(DNN)随后通过仿真测试，并用于实验中检索计算重影成像(CGI)结果。测试阶段中，CGI算法分别从MNIST手写数字和方块风格数字的测试图像生成重建图像，后者与训练组的图像存在差异。如图2(b)所示，输入重建测试图像后，训练好的DNN会生成CGIDL结果。通过对比CGIDL与测试图像的差异，我们可以评估训练DNN的质量。性能良好的DNN可用于实验中检索CGI结果。

The schematic of the experiment is shown in Fig. 2(c). A CW laser is used to illuminate the DMD, on which the noise patterns are loaded. The pattern generated by the DMD is then projected onto the object. In our experiment, the size of the noise patterns is $216\times392$ DMD pixels (54 $\times$ 98 independent pixels), in which the independent changeable mirrors count for $4\times4$ pixels. Each DMD pixel is $16\mu m\times16\mu m$ in size.

实验示意图如图 2(c) 所示。实验中采用连续波 (CW) 激光器照射加载了噪声图案的数字微镜器件 (DMD)，随后由 DMD 生成的图案被投射到目标物体上。本实验采用的噪声图案尺寸为 $216\times392$ DMD 像素 (54 $\times$ 98 个独立像素)，其中每个可独立控制的微镜对应 $4\times4$ 像素区域。每个 DMD 像素的物理尺寸为 $16\mu m\times16\mu m$。

In the CGI process, the quality of the images is proportional to the sampling rate, which is the ratio between the number of illumination patterns $N_{\mathrm{pattern}}$ and $N_{\mathrm{pixel}}$ [45, 46]:

在CGI过程中，图像质量与采样率成正比，即照明模式数量$N_{\mathrm{pattern}}$与像素数量$N_{\mathrm{pixel}}$之比 [45, 46]:

$$
\beta=N_{\mathrm{pattern}}/N_{\mathrm{pixel}}.
$$

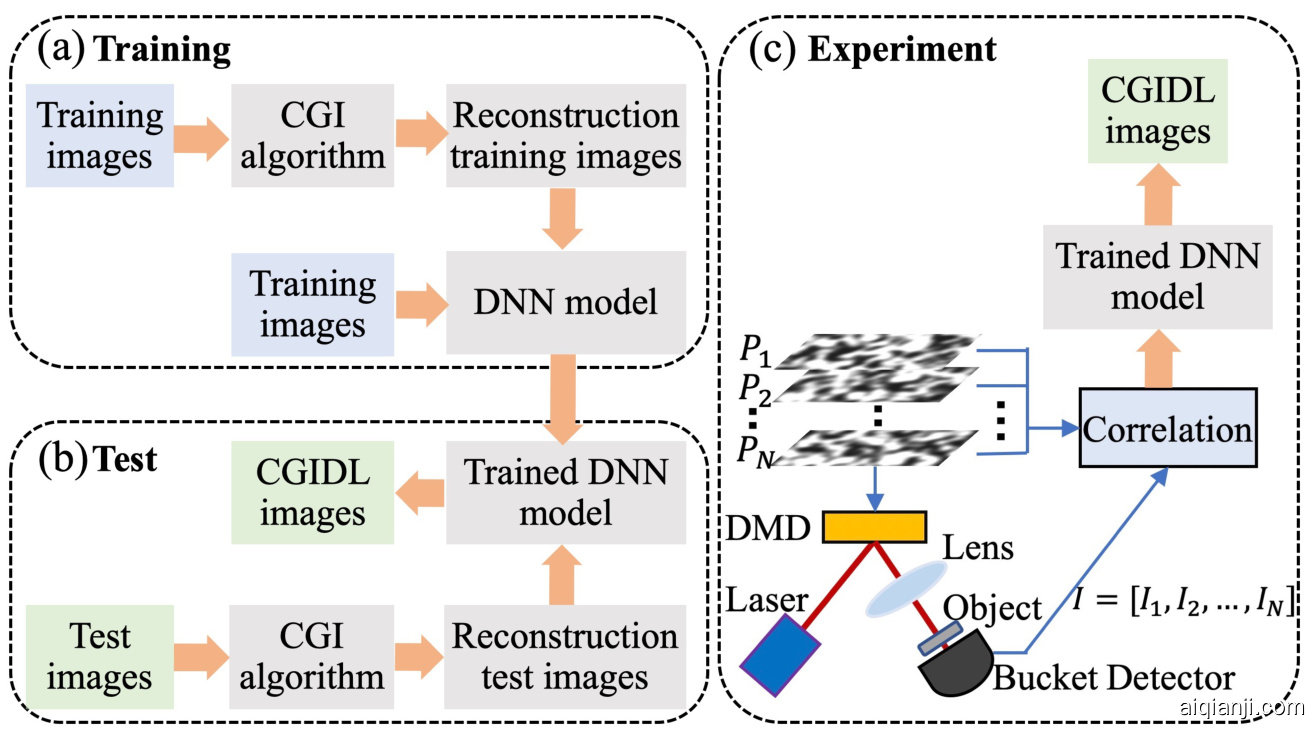
FIG. 2: The flow chart of CGIDL consists of three parts: (a) training, (b) test, and (c) experiment. The DNN model is trained with CGI results from database via simulation. The simulation testing process and experimental measuments use both the handwriting digits and block style digits. The experimental part for CGI uses pink noise and white noise speckle patterns, and their CGI results are ameliorated by trained DNN model.

图 2: CGIDL的流程图包含三部分: (a) 训练, (b) 测试, (c) 实验。深度神经网络(DNN)模型通过仿真使用数据库中的CGI结果进行训练。仿真测试过程和实验测量同时使用手写数字和方块风格数字。CGI实验部分采用粉红噪声和白噪声散斑图案, 其CGI结果通过训练好的DNN模型进行优化。

In the following, We compared the trained network using white noise speckle patterns (DL white) and pink noise speckle patterns (DL pink), as well as the conventional CGI (CGI white) in terms of reconstruction performance with respect to the sampling ratio $\beta$ .

在以下内容中，我们比较了使用白噪声散斑模式（DL white）和粉红噪声散斑模式（DL pink）训练的网络，以及传统计算重影成像（CGI white）在不同采样率 $\beta$ 下的重建性能。

III. SIMULATION

III. 仿真

To test the robustness of our method to different datasets, noise, and its performs at different sampling rates, we performed a set of simulations. Two sets of testing images are used in the simulation. One of which is the handwriting digits 1-9 from the training set, the other is the block style digits 1-9, which are completely independent of training images. These images have $28\times28$ pixels and are resized into $54\times98$ by widening and amplification. We started our simulation from the comparison of the CGI white, DL white and DL pink without noise at $\beta=5%$ , as shown in Fig. 3. The upper part is with the handwriting digits 1-9, the lower part is with the block style digits 1-9. Apparently, at this low sampling rate, the traditional CGI method fails to retrieve the images in both cases. On the other hand, both DL methods work much better than the traditional CGI. For digits from the training dataset, both methods work almost equally well. For digits from outside the training dataset, DL pink works already better than DL white. For example, the DL white barely can distinguish digits ’3’ and ’8’, but DL pink can retrieve all the digits images.

为了测试我们的方法对不同数据集、噪声以及不同采样率下的鲁棒性，我们进行了一系列模拟实验。模拟中使用了两组测试图像：一组是训练集中的手写数字1-9，另一组是与训练图像完全独立的方块风格数字1-9。这些图像具有$28\times28$像素，通过加宽和放大调整为$54\times98$像素。我们从无噪声条件下$\beta=5%$采样率时CGI白光、DL白光和DL粉光的对比开始模拟，如图3所示。上半部分为手写数字1-9，下半部分为方块风格数字1-9。显然，在这种低采样率下，传统CGI方法在两种情况下都无法重建图像。而两种DL方法的表现都远优于传统CGI。对于训练数据集中的数字，两种方法表现几乎相当；对于训练集外的数字，DL粉光已优于DL白光。例如DL白光几乎无法区分数字"3"和"8"，但DL粉光能重建所有数字图像。

In real application, there always exist noise in the measurement. It is therefore worthwhile checking the performances of different methods under the influence of noise. We then performed another set of simulations with added grayscale random noise. The signal-to-noise ratio (SNR) in logarithmic decibel scale is defined as

在实际应用中，测量数据总是存在噪声。因此，有必要检验不同方法在噪声影响下的性能表现。我们随后进行了另一组添加灰度随机噪声的仿真实验。信噪比 (SNR) 以对数分贝尺度定义为

$$
\mathrm{SNR}=10\log{\frac{P_{\mathrm{s}}}{P_{\mathrm{b}}}},
$$

where $P_{\mathrm{s}}$ is the average signal and $P_{\mathrm{b}}$ is the average noise background. Here the SNR is set to be 4.77dB. As s

[论文翻译]通过非实验性深度学习实现0.8%奈奎斯特计算重影成像

原文地址：https://arxiv.org/pdf/2108.07673v1