Draft-and-Revise: Effective Image Generation with Contextual RQ-Transformer
基于上下文的高效图像生成
Abstract
摘要
Although auto regressive models have achieved promising results on image generation, their unidirectional generation process prevents the resultant images from fully reflecting global contexts. To address the issue, we propose an effective image generation framework of Draft-and-Revise with Contextual RQ-transformer to consider global contexts during the generation process. As a generalized VQ-VAE, RQ-VAE first represents a high-resolution image as a sequence of discrete code stacks. After code stacks in the sequence are randomly masked, Contextual RQTransformer is trained to infill the masked code stacks based on the unmasked contexts of the image. Then, Contextual RQ-Transformer uses our two-phase decoding, Draft-and-Revise, and generates an image, while exploiting the global contexts of the image during the generation process. Specifically. in the draft phase, our model first focuses on generating diverse images despite rather low quality. Then, in the revise phase, the model iterative ly improves the quality of images, while preserving the global contexts of generated images. In experiments, our method achieves state-of-the-art results on conditional image generation. We also validate that the Draft-and-Revise decoding can achieve high performance by effectively controlling the quality-diversity trade-off in image generation.
虽然自回归模型在图像生成方面取得了显著成果,但其单向生成过程导致生成图像无法充分反映全局上下文。为解决这一问题,我们提出了一种基于上下文RQ-Transformer的"草图-修订"图像生成框架,在生成过程中兼顾全局上下文。作为广义VQ-VAE,RQ-VAE首先将高分辨率图像表示为离散代码堆栈序列。随机掩码序列中的部分代码堆栈后,上下文RQ-Transformer通过训练学习基于未掩码上下文填充被掩码部分。随后,该模型采用我们提出的两阶段解码策略——"草图-修订"进行图像生成,整个过程充分利用图像全局上下文。具体而言:在草图阶段,模型优先生成多样性高但质量较低的图像;在修订阶段,通过迭代优化提升图像质量,同时保持生成图像的全局一致性。实验表明,我们的方法在条件图像生成任务上达到了最先进水平,并验证了"草图-修订"解码能通过有效控制质量-多样性平衡实现卓越性能。
1 Introduction
1 引言
Learning discrete representations of images enables auto regressive (AR) models to achieve promising results on high-resolution image generation. Here, an image is encoded into a feature map, which is represented as a sequence of discrete codes [13, 37] or code stacks [26]. Then, an AR model generates a sequence of codes in the raster scan order and decodes the codes into an image. Consequently, AR models show high performance and s cal ability on large-scale datasets [13, 26, 30].
学习图像的离散表示使自回归 (AR) 模型能够实现高分辨率图像生成的良好效果。该方法将图像编码为特征图,表示为离散代码序列 [13, 37] 或代码堆栈 [26]。随后,AR 模型按光栅扫描顺序生成代码序列,并将代码解码为图像。因此,AR 模型在大规模数据集上展现出高性能和可扩展性 [13, 26, 30]。
Despite the promising results of AR models, we postulate that the ability of AR models is limited due to the lack of considering global contexts in the generation process. Specifically, since AR models generate images by sequentially predicting the next code and attending to only precedent codes generated, they neither exploit the later part of the generated image nor consider the global contexts during generation. For example, Figure 1 (middle) shows that an AR model fails to generate a coherent image, when it is asked to inpaint the masked region of Figure 1 (left) with a school bus.
尽管AR模型取得了令人瞩目的成果,但我们认为其能力存在局限性,原因在于生成过程中缺乏对全局上下文(global contexts)的考量。具体而言,由于AR模型通过顺序预测下一个编码(code)并仅关注已生成的前序编码来生成图像,它们既未利用已生成图像的后半部分信息,也未在生成过程中考虑全局上下文。例如,图1(中)显示:当要求AR模型用校车填充图1(左)的掩码区域时,它未能生成连贯的图像。
Such a failure is due to the inability of AR models to refer to the context of traffic lane on the right side of the masked region.
这种失败是由于AR模型无法参考被遮蔽区域右侧的车道上下文所致。
To address this issue, we propose an effective image generation framework, Draft-and-Revise, with a contextual transformer to exploit the global contexts of images. Given a randomly masked image, the contextual transformer is first trained to infill the masks by bidirectional self-attentions similarly to BERT [8].
为解决这一问题,我们提出了一种高效的图像生成框架 Draft-and-Revise,采用上下文感知 Transformer 来挖掘图像的全局上下文信息。给定一张随机掩码的图像,该上下文感知 Transformer 首先通过类似 BERT [8] 的双向自注意力机制训练来填充掩码区域。

Figure 1: Examples of image inpainting by an AR model (middle) and ours (right).
图 1: AR模型(中)与本文方法(右)的图像修复效果对比示例。
To fully leverage the contextual prediction in generation, we propose Draft-and-Revise decoding which has two phases, draft and revise, imitating the image generation process of a human expert who draws a draft first and iterative ly revises the draft to improve its quality. In the draft phase, the model first infills an empty image to generate a draft image with diverse contents despite the rather low-quality. In the revise phase, the visual quality of the draft is iterative ly improved, while the global contexts of the draft are preserved and exploited. Consequently, our Draft-and-Revise with contextual transformer effectively generates high-quality images with diverse contents.
为充分发挥生成过程中的上下文预测能力,我们提出草稿-修订解码(Draft-and-Revise decoding)方法,该方法模仿人类专家先绘制草稿再迭代修订的图像生成流程,包含草稿和修订两个阶段。在草稿阶段,模型通过填充空白图像生成内容多样但质量较低的初始草稿;在修订阶段,系统在保留并利用草稿全局上下文的同时,迭代提升其视觉质量。最终,我们基于上下文Transformer的草稿-修订方法能高效生成内容多样化的高质量图像。
We use residual-quantized VAE (RQ-VAE) [26] to implement our image generation framework, since RQ-VAE generalizes vector-quantized VAE (VQ-VAE) [37] by representing an image as a sequence of code stacks instead of a sequence of codes. Then, we propose Contextual RQ-Transformer as a contextual transformer for masked code stack modeling of RQ-VAE. Specifically, given a sequence of randomly masked code stacks, Contextual RQ-Transformer first uses a bidirectional transformer to capture the global contexts of unmasked code stacks. Based on the global contexts, the masked code stacks are predicted in parallel, while the codes in each masked code stack are sequentially predicted. In experiments, our Draft-and-Revise framework with Contextual RQ-Transformer achieves state-ofthe-art results on conditional image generation and remarkable improvements on image inpainting. In addition, we demonstrate that Draft-and-Revise decoding can effectively control the quality-diversity trade-off in image generation to achieve high performance.
我们采用残差量化变分自编码器 (RQ-VAE) [26] 来实现图像生成框架,因为 RQ-VAE 通过将图像表示为码堆序列而非单一码序列,推广了向量量化变分自编码器 (VQ-VAE) [37]。随后,我们提出上下文感知 RQ-Transformer 作为 RQ-VAE 掩码码堆建模的上下文 Transformer。具体而言,给定随机掩码的码堆序列,上下文感知 RQ-Transformer 首先使用双向 Transformer 捕捉未掩码码堆的全局上下文。基于全局上下文,模型并行预测被掩码的码堆,同时逐序预测每个掩码码堆中的编码。实验表明,采用上下文感知 RQ-Transformer 的"起草-修订"框架在条件图像生成任务中达到最先进水平,并在图像修复任务中取得显著提升。此外,我们验证了"起草-修订"解码机制能有效调控图像生成中质量-多样性的平衡,从而实现卓越性能。
The main contributions of this paper are summarized as follows. 1) We propose an intuitive and powerful framework, Draft-and-Revise, for image generation based on a bidirectional transformer. 2) We propose Contextual RQ-Transformer for masked code stack modeling of RQ-VAE and empirically show that the proposed model with Draft-and-Revise decoding achieves state-of-the-art results on class- and text-conditional image generation benchmarks. 3) An extensive ablation study validates the effectiveness of Draft-and-Revise decoding on controlling the quality-diversity trade-off and its capability to generate high-quality images with diverse contents.
本文的主要贡献总结如下。1) 我们提出了一种直观且强大的框架 Draft-and-Revise (草稿与修订),用于基于双向 Transformer 的图像生成。2) 我们提出了 Contextual RQ-Transformer 用于 RQ-VAE 的掩码代码堆栈建模,并通过实验证明,采用 Draft-and-Revise 解码的该模型在类别和文本条件图像生成基准测试中取得了最先进的结果。3) 广泛的消融研究验证了 Draft-and-Revise 解码在控制质量-多样性权衡方面的有效性,以及其生成具有多样化内容的高质量图像的能力。
2 Related Work
2 相关工作
Discrete Representation for Image Generation By representing an image as a sequence of codes, VQ-VAE [37] becomes an important part for high-resolution image generation [6, 10, 15, 26, 30, 37], but suffers from low quality of reconstructed images. However, VQGAN [13] significantly improves the perceptual quality of reconstructed images by adding the adversarial and perceptual losses into the training objective of VQ-VAE. As a generalized approach of VQ-VAE and VQGAN, RQ-VAE [26] represents an image as a sequence of code stacks, which consists of ordered codes, and reduces the sequence length, while preserving the reconstruction quality. Then, RQ-Transformer [26] achieves high performance with lower computational costs on generating high-resolution images. However, as an AR model of RQ-VAE, RQ-Transformer cannot capture the global contexts of generated images.
离散表征在图像生成中的应用
通过将图像表示为一系列编码,VQ-VAE [37] 成为高分辨率图像生成 [6, 10, 15, 26, 30, 37] 的重要组成部分,但存在重建图像质量较低的问题。然而,VQGAN [13] 通过在 VQ-VAE 的训练目标中加入对抗损失和感知损失,显著提升了重建图像的感知质量。作为 VQ-VAE 和 VQGAN 的通用方法,RQ-VAE [26] 将图像表示为编码堆栈序列(由有序编码组成),在保持重建质量的同时减少了序列长度。随后,RQ-Transformer [26] 以更低的计算成本实现了高分辨率图像生成的高性能。但作为 RQ-VAE 的自回归 (AR) 模型,RQ-Transformer 无法捕捉生成图像的全局上下文。
Generation Tasks with Bidirectional Transformers To overcome the limitation of AR models on unidirectional architecture, bidirectional transformers have been used for generative tasks. Similar to the pre training objective of BERT [8], a bidirectional transformer is trained to infill a random mask. Then, accompanied with an iterative decoding method [14, 28, 34, 38], the model can generate texts [14], images [6], or videos [16, 40]. Recently, discrete diffusion models [1, 4, 12, 15] also uses bidirectional transformers to generate an image. Given a partially corrupted by random code replacement [1, 12] or randomly masked [1, 4, 15] sequence of codes, diffusion models are trained to gradually denoise the corrupted codes or infill the masks. The training of discrete diffusion models with an absorbing state [1] is the same to infill randomly masked sequence [6, 4]. However, different from the reverse process of diffusion models, our decoding method has explicit two phases to generate high-quality images with diverse contents.
使用双向Transformer进行生成任务
为克服自回归(AR)模型在单向架构上的局限性,双向Transformer被用于生成任务。与BERT[8]的预训练目标类似,双向Transformer通过训练来填充随机掩码。随后,结合迭代解码方法[14,28,34,38],该模型可生成文本[14]、图像[6]或视频[16,40]。近期,离散扩散模型[1,4,12,15]也采用双向Transformer生成图像。给定部分被随机代码替换[1,12]或随机掩码[1,4,15]破坏的代码序列,扩散模型通过训练逐步去噪被破坏的代码或填充掩码。采用吸收态[1]的离散扩散模型训练过程与随机掩码序列填充[6,4]相同。但与扩散模型的反向过程不同,我们的解码方法通过显式的两阶段流程生成内容多样化的高质量图像。
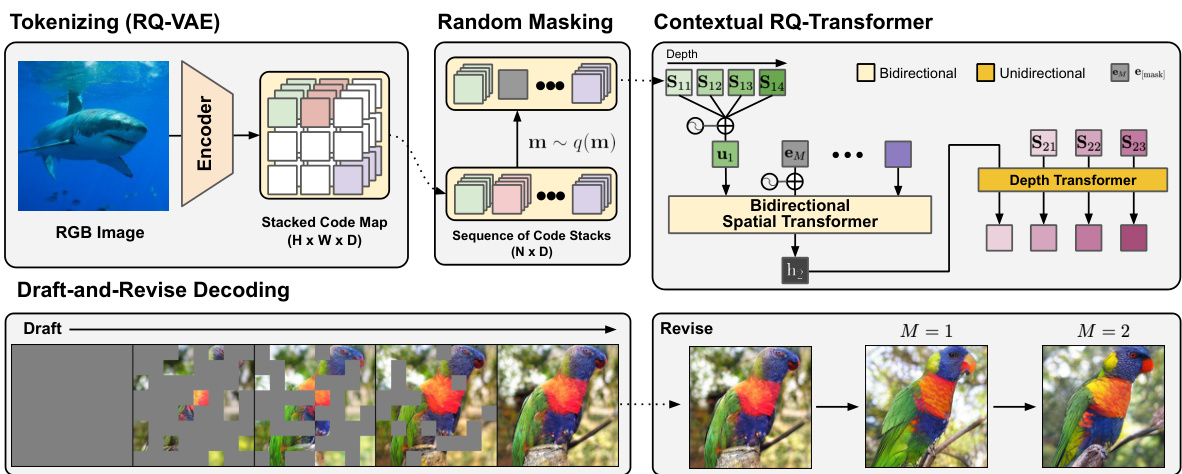
Figure 2: The overview of Draft-and-Revise framework with Contextual RQ-Transformer. Our framework exploits global contexts of images to generate high-quality images with diverse contents.
图 2: 基于上下文 RQ-Transformer 的起草-修订框架概览。该框架利用图像的全局上下文生成内容多样化的高质量图像。
3 Draft-and-Revise Framework for Effective Image Generation
3 高效图像生成的草稿-修订框架
In this section, we propose our Draft-and-Revise framework for effective image generation using bidirectional contexts of images. We first review RQ-VAE [26] as a generalization of VQ-VAE. Then, we propose Contextual RQ-Transformer which is trained to infill a randomly masked sequence of code stacks of RQ-VAE by understanding bidirectional contexts of unmasked parts in the sequence. Lastly, we propose draft-and-revise decoding for a bidirectional transformer to effectively generate high-quality images exploiting global contexts of images. Figure 2 provides the overview of our proposed framework, including Contextual RQ-Transformer and Draft-and-Revise decoding.
在本节中,我们提出了利用图像双向上下文进行高效图像生成的 Draft-and-Revise 框架。首先,我们将 RQ-VAE [26] 作为 VQ-VAE 的泛化形式进行回顾。接着,我们提出 Contextual RQ-Transformer,该模型通过理解序列中未掩码部分的双向上下文,学习填充 RQ-VAE 随机掩码的代码堆栈序列。最后,我们针对双向 Transformer 提出 draft-and-revise 解码策略,以利用图像的全局上下文高效生成高质量图像。图 2 展示了我们提出的框架概览,包括 Contextual RQ-Transformer 和 Draft-and-Revise 解码流程。
3.1 Residual-Quantized Variation al Auto encoder (RQ-VAE)
3.1 残差量化变分自编码器 (RQ-VAE)
RQ-VAE [26] represents an image as a sequence of code stacks. Let a codebook $\mathcal{C}={(k,{\bf e}(k))}{k\in[K]}$ include pairs of a code $k$ and its code embedding $\mathbf{e}(k)\in\mathbb{R}^{n_{z}}$ , where $K=|\mathcal{C}|$ is the codebook size and $n_{z}$ is the dimensionality of $\mathbf{e}(k)$ . Given a vector $\mathbf{z}\in\mathbb{R}^{n_{z}}$ , $\boldsymbol{\mathcal{Q}}(\mathbf{z};\mathcal{C})$ is defined as the code of $\mathbf{z}$ :
RQ-VAE [26] 将图像表示为一系列代码堆栈。设码本 $\mathcal{C}={(k,{\bf e}(k))}{k\in[K]}$ 包含代码 $k$ 与其嵌入向量 $\mathbf{e}(k)\in\mathbb{R}^{n_{z}}$ 的配对,其中 $K=|\mathcal{C}|$ 为码本大小,$n_{z}$ 是 $\mathbf{e}(k)$ 的维度。给定向量 $\mathbf{z}\in\mathbb{R}^{n_{z}}$,定义 $\boldsymbol{\mathcal{Q}}(\mathbf{z};\mathcal{C})$ 为 $\mathbf{z}$ 的对应代码:
$$
\mathcal{Q}(\mathbf{z};\mathcal{C})=\arg\operatorname*{min}{\boldsymbol{k}}\left|\mathbf{z}-\mathbf{e}(\boldsymbol{k})\right|_{2}^{2}.
$$
$$
\mathcal{Q}(\mathbf{z};\mathcal{C})=\arg\operatorname*{min}{\boldsymbol{k}}\left|\mathbf{z}-\mathbf{e}(\boldsymbol{k})\right|_{2}^{2}.
$$
Then, RQ with depth $D$ represents a vector as a code stack which consists of $D$ codes:
然后,深度为 $D$ 的 RQ 将一个向量表示为由 $D$ 个代码组成的代码栈:
$$
\mathcal{R Q}(\mathbf{z};\mathcal{C},D)=(k_{1},\cdot\cdot\cdot,k_{D})\in[K]^{D},
$$
$$
\mathcal{R Q}(\mathbf{z};\mathcal{C},D)=(k_{1},\cdot\cdot\cdot,k_{D})\in[K]^{D},
$$
where $k_{d}$ is the $d$ -th code of $\mathbf{z}$ . Specifically, RQ first initializes the 0-th residual vector as $\mathbf{r}{0}=\mathbf{z}$ , and then recursively disc ret ize s a residual vector $\mathbf{r}{d-1}$ and computes the next residual vector $\mathbf{r}_{d}$ as
其中 $k_{d}$ 是 $\mathbf{z}$ 的第 $d$ 个编码。具体而言,RQ首先将第0个残差向量初始化为 $\mathbf{r}{0}=\mathbf{z}$,然后递归地对残差向量 $\mathbf{r}{d-1}$ 进行离散化处理,并计算下一个残差向量 $\mathbf{r}_{d}$ 为
$$
k_{d}=\mathcal{Q}(\mathbf{r}{d-1};\mathcal{C}),\qquad\mathbf{r}{d}=\mathbf{r}{d-1}-\mathbf{e}(k_{d}),
$$
$$
k_{d}=\mathcal{Q}(\mathbf{r}{d-1};\mathcal{C}),\qquad\mathbf{r}{d}=\mathbf{r}{d-1}-\mathbf{e}(k_{d}),
$$
for $d\in[D]$ . Finally, $\mathbf{z}$ is approximated by the sum of the $D$ code embeddings $\begin{array}{r}{\hat{\mathbf{z}}:=\sum_{d=1}^{D}\mathbf{e}(k_{d})}\end{array}$ . We remark that RQ is a generalized version of VQ, as RQ with $D=1$ is equivalent t o VQ. For $D>1$ , RQ conducts a finer approximation of $\mathbf{z}$ as the quantization errors are sequentially reduced as $d$ increases. Here, the coarse-to-fine approximation ensures the $D$ codes to be sequentially dependent.
对于 $d\in[D]$。最终,$\mathbf{z}$ 由 $D$ 个编码嵌入的和近似表示:$\begin{array}{r}{\hat{\mathbf{z}}:=\sum_{d=1}^{D}\mathbf{e}(k_{d})}\end{array}$。需要说明的是,RQ (Residual Quantization) 是 VQ (Vector Quantization) 的广义版本,因为当 $D=1$ 时 RQ 等价于 VQ。对于 $D>1$ 的情况,RQ 通过对 $\mathbf{z}$ 进行更精细的近似,随着 $d$ 的增加逐步减小量化误差。这里的由粗到精 (coarse-to-fine) 近似确保了 $D$ 个编码的顺序依赖性。
RQ-VAE represents an image as a map of code stacks. Specifically, a given image $\mathbf{X}$ is first converted to a low-resolution feature map $\mathbf{Z}=\dot{E}(\mathbf{X})\in\mathbb{R}^{H\times W\times\dot{n_{z}}}$ , and then each feature vector $\mathbf{Z}_{h w}$ at spatial position $(h,w)$ is disc ret i zed into a code stack by RQ with depth $D$ . As a result, we get a map of code stacks $\mathbf{S}\overset{'}{\in}[K]^{H\times W\times D}$ . Further details of RQ-VAE are referred to Appendix.
RQ-VAE将图像表示为代码堆栈的映射。具体而言,给定图像$\mathbf{X}$首先被转换为低分辨率特征图$\mathbf{Z}=\dot{E}(\mathbf{X})\in\mathbb{R}^{H\times W\times\dot{n_{z}}}$,然后通过深度为$D$的残差量化(RQ)将空间位置$(h,w)$处的每个特征向量$\mathbf{Z}_{h w}$离散化为一个代码堆栈。最终我们得到代码堆栈映射$\mathbf{S}\overset{'}{\in}[K]^{H\times W\times D}$。RQ-VAE的更多细节请参阅附录。
3.2 Contextual Transformer for Image Generation with Global Contexts
3.2 基于全局上下文的图像生成上下文Transformer
As a bidirectional transformer for RQ-VAE, we propose Contextual RQ-Transformer for image generation based on a contextual understanding of images. First, we adopt the pre training of BERT [8] to formulate a masked code stack modeling of RQ-VAE. Then, we introduce how Contextual RQTransformer infills the randomly masked code stacks after reading the given contextual information.
作为RQ-VAE的双向Transformer,我们提出了基于图像上下文理解的Contextual RQ-Transformer用于图像生成。首先,我们采用BERT[8]的预训练方法来构建RQ-VAE的掩码代码堆栈建模。接着,我们介绍了Contextual RQTransformer在读取给定上下文信息后如何填充随机掩码的代码堆栈。
3.2.1 Masked Code Stack Modeling of RQ-VAE
3.2.1 RQ-VAE 的掩码代码堆栈建模
By adopting the pre training of BERT [8], we formulate the masked code stack modeling of RQ-VAE with a contextual transformer to generate an image by iterative mask-infilling as non-AR models [14]. We first convert the map $\mathbf{S}\in[\breve{K}]^{H\times W\times D}$ into a sequence of code stacks $\mathbf{\check{S}}^{\prime}\in[K]^{N\times D}$ using the raster-scan ordering, where $N=H W$ and $\mathbf{S}{n}^{\prime}=(\mathbf{S}{n1}^{\prime},\cdot\cdot\cdot,\mathbf{S}{n D}^{\prime})\in[K]^{D}$ for $n\in[N]$ . We denote $\mathbf{S}^{\prime}$ as S for the brevity of notation. A mask vector $\mathbf{m}$ is defined as a binary vector $\mathbf{m}\in{0,1}^{N}$ to indicate the spatial positions to be masked.
通过采用BERT [8]的预训练方法,我们利用上下文Transformer对RQ-VAE进行掩码代码堆栈建模,以非自回归模型[14]的方式通过迭代掩码填充生成图像。首先将地图$\mathbf{S}\in[\breve{K}]^{H\times W\times D}$转换为代码堆栈序列$\mathbf{\check{S}}^{\prime}\in[K]^{N\times D}$(采用光栅扫描顺序),其中$N=H W$且$\mathbf{S}_{n}^{\prime}=(\mathbf{S}_{n1}^{\prime},\cdot\cdot\cdot,\mathbf{S}{n D}^{\prime})\in[K]^{D}$($n\in[N]$)。为简化表示,将$\mathbf{S}^{\prime}$记作S。定义掩码向量$\mathbf{m}$为二进制向量$\mathbf{m}\in{0,1}^{N}$,用于指示待掩码的空间位置。
where [MASK] is a mask token to substitute for ${\bf S}{n d}$ if $\mathbf{m}{n}=1$ . Given a random mask vector ${\bf m}\sim q({\bf m})$ , the masked code stacks given $\mathbf{S}_{\backslash\mathbf{m}}$ are modeled as
其中 [MASK] 是一个掩码token (mask token),当 $\mathbf{m}{n}=1$ 时用于替代 ${\bf S}_{n d}$。给定随机掩码向量 ${\bf m}\sim q({\bf m})$,被掩码的代码堆叠 $\mathbf{S}{\backslash\mathbf{m}}$ 被建模为
$$
\prod_{n:\mathbf{m}{n}=1}p(\mathbf{S}{n}|\mathbf{S}{\backslash\mathbf{m}})=\prod_{n:\mathbf{m}{n}=1}\prod_{d=1}^{D}p(\mathbf{S}{n d}|\mathbf{S}{n,<d},\mathbf{S}_{\backslash\mathbf{m}}),
$$
$$
\prod_{n:\mathbf{m}{n}=1}p(\mathbf{S}{n}|\mathbf{S}{\backslash\mathbf{m}})=\prod_{n:\mathbf{m}{n}=1}\prod_{d=1}^{D}p(\mathbf{S}{n d}|\mathbf{S}{n,<d},\mathbf{S}_{\backslash\mathbf{m}}),
$$
wmhaserkei $q(\mathbf{m})$ iitsi oan sm aarsek rd a in sd troi b mult yi ocnh owshene.r eI nthstee amda osfk ifinxgi npgo rtthieo np $\textstyle\sum_{n=1}^{N}\mathbf{m}{i}/N$ ians $(0,1]$ aRsT ,w terlali naisn tgh ea $15%$ model with a random masking portion from $(0,1]$ enables the model to generate new images based on various masking patterns including $\mathbf{m}_{n}=1$ for all $n$ . We explain the details of $q(\mathbf{m})$ in Section 3.2.3.
wmhaserkei $q(\mathbf{m})$ iitsi oan sm aarsek rd a in sd troi b mult yi ocnh owshene.r eI nthstee amda osfk ifinxgi npgo rtthieo np $\textstyle\sum_{n=1}^{N}\mathbf{m}{i}/N$ ians $(0,1]$ aRsT ,w terlali naisn tgh ea $15%$ 模型采用从 $(0,1]$ 随机采样的掩码比例,使模型能够基于包括全 $n$ 的 $\mathbf{m}_{n}=1$ 在内的多种掩码模式生成新图像。我们将在第3.2.3节详细说明 $q(\mathbf{m})$ 的具体实现。
The left-hand side of Eq. 5 implies that all masked code stacks can be decoded in parallel, after extracting contextual information from $\mathbf{S}{\backslash\mathbf{m}}$ . If $D=1$ , Eq. 5 becomes equivalent to conventional masked token modeling of texts [8] and images [6, 16] where a single token at each masked position is predicted. For $D>1$ , the $D$ codes of $\mathbf{S}_{n}$ are auto regressive ly predicted, as they are sequentially computed in Eq. 3 for a coarse-to-fine approximation and hence well-suited for an AR prediction.
式5的左侧表明,所有掩码代码堆栈都可以在从$\mathbf{S}{\backslash\mathbf{m}}$中提取上下文信息后并行解码。若$D=1$,式5便等同于传统的文本[8]和图像[6,16]掩码token建模,其中每个掩码位置仅预测单个token。当$D>1$时,$\mathbf{S}_{n}$的$D$个代码以自回归方式预测,如式3中为进行由粗到精的近似而顺序计算的那样,因此非常适合自回归预测。
3.2.2 Contextual RQ-Transformer
3.2.2 上下文感知 RQ-Transformer
We modify the previous RQ-Transformer [26] for masked code stack modeling with bidirectional contexts in Eq. 5. Contextual RQ-Transformer consists of Bidirectional Spatial Transformer and Depth Transformer: Bidirectional Spatial Transformer understands contextual information in the unmasked code stacks using bidirectional self-attentions, and Depth Transformer infills the masked code stacks in parallel, by auto regressive ly predicting the $D$ codes at each position.
我们对之前的RQ-Transformer [26]进行了修改,采用公式5中的双向上下文进行掩码代码堆栈建模。上下文感知RQ-Transformer由双向空间Transformer和深度Transformer组成:双向空间Transformer通过双向自注意力机制理解未掩码代码堆栈中的上下文信息,深度Transformer则通过自回归预测每个位置的$D$个代码,并行填充被掩码的代码堆栈。
Bidirectional Spatial Transformer Given a masked sequence of code stacks $\mathbf{S}{\backslash\mathbf{m}}$ , bidirectional spatial transformer first embeds $\mathbf{S}_{\backslash\mathbf{m}}$ using the code embeddings of RQ-VAE as
双向空间Transformer 给定一个掩码后的代码堆栈序列 $\mathbf{S}{\backslash\mathbf{m}}$,双向空间Transformer首先使用RQ-VAE的代码嵌入对 $\mathbf{S}_{\backslash\mathbf{m}}$ 进行编码
where $\mathrm{PE}{N}(n)$ is an embedding for position $n$ , and ${\bf e}{[\mathrm{MASK}]}\in\mathbb{R}^{n_{z}}$ is an embedding for [MASK]. Then, the bidirectional self-attention blocks, $f_{\theta}^{\mathrm{spatial}}$ , extracts the context vector ${\bf h}{n}$ to predict $\mathbf{S}_{n}$ as
其中 $\mathrm{PE}{N}(n)$ 是位置 $n$ 的嵌入,${\bf e}{[\mathrm{MASK}]}\in\mathbb{R}^{n_{z}}$ 是 [MASK] 的嵌入。然后,双向自注意力块 $f_{\theta}^{\mathrm{spatial}}$ 提取上下文向量 ${\bf h}{n}$ 以预测 $\mathbf{S}_{n}$,具体为
$$
({\bf h}{1},\cdot\cdot\cdot{\bf\nabla},{\bf h}{N})=f_{\theta}^{\mathrm{spatial}}({\bf u}{1},\cdot\cdot\cdot{\bf\nabla},{\bf u}_{N}).
$$
$$
({\bf h}{1},\cdot\cdot\cdot{\bf\nabla},{\bf h}{N})=f_{\theta}^{\mathrm{spatial}}({\bf u}{1},\cdot\cdot\cdot{\bf\nabla},{\bf u}_{N}).
$$
Depth Transformer Depth transformer auto regressive ly predicts ${\bf S}{n}=({\bf S}{n1},\cdot\cdot\cdot,{\bf S}{n D})$ at a masked position. The input of depth transformer $(\mathbf{\bar{v}}{n d})_{d=1}^{D}$ is defined as
深度 Transformer 深度 Transformer 以自回归方式预测掩码位置处的 ${\bf S}{n}=({\bf S}{n1},\cdot\cdot\cdot,{\bf S}{n D})$。深度 Transformer 的输入 $(\mathbf{\bar{v}}{n d})_{d=1}^{D}$ 定义为
Algorithm 1 UPDATE of S
算法 1: S的UPDATE操作
Algorithm 2 Draft-and-Revise decoding
算法 2: 起草-修订解码 (Draft-and-Revise decoding)
where $\mathrm{PE}{D}(d)$ is the positional embedding for depth $d$ . Then, depth transformer f θdepth, which consists of causal attention blocks, outputs the logit $\mathbf{p}{n d}$ to predict ${\bf S}_{n d}$ as
其中 $\mathrm{PE}{D}(d)$ 是深度 $d$ 的位置编码。随后,由因果注意力块构成的深度Transformer $f_{\theta}^{\text{depth}}$ 输出对数概率 $\mathbf{p}{n d}$ 以预测 ${\bf S}_{n d}$
$$
\mathbf{p}{n d}=f_{\theta}^{\mathrm{depth}}(\mathbf{v}{n1},\cdots,\mathbf{v}{n d})\quad\mathrm{and}\quad p_{\theta}(\mathbf{S}{n d}=k|\mathbf{S}{n,<d},\mathbf{S}{\setminus\mathbf{m}})=\mathrm{softmax}(\mathbf{p}{n d})_{k}.
$$
We remark that the architecture of Contextual RQ-Transformer subsumes bidirectional transformers. Specifically, RQ-Transformer with $D=1$ is equivalent to a bidirectional transformer since the depth transformer becomes a multilayer perceptron with layer normalization [2].
我们注意到,Contextual RQ-Transformer 的架构包含了双向 Transformer (bidirectional transformer)。具体而言,当 $D=1$ 时,RQ-Transformer 等价于一个双向 Transformer,因为深度 Transformer 会退化为带层归一化 (layer normalization) 的多层感知机 [2]。
3.2.3 Training of Contextual RQ-Transformer
3.2.3 上下文 RQ-Transformer 训练
For the training of Contextual RQ-Transformer, let us define a mask distribution $q(\mathbf{m})$ with a mask scheduling function $\gamma$ . Following previous approaches [6, 14, 16], $\gamma$ is chosen to be decreasing and to satisfy $\gamma(0)=1$ and $\gamma(1)=0$ . Then, ${\bf m}\sim q({\bf m})$ is specified as
在训练Contextual RQ-Transformer时,我们定义一个掩码分布$q(\mathbf{m})$和掩码调度函数$\gamma$。沿用先前方法[6, 14, 16],选择$\gamma$为递减函数并满足$\gamma(0)=1$和$\gamma(1)=0$。于是,${\bf m}\sim q({\bf m})$被定义为
$$
r\sim\mathrm{Unif}([0,1))
$$
$$
r\sim\mathrm{Unif}([0,1))
$$
$$
\mathbf{m}\sim\mathrm{Unif}({\mathbf{m}:|\mathbf{m}|=\lceil\gamma(r)\cdot N\rceil}),
$$
$$
\mathbf{m}\sim\mathrm{Unif}({\mathbf{m}:|\mathbf{m}|=\lceil\gamma(r)\cdot N\rceil}),
$$
where $\begin{array}{r}{|{\bf m}|=\sum_{n\in[N]}{\bf m}_{n}}\end{array}$ is the count of masked positions. Finally, the training objective of Contextual RQ -Transformer is to minimize the negative log-likelihood of masked code stacks:
其中 $\begin{array}{r}{|{\bf m}|=\sum_{n\in[N]}{\bf m}_{n}}\end{array}$ 表示被遮蔽位置的总数。最终,Contextual RQ-Transformer 的训练目标是最小化被遮蔽代码堆栈的负对数似然:
$$
\mathcal{L}=\mathbb{E}{\mathbf{m}\sim q(\mathbf{m})}\left[\mathbb{E}{\mathbf{S}}\left[\sum_{n:\mathbf{m}{n}=1}\sum_{d=1}^{D}-\log p_{\theta}(\mathbf{S}{n d}\vert\mathbf{S}_{n,<d},\mathbf{S}_{\setminus\mathbf{m}})\right]\right].
$$
$$
\mathcal{L}=\mathbb{E}{\mathbf{m}\sim q(\mathbf{m})}\left[\mathbb{E}{\mathbf{S}}\left[\sum_{n:\mathbf{m}{n}=1}\sum_{d=1}^{D}-\log p_{\theta}(\mathbf{S}{n d}\vert\mathbf{S}_{n,<d},\mathbf{S}_{\setminus\mathbf{m}})\right]\right].
$$
3.3 Draft-and-Revise: Two-Phase Decoding with Global Contexts of Generated Imaegs
3.3 起草-修订:基于生成图像全局上下文的两阶段解码
We propose a decoding algorithm, Draft-and-Revise, which uses Contextual RQ-Transformer to effectively generate high-quality images with diverse visual contents. We introduce the details of Draft-and-Revise decoding and then explain how the two-phase decoding can effectively control the quality-diversity trade-off of generated images.
我们提出了一种解码算法Draft-and-Revise,该算法利用Contextual RQ-Transformer有效生成具有多样化视觉内容的高质量图像。我们将详细介绍Draft-and-Revise解码的细节,并解释两阶段解码如何有效控制生成图像的质量与多样性权衡。
We define a partition $\pmb{\Pi}=(\mathbf{m}^{1},\cdot\cdot\cdot\mathbf{\Omega},\mathbf{m}^{T})$ as a collection of pairwise disjoint $T$ mask vectors to cover all spatial positions, where $\begin{array}{r}{\sum_{t=1}^{T}\mathbf{m}_{n}^{t}=1}\end{array}$ for all $n\in[N]$ . A partition $\mathbf{II}$ is sampled from the distribution $p(\mathbf{I};T)$ .
我们定义分区 $\pmb{\Pi}=(\mathbf{m}^{1},\cdot\cdot\cdot\mathbf{\Omega},\mathbf{m}^{T})$ 为覆盖所有空间位置的 $T$ 个两两互不重叠的掩码向量集合,其中对于所有 $n\in[N]$ 满足 $\begin{array}{r}{\sum_{t=1}^{T}\mathbf{m}_{n}^{t}=1}\end{array}$。分区 $\mathbf{II}$ 从分布 $p(\mathbf{I};T)$ 中采样得到.
We first define a procedure UPDATE $(\mathbf{S},\boldsymbol{\Pi})$ to update $\mathbf{S}$ as described in Algorithm 1, which updates $\mathbf{S}{n}$ with $\mathbf{m}_{n}^{t}=1$ for $t\in[T]$ . Then, Draft-and-Revise decoding in Algorithm 2 generates a draft from the empty sequence of code stacks and improves the quality of the draft.
我们首先定义一个过程 UPDATE $(\mathbf{S},\boldsymbol{\Pi})$ 来更新 $\mathbf{S}$ ,如算法 1 所述,该过程用 $\mathbf{m}{n}^{t}=1$ 更新 $\mathbf{S}_{n}$ ,其中 $t\in[T]$ 。然后,算法 2 中的 Draft-and-Revise 解码从空的代码栈序列生成草稿,并提高草稿的质量。
Table 1: FIDs, ISs, Precisions, and Recalls for class-conditional generation on ImageNet [7]. † denotes the use of pretrained classifier for rejection sampling, gradient guidance, or training.
表 1: ImageNet [7] 上类别条件生成的 FID、IS、精确度和召回率。† 表示使用了预训练分类器进行拒绝采样、梯度引导或训练。
| 模型 | 参数量 | 分辨率 | FID↓ | IS↑ | 精确度↑ | 召回率↑ |
|---|---|---|---|---|---|---|
| BigGAN-deep [5] | 112M | - | 6.95 | 202.6 | 0.87 | 0.23 |
| StyleGAN-XL [33] | 166M | 2.3 | 262.1 | 0.78 | 0.53 | |
| ADM [9] | 554M | 10.94 | 101.0 | 0.69 | 0.63 | |
| ADM-G [9] | 608M | 4.59 | 186.7 | 0.82 | 0.52 | |
| ImageBART [12] | 3.5B | 16x16x1 | 21.19 | 61.6 | ||
| VQ-Diffusion [15] | 518M | 16x16x1 | 11.89 | |||
| LDM-8 [31] | 395M | 32×32 | 15.51 | 79.03 | 0.65 | 0.63 |
| LDM-8-Gt [31] | 506M | 32×32 | 7.76 | 209.52 | 0.84 | 0.35 |
| MaskGIT [6] | 227M | 16×16x1 | 6.18 | 182.1 | 0.80 | 0.51 |
| VQ-GAN [13] | 1.4B | 16×16x1 | 15.78 | 74.3 | ||
| RQ-Transformer [26] | 1.4B | 8×8×4 | 8.71 | 119.0 | 0.71 | 0.58 |
| RQ-Transformer [26] | 3.8B | 8×8×4 | 7.55 | 134.0 | 0.73 | 0.58 |
| RQ-Transformer [26] | 3.8B | 8×8×4 | 3.80 | 323.7 | 0.82 | 0.50 |
| ContextualRQ-Transformer | 371M | 8×8×4 | 5.45 | 172.6 | 0.81 | 0.49 |
| Contextual RQ-Transformer | 821M | 8×8×4 | 3.45 | 221.9 | 0.82 | 0.52 |
| ContextualRQ-Transformer | 1.4B | 8×8×4 | 3.41 | 224.6 | 0.79 | 0.54 |
| 验证数据 | 1.62 | 234.0 | 0.75 | 0.67 |
Draft phase In the draft phase, our model gradually infills the empty sequence of code stacks to generate a draft image, considering the global contexts of infilled code stacks. Let $\mathbf{S}^{\mathrm{empty}}$ be an empty sequence of code stacks with $\begin{array}{r}{\mathbf{S}{n}^{\mathrm{empty}}=[\mathbf{MASK}]^{D}}\end{array}$ for all $n$ . Given a partition size $T{\mathrm{draft}}$ , our model generates a draft image as
草案阶段
在草案阶段,我们的模型逐步填充代码堆栈的空序列以生成草案图像,同时考虑已填充代码堆栈的全局上下文。设$\mathbf{S}^{\mathrm{empty}}$为一个空代码堆栈序列,其中对所有$n$满足$\begin{array}{r}{\mathbf{S}{n}^{\mathrm{empty}}=[\mathbf{MASK}]^{D}}\end{array}$。给定分区大小$T{\mathrm{draft}}$,我们的模型生成草案图像的过程如下:
$$
\mathbf{S}^{\mathrm{draft}}=\mathrm{UPDATE}(\mathbf{S}^{\mathrm{empty}},\Pi;\theta)\quad\mathrm{where}\quad\Pi\sim p(\Pi;T_{\mathrm{draft}}).
$$
$$
\mathbf{S}^{\mathrm{draft}}=\mathrm{UPDATE}(\mathbf{S}^{\mathrm{empty}},\Pi;\theta)\quad\mathrm{where}\quad\Pi\sim p(\Pi;T_{\mathrm{draft}}).
$$
Revise phase The generated draft $\mathbf{S}^{\mathrm{draft}}$ is repeatedly revised to improve the visual quality of the image, while preserving the overall structure of the draft. Given a partition size $T_{\mathrm{revise}}$ and the number of updates $M$ , the draft $\mathbf{S}^{0}=\mathbf{S}^{\mathrm{draft}}$ is repeatedly updated $M$ times as
修订阶段 生成的草图 $\mathbf{S}^{\mathrm{draft}}$ 会经过多次修订以提升图像视觉质量,同时保持草图的整体结构。给定分区大小 $T_{\mathrm{revise}}$ 和更新次数 $M$,初始草图 $\mathbf{S}^{0}=\mathbf{S}^{\mathrm{draft}}$ 会被重复更新 $M$ 次
$$
\mathbf{S}^{m}=\mathbf{U}\mathbf{P}\mathbf{D}\mathbf{A}\mathrm{TE}(\mathbf{S}^{m-1},\Pi;\theta)\quad\mathrm{where}\quad\Pi\sim p(\Pi;T_{\mathrm{revise}})\quad\mathrm{for}m=1,\cdots,M.
$$
$$
\mathbf{S}^{m}=\mathbf{U}\mathbf{P}\mathbf{D}\mathbf{A}\mathrm{TE}(\mathbf{S}^{m-1},\Pi;\theta)\quad\mathrm{where}\quad\Pi\sim p(\Pi;T_{\mathrm{revise}})\quad\mathrm{for}m=1,\cdots,M.
$$
Note that Draft-and-Revise is not a tailored method, since we can adopt any mask-infilling-based generation method [4, 6] for UPDATE in Algorithm 1. For example, confidence-based decoding [6, 16], which iterative ly updates S from high-confidence to low-confidence predictions, can be used for UPDATE. However, we find that confidence-based decoding generates low-diversity images with oversimplified contents, since a model tends to predict simple visual patterns with high confidence. In addition, confidence-based decoding often leads to biased unmasking patterns, which are not used in training, as shown in Appendix. Thus, we use a uniformly random partition $\mathbf{II}$ in UPDATE as the most simplified rule, leaving investigations on sophisticated update methods as future work.
请注意,Draft-and-Revise并非定制化方法,因为我们可以采用任何基于掩码填充的生成方法 [4, 6] 来实现算法1中的UPDATE步骤。例如,基于置信度的解码 [6, 16] 会从高置信度到低置信度逐步更新S,也可用于UPDATE。但我们发现,由于模型倾向于预测高置信度的简单视觉模式,基于置信度的解码会生成内容过度简化且多样性不足的图像。此外,如附录所示,该方法常导致训练中未使用的偏置性解掩模式。因此,我们采用最简单的规则——在UPDATE中使用均匀随机分割 $\mathbf{II}$,将复杂更新方法的研究留作未来工作。
We postulate that our Draft-and-Revise can generate high-quality images with diverse contents by explicitly dividing two phases. Specifically, a model first generates draft images with diverse visual contents despite the rather low quality of drafts. After semantically diverse images are generated as drafts, we use sampling strategies such as temperature scaling [19] and classifier-free guidance [20] in the revise phase to improve the visual quality of the drafts, while preserving the major semantic contents in drafts. Thus, our method can improve the performance of image generation by effectively controlling the quality-diversity trade-off. In addition, we emphasize that the two-phased decoding is intuitive and resembles the image generation process of human experts, who repeatedly refine their works to improve the quality after determining the overall contents first.
我们假设,通过明确划分两个阶段,我们的"起草-修订"(Draft-and-Revise)方法能够生成内容多样且高质量的图像。具体而言,模型首先生成视觉内容多样但质量较低的起草图像。在生成语义多样的起草图像后,我们在修订阶段采用温度缩放[19]和无分类器引导[20]等采样策略来提升起草图像的视觉质量,同时保留其中的主要语义内容。因此,我们的方法能通过有效控制质量-多样性权衡来提升图像生成性能。此外需要强调的是,这种两阶段解码方式直观地模拟了人类专家的图像创作流程——专家们总是先确定整体内容,再通过反复润色来提升作品质量。
4 Experiments
4 实验
In this section, we show that our Draft-and-Revise with Contextual RQ-Transformer can outperform previous approaches for class- and text-conditional image generation. In addition, we conduct an extensive ablation study to understand the effects of Draft-and-Revise decoding on the quality and diversity of generated images, and the sampling speed. We use the publicly released RQ-VAE [26] to represent a $256\times256$ resolution of images as $8\times8\times4$ codes. For a fair comparison, we make Contextual RQ-Transformer have the same model size as the previous RQ-Transformer [26]. For training, the quarter-period of cosine is used as the mask scheduling function $\gamma$ in Eq. 10 following the previous studies [6, 27]. We include the implementation details in Appendix.
在本节中,我们展示了基于上下文RQ-Transformer的起草-修订策略在类别和文本条件图像生成任务中优于先前方法。此外,我们通过大量消融实验研究了起草-修订解码对生成图像质量、多样性以及采样速度的影响。实验采用公开的RQ-VAE[26]将256×256分辨率图像表示为8×8×4的编码。为公平比较,上下文RQ-Transformer与先前RQ-Transformer[26]保持相同模型规模。训练阶段沿用前人研究[6,27]的方案,将余弦函数的四分之一周期作为公式10中的掩码调度函数γ。具体实现细节详见附录。

Figure 3: The examples of generated $256\times256$ images of our model trained on (Top) ImageNet and (Bottom) CC-3M. The used text conditions are "Sunset over the skyline of a {beach, city}.", "an avocado {in the desert, on the seashore}.", and "a painting of a {dog, cat} with sunglasses.".
图 3: 我们的模型在 (上) ImageNet 和 (下) CC-3M 数据集上训练后生成的 $256\times256$ 图像示例。使用的文本条件为 "Sunset over the skyline of a {beach, city}.", "an avocado {in the desert, on the seashore}.", 以及 "a painting of a {dog, cat} with sunglasses."。
4.1 Class-conditional Image Generation
4.1 类别条件图像生成
We train Contextual RQ-Transformer with 371M, 821M, and 1.4B parameters on ImageNet [7] for class-conditional image generation. For Draft-and-Revise decoding, we use $T_{\mathrm{draft}}=64$ , $T_{\mathrm{revise}}=2$ , and $M=2$ . We use temperature scaling [19] and classifier-free guidance [20] only in the revise phase, while none of the strategies are applied in the draft phase. Fréchet Inception Distance (FID) [18], Inception Score (IS) [32], and Precision and Recall [25] are used for evaluation measures.
我们在ImageNet [7]数据集上训练了参数量为3.71亿、8.21亿和14亿的Contextual RQ-Transformer,用于类别条件图像生成。在Draft-and-Revise解码过程中,设定草稿阶段步长$T_{\mathrm{draft}}=64$、修订阶段步长$T_{\mathrm{revise}}=2$以及修订轮次$M=2$。温度缩放[19]和分类器无关引导[20]策略仅应用于修订阶段,草稿阶段不采用任何优化策略。评估指标采用Fréchet Inception距离(FID) [18]、Inception分数(IS) [32]以及精确率与召回率[25]。
Table 1 shows that Contextual RQ-Transformer significantly outperforms the previous approaches. Notably, Contextual RQ-Transformer with 371M parameters outperforms RQ-Transformers with 1.4B and 3.8B parameters on all evaluation measures, despite having only about $4.2\times$ and $11.4\times$ fewer parameters. In addition, the performance is improved as the number of parameters increases to 821M and 1.4B. Contextual RQ-Transformer can achieve the lower FID score without a pretrained classifier than ADM-G and 3.8B parameters of RQ-Transformer with the use of pretrained classifier. StyleGAN-XL also uses a pretrained classifier during both training and image generation and achieves the lowest FID in Table 1. However, our model with 1.4B parameters has higher precision and recall than StyleGAN-XL, implying that our model generates images of better fidelity and diversity without a pretrained classifier. Our high performance without a classifier is remarkable, since the gradient guidance and rejection sampling are the tailored techniques to the model-based evaluation metrics in Table 1. Considering that the performance is marginally improved as the number of parameters increases from 821M to 1.4B, an improved RQ-VAE can boost the performance of Contextual RQ-Transformer, since the reconstruction quality determines the best results of generated images.
表 1 显示,Contextual RQ-Transformer 显著优于先前的方法。值得注意的是,参数量仅为 3.71 亿的 Contextual RQ-Transformer 在所有评估指标上均优于参数量达 14 亿和 38 亿的 RQ-Transformer,尽管其参数量分别减少了约 $4.2\times$ 和 $11.4\times$。此外,当参数量增至 8.21 亿和 14 亿时,性能也相应提升。在不使用预训练分类器的情况下,Contextual RQ-Transformer 能获得比 ADM-G 和 38 亿参数 RQ-Transformer (使用预训练分类器) 更低的 FID 分数。StyleGAN-XL 在训练和图像生成阶段均使用预训练分类器,因此在表 1 中取得了最低的 FID 值。但我们 14 亿参数的模型在精度和召回率上均优于 StyleGAN-XL,这表明我们的模型无需预训练分类器即可生成保真度和多样性更优的图像。我们的模型在不使用分类器的情况下仍能保持高性能,这一点尤为突出,因为梯度引导和拒绝采样是针对表 1 中基于模型的评估指标量身定制的技术。考虑到参数量从 8.21 亿增至 14 亿时性能提升有限,改进的 RQ-VAE 有望进一步提升 Contextual RQ-Transformer 的性能,因为重建质量决定了生成图像的最佳效果。
4.2 Text-conditional Image Generation
4.2 文本条件图像生成
We train Contextual RQ-Transformer with 366M and 654M parameters on CC-3M [36] for text-to-image (T2I) generation. We use Byte Pair Encoding [35, 39] to encode a text condition into 32 tokens. We also report CLIPscore [29] with ViT-B/32 [11] to measure the correspondence between texts and images.
我们在CC-3M [36]数据集上训练了参数量为3.66亿和6.54亿的Contextual RQ-Transformer模型,用于文生图 (T2I) 任务。采用字节对编码 (Byte Pair Encoding) [35, 39] 将文本条件编码为32个token。同时使用ViT-B/32 [11]架构计算CLIPscore [29] 指标来评估文本与图像的对应关系。
Contextual RQ-Transformer in Table 2 outperforms the previous T2I generation models. Contextual RQ-Transformer with 366M parameters achieves better FID than RQ-Transformer
表 2 中的 Contextual RQ-Transformer 在性能上超越了之前的 T2I (Text-to-Image) 生成模型。参数量为 3.66 亿的 Contextual RQ-Transformer 在 FID 指标上优于 RQ-Transformer。
Table 2: FIDs and CLIP scores [29] on the validation dataset of CC-3M [36] for T2I generation.
| Params | FID↓ | CLIP-s↑ | |
| VQ-GAN[13] ImageBART [12] LDM-4 [31] | 600M 2.8B 645M | 28.86 22.61 17.01 | 0.20 0.23 0.24 |
| RQ-Transformer[26] Ours | 654M 366M | 12.33 10.44 | 0.26 0.26 |
| Ours | 654M | 9.65 | 0.26 |
表 2: CC-3M [36] 验证数据集上文本到图像 (T2I) 生成的 FID 和 CLIP 分数 [29]。
| 模型 | 参数量 | FID↓ | CLIP-s↑ |
|---|---|---|---|
| VQ-GAN[13] ImageBART [12] LDM-4 [31] | 600M 2.8B 645M | 28.86 22.61 17.01 | 0.20 0.23 0.24 |
| RQ-Transformer[26] Ours | 654M 366M | 12.33 10.44 | 0.26 0.26 |
| Ours | 654M | 9.65 | 0.26 |
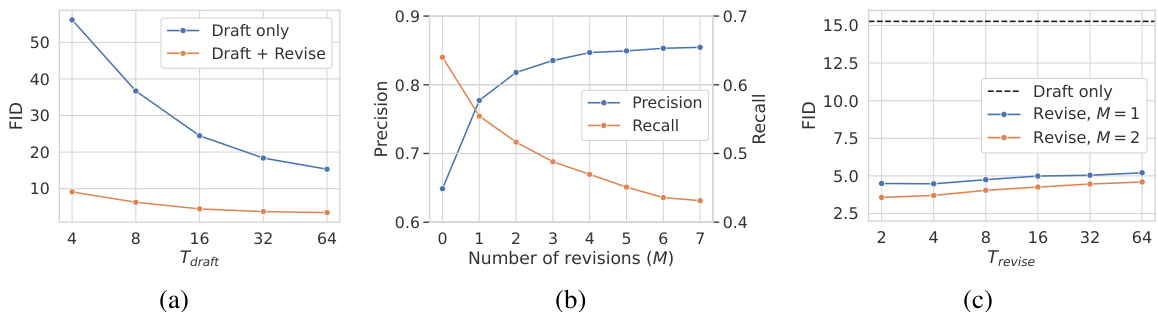
Figure 4: Ablation study on Draft-and-Revise decoding in Section 4.4. (a) FID subject to $T_{\mathrm{draft}}$ . (b) Precision and recall subject to $M$ . (c) FID subject to $T_{\mathrm{revise}}$ .
图 4: 第4.4节中 Draft-and-Revise 解码的消融研究。(a) 随 $T_{\mathrm{draft}}$ 变化的 FID。(b) 随 $M$ 变化的精确率和召回率。(c) 随 $T_{\mathrm{revise}}$ 变化的 FID。

Figure 5: Examples of generated images in the draft phase (left) and revise phases at $M=1,2,3,4,5$ . The draft images are generated with $T_{\mathrm{draft}}=8$ (top) and $T_{\mathrm{draft}}=64$ (bottom), respectively.
图 5: 草稿阶段(左)与修订阶段在$M=1,2,3,4,5$时生成的图像示例。顶部草稿图像使用$T_{\mathrm{draft}}=8$生成,底部使用$T_{\mathrm{draft}}=64$生成。
with 654M parameters, and outperforms ImageBART and LDM-4, although our model has $12\times$ fewer parameters than ImageBART. When we increase the number of parameters to 654M, our model achieves state-of-the-art FID on CC-3M. Meanwhile, our model does not improve the CLIP score of RQ-Transformer, but achieves competitive results with fewer parameters. In Figure 3, our model generates images with unseen texts in CC-3M.
参数规模为6.54亿时,我们的模型性能超越ImageBART和LDM-4,尽管参数量比ImageBART少$12\times$。当参数量增至6.54亿,我们的模型在CC-3M数据集上取得了当前最优的FID分数。虽然未能提升RQ-Transformer的CLIP分数,但以更少参数实现了具有竞争力的结果。图3展示了我们的模型根据CC-3M未见文本生成的图像。
4.3 Conditional Image Inpainting
4.3 条件图像修复
We conduct conditional image inpainting where a model infills a masked area according to the given condition and contexts. Figure 1 shows the example of image inpainting by RQ-Transformer (middle) and Contextual RQ-Transformer (right), when the class-condition is school bus. RQ-Transformer cannot attend to the right and bottom sides of the masked area and fails to generate a coherent image with given contexts. However, our model can complete the image to be coherent with given contexts by exploiting global contexts. We attach more examples of image inpainting in Appendix.
我们进行了条件图像修复任务,模型根据给定条件和上下文对掩码区域进行填充。图1展示了当类别条件为校车时,RQ-Transformer(中)和Contextual RQ-Transformer(右)的图像修复示例。RQ-Transformer无法关注掩码区域的右侧和底部,未能生成与给定上下文连贯的图像。而我们的模型通过利用全局上下文,能够完成与给定上下文一致的图像修复。更多图像修复示例详见附录。
4.4 Ablation Study on Draft-and-Revise
4.4 草拟-修订机制的消融研究
We conduct an extensive ablation study to demonstrate the effectiveness of Draft-and-Revise decoding of our framework. We use Contextual RQ-Transformer with 821M parameters trained on ImageNet.
我们进行了广泛的消融研究,以验证框架中 Draft-and-Revise 解码策略的有效性。实验采用基于 ImageNet 训练的 8.21 亿参数 Contextual RQ-Transformer 模型。
Quality improvement of draft images in the revise phase Figure 4(a) shows the effects of $T_{\mathrm{draft}}$ on draft images and their quality improvement in the revised phase with $T_{\mathrm{revise}}=2$ and $M=2$ In the draft phase, FID is improved as $T_{\mathrm{draft}}$ increases from 4 to 64. At each inference, Contextual RQ-Transformer generates ${N}/{T_{\mathrm{{draft}}}}$ code stacks in parallel, starting with the empty sequence. Thus, the model with a large $T_{\mathrm{draft}}$ generates a small number of code stacks at each inference and can avoid generating incoherent code stacks in the early stage of the draft phase. Although FIDs in the draft phase are worse, they are significantly improved in the revise phase as shown in Figure 5.
修订阶段草稿图像的质量提升
图4(a)展示了$T_{\mathrm{draft}}$对草稿图像的影响及其在修订阶段的质量改进情况($T_{\mathrm{revise}}=2$,$M=2$)。在草稿阶段,随着$T_{\mathrm{draft}}$从4增加到64,FID (Fréchet Inception Distance) 指标逐步改善。每次推理时,Contextual RQ-Transformer会从空序列开始并行生成${N}/{T_{\mathrm{{draft}}}}$个代码栈。因此,较大$T_{\mathrm{draft}}$的模型每次推理生成的代码栈数量较少,能够避免在草稿阶段早期生成不连贯的代码栈。尽管草稿阶段的FID值较差,但如图5所示,这些图像在修订阶段得到了显著改善。
Effect of $M$ and $T_{\mathbf r\mathbf e\mathbf v{i s e}}$ in the revise phase Figure 4(b) shows the effects of the number of updates $M$ in the revise phase on the quality and diversity of generated images. Since the quality-diversity trade-off exists as the updates are repeated, we select $M=2$ as the default hyper parameter to balance the precision and recall, considering that the increase of precision starts to slow down. Interestingly, Figure 5 shows that the overall contents remain unchanged even after $M>2$ . Thus, we claim that Draft-and-Revise decoding does not harm the perceptual diversity of generated images throughout the revise phase despite the consistent deterioration of recall.
$M$ 和 $T_{\mathbf r\mathbf e\mathbf v{i s e}}$ 在修订阶段的影响
图 4(b) 展示了修订阶段更新次数 $M$ 对生成图像质量和多样性的影响。由于重复更新会存在质量-多样性权衡,考虑到精度增长开始放缓,我们选择 $M=2$ 作为默认超参数以平衡精度和召回率。有趣的是,图 5 显示即使 $M>2$ 后整体内容仍保持不变。因此,我们主张尽管召回率持续下降,但 Draft-and-Revise 解码在整个修订阶段不会损害生成图像的感知多样性。
Figure 4(c) shows the effects of $T_{\mathrm{revise}}$ on the quality of generated images. The FIDs are significantly improved in the revise phase regardless of the choice of $T_{\mathrm{revise}}$ , but increasing $T_{\mathrm{revise}}$ slightly deteriorates FIDs. We remark that some code stacks of a draft can be erroneous due to its low quality, and a model with large $T_{\mathrm{revise}}$ slowly updates a small number of code stacks at once in the revise phase. Therefore, the updates with large $T_{\mathrm{revise}}$ can be more influenced by the erroneous code stacks. Although $T_{\mathrm{revise}}=2$ updates half of an image at once, our draft-and-revise decoding successfully improves the quality of generated images, while preserving the global contexts of drafts, as shown in Figure 5. The study on self-supervised learning [17] also reports similar results, where a masked auto-encoder reconstructs the global contexts of an image after masking half of the image.
图 4(c) 展示了 $T_{\mathrm{revise}}$ 对生成图像质量的影响。无论 $T_{\mathrm{revise}}$ 如何选择,修订阶段的 FID (Frechet Inception Distance) 均显著改善,但增大 $T_{\mathrm{revise}}$ 会轻微劣化 FID。我们注意到,由于草稿质量较低,其部分代码堆栈可能存在错误,而较大 $T_{\mathrm{revise}}$ 的模型会在修订阶段缓慢地一次性更新少量代码堆栈。因此,较大 $T_{\mathrm{revise}}$ 的更新更容易受到错误代码堆栈的影响。尽管 $T_{\mathrm{revise}}=2$ 会一次性更新半数图像区域,但如图 5 所示,我们的"起草-修订"解码方法在保持草稿全局上下文的同时,成功提升了生成图像质量。自监督学习研究 [17] 也报告了类似结论:当图像半数区域被遮蔽时,掩码自编码器仍能重建图像的全局上下文。
Quality-diversity control of Draft-and-Revise Our Draft-and-Revise decoding can effectively control the quality-diversity trade-off in generated images. Table 3 shows FID, precision (P), and recall (R) according to the use of classifier-free guidance [20] with a scale of 1.8, while applying temperature scaling with 0.8 only to the revise phase. Contextual RQ-Transformer without the guidance already outperforms RQ-Transformer with 3.8B parameters and demonstrates the effectiveness of our framework. When the guidance is used for both draft and revise phases, the precision dramatically increases but the recall decreases to 0.33. Consequently, FID becomes worse due to the lack of diversity in generated images. However, when the guidance is applied only to the revise phase, our model achieves the lowest FID, as the quality and diversity are well-balanced. Thus, the explicitly separated two phases of Draft-and-Revise can effectively control the issue of quality-diversity trade-off by generating diverse drafts and then improving their quality.
草案修订的质量-多样性控制
我们的草案修订解码方法能有效控制生成图像的质量与多样性权衡。表3展示了在使用分类器无引导[20](尺度为1.8)且仅在修订阶段应用温度缩放(0.8)时的FID、精确度(P)和召回率(R)。未使用引导的Contextual RQ-Transformer已优于具有38亿参数的RQ-Transformer,证明了我们框架的有效性。当引导同时应用于草案和修订阶段时,精确度显著提升但召回率降至0.33,导致FID因生成图像多样性不足而恶化。然而,当引导仅应用于修订阶段时,我们的模型实现了最低FID,因为质量与多样性达到了良好平衡。因此,明确分离的草案修订两阶段可
