Linguistic Knowledge as Memory for Recurrent Neural Networks

语言知识作为循环神经网络的记忆体

Abstract

摘要

Training recurrent neural networks to model long term dependencies is difficult. Hence, we propose to use external linguistic knowledge as an explicit signal to inform the model which memories it should utilize. Specifically, external knowledge is used to augment a sequence with typed edges between arbitrarily distant elements, and the resulting graph is decomposed into directed acyclic subgraphs. We introduce a model that encodes such graphs as explicit memory in recurrent neural networks, and use it to model co reference relations in text. We apply our model to several text comprehension tasks and achieve new state-of-the-art results on all considered benchmarks, including CNN, bAbi, and LAMBADA. On the bAbi QA tasks, our model solves 15 out of the 20 tasks with only 1000 training examples per task. Analysis of the learned representations further demonstrates the ability of our model to encode fine-grained entity information across a document.

训练循环神经网络 (RNN) 建模长程依赖关系具有挑战性。为此，我们提出利用外部语言学知识作为显式信号，指导模型选择应使用的记忆内容。具体而言，该方法通过为序列中任意距离元素添加类型化边来构建增强图，并将该图分解为有向无环子图。我们提出了一种新模型，可将此类图结构编码为循环神经网络中的显式记忆，并用于文本共指关系建模。在多个文本理解任务上的实验表明，我们的模型在CNN、bAbi和LAMBADA等基准测试中均取得了最先进性能。在bAbi问答任务中，模型仅需每个任务1000个训练样本即可解决20个任务中的15个。对学习表征的分析进一步表明，该模型能够跨文档编码细粒度实体信息。

1. Introduction

1. 引言

Sequential data appears in many real world applications involving natural language, videos, speech and financial markets. Predictions involving such data require accurate modeling of dependencies between elements of the sequence which may be arbitrarily far apart. Deep learning offers the promise of extracting these dependencies in a purely data driven manner, with Recurrent Neural Networks (RNNs) being the architecture of choice. RNNs show excellent performance when the dependencies of interest range short spans of the sequence, however they can be notoriously hard to train to discover longer range dependencies (Koutnik et al., 2014; Bengio et al., 1994).

序列数据广泛存在于自然语言、视频、语音和金融市场等现实应用中。对此类数据进行预测需要精确建模序列元素间的依赖关系，这些依赖可能跨越任意距离。深度学习提供了以纯数据驱动方式提取这些依赖关系的潜力，其中循环神经网络 (RNN) 是首选架构。当目标依赖关系仅涉及短序列跨度时，RNN 表现出优异性能，但众所周知其难以训练以发现长程依赖关系 (Koutnik et al., 2014; Bengio et al., 1994)。

Hochreiter & Schmid huber (1997) introduced Long Short Term Memory (LSTM) networks which use a special unit called the Constant Error Carousel (CEC) to alleviate this problem. The CEC has a memory cell with a constant linear connection to itself which allows gradients to flow over long distances. Cho et al. (2014b) introduced a simplified version of LSTMs called Gated Recurrent Units (GRU) with has one less gate, and consequently fewer parameters. Both LSTMs and GRUs have been hugely popular for modeling sequence data (Sutskever et al., 2014; Kiros et al., 2015; Oord et al., 2016).

Hochreiter & Schmidhuber (1997) 提出了长短期记忆网络 (LSTM)，通过名为恒定误差传送带 (CEC) 的特殊单元缓解该问题。CEC 具有一个与自身保持恒定线性连接的记忆单元，使梯度能够长距离传播。Cho 等人 (2014b) 提出了简化版 LSTM——门控循环单元 (GRU)，其减少了一个门结构，参数量更少。LSTM 和 GRU 在序列数据建模中广受欢迎 (Sutskever 等人, 2014; Kiros 等人, 2015; Oord 等人, 2016)。

Despite these extensions, empirical studies have shown that it is still difficult to train RNNs with long-range dependencies (see for example, (Cho et al., 2014a)). One suggested explanation for this is that the network must propagate all the information in a single fixed-size vector, which may be infeasible. This led to the introduction of the attention mechanism (Bahdanau et al., 2014) which adapts the sequence model with a more explicit form of long term memory. At each time step $t$ , the model can perform a “soft”- lookup over all previous outputs through a weighted average $\sum_{i=1}^{\star-1}\alpha_{i}h_{i}$ . The weights $\alpha_{i}$ are the outputs of another net work whose parameters are learned from data. Augmenting sequence models with attention has lead to significant improvements in various language modeling domains (Hermann et al., 2015). Other architectures, such as Memory Networks (Weston et al., 2014), further build on this idea by introducing a memory module for the soft-lookup operation, and a number of models allow the RNN to hold differentiable “memories” of past elements to discover long range correlations (Graves et al., 2014). However, Daniluk et al. (2017) showed that even memory-augmented neural models do not look beyond the immediately preceding time steps. Clearly, training RNNs to discover long range dependencies without an explicit signal is challenging.

尽管有这些扩展，实证研究表明，训练具有长程依赖性的循环神经网络 (RNN) 仍存在困难 (例如参见 (Cho et al., 2014a)) 。对此的一种解释是，网络必须在单个固定大小的向量中传播所有信息，这可能难以实现。这促使注意力机制 (Bahdanau et al., 2014) 的引入，该机制通过更显式的长期记忆形式来调整序列模型。在每个时间步 $t$，模型可以通过加权平均 $\sum_{i=1}^{\star-1}\alpha_{i}h_{i}$ 对所有先前输出进行"软"查找。权重 $\alpha_{i}$ 是另一个网络的输出，其参数从数据中学习得到。通过注意力增强序列模型，已在各种语言建模领域取得显著改进 (Hermann et al., 2015)。其他架构，如记忆网络 (Weston et al., 2014)，进一步扩展了这一思想，引入用于软查找操作的内存模块，并且许多模型允许 RNN 保存过去元素的可微分"记忆"以发现长程相关性 (Graves et al., 2014)。然而，Daniluk 等人 (2017) 表明，即使是内存增强的神经模型也不会关注超过紧邻时间步的内容。显然，在没有显式信号的情况下训练 RNN 发现长程依赖关系具有挑战性。

In this paper we do not attempt to solve this problem. Instead we argue that in many applications, information about long-term dependencies may be readily available in the form of symbolic knowledge. As an example, consider the sequence of text shown in Figure 1. Standard preprocessing tools can be used to extract relations such as coreference and hypernymy between pairs of tokens, which can be added as extra edges in addition to the sequential links between elements. We argue that these extra signals can be used to provide the RNN model with locations of an explicit memory of distant elements when computing the representation of the current element. The content of a memory is the representation of the linked element, and edge labels can distinguish different types of memories. In this manner symbolic knowledge can guide the propagation of information through a recurrent network.

本文中我们并不试图解决这一问题。相反，我们认为在许多应用场景中，关于长期依赖关系的信息可以很容易地以符号知识的形式获取。以图1所示的文本序列为例，标准预处理工具可用于提取token对之间的共指关系和上下位关系，这些关系可以作为额外边添加到元素间的顺序链接之上。我们主张这些额外信号能为RNN模型在计算当前元素表征时，提供远距离元素的显式记忆定位功能。记忆内容即被链接元素的表征，而边标签可区分不同类型的记忆。通过这种方式，符号知识能引导信息在循环网络中的传播。

Technically, incorporating these “skip connections” into the sequence converts it into a graph with cycles. Graph based neural networks (Scarselli et al., 2009) can be used to handle such data, but they are computationally expensive when the number of nodes in the graph is large. Instead, we utilize the order inherent in the the un augmented sequence to decompose the graph into two Directed Acyclic Graphs (DAGs) with a topological ordering. We introduce the Memory as Acyclic Graph Encoding RNN (MAGERNN) framework to compute the representation of such graphs while touching every node only once, and implement a GRU version of it called MAGE-GRU. MAGERNN learns separate representations for propagation along each edge type, which leads to superior performance empirically. In cases where there is at most a single incoming edge of a particular type at a node, it reduces to a memory augmented regular RNN whose memory access is determined by a symbolic signal.

从技术上讲，将这些"跳跃连接"融入序列会将其转化为带环图。基于图的神经网络 [20] 可以处理此类数据，但当图中节点数量庞大时计算成本高昂。为此，我们利用原始序列的固有顺序将图分解为两个具有拓扑排序的有向无环图 (DAG)。我们提出记忆增强型有向无环图编码循环神经网络 (MAGERNN) 框架，该框架能在仅访问每个节点一次的情况下计算此类图的表示，并实现了其门控循环单元版本 MAGE-GRU。MAGERNN 会为每种边类型的传播学习独立表示，实验表明这能带来更优性能。当节点处特定类型的入边最多只有一条时，该方法可简化为由符号信号控制内存访问的常规记忆增强循环神经网络。

We use MAGE-RNN to model co reference relations for text comprehension tasks, where answers to a query have to be extracted from a context document. Tokens in a document are connected by a co reference relation if they refer to the same underlying entity. Identifying such relations is important for developing an understanding of the document, and hence we augment RNN architectures for text comprehension with an explicit memory of coreferent mentions. MAGE-GRU leads to a consistent improvement over the vanilla GRU, as well as a baseline where the coreference information is added as input features to the model. By further replacing GRU units in existing reading comprehension models with MAGE-GRUs we achieve stateof-the-art performance on three well studied benchmarks – the bAbi QA tasks, the LAMBADA dataset, and the CNN dataset. An analysis of the learned representations by the model also show its effectiveness in encoding fine-grained information about the entities in a document.

我们使用MAGE-RNN对文本理解任务中的共指关系进行建模，这类任务需要从上下文文档中提取查询的答案。如果文档中的Token指向同一实体，则通过共指关系连接。识别这类关系对于理解文档至关重要，因此我们在RNN架构中增加了显式的共指提及记忆机制来增强文本理解能力。MAGE-GRU相比原始GRU以及仅将共指信息作为输入特征的基线模型实现了持续改进。通过将现有阅读理解模型中的GRU单元替换为MAGE-GRU，我们在三个经典基准测试（bAbi QA任务、LAMBADA数据集和CNN数据集）上达到了最先进的性能。对该模型学习表征的分析也表明其在编码文档实体细粒度信息方面的有效性。

2. Related Work

2. 相关工作

Augmenting the sequence with these extra links converts it from a chain to a more general graph structure. Models such as the Graph Neural Networks (Scarselli et al., 2009) and Gated Graph Sequence Neural Networks (Li et al., 2016) can be used to handle such data. The basic idea in these architectures is to update the representation of every single node at every time-step, based on the incoming representations of their neighbours. Depending on the optimization procedure, the updates are either performed till the representations converge, or for a fixed number of time-steps. The resulting complexity is $O(N T)$ , where $N$ is the number of nodes, and $T$ is the number of time-steps. To fully propagate information in the graph, $T$ should be at least the width of the graph. Though in practice it is possible to obtain an approximation with a smaller $T$ , training graph-based neural networks is computationally expensive compared to RNNs, which have complexity only $O(N)$ .

通过这些额外链接增强序列，将其从链式结构转换为更通用的图结构。可以使用图神经网络 (Graph Neural Networks) (Scarselli et al., 2009) 和门控图序列神经网络 (Gated Graph Sequence Neural Networks) (Li et al., 2016) 等模型来处理此类数据。这些架构的基本思想是：在每一个时间步，基于相邻节点的输入表征来更新每个单一节点的表征。根据优化过程的不同，更新操作会持续到表征收敛或执行固定次数的时间步。最终复杂度为 $O(N T)$ ，其中 $N$ 是节点数量， $T$ 是时间步数。要在图中完全传播信息， $T$ 至少应为图的宽度。尽管在实践中可以用较小的 $T$ 获得近似解，但与复杂度仅为 $O(N)$ 的循环神经网络 (RNN) 相比，基于图的神经网络训练计算成本更高。

Trees are another commonly encountered graph structure, and Tai et al. (2015) proposed Tree-Structured LSTMs for handling such data. However, that work focused solely on dependency parses of textual data and ignored its inherent sequential ordering, whereas here we argue for a more general approach which can incorporate many types of edges between tokens, including sequential ones. The resulting MAGE-RNN formulation can be viewed as an extension of Tree-Structured LSTMs.

树是另一种常见的图结构，Tai等人(2015)提出了Tree-Structured LSTM来处理此类数据。然而，该工作仅关注文本数据的依存句法分析，忽略了其固有的顺序性。本文主张采用更通用的方法，能够整合token之间的多种边类型(包括顺序边)。由此产生的MAGE-RNN公式可视为Tree-Structured LSTM的扩展。

Shuai et al. (2016) proposed a similar idea to ours, which employs RNNs on DAGs of image pixels. However, their model focuses on images and does not handle typed edges. In contrast, our work provides a novel perspective on incorporating symbolic knowledge as links to sequential data. Moreover, in terms of model architectures, our model explicitly handles typed edges by using separate parameter matrices and split hidden states, which are key to improved performance.

Shuai等人 (2016) 提出了与我们类似的思路，即在图像像素的有向无环图 (DAG) 上应用循环神经网络 (RNN)。但他们的模型仅针对图像数据，且未处理带类型的边。相比之下，我们的工作为将符号知识作为链接融入序列数据提供了全新视角。此外，在模型架构方面，我们通过使用独立参数矩阵和分割隐藏状态显式处理带类型的边，这正是性能提升的关键所在。

The importance of reference resolution for reading comprehension was previously studied in Wang et al. (2017). They showed that models which utilize explicit coreference information, for example via the attention sum mechanism (see Section 4.1), tend to perform better than those which do not. The suggested solution in that work was to add this information as extra features to the input of the model This approach forms our “one-hot” baseline. Here we take that idea further by proposing a modification to the structure of the reader itself for handling co reference, and show that doing so leads to further performance improvement, and interpret able output representations. Our model is also related to the Recurrent Entity Networks architecture (Henaff et al., 2016). In fact, with perfect coreference information, each chain corresponds to an entity in the story, plus one chain for the sequential context. However, the MAGE-RNN model allows these chains to interact with each other, unlike recurrent entity networks (for example, the local context around the mention of an entity can inform the co reference representation of that entity and vice versa). It is also possible to incorporate other types of symbolic knowledge beyond co reference in MAGE-RNNs.

Wang等人 (2017) 先前研究了指代消解对阅读理解的重要性。研究表明，利用显式共指信息（例如通过注意力求和机制，见第4.1节）的模型通常优于未使用该信息的模型。该研究提出的解决方案是将此类信息作为额外特征输入模型，这构成了我们的"one-hot"基线。本文进一步拓展该思路，通过修改阅读器结构本身来处理共指关系，实验表明该方法能带来性能提升并生成可解释的输出表征。我们的模型与循环实体网络架构 (Henaff等人, 2016) 也存在关联。实际上，在完美共指信息条件下，每条链对应故事中的一个实体外加一条序列上下文链。但与循环实体网络不同，MAGE-RNN模型允许这些链相互交互（例如，实体提及的局部上下文可以影响该实体的共指表征，反之亦然）。MAGE-RNN还可整合除共指外的其他符号知识类型。

Recently, there has been interest in incorporating symbolic knowledge, such as that from a Knowledge Base or coreference information, within RNN-based language models (Yang et al., 2016; Ahn et al., 2016). However, rather than incorporating this knowledge within the structure of the RNN, these works instead use the output representation learned by the RNN to model latent variables which decide when to select the next token from the full vocabulary or a restricted vocabulary from the knowledge source. This approach is specific to the task of predicting the next token in a sequence. Our work is aimed at the more general problem of learning suitable representations of text.

最近，研究者们开始关注如何将符号知识（如来自知识库或共指信息的知识）整合到基于RNN的语言模型中 (Yang et al., 2016; Ahn et al., 2016)。然而，这些工作并非在RNN结构中直接融入知识，而是利用RNN学习到的输出表示来建模潜在变量，这些变量决定何时从完整词表或知识源的受限词表中选择下一个token。这种方法专门针对序列中预测下一个token的任务。我们的研究则针对更通用的文本表示学习问题。

Figure 1. A sequence of text augmented with extra links. Red edges denote co reference relations, and green edges denote hypo/hypernymy. Black edges denote usual sequential links.

图 1: 带有额外链接的文本序列。红色边表示共指关系，绿色边表示上下位关系。黑色边表示常规顺序链接。

3. Methods

3. 方法

3.1. From Sequences to DAGs

3.1. 从序列到有向无环图

Suppose that along with the input sequence $x_{1},\dots,x_{T}$ , where $x_{i}\in\mathbb{R}^{d_{i n}}$ , we are also given information about which pairs of elements connect with each other. Further, suppose that these extra “edges” are typed—i.e., they belong to one of several different categories. Such extra information is common in Natural Language Processing (NLP). For example, one type of edge might connect multiple mentions of the same entity (co reference), while another type of edge might connect generic terms to their specific instances (hyponymy and hypernymy). Figure 1 shows a simple example. Any piece of text can be augmented in this manner by running standard preprocessing tools such as coreference taggers and entity linkers.

假设除了输入序列 $x_{1},\dots,x_{T}$ (其中 $x_{i}\in\mathbb{R}^{d_{i n}}$) 之外，我们还获得了关于哪些元素对彼此连接的信息。此外，假设这些额外的"边"是有类型的——即它们属于几种不同类别之一。此类额外信息在自然语言处理 (NLP) 中很常见。例如，一种边可能连接同一实体的多次提及 (共指)，而另一种边可能将通用术语连接到其特定实例 (下位词和上位词)。图 1 展示了一个简单示例。通过运行共指标注器和实体链接器等标准预处理工具，可以以这种方式增强任何文本。

Let $\boldsymbol{\mathcal{G}}=(\mathcal{X},\mathcal{E})$ denote the resulting directed graph which includes the sequential edges between consecutive elements, as well as the extra typed edges. The nodes $\mathcal{X}=$ ${x_{i}}_{i=1}^{T}$ correspond to the elements of the original sequence, and edges ${\mathcal{E}}_{0}={(x,x^{\prime},e)}$ are tuples consisting of the source, target and type of the link. The graph $\mathcal{G}$ results from augmenting the edges in $\mathcal{E}_{0}$ with inverse edges. More formally, for each edge $(x,x^{\prime},e)\in\mathcal{E}_{0}$ , we add an edge $(x^{\prime},x,e^{\prime})$ to the graph with $e^{\prime}$ being the (artificial) inverse edge type of $e$ . The resulting edge set with both original and inverse edges is denoted as $\mathcal{E}$ . By definition, the graph $\mathcal{G}$ is a directed cyclic graph in general, but we can use the inherent order of the original sequence to decompose this into two subgraphs in the forward and backward directions respectively. The forward subgraph can be defined as $\mathcal{G}_{f}=(\mathcal{X},\mathcal{E}_{f})$ , where $\mathcal{E}_{f}={(x_{i},x_{j},e_{f})\in\mathcal{E}:$ $i<j}$ . Here $i$ and $j$ are indices into the original sequence. The backward graph is defined analogously, with $\mathcal{E}_{b}={(x_{i},x_{j},e_{b})\in\mathcal{E}:i>j}$ . By construction, ${\mathcal G}_{f}$ and $\mathcal{G}_{b}$ are DAGs, i.e., they do not contain cycles. We denote the set of all forward edge types by $E_{f}$ and all backward edge types by $E_{b}$ .

设 $\boldsymbol{\mathcal{G}}=(\mathcal{X},\mathcal{E})$ 表示最终得到的有向图，其中包含连续元素间的顺序边和额外类型边。节点 $\mathcal{X}=$ ${x_{i}}_{i=1}^{T}$ 对应原始序列的元素，边 ${\mathcal{E}}_{0}={(x,x^{\prime},e)}$ 是由链接的源节点、目标节点和类型组成的三元组。图 $\mathcal{G}$ 是通过在 $\mathcal{E}_{0}$ 中增加反向边得到的。更正式地说，对于每条边 $(x,x^{\prime},e)\in\mathcal{E}_{0}$ ，我们向图中添加一条边 $(x^{\prime},x,e^{\prime})$ ，其中 $e^{\prime}$ 是 $e$ 的（人工）反向边类型。包含原始边和反向边的最终边集记为 $\mathcal{E}$ 。根据定义，图 $\mathcal{G}$ 通常是一个有向循环图，但我们可以利用原始序列的固有顺序将其分解为分别沿正向和反向的两个子图。正向子图定义为 $\mathcal{G}_{f}=(\mathcal{X},\mathcal{E}_{f})$ ，其中 $\mathcal{E}_{f}={(x_{i},x_{j},e_{f})\in\mathcal{E}:$ $i<j}$ 。这里 $i$ 和 $j$ 是原始序列的索引。反向图的定义类似，其中 $\mathcal{E}_{b}={(x_{i},x_{j},e_{b})\in\mathcal{E}:i>j}$ 。根据构造， ${\mathcal G}_{f}$ 和 $\mathcal{G}_{b}$ 是有向无环图（DAG），即它们不包含循环。我们将所有正向边类型的集合记为 $E_{f}$ ，所有反向边类型的集合记为 $E_{b}$ 。

For every DAG there exists a topological ordering of its nodes in a sequence such that all edges in the graph are directed from preceding nodes to succeeding nodes in the sequence. For ${\mathcal G}{f}$ (respectively $\mathcal{G}_{b}$ ) defined above, one such ordering is immediately available – the forward sequence order $(1,2,\ldots,T)$ (respectively the backward order $(T,T-1,\dots,1))$ . The existence of such an ordering makes DAGs particularly amenable to be modeled using RNNs, and below we discuss an architecture for doing so.

对于每个有向无环图(DAG)，其节点都存在一种拓扑排序序列，使得图中所有边都从序列中的前驱节点指向后继节点。对于上述定义的 ${\mathcal G}{f}$ (相应地 $\mathcal{G}_{b}$)，可以立即获得一种这样的排序——前向序列顺序 $(1,2,\ldots,T)$ (相应地是后向顺序 $(T,T-1,\dots,1))$。这种排序的存在使得DAG特别适合用RNN建模，下面我们将讨论实现这一目标的架构。

3.2. MAGE-GRUs

3.2. MAGE-GRUs

We present our framework as an adaptation of Gated Recurrent Units, called MAGE-GRU; however similar extensions can be derived for any recurrent neural network. MAGEGRU uses separate networks for the forward and backward subgraphs respectively. We present the updates only for the forward subgraph, since the backward subgraph is processed analogously.

我们提出的框架是对门控循环单元 (Gated Recurrent Units) 的改进，称为 MAGE-GRU；不过类似的扩展可以应用于任何循环神经网络。MAGE-GRU 分别为前向子图和反向子图使用独立的网络。由于反向子图的处理方式类似，我们仅展示前向子图的更新过程。

Miller et al. (2016) and Daniluk et al. (2017) argue that overloaded use of state representations as both memory content and address makes training of the network difficult, and decompose these two functions by parameter izing them separately. Similarly, we decompose the hidden states in the GRUs and maintain a separate hidden state vector $h_{t}^{e}\in\mathbb{R}^{d_{e}}$ for each edge type in $\mathcal{E}_{f}$ . The intuition behind this is that, for example, the representation flowing through the black edges in Figure 1 need not be the same as that flowing through the red or green edges.

Miller等人 (2016) 和Daniluk等人 (2017) 指出，将状态表示同时作为记忆内容和地址的过载使用会使网络训练变得困难，因此通过分别参数化来分解这两种功能。类似地，我们分解了GRU中的隐藏状态，并为$\mathcal{E}{f}$中的每种边类型维护了一个单独的隐藏状态向量$h{t}^{e}\in\mathbb{R}^{d_{e}}$。其背后的直觉是，例如，流经图1中黑色边的表示不必与流经红色或绿色边的表示相同。

As $t$ varies from 1 to $T$ , the hidden states are updated in the topological order defined by the sequence and, importantly, the update for each edge state depends on the current state of all incoming edges at $x_{t}$ . Specifically, define

随着 $t$ 从 1 变化到 $T$，隐藏状态按照序列定义的拓扑顺序更新，且关键在于每条边的状态更新取决于 $x_{t}$ 处所有入边的当前状态。具体定义为

$$
\mathcal{T}{f}(x_{t})={(t^{\prime},e):(x_{t^{\prime}},x_{t},e)\in\mathcal{E}_{f}}
$$

$$
\mathcal{T}{f}(x_{t})={(t^{\prime},e):(x_{t^{\prime}},x_{t},e)\in\mathcal{E}_{f}}
$$

as the set of incoming edges at node $x$ , along with the index of their sources. Then the next state is given by

作为节点 $x$ 的入边集合及其源节点索引。下一状态由以下公式给出：

$$
\begin{array}{l}{{r_{t}^{e}=\sigma\big(W_{r}^{e}x_{t}+\displaystyle\sum_{(t^{\prime},e^{\prime})\in{\cal Z}{f}(x_{t})}U_{r}^{e,e^{\prime}}h_{t^{\prime}}^{e^{\prime}}+b_{r}^{e}\big)}}\ {{z_{t}^{e}=\sigma\big(W_{z}^{e}x_{t}+\displaystyle\sum_{(t^{\prime},e^{\prime})\in{\cal Z}{f}(x_{t})}U_{z}^{e,e^{\prime}}h_{t^{\prime}}^{e^{\prime}}+b_{z}^{e}\big)}}\ {{\tilde{h}{t}^{e}=\operatorname{tanh}\bigl(W_{h}^{e}x_{t}+r_{t}^{e}\odot\displaystyle\sum_{(t^{\prime},e^{\prime})\in{\cal Z}{f}(x_{t})}U_{h}^{e,e^{\prime}}h_{t^{\prime}}^{e^{\prime}}+b_{h}^{e}\bigr)}}\ {{h_{t}^{e}=\big(1-z_{t}^{e}\big)\odot h_{t-1}^{e}+z_{t}^{e}\odot\tilde{h}_{t}^{e}}}\end{array}
$$

$$
\begin{array}{l}{{r_{t}^{e}=\sigma\big(W_{r}^{e}x_{t}+\displaystyle\sum_{(t^{\prime},e^{\prime})\in{\cal Z}{f}(x_{t})}U_{r}^{e,e^{\prime}}h_{t^{\prime}}^{e^{\prime}}+b_{r}^{e}\big)}}\ {{z_{t}^{e}=\sigma\big(W_{z}^{e}x_{t}+\displaystyle\sum_{(t^{\prime},e^{\prime})\in{\cal Z}{f}(x_{t})}U_{z}^{e,e^{\prime}}h_{t^{\prime}}^{e^{\prime}}+b_{z}^{e}\big)}}\ {{\tilde{h}{t}^{e}=\operatorname{tanh}\bigl(W_{h}^{e}x_{t}+r_{t}^{e}\odot\displaystyle\sum_{(t^{\prime},e^{\prime})\in{\cal Z}{f}(x_{t})}U_{h}^{e,e^{\prime}}h_{t^{\prime}}^{e^{\prime}}+b_{h}^{e}\bigr)}}\ {{h_{t}^{e}=\big(1-z_{t}^{e}\big)\odot h_{t-1}^{e}+z_{t}^{e}\odot\tilde{h}_{t}^{e}}}\end{array}
$$

for each $e\in E_{f}.W_{r,z,h}^{e}$ re,z,h and U re,,ze,h are parameter matrices of size de × din and de × de′ respectively, and bre,z,h are

对于每个 $e\in E_{f}.W_{r,z,h}^{e}$，re,z,h 和 U re,,ze,h 分别是大小为 de × din 和 de × de′ 的参数矩阵，bre,z,h 是

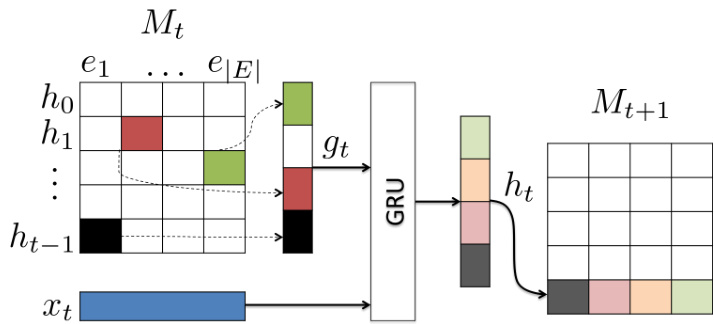
Figure 2. Operation of the chain-decomposed MAGE-GRU. $M_{t}$ denotes the block of memories for each edge type and preceding time-steps.

图 2: 链式分解 MAGE-GRU 的操作流程。$M_{t}$ 表示每种边类型及先前时间步的记忆块。

parameter vectors of size $d_{e}$ . The output representation at time step $t$ is given by,

参数向量大小为 $d_{e}$。时间步 $t$ 的输出表示由下式给出：

$$
h_{t}=h_{t}^{e_{1}}|h_{t}^{e_{2}}|\ldots|h_{t}^{e_{|E_{f}|}},
$$

$$
h_{t}=h_{t}^{e_{1}}|h_{t}^{e_{2}}|\ldots|h_{t}^{e_{|E_{f}|}},
$$

where $h_{t}\in\mathbb{R}^{\sum_{e}d_{e}}$ , and $\parallel$ denotes concatenation. Output for the forward subgraph is given by $H_{f}=[h_{1},\dots,h_{T}]$ . Similarly, we can obtain the output of the backward subgraph $H_{b}$ , and concatenate with $H_{f}$ such that elements of the original sequence line up. The collection of all previous output representations $M_{t}=[h_{0};h_{1};\ldots;h_{t-1}]$ can be viewed as the memory available to the recurrent model at time-step $t$ .

其中 $h_{t}\in\mathbb{R}^{\sum_{e}d_{e}}$ ，且 $\parallel$ 表示拼接操作。前向子图的输出为 $H_{f}=[h_{1},\dots,h_{T}]$ 。同理可得后向子图输出 $H_{b}$ ，并与 $H_{f}$ 按原序列位置对齐拼接。所有历史输出表示的集合 $M_{t}=[h_{0};h_{1};\ldots;h_{t-1}]$ 可视为循环模型在时间步 $t$ 时的记忆单元。

In the case of co reference, or any relation where there is at most one incoming edge of a particular type at any node, the DAG can be decomposed into a collection of independent chains. Then the updates for each $e$ in (2) can be trivially combined into one regular GRU update, as depicted in Figure 2. To see this, define $g_{t}=g_{t}^{e_{1}}\Vert g_{t}^{e_{2}}\Vert\dots\Vert g^{e_{|E|}}$ where $g_{t}^{e_{i}}=h_{t^{\prime}}^{e_{i}}$ , if $\exists(t^{\prime},e_{i})\in\mathbb{Z}(x_{t})$ , else $g_{t}^{e_{i}}=0$ . In other words, $g_{t}^{e_{i}}$ holds the hidden state of the node connecting to $x_{t}$ via edge $e$ , if there is such a node. Then, by stacking the matrices W e, U ∗e,e′ and the vector $b_{*}^{e}$ for all $e,e^{\prime}$ , we obtain the following combined updates:

在共指或任何关系中，若某节点最多只有一条特定类型的入边，则该有向无环图(DAG)可分解为一组独立链。此时，(2)式中每个$e$的更新可简单合并为一次常规GRU更新，如图2所示。具体而言，定义$g_{t}=g_{t}^{e_{1}}\Vert g_{t}^{e_{2}}\Vert\dots\Vert g^{e_{|E|}}$，其中当$\exists(t^{\prime},e_{i})\in\mathbb{Z}(x_{t})$时$g_{t}^{e_{i}}=h_{t^{\prime}}^{e_{i}}$，否则$g_{t}^{e_{i}}=0$。换言之，若存在通过边$e$连接至$x_{t}$的节点，则$g_{t}^{e_{i}}$保存该节点的隐状态。通过堆叠所有$e,e^{\prime}$对应的矩阵W e、U ∗e,e′和向量$b_{*}^{e}$，我们得到以下组合更新式：

$$
\begin{array}{r l}&{r_{t}=\sigma(W_{r}x_{s_{t}}+U_{r}g_{t}+b_{r})}\ &{z_{t}=\sigma(W_{z}x_{s_{t}}+U_{z}g_{t}+b_{z})}\ &{\tilde{h}_{t}=\operatorname{tanh}(W_{h}x_{s_{t}}+r_{t}\odot U_{h}g_{t}+b_{h})}\ &{h_{t}=(1-z_{t})\odot h_{t-1}+z_{t}\odot\tilde{h}_{t},}\end{array}
$$

$$
\begin{array}{r l}&{r_{t}=\sigma(W_{r}x_{s_{t}}+U_{r}g_{t}+b_{r})}\ &{z_{t}=\sigma(W_{z}x_{s_{t}}+U_{z}g_{t}+b_{z})}\ &{\tilde{h}_{t}=\operatorname{tanh}(W_{h}x_{s_{t}}+r_{t}\odot U_{h}g_{t}+b_{h})}\ &{h_{t}=(1-z_{t})\odot h_{t-1}+z_{t}\odot\tilde{h}_{t},}\end{array}
$$

which are the usual GRU updates, but with the recurrent state replaced by $g_{t}$ . Finally, we must slice the output vector $h_{t}$ back into its constituents $h_{t}^{e}$ for all $e\in E_{f}$ by extracting the appropriate dimensions.

这是常规的GRU更新步骤，但循环状态被替换为$g_{t}$。最后，我们必须通过提取相应维度将输出向量$h_{t}$重新切分为其组成部分$h_{t}^{e}$（对于所有$e\in E_{f}$）。

3.3. Multiple Sequences

3.3. 多序列

In certain applications, we have multiple sequences whose elements interact with each other via known relationships. Continuing with our motivating example, Figure 3 shows an example where the first sequence is a context passage and the second sequence is a question posed over the passage. The sequences are further augmented with coreference and hypernymy relations, resulting in an undirected cyclic graph.

在某些应用中，我们会遇到多个序列之间通过已知关系相互作用的场景。延续前文的示例，图 3: 展示了一个案例：第一个序列是上下文段落，第二个序列是针对该段落提出的问题。这些序列通过共指关系和上下位关系进一步扩展，最终形成一个无向循环图。

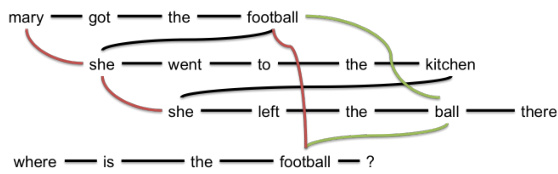
Figure 3. Two sequences of text augmented with extra links. Red edges denote co reference relations, and green edges denote hypo/hyper-nymy. Black edges denote usual sequential links.

图 3: 带有额外链接的两段文本增强示意图。红色边表示共指关系，绿色边表示上下位关系。黑色边表示常规顺序链接。

We would like to decompose this graph into a collection of DAGs and use the MAGE-GRU presented above to learn representations of the elements in the sequences. Also, we would like to preserve the order of the original sequences in the decomposed DAGs. Suppose we have $S$ sequences $X_{1},\dots,X_{S}$ . One way to do this is as follows: for each permutation of the collection of sequences $(X_{k_{1}},X_{k_{2}},\ldots,X_{k_{S}})$ , treat it as a single long sequence and decompose into forward and backward subgraphs as described in Section 3.1. However, this results in $2S!$ DAGs, which is expensive except for very small $S$ . Instead, we propose here taking one random permutation of the sequences and decomposing it into the forward and backward subgraphs. In this manner, each edge in the graph is still traversed twice (once in both directions), without incurring any additional cost compared to processing the sequences individually. Moreover, multi-layer extensions of the MAGE-GRU can allow information to flow through arbitrary paths through the graph.

我们希望能将该图分解为一组有向无环图(DAG)，并利用前文提出的MAGE-GRU来学习序列元素的表征。同时，我们希望在被分解的有向无环图中保留原始序列的顺序。假设我们有$S$个序列$X_{1},\dots,X_{S}$，具体实现方式如下：对于序列集合的每个排列$(X_{k_{1}},X_{k_{2}},\ldots,X_{k_{S}})$，将其视为单个长序列并按3.1节所述方法分解为前向和后向子图。但这种方法会产生$2S!$个有向无环图，除非$S$值极小，否则计算成本极高。为此，我们提出采用随机排列序列的方案，将其分解为前向和后向子图。这种方式仍能保证图中每条边被遍历两次（正反方向各一次），且与单独处理各序列相比不会产生额外成本。此外，MAGE-GRU的多层扩展结构允许信息通过图中的任意路径流动。

4. Experiments

4. 实验

4.1. Text Comprehension with Co reference

4.1. 带共指消解的文本理解

Text comprehension tasks involve tuples of the form $(d,q,a)$ , where $d$ is a context document and $q$ is a ques- tion whose answer $a$ can be inferred from reading $d$ . In the extractive setting the answer is a span of text in the context document. Often a set of candidates $\mathcal{C}$ is available, in which case the task becomes a classification task. Several large-scale benchmarks (Rajpurkar et al., 2016; Onishi et al., 2016) and deep learning models (Munkhdalai & Yu, 2016) have been proposed for this task recently.

文本理解任务涉及形式为 $(d,q,a)$ 的元组，其中 $d$ 是上下文文档，$q$ 是一个问题，其答案 $a$ 可通过阅读 $d$ 推断得出。在抽取式设定中，答案是上下文文档中的一段文本。通常还会提供一组候选答案 $\mathcal{C}$，此时任务就转化为分类任务。针对该任务，近期已提出了多个大规模基准测试 (Rajpurkar et al., 2016; Onishi et al., 2016) 和深度学习模型 (Munkhdalai & Yu, 2016)。

Comprehending a document requires complex reasoning processes and prior knowledge on the part of the reader. One of these processes is co reference resolution, where the reader must identify expressions in text referring to the same entity (see red edges in Figures 1, 3). Chu et al. (2016) show that existing state-of-the art models have poor performance in cases where some form of co reference resolution is required. A separate line of work (Clark & Manning, 2015), however, has led to the development of sophisticated co reference an not at or s 1, and here we use these annotations over document and question pairs as an explicit memory signal for an RNN reader. The intuition is that when processing referring expressions, the model should also receive information about previous mentions of the referent entity.

理解文档需要读者具备复杂的推理过程和先验知识。其中一项关键过程是共指消解 (coreference resolution) ，即识别文本中指向同一实体的不同表述（见图 1、图 3 中的红色边）。Chu 等人 (2016) 的研究表明，现有最先进模型在需要共指消解的场景中表现欠佳。而 Clark 和 Manning (2015) 的独立研究则开发了成熟的共指标注工具，本文将这些文档与问题对的标注作为 RNN 阅读器的显式记忆信号。其核心思想是：当模型处理指代表达时，应同时获取该实体先前被提及的信息。

We study the effect of adding an explicit co reference signal to RNN based models for three well studied text comprehension benchmarks. Following previous work (Hermann et al., 2015; Kadlec et al., 2016) our basic architecture consists of bidirectional GRUs to encode the document and query into a matrix $H^{d}=[h_{1}^{d},\ldots,h_{|d|}^{d}]$ and vector $h^{q}$ respectively. Next the query vector is used to compute an attention distribution over the document,

我们研究了在基于RNN的模型中添加显式共指信号对三个经过充分研究的文本理解基准的影响。遵循先前工作 (Hermann et al., 2015; Kadlec et al., 2016) 的基本架构，我们使用双向GRU将文档和查询分别编码为矩阵 $H^{d}=[h_{1}^{d},\ldots,h_{|d|}^{d}]$ 和向量 $h^{q}$。接着利用查询向量计算文档上的注意力分布，

$$
\alpha=\mathrm{softmax}\left(h^{q}\right)^{T}H^{d}
$$

$$
\alpha=\mathrm{softmax}\left(h^{q}\right)^{T}H^{d}
$$

For extractive tasks, we use this attention distribution directly to predict the answer, using the attention-sum mechanism suggested by Kadlec et al. (2016). Hence, the probability of selecting token $w$ as the answer is given by $\textstyle\sum_{i\in I(w,d)}\alpha_{i}$ , where $I(w,d)$ is the set of positions $w$ occurs in $d$ . For classification tasks, we select the answer among the candidates $\mathcal{C}$ as follows:

对于抽取式任务，我们直接使用这种注意力分布来预测答案，采用 Kadlec 等人 (2016) 提出的注意力求和机制。因此，选择 token $w$ 作为答案的概率由 $\textstyle\sum_{i\in I(w,d)}\alpha_{i}$ 给出，其中 $I(w,d)$ 是 $w$ 在文档 $d$ 中出现的位置集合。对于分类任务，我们按以下方式从候选集 $\mathcal{C}$ 中选择答案：

$$
\begin{array}{l}{{\displaystyle h^{d}=\alpha^{T}H^{d}}}\ {{\displaystyle p_{\mathcal{C}}=\mathrm{softmax}((h^{d})^{T}W_{\mathcal{C}})}}\ {{\displaystyle\hat{a}=\mathrm{argmax}_{\mathcal{C}}p_{\mathcal{C}}}}\end{array}
$$

$$
\begin{array}{l}{{\displaystyle h^{d}=\alpha^{T}H^{d}}}\ {{\displaystyle p_{\mathcal{C}}=\mathrm{softmax}((h^{d})^{T}W_{\mathcal{C}})}}\ {{\displaystyle\hat{a}=\mathrm{argmax}_{\mathcal{C}}p_{\mathcal{C}}}}\end{array}
$$

where $W_{\mathcal{C}}$ is a lookup table of output embeddings, one for each candidate.

其中 $W_{\mathcal{C}}$ 是输出嵌入的查找表，每个候选对应一个。

To test our contribution, we replace the pair of bi-GRUs with the single MAGE-GRU model described for multiple sequences for computing the document and query representations, and compare the final performance. As a baseline we also compare to the setting where co reference information is added as extra features at the input of the GRU. Let $M$ be the number of co reference chains for the $(d,q)$ pair: we append a one-hot vector $o_{t}\in{0,1}^{M}$ to the input of the GRU $x_{t}$ indicating which co reference chain, if any, that token is a part of. Such additional features were shown to be useful by Wang et al. (2017). Henceforth, we refer to this baseline as “one-hot”.

为验证我们的贡献，我们将用于计算文档和查询表示的双向GRU对替换为所述多序列处理的单一MAGE-GRU模型，并比较最终性能。作为基线，我们还对比了在GRU输入端添加共指信息作为额外特征的设置。设$(d,q)$对的共指链数量为$M$：我们在GRU输入$x_{t}$后附加一个独热向量$o_{t}\in{0,1}^{M}$，用于指示该token所属的共指链（若存在）。Wang等人(2017)已证明此类附加特征的有效性。下文将该基线称为"one-hot"。

Dhingra et al. (2016) presented a multi-layer architecture called GA Reader for text comprehension which achieves state of the art performance over several datasets. To further test whether our model can improve over this competitive baseline, we replace the bi-GRU at every layer of the GA Reader with our proposed MAGE-GRU.

Dhingra等人(2016)提出了一种名为GA Reader的多层架构用于文本理解，该架构在多个数据集上实现了最先进的性能。为了进一步测试我们的模型是否能超越这一强劲基线，我们用提出的MAGE-GRU替换了GA Reader每一层的双向GRU。

4.2. Performance Comparison

4.2. 性能对比

Story Based QA: Our first benchmark is the bAbi dataset from Weston et al. (2015), a set of 20 toy tasks aimed at measuring the ability of agents to reason about natural language. In each task the agent is presented with a simple story about entities in operating in an environment, followed by a question about the final state of that environment. Different tasks measure different reasoning abilities on the part of the agent, including chaining facts, counting, deduction, induction and others. An example2 is shown in Figure 3. The official release of the dataset3 comes with two versions, we focus on the more difficult 1K split in this work. Following Seo et al. (2017b), we ran 10 random initi aliz at ions of the model and report the test set performance for the model with the best validation set performance.

基于故事的问答：我们的首个基准测试是Weston等人(2015)提出的bAbi数据集，该数据集包含20个玩具任务，旨在评估智能体对自然语言的推理能力。每个任务中，智能体会接收