Piece of Table: A Divide-and-Conquer Approach for Selecting Sub-Tables in Table Question Answering

Abstract

Applying language models (LMs) to tables is challenging due to the inherent structural differences between twodimensional tables and one-dimensional text for which the LMs were originally designed. Furthermore, when applying linearized tables to LMs, the maximum token lengths often imposed in self-attention calculations make it difficult to comprehensively understand the context spread across large tables. To address these challenges, we present PieTa (Piece of Table), a new framework for sub-table-based question answering $^{\prime}Q A)$ . PieTa operates through an iterative process of dividing tables into smaller windows, using LMs to select relevant cells within each window, and merging these cells into a sub-table. This multi-resolution approach captures dependencies across multiple rows and columns while avoiding the limitations caused by long context inputs. Instantiated as a simple iterative sub-table union algorithm, PieTa demonstrates improved performance over previous sub-table-based QA approaches.

1. Introduction

Tables effectively mitigate data complexity by organizing information into curated rows and columns, making them more accessible and comprehensible than plain text. Consequently, various natural language processing (NLP) tasks, including table question answering (QA), have emerged to extract and interpret information from structured data [12, 14, 20].

However, applying (large) language models (LMs) to tables is challenging due to the inherent structural differences between tables and text. Text familiar to LMs is onedimensional and is read in a linear direction (e.g., in raster order), with contextual relationships confined within sentences. The meaning of a sentence can change significantly if the order of tokens is altered. In contrast, tables are inherently two-dimensional, requiring both horizontal and vertical reading. Often, there is no clear context between table cells as there is in text, and changing the order of columns or rows does not alter the meaning [6].

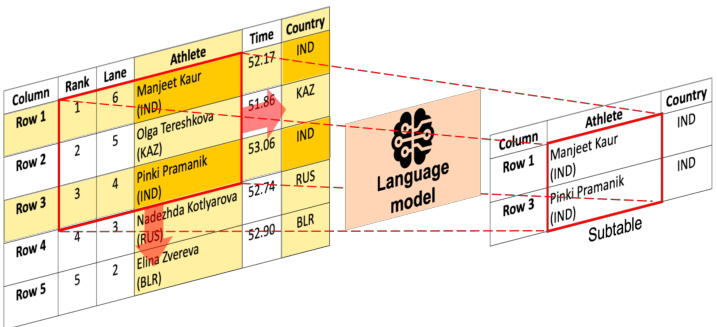
Question:Tell me the number of athletes from India. Figure 1. An overview of the proposed PieTa (Piece of Table) framework. Given an input table and a question, our algorithm synthesizes a sub-table for subsequent answering by iterative ly dividing the table into smaller windows, using language models to select relevant cells within these windows (thereby generating intermediate sub-tables), and merging these intermediate sub-tables. This process is repeated until the final sub-table is formed.

Recent advances in table QA have focused on accommodating these differences. For example, Jiang et al. [3], Liu et al. [9] employed table QA-specific pre-training objectives guided by auxiliary SQL queries. However, these methods are limited by the need for paired table-SQL training sets and struggle with large tables or those with many irrelevant entries [15]. Alternatively, Herzig et al. [2], Yang et al. [17], Yin et al. [19] explored positional embeddings applied to linearized tables. A major limitation of these holistic approaches is the computational constraint of transformerbased models, which typically restrict self-attention to 512 or 1,024 tokens, insufficient for handling large tables with thousands of rows (see Sec. 4).

To overcome the limitations of holistic approaches, other methods focus on pre-articulating relevant information from tables. These methods first use LMs to translate the given questions into logical formats suited for tabular data retrieval, such as SQL or Python scripts [1, 13]. Ideally, when wellgenerated, such code can retrieve relevant information effectively, enabling the subsequent QA process to bypass irrelevant distractions. However, generating flexible programs versatile enough to cover wide variations in table remains a significant challenge [10].

Sub-table selection methods aim to balance and mitigate the limitations of both holistic approaches and code generation methods. These methods first reduce the search space by extracting a relevant sub-table, which is then fed to a table QA reader to construct the final answer.

For example, Lin et al. [7]’s inner table retriever (ITR) selects rows and columns that align with the given question by calculating the similarity between the question and each individual row or column. This approach is computationally efficient and effective for answering simple questions. However, it can struggle to capture dependencies across multiple rows and/or columns. For instance, when answering the question Which was the next aircraft that came into service after Cessna 404 Titan?, ITR faces challenges because it must identify the aircraft that started the service after the Cessna 404 Titan without information on when it started the service.

Ye et al. [18]’s Dater algorithm attempts to address this limitation by employing LM in-context learning to jointly select multiple rows. While this approach offers improved performance over independent row selection, it inherits the limitation of one-dimensional LMs applied to two-dimensional tables, similar to the challenges encountered when using LMs to generate answers directly from linearized tables. Furthermore, LMs generally struggle to understand and combine long context inputs [8, 16], a challenge particularly pronounced in table QA involving large tables.

In this paper, we present PieTa (Piece of Table), a new framework for sub-table-based QA. PieTa operates through three main steps: In the Divide step, a given table is decomposed into smaller windows. In the subsequent Conquer step, an LM selects cells from each window that match the given question (Fig. 1), constructing intermediate sub-tables. Finally, in the Combination step, the extracted intermediate sub-tables from individual windows are merged to form a new table. This process is repeated, treating the resulting table as the new input, until the final sub-table is constructed.

PieTa captures and exploits dependencies across multiple rows or columns while avoiding the challenge of combining long context inputs. This is achieved through a multiresolution combination approach that enables the capture of long-term dependencies within the original table. Evaluated on the WikiSQL dataset [20], PieTa demonstrates significantly improved QA accuracy and sub-table selection performance.

2. Related work

Holistic table QA readers. In table QA, a reader, often implemented as a language model (LM), generates an answer for a given question based on a complete table or a preprocessed sub-table. The TAPEX reader, for instance, mimics an SQL execution engine by synthesizing answers from tables using SQL query pairs [9]. It employs the BART backbone model [5], initially trained on synthetic SQL queries and later fine-tuned to answer natural language questions.

Generating large-scale, high-quality pairs of tables and corresponding SQL queries to articulate clear answers for large tables can be costly. OmniTab simplified this by replacing sophisticated SQL queries with plain text descriptions [3]. It assumes each table has an accompanying textual description, which it retrieves and uses for pre-training before fine-tuning on table QA tasks.

These holistic approaches inherit the limitation of LMs when applied to large tables, as typically only a small subset of cells in the table is relevant to a given question [15]. Our approach efficiently selects relevant cells from the table, helping guide these readers to generate improved answers.

Guiding readers through subset selection. Filtering irrelevant and redundant information from a table per question can help LM readers avoid distraction. Sub-table selection methods achieve this by constructing a tailored sub-table for each question. Lin et al. [7] fine-tuned dense passage retriever encoders [4] to select relevant rows and columns, with their inner table retriever (ITR) using supervised contrastive loss by labeling rows and columns containing answer cells from the WikiSQL dataset as positive. Originally, this technique was designed to keep the input table size within the maximum token limit that an LM can handle, and therefore, it does not directly construct a minimum sub-table that balances precision and recall. While extending this technique to filter irrelevant information is feasible, it cannot capture dependencies across multiple rows or columns (Sec. 1). In contrast, our method can significantly reduce sub-table size while retaining relevant information, leading to improved QA performance.

Dater [18] employs LM in-context learning to synthesize a sub-table and sub-query pair from the given table and question. However, this approach requires extended prompts for the LM to fully comprehend the table structure and devise an effective selection strategy, which becomes a severe burden for large tables. Generally, the effectiveness of LMs can degrade when dealing with extremely long prompts [8, 16]. TabSQLify [11] selects a subset of rows (with full columns) as input to LMs to generate SQL queries for sub-table selection, leading to significantly improved table QA results. Similar to Dater, it relies on LM in-context learning, facing the same challenge of requiring extended prompts. Our approach mitigates this issue by preemptively breaking down large tables into smaller windows, allowing LMs to focus on extracting relevant cells within each window, thereby alleviating the burden of processing long prompts.

3. Divide-and-conquer sub-table selection

Table question answering (QA) aims to accurately interpret, analyze, and respond to natural language questions based on table. Formally, the task is to generate an answer $A$ given a table $T$ and a human-understandable question $Q$ . The answer $A$ can be a number, word, phrase, sentence, or other forms depending on the types of questions and tables. It is either extracted directly from $T$ or synthesized from the information within $T$ by the reader $\mathcal{R}$ .

In sub-table-based QA approaches, a selector $s$ first generates a sub-table $T_{s}$ from $T$ , which are then fed to the reader $\mathcal{R}$ to generate the final answer:

$$
A=\mathcal{R}(T_{s},Q),T_{s}=S(T,Q).
$$

For the selector $s$ , we fine-tune the output layer of Llama3 (Sec. 3.2). For the reader $\mathcal{R}$ , we employ OmniTab [3], which was originally fine-tuned on the WikiSQL dataset (Sec. 4).

Our study focuses on improving the selector $s$ , and therefore, we do not alter readers. However, in principle, joint tuning of $\mathcal{R}$ and $s$ is feasible.

3.1. Sub-table selection

Our sub-table selection algorithm iterative ly applies three main steps. In the Divide step, the input table $T$ is partitioned into small overlapping windows ${W_{i}}{i=1}^{N}$ of size $w\times w$ using a moving window approach (Algorithm 2). In the Conquer step, the selector $s$ extracts a sub-window $V{i}$ within each window $W_{i}$ based on the input question $Q$ as guided by a prompt instruction $\mathcal{P}$ (Sec. 3.2 and Fig. A.1):

$$
V_{i}={\cal S}({\mathcal{P}}(W_{i},Q)).
$$

The Combination step merges the generated sub-windows a{s t}hie= 1set union of all cells in the sub-windows ${V_{i}}{i=1}^{N}$ into a new table $T^{t}$ . Specifically, $T^{t}$ is obtained ${V{i}}_{i=1}^{N}$ These steps are repeated, taking $T^{t}$ as the new input $T$ for the Divide step in each iteration $t$ , until the generated table $T^{t}$ is no longer updated. The complete sub-table selection process is outlined in Algorithm 1.

3.2. Instruction tuning the selector

We construct the selector $s$ by fine-tuning the output layer of the Llama3-8B-Instruct model,* while in principle, our method is applicable to any LM selector that can understand tables with a small window size.

Algorithm 1 SUB TABLE SELECTION $(S)$ .

Data generation. The training data are generated by sampling input windows (of size $w\times w$ ) from the WikiSQL training set of tables and questions, and creating the corresponding target sub-windows. Unlike previous approaches [18], which only predict the column and the row indices of the target, our selector additionally predicts the corresponding cell values. Providing such explicit guides leads to improved performance (see Sec. 4.3).

We refer to the columns with cells matching the conditions specified in the question as condition columns. Each cell in a condition column may or may not satisfy the corresponding condition. Similarly, the column containing the exact cell values that the question seeks is referred to as the answer column. For example, for the question presented in Fig. 2, Horwood, Total, and Result are the condition columns, while Goodman is an answer column.

For each training window $W_{i}$ sampled from a table $T$ with a corresponding question $Q$ , the target sub-window $V_{i}$ is constructed by first selecting all condition and answer columns within $W_{i}$ . Then, for these selected columns, only the rows that satisfy all the conditions present in $W_{i}$ are further selected.

Figure 2 illustrates the resulting training data generation process. The first window $W_{1}$ contains two condition columns, Total and Result. The target sub-window $V_{1}$ is then generated from the cells in these columns that jointly satisfy the conditions safe and total score of 31. The second window $W_{2}$ includes a condition column Horwood and an answer column Goodman. The target $V_{2}$ is created from the subset of these columns in $W_{2}$ that satisfy the condition 7 from Horwood. Since no such cells actually exist, $V_{2}$ is constructed as an empty table containing only the column header information. The third window $W_{3}$ contains only an answer column; since there is no condition imposed, all cells from this column are included in $V_{3}$ . This target window generation strategy allows the selector $s$ to focus solely on the input windows $W$ when making predictions. See Sec. 3.3

Question: What score did Goodman give to all songs with safe results , which received a 7 from Horwood and have a total score of 31 ?

for details.

Sampling training windows. A straightforward approach to generate the training data (pairs of input $W_{i}$ and the corresponding target $V_{i}$ sub-windows) for fine-tuning the selector $s$ is to randomly sample from the given input tables $T$ and the corresponding questions $Q$ . However, we observed in preliminary experiments that such naive sampling leads $s$ to generate meaningless single-column target tables. This can be attributed to the resulting imbalance in the target window sizes: For a given input window $W$ of size $w\times w$ there can be $w(w+1)+1$ different sizes of the underlying target window (including the window of size zero): ${0\times0,1\times1,\ldots,1\times w,\ldots,w\times1,\ldots,w\times w}$ . $1\times0$ $2\times0,\ldots$ , and $w\times0$ are excluded because the table cannot be made without the column. Among them, cases where only one column is selected as the target predominate (Fig. A.2), while cases where the entire input window $W$ becomes the target are rare: This would require all columns in $W$ correspond to either the condition or answer columns, and all cells therein satisfy the question presented in the question. Therefore, we explicitly balance the target window size distribution when sampling the training set. Details of this process and the corresponding examples are presented in Appendix A.3.

3.3. Discussion

The crux of our approach lies in the multi-resolution al table formation technique, which builds upon table (sub-)windows. In images, neighboring pixels often exhibit strong correlations, justifying the use of small windows e.g. convolutional kernels in convolutional neural networks (CNNs) and attention windows in vision transformers. However, tables do not necessarily have such a spatial structure: For example, in the table in Fig. 3, the neighboring cells 1995-1997 and 1998-2001 are more similar within the Years produced column. Conversely, the cells in the Model 725tds row do not have such a relationship (e.g., 1995-2001 is not more strongly related to M51D25 turbocharged I6 than Diesel). In this context, employing sub-windows might initially seem to introduce unnecessary restrictions.

Figure 2. An example of generated training data. The table $T$ and the question $Q$ are sourced from WikiSQL train dataset [20]. Three conditions and the corresponding cell values are color-coded. The four example input windows ${W_{i}}{i=1}^{4}$ , arranged in raster order, are highlighted with orange boxes, and the corresponding training targets ${V{i}}_{i=1}^{4}$ are displayed on the right. Table 1. Performance of two table QA readers (measured in exact match $%$ ) across three different sub-table types in the WikiSQL dataset. The union table we aim for is not only easier to attain compared to the gold table, but its performance is also on par with that of the gold table.

We demonstrate that the set union-based sub-window combination approach can effectively overcome such potential restrictions while ensuring focused answer generation by constructing moderately-sized final sub-tables. Suppose that the following question is presented for the table in Fig. 3: List each of models with diesel fuel produced from 1988-2001. An ideal sub-table for QA in this case would be the intersection of cells satisfying the conditions diesel fuel and 1998-2001, along with their corresponding cell values in the Engine column (see the table at the bottom of the right column in Fig. 3).

Directly identifying such a gold table would require a comprehensive understanding of the entire table. Instead, our algorithm iterative ly merges sub-window found within each window. For example, by taking the cells that have Diesel or the cells that match 1998-2001 and merging them as a sub-table, our algorithm effectively takes a union of them (the table in the upper right column of Fig. 3).

This union approach offers significant advantages: First, identifying a relevant sub-window within a window is much easier than pinpointing the gold table (which effectively acts as intersection of conditions across the entire table), as the

Original table

Question: List each of the models with diesel fuel produced from 1998-2001 . Target: M57D30 turbocharged I6, M67D40 turbocharged V8

Output: M57D30 turbocharged I6, M67D40 turbocharged V8 ❌ Output: 730d, 750d Output: M57D30 turbocharged I6, M67D40 turbocharged V8

Union table Gold table

Figure 3. Examples of (sub-)tables and the corresponding QA results. The original table has two condition columns (Fuel and Years produced) and one answer column Engine, which respectively match the conditions and expected outcomes presented in the question. Two conditions and the corresponding cell values are color-coded. The union table consists of rows satisfying at least one condition, while the underlying gold table consists of rows satisfying all conditions. Estimating the gold table is challenging as it requires a comprehensive understanding of the entire input table. The answers below the respective tables are the corresponding outputs of the OmniTab reader. Feeding the original complete table leads to incorrect results, while both the gold and union table produce correct answers.

selection module (LMs) can focus exclusively on the cells within the window. Our training target generation process aligns with this objective: Each target sub-window is constructed based only on the conditions and outputs present within the corresponding input window. Furthermore, we empirically validated that the size of the resulting union sub-tables, while larger than the underlying gold tables, is substantially smaller than the original complete tables, facilitating subsequent answer generation steps. In our experiments, the number of cells in the union table decreased to an average of $13.91%$ compared to the original table. Combining these strengthens, our union approach offers comparable performance to using the underlying gold table. Table 1 shows an example of building sub-tables, demonstrating significant improvements in final table QA performance.

4. Experiments

4.1. Experimental settings

We evaluate the performance of our table QA algorithm using the WikiSQL dataset [20]. WikiSQL comprises tables extracted from Wikipedia, spanning a variety of domains. The dataset includes questions requring aggregation, c