Improving Machine Reading Comprehension with Single-choice Decision and Transfer Learning

通过单项选择决策和迁移学习提升机器阅读理解能力

Abstract

摘要

Multi-choice Machine Reading Comprehension (MMRC) aims to select the correct answer from a set of options based on a given passage and question. Due to task specific of MMRC, it is non-trivial to transfer knowledge from other MRC tasks such as SQuAD, Dream. In this paper, we simply reconstruct multi-choice to single-choice by training a binary classification to distinguish whether a certain answer is correct. Then select the option with the highest confidence score. We construct our model upon ALBERT-xxlarge model and estimate it on the RACE dataset. During training, We adopt AutoML strategy to tune better parameters. Experimental results show that the single-choice is better than multi-choice. In addition, by transferring knowledge from other kinds of MRC tasks, our model achieves a new state-of-the-art results in both single and ensemble settings.

多项选择机器阅读理解 (Multi-choice Machine Reading Comprehension, MMRC) 旨在根据给定文章和问题从一组选项中选择正确答案。由于 MMRC 的任务特殊性，从 SQuAD、Dream 等其他机器阅读理解任务迁移知识并非易事。本文通过训练一个二元分类器来区分某个答案是否正确，从而将多项选择重构为单项选择，然后选择置信度分数最高的选项。我们在 ALBERT-xxlarge 模型基础上构建模型，并在 RACE 数据集上进行评估。训练过程中，我们采用 AutoML 策略调整更优参数。实验结果表明，单项选择优于多项选择。此外，通过从其他类型的机器阅读理解任务迁移知识，我们的模型在单模型和集成设置下均取得了新的最先进结果。

1 Introduction

1 引言

The last several years have seen a land rush in research on machine reading (MRC) comprehension and various dataset have been proposed such as SQuAD1.1, SQuAD2.0, NewsQA and CoQA (Rajpurkar et al., 2016; Trischler et al., 2016; Reddy et al., 2019). Different from the above which are extractive MRC, RACE is a multi-choice MRC dataset (MMRC) proposed by (Lai et al., 2017). RACE was extracted from middle and high school English examinations in China. Figure 1 shows an example passage and two related questions from RACE. The key difference between RACE and previously released machine comprehension datasets is that the answers in RACE often cannot be directly extracted from the passages, as illustrated by the two example questions (Q1 & Q2)

过去几年见证了机器阅读理解(MRC)研究的热潮，各类数据集如SQuAD1.1、SQuAD2.0、NewsQA和CoQA相继提出 (Rajpurkar et al., 2016; Trischler et al., 2016; Reddy et al., 2019)。不同于上述抽取式MRC数据集，RACE是由(Lai et al., 2017)提出的多项选择MRC数据集(MMRC)，其内容选自中国初高中英语考试试题。图1展示了RACE中的一篇示例文章及两个相关问题。RACE与先前发布的机器阅读理解数据集的关键区别在于，其答案往往无法直接从文章中抽取，如示例问题(Q1和Q2)所示。

Passage: For the past two years, 8-year-old Harli Jordean from Stoke Newington, London, has been selling marbles . His successful marble company, Marble King, sells all things marble-related - from affordable tubs of the glass playthings to significantly expensive items like Duke of York solitaire tables - sourced, purchased and processed by the mini-CEO himself. ”I like having my own company. I like being the boss,” Harli told the Mirror....Tina told The Daily Mail. ”At the moment he is annoying me by creating his own Marble King marbles - so that could well be the next step for him.”

过去两年，伦敦斯托克纽因顿的8岁男孩Harli Jordean一直在销售弹珠。他创立的弹珠公司Marble King经营各类弹珠产品——从价格亲民的玻璃弹珠桶，到约克公爵弹珠台等高端商品——这些都由这位小CEO亲自采购、加工。Harli向《镜报》表示："我喜欢拥有自己的公司，喜欢当老板"...Tina告诉《每日邮报》："他现在正忙着自制Marble King品牌弹珠，这很可能是他的下一步计划。"

Q1: Harli’s Marble Company became popular as soon as he launched it because .

Q1: Harli的弹珠公司一经推出就大受欢迎，原因是。

A: it was run by ”the world’s youngest CEO” B: it filled the gap of online marble trade C: Harli was fascinated with marble collection D: Harli met the growing demand of the customers

A: 它由"世界上最年轻的CEO"运营
B: 它填补了在线大理石交易的空白
C: Harli 对大理石收藏着迷
D: Harli 满足了客户日益增长的需求

Q2: How many mass media are mentioned in the passage?

Q2: 文中提到了多少种大众媒体？

A: One B: Two C: Three D: Four

A: 一 B: 二 C: 三 D: 四

Table 1: An example passage and two related multichoice questions. The ground-truth answers are in bold.

表 1: 示例段落及两道相关选择题。正确答案以粗体显示。

in Table 1. Thus, answering these questions needs inferences.

表1: 因此，回答这些问题需要进行推理。

Recently, pretrained language models (LM) such as BERT (Devlin et al., 2018), RoBERTa (Liu et al., 2019), ALBERT (Lan et al., 2019) have achieved great success on MMRC tasks. Notably, Megatron-LM (Shoeybi et al., 2019) which is a 48 layer BERT with 3.9 billion parameters yields the highest score on the RACE leader board in both single and ensemble settings. The key point to model MMRC is: first encode the context, question, options with BERT like LM, then add a matching network on top of BERT to score the options. Generally, the matching network can be various (Ran et al., 2019; Zhang et al., 2020; Zhu et al., 2020). Ran et al. (2019) proposes an option comparison network (OCN) to compare options at word-level to better identify their correlations to help reasoning. Zhang et al. (2020) proposes a dual co-matching network (DCMN) which models the relationship among passage, question and answer options bidirectional ly. All these matching networks show promising improvements com- pared with pretrained language models. One point they have in common is that the answer together with the distract or s are jointly considered which we name multi-choice models. We argue that the options can be concerned separately for two reasons, 1) when human works on MMRC problem, they always consider the options one by one and select the one with the highest confidence. 2) MMRC suffers from the data scarcity problem. Multi-choice models are inconvenient to take advantage of other MRC dataset.

近年来，预训练语言模型（LM）如BERT (Devlin et al., 2018)、RoBERTa (Liu et al., 2019)、ALBERT (Lan et al., 2019)在多项阅读理解（MMRC）任务中取得了显著成功。值得注意的是，拥有48层结构和39亿参数的Megatron-LM (Shoeybi et al., 2019)在RACE排行榜的单模型和集成模型设置中均获得最高分。建模MMRC的关键在于：首先使用BERT类语言模型编码上下文、问题和选项，然后在BERT顶部添加匹配网络对选项进行评分。通常，匹配网络可以有多种形式 (Ran et al., 2019; Zhang et al., 2020; Zhu et al., 2020)。Ran等人 (2019)提出选项比较网络（OCN），通过词级比较选项以更好识别其相关性来辅助推理。Zhang等人 (2020)提出双向共匹配网络（DCMN），双向建模文章、问题与选项之间的关系。相比预训练语言模型，这些匹配网络均显示出显著改进。它们的共同点是联合考虑正确答案与干扰项，我们称之为多选模型。我们认为选项可以单独考虑基于两点：1) 人类处理MMRC问题时总是逐个评估选项并选择置信度最高的；2) MMRC存在数据稀缺问题，多选模型难以利用其他MRC数据集。

In this paper, we propose a single-choice model for MMRC. Our model considers the options separately. The key component of our method is a binary classification network on top of pretrained language models. For each option of a given context and question, we calculate a confidence score. Then we select the one with the highest score as the final answer. In both training and decoding, the right answer and the distractors are modeled independently. Our proposed method gets rid of the multi-choice framework, and can leverage amount of other resources. Taking SQuAD as an example, we can take a context, one of its question and the corresponding answer as a positive instance for our classification with golden label 1. In this way many QA dataset can be used to enhance RACE. Experimental results show that single-choice model performs better than multi-choice models, in addition by transferring knowledge from other QA dataset, our single model achieves $90.7%$ and ensemble model achieves $91.4%$ , both are the best score on the leader board.

本文提出了一种用于MMRC的单选项模型。我们的模型对选项进行独立考量，其核心是在预训练语言模型基础上构建的二分类网络。针对给定上下文和问题的每个选项，我们会计算置信度分数，最终选择得分最高的选项作为答案。在训练和解码过程中，正确答案与干扰项均被独立建模。该方法摆脱了多选项框架限制，并能充分利用其他资源：以SQuAD为例，我们可以将上下文、问题及其对应答案作为正样本（标注为1）用于分类训练。通过这种方式，众多QA数据集都能用于增强RACE。实验结果表明，单选项模型性能优于多选项模型，此外通过迁移其他QA数据集的知识，我们的单模型达到$90.7%$，集成模型达到$91.4%$，两者均位列排行榜首位。

2 Task Description

2 任务描述

Multi-choice MRC (MMRC) can be represented as a triple $<P,Q,A>$ , where $P=s_{1},s_{2},...,s_{m}$ is an article consist of multiple sentences $s,~Q$ is a question asked upon the article and $\textit{A}=$ ${A_{1},...A_{n}}$ is a set of candidate answers. Only one answer in $A$ is correct and others are distractors. The purpose of the MMRC is to select the right one. RACE is one kind of MMRC task, which is created by domain experts to test students’ reading comprehension skills, consequently requiring non-trivial reasoning techniques. Each article in RACE has several questions and the questions always have 4 candidate answers, one answer and three distract or s.

多项选择阅读理解 (MMRC) 可以表示为一个三元组 $<P,Q,A>$，其中 $P=s_{1},s_{2},...,s_{m} $ 是由多个句子 $s$ 组成的文章，$Q$ 是基于文章提出的问题，$\textit{A}=$ ${A_{1},...A_{n}}$ 是一组候选答案。$A$ 中只有一个正确答案，其余为干扰项。MMRC 的目标是选出正确答案。RACE 是一种 MMRC 任务，由领域专家设计用于测试学生的阅读理解能力，因此需要非平凡的推理技巧。RACE 中的每篇文章包含若干问题，每个问题始终有 4 个候选答案（1 个正确答案和 3 个干扰项）。

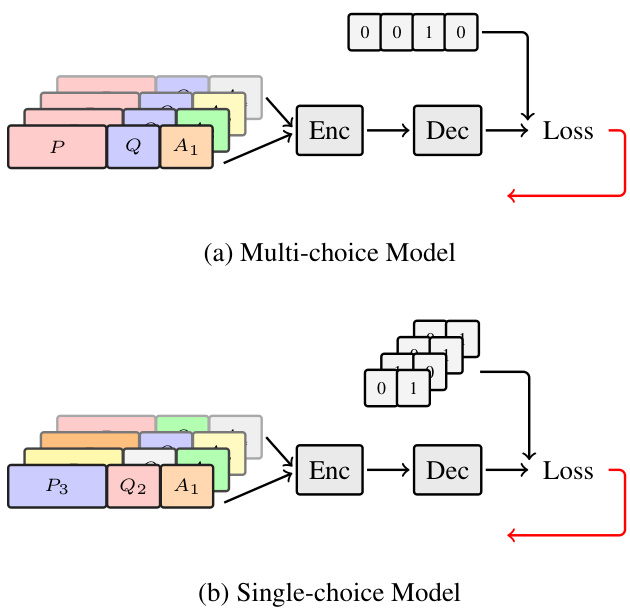
Figure 1: An overview of Standard Model and Singlechoice Model.

图 1: 标准模型与单项选择模型概览。

3 Methods

3 方法

Previous works have verified the effectiveness of Pretrained language models such as BERT, XLNet,Roberta and Albert in Multi-choice MRC tasks. Pretrained language models are used as encoder to get the global context representation. After that, a decoder is employed to find the correct answer given all the information contained in the global representation. Let $P,Q$ , and ${A_{1},...A_{n}}$ denote the passage, question and option set separately. The input of Pretrained encoder is defined as $\left(P\oplus Q\oplus A_{i}\right)$ , the concatenation of $P$ , $Q$ and $A_{i}$ one of the option in candidate set. Moreover, for the same question, the inputs with different options are concatenated together as a complete training sample, which is more intuitive and similar to human that select the correct answer compared with other options. After encoding all the inputs for a single question, the contextual represent at ions $T={T_{C L S1},...,T_{C L S n}}$ is used to classify which is the correct answer given passage and question(see Figure2(a)). An single full connection layer is added to compute the probability $p({A_{1},...A_{n}}|P,Q)$ for all the answers and the ground truth $y$ is the index of correct answer in candidates. $T\in\mathbb{R}^{n\times h}$ , $n$ denotes the number of the options in candidate set. We define the score to be:

先前的研究已验证了BERT、XLNet、Roberta和Albert等预训练语言模型(pretrained language models)在多选题阅读理解(Multi-choice MRC)任务中的有效性。预训练语言模型作为编码器获取全局上下文表征，随后通过解码器基于全局表征信息找出正确答案。设$P,Q$和${A_{1},...A_{n}}$分别表示文章、问题和选项集合，预训练编码器的输入定义为$\left(P\oplus Q\oplus A_{i}\right)$，即文章$P$、问题$Q$与候选选项$A_{i}$的拼接。对于同一问题，不同选项的输入会拼接为完整训练样本，这种设计更符合人类对比选项选出正确答案的认知方式。编码单个问题的所有输入后，上下文表征$T={T_{C L S1},...,T_{C L S n}}$用于结合文章和问题分类正确选项(见图2(a))。通过单层全连接网络计算所有答案的概率$p({A_{1},...A_{n}}|P,Q)$，真实标签$y$为正确选项在候选集中的索引。其中$T\in\mathbb{R}^{n\times h}$，$n$表示候选选项数量。我们定义得分函数为：

$$
p({A_{1},...A_{n}}|P,Q)=\sigma(W T+b)
$$

$$
p({A_{1},...A_{n}}|P,Q)=\sigma(W T+b)
$$

where $W\in\mathbb{R}^{h\times1}$ is the weight and $b$ is the bias. Parameter matrices are finetuned based on pretrained language model with the cross entropy loss function which is formulated as:

其中 $W\in\mathbb{R}^{h\times1}$ 是权重，$b$ 是偏置。参数矩阵基于预训练语言模型使用交叉熵损失函数进行微调，该函数公式为：

$$
\mathrm{\Delta}\log\mathrm{\Delta}=\mathrm{\Delta}-\sum{y\log(p)}
$$

$$
\mathrm{\Delta}\log\mathrm{\Delta}=\mathrm{\Delta}-\sum{y\log(p)}
$$

3.1 Single-choice Model

3.1 单选题模型

As all input sequences with the same passage and question are tied together, each training sample contain much duplicate content. For example, the passage with multiple sentences repeat $n$ times in a single training sample which may degrade the diversity in each training step. Moreover, this method need to fix the data format that each question must have the same number of options which is also inconvenient to take advantage of other MRC datasets.

由于所有具有相同段落和问题的输入序列都被绑定在一起，每个训练样本包含大量重复内容。例如，包含多个句子的段落会在单个训练样本中重复 $n$ 次，这可能降低每个训练步骤的多样性。此外，这种方法需要固定数据格式，要求每个问题必须具有相同数量的选项，这也不利于利用其他机器阅读理解（MRC）数据集。

Alternatively, we reconstruct the multi-choice to single-choice. We just need to distinguish whether the answer is correct without considering other options in the candidate set. By this way, we keep the diversity in training batches and relax the constraints on multi-choice framework.

或者，我们将多选题重构为单选题。只需判断答案是否正确，而无需考虑候选集中的其他选项。这种方法保持了训练批次的多样性，同时放宽了对多选题框架的限制。

Instead of concatenate all inputs with the same question together, we just encode a single input and use its contextual representations $T_{C L S i}$ to classify whether the answer is correct (see Figure2(b)). The ground truth is $y\in{0,1}$ , Thus we re-define the score $g(P,Q,A_{i})$ as:

我们没有将所有相同问题的输入拼接在一起，而是仅编码单个输入，并利用其上下文表示 $T_{CLSi}$ 来判断答案是否正确（见图2(b)）。真实标签为 $y\in{0,1}$，因此我们将得分 $g(P,Q,A_{i})$ 重新定义为：

$$
g(P,Q,A_{i})=\sigma(W T_{C L S i}+b)
$$

$$
g(P,Q,A_{i})=\sigma(W T_{C L S i}+b)
$$

where $W\in\mathbb{R}^{h\times l a b e l}$ . Correspondingly, the cross entropy loss function can be re-formulated as:

其中 $W\in\mathbb{R}^{h\times l a b e l}$ 。相应地，交叉熵损失函数可重新表述为：

$$
\begin{array}{r c l}{{\mathrm{loss}}}&{{=}}&{{\displaystyle-\sum y\log(g(P,Q,A_{i}))}}\ {{}}&{{+}}&{{\displaystyle(1-y)\log(1-g(P,Q,A_{i}))}}\end{array}
$$

$$
\begin{array}{r c l}{{\mathrm{loss}}}&{{=}}&{{\displaystyle-\sum y\log(g(P,Q,A_{i}))}}\ {{}}&{{+}}&{{\displaystyle(1-y)\log(1-g(P,Q,A_{i}))}}\end{array}
$$

In the end, to get the correct answers, we select the top-n answers with respect to score. Here $n$ denotes the number of correct answers. E.g., $n{=}1$ in RACE.

最终，为了得到正确答案，我们根据分数选择前n个答案。这里$n$表示正确答案的数量。例如，在RACE中$n{=}1$。

Figure 2: Overview of our AutoML architecture.

图 2: 我们的 AutoML 架构概览。

3.2 Transfer Learning

3.2 迁移学习

In this section, We propose a simple yet effective strategy to transfer knowledge from other QA dataset. As the single-choice model relax the constraints on multi-choice framework, more QA datasets such as SQuAD2.0, ARC, CoQA and DREAM can be used to enhance RACE. It consists of three steps:

在本节中，我们提出了一种简单而有效的策略，用于从其他问答数据集迁移知识。由于单选题模型放宽了对多选题框架的限制，更多问答数据集（如 SQuAD2.0、ARC、CoQA 和 DREAM）可用于增强 RACE。该策略包含三个步骤：

(1) we preprocess data with different formats to the same input type as mentioned in section 3. For multiple-choice MRC datasets, like DREAM and ARC, we concatenate each option with corresponding context and question. And for extractive MRC datasets like SQuAD2.0 and CoQA, we take the context (passage or dialog), one of its question and corresponding answer as a positive instance for the binary classification.

(1) 我们将不同格式的数据预处理为第3节提到的统一输入类型。对于选择题型MRC数据集(如DREAM和ARC)，我们将每个选项与对应上下文和问题拼接。对于抽取型MRC数据集(如SQuAD2.0和CoQA)，我们取上下文(段落或对话)、其中一个问题及其对应答案作为二分类的正样本。

(2) We collect and corrupt the pre processed data from different QA datasets and then train the binary classification on this mixed data. We find that the model benefits a lot from the large amount of MRC datasets.

(2) 我们从不同问答(QA)数据集中收集并破坏预处理后的数据，然后基于这些混合数据训练二元分类模型。研究发现模型能从大量机器阅读理解(MRC)数据集中显著