MASS-EDITING MEMORY IN A TRANSFORMER
在Transformer中批量编辑记忆
Kevin Meng1,2 Arnab Sen Sharma2 Alex Andonian1 Yonatan Belinkov† 3 David Bau2 1MIT CSAIL 2 Northeastern University 3Technion – IIT
Kevin Meng1,2 Arnab Sen Sharma2 Alex Andonian1 Yonatan Belinkov† 3 David Bau2 1MIT CSAIL 2东北大学 3以色列理工学院
ABSTRACT
摘要
Recent work has shown exciting promise in updating large language models with new memories, so as to replace obsolete information or add specialized knowledge. However, this line of work is predominantly limited to updating single associations. We develop MEMIT, a method for directly updating a language model with many memories, demonstrating experimentally that it can scale up to thousands of associations for GPT-J (6B) and GPT-NeoX (20B), exceeding prior work by orders of magnitude. Our code and data are at memit.baulab.info.
近期研究在更新大语言模型记忆方面展现出令人振奋的潜力,旨在替换过时信息或添加专业知识。然而这类工作目前主要局限于更新单一关联。我们开发了MEMIT方法,可直接为语言模型批量更新记忆,实验证明该方法能在GPT-J (6B)和GPT-NeoX (20B)模型上实现数千条关联的更新,规模超越前人工作数个量级。代码与数据详见memit.baulab.info。
1 INTRODUCTION
1 引言
How many memories can we add to a deep network by directly editing its weights?
通过直接编辑权重,我们能为深度网络增添多少记忆?
Although large auto regressive language models (Radford et al., 2019; Brown et al., 2020; Wang & Komatsu zak i, 2021; Black et al., 2022) are capable of recalling an impressive array of common facts such as “Tim Cook is the CEO of Apple” or “Polaris is in the constellation Ursa Minor” (Petroni et al., 2020; Brown et al., 2020), even very large models are known to lack more specialized knowledge, and they may recall obsolete information if not updated periodically (Lazaridou et al., 2021; Agarwal & Nenkova, 2022; Liska et al., 2022). The ability to maintain fresh and customizable information is desirable in many application domains, such as question answering, knowledge search, and content generation. For example, we might want to keep search models updated with breaking news and recently-generated user feedback. In other situations, authors or companies may wish to customize models with specific knowledge about their creative work or products. Because re-training a large model can be prohibitive (Patterson et al., 2021) we seek methods that can update knowledge directly.
虽然大型自回归语言模型 (Radford et al., 2019; Brown et al., 2020; Wang & Komatsuzaki, 2021; Black et al., 2022) 能够回忆大量常见事实,例如"Tim Cook是苹果公司CEO"或"北极星位于小熊座" (Petroni et al., 2020; Brown et al., 2020),但即使是超大规模模型也已知缺乏更专业的知识,且若未定期更新可能会回忆过时信息 (Lazaridou et al., 2021; Agarwal & Nenkova, 2022; Liska et al., 2022)。保持信息新鲜度和可定制性的能力在问答系统、知识搜索和内容生成等众多应用领域都至关重要。例如,我们可能希望让搜索模型持续更新突发新闻和最新用户反馈。在其他场景中,作者或企业可能希望用特定创作或产品知识来定制模型。由于重新训练大模型成本过高 (Patterson et al., 2021),我们寻求能够直接更新知识的方法。
To that end, several knowledge-editing methods have been proposed to insert new memories directly into specific model parameters. The approaches include constrained fine-tuning (Zhu et al., 2020), hyper network knowledge editing (De Cao et al., 2021; Hase et al., 2021; Mitchell et al., 2021; 2022), and rank-one model editing (Meng et al., 2022). However, this body of work is typically limited to updating at most a few dozen facts; a recent study evaluates on a maximum of 75 (Mitchell et al., 2022) whereas others primarily focus on single-edit cases. In practical settings, we may wish to update a model with hundreds or thousands of facts simultaneously, but a naive sequential application of current state-of-the-art knowledge-editing methods fails to scale up (Section 5.2).
为此,研究者们提出了多种知识编辑方法,用于将新记忆直接植入特定模型参数。这些方法包括约束微调 (Zhu et al., 2020) 、超网络知识编辑 (De Cao et al., 2021; Hase et al., 2021; Mitchell et al., 2021; 2022) 以及秩一模型编辑 (Meng et al., 2022) 。然而,这类工作通常仅限于更新最多几十条事实:近期研究最多评估了75条 (Mitchell et al., 2022) ,而其他研究主要关注单次编辑场景。在实际应用中,我们可能希望同时更新模型数百或数千条事实,但简单地顺序应用当前最先进的知识编辑方法无法实现规模化扩展 (第5.2节) 。
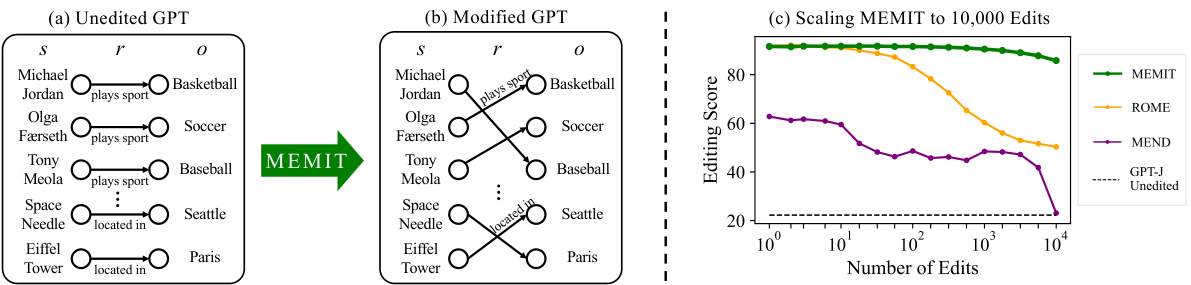
Figure 1: MEMIT is capable of updating thousands of memories at once. (a) Language models can be viewed as knowledge bases containing memorized tuples $(s,r,o)$ , each connecting some subject $s$ to an object $o$ via a relation $r$ , e.g., ( $s=$ Michael Jordan, $r=$ plays sport, $o=$ basketball). (b) MEMIT modifies transformer weights to edit memories, e.g., “Michael Jordan now plays the sport baseball,” while (c) maintaining generalization, specificity, and fluency at scales beyond other methods. As Section 5.2.2 details, editing score is the harmonic mean of efficacy, generalization, and specificity metrics.
图 1: MEMIT能够一次性更新数千条记忆。(a) 语言模型可视为包含记忆元组$(s,r,o)$的知识库,每个元组通过关系$r$将主体$s$与客体$o$关联,例如($s=$Michael Jordan,$r=$plays sport,$o=$basketball)。(b) MEMIT通过修改Transformer权重来编辑记忆,例如"Michael Jordan now plays the sport baseball",同时(c)在规模上保持泛化性、特异性和流畅性优于其他方法。如第5.2.2节所述,编辑分数是效力、泛化性和特异性指标的调和平均值。
We propose MEMIT, a scalable multi-layer update algorithm that uses explicitly calculated parameter updates to insert new memories. Inspired by the ROME direct editing method (Meng et al., 2022), MEMIT targets the weights of transformer modules that we determine to be causal mediators of factual knowledge recall. Experiments on GPT-J (6B parameters; Wang & Komatsu zak i 2021) and GPT-NeoX (20B; Black et al. 2022) demonstrate that MEMIT can scale and successfully store thousands of memories in bulk. We analyze model behavior when inserting true facts, counter factual s, 27 specific relations, and different mixed sets of memories. In each setting, we measure robustness in terms of generalization, specificity, and fluency while comparing the scaling of MEMIT to rank-one, hyper network, and fine-tuning baselines.
我们提出MEMIT,这是一种可扩展的多层更新算法,通过显式计算参数更新来插入新记忆。受ROME直接编辑方法(Meng等,2022)的启发,MEMIT针对Transformer模块中我们确定为事实知识回忆因果介质的权重进行修改。在GPT-J(60亿参数;Wang & Komatsuzaki 2021)和GPT-NeoX(200亿;Black等 2022)上的实验表明,MEMIT能够扩展并成功批量存储数千条记忆。我们分析了插入真实事实、反事实、27种特定关系以及不同混合记忆集时的模型行为。在每种设置中,我们从泛化性、特异性和流畅性三个维度测量鲁棒性,同时将MEMIT与秩一法、超网络和微调基线进行扩展性对比。
2 RELATED WORK
2 相关工作
Scalable knowledge bases. The representation of world knowledge is a core problem in artificial intelligence (Richens, 1956; Minsky, 1974), classically tackled by constructing knowledge bases of real-world concepts. Pioneering hand-curated efforts (Lenat, 1995; Miller, 1995) have been followed by web-powered knowledge graphs (Auer et al., 2007; Bollacker et al., 2007; Suchanek et al., 2007; Havasi et al., 2007; Carlson et al., 2010; Dong et al., 2014; Vrandecic & Krotzsch, 2014; Bosselut et al., 2019) that extract knowledge from large-scale sources. Structured knowledge bases can be precisely queried, measured, and updated (Davis et al., 1993), but they are limited by sparse coverage of uncatalogued knowledge, such as commonsense facts (Weikum, 2021).
可扩展知识库。世界知识的表示是人工智能领域的核心问题 (Richens, 1956; Minsky, 1974),传统方法通过构建现实世界概念的知识库来解决。继早期人工编纂的知识库 (Lenat, 1995; Miller, 1995) 之后,出现了基于网络的知识图谱 (Auer et al., 2007; Bollacker et al., 2007; Suchanek et al., 2007; Havasi et al., 2007; Carlson et al., 2010; Dong et al., 2014; Vrandecic & Krotzsch, 2014; Bosselut et al., 2019),这些知识图谱从大规模数据源中提取知识。结构化知识库可以进行精确查询、度量和更新 (Davis et al., 1993),但其局限性在于对未编目知识(如常识性事实)的覆盖不足 (Weikum, 2021)。
Language models as knowledge bases. Since LLMs can answer natural-language queries about real-world facts, it has been proposed that they could be used directly as knowledge bases (Petroni et al., 2019; Roberts et al., 2020; Jiang et al., 2020; Shin et al., 2020). However, LLM knowledge is only implicit; responses are sensitive to specific phrasings of the prompt (Elazar et al., 2021; Petroni et al., 2020), and it remains difficult to catalog, add, or update knowledge (AlKhamissi et al., 2022). Nevertheless, LLMs are promising because they scale well and are un constrained by a fixed schema (Safavi & Koutra, 2021). In this paper, we take on the update problem, asking how the implicit knowledge encoded within model parameters can be mass-edited.
语言模型作为知识库。由于大语言模型能够回答关于现实世界事实的自然语言查询,有人提出可以直接将其用作知识库 (Petroni et al., 2019; Roberts et al., 2020; Jiang et al., 2020; Shin et al., 2020)。然而,大语言模型的知识仅具有隐式特性:其响应易受提示词具体表述的影响 (Elazar et al., 2021; Petroni et al., 2020),且知识的编目、添加或更新仍存在困难 (AlKhamissi et al., 2022)。尽管如此,大语言模型仍具潜力,因其具备良好的扩展性且不受固定模式约束 (Safavi & Koutra, 2021)。本文聚焦知识更新问题,探讨如何对编码在模型参数中的隐式知识进行批量编辑。
Hyper network knowledge editors. Several meta-learning methods have been proposed to edit knowledge in a model. Sinitsin et al. (2019) proposes a training objective to produce models amenable to editing by gradient descent. De Cao et al. (2021) proposes a Knowledge Editor (KE) hyper network that edits a standard model by predicting updates conditioned on new factual statements. In a study of KE, Hase et al. (2021) find that it fails to scale beyond a few edits, and they scale an improved objective to 10 beliefs. MEND (Mitchell et al., 2021) also adopts meta-learning, inferring weight updates from the gradient of the inserted fact. To scale their method, Mitchell et al. (2022) proposes SERAC, a system that routes rewritten facts through a different set of parameters while keeping the original weights unmodified; they demonstrate scaling up to 75 edits. Rather than meta-learning, our method employs direct parameter updates based on an explicitly computed mapping.
超网络知识编辑器。已有多种元学习方法被提出用于编辑模型中的知识。Sinitsin等人(2019)提出了一种训练目标,使模型能够通过梯度下降进行编辑。De Cao等人(2021)提出了一种知识编辑器(KE)超网络,通过基于新事实陈述预测更新来编辑标准模型。Hase等人(2021)在对KE的研究中发现,该方法难以扩展到少量编辑之外,他们将改进后的目标扩展到10个信念。MEND(Mitchell等人,2021)也采用元学习,从插入事实的梯度推断权重更新。为了扩展其方法,Mitchell等人(2022)提出了SERAC系统,该系统通过不同的参数集路由重写事实,同时保持原始权重不变;他们展示了扩展到75次编辑的能力。与元学习不同,我们的方法基于显式计算映射直接进行参数更新。
Direct model editing. Our work most directly builds upon efforts to localize and understand the internal mechanisms within LLMs (Elhage et al., 2021; Dar et al., 2022). Based on observations from Geva et al. (2021; 2022) that transformer MLP layers serve as key–value memories, we narrow our focus to them. We then employ causal mediation analysis (Pearl, 2001; Vig et al., 2020; Meng et al., 2022), which implicates a specific range of layers in recalling factual knowledge. Previously, Dai et al. (2022) and Yao et al. (2022) have proposed editing methods that alter sparse sets of neurons, but we adopt the classical view of a linear layer as an associative memory (Anderson, 1972; Kohonen, 1972). Our method is closely related to Meng et al. (2022), which also updates GPT as an explicit associative memory. Unlike the single-edit approach taken in that work, we modify a sequence of layers and develop a way for thousands of modifications to be performed simultaneously.
直接模型编辑。我们的工作最直接建立在定位和理解大语言模型内部机制的研究基础上 (Elhage et al., 2021; Dar et al., 2022)。基于Geva等人 (2021; 2022) 关于Transformer的MLP层作为键值存储的观察,我们将研究范围缩小到这些层。随后采用因果中介分析 (Pearl, 2001; Vig et al., 2020; Meng et al., 2022),该方法揭示了特定层范围在事实知识回忆中的作用。此前,Dai等人 (2022) 和Yao等人 (2022) 提出了修改稀疏神经元集的编辑方法,但我们采用线性层作为关联记忆的经典观点 (Anderson, 1972; Kohonen, 1972)。我们的方法与Meng等人 (2022) 密切相关,后者也将GPT更新为显式关联记忆。不同于该研究的单次编辑方法,我们修改了一系列层,并开发了同时执行数千次修改的技术。
3 PRELIMINARIES: LANGUAGE MODELING AND MEMORY EDITING
3 基础知识:语言建模与记忆编辑
The goal of MEMIT is to modify factual associations stored in the parameters of an auto regressive LLM. Such models generate text by iterative ly sampling from a conditional token distribution
MEMIT的目标是修改自回归大语言模型参数中存储的事实关联。这类模型通过从条件token分布中迭代采样来生成文本。
$\mathbb{P}\left[x_{[t]}\mid x_{[1]},\ldots,x_{[E]}\right]$ parameterized by a $D$ -layer transformer decoder, $G$ (Vaswani et al., 2017):
$\mathbb{P}\left[x_{[t]}\mid x_{[1]},\ldots,x_{[E]}\right]$ 由 $D$ 层 Transformer 解码器 $G$ 参数化 (Vaswani et al., 2017):
$$
\begin{array}{r}{\mathbb{P}\left[x_{[t]}|x_{[1]},\ldots,x_{[E]}\right]\triangleq G([x_{[1]},\ldots,x_{[E]}])=\operatorname{softmax}\left(W_{y}h_{[E]}^{D}\right),}\end{array}
$$
$$
\begin{array}{r}{\mathbb{P}\left[x_{[t]}|x_{[1]},\ldots,x_{[E]}\right]\triangleq G([x_{[1]},\ldots,x_{[E]}])=\operatorname{softmax}\left(W_{y}h_{[E]}^{D}\right),}\end{array}
$$
where $h_{[E]}^{D}$ is the transformer’s hidden state representation at the final layer $D$ and ending token $E$ . This state is computed using the following recursive relation:
其中 $h_{[E]}^{D}$ 是Transformer在最终层 $D$ 和结束token $E$ 处的隐藏状态表示。该状态通过以下递归关系计算:
$$
\begin{array}{r l}&{{\boldsymbol{h}}_ {[t]}^{l}(\boldsymbol{x})={\boldsymbol{h}}_ {[t]}^{l-1}(\boldsymbol{x})+a_{[t]}^{l}(\boldsymbol{x})+m_{[t]}^{l}(\boldsymbol{x})}\ &{\quad\mathrm{where~}a^{l}=\mathrm{attn}^{l}\left({\boldsymbol{h}}_ {[1]}^{l-1},{\boldsymbol{h}}_ {[2]}^{l-1},\dots,{\boldsymbol{h}}_ {[t]}^{l-1}\right)}\ &{\quad m_{[t]}^{l}={\boldsymbol{W}}_ {o u t}^{l}\sigma\left({\boldsymbol{W}}_ {i n}^{l}\gamma\left({\boldsymbol{h}}_{[t]}^{l-1}\right)\right),}\end{array}
$$
$$
\begin{array}{r l}&{{\boldsymbol{h}}_ {[t]}^{l}(\boldsymbol{x})={\boldsymbol{h}}_ {[t]}^{l-1}(\boldsymbol{x})+a_{[t]}^{l}(\boldsymbol{x})+m_{[t]}^{l}(\boldsymbol{x})}\ &{\quad\mathrm{where~}a^{l}=\mathrm{attn}^{l}\left({\boldsymbol{h}}_ {[1]}^{l-1},{\boldsymbol{h}}_ {[2]}^{l-1},\dots,{\boldsymbol{h}}_ {[t]}^{l-1}\right)}\ &{\quad m_{[t]}^{l}={\boldsymbol{W}}_ {o u t}^{l}\sigma\left({\boldsymbol{W}}_ {i n}^{l}\gamma\left({\boldsymbol{h}}_{[t]}^{l-1}\right)\right),}\end{array}
$$
$h_{[t]}^{0}(x)$ is the embedding of token $x_{[t]}$ , and $\gamma$ is layernorm. Note that we have written attention and MLPs in parallel as done in Black et al. (2021) and Wang & Komatsu zak i (2021).
$h_{[t]}^{0}(x)$ 是 token $x_{[t]}$ 的嵌入向量,$\gamma$ 是层归一化 (layernorm)。注意,我们按照 Black 等人 (2021) 以及 Wang 和 Komatsuzaki (2021) 的方式将注意力机制和 MLP 并行处理。
Large language models have been observed to contain many memorized facts (Petroni et al., 2020; Brown et al., 2020; Jiang et al., 2020; Chowdhery et al., 2022). In this paper, we study facts of the form (subject $s$ , relation $r$ , object $o$ ), e.g., $s=$ Michael Jordan, $r=$ plays sport, $o=$ basketball). A generator $G$ can recall a memory for $(s_{i},r_{i},*)$ if we form a natural language prompt $p_{i}=p(s_{i},r_{i})$ such as “Michael Jordan plays the sport of” and predict the next token(s) representing $o_{i}$ . Our goal is to edit many memories at once. We formally define a list of edit requests as:
研究发现大语言模型中存储了大量事实性知识 (Petroni et al., 2020; Brown et al., 2020; Jiang et al., 2020; Chowdhery et al., 2022)。本文研究形式为 (主体 $s$ , 关系 $r$ , 客体 $o$ ) 的三元组事实,例如 $s=$ Michael Jordan, $r=$ 从事运动, $o=$ 篮球)。当构建自然语言提示 $p_{i}=p(s_{i},r_{i})$ 如"Michael Jordan从事的运动是"时,生成器 $G$ 若能预测表示 $o_{i}$ 的后续token,则视为成功调用了 $(s_{i},r_{i},*)$ 的记忆。我们的目标是实现批量记忆编辑,将编辑请求列表形式化定义为:
$$
\mathcal{E}={(s_{i},r_{i},o_{i})|i}\mathrm{ s.t. }\vec{\beta}i,j.\left(s_{i}=s_{j}\right)\wedge(r_{i}=r_{j})\wedge(o_{i}\neq o_{j}).
$$
$$
\mathcal{E}={(s_{i},r_{i},o_{i})|i}\mathrm{ s.t. }\vec{\beta}i,j.\left(s_{i}=s_{j}\right)\wedge(r_{i}=r_{j})\wedge(o_{i}\neq o_{j}).
$$
The logical constraint ensures that there are no conflicting requests. For example, we can edit Michael Jordan to play $o_{i}=$ “baseball”, but then we exclude associating him with professional soccer.
逻辑约束确保不存在冲突的请求。例如,我们可以将Michael Jordan编辑为参与 $o_{i}=$ "棒球(baseball)",但这样就排除了他与职业足球的关联。
What does it mean to edit a memory well? At a superficial level, a memory can be considered edited after the model assigns a higher probability to the statement “Michael Jordan plays the sport of baseball” than to the original prediction (basketball); we say that such an update is effective. Yet it is important to also view the question in terms of generalization, specificity, and fluency:
如何才算编辑好一段记忆?从表面上看,当模型对"Michael Jordan从事棒球运动"这一陈述赋予的概率高于原始预测(篮球)时,即可认为记忆已被编辑;我们称这种更新是有效的。但更重要的是从泛化性、特异性和流畅性三个维度来审视这个问题:
• To test for generalization, we can rephrase the question: “What is Michael Jordan’s sport? What sport does he play professionally?” If the modification of $G$ is superficial and overfitted to the specific memorized prompt, such predictions will fail to recall the edited memory, “baseball.” • Conversely, to test for specificity, we can ask about similar subjects for which memories should not change: “What sport does Kobe Bryant play? What does Magic Johnson play?” These tests will fail if the updated $G$ indiscriminately regurgitates “baseball” for subjects that were not edited. • When making changes to a model, we must also monitor fluency. If the updated model generates disfluent text such as “baseball baseball baseball baseball,” we should count that as a failure.
• 为测试泛化性,我们可以改写问题:"迈克尔·乔丹从事什么运动?他以什么运动为职业?"如果对$G$的修改是表面化的,并且过度拟合了特定的记忆提示,这类预测将无法回忆起被编辑的记忆"棒球"。
• 相反地,为测试特异性,我们可以询问不应改变记忆的相似主体:"科比·布莱恩特从事什么运动?魔术师约翰逊从事什么运动?"如果更新后的$G$不加区分地对未经编辑的主体重复输出"棒球",这些测试就会失败。
• 修改模型时,我们还必须监控流畅性。如果更新后的模型生成诸如"棒球棒球棒球棒球"之类不流畅的文本,应将其视为失败案例。
4 METHOD
4 方法
MEMIT inserts memories by updating transformer mechanisms that have recently been elucidated using causal mediation analysis (Meng et al., 2022). In GPT-2 XL, we found that there is a sequence of critical MLP layers $\mathcal{R}$ that mediate factual association recall at the last subject token $S$ (Figure 2). MEMIT operates by (i) calculating the vector associations we want the critical layers to remember, then (ii) storing a portion of the desired memories in each layer $l\in\mathcal R$ .
MEMIT通过更新最近通过因果中介分析 (Meng et al., 2022) 阐明的Transformer机制来插入记忆。在GPT-2 XL中,我们发现存在一系列关键MLP层 $\mathcal{R}$ ,它们在最后一个主体token $S$ 处中介事实关联回忆 (图 2)。MEMIT的操作方式是:(i) 计算我们希望关键层记住的向量关联,然后 (ii) 将部分所需记忆存储在每个层 $l\in\mathcal R$ 中。
Throughout this paper, our focus will be on states representing the last subject token $S$ of prompt $p_{i}$ , so we shall abbreviate $h_{i}^{l}=h_{[S]}^{l}(p_{i})$ . Similarly, $m_{i}^{l}$ and $a_{i}^{l}$ denote $m_{[S]}^{l}(p_{i})$ and $a_{[S]}^{l}(p_{i})$ .
在本文中,我们将重点关注表示提示 $p_{i}$ 最后一个主题token $S$ 的状态,因此我们将简写为 $h_{i}^{l}=h_{[S]}^{l}(p_{i})$ 。类似地,$m_{i}^{l}$ 和 $a_{i}^{l}$ 分别表示 $m_{[S]}^{l}(p_{i})$ 和 $a_{[S]}^{l}(p_{i})$ 。
4.1 IDENTIFYING THE CRITICAL PATH OF MLP LAYERS
4.1 识别 MLP 层的关键路径
Figure 3 shows the results of applying causal tracing to the larger GPT-J (6B) model; for implementation details, see Appendix A. We measure the average indirect causal effect of each $h_{i}^{l}$ on a sample of memory prompts $p_{i}$ , with either the Attention or MLP modules for token $S$ disabled. The results confirm that GPT-J has a concentration of mediating states $h_{i}^{l}$ ; moreover, they highlight a mediating causal role for a range of MLP modules, which can be seen as a large gap between the effect of single states (purple bars in Figure 3) and the effects with MLP severed (green bars); this gap diminishes after layer 8. Unlike Meng et al. (2022) who use this test to identify a single edit layer, we select the whole range of critical MLP layers $l\in\mathcal R$ . For GPT-J, we have $\mathcal{R}={3,\bar{4},5,6,7,\dot{8}}$ .
图 3: 展示了在更大的 GPT-J (6B) 模型上应用因果追踪的结果,具体实现细节参见附录 A。我们测量了每个 $h_{i}^{l}$ 对记忆提示样本 $p_{i}$ 的平均间接因果效应,其中 Token $S$ 的注意力模块或 MLP 模块被禁用。结果证实 GPT-J 具有中介状态 $h_{i}^{l}$ 的集中性;此外,它们突显了一系列 MLP 模块的中介因果作用,这可以看作是单状态效应(图 3 中的紫色条)与 MLP 切断效应(绿色条)之间的巨大差距,该差距在第 8 层后减小。与 Meng 等人 (2022) 使用此测试识别单个编辑层不同,我们选择了关键 MLP 层 $l\in\mathcal R$ 的整个范围。对于 GPT-J,我们有 $\mathcal{R}={3,\bar{4},5,6,7,\dot{8}}$。
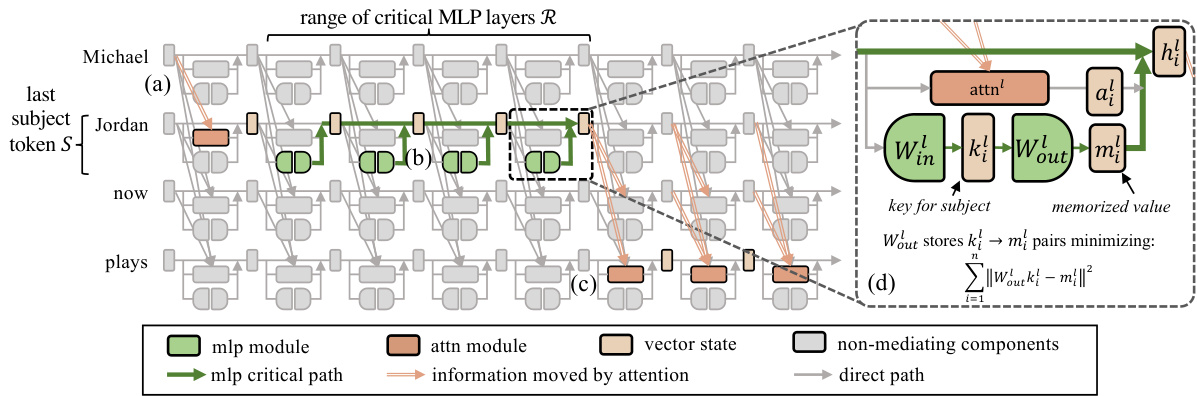
Figure 2: MEMIT modifies transformer parameters on the critical path of MLP-mediated factual recall. We edit stored associations based on observed patterns of causal mediation: (a) first, the early-layer attention modules gather subject names into vector representations at the last subject token $S$ . (b) Then MLPs at layers $l\in\mathcal R$ read these encodings and add memories to the residual stream. (c) Those hidden states are read by attention to produce the output. (d) MEMIT edits memories by storing vector associations in the critical MLPs.
图 2: MEMIT通过修改MLP介导的事实回忆关键路径上的Transformer参数实现编辑。我们基于观察到的因果中介模式修改存储关联:(a) 首先,浅层注意力模块将主语名称汇集到最后一个主语token $S$ 的向量表示中。(b) 随后位于层 $l\in\mathcal R$ 的MLP读取这些编码,并向残差流添加记忆。(c) 这些隐藏状态被注意力模块读取以生成输出。(d) MEMIT通过在关键MLP中存储向量关联来实现记忆编辑。
Given that a range of MLPs play a joint mediating role in recalling facts, we ask: what is the role of one MLP in storing a memory? Each token state in a transformer is part of the residual stream that all attention and MLP modules read from and write to (Elhage et al., 2021). Unrolling Eqn. 2 for $h_{i}^{L^{-}}=h_{[S]}^{L}(p_{i})$ :
鉴于多个MLP在事实回忆中共同发挥中介作用,我们提出疑问:单个MLP在记忆存储中扮演什么角色?Transformer中的每个Token状态都是残差流的一部分,所有注意力模块和MLP模块都从中读取并写入 (Elhage et al., 2021) 。展开公式2中的 $h_{i}^{L^{-}}=h_{[S]}^{L}(p_{i})$ 可得:
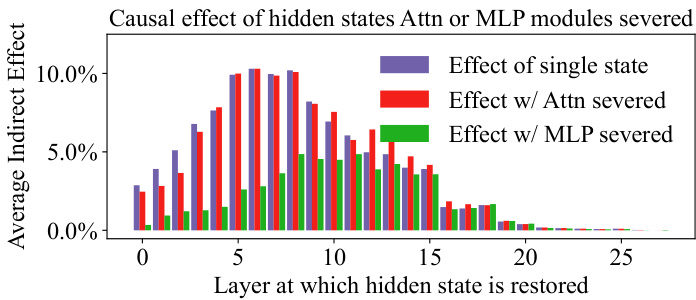
Figure 3: A critical mediating role for mid-layer MLPs.
图 3: 中间层 MLP 的关键中介作用。
$$
h_{i}^{L}=h_{i}^{0}+\sum_{l=1}^{L}a_{i}^{l}+\sum_{l=1}^{L}m_{i}^{l}.
$$
$$
h_{i}^{L}=h_{i}^{0}+\sum_{l=1}^{L}a_{i}^{l}+\sum_{l=1}^{L}m_{i}^{l}.
$$
Eqn. 6 highlights that each individual
式 6 强调每个个体
MLP contributes by adding to the memory at $h_{i}^{L}$ (Figure 2b), which is later read by last-token attention modules (Figure 2c). Therefore, when writing new memories into $G$ , we can spread the desired changes across all the critical layers $m_{i}^{l}$ for $l\in\mathcal R$ .
MLP通过向$h_{i}^{L}$处的记忆添加内容做出贡献 (图 2b),这些内容随后会被最后token注意力模块读取 (图 2c)。因此,当向$G$写入新记忆时,我们可以将所需的变化扩散到所有关键层$m_{i}^{l}$,其中$l\in\mathcal R$。
4.2 BATCH UPDATE FOR A SINGLE LINEAR ASSOCIATIVE MEMORY
4.2 单一线性联想记忆的批量更新
In each individual layer $l$ , we wish to store a large batch of $u\gg1$ memories. This section derives an optimal single-layer update that minimizes the squared error of memorized associations, assuming that the layer contains previously-stored memories that should be preserved. We denote $W_{0}\triangleq W_{o u t}^{l}$ (Eqn. 4, Figure 2) and analyze it as a linear associative memory (Kohonen, 1972; Anderson, 1972) that associates a set of input keys $k_{i}\triangleq k_{i}^{l}$ (encoding subjects) to corresponding memory values $m_{i}\triangleq m_{i}^{l}$ (encoding memorized properties) with minimal squared error:
在每一层$l$中,我们希望存储大批量$u\gg1$的记忆。本节推导出在假设该层包含需要保留的先前存储记忆的情况下,能最小化记忆关联平方误差的最优单层更新。我们将$W_{0}\triangleq W_{o u t}^{l}$(公式4,图2)表示为一个线性联想记忆(Kohonen, 1972; Anderson, 1972),它以最小平方误差将一组输入键$k_{i}\triangleq k_{i}^{l}$(编码主体)与对应的记忆值$m_{i}\triangleq m_{i}^{l}$(编码记忆属性)相关联:
$$
W_{0}\triangleq\underset{\hat{W}}{\operatorname{argmin}}\sum_{i=1}^{n}\left|\hat{W}k_{i}-m_{i}\right|^{2}.
$$
$$
W_{0}\triangleq\underset{\hat{W}}{\operatorname{argmin}}\sum_{i=1}^{n}\left|\hat{W}k_{i}-m_{i}\right|^{2}.
$$
If we stack keys and memories as matrices $K_{0}=[k_{1}\mid k_{2}\mid\cdots\mid k_{n}]$ and $M_{0}=[m_{1}\mid m_{2}\mid\cdots\mid m_{n}]$ , then Eqn. 7 can be optimized by solving the normal equation (Strang, 1993, Chapter 4):
如果将键和记忆堆叠为矩阵 $K_{0}=[k_{1}\mid k_{2}\mid\cdots\mid k_{n}]$ 和 $M_{0}=[m_{1}\mid m_{2}\mid\cdots\mid m_{n}]$ ,那么通过求解正规方程 (Strang, 1993, Chapter 4) 可以优化公式 7:
$$
W_{0}K_{0}K_{0}^{T}=M_{0}K_{0}^{T}.
$$
$$
W_{0}K_{0}K_{0}^{T}=M_{0}K_{0}^{T}.
$$
Suppose that pre-training sets a transformer MLP’s weights to the optimal solution $W_{0}$ as defined in Eqn. 8. Our goal is to update $W_{0}$ with some small change $\Delta$ that produces a new matrix $W_{1}$ with
假设预训练将 Transformer MLP 的权重设置为公式 8 中定义的最优解 $W_{0}$。我们的目标是用一个小的变化 $\Delta$ 来更新 $W_{0}$,从而生成一个新的矩阵 $W_{1}$。
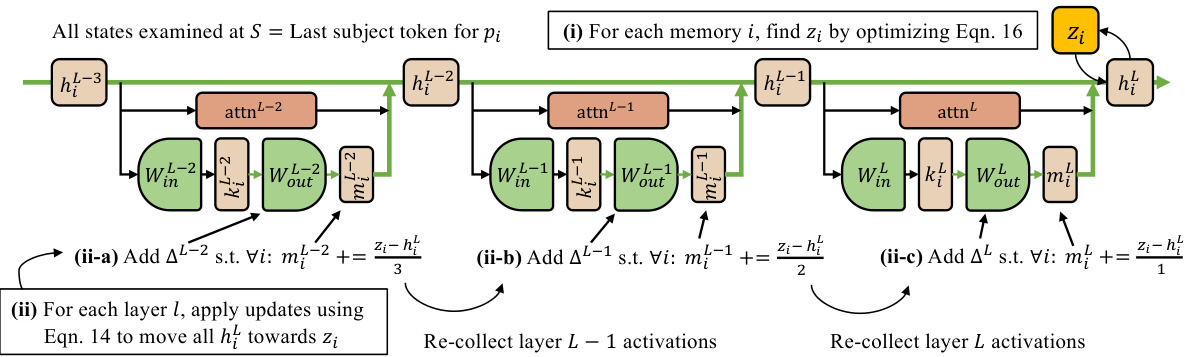
Figure 4: The MEMIT update. We first (i) replace $h_{i}^{l}$ with the vector $z_{i}$ and optimize Eqn. 16 so that it conveys the new memory. Then, after all $z_{i}$ are calculated we (ii) iterative ly insert a fraction of the residuals for all $z_{i}$ over the range of critical MLP modules, executing each layer’s update by applying Eqn. 14. Because changing one layer will affect activation s of downstream modules, we recollect activation s after each iteration.
图 4: MEMIT更新过程。我们首先(i)用向量$z_{i}$替换$h_{i}^{l}$并优化公式16,使其传递新记忆。随后在所有$z_{i}$计算完成后,(ii)我们在关键MLP模块范围内迭代插入各$z_{i}$的部分残差,通过应用公式14执行每层更新。由于单层修改会影响下游模块的激活值,我们在每次迭代后重新收集激活值。
a set of additional associations. Unlike Meng et al. (2022), we cannot solve our problem with a constraint that adds only a single new association, so we define an expanded objective:
一组额外关联。与Meng等人(2022)不同,我们无法通过仅添加单个新关联的约束条件来解决该问题,因此定义了一个扩展目标:
$$
W_{1}\triangleq\underset{\hat{W}}{\operatorname{argmin}}\left(\sum_{i=1}^{n}\left|{\hat{W}}k_{i}-m_{i}\right|^{2}+\sum_{i=n+1}^{n+u}\left|{\hat{W}}k_{i}-m_{i}\right|^{2}\right).
$$
$$
W_{1}\triangleq\underset{\hat{W}}{\operatorname{argmin}}\left(\sum_{i=1}^{n}\left|{\hat{W}}k_{i}-m_{i}\right|^{2}+\sum_{i=n+1}^{n+u}\left|{\hat{W}}k_{i}-m_{i}\right|^{2}\right).
$$
We can solve Eqn. 9 by again applying the normal equation, now written in block form:
我们可以通过再次应用正规方程来求解方程9,现在以分块形式表示:
$$
W_{1}\left[K_{0}\quad K_{1}\right]\left[K_{0}\quad K_{1}\right]^{T}=\left[M_{0}\quad M_{1}\right]\left[K_{0}\quad K_{1}\right]^{T}
$$
$$
W_{1}\left[K_{0}\quad K_{1}\right]\left[K_{0}\quad K_{1}\right]^{T}=\left[M_{0}\quad M_{1}\right]\left[K_{0}\quad K_{1}\right]^{T}
$$
$$
\begin{array}{r l}{\mathrm{{1}d s t o. }}&{{}(W_{0}+\Delta)(K_{0}K_{0}^{T}+K_{1}K_{1}^{T})=M_{0}K_{0}^{T}+M_{1}K_{1}^{T}}\end{array}
$$
$$
\begin{array}{r l}{\mathrm{{1}d s t o. }}&{{}(W_{0}+\Delta)(K_{0}K_{0}^{T}+K_{1}K_{1}^{T})=M_{0}K_{0}^{T}+M_{1}K_{1}^{T}}\end{array}
$$
$$
W_{0}K_{0}K_{0}^{T}+W_{0}K_{1}K_{1}^{T}+\Delta K_{0}K_{0}^{T}+\Delta K_{1}K_{1}^{T}=M_{0}K_{0}^{T}+M_{1}K_{1}^{T}
$$
$$
W_{0}K_{0}K_{0}^{T}+W_{0}K_{1}K_{1}^{T}+\Delta K_{0}K_{0}^{T}+\Delta K_{1}K_{1}^{T}=M_{0}K_{0}^{T}+M_{1}K_{1}^{T}
$$
$$
\mathrm{ing Eqn. 8 from Eqn.~12:}\quad\Delta(K_{0}K_{0}^{T}+K_{1}K_{1}^{T})=M_{1}K_{1}^{T}-W_{0}K_{1}K_{1}^{T}.
$$
$$
\mathrm{由式 8 减式 12 得:}\quad\Delta(K_{0}K_{0}^{T}+K_{1}K_{1}^{T})=M_{1}K_{1}^{T}-W_{0}K_{1}K_{1}^{T}.
$$
A succinct solution can be written by defining two additional quantities: $C_{0}\triangleq K_{0}K_{0}^{T}$ , a constant proportional to the uncentered covariance of the pre-existing keys, and $R\triangleq M_{1}-W_{0}K_{1}$ , the residual error of the new associations when evaluated on old weights $W_{0}$ . Then Eqn. 13 can be simplified as:
通过定义两个额外的量可以写出简洁的解法:$C_{0}\triangleq K_{0}K_{0}^{T}$(与已有键(key)的非中心化协方差成比例的常量),以及$R\triangleq M_{1}-W_{0}K_{1}$(用旧权重$W_{0}$评估新关联时的残差)。于是式(13)可简化为:
$$
\Delta=R K_{1}^{T}(C_{0}+K_{1}K_{1}^{T})^{-1}.
$$
$$
\Delta=R K_{1}^{T}(C_{0}+K_{1}K_{1}^{T})^{-1}.
$$
Since pre training is opaque, we do not have access to $K_{0}$ or $M_{0}$ . Fortunately, computing Eqn. 14 only requires an aggregate statistic $C_{0}$ over the previously stored keys. We assume that the set of previously memorized keys can be modeled as a random sample of inputs, so that we can compute
由于预训练过程不透明,我们无法获取$K_{0}$或$M_{0}$。幸运的是,计算方程14仅需基于先前存储密钥的聚合统计量$C_{0}$。我们假设先前记忆的密钥集合可建模为输入数据的随机样本,从而能够进行计算。
$$
C_{0}=\lambda\cdot\mathbb{E}_{k}\left[k k^{T}\right]
$$
$$
C_{0}=\lambda\cdot\mathbb{E}_{k}\left[k k^{T}\right]
$$
by estimating $\mathbb{E}_{k}\left[k k^{T}\right]$ , an uncentered covariance statistic collected using an empirical sample of vector inputs to the lay er. We must also select $\lambda$ , a hyper parameter that balances the weighting of new v.s. old associations; a typical value is $\lambda=1.5\times\bar{1}0^{4}$ .
通过估计 $\mathbb{E}_{k}\left[k k^{T}\right]$ ,即使用该层向量输入的实证样本收集的非中心化协方差统计量。我们还需选择超参数 $\lambda$ ,用于平衡新旧关联的权重;典型值为 $\lambda=1.5\times\bar{1}0^{4}$ 。
4.3 UPDATING MULTIPLE LAYERS
4.3 更新多层结构
We now define the overall update algorithm (Figure 4). Inspired by the observation that robustness is improved when parameter change magnitudes are minimized (Zhu et al., 2020), we spread updates evenly over the range of mediating layers $\mathcal{R}$ . We define a target layer $L\triangleq\operatorname*{max}(\mathcal{R})$ at the end of the mediating layers, at which the new memories should be fully represented. Then, for each edit $(s_{i},r_{i},o_{i})\in\mathbf{\bar{\mathcal{E}}}$ , we (i) compute a hidden vector $z_{i}$ to replace $h_{i}^{L}$ such that adding $\delta_{i}\triangleq z_{i}-h_{i}^{L}$ to the hidden state at layer $L$ and token $T$ will completely convey the new memory. Finally, one layer at a time, we (ii) modify the MLP at layer $l$ , so that it contributes an approximately-equal portion of the change $\delta_{i}$ for each memory $i$ .
我们现在定义整体更新算法(图4)。受参数变化幅度最小时鲁棒性会提升这一观察的启发(Zhu et al., 2020),我们将更新均匀分布在中间层范围$\mathcal{R}$上。我们在中间层末端定义目标层$L\triangleq\operatorname*{max}(\mathcal{R})$,新记忆应在此层完全呈现。然后,对于每个编辑$(s_{i},r_{i},o_{i})\in\mathbf{\bar{\mathcal{E}}}$,我们(i)计算隐藏向量$z_{i}$以替换$h_{i}^{L}$,使得在层$L$和token$T$处向隐藏状态添加$\delta_{i}\triangleq z_{i}-h_{i}^{L}$将完整传递新记忆。最后,我们逐层(ii)修改层$l$的MLP,使其为每个记忆$i$贡献近似等量的变化$\delta_{i}$。
(i) Computing $z_{i}$ . For the $i$ th memory, we first compute a vector $z_{i}$ that would encode the association $(s_{i},r_{i},o_{i})$ if it were to replace $h_{i}^{L}$ at layer $L$ at token $S$ . We find $z_{i}=h_{i}^{L}+\delta_{i}$ by optimizing the residual vector $\delta_{i}$ using gradient descent:
(i) 计算 $z_{i}$。对于第 $i$ 个记忆单元,我们首先计算向量 $z_{i}$,该向量将编码关联 $(s_{i},r_{i},o_{i})$,前提是它要在第 $L$ 层的 token $S$ 处替换 $h_{i}^{L}$。我们通过梯度下降优化残差向量 $\delta_{i}$,得到 $z_{i}=h_{i}^{L}+\delta_{i}$:
$$
z_{i}=h_{i}^{L}+\underset{\delta_{i}}{\mathrm{argmin}}\frac{1}{P}\sum_{j=1}^{P}-\log\mathbb{P}_ {G(h_{i}^{L}+=\delta_{i})}\left[o_{i}\mid x_{j}\oplus p(s_{i},r_{i})\right].
$$
$$
z_{i}=h_{i}^{L}+\underset{\delta_{i}}{\mathrm{argmin}}\frac{1}{P}\sum_{j=1}^{P}-\log\mathbb{P}_ {G(h_{i}^{L}+=\delta_{i})}\left[o_{i}\mid x_{j}\oplus p(s_{i},r_{i})\right].
$$
In words, we optimize $\delta_{i}$ to maximize the model’s prediction of the desired object $o_{i}$ , given a set of factual prompts ${x_{j}\oplus p(s_{i},r_{i})}$ that concatenate random prefixes $x_{j}$ to a templated prompt to aid generalization across contexts. $\acute{G}(h_{i}^{L}+=\delta_{i})$ indicates that we modify the transformer execution by substituting the modified hidden state $z_{i}$ for $\dot{h}_{i}^{L}$ ; this is called “hooking” in popular ML libraries.
我们用语言描述就是:通过优化 $\delta_{i}$ 来最大化模型对目标对象 $o_{i}$ 的预测概率,其中输入是一组事实提示 ${x_{j}\oplus p(s_{i},r_{i})}$ ——这些提示将随机前缀 $x_{j}$ 与模板化提示拼接,以提升跨上下文的泛化能力。 $\acute{G}(h_{i}^{L}+=\delta_{i})$ 表示我们通过用修改后的隐藏状态 $z_{i}$ 替换 $\dot{h}_{i}^{L}$ 来改变 Transformer 的执行过程,这种操作在主流机器学习库中被称为"hooking"。
(ii) Spreading $z_{i}-h_{i}^{L}$ over layers. We seek delta matrices $\Delta^{l}$ such that:
(ii) 将 $z_{i}-h_{i}^{L}$ 分散到各层。我们需要找到增量矩阵 $\Delta^{l}$ 使得:
$$
\begin{array}{r l}&{\mathrm{ting}\hat{W}_ {o u t}^{l}:=W_{o u t}^{l}+\Delta^{l}\mathrm{ for all }l\in\mathcal{R}\mathrm{ optimizes }\displaystyle\operatorname*{min}_ {{\Delta^{l}}}\sum_{i}\Big|z_{i}-\hat{h}_ {i}^{L}\Big|^{2},}\ &{\mathrm{where}\hat{h}_ {i}^{L}=h_{i}^{0}+\displaystyle\sum_{l=1}^{L}a_{i}^{l}+\displaystyle\sum_{l=1}^{L}\hat{W}_ {o u t}^{l}\sigma\left(W_{i n}^{l}\gamma\left(h_{t}^{l-1}\right)\right).}\end{array}
$$
$$
\begin{array}{r l}&{\mathrm{令}\hat{W}_ {o u t}^{l}:=W_{o u t}^{l}+\Delta^{l}\mathrm{ 对所有 }l\in\mathcal{R}\mathrm{ 优化 }\displaystyle\operatorname*{min}_ {{\Delta^{l}}}\sum_{i}\Big|z_{i}-\hat{h}_ {i}^{L}\Big|^{2},}\ &{\mathrm{其中}\hat{h}_ {i}^{L}=h_{i}^{0}+\displaystyle\sum_{l=1}^{L}a_{i}^{l}+\displaystyle\sum_{l=1}^{L}\hat{W}_ {o u t}^{l}\sigma\left(W_{i n}^{l}\gamma\left(h_{t}^{l-1}\right)\right).}\end{array}
$$
Because edits to any layer will influence all following layers’ activation s, we calculate $\Delta^{l}$ iterative ly in ascending layer order (Figure 4ii-a,b,c). To compute each individual $\Delta^{l}$ , we need the corresponding keys $K^{l}=\mathbf{\overline{{[}}\it{k_{1}^{l}\mathrm{ \overline{{ }}{ | \cdot \cdot \cdot | } }}}k_{n}^{l}\mathbf{\bar{\Psi}}]$ and memories $M^{l}=[\dot{m}_ {1}^{l}\mid\cdots\mid m_{n}^{l}]$ to insert using Eqn. 14. Each key $k_{i}^{\check{l}}$ is computed as the input to $W_{o u t}^{l}$ at each layer $l$ (Figure 2d):
由于对任何层的编辑都会影响后续所有层的激活,我们按升序层序迭代计算 $\Delta^{l}$ (图 4ii-a,b,c)。为计算每个独立的 $\Delta^{l}$,需要对应的键 $K^{l}=\mathbf{\overline{{[}}\it{k_{1}^{l}\mathrm{ \overline{{ }}{ | \cdot \cdot \cdot | } }}}k_{n}^{l}\mathbf{\bar{\Psi}}]$ 和记忆 $M^{l}=[\dot{m}_ {1}^{l}\mid\cdots\mid m_{n}^{l}]$ 以便通过公式14进行插入。每个键 $k_{i}^{\check{l}}$ 的计算方式是作为每层 $l$ 中 $W_{o u t}^{l}$ 的输入(图 2d):
$$
k_{i}^{l}=\frac{1}{P}\sum_{j=1}^{P}k(x_{j}+s_{i}),\mathrm{ where }k(x)=\sigma\left(W_{i n}^{l}\gamma\left(h_{i}^{l-1}(x)\right)\right).
$$
$$
k_{i}^{l}=\frac{1}{P}\sum_{j=1}^{P}k(x_{j}+s_{i}),\mathrm{ where }k(x)=\sigma\left(W_{i n}^{l}\gamma\left(h_{i}^{l-1}(x)\right)\right).
$$
$m_{i}^{l}$ is then computed as the sum of its current value and a fraction of the remaining top-level residual:
$m_{i}^{l}$ 的计算方式为其当前值加上剩余顶层残差的一部分:
where the denominator of $r_{i}$ spreads the residual out evenly. Algorithm 1 summarizes MEMIT, and additional implementation details are offered in Appendix B.
其中$r_{i}$的分母将残差均匀分布。算法1总结了MEMIT方法,附录B提供了更多实现细节。
Algorithm 1: The MEMIT Algorithm
算法 1: MEMIT算法
| Data: Requested edits & = {(s, r, o)}, generator G, layers to edit S, covariances Cl Result:Modified generator containing edits from & | ||
| for Si,ri,O E & do I/ Compute target % vectors for every memory i | ||
| optimize 8 ←argmins: ∑§=1 - log PG(h +=8a) [o | x, p(si, ri)] (Eqn. 16) | ||
| i←h+ | ||
| 4end sforl∈Rdo | // Perform update: spread changes over layers | |
| h ← h-1 + a + m (Eqn. 2) for si,ri,O E & do | // Run layer I with updated weights | |
| 8 | k←k =∑=1 k(xj + si) (Eqn. 19) | |
| // Distribute residual over remaining layers | ||
| 10 | end | |
| 11 | Kl ←[k,,k] | |
| 12 | R←[r..r] | |
| 13 | △ ← RlKlT (Cl + Kl KiT)-1 (Eqn. 14) | |
| 14 | Wl ←Wl + △ | // Update layer I MLP weights in model |
| 15 end | ||
数据:请求编辑集 & = {(s, r, o)},生成器 G,待编辑层 S,协方差 Cl
结果:包含 & 编辑的修改后生成器
对于 Si,ri,O ∈ & 执行
// 为每个记忆 i 计算目标向量
优化 δ ← argminδ ∑i=1 -log PG(h+δai) [o | x, p(si, ri)] (公式 16)
i←h+
4结束
对于 l∈R 执行
// 执行更新:将变化传播到各层
h ← hl-1 + al + ml (公式 2)
对于 si,ri,O ∈ & 执行
// 使用更新后的权重运行第 l 层
8
k←k =∑j=1 k(xj + si) (公式 19)
// 将残差分配到剩余层
10
结束
11
Kl ←[k1,...,k]
12
R←[r1..r]
13
△ ← RlKlT (Cl + Kl KlT)-1 (公式 14)
14
Wl ←Wl + △
// 更新模型中第 l 层 MLP 权重
15 结束
5 EXPERIMENTS
5 实验
5.1 MODELS AND BASELINES
5.1 模型与基线
We run experiments on two auto regressive LLMs: GPT-J (6B) and GPT-NeoX (20B). For baselines, we first compare with a naive fine-tuning approach that uses weight decay to prevent forgetfulness (FT-W). Next, we experiment with MEND, a hyper network-based model editing approach that edits multiple facts at the same time (Mitchell et al., 2021). Finally, we run a sequential version of ROME (Meng et al., 2022): a direct model editing method that iterative ly updates one fact at a time. The recent SERAC model editor (Mitchell et al., 2022) does not yet have public code, so we cannot compare with it at this time. See Appendix B for implementation details.
我们在两个自回归大语言模型上进行了实验:GPT-J (6B) 和 GPT-NeoX (20B)。作为基线方法,首先与采用权重衰减防止遗忘的简单微调方法 (FT-W) 进行比较。接着测试了基于超网络的模型编辑方法 MEND (Mitchell et al., 2021),该方法可同时编辑多个事实。最后运行了 ROME (Meng et al., 2022) 的序列版本:这种直接模型编辑方法每次迭代更新一个事实。近期提出的 SERAC 模型编辑器 (Mitchell et al., 2022) 尚未公开代码,因此暂时无法进行比较。具体实现细节参见附录 B。
5.2 MEMIT SCALING
5.2 MEMIT 扩展
5.2.1 EDITING 10K MEMORIES IN ZSRE
5.2.1 在ZSRE中编辑10K记忆
We first test MEMIT on zsRE (Levy et al., 2017), a question-answering task from which we extract 10,000 real-world facts; zsRE tests MEMIT’s ability to add correct information. Because zsRE does not contain generation tasks, we evaluate solely on prediction-based metrics. Efficacy
我们首先在zsRE (Levy et al., 2017) 上测试MEMIT,这是一个问答任务,从中我们提取了10,000个真实世界的事实;zsRE测试了MEMIT添加正确信息的能力。由于zsRE不包含生成任务,我们仅基于预测指标进行评估。有效性
Table 1: 10,000 zsRE Edits on GPT-J (6B).
| Editor | Score↑ | Efficacy ↑ | Paraphrase ↑ | Specificity↑ |
| GPT-J | 26.4 | 26.4 (±0.6) | 25.8 (±0.5) | 27.0 (±0.5) |
| FT-W | 42.1 | 69.6 (±0.6) | 64.8 (±0.6) | 24.1 (±0.5) |
| MEND | 20.0 | 19.4 (±0.5) | 18.6 (±0.5) | 22.4 (±0.5) |
| ROME | 2.6 | 21.0 (±0.7) | 19.6 (±0.7) | 0.9 (±0.1) |
| MEMIT | 50.7 | 96.7 (±0.3) | 89.7 (±0.5) | 26.6 (±0.5) |
表 1: GPT-J (6B) 上的 10,000 次 zsRE 编辑
| Editor | Score↑ | Efficacy ↑ | Paraphrase ↑ | Specificity↑ |
|---|---|---|---|---|
| GPT-J | 26.4 | 26.4 (±0.6) | 25.8 (±0.5) | 27.0 (±0.5) |
| FT-W | 42.1 | 69.6 (±0.6) | 64.8 (±0.6) | 24.1 (±0.5) |
| MEND | 20.0 | 19.4 (±0.5) | 18.6 (±0.5) | 22.4 (±0.5) |
| ROME | 2.6 | 21.0 (±0.7) | 19.6 (±0.7) | 0.9 (±0.1) |
| MEMIT | 50.7 | 96.7 (±0.3) | 89.7 (±0.5) | 26.6 (±0.5) |
measures the proportion of cases where $o$ is the argmax generation given $p(s,r)$ , Paraphrase is the same metric but applied on paraphrases, Specificity is the model’s argmax accuracy on a randomly-sampled unrelated fact that should not have changed, and Score is the harmonic mean of the three aforementioned scores; Appendix C contains formal definitions. As Table 1 shows, MEMIT performs best at 10,000 edits; most memories are recalled with generalization and minimal bleedover. Interestingly, simple fine-tuning FT-W performs better than the baseline knowledge editing methods MEND and ROME at this scale, likely because its objective is applied only once.
衡量在给定 $p(s,r)$ 时 $o$ 作为 argmax 生成结果的比例,Paraphrase 是相同指标但应用于改写文本,Specificity 是模型在随机采样的无关事实上不应发生变化的 argmax 准确率,Score 是上述三个分数的调和平均数;附录 C 包含正式定义。如表 1 所示,MEMIT 在 10,000 次编辑时表现最佳,大多数记忆都能被召回且具有泛化性和最小的干扰。有趣的是,在这个规模下,简单的微调方法 FT-W 优于基线知识编辑方法 MEND 和 ROME,这可能是因为其目标函数仅应用一次。
5.2.2 COUNTER FACT SCALING CURVES
5.2.2 反事实缩放曲线
Next, we test MEMIT’s ability to add counter factual information using COUNTER FACT, a collection of 21,919 factual statements (Meng et al. (2022), Appendix C). We first filter conflicts by removing facts that violate the logical condition in Eqn. 5 (i.e., multiple edits modify the same $(s,r)$ prefix to different objects). For each problem size $n\in{1,2,3,6,10,18,32$ , $56,100,178,3\mathrm{i}\mathrm{i}\overline{{6}},562,1000,1778,316\dot{2},5623,10000}^{1},$ , $n$ counter factual s are inserted.
接下来,我们测试MEMIT通过COUNTER FACT数据集(包含21,919条反事实陈述[Meng et al. (2022), 附录C])添加反事实信息的能力。首先通过移除违反公式5逻辑条件(即多个编辑将相同$(s,r)$前缀修改为不同对象)的事实来过滤冲突。针对每个问题规模$n\in{1,2,3,6,10,18,32$, $56,100,178,3\mathrm{i}\mathrm{i}\overline{{6}},562,1000,1778,316\dot{2},5623,10000}^{1}$,插入$n$条反事实陈述。
Following Meng et al. (2022), we report several metrics designed to test editing desiderata. Efficacy Success $\mathbf{\mu}(\mathbf{ES})$ evaluates editing success and is the proportion of cases for which the new object $o_{i}$ ’s probability is greater than the probability of the true real-world object $o_{i}^{c}$ :2 $\mathbb{E}_ {i}\left[\mathbb{P}_ {G}\left[o_{i}\mid p(s_{i},\bar{r}_ {i})\right]>\mathbb{P}_ {G}\left[o_{i}^{c}\mid\bar{p}(s_{i},r_{i})\right]\right]$ . Paraphrase Success (PS) is a generalization measure defined similarly, except $G$ is prompted with rephrasing s of the original statement. For testing specificity, Neighborhood Success (NS) is defined similarly, but we check the probability $G$ assigns to the correct answer $o_{i}^{c}$ (instead of $o_{i}$ ), given prompts about distinct but semantically-related subjects (instead of $s_{i}$ ). Editing Score (S) aggregates metrics by taking the harmonic mean of ES, PS, NS.
遵循 Meng 等人 (2022) 的方法,我们报告了几种用于测试编辑需求的指标。效能成功率 (Efficacy Success, μ(ES)) 评估编辑成功情况,计算新对象 $o_{i}$ 的概率高于真实世界对象 $o_{i}^{c}$ 概率的案例比例:2 $\mathbb{E}_ {i}\left[\mathbb{P}_ {G}\left[o_{i}\mid p(s_{i},\bar{r}_ {i})\right]>\mathbb{P}_ {G}\left[o_{i}^{c}\mid\bar{p}(s_{i},r_{i})\right]\right]$。改写成功率 (Paraphrase Success, PS)) 是类似定义的泛化度量,区别在于用原始语句的改写版本提示 $G$。为测试特异性,邻域成功率 (Neighborhood Success, NS)) 采用类似定义,但检查 $G$ 在给定与不同但语义相关主题 (而非 $s_{i}$) 的提示时,对正确答案 $o_{i}^{c}$ (而非 $o_{i}$) 赋予的概率。编辑分数 (Editing Score, S)) 通过取 ES、PS、NS 的调和平均值来聚合指标。
We are also interested in measuring generation quality of the updated model. First, we check that $G$ ’s generations are semantically consistent with the new object using a Reference Score (RS), which is collected by generating text about $s$ and checking its TF-IDF similarity with a reference Wikipedia text about $o$ . To test for fluency degradation due to excessive repetition, we measure Generation Entropy (GE), computed as the weighted sum of the entropy of bi- and tri-gram $n$ -gram distributions of the generated text. See Appendix C for further details on metrics.
我们还关注评估更新后模型的生成质量。首先通过参考分数(RS)验证生成器$G$的输出与新对象语义一致性,该分数通过生成关于$s$的文本并计算其与维基百科参考文本$o$的TF-IDF相似度获得。为检测过度重复导致的流畅性下降,我们计算生成熵(GE),即生成文本中二元组和三元组$n$-gram分布熵的加权和。具体指标说明详见附录C。
Figure 5 plots performance v.s. number of edits on log scale, up to 10,000 facts. ROME performs well up to $n=10$ but degrades starting at $n=32$ . Similarly, MEND performs well at $n=1$ but rapidly declines at $n=6$ , losing all efficacy before $n=1{,}000$ and, curiously, having negligible effect on the model at $n=10{,}000$ (the high specificity score is achieved by leaving the model nearly unchanged). MEMIT performs best at large $n$ . At small $n$ , ROME achieves better generalization at the cost of slightly lower specificity, which means that ROME’s edits are more robust under rephrasing s, likely due to that method’s hard equality constraint for weight updates, compared to MEMIT’s soft error minimization. Table 2 provides a direct numerical comparison at 10,000 edits on both GPT-J and GPT-NeoX. FT-W3 does well on probability-based metrics but suffers from complete generation failure, indicating significant model damage.
图 5: 绘制了性能与对数尺度上编辑数量(最多10,000条事实)的关系。ROME在 $n=10$ 时表现良好,但从 $n=32$ 开始性能下降。类似地,MEND在 $n=1$ 时表现优异,但在 $n=6$ 时迅速衰退,在 $n=1{,}000$ 前完全失效,有趣的是,在 $n=10{,}000$ 时对模型的影响微乎其微(高特异性得分是通过几乎不改变模型实现的)。MEMIT在大规模 $n$ 时表现最佳。在小规模 $n$ 时,ROME以略微降低特异性为代价实现了更好的泛化能力,这意味着ROME的编辑在句式改写下更稳健,这可能是因为该方法对权重更新采用了硬性等式约束,而MEMIT采用的是软性误差最小化。表 2: 提供了GPT-J和GPT-NeoX在10,000次编辑时的直接数值对比。FT-W3在基于概率的指标上表现良好,但出现了完全生成失败的情况,表明模型受到了严重损害。
Appendix B provides a runtime analysis of all four methods on 10,000 edits. We find that MEND is fastest, taking 98 sec. FT is second at around $29\mathrm{{min}}$ , while MEMIT and ROME are the slowest at
附录 B 提供了四种方法在 10,000 次编辑上的运行时间分析。我们发现 MEND 速度最快,耗时 98 秒。FT 次之,约为 $29\mathrm{{min}}$,而 MEMIT 和 ROME 最慢。
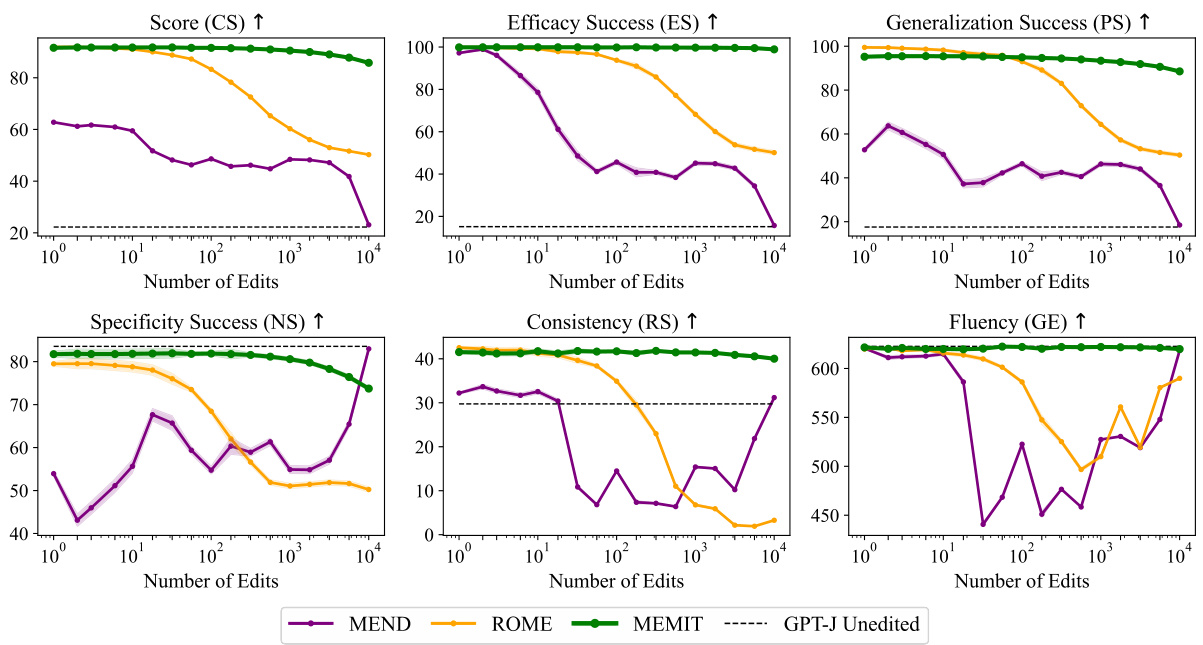
Figure 5: MEMIT scaling curves plot editing performance against problem size (log-scale). The dotted line indicates GPT-J’s pre-edit performance; specificity (NS) and fluency (GE) should stay close to the baseline. $95%$ confidence intervals are shown as areas.
图 5: MEMIT扩展曲线展示了编辑性能随问题规模(对数尺度)的变化。虚线表示GPT-J的预编辑性能;特异性(NS)和流畅度(GE)应保持接近基线水平。95%置信区间以区域形式显示。
Table 2: Numerical results on COUNTER FACT for 10,000 edits.
| Editor | Score | Efficacy | Generalization | Specificity | Fluency | Consistency |
| S↑ | ES ↑ | PS ↑ | NS ↑ | GE↑ | RS ↑ | |
| GPT-J | 22.4 | 15.2 (0.7) | 17.7 (0.6) | 83.5 (0.5) | 622.4 (0.3) | 29.4 (0.2) |
| FT-W | 67.6 | 99.4 (0.1) | 77.0 (0.7) | 46.9 (0.6) | 293.9 (2.4) | 15.9 (0.3) |
| MEND | 23.1 | 15.7 (0.7) | 18.5 (0.7) | 83.0 (0.5) | 618.4 (0.3) | 31.1 (0.2) |
| ROME | 50.3 | 50.2 (1.0) | 50.4 (0.8) | 50.2 (0.6) | 589.6 (0.5) | 3.3 (0.0) |
| MEMIT | 85.8 | 98.9 (0.2) | 88.6 (0.5) | 73.7 (0.5) | 619.9 (0.3) | 40.1 (0.2) |
| GPT-NeoX | 23.7 | 16.8 (1.9) | 18.3 (1.7) | 81.6 (1.3) | 620.4 (0.6) | 29.3 (0.5) |
| MEMIT | 82.0 | 97.2 (0.8) | 82.2 (1.6) | 70.8 (1.4) | 606.4 (1.0) | 36.9 (0.6) |
表 2: COUNTER FACT数据集上10,000次编辑的数值结果
| Editor | Score | Efficacy | Generalization | Specificity | Fluency | Consistency |
|---|---|---|---|---|---|---|
| S↑ | ES ↑ | PS ↑ | NS ↑ | GE↑ | RS ↑ | |
| GPT-J | 22.4 | 15.2 (0.7) | 17.7 (0.6) | 83.5 (0.5) | 622.4 (0.3) | 29.4 (0.2) |
| FT-W | 67.6 | 99.4 (0.1) | 77.0 (0.7) | 46.9 (0.6) | 293.9 (2.4) | 15.9 (0.3) |
| MEND | 23.1 | 15.7 (0.7) | 18.5 (0.7) | 83.0 (0.5) | 618.4 (0.3) | 31.1 (0.2) |
| ROME | 50.3 | 50.2 (1.0) | 50.4 (0.8) | 50.2 (0.6) | 589.6 (0.5) | 3.3 (0.0) |
| MEMIT | 85.8 | 98.9 (0.2) | 88.6 (0.5) | 73.7 (0.5) | 619.9 (0.3) | 40.1 (0.2) |
| GPT-NeoX | 23.7 | 16.8 (1.9) | 18.3 (1.7) | 81.6 (1.3) | 620.4 (0.6) | 29.3 (0.5) |
| MEMIT | 82.0 | 97.2 (0.8) | 82.2 (1.6) | 70.8 (1.4) | 606.4 (1.0) | 36.9 (0.6) |
$7.44\mathrm{hr}$ and $12.29\mathrm{hr}$ , respectively. While MEMIT’s execution time is high relative to MEND and FT, we note that its current implementation is naive and does not batch the independent $z_{i}$ optimization s, instead computing each one in series. These computations are actually “embarrassingly parallel” and thus could be batched.
$7.44\mathrm{hr}$ 和 $12.29\mathrm{hr}$。虽然 MEMIT 的执行时间相对于 MEND 和 FT 较高,但我们注意到其当前实现较为原始,未对独立的 $z_{i}$ 优化进行批处理,而是逐个串行计算。这些计算实际上是"高度可并行"的,因此可以进行批处理。
5.3 EDITING DIFFERENT CATEGORIES OF FACTS
5.3 编辑不同类别的事实
For insight into MEMIT’s performance on different types of facts, we pick the 27 categories from COUNTER FACT that have at least 300 cases each, and assess each algorithm’s performance on those cases. Figure 6a shows that MEMIT achieves better overall scores compared to FT and MEND in all categories. It also reveals that some relations are harder to edit compared to others; for example, each of the editing algorithms faced difficulties in changing the sport an athlete plays. Even on harder cases, MEMIT outperforms other methods by a clear margin.
为了深入了解MEMIT在不同类型事实上的表现,我们从COUNTER FACT中选取了27个类别(每个类别至少包含300个案例),并评估各算法在这些案例上的表现。图6a显示,MEMIT在所有类别中的综合得分均优于FT和MEND。同时表明某些关系比其他关系更难编辑,例如所有编辑算法在修改运动员从事的运动项目时都遇到困难。即使在较难的案例上,MEMIT仍以明显优势超越其他方法。
Model editing methods are known to occasionally suffer from a trade-off between attaining high generalization and good specificity. This trade-off is clearly visible for MEND in Figure 6b. FT consistently fails to achieve good specificity. Overall, MEMIT achieves a higher score in both dimensions, although it also exhibits a trade-off in editing some relations such as P127 (“product owned by company”) and P641 (“athlete plays sport”).
已知模型编辑方法偶尔需要在实现高泛化性和良好特异性之间进行权衡。这种权衡在图6b中MEND的表现尤为明显。FT始终难以达到良好的特异性。总体而言,MEMIT在这两个维度上都取得了更高的分数,尽管在编辑某些关系(如P127("公司拥有的产品")和P641("运动员从事的运动"))时也表现出类似的权衡。
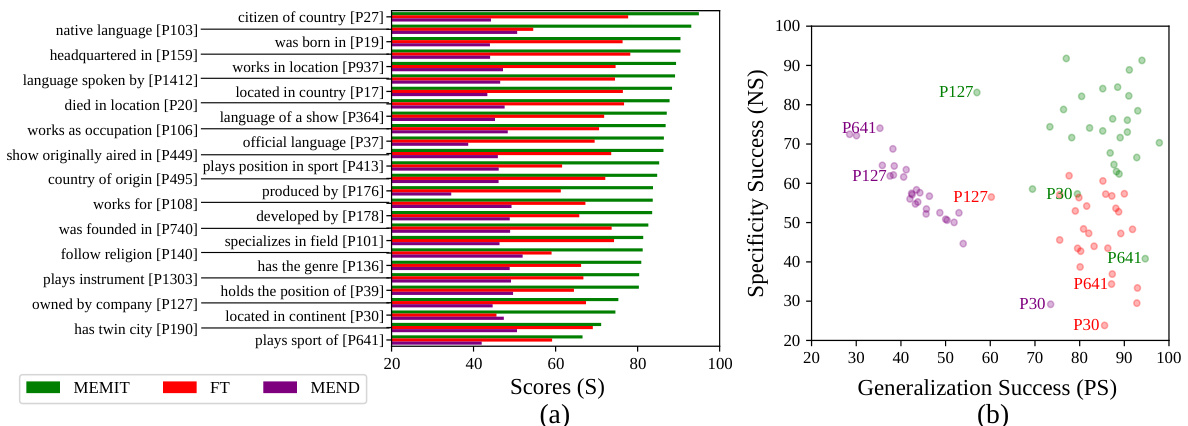
Figure 6: (a) Category-wise rewrite scores achieved by different approaches in editing 300 similar facts. (b) Category-wise specificity vs generalization scores by different approaches on 300 edits.
图 6: (a) 不同方法在编辑300条相似事实时取得的分类重写分数。(b) 不同方法在300次编辑上的分类特异性与泛化性分数对比。

Figure 7: When comparing mixes of edits, MEMIT gives consistent near-linear (near-average) performance while scaling up to 700 facts.
图 7: 在比较混合编辑时,MEMIT 在扩展到 700 个事实时仍能保持接近线性 (接近平均) 的性能。
5.4 EDITING DIFFERENT CATEGORIES OF FACTS TOGETHER
5.4 同时编辑不同类别的事实
To investigate whether the scaling of MEMIT is sensitive to differences in the diversity of the memories being edited together, we sample sets of cases $\mathcal{E}_ {m i x}$ that mix two different relations from the COUNTER FACT dataset. We consider four scenarios depicted in Figure 7, where the relations have similar or different classes of subjects or objects. In all of the four cases, MEMIT’s performance on $\mathcal{E}_{m i x}$ is close to the average of the performance of each relation without mixing. This provides support to the hypothesis that the scaling of MEMIT is neither positively nor negatively affected by the diversity of the memories being edited. Appendix D contains implementation details.
为了研究MEMIT的扩展性是否对同时编辑的记忆多样性差异敏感,我们从COUNTER FACT数据集中抽样了混合两种不同关系的案例集$\mathcal{E}_ {m i x}$。我们考虑了图7中描述的四种场景,其中关系的主体或客体类别相似或不同。在所有四种情况下,MEMIT在$\mathcal{E}_{m i x}$上的表现接近于未混合时各关系表现的平均值。这支持了以下假设:MEMIT的扩展性既不受被编辑记忆多样性的正面影响,也不受其负面影响。附录D包含实现细节。
6 DISCUSSION AND CONCLUSION
6 讨论与结论
We have developed MEMIT, a method for editing factual memories in large language models by directly manipulating specific layer parameters. Our method scales to much larger sets of edits (100x) than other approaches while maintaining excellent specificity, generalization, and fluency.
我们开发了MEMIT方法,通过直接操控特定层参数来实现大语言模型中的事实记忆编辑。该方法支持比其他方法更大规模的编辑量(100倍),同时保持出色的特异性、泛化性和流畅性。
Our investigation also reveals some challenges: certain relations are more difficult to edit with robust specificity, yet even on challenging cases we find that MEMIT outperforms other methods by a clear margin. The knowledge representation we study is also limited in scope to working with directional $(s,r,o)$ relations: it does not cover spatial or temporal reasoning, mathematical knowledge, linguistic knowledge, procedural knowledge, or even symmetric relations. For example, the association that “Tim Cook is CEO of Apple” must be processed separately from the opposite association that “The CEO of Apple is Tim Cook.”
我们的调查还揭示了一些挑战:某些关系难以通过稳健的特异性进行编辑,但即使在具有挑战性的案例中,我们发现MEMIT仍明显优于其他方法。我们研究的知识表示在范围上也仅限于处理定向$(s,r,o)$关系:它不涵盖空间或时间推理、数学知识、语言知识、程序性知识,甚至对称关系。例如,"Tim Cook是Apple的CEO"这一关联必须与相反的关联"Apple的CEO是Tim Cook"分开处理。
Despite these limitations, it is noteworthy that large-scale model updates can be constructed using an explicit analysis of internal computations. Our results raise a question: might interpret ability-based methods become a commonplace alternative to traditional opaque fine-tuning approaches? Our positive experience brings us optimism that further improvements to our understanding of network internals will lead to more transparent and practical ways to edit, control, and audit models.
尽管存在这些限制,值得注意的是,我们可以通过对内部计算的显式分析来构建大规模模型更新。我们的研究结果提出了一个问题:基于可解释性的方法是否会成为传统不透明微调方法的常见替代方案?我们的积极经验使我们乐观地认为,随着对网络内部机制理解的进一步深入,将催生出更透明、更实用的模型编辑、控制和审计方法。
7 ETHICAL CONSIDERATIONS
7 伦理考量
Although we test a language model’s ability to serve as a knowledge base, we do not find these models to be a reliable source of knowledge, and we caution readers that a LLM should not be used as an authoritative source of facts. Our memory-editing methods shed light on the internal mechanisms of models and potentially reduce the cost and energy needed to fix errors in a model, but the same methods might also enable a malicious actor to insert false or damaging information into a model that was not originally present in the training data.
虽然我们测试了语言模型作
