DeepMAD: Mathematical Architecture Design for Deep Convolutional Neural Network
DeepMAD: 深度卷积神经网络的数学架构设计
Abstract
摘要
The rapid advances in Vision Transformer (ViT) refresh the state-of-the-art performances in various vision tasks, overshadowing the conventional CNN-based models. This ignites a few recent striking-back research in the CNN world showing that pure CNN models can achieve as good performance as ViT models when carefully tuned. While encouraging, designing such high-performance CNN models is challenging, requiring non-trivial prior knowledge of network design. To this end, a novel framework termed Mathematical Architecture Design for Deep CNN (Deep $M A D^{1}$ ) is proposed to design high-performance CNN models in a principled way. In DeepMAD, a CNN network is modeled as an information processing system whose expressiveness and effectiveness can be analytically formulated by their structural parameters. Then a constrained mathematical programming (MP) problem is proposed to optimize these structural parameters. The MP problem can be easily solved by off-the-shelf MP solvers on CPUs with a small memory footprint. In addition, DeepMAD is a pure mathematical framework: no GPU or training data is required during network design. The superiority of DeepMAD is validated on multiple large-scale computer vision benchmark datasets. Notably on ImageNet-1k, only using conventional convolutional layers, DeepMAD achieves $0.7%$ and $1.5%$ higher top-1 accuracy than ConvNeXt and Swin on Tiny level, and $0.8%$ and $0.9%$ higher on Small level.
视觉Transformer (ViT) 的快速发展刷新了各类视觉任务的最优性能,使传统基于CNN的模型相形见绌。这引发了CNN领域近期几项引人注目的反击性研究,表明经过精心调优的纯CNN模型可以达到与ViT模型相当的性能。尽管这一结果令人鼓舞,但设计此类高性能CNN模型颇具挑战性,需要深厚的网络设计先验知识。为此,我们提出了一种称为深度CNN数学架构设计 (Deep $M A D^{1}$) 的新框架,以系统化的方式设计高性能CNN模型。在DeepMAD中,CNN网络被建模为一个信息处理系统,其表达能力和有效性可通过结构参数进行解析建模。随后提出一个约束数学规划 (MP) 问题来优化这些结构参数,该MP问题可由现成的MP求解器在CPU上轻松求解,且内存占用极小。此外,DeepMAD是一个纯数学框架:在网络设计阶段无需GPU或训练数据。DeepMAD的优越性在多个大规模计算机视觉基准数据集上得到验证。值得注意的是在ImageNet-1k上,仅使用传统卷积层,DeepMAD在Tiny级别比ConvNeXt和Swin分别高出$0.7%$和$1.5%$的top-1准确率,在Small级别分别高出$0.8%$和$0.9%$。
1. Introduction
1. 引言
Convolutional neural networks (CNNs) have been the predominant computer vision models in the past decades [23,31,41,52,63]. Until recently, the emergence of
卷积神经网络 (Convolutional Neural Networks, CNNs) 在过去几十年一直是计算机视觉领域的主导模型 [23,31,41,52,63]。直到最近,随着
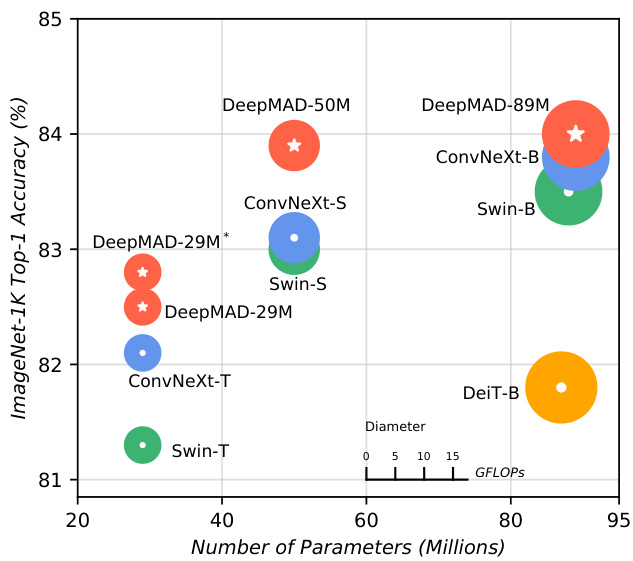
Figure 1. Comparison between DeepMAD models, Swin [40] and ConvNeXt [41] on ImageNet-1k. DeepMAD achieves better performance than Swin and ConvNeXt with the same scales.
图 1: DeepMAD模型与Swin [40]和ConvNeXt [41]在ImageNet-1k上的对比。在相同规模下,DeepMAD实现了优于Swin和ConvNeXt的性能。
Vision Transformers (ViTs) [18, 40, 64] establishes a novel deep learning paradigm surpassing CNN models [40, 64] thanks to the innovation of self-attention [66] mechanism and other dedicated components [3, 17, 28, 29, 55] in ViTs.
视觉Transformer (ViT) [18, 40, 64] 通过自注意力 (self-attention) [66] 机制和其他专用组件 [3, 17, 28, 29, 55] 的创新,建立了一种超越CNN模型 [40, 64] 的新型深度学习范式。
Despite the great success of ViT models in the 2020s, CNN models still enjoy many merits. First, CNN models do not require self-attention modules which require quadratic computational complexity in token size [45]. Second, CNN models usually generalize better than ViT models when trained on small datasets [41]. In addition, convolutional operators have been well-optimized and tightly integrated on various hardware platforms in the industry, like IoT [5].
尽管ViT模型在2020年代取得了巨大成功,CNN模型仍具备诸多优势。首先,CNN模型无需自注意力模块(该模块的token数量会导致二次方计算复杂度)[45]。其次,在小规模数据集训练时,CNN模型通常比ViT模型具有更好的泛化能力[41]。此外,卷积算子已在物联网(IoT)[5]等工业级硬件平台上实现了深度优化和紧密集成。
Considering the aforementioned advantages, recent researches try to revive CNN models using novel architecture designs [16,22,41,77]. Most of these works adopt ViT components into CNN models, such as replacing the attention matrix with a convolutional counterpart while keeping the macro structure of ViTs. After modifications, these modern CNN backbones are considerably different from the conventional ResNet-like CNN models. Although these efforts abridge the gap between CNNs and ViTs, designing such high-performance CNN models requires dedicated efforts in structure tuning and non-trivial prior knowledge of network design, therefore is time-consuming and difficult to generalize and customize.
考虑到上述优势,近期研究尝试通过新颖的架构设计复兴CNN模型 [16,22,41,77]。这些工作大多将ViT组件引入CNN模型,例如在保持ViT宏观结构的同时用卷积替代注意力矩阵。经过改造后,这些现代CNN骨干网络与传统类ResNet的CNN模型存在显著差异。尽管这些努力缩小了CNN与ViT之间的差距,但设计此类高性能CNN模型需要对结构调优投入大量精力,并具备网络设计的非平凡先验知识,因此耗时且难以泛化和定制。
In this work, a novel design paradigm named Mathematical Architecture Design (DeepMAD) is proposed, which designs high-performance CNN models in a principled way. DeepMAD is built upon the recent advances of deep learning theories [8, 48, 50]. To optimize the architecture of CNN models, DeepMAD innovates a constrained mathematical programming (MP) problem whose solution reveals the optimized structural parameters, such as the widths and depths of the network. Particularly, DeepMAD maximizes the differential entropy [26,32,59,60,68,78] of the network with constraints from the perspective of effectiveness [50]. The effectiveness controls the information flow in the network which should be carefully tuned so that the generated networks are well behaved. The dimension of the proposed MP problem in DeepMAD is less than a few dozen. Therefore, it can be solved by off-the-shelf MP solvers nearly instantly on CPU. NO GPU is required and no deep model is created in memory2. This makes DeepMAD lightning fast even on CPU-only servers with a small memory footprint. After solving the MP problem, the optimized CNN architecture is derived from the MP solution.
在本工作中,我们提出了一种名为数学架构设计(DeepMAD)的新范式,以系统化方式设计高性能CNN模型。DeepMAD基于深度学习理论的最新进展[8,48,50]。为优化CNN模型架构,DeepMAD创新性地构建了一个约束数学规划(MP)问题,其解可揭示网络宽度、深度等优化后的结构参数。特别地,DeepMAD从有效性[50]角度出发,在约束条件下最大化网络的微分熵[26,32,59,60,68,78]。有效性控制着网络中的信息流动,需精细调节以确保生成网络的良好表现。DeepMAD中MP问题的维度不超过几十维,因此可通过现成MP求解器在CPU上即时求解,无需GPU且不占用内存创建深度模型2。这使得DeepMAD即便在仅配备CPU的低内存服务器上也能闪电般快速运行。求解MP问题后,优化后的CNN架构即可从MP解中导出。
DeepMAD is a mathematical framework to design optimized CNN networks with strong theoretical guarantees and state-of-the-art (SOTA) performance. To demonstrate the power of DeepMAD, we use DeepMAD to optimize CNN architectures only using the conventional convolutional layers [2,54] as building blocks. DeepMAD achieves comparable or better performance than ViT models of the same model sizes and FLOPs. Notably, DeepMAD achieves $82.8%$ top-1 accuracy on ImageNet-1k with $4.5\mathrm{G}$ FLOPs and 29M Params, outperforming ConvNeXt-Tiny $(82.1%)$ [41] and Swin-Tiny $(81.3%)$ [40] at the same scale; DeepMAD also achieves $77.7%$ top-1 accuracy at the same scale as ResNet-18 [21] on ImageNet-1k, which is $8.9%$ better than He’s original ResNet-18 $(70.9%)$ and is even comparable to He’s ResNet-50 $(77.4%)$ . The contributions of this work are summarized as follows:
DeepMAD 是一种数学框架,用于设计具有强大理论保证和最先进 (SOTA) 性能的优化 CNN 网络。为了展示 DeepMAD 的强大能力,我们仅使用传统卷积层 [2,54] 作为构建模块来优化 CNN 架构。DeepMAD 在相同模型大小和 FLOPs 下实现了与 ViT 模型相当或更优的性能。值得注意的是,DeepMAD 在 ImageNet-1k 上以 4.5G FLOPs 和 29M 参数量实现了 82.8% 的 top-1 准确率,优于同规模的 ConvNeXt-Tiny (82.1%) [41] 和 Swin-Tiny (81.3%) [40];DeepMAD 在 ImageNet-1k 上与 ResNet-18 [21] 相同规模下实现了 77.7% 的 top-1 准确率,比 He 的原始 ResNet-18 (70.9%) 高出 8.9%,甚至与 He 的 ResNet-50 (77.4%) 相当。本工作的贡献总结如下:
• A Mathematical Architecture Design paradigm, DeepMAD, is proposed for high-performance CNN architecture design. • DeepMAD is backed up by modern deep learning theories [8, 48, 50]. It solves a constrained mathematical programming (MP) problem to generate optimized
• 提出了一种高性能CNN架构设计的数学架构设计范式DeepMAD。
• DeepMAD基于现代深度学习理论 [8, 48, 50],通过求解约束数学规划(MP)问题来生成优化方案。
CNN architectures. The MP problem can be solved on CPUs with a small memory footprint. • DeepMAD achieves SOTA performances on multiple large-scale vision datasets, proving its superiority. Even only using the conventional convolutional layers, DeepMAD designs high-performance CNN models comparable to or better than ViT models of the same model sizes and FLOPs. • DeepMAD is transferable across multiple vision tasks, including image classification, object detection, semantic segmentation and action recognition, with consistent performance improvements.
CNN架构。MP问题可以在内存占用较小的CPU上解决。
• DeepMAD在多个大规模视觉数据集上实现了SOTA性能,证明了其优越性。即使仅使用传统卷积层,DeepMAD设计的高性能CNN模型也能达到或优于相同模型规模和FLOPs的ViT模型。
• DeepMAD可迁移至多种视觉任务,包括图像分类、目标检测、语义分割和动作识别,且性能提升一致。
2. Related Works
2. 相关工作
In this section, we briefly survey the recent works of modernizing CNN networks, especially the works inspired by transformer architectures. Then we discuss related works in information theory and theoretical deep learning.
在本节中,我们简要综述了现代化CNN网络的最新研究,特别是受Transformer架构启发的成果。随后探讨了信息论和理论深度学习领域的相关研究。
2.1. Modern Convolutional Neural Networks
2.1. 现代卷积神经网络
Convolutional deep neural networks are popular due to their conceptual simplicity and good performance in computer vision tasks. In most studies, CNNs are usually manually designed [16, 21, 23, 41, 57, 63]. These pre-defined architectures heavily rely on human prior knowledge and are difficult to customize, for example, tailored to some given FLOPs/Params budgets. Recently, some works use AutoML [10,33,35,37,56,62,75] to automatically generate high-performance CNN architectures. Most of these methods are data-dependent and require lots of computational resources. Even if one does not care about the computational cost of AutoML, the patterns generated by AutoML algorithms are difficult to interpret. It is hard to justify why such architectures are preferred and what theoretical insight we can learn from these results. Therefore, it is important to explore the architecture design in a principled way with clear theoretical motivation and human readability.
卷积深度神经网络因其概念简单且在计算机视觉任务中表现良好而广受欢迎。在大多数研究中,CNN通常采用人工设计[16,21,23,41,57,63]。这些预定义架构高度依赖人类先验知识,难以定制化(例如适配特定FLOPs/参数量预算)。近年来,部分研究开始采用AutoML[10,33,35,37,56,62,75]自动生成高性能CNN架构。这些方法大多依赖数据且需消耗大量计算资源。即便不考虑AutoML的计算成本,其算法生成的模式也难以解释——我们无法明确判定此类架构的优越性成因,或从中获得理论洞见。因此,通过具有清晰理论动机且可被人理解的原则性方法探索架构设计至关重要。
The Vision Transformer (ViT) is a rapid-trending topic in computer vision [18, 40, 64]. The Swin Transformer [40] improves the computational efficiency of ViTs using a CNN-like stage-wise design. Inspired by Swin Transformer, recent researches combine CNNs and ViTs, leading to more efficient architectures [16, 22, 40, 41, 77]. For example, MetaFormer [77] shows that the attention matrix in ViTs can be replaced by a pooling layer. ConvNext [41] mimics the attention layer using depth-wise convolution and uses the same macro backbone as Swin Transformer [40]. RepLKNet [16] scales up the kernel sizes beyond $31\times31$ to capture global receptive fields as attention. All these efforts demonstrate that CNN models can achieve as good performance as ViT models when tuned carefully. However, these modern CNNs require non-trivial prior knowledge when designing therefore are difficult to generalize and customize.
视觉Transformer (ViT) 是计算机视觉领域快速兴起的热点课题 [18, 40, 64]。Swin Transformer [40] 通过类CNN的层级式设计提升了ViT的计算效率。受Swin Transformer启发,近期研究将CNN与ViT相结合,催生出更高效的架构 [16, 22, 40, 41, 77]。例如MetaFormer [77] 证明ViT中的注意力矩阵可被池化层替代;ConvNext [41] 使用深度卷积模拟注意力层,并采用与Swin Transformer [40] 相同的宏观骨干网络;RepLKNet [16] 将卷积核尺寸扩展至 $31\times31$ 以上以捕获类似注意力的全局感受野。这些成果表明,经过精心调优的CNN模型能达到与ViT模型相当的性能。然而,这些现代CNN在设计时需要大量先验知识,因此难以泛化和定制化。
2.2. Information Theory in Deep Learning
2.2. 深度学习中的信息论
Information theory is a powerful instrument for studying complex systems such as deep neural networks. The Principle of Maximum Entropy [26, 32] is one of the most widely used principles in information theory. Several previous works [8, 50, 53, 60, 78] attempt to establish the connection between the information entropy and the neural network architectures. For example, [8] tries to interpret the learning ability of deep neural networks using subspace entropy reduction. [53] studies the information bottleneck in deep architectures and explores the entropy distribution and information flow in deep neural networks. [78] proposes the principle of maximal coding rate reduction for optimization. [60] designs efficient object detection networks via maximizing multi-scale feature map entropy. The monograph [50] analyzes the mutual information between different neurons in an MLP model. In DeepMAD, the entropy of the model itself is considered instead of the coding rate reduction as in [8]. The effectiveness is also proposed to show that only maximizing entropy as in [60] is not enough.
信息论是研究深度神经网络等复杂系统的有力工具。最大熵原理 (Principle of Maximum Entropy) [26, 32] 是信息论中应用最广泛的原则之一。先前多项研究 [8, 50, 53, 60, 78] 试图建立信息熵与神经网络架构之间的联系。例如,[8] 尝试通过子空间熵减来解释深度神经网络的学习能力。[53] 研究了深度架构中的信息瓶颈,探索了深度神经网络中的熵分布与信息流动。[78] 提出了最大编码率降低的优化原则。[60] 通过最大化多尺度特征图熵来设计高效的目标检测网络。专著 [50] 分析了 MLP 模型中不同神经元间的互信息。在 DeepMAD 中,考虑的是模型自身的熵而非 [8] 中的编码率降低。研究还表明,仅如 [60] 那样最大化熵是不够的。
3. Mathematical Architecture Design for MLP
3. MLP 的数学架构设计
In this section, we study the architecture design for Multiple Layer Perceptron (MLP) using a novel mathematical programming (MP) framework. We then generalize this technique to CNN models in the next section. To derive the MP problem for MLP, we first define the entropy of the MLP which controls its expressiveness, followed by a constraint which controls its effectiveness. Finally, we maximize the entropy objective function subject to the effectiveness constraint.
在本节中,我们研究使用新型数学规划 (MP) 框架设计多层感知机 (MLP) 的架构。下一节将把该技术推广到 CNN 模型。为推导 MLP 的 MP 问题,首先定义控制其表达能力的 MLP 熵,再引入控制其有效性的约束条件,最终在有效性约束下最大化熵目标函数。
3.1. Entropy of MLP models
3.1. MLP模型的熵
Suppose that in an $L$ -layer MLP $f(\cdot)$ , the $i$ -th layer has $w_{i}$ input channels and $w_{i+1}$ output channels. The output $\mathbf{x}{i+1}$ and the input $\mathbf{x}{i}$ are connected by $\mathbf{x}{i+1}=\mathbf{M}{i}\mathbf{x}{i}$ where $\mathbf{M}{i}\in\mathbb{R}^{w_{i+1}\times w_{i}}$ is trainable weights. Following the entropy analysis in [8], the entropy of the MLP model $f(\cdot)$ is given in Theorem 1.
假设在一个 $L$ 层 MLP $f(\cdot)$ 中,第 $i$ 层有 $w_{i}$ 个输入通道和 $w_{i+1}$ 个输出通道。输出 $\mathbf{x}{i+1}$ 与输入 $\mathbf{x}{i}$ 通过 $\mathbf{x}{i+1}=\mathbf{M}{i}\mathbf{x}{i}$ 连接,其中 $\mathbf{M}{i}\in\mathbb{R}^{w_{i+1}\times w_{i}}$ 是可训练权重。根据 [8] 中的熵分析,该 MLP 模型 $f(\cdot)$ 的熵由定理 1 给出。
Theorem 1. The normalized Gaussian entropy upper bound of the MLP $f(\cdot)$ is
定理1. MLP $f(\cdot)$ 的归一化高斯熵上界为
$$
H_{f}=w_{L+1}\sum_{i=1}^{L}\log(w_{i}).
$$
$$
H_{f}=w_{L+1}\sum_{i=1}^{L}\log(w_{i}).
$$
The proof is given in Appendix A. The entropy measures the expressiveness of the deep network [8, 60]. Following the Principle of Maximum Entropy [26, 32], we propose to maximize the entropy of MLP under given computational budgets.
证明过程见附录A。熵用于衡量深度网络的表达能力 [8, 60]。基于最大熵原理 [26, 32],我们提出在给定计算预算下最大化MLP的熵。
However, simply maximizing entropy defined in Eq. (1) leads to an over-deep network because the entropy grows exponentially faster in depth than in width according to the Theorem 1. An over-deep network is difficult to train and hinders effective information propagation [50]. This observation inspires us to look for another dimension in deep architecture design. This dimension is termed effectiveness presented in the next subsection.
然而,单纯最大化式(1)定义的熵会导致网络过深。根据定理1,熵随深度增长的速度远快于随宽度增长的速度。过深的网络难以训练,并会阻碍有效信息传播[50]。这一观察启发我们在深度架构设计中寻找另一个维度,该维度被称为有效性,将在下一小节中介绍。
3.2. Effectiveness Defined in MLP
3.2. MLP中定义的有效性
An over-deep network can be considered as a chaos system that hinders effective information propagation. For a chaos system, when the weights of the network are randomly initialized, a small perturbation in low-level layers of the network will lead to an exponentially large perturbation in the high-level output of the network. During the back-propagation, the gradient flow cannot effectively propagate through the whole network. Therefore, the network becomes hard to train when it is too deep.
过深的网络可视为阻碍有效信息传播的混沌系统。对于混沌系统而言,当网络权重随机初始化时,网络低层的微小扰动会导致高层输出产生指数级放大的扰动。在反向传播过程中,梯度流无法有效贯穿整个网络。因此,网络过深时会难以训练。
Inspired by the above observation, in DeepMAD we propose to control the depth of network. Intuitively, a 100- layer network is relatively too deep if its width is only 10 channels per layer or is relatively too shallow if its width is 10000 channels per layer. To capture this relative-depth intuition rigorously, we import the metric termed network effectiveness for MLP from the work [50]. Suppose that an MLP has $L$ -layers and each layer has the same width $w$ , the effectiveness of this MLP is defined by
受上述观察启发,我们在DeepMAD中提出控制网络深度的方法。直观来看,一个100层网络若每层宽度仅为10个通道则相对过深,若每层宽度达10000个通道则相对过浅。为严谨量化这种相对深度关系,我们引入文献[50]中针对MLP (Multilayer Perceptron) 提出的网络有效性指标。假设某MLP具有$L$层且每层宽度均为$w$,其有效性定义为
$$
\rho=L/w.
$$
$$
\rho=L/w.
$$
Usually, $\rho$ should be a small constant. When $\rho\to0$ , the MLP behaves like a single-layer linear model; when $\rho\rightarrow$ $\infty$ , the MLP is a chaos system. There is an optimal $\rho^{*}$ for MLP such that the mutual information between the input and the output are maximized [50].
通常,$\rho$ 应为一个较小的常数。当 $\rho\to0$ 时,多层感知机 (MLP) 表现得像一个单层线性模型;当 $\rho\rightarrow\infty$ 时,MLP 则是一个混沌系统。对于 MLP 而言,存在一个最优的 $\rho^{*}$,使得输入与输出之间的互信息达到最大值 [50]。
In DeepMAD, we propose to constrain the effectiveness when designing the network. An unaddressed issue is that Eq. (2) assumes the MLP has uniform width but in practice, the width $w_{i}$ of each layer can be different. To address this issue, we propose to use the average width of MLP in Eq. (2).
在DeepMAD中,我们提出在设计网络时约束其有效性。一个未解决的问题是方程(2)假设MLP具有均匀宽度,但实际上每层的宽度$w_{i}$可能不同。为解决这一问题,我们建议在方程(2)中使用MLP的平均宽度。
Proposition 1. The average width of an $L$ layer MLP $f(\cdot)$ is defined by
命题1. 一个$L$层MLP(多层感知机) $f(\cdot)$ 的平均宽度定义为
$$
\bar{w}=(\prod_{i=1}^{L}w_{i})^{1/L}=\exp\left(\frac{1}{L}\sum_{i=1}^{L}\log w_{i}\right).
$$
$$
\bar{w}=(\prod_{i=1}^{L}w_{i})^{1/L}=\exp\left(\frac{1}{L}\sum_{i=1}^{L}\log w_{i}\right).
$$
Proposition 1 uses geometric average instead of arithmetic average of $w_{i}$ to define the average width of MLP. This definition is derived from the entropy definition in Eq. (1). Please check Appendix B for details. In addition, geometric average is more reasonable than arithmetic average. Suppose an MLP has a zero width in some layer. Then the information cannot propagate through the network. Therefore, its “equivalent width” should be zero.
命题1采用几何平均数而非算术平均数来定义MLP的平均宽度$w_{i}$。该定义源自公式(1)中的熵定义,详见附录B。此外,几何平均数比算术平均数更合理。假设某层MLP宽度为零,信息将无法通过网络传播,因此其"等效宽度"应为零。
In real-world applications, the optimal value of $\rho$ depends on the building blocks. We find that $\rho\in[0.1,2.0]$ usually gives good results in most vision tasks.
在实际应用中,$\rho$ 的最佳值取决于具体构建模块。我们发现,在大多数视觉任务中,$\rho\in[0.1,2.0]$ 通常能取得良好效果。
4. Mathematical Architecture Design for CNN
4. CNN的数学架构设计
In this section, the definitions of entropy and the effectiveness are generalized from MLP to CNN. Then three empirical guidelines are introduced inspired by the best engineering practice. At last, the final mathematical formulation of DeepMAD is presented.
本节将熵和有效性的定义从多层感知机 (MLP) 推广到卷积神经网络 (CNN),随后根据最佳工程实践提炼出三条经验准则,最后给出DeepMAD的完整数学表述。
4.1. From MLP to CNN
4.1. 从MLP到CNN
A CNN operator is essentially a matrix multiplication with a sliding window. Suppose that in the $i$ -th CNN layer, the number of input channels is $c_{i}$ , the number of output channels is $c_{i+1}$ , the kernel size is $k_{i}$ , group is $g_{i}$ . Then this CNN operator is equivalent to a matrix multiplication $W_{i}\in\mathbb{R}^{c_{i+1}\times c_{i}k_{i}^{2}/g_{i}}$ . Therefore, the “width” of this CNN layer is projected to $c_{i}k_{i}^{2}/g_{i}$ in Eq. (1).
CNN算子本质上是一个带滑动窗口的矩阵乘法。假设在第$i$个CNN层中,输入通道数为$c_{i}$,输出通道数为$c_{i+1}$,卷积核尺寸为$k_{i}$,分组数为$g_{i}$。则该CNN算子等价于矩阵乘法$W_{i}\in\mathbb{R}^{c_{i+1}\times c_{i}k_{i}^{2}/g_{i}}$。因此,该CNN层的"宽度"在公式(1)中被投影为$c_{i}k_{i}^{2}/g_{i}$。
A new dimension in CNN feature maps is the resolution $r_{i}\times r_{i}$ at the $i\cdot$ -th layer. To capture this, we propose the following definition of entropy for CNN networks.
CNN特征图的一个新维度是第$i$层的分辨率$r_{i}\times r_{i}$。为了捕捉这一点,我们提出了以下CNN网络的熵定义。
Proposition 2. For an $L$ -layer CNN network $f(\cdot)$ parameterized by ${c_{i},k_{i},g_{i},r_{i}}_{i=1}^{L}$ , its entropy is defined by
命题2. 对于一个由参数 ${c_{i},k_{i},g_{i},r_{i}}_{i=1}^{L}$ 定义的 $L$ 层CNN网络 $f(\cdot)$ ,其熵定义为
$$
H_{L}\triangleq\log(r_{L+1}^{2}c_{L+1})\sum_{i=1}^{L}\log(c_{i}k_{i}^{2}/g_{i}).
$$
$$
H_{L}\triangleq\log(r_{L+1}^{2}c_{L+1})\sum_{i=1}^{L}\log(c_{i}k_{i}^{2}/g_{i}).
$$
In Eq. (4), we use a similar definition of entropy as in Eq. (1). We use $\log(r_{L+1}^{2}c_{L+1})$ instead of $(r_{L+1}^{2}c_{L+1})$ in Eq. (4). This is because a nature image is highly compressible so the entropy of an image or feature map does not scale up linearly in its volume $O(r_{i}^{2}\times c_{i})$ . Inspired by [51], taking logarithms can better formulate the ground-truth entropy for natural images.
在式 (4) 中,我们采用了与式 (1) 类似的熵定义。不同于式 (1) 使用 $(r_{L+1}^{2}c_{L+1})$ ,我们在式 (4) 中采用 $\log(r_{L+1}^{2}c_{L+1})$ 。这是因为自然图像具有高度可压缩性,图像或特征图的熵不会随其体积 $O(r_{i}^{2}\times c_{i})$ 线性增长。受 [51] 启发,取对数能更准确地描述自然图像的真实熵。
4.2. Three Empirical Guidelines
4.2. 三项实证准则
We find that the following three heuristic rules are beneficial to architecture design in DeepMAD. These rules are inspired by the best engineering practices.
我们发现以下三条启发式规则对DeepMAD的架构设计有益。这些规则源自最佳工程实践。
• Guideline 1. Weighted Multiple-Scale Entropy CNN networks usually contain down-sampling layers which split the network into several stages. Each stage captures features at a certain scale. To capture the entropy at different scales, we use a weighted summation to ensemble entropy of the last layer in each stage to obtain the entropy of the network as in [60]. • Guideline 2. Uniform Stage Depth We require the depth of each stage to be uniformly distributed as much as possible. We use the variance of depths to measure the uniformity of depth distribution.
• 准则1. 加权多尺度熵 CNN网络通常包含下采样层,这些层将网络划分为多个阶段。每个阶段捕获特定尺度的特征。为了捕捉不同尺度的熵,我们采用加权求和的方式集成每个阶段最后一层的熵,从而获得网络的熵,如[60]所述。
• 准则2. 均匀阶段深度 我们要求每个阶段的深度尽可能均匀分布。使用深度方差来衡量深度分布的均匀性。
• Guideline 3. Non-Decreasing Number of Channels We require that channel number of each stage is nondecreasing along the network depth. This can prevent high-level stages from having small widths. This guideline is also a common practise in a lot of manually designed networks.
• 准则3. 通道数非递减
我们要求每个阶段的通道数随网络深度非递减。这可以防止高层级阶段出现宽度过小的情况。该准则也是许多人工设计网络的常见做法。
4.3. Final DeepMAD Formula
4.3. 最终 DeepMAD 公式
We gather everything together and present the final mathematical programming problem for DeepMAD. Suppose that we aim to design an $L$ -layer CNN model $f(\cdot)$ with $M$ stages. The entropy of the $i$ -th stage is denoted as $H_{i}$ defined in Eq. (4). Within each stage, all blocks use the same structural parameters (width, kernel size, etc.). The width of each CNN layer is defined by $w_{i}=c_{i}k_{i}^{2}/g_{i}$ . The depth of each stage is denoted as $L_{i}$ for $i=1,2,\cdots,M$ . We propose to optimize ${w_{i},L_{i}}$ via the following mathematical programming (MP) problem:
我们将所有内容整合起来,呈现DeepMAD的最终数学规划问题。假设我们要设计一个具有$M$个阶段的$L$层CNN模型$f(\cdot)$。第$i$个阶段的熵由式(4)定义的$H_{i}$表示。在每个阶段内,所有块使用相同的结构参数(宽度、核大小等)。每个CNN层的宽度由$w_{i}=c_{i}k_{i}^{2}/g_{i}$定义。每个阶段的深度表示为$i=1,2,\cdots,M$的$L_{i}$。我们提出通过以下数学规划(MP)问题优化${w_{i},L_{i}}$:
$$
\begin{array}{r l}{\displaystyle\operatorname{max}{w_{i},L_{i}}}&{\displaystyle\sum_{i=1}^{M}\alpha_{i}H_{i}-\beta Q,}\ {\mathrm{s.t.}}&{L\cdot(\displaystyle\prod_{i=1}^{L}w_{i})^{-1/L}\leq\rho_{0},}\ &{\mathrm{FLOPs}[f(\cdot)]\leq\mathrm{budget},}\ &{\mathrm{Params}[f(\cdot)]\leq\mathrm{budget},}\ &{Q\triangleq\exp[\mathrm{Var}(L_{1},L_{2},\cdots,L_{M})],}\ &{w_{1}<w_{2}<\cdots<w_{L}.}\end{array}
$$
$$
\begin{array}{r l}{\displaystyle\operatorname*{max}{w_{i},L_{i}}}&{\displaystyle\sum_{i=1}^{M}\alpha_{i}H_{i}-\beta Q,}\ {\mathrm{s.t.}}&{L\cdot(\displaystyle\prod_{i=1}^{L}w_{i})^{-1/L}\leq\rho_{0},}\ &{\mathrm{FLOPs}[f(\cdot)]\leq\mathrm{budget},}\ &{\mathrm{Params}[f(\cdot)]\leq\mathrm{budget},}\ &{Q\triangleq\exp[\mathrm{Var}(L_{1},L_{2},\cdots,L_{M})],}\ &{w_{1}<w_{2}<\cdots<w_{L}.}\end{array}
$$
In the above MP formulation, ${\alpha_{i},\beta,\rho_{0}}$ are hyperparameters. ${\alpha_{i}}$ are the weights of entropies at different scales. For CNN models with 5 down-sampling layers, ${\alpha_{i}}={1,1,1,1,8}$ is suggested in most vision tasks. $Q$ penalizes the objective function if the network has nonuniform depth distribution across stages. We set $\beta=10$ in our experiments. $\rho_{0}$ controls the effectiveness of the network whose value is usually tuned in range [0.1, 2.0]. The last two inequalities control the computational budgets. This MP problem can be easily solved by off-the-shelf solvers for constrained non-linear programming [4, 44].
在上述 MP (Mathematical Programming) 公式中,${\alpha_{i},\beta,\rho_{0}}$ 是超参数。${\alpha_{i}}$ 表示不同尺度下熵的权重。对于具有 5 个下采样层的 CNN (Convolutional Neural Network) 模型,在大多数视觉任务中建议使用 ${\alpha_{i}}={1,1,1,1,8}$。$Q$ 会在网络各阶段的深度分布不均匀时对目标函数施加惩罚。实验中我们设定 $\beta=10$。$\rho_{0}$ 控制网络的有效性,其值通常在 [0.1, 2.0] 范围内调整。最后两个不等式用于控制计算预算。该 MP 问题可通过现成的约束非线性规划求解器轻松解决 [4, 44]。
5. Experiments
5. 实验
Experiments are developed at three levels. First, the relationship between the model accuracy and the model effec ti ve ness is investigated on CIFAR-100 [30] to verify our effective theory in Section 4.3. Then, DeepMAD is used to design better ResNets and mobile networks. To demonstrate the power of DeepMAD, we design SOTA CNN models using DeepMAD with the conventional convolutional layers. Performances on ImageNet-1K [15] are reported with comparison to popular modern CNN and ViT models.
实验分为三个层面展开。首先,在CIFAR-100 [30]上探究模型精度与模型效能的关系,以验证第4.3节提出的有效理论。随后,使用DeepMAD工具优化ResNet和移动网络架构。为展示DeepMAD的潜力,我们基于传统卷积层设计出SOTA CNN模型,并在ImageNet-1K [15]数据集上对比当前主流CNN与ViT模型报告性能表现。
Finally, the CNN models designed by DeepMAD are transferred to multiple down-streaming tasks, such as MS COCO [36] for object detection, ADE20K [82] for semantic segmentation and UCF101 [58] / Kinetics 400 [27] for action recognition. Consistent performance improvements demonstrate the excellent transfer ability of DeepMAD models.
最终,DeepMAD设计的CNN模型被迁移到多个下游任务中,例如目标检测任务MS COCO [36]、语义分割任务ADE20K [82],以及动作识别任务UCF101 [58]/Kinetics 400 [27]。一致的性能提升证明了DeepMAD模型出色的迁移能力。
5.1. Training Settings
5.1. 训练设置
Following previous works [72, 74], SGD optimizer with momentum 0.9 is adopted to train DeepMAD models. The weight decay is 5e-4 for CIFAR-100 dataset and 4e-5 for ImageNet-1k. The initial learning rate is 0.1 with batch size of 256. We use cosine learning rate decay [43] with 5 epochs of warm-up. The number of training epochs is 1,440 for CIFAR-100 and 480 for ImageNet-1k. All experiments use the following data augmentations [47]: mixup [80], label-smoothing [61], random erasing [81], random crop/resize/flip/lighting, and Auto-Augment [14].
遵循先前工作 [72, 74],采用动量(momentum)为0.9的SGD优化器训练DeepMAD模型。CIFAR-100数据集的权重衰减(weight decay)为5e-4,ImageNet-1k为4e-5。初始学习率为0.1,批量大小(batch size)为256。我们使用余弦学习率衰减 [43] 并包含5轮热身训练(warm-up)。CIFAR-100的训练轮次(epoch)为1,440次,ImageNet-1k为480次。所有实验均采用以下数据增强方法 [47]:mixup [80]、标签平滑(label-smoothing) [61]、随机擦除(random erasing) [81]、随机裁剪/缩放/翻转/光照调整,以及自动增强(Auto-Augment) [14]。
5.2. Building Blocks
5.2. 基础构建模块
To align with ResNet family [21], Section 5.4 uses the same building blocks as ResNet-50. To align with ViT models [18, 40, 64], DeepMAD uses MobileNet-V2 [23] blocks followed by SE-block [24] as in Efficient Net [63] to design high performance networks.
为与ResNet系列[21]保持一致,第5.4节采用与ResNet-50相同的构建模块。为与ViT模型[18,40,64]对齐,DeepMAD采用Efficient Net[63]中的MobileNet-V2[23]模块接SE模块[24]来设计高性能网络。
5.3. Effectiveness on CIFAR-100
5.3. CIFAR-100 上的有效性
The effectiveness $\rho$ is an important hyper-parameter in DeepMAD. This experiment demonstrate how $\rho$ affects the architectures in DeepMAD. To this end, 65 models are randomly generated using ResNet blocks, with different depths and widths. All models have the same FLOPs (0.04G) and Params (0.27M) as ResNet-20 [25] for CIFAR-100. The effectiveness $\rho$ varies in range [0.1, 1.0].
有效性 $\rho$ 是DeepMAD中的一个重要超参数。本实验展示了 $\rho$ 如何影响DeepMAD的架构。为此,我们使用ResNet块随机生成了65个模型,这些模型具有不同的深度和宽度。所有模型在CIFAR-100上的FLOPs (0.04G) 和参数量 (0.27M) 均与ResNet-20 [25] 相同。有效性 $\rho$ 的变化范围为[0.1, 1.0]。
These randomly generated models are trained on CIFAR-100. The effectiveness $\rho$ , top-1 accuracy and network entropy for each model are plotted in Figure 2. We can find that the entropy increases with $\rho$ monotonically. This is because the larger the $\rho$ is, the deeper the network is, and thus the greater the entropy as described in Section 3.1. However, as shown in Figure 2, the model accuracy does not always increase with $\rho$ and entropy. When $\rho$ is small, the model accuracy is proportional to the model entropy; when $\rho$ is too large, such relationship no longer exists. Therefore, $\rho$ should be contrained in a certain “effective” range in DeepMAD.
这些随机生成的模型在CIFAR-100上进行训练。图2展示了每个模型的有效性$\rho$、top-1准确率和网络熵值。我们可以发现,熵值随$\rho$单调递增。这是因为$\rho$越大,网络越深,如第3.1节所述,熵值也就越大。然而,如图2所示,模型准确率并不总是随$\rho$和熵值增加而提升。当$\rho$较小时,模型准确率与模型熵值成正比;但当$\rho$过大时,这种关系便不复存在。因此,在DeepMAD中应将$\rho$约束在某个"有效"范围内。
Figure 3 gives more insights into the effectiveness hypothesis in Section 3.2. The architectures around $\rho{}={}$ ${0.1,0.5,1.0}$ are selected and grouped by $\rho$ . When $\rho$ is small ( $\mathrm{\bf\ddot{\rho}}$ is around 0.1), the network is effective in information propagation so we observe a strong correlation between network entropy and network accuracy. But these models are too shallow to obtain high performance. When $\rho$ is too large $(\rho~\approx~1.0)$ , the network approaches a chaos system therefore no clear correlation between network entropy and network accuracy. When $\rho$ is around 0.5, the network can achieve the best performance and the correlation between the network entropy and network accuracy reaches 0.77.
图 3: 进一步验证了第3.2节中的有效性假设。我们选取并按照 $\rho$ 值分组展示了 $\rho{}={}$ ${0.1,0.5,1.0}$ 附近的架构。当 $\rho$ 值较小时 ( $\mathrm{\bf\ddot{\rho}}$ 约为0.1),网络在信息传播方面效率较高,因此我们观察到网络熵与网络准确率之间存在强相关性。但这些模型过于浅层,难以获得高性能。当 $\rho$ 值过大时 $(\rho~\approx~1.0)$,网络接近混沌系统,因此网络熵与网络准确率之间无明显相关性。当 $\rho$ 值约为0.5时,网络能达到最佳性能,此时网络熵与网络准确率之间的相关性达到0.77。
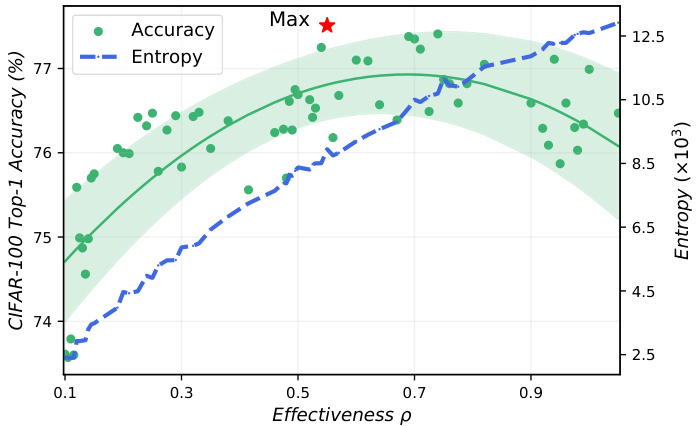
Figure 2. Effectiveness $\rho$ v.s. top-1 accuracy and entropy of each generated model on CIFAR-100. The best model is marked by a star. The entropy increases with $\rho$ monotonically but the model accuracy does not. The optimal $\rho^{*}\approx0.5$ .
图 2: 各生成模型在 CIFAR-100 上的有效性 $\rho$ 与 top-1 准确率和熵的关系。最佳模型用星号标记。熵随 $\rho$ 单调递增,但模型准确率并非如此。最优 $\rho^{*}\approx0.5$。
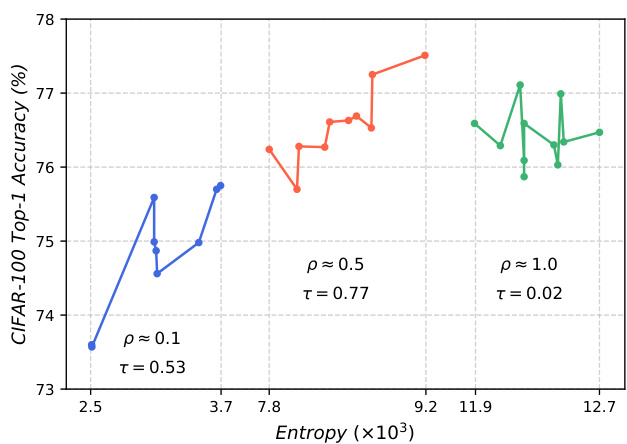
Figure 3. The architectures around $\rho={0.1,0.5,1.0}$ are selected and grouped by $\rho$ . Kendall coefficient $\tau$ [1] is used to measure the correlation.
图 3: 围绕 $\rho={0.1,0.5,1.0}$ 的架构被选出并按 $\rho$ 分组。Kendall系数 $\tau$ [1] 用于衡量相关性。
5.4. DeepMAD for ResNet Family
5.4. 面向ResNet家族的DeepMAD
ResNet family is one of the most popular and classic CNN models in deep learning. We use DeepMAD to redesign ResNet and show that the DeepMAD can generate much better ResNet models. The effectiveness $\rho$ for those original ResNets is computed for easy comparison. First, we use DeepMAD to design a new architecture DeepMADR18 which has the same model size and FLOPs as ResNet18. $\rho$ is tuned in range ${0.1,0.3,0.5,0.7}$ for DeepMADR18. $\rho=0.3$ gives the best architecture. Then, $\rho=0.3$ is fixed in the design of DeepMAD-R34 and DeepMADR50 which align with ResNet-34 and Resnet-50 respectively. As shown in Table 1, compared to He’s original results, DeepMAD-R18 achieves $6.8%$ higher accuracy than ResNet-18 and is even comparable to ResNet-50. Besides, DeepMAD-R50 achieves $3.2%$ better accuracy than the ResNet-50. To ensure the fairness in comparison, the performances of ResNet family under the fair training setting are reported. With our training recipes, the accuracies of ResNet models improved around $1.5%$ . DeepMAD still outperforms the ResNet family by a large margin when both are trained fairly. The inferior performance of ResNet family can be explained by their small $\rho$ which limits their model entropy. This phenomenon again validates our theory discussed in Section 4.3.
ResNet 系列是深度学习中最流行且经典的 CNN (Convolutional Neural Network) 模型之一。我们使用 DeepMAD 重新设计 ResNet,结果表明 DeepMAD 能生成更优的 ResNet 模型。为便于比较,计算了原始 ResNet 模型的有效性指标 $\rho$。首先,我们利用 DeepMAD 设计了与 ResNet-18 参数量和 FLOPs 相同的新架构 DeepMAD-R18,并在 ${0.1,0.3,0.5,0.7}$ 范围内调节 $\rho$ 值。当 $\rho=0.3$ 时获得最佳架构。随后,在设计与 ResNet-34/50 对应的 DeepMAD-R34 和 DeepMAD-R50 时固定 $\rho=0.3$。如表 1 所示,相比 He 的原始结果,DeepMAD-R18 准确率比 ResNet-18 高出 $6.8%$,甚至可与 ResNet-50 媲美;DeepMAD-R50 则比 ResNet-50 提升 $3.2%$。为确保公平对比,我们报告了 ResNet 系列在统一训练设置下的性能。采用我们的训练方案后,ResNet 模型准确率提升约 $1.5%$,但 DeepMAD 仍大幅领先。ResNet 系列性能较弱可归因于其较小的 $\rho$ 值限制了模型熵,该现象再次验证了第 4.3 节的理论分析。
Table 1. DeepMAD v.s. ResNet on ImageNet-1K, using ResNet building block. $\dagger$ : model trained by our pipeline. $\rho$ is tuned for DeepMAD-R18. DeepMAD achieves consistent improvements compared with ResNet18/34/50 with the same Params and FLOPs.
表 1: DeepMAD 与 ResNet 在 ImageNet-1K 上的对比 (使用 ResNet 基础模块)。$\dagger$: 采用本论文训练流程的模型。$\rho$ 为 DeepMAD-R18 调整参数。在参数量 (Params) 和计算量 (FLOPs) 相同的情况下,DeepMAD 相比 ResNet18/34/50 实现了稳定提升。
| 模型 | 参数量 | 计算量 | 准确率 (%) |
|---|---|---|---|
| ResNet-18 [21] | 11.7M | 1.8G 0.01 | 70.9 |
| ResNet-18$\dagger$ | 11.7M | 1.8G 0.01 | 72.2 |
| DeepMAD-R18 | 11.7M | 1.8G 0.1 | 76.9 |
| DeepMAD-R18 | 11.7M | 1.8G 0.3 | 77.7 |
| DeepMAD-R18 | 11.7M | 1.8G 0.5 | 77.5 |
| DeepMAD-R18 | 11.7M | 1.8G 0.7 | 75.7 |
| ResNet-34 [21] | 21.8M | 3.6G 0.02 | 74.4 |
| ResNet-34$\dagger$ | 21.8M | 3.6G 0.02 | 75.6 |
| DeepMAD-R34 | 21.8M | 3.6G 0.3 | 79.7 |
| ResNet-50 [21] | 25.6M | 4.1G 0.09 | 77.4 |
| ResNet-50$\dagger$ | 25.6M | 4.1G 0.09 | 79.3 |
| DeepMAD-R50 | 25.6M | 4.1G 0.3 | 80.6 |
5.5. DeepMAD for Mobile CNNs
5.5. 面向移动端CNN的DeepMAD
We use DeepMAD to design mobile CNN models for further exploration. Following previous works, MobileNetV2 block with SE-block are used to build new models. $\rho$ is tuned at Efficient Net-B0 scale in the range of ${0.3,0.5,1.0 $ , $ 1.5,2.0 } $ for DeepMAD-B0, and $\rho=0.5$ achieves the best result. Then, we transfer the optimal $\rho$ for DeepMAD-B0 to DeepMAD-MB. As shown in Table 2, the DeepMADB0 achieves $76.1%$ top-1 accuracy which is comparable with the Efficient Net-B0 $(76.3%)$ . It should be noted that Efficient Net-B0 is designed by brute-force grid search which takes around 3800 GPU days [67]. The performance of the DeepMAD-B0 is comparable to the Efficient Net-B0 by simply solving an MP problem on CPU in a few minutes. Aligned with MobileNet-V2 on Params and FLOPs, DeepMAD-MB achieves $72.3%$ top-1 accuracy which is 0.3% higher in accuracy.
我们使用DeepMAD来设计移动端CNN模型以进行进一步探索。遵循先前工作,采用带SE模块的MobileNetV2块构建新模型。在EfficientNet-B0规模下调整参数$\rho$,取值范围为${0.3,0.5,1.0 $,$ 1.5,2.0}$,其中$\rho=0.5$时DeepMAD-B0取得最佳效果。随后将该最优$\rho$值迁移至DeepMAD-MB。如表2所示,DeepMAD-B0以$76.1%$的top-1准确率与EfficientNet-B0 $(76.3%)$ 相当。值得注意的是,EfficientNet-B0是通过耗时约3800 GPU天的暴力网格搜索[67]设计的,而DeepMAD-B0仅需在CPU上求解MP问题数分钟即可获得相近性能。在参数量和FLOPs与MobileNet-V2对齐的情况下,DeepMAD-MB以$72.3%$的top-1准确率实现了0.3%的性能提升。
Table 2. DeepMAD under mobile setting. Top-1 accuracy on ImageNet-1K. $\rho$ is tuned for DeepMAD-B0.
表 2: 移动场景下的DeepMAD。ImageNet-1K的Top-1准确率。$\rho$为DeepMAD-B0调整值。
| Model | #Param. | FLOPs | p Acc. (%) |
|---|---|---|---|
| EffNet-B0 [63] | 5.3M | 390M 0.6 | 76.3 |
| DeepMAD-BO | 5.3M | 390M 0.3 | 74.3 |
| DeepMAD-BO | 5.3M | 390M 0.5 | 76.1 |
| DeepMAD-BO | 5.3M | 390M 1.0 | 75.9 |
| DeepMAD-BO | 5.3M | 390M 1.5 | 75.7 |
| DeepMAD-BO | 5.3M | 390M 2.0 | 74.9 |
| MobileNet-V2 [23] | 3.5M | 320M 0.9 | 72.0 |
| DeepMAD-MB | 3.5M | 320M 0.5 | 72.3 |
Table 3. DeepMAD v.s. SOTA ViT and CNN models on ImageNet-1K. $\rho=0.5$ for all DeepMAD models. DeepMAD $29\mathbf{M}^{*}$ : uses $288\mathrm{x}288$ resolution while the Params and FLOPs keeps the same as DeepMAD-29M.
表 3: DeepMAD 与当前最优 ViT 和 CNN 模型在 ImageNet-1K 上的对比。所有 DeepMAD 模型的 $\rho=0.5$。DeepMAD $29\mathbf{M}^{*}$ 使用 $288\mathrm{x}288$ 分辨率,同时参数量和 FLOPs 与 DeepMAD-29M 保持一致。
| 模型 | 分辨率 | 参数量 | FLOPs | 准确率 (%) |
|---|---|---|---|---|
| ResNet-50 [21] | 224 | 26 M | 4.1G | 77.4 |
| DeiT-S [64] | 224 | 22 M | 4.6G | 79.8 |
| PVT-Small [71] | 224 | 25 M | 3.8G | 79.8 |
| Swin-T [40] | 224 | 29 M | 4.5 G | 81.3 |
| TNT-S [19] | 224 | 24 M | 5.2G | 81.3 |
| T2T-ViTt-14 [79] | 224 | 22 M | 6.1 G | 81.7 |
| ConvNeXt-T [41] | 224 | 29 M | 4.5 G | 82.1 |
| SLaK-T [39] | 224 | 30 M | 5.0G | 82.5 |
| DeepMAD-29M | 224 | 29 M | 4.5 G | 82.5 |
| DeepMAD-29M* | 288 | 29 M | 4.5 G | 82.8 |
| ResNet-101 [21] | 224 | 45 M | 7.8G | 78.3 |
| ResNet-152 [21] | 224 | 60 M | 11.5G | 79.2 |
| PVT-Large [71] | 224 | 61 M | 9.8 G | 81.7 |
| T2T-ViTt-19 [79] | 224 | 39 M | 9.8 G | 82.2 |
| T2T-ViTt-24 [79] | 224 | 64 M | 15.0G | 82.6 |
| TNT-B [19] | 224 | 66 M | 14.1 G | 82.9 |
| Swin-S [40] | 224 | 50M | 8.7G | 83.0 |
| ConvNeXt-S [41] | 224 | 50M | 8.7G | 83.1 |
| SLaK-S [39] | 224 | 55M | 9.8 G | 83.8 |
| DeepMAD-50M | 224 | 50 M | 8.7G | 83.9 |
| DeiT-B/16 [64] | 224 | 87M | 17.6G | 81.8 |
| RepLKNet-31B [16] | 224 | 79 M | 15.3 G | 83.5 |
| Swin-B [40] | 224 | 88 M | 15.4G | 83.5 |
| ConvNeXt-B [41] | 224 | 89 M | 15.4G | 83.8 |
| SLaK-B [39] | 224 | 95M | 17.1 G | 84.0 |
| DeepMAD-89M | 224 | 89 M | 15.4 G | 84.0 |
5.6. DeepMAD for SOTA
5.6. 实现SOTA的DeepMAD
We use DeepMAD to design a SOTA CNN model for ImageNet-1K classification. The conventional MobileNetV2 building block with SE module is used. This DeepMAD network is aligned with Swin-Tiny [40] at 29M Params and 4.5G FLOPs therefore is labeled as DeepMAD-29M. As shown in Table 3, DeepMAD-29M outperforms or is comparable to SOTA ViT models as well as recent modern CNN models. DeepMAD-29M achieves $82.5%$ , which is $2.7%$ higher accuracy than DeiT-S [64] and $1.2%$ higher accuracy than the Swin-T [40]. Meanwhile, DeepMAD-29M is $0.4%$ higher than the ConvNeXt-T [41] which is inspired by the transformer architecture. DeepMAD also designs networks with larger resolution (288), DeepMAD ${29}\mathbf{M}^{}$ , while keeping the FLOPs and Params not changed. DeepMAD $\boldsymbol{29}\mathbf{M}^{*}$ reaches $82.8%$ accuracy and is comparable to Swin-S [40] and ConvNeXt-S [41] with nearly half of their FLOPs. Deep-MAD also achieves better performance on small and base level. Especially, DeepMAD-50M can achieve even better performance than ConvNeXt-B with nearly half of its scale. It proves only with the conventional convolutional layers as building blocks, Deep-MAD achieves comparable or better performance than ViT models.
我们使用DeepMAD为ImageNet-1K分类设计了一个SOTA CNN模型。该模型采用带SE模块的传统MobileNetV2构建块。该DeepMAD网络在参数量(29M)和计算量(4.5G FLOPs)上与Swin-Tiny [40]对齐,因此标记为DeepMAD-29M。如表3所示,DeepMAD-29M优于或持平于SOTA ViT模型及近期现代CNN模型。DeepMAD-29M达到82.5%准确率,比DeiT-S [64]高2.7%,比Swin-T [40]高1.2%。同时,DeepMAD-29M比受Transformer架构启发的ConvNeXt-T [41]高0.4%。DeepMAD还设计了更高分辨率(288)的网络DeepMAD ${29}\mathbf{M}^{}$,同时保持FLOPs和参数量不变。DeepMAD $\boldsymbol{29}\mathbf{M}^{*}$达到82.8%准确率,与计算量近乎翻倍的Swin-S [40]和ConvNeXt-S [41]性能相当。DeepMAD在小型和基础级模型上也表现更优。特别是DeepMAD-50M能以近乎半数的规模实现优于ConvNeXt-B的性能。这证明仅使用传统卷积层作为构建块,DeepMAD即可实现与ViT模型相当或更优的性能。
5.7. Downstream Experiments
5.7. 下游实验
To demonstrate the transfer ability of models designed by DeepMAD, the models solved by DeepMAD play as the backbones on downstream tasks including object detection, semantic segmentation and action recognition.
为验证DeepMAD设计模型的迁移能力,由DeepMAD求解的模型在下游任务中作为主干网络,包括目标检测、语义分割和行为识别。
Object Detection on MS COCO MS COCO is a widely used dataset in object detection. It has 143K images and 80 object categories. The experiments are evaluated on MS COCO [36] with the official training/testing splits. The results in Table 4 are evaluated on val-2017. We use two detection frameworks, FCOS [70] and GFLV2 [34], implemented by mm detection [9]. The DeepMAD-R50 model plays as the backbone of these two detection frameworks. The models are initialized with pre-trained weights on ImageNet and trained for 2X (24 epoches). The multi-scale training trick is also used for the best performance. As shown in Table 4, DeepMAD-R50 achieves 40.0 AP with FCOS [70] , which is 1.5 AP higher than ResNet-50. It also achieves 44.9 AP with GFLV2 [34], which is $1.0\mathrm{AP}$ higher than Re
